Fracture Parameters of Cement Mortar with Different Structural Dimensions Under the Direct Tension Test
Abstract
1. Introduction
2. Uniaxial Tension Test of Size Effects
3. Uniaxial Cauchy Stress According to 3D Image Analysis
4. Size Effect of Mortar Specimens under Uniaxial Tension
5. Measurement of Mode I Fracture Energy Based on the Cauchy Stress
6. Conclusions
- The fractured surfaces were scanned using a 3D scanner and we calculated Cauchy stresses to evaluate the fracture energy precisely by using final fractured surface. The actual fractured surfaces were larger than the initial section, so the fracture stresses were calculated according to the Cauchy stress principle. It is important to quantify the mode I fracture energy based on experimental test data. Smaller specimen group shows relatively larger differences between fractured and initial sections.
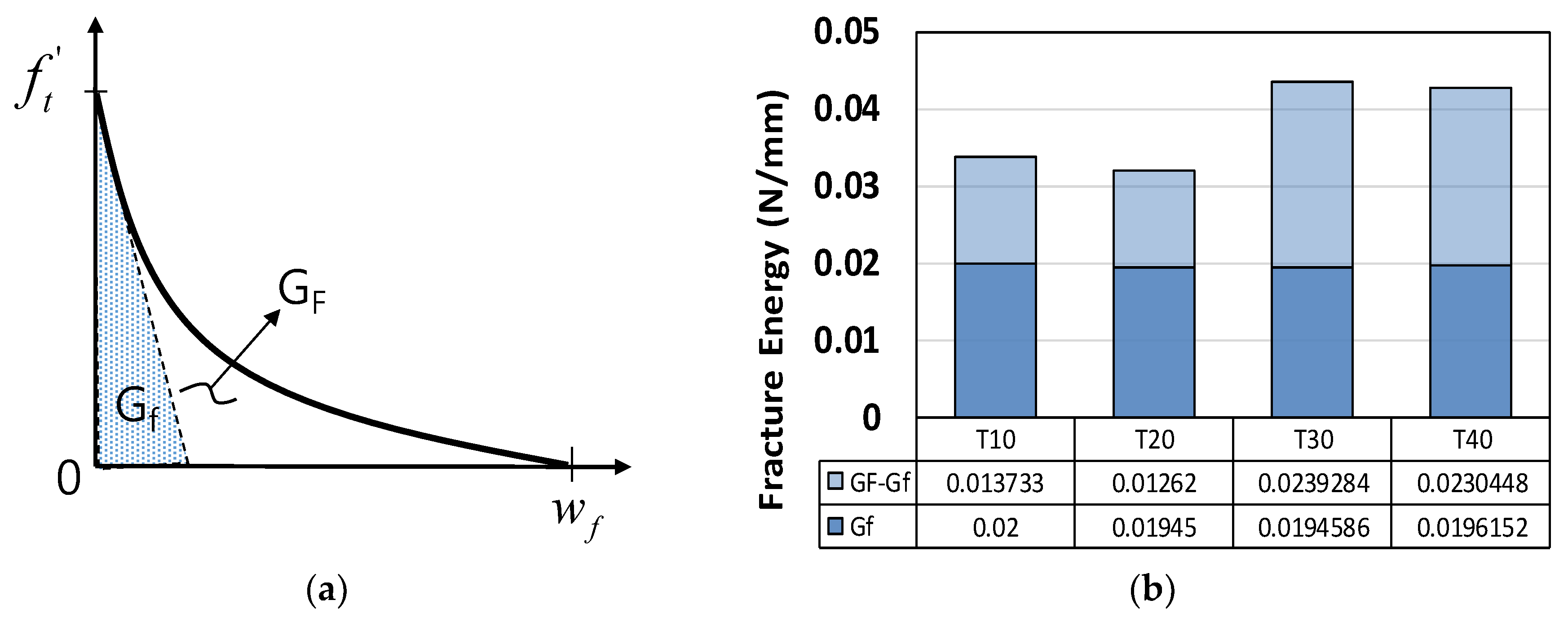
- The average GF/Gf ratio for the mortar specimens was 1.94, which is lower than the typical value for concrete, of 2.5. The direct tension test on the double-notched mortar specimens with no major inclusion yielded a small FPZ after tensile crack initiation, so that the tail portion of the softening branch was also relatively small. This led to a decrease in the GF/Gf ratio. We verified this via a nonlinear fracture mechanics simulation, which agreed well with our experimental results.
- We investigated the size effect for four different specimens with d/a held constant, to eliminate shape effects. The traditional LEFM-based prediction and the Bažant size effect law predict a gradient of 1/2 in the case of relatively large specimens. Typical laboratory-scaled specimens usually exhibit gradients below 1/2 in the case of concrete; thus, nonlinear fracture mechanics should be used to estimate tensile strength in terms of structural dimensions. In the case of our mortar specimens, the slope value, 1/0.727, violated either the LEFM theory and Bažant size effect law, which was unexpected because LEFM predicts a strong size effect. More observations are required to explore this according to variations in d/a. In order to explore this discrepancy, different direct tensile test specimen could be applied; (a) un-notched specimen, (b) one-side single-notched specimen, and (c) double-notched specimen. Notch sensitivity may lead to different extent of FPZ and tensile strength change in accordance with specimen size.
Author Contributions
Funding
Conflicts of Interest
References
- Van Vliet, M.R.A. Size Effect in Tensile Fracture of Concrete and Rock. Ph.D. Thesis, TU-Delft, Delft, The Netherlands, 2000; p. 192. [Google Scholar]
- Rilem, T.Q.F.S. Quasibrittle fracture scaling and size effect-Final report. Mat. Struct. 2004, 37, 547–568. [Google Scholar] [CrossRef][Green Version]
- Van Mier, J.G.M. Concrete Fracture: A Multiscale Approach; CRC Press: Boca Raton, FL, USA, 2013; pp. 1–357. [Google Scholar]
- Bažant, Z. Size effect in blunt fracture: Concrete, Rock, Metal. ASCE J. Eng. Mech. 1984, 110, 518–535. [Google Scholar] [CrossRef]
- Bažant, Z.; Planas, J. Fracture and Size Effect in Concrete and other Quasibrittle Materials; CRC Press: Boca Raton, FL, USA, 1997; pp. 1–640. [Google Scholar]
- Bažant, Z.; Kim, J.-K.; Pfeiffer, P.A. Nonlinear fracture properties from size effect tests. J. Strut. Eng. 1986, 112, 289–307. [Google Scholar] [CrossRef]
- Karihaloo, B.L.; Carpintreri, A.; Elices, M. Fracture mechanics of cement mortar and plain concrete. Adv. Cem. Based Mat. 1993, 1, 92–105. [Google Scholar] [CrossRef]
- Bažant, Z.; Oh, B.H. Crack band theory for fracture of concrete. Mat. Constr. 1983, 16, 155–177. [Google Scholar] [CrossRef]
- Bažant, Z. Concrete fracture models: Testing and practice. Eng. Fract. Mech. 2002, 69, 165–205. [Google Scholar] [CrossRef]
- Van Vliet, M.R.A.; Van Mier, J.G.M. Size effect of concrete in uniaxial tension. Trans. Eng. Sci. 1996, 13, 823–830. [Google Scholar]
- Bažant, Z.; Daniel, I.; Li, Z. Size effect and fracture characteristics of composite laminates. J. Eng. Mat. Tech. 1996, 118, 317–324. [Google Scholar] [CrossRef]
- Kozul, R.; Darwin, D. Effects of Aggregate Type, Size, and Content on Concrete Strength and Fracture Energy; SM Report No. 43; University of Kansas: Lawrence, KS, USA, 1997; pp. 1–98. [Google Scholar]
- Nishikawa, T.; Ito, S.; Awaji, H. Fracture mechanics and microstructure of cement mortar. In Proceedings of the FRAMCOS-3, Gifu, Japan, 12–16 October 1998; pp. 223–232. [Google Scholar]
- Van Vliet, M.R.A.; Van Mier, J.G.M. Effect of strain gradients on the size of concrete in uniaxial tension. In Fracture Scaling; Springer: Dordrecht, The Netherlands, 1999; Volume 95, pp. 195–219. [Google Scholar]
- Van Vliet, M.R.A. Size effect of concrete and sandstone. Heron 2000, 45, 91–108. [Google Scholar]
- Zheng, W.; Kwan, A.K.H.; Lee, P.K.K. Direct tension test of concrete. Mat. J. 2001, 98, 63–71. [Google Scholar]
- Zhu, Y.; Xu, S.L. Fracture properties of cement paste and mortar: An experimental investigation. In Proceedings of the International Association of Fracture Mechanics for Concrete and Concrete Structures, FRAMCOS-6, Catania, Italy, 17–22 June 2007; pp. 1–7. [Google Scholar]
- Xu, S.; Zhu, Y. Experiment studies on fracture energy of cement paste and mortar. In Key Engineering Materials; Trans Tech Publications: Zürich, Switzerland, 2007; Volume 348–349, pp. 169–172. [Google Scholar]
- Aliha, M.R.M.; Ayatollahi, M.R. Brittle fracture evaluation of a fine grain cement mortar in combined tensile-shear deformation. Fatigue Fract. Eng. Mat. Struct. 2009, 32, 987–994. [Google Scholar] [CrossRef]
- Wang, J.J.A.; Liu, K.C.; Naus, D. A new test method for determining the strength and fracture toughness of cement mortar and concrete. In Proceedings of the ASME Pressure Vessels and Piping Conference, Prague, Czech Republic, 26–30 July 2009; American Society of Mechanical Engineers: New York, NY, USA, 2009; Volume 6, pp. 13–19. [Google Scholar]
- Chen, X.; Wu, S.; Zhou, J. Strength values of cementitious materials in bending and tension test methods. J. Mat. Civ. Eng. 2014, 26, 484–490. [Google Scholar] [CrossRef]
- Zhou, J.; Qian, P.; Chen, X. Stress-strain behavior of cementitious materials with different sizes. Sci. World J. 2014, 2014, 919154. [Google Scholar] [CrossRef] [PubMed]
- Del Viso, J.R.; Carmona, J.R.; Ruiz, G. Size and shape effects on the compressive strength of high strength concrete. Cem. Concr. Res. 2008, 38, 386–395. [Google Scholar] [CrossRef]
- Chupanit, P.; Roesler, J.R. Fracture energy approach to characterize concrete crack surface roughness and shear stiffness. J. Mat. Civ. Eng. 2008, 20, 275–282. [Google Scholar] [CrossRef]
- Volokh, K.Y. Characteristic length of damage localization in concrete. Mech. Res. Comm. 2013, 51, 29–31. [Google Scholar] [CrossRef]
- Cifuentes, H.; Alcalde, M.; Medina, F. Comparison of the size-independent fracture energy of concrete obtained by two test methods. In Proceedings of the FRAMCOS-8, Toledo, Spain, 10–14 March 2013; pp. 1–6. [Google Scholar]
- Fernandez-Canteli, A.; Castanon, L.; Nieto, B.; Lozano, M. Determining fracture energy parameters of concrete from the modified compact tension test. Frattura Integrità Strut. 2014, 30, 383–393. [Google Scholar] [CrossRef]
- Toward a Rational Understanding of Shear in Beams and Slabs; CEB-FIP Bulletin: Zürich, Switzerland, 2016; Volume 85, pp. 214–218.
- Uday, N.P. Experimental determination of fracture energy by RILEM method. Int. J. Eng. Sci. 2017, 6, 106–115. [Google Scholar] [CrossRef]
- To, T.; Celarie, F.; Roux-Langlois, C.; Bazin, A.; Gueguen, Y.; Orain, H.; Le Fur, M.; Burgaund, V.; Rouxel, T. Fracture toughness, fracture energy and slow crack growth of glass as investigated by the single-edge precracked beam (SEPB) and Chevron-notched beam (CNB) methods. Acta Mat. 2018, 146, 1–11. [Google Scholar] [CrossRef]
- Ko, S.; Chan, K.; Hawkins, R.; Jayaram, R.; Lynch, C.; El Mamoune, R.; Nguyen, M.; Pekhotin, N.; Stokes, N.; Wu, D.; et al. Experimental and numerical characterization of the intra-laminar fracturing behavior in discontinuous fiber composite structures. In Proceedings of the 33th ASC Conference, Seattle, WA, USA, 24–26 September 2018; pp. 1–15. [Google Scholar]
- Werner, S.; Kustermann, A.; Thienel, C. Analyzing the influence of maximum aggregate size upon the concrete behavior under projectile impact by means of fracture mechanic and surface analytic methods. In Proceedings of the 9th fib International Ph.D. Symposium in Civil Engineering, Karlsruhe, Germany, 22–25 July 2013; pp. 1–8. [Google Scholar]
- Hordiijk, D.A. Local Approach to Fatigue of Concrete. Ph.D. Thesis, TU-Delft, Delft, The Netherlands, 1991. [Google Scholar]
- Atena Theory Manual; Cervenka Consulting: Praha, Czech Republic, 2013.
- Hillerborg, A. The theoretical basis of a method to determine the fracture energy GF of concrete. Mat. Struct. 1985, 18, 291–296. [Google Scholar] [CrossRef]
- Bažant, Z.; Pfeiffer, P.A. Determination of fracture energy from size effect and brittleness number. ACI Mat. J. 1987, 84, 463–480. [Google Scholar]


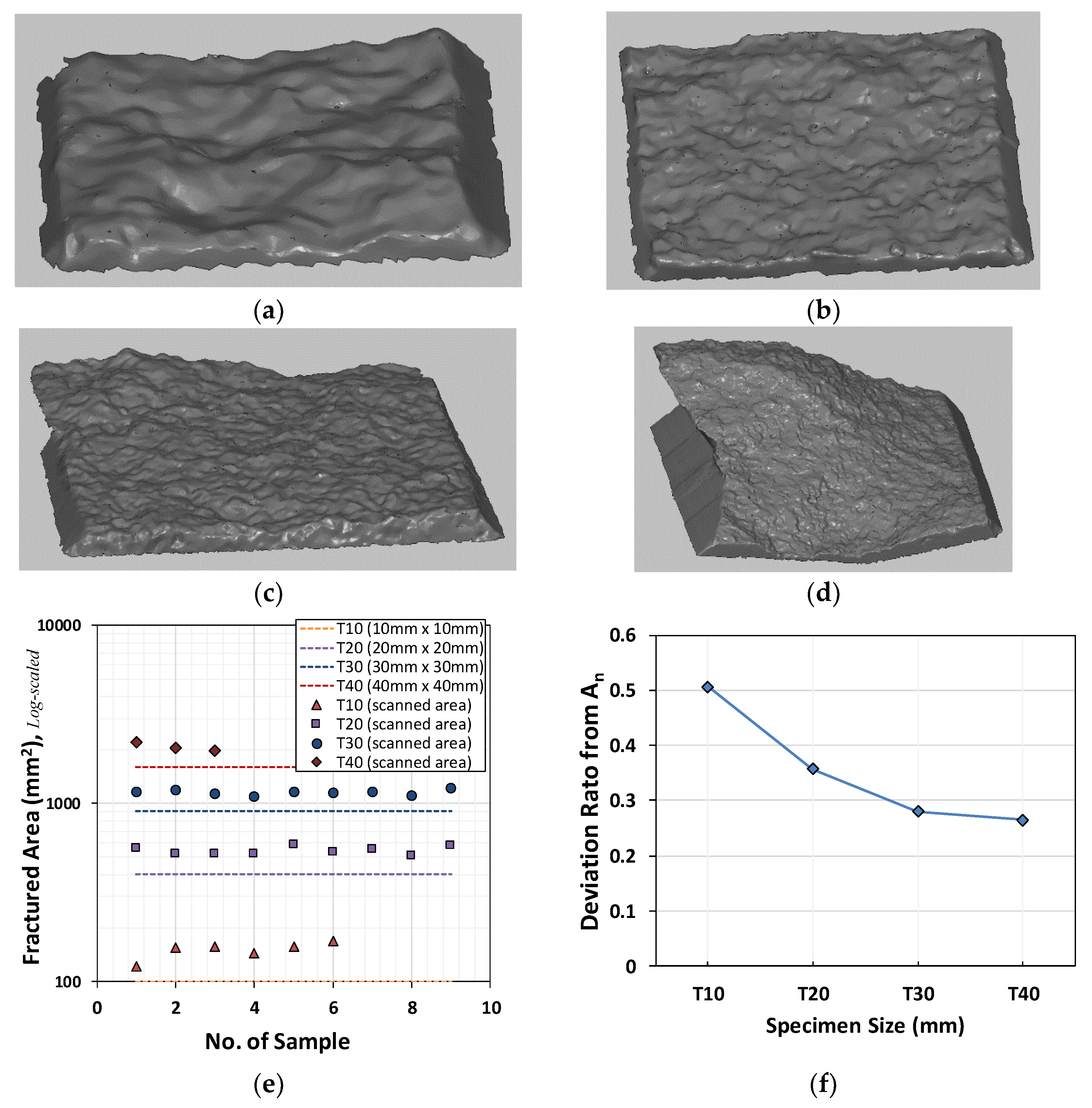
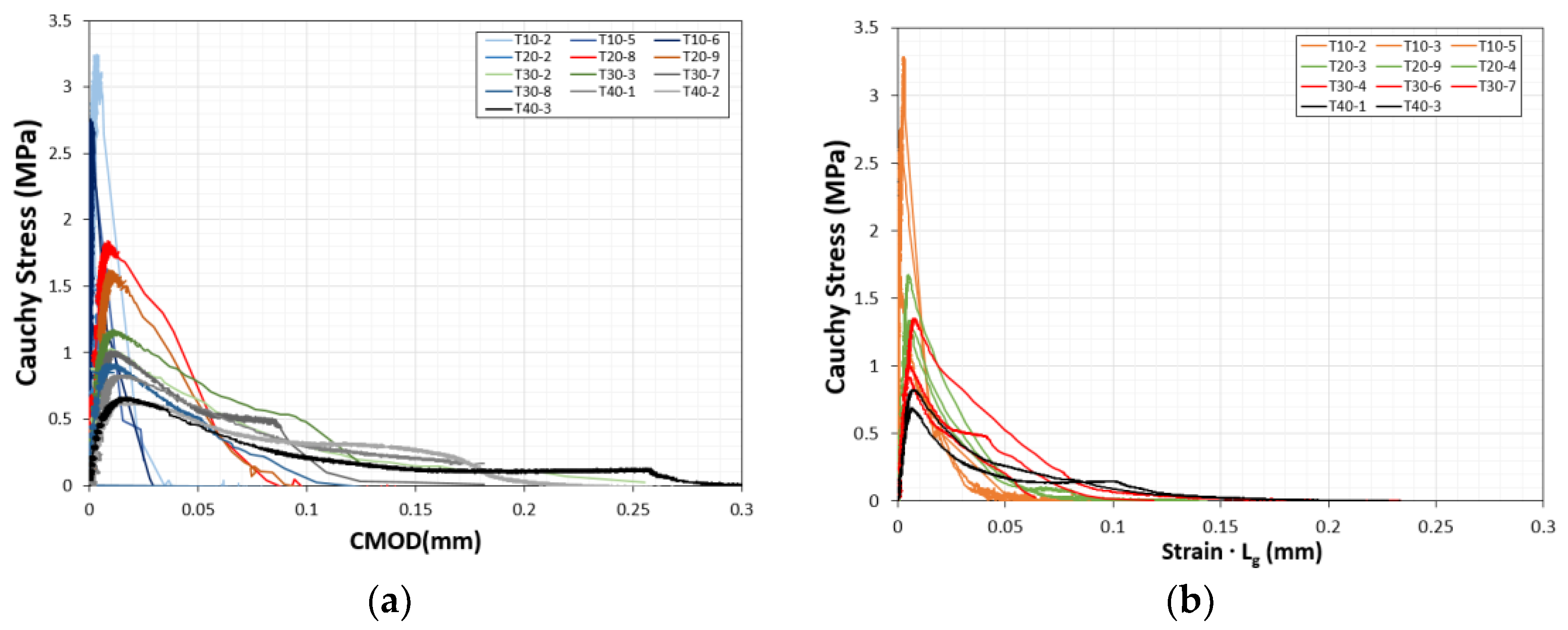








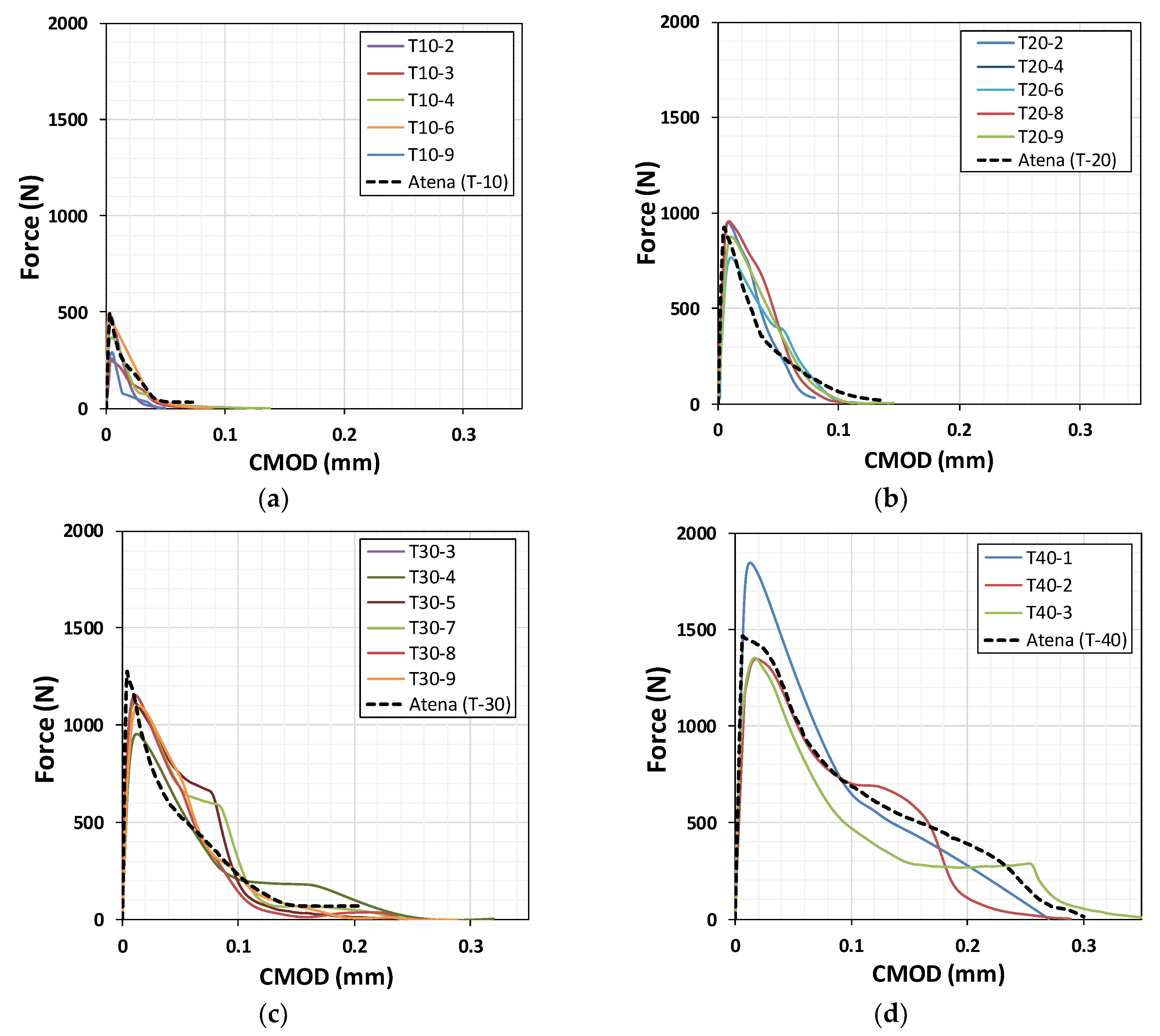

| Specimen Label | h0 | h1 | h2 | h3 | h4 | w0 | w1 | w2 | a | b | Ao (mm2) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| T-10 | 165.0 | 42.5 | 20.0 | 17.5 | 5.0 | 30.0 | 15.0 | 10.0 | 2.5 | 10.0 | 100 |
| T-20 | 330.0 | 85.0 | 40.0 | 35.0 | 10.0 | 60.0 | 30.0 | 20.0 | 5.0 | 20.0 | 400 |
| T-30 | 495.0 | 127.5 | 60.0 | 52.5 | 15.0 | 90.0 | 45.0 | 30.0 | 7.5 | 30.0 | 900 |
| T-40 | 660.0 | 170.0 | 80.0 | 70.0 | 20.0 | 120.0 | 60.0 | 40.0 | 10.0 | 40.0 | 1600 |
| Specimen Label | Avg. Cauchy Stress (MPa) | Estimated Tensile Stress (MPa) |
|---|---|---|
| T-10 | 2.577 | 2.327 |
| T-20 | 1.591 | 1.583 |
| T-30 | 1.088 | 1.085 |
| T-40 | 0.719 | 0.723 |
| Specimen Label | PK Stress | Cauchy Stress | LEFM | Bažant (n = 3, k1 = 1, m = 2) | Modified Bažant (n = 3, k1 = 0.375, m = 0.727) |
|---|---|---|---|---|---|
| T-10 | 3.89 | 2.58 | 3.16 | 4.09 | 2.78 |
| T-20 | 2.15 | 1.59 | 2.20 | 3.21 | 1.51 |
| T-30 | 1.39 | 1.09 | 1.80 | 2.73 | 0.99 |
| T-40 | 0.94 | 0.72 | 1.56 | 2.41 | 0.72 |
| Specimen Label | ft’(MPa) | wf (mm) | Gf (N/mm) | GF (N/mm) | GF/Gf | α |
|---|---|---|---|---|---|---|
| T-10 | 2.58 | 0.0333 | 0.02 | 0.0337 | 1.685 | 2.55 |
| T-20 | 1.59 | 0.0910 | 0.01945 | 0.0321 | 1.650 | 4.51 |
| T-30 | 1.09 | 0.1450 | 0.01946 | 0.0434 | 2.230 | 3.64 |
| T-40 | 0.72 | 0.2450 | 0.01962 | 0.0427 | 2.176 | 4.13 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rhee, I.; Lee, J.S.; Roh, Y.-S. Fracture Parameters of Cement Mortar with Different Structural Dimensions Under the Direct Tension Test. Materials 2019, 12, 1850. https://doi.org/10.3390/ma12111850
Rhee I, Lee JS, Roh Y-S. Fracture Parameters of Cement Mortar with Different Structural Dimensions Under the Direct Tension Test. Materials. 2019; 12(11):1850. https://doi.org/10.3390/ma12111850
Chicago/Turabian StyleRhee, Inkyu, Jun Seok Lee, and Young-Sook Roh. 2019. "Fracture Parameters of Cement Mortar with Different Structural Dimensions Under the Direct Tension Test" Materials 12, no. 11: 1850. https://doi.org/10.3390/ma12111850
APA StyleRhee, I., Lee, J. S., & Roh, Y.-S. (2019). Fracture Parameters of Cement Mortar with Different Structural Dimensions Under the Direct Tension Test. Materials, 12(11), 1850. https://doi.org/10.3390/ma12111850






