Using the Steady-State Chloride Migration Test to Evaluate the Self-Healing Capacity of Cracked Mortars Containing Crystalline, Expansive, and Swelling Admixtures
Abstract
:1. Introduction
2. Theoretical Background
3. Experimental Program
3.1. Test Outline
3.2. Materials and Mix Proportions
3.3. Preparation of Cracked Specimens
3.4. Steady-State Chloride Migration Test
4. Results and Discussion
4.1. Effect of Electrical Potential
4.2. Effect of Crystalline and Expansive Admixtures on the Self-Healing of Cracks
4.3. Evaluation of Self-Healing Capacity
5. Conclusions
- (1)
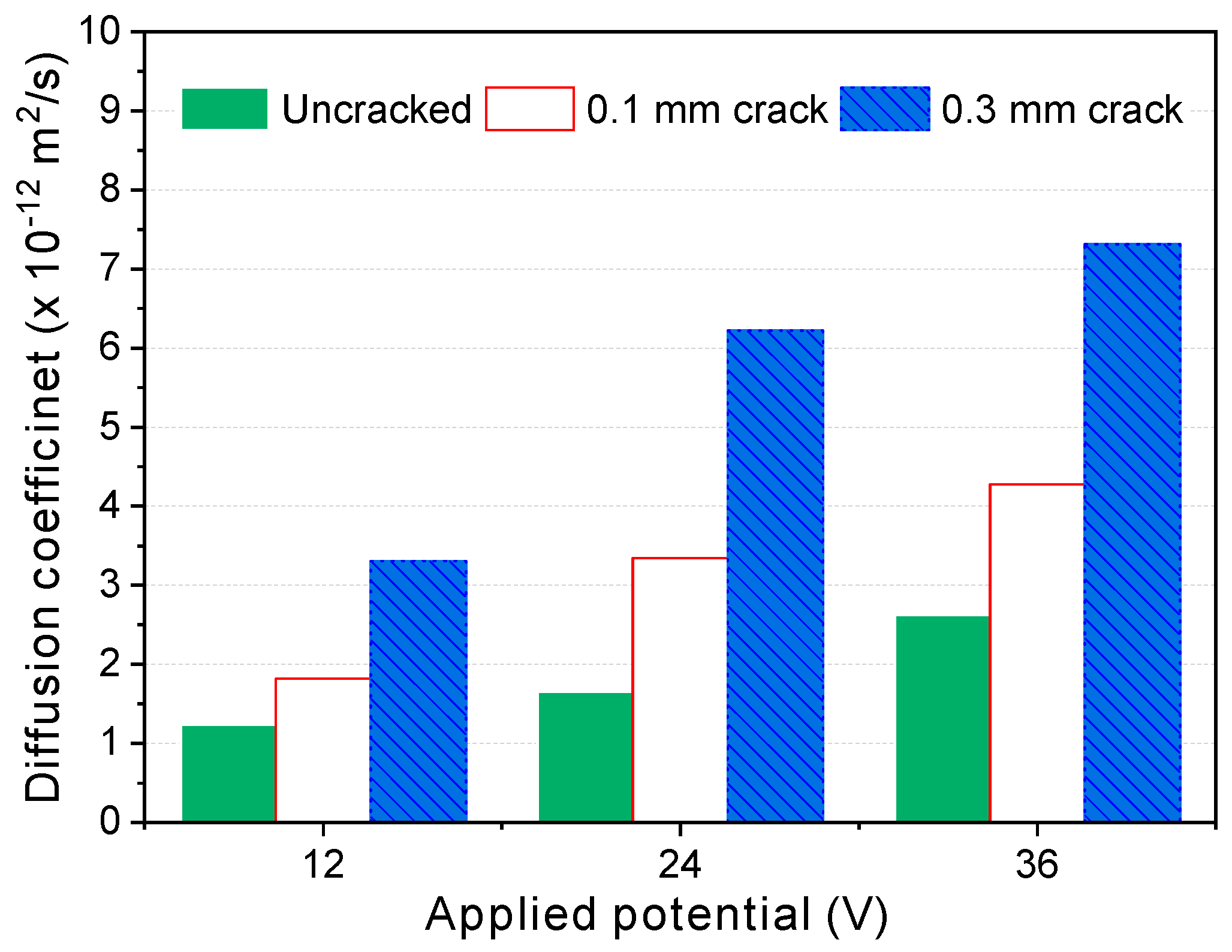
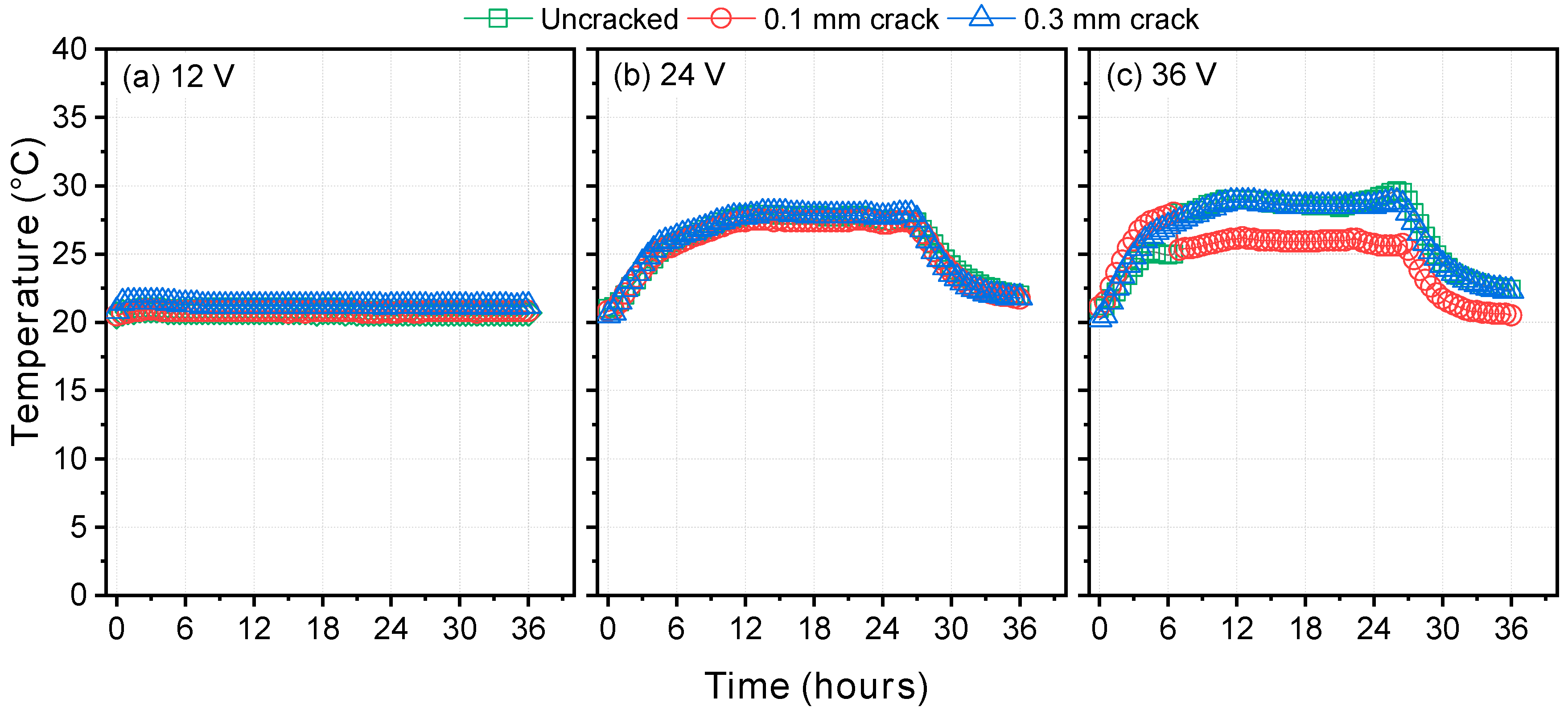
- In the steady-state migration test, the time to reach the quasi-steady-state decreased and the diffusion coefficients increased with increasing potential. This is attributed to both the effect of the potential drop inside the migration cell and the self-healing that occurred during the test. Therefore, it is necessary to minimize the test duration by choosing a high potential, though it remains important that the temperature does not rise too high during the test. Within the scope of this study, 36 V was selected as the most appropriate potential, under which the temperature rise was less than 10 °C, and the test duration could be reduced to as low as 24 to 36 h. Under those conditions, the repeatability of the test was quite high, and the deviations between different test specimens were low enough.
- (2)
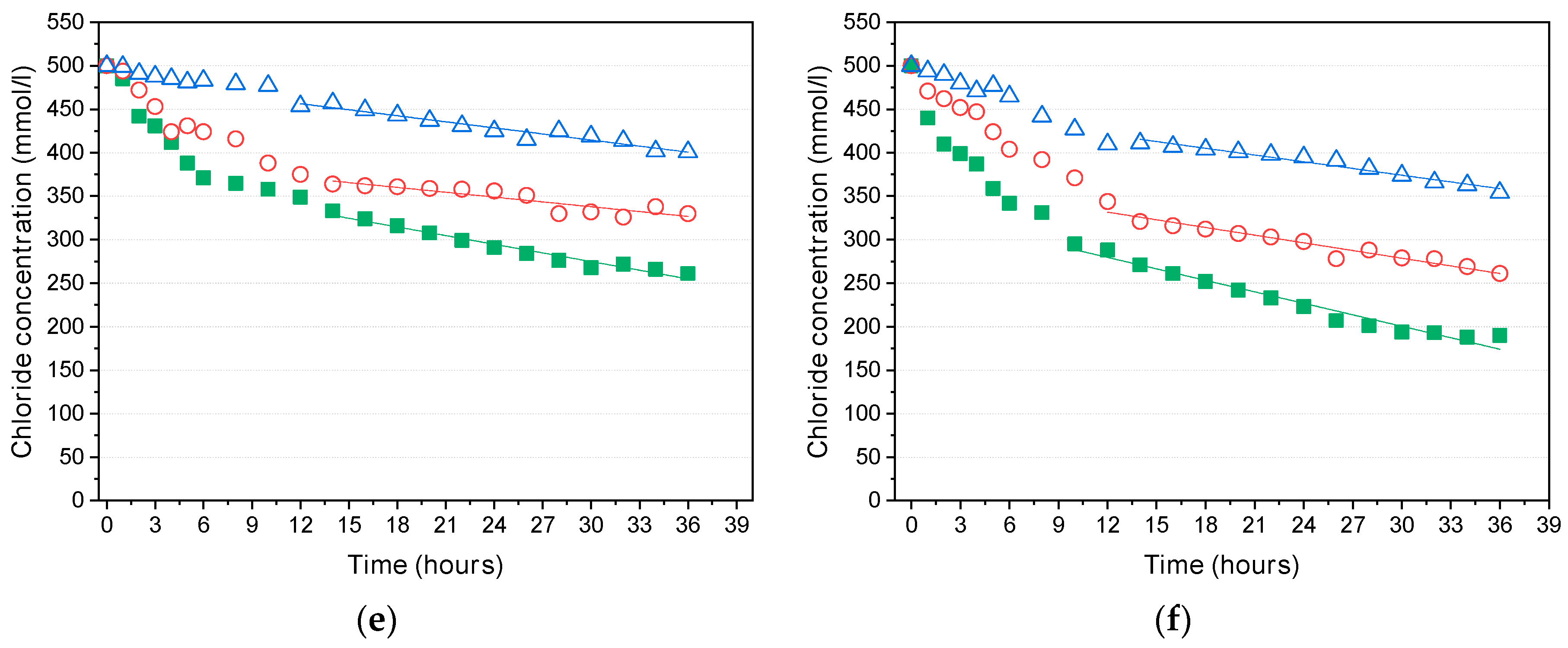
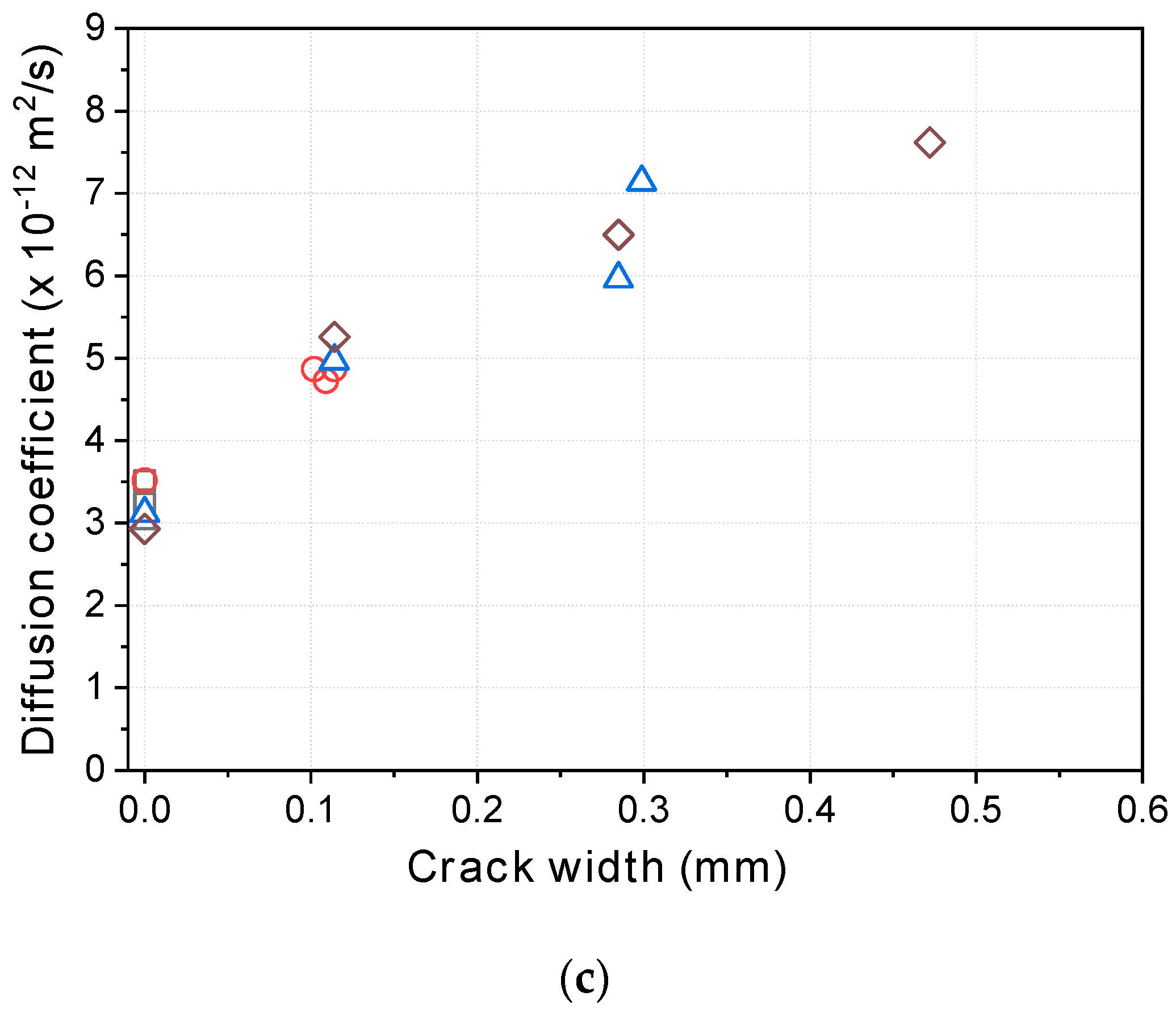
- The diffusion coefficients obtained from the steady-state diffusion coefficients under the high potential (36 V) increased almost linearly in proportion to the crack width, and the threshold crack width suggested by previous research—the point at which the diffusion coefficient suddenly increases—was not observed before healing. After a certain period of healing, the diffusion coefficients decreased regardless of the mixture type. Up to a certain crack width, the diffusion coefficients decreased to almost the same level as the uncracked specimens. This strongly suggests that the threshold crack width can be attributed to the self-healing of cracks during the test.
- (3)
- For larger crack widths, on the other hand, the recovery of the diffusion coefficients depended on the mixture. The mixture incorporating calcium sulfoaluminate as an expansive admixture and bentonite as a swelling agent together with a crystalline admixture including Na2CO3 and organic calcium ions showed better self-healing performance than the mixture incorporating only the crystalline admixture. Also, depending on the types of self-healing techniques, it is noted that there is a limit in the crack width that can be healed.
- (4)
- The self-healing capacity with respect to resistance to chloride penetration can be evaluated using the steady-state migration test, and an index for the recovery of resistance to chloride penetration due to self-healing can be defined using the rate of chloride ions that pass through the crack. The proposed index can be used to quantitatively compare self-healing techniques. Also, the proposed evaluation method using the steady-state migration test under higher potential can give a more accurate result because the diffusion coefficient can be measured in a relatively short time by preventing the occurrence of self-healing during the test.
Author Contributions
Funding
Conflicts of Interest
References
- Jang, S.Y.; Kim, B.S.; Oh, B.H. Effect of crack width on chloride diffusion coefficients of concrete by steady-state migration tests. Cem. Concr. Res. 2011, 41, 9–19. [Google Scholar] [CrossRef]
- Shah, V.; Scrivener, K.; Bhattacharjee, B.; Bishnoi, S. Changes in microstructure characteristics of cement paste on carbonation. Cem. Concr. Res. 2018, 109, 184–197. [Google Scholar] [CrossRef]
- Van Belleghem, B.; Kessler, S.; Van den Heede, P.; Van Tittelboom, K.; De Belie, N. Chloride induced reinforcement corrosion behavior in self-healing concrete with encapsulated polyurethane. Cem. Concr. Res. 2018, 113, 130–139. [Google Scholar] [CrossRef]
- Ferrara, L.; Krelani, V.; Moretti, F.; Flores, M.R.; Ros, P.S. Effects of autogenous healing on the recovery of mechanical performance of High Performance Fibre Reinforced Cementitious Composites (HPFRCCs): Part 1. Cem. Concr. Compos. 2017, 83, 76–100. [Google Scholar] [CrossRef] [Green Version]
- Mihashi, H.; Nishiwaki, T. Development of engineered self-healing and self-repairing concrete-state-of-the-art report. J. Adv. Concr. Technol. 2012, 10, 170–184. [Google Scholar] [CrossRef]
- Van Tittelboom, K.; De Belie, N. Self-healing in cementitious materials—A review. Materials 2013, 6, 2182–2217. [Google Scholar] [CrossRef] [PubMed]
- Ahn, T.-H.; Kishi, T. Crack self-healing behavior of cementitious composites incorporating various mineral admixtures. J. Adv. Concr. Technol. 2010, 8, 171–186. [Google Scholar] [CrossRef]
- De Nardi, C.; Bullo, S.; Ferrara, L.; Ronchin, L.; Vavasori, A. Effectiveness of crystalline admixtures and lime/cement coated granules in engineered self-healing capacity of lime mortars. Mater. Struct. 2017, 50, 191. [Google Scholar] [CrossRef]
- Azarsa, P.; Gupta, R.; Biparva, A. Assessment of self-healing and durability parameters of concretes incorporating crystalline admixtures and Portland Limestone Cement. Cem. Concr. Compos. 2019, 99, 17–31. [Google Scholar] [CrossRef]
- Ferrara, L.; Mullem, T.V.; Alonso, M.C.; Antonaci, P.; Borg, R.P.; Cuenca, E.; Jefferson, A.; Ng, P.-L.; Peled, A.; Roig-Flores, M.; et al. Experimental characterization of the self-healing capacity of cement based materials and its effects on the material performance: A state of the art report by COST Action SARCOS WG2. Constr. Build. Mater. 2018, 167, 115–142. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.X.D.; Wong, H.S.; Buenfeld, N.R. Self-sealing of cracks in concrete using superabsorbent polymers. Cem. Concr. Res. 2016, 79, 194–208. [Google Scholar] [CrossRef] [Green Version]
- Van Belleghem, B.; Van den Heede, P.; De Belie, N. Resistance to Chloride Penetration of Self-Healing Concrete with Encapsulated Polyurethane. In Proceedings of the 4th International Conference on Sustainable Construction Materials and Technologies (SCMT4), Las Vegas, NV, USA, 7–11 August 2016; pp. 1386–1395. [Google Scholar]
- Souradeep, G.; Kua, H.W. Encapsulation technology and techniques in self-healing concrete. J. Mater. Civ. Eng. 2016, 28, 04016165. [Google Scholar] [CrossRef]
- Aldea, C.-M.; Song, W.; Popovics, J.S.; Shah, S.P. Extent of healing of cracked normal strength concrete. J. Mater. Civ. Eng. 2000, 12, 92–96. [Google Scholar] [CrossRef]
- Cuenca, E.; Tejedor, A.; Ferrara, L. A methodology to assess crack-sealing effectiveness of crystalline admixtures under repeated cracking-healing cycles. Constr. Build. Mater. 2018, 179, 619–632. [Google Scholar] [CrossRef]
- Muhammad, N.Z.; Shafaghat, A.; Keyvanfar, A.; Majid, M.Z.A.; Ghoshal, S.K.; Yasouj, S.E.M.; Ganiyu, A.A.; Kouchaksaraei, M.S.; Kamyab, H.; Taheri, M.M.; et al. Tests and methods of evaluating the self-healing efficiency of concrete: A review. Constr. Build. Mater. 2016, 112, 1123–1132. [Google Scholar] [CrossRef]
- Darquennes, A.; Olivier, K.; Benboudjema, F.; Gagné, R. Self-healing at early-age, a way to improve the chloride resistance of blast-furnace slag cementitious materials. Constr. Build. Mater. 2016, 113, 1017–1028. [Google Scholar] [CrossRef]
- Şahmaran, M. Effect of flexure induced transverse crack and self-healing on chloride diffusivity of reinforced mortar. J. Mater. Sci. 2007, 42, 9131–9136. [Google Scholar] [CrossRef]
- Standard Method of Test for Resistance of Concrete to Chloride Ion Penetration; AASHTO T259; American Association of State Highway and Transportation Officials: Washington, DC, USA, 1986.
- Standard Test Method for Determining the Penetration of Chloride Ion into Concrete by Ponding; ASTM C1543-10a; ASTM: West Conshohocken, PA, USA, 2000.
- Products and Systems for the Protection and Repair of Concrete Structures Test Methods Measurement of Chloride Ion Ingress; EN 13396; CEN: London, UK, 2004.
- Concrete, Hardened: Accelerated Chloride Penetration; NT Build 443; Nordtest: Slettetoften, Taastrupl, Denmark, 1995.
- Standard Test Method for Determining the Apparent Chloride Diffusion Coefficient of Cementitious Mixtures by Bulk Diffusion; ASTM C1556; ASTM: West Conshohocken, PA, USA, 2004.
- Standard Method of Test for Electrical Indication of Concrete’s Ability to Resist Chloride Ion Penetration; AASHTO T277; American Association of State Highway and Transportation Officials: Washington, DC, USA, 1993.
- Standard Test Method for Electrical Indication of Concrete’s Ability to Resist Chloride Ion Penetration; ASTM C1202; ASTM: West Conshohocken, PA, USA, 1981.
- Concrete, Mortar and Cement-Based Repair Materials: Chloride Diffusion Coefficient from Migration Cell Experiments; NT Build 355; Nordtest: Slettetoften, Taastrupl, Denmark, 1997.
- Chloride Migration Coefficient from Non-Stady-State Migration Experiments; NT Build 492; Nordtest: Slettetoften, Slettetoften, Denmark, 1999.
- Jacobsen, S.; Marchand, J.; Boisvert, L. Effect of cracking and healing on chloride transport in OPC concrete. Cem. Concr. Res. 1996, 26, 869–881. [Google Scholar] [CrossRef]
- Maes, M.; De Belie, N. Resistance of concrete and mortar against combined attack of chloride and sodium sulphate. Cem. Concr. Compos. 2014, 53, 59–72. [Google Scholar] [CrossRef]
- Ye, H.; Tian, Y.; Jin, N.; Jin, X.; Fu, C. Influence of cracking on chloride diffusivity and moisture influential depth in concrete subjected to simulated environmental conditions. Constr. Build. Mater. 2013, 47, 66–79. [Google Scholar] [CrossRef]
- Lim, C.C.; Gowripalan, N.; Sirivivatnanon, V. Microcracking and chloride permeability of concrete under uniaxial compression. Cem. Concr. Compos. 2000, 22, 353–360. [Google Scholar] [CrossRef]
- Tegguer, A.D.; Bonnet, S.; Khelidj, A.; Baroghel-Bouny, V. Effect of uniaxial compressive loading on gas permeability and chloride diffusion coefficient of concrete and their relationship. Cem. Concr. Res. 2013, 52, 131–139. [Google Scholar] [CrossRef] [Green Version]
- Şahmaran, M.; Yildirim, G.; Erdem, T.K. Self-healing capability of cementitious composites incorporating different supplementary cementitious materials. Cem. Concr. Compos. 2013, 35, 89–101. [Google Scholar] [CrossRef] [Green Version]
- Win, P.P.; Watanabe, M.; Machida, A. Penetration profile of chloride ion in cracked reinforced concrete. Cem. Concr. Res. 2004, 34, 1073–1079. [Google Scholar] [CrossRef]
- Ye, H.; Jin, N.; Jin, X.; Fu, C. Model of chloride penetration into cracked concrete subject to drying—Wetting cycles. Constr. Build. Mater. 2012, 36, 259–269. [Google Scholar] [CrossRef]
- Akhavan, A.; Rajabipour, F. Evaluating ion diffusivity of cracked cement paste using electrical impedance spectroscopy. Mater. Struct. 2013, 46, 697–708. [Google Scholar] [CrossRef]
- Djerbi, A.; Bonnet, S.; Khelidj, A.; Baroghel-bouny, V. Influence of traversing crack on chloride diffusion into concrete. Cem. Concr. Res. 2008, 38, 877–883. [Google Scholar] [CrossRef] [Green Version]
- Konin, A.; François, R.; Arliguie, G. Penetration of chlorides in relation to the microcracking state into reinforced ordinary and high strength concrete. Mater. Struct. 1998, 31, 310–316. [Google Scholar] [CrossRef]
- Mu, S.; De Schutter, G.; Ma, B. Non-steady state chloride diffusion in concrete with different crack densities. Mater. Struct. 2013, 46, 123–133. [Google Scholar] [CrossRef]
- Gowripalan, N.; Sirivivatnanon, V.; Lim, C.C. Chloride diffusivity of concrete cracked in flexure. Cem. Concr. Res. 2000, 30, 725–730. [Google Scholar] [CrossRef]
- Tang, L.; Nilsson, L.-O.; Basheer, P.A.M. Resistance of Concrete to Chloride Ingress: Testing and Modelling; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Edvardsen, C. Water permeability and autogeneous healing of cracks in concrete. ACI Mater. J. 1999, 96, 448–454. [Google Scholar]
- Tang, L.; Nilsson, L.-O. Rapid Determination of the chloride diffusivity in concrete by applying an electrical field. ACI Mater. J. 1993, 89, 49–53. [Google Scholar]
- Andrade, C. Calculation of chloride diffusion coefficients in concrete from ionic migration measurements. Cem. Concr. Res. 1993, 23, 724–742. [Google Scholar] [CrossRef]
- Page, C.; Short, N.R.; El Tarras, A. Diffusion of chloride ions in hardened cement pastes. Cem. Concr. Res. 1981, 11, 395–406. [Google Scholar] [CrossRef]
- Shin, K.J.; Bae, W.; Choi, S.-W.; Son, M.W.; Lee, K.M. Parameters influencing water permeability coefficient of cracked concrete specimens. Constr. Build. Mater. 2017, 151, 907–915. [Google Scholar] [CrossRef]
- Thermo Scientific. User Guide Chloride Ion Selective Electrode; Thermo Fisher Scientific Inc.: Waltham, MA, USA, 2008. [Google Scholar]
- Standard Test Methods for Chloride Ion in Water; ASTM D512-99; ASTM: West Conshohocken, PA, USA, 1999.
- Lee, W.-J.; Hwang, J.-S.; Ahn, S.-W.; Lee, K.M. Water permeability performance evaluation of mortar containing crack self-healing mineral admixtures. J. Recycl. Constr. Resour. 2016, 4, 463–469. (In Korean) [Google Scholar]
- Park, B.; Choi, Y.C. Quantitative evaluation of crack self-healing in cement-based materials by absorption test. Constr. Build. Mater. 2018, 184, 1–10. [Google Scholar] [CrossRef]
- McGrath, P.F.; Hooton, R.D. Influence of voltage on chloride diffusion coefficients from chloride migration tests. Cem. Concr. Res. 1996, 26, 1239–1244. [Google Scholar] [CrossRef]
- Yildirim, G.; Aras, G.H.; Banyhussan, Q.S.; Şahmaran, M.; Lachemi, M. Estimating the self-healing capability of cementitious composites through non-destructive electrical-based monitoring. NDT E Int. 2015, 76, 26–37. [Google Scholar] [CrossRef]












| Test Time | No. of Test Cycles | Target Crack Widths | |||
|---|---|---|---|---|---|
| “Mix. ID”-UC | “Mix. ID”-C0.1 | “Mix. ID”-C0.3 | “Mix. ID”-C0.5 | ||
| Before healing | #1 | Uncracked | Uncracked | Uncracked | Uncracked |
| #2 | Uncracked | 0.1 mm | 0.1 mm | 0.1 mm | |
| #3 | Uncracked | 0.1 mm | 0.3 mm | 0.3 mm | |
| #4 | Uncracked | 0.1 mm | 0.3 mm | 0.5 mm | |
| After healing of 28 and 56 days | #1 | Uncracked | 0.1 mm | 0.3 mm | 0.5 mm |
| Mixture ID | Mixture Proportions (kg/m3) | 28-Day Compressive Strength (MPa) | Slump Flow (mm) | ||||
|---|---|---|---|---|---|---|---|
| Water | Cement | Crystalline Admixture | Expansive Admixture | Sand | |||
| OPC | 273.2 | 683 | - | - | 1366 | 54.6 | 170 |
| SH-A | 273.2 | 683 | 20.5 | - | 1345.5 | 47.3 | 165 |
| SH-B | 273.2 | 683 | 20.5 | 20.5 | 1325 | 49.6 | 169 |
| Potential Applied | Target Crack Width (µm) | Measured (Mean) Crack Width (µm) | Difference (%) |
|---|---|---|---|
| 36 V | 100 | 110 | +10.0 |
| 300 | 300 | 0.0 | |
| 24 V | 100 | 107 | +7.0 |
| 300 | 293 | −2.3 | |
| 12 V | 100 | 106 | +6.0 |
| 300 | 312 | +4.0 |
| Literature | Specimen | Mixture | Initial Curing (Days) | Diffusion Coefficient of Uncracked Specimens after Initial Curing (×10−12 m2/s) | Crack Width (mm) | Healing Age (Days) | Diffusion Coefficient of Cracked Specimens (×10−12 m2/s) | Reduction Ratio (%) |
|---|---|---|---|---|---|---|---|---|
| Darquennes et al. (2016) [17] | Mortar cylinder with 110 mm diameter and 30 mm thickness | 100% OPC (water/cement = 0.50) | 7 | 2.99 | 0.126 | 0 | 6.43 | - |
| 14 | 4.50 | 30.0 | ||||||
| 21 | 4.00 | 37.8 | ||||||
| 50% OPC + 50% GGBFS (water/binder = 0.52) | 7 | 2.90 | 0.152 | 0 | 7.39 | - | ||
| 14 | 4.00 | 45.9 | ||||||
| 21 | 3.30 | 55.3 | ||||||
| This study | Mortar cylinder with 100 mm diameter and 50 mm thickness | OPC | 28 | 2.63 | 0.103 | 0 | 3.23 | - |
| 28 | 2.42 | 25.1 | ||||||
| 56 | 2.08 | 35.6 | ||||||
| SH-A | 28 | 2.44 | 0.114 | 0 | 4.37 | - | ||
| 28 | 2.26 | 48.3 | ||||||
| 56 | 2.09 | 52.2 | ||||||
| SH-B | 28 | 2.93 | 0.123 | 0 | 5.26 | - | ||
| 28 | 2.36 | 55.1 | ||||||
| 56 | 1.91 | 63.7 |
| Evaluation Methods | Test Duration | Pros | Cons |
|---|---|---|---|
| Ponding test (AASHTO T259 [19], ASTM C1543 [20]) | 90–180 days |
|
|
| Coulomb test (ASTM C1202 [25]) | 6 h |
|
|
| Electrical impedance test [36,52] | 5–30 min (after drying for 24 h) |
|
|
| Non-steady-state migration test (NT Build 492 [27]) | 24–96 h |
|
|
| Steady-state migration test (NT Build 355 [26]) | 7 days |
|
|
| The proposed method (Modified steady-state migration test) | 24–36 h (under 36 V) |
|
|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abro, F.u.R.; Buller, A.S.; Lee, K.-M.; Jang, S.Y. Using the Steady-State Chloride Migration Test to Evaluate the Self-Healing Capacity of Cracked Mortars Containing Crystalline, Expansive, and Swelling Admixtures. Materials 2019, 12, 1865. https://doi.org/10.3390/ma12111865
Abro FuR, Buller AS, Lee K-M, Jang SY. Using the Steady-State Chloride Migration Test to Evaluate the Self-Healing Capacity of Cracked Mortars Containing Crystalline, Expansive, and Swelling Admixtures. Materials. 2019; 12(11):1865. https://doi.org/10.3390/ma12111865
Chicago/Turabian StyleAbro, Fahad ul Rehman, Abdul Salam Buller, Kwang-Myong Lee, and Seung Yup Jang. 2019. "Using the Steady-State Chloride Migration Test to Evaluate the Self-Healing Capacity of Cracked Mortars Containing Crystalline, Expansive, and Swelling Admixtures" Materials 12, no. 11: 1865. https://doi.org/10.3390/ma12111865
APA StyleAbro, F. u. R., Buller, A. S., Lee, K.-M., & Jang, S. Y. (2019). Using the Steady-State Chloride Migration Test to Evaluate the Self-Healing Capacity of Cracked Mortars Containing Crystalline, Expansive, and Swelling Admixtures. Materials, 12(11), 1865. https://doi.org/10.3390/ma12111865








