Periodic Metallo-Dielectric Structures: Electromagnetic Absorption and its Related Developed Temperatures
Abstract
:1. Introduction
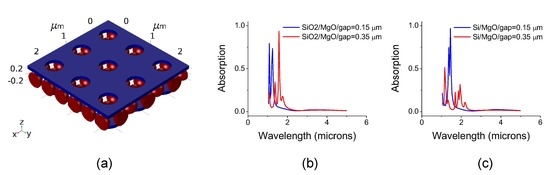
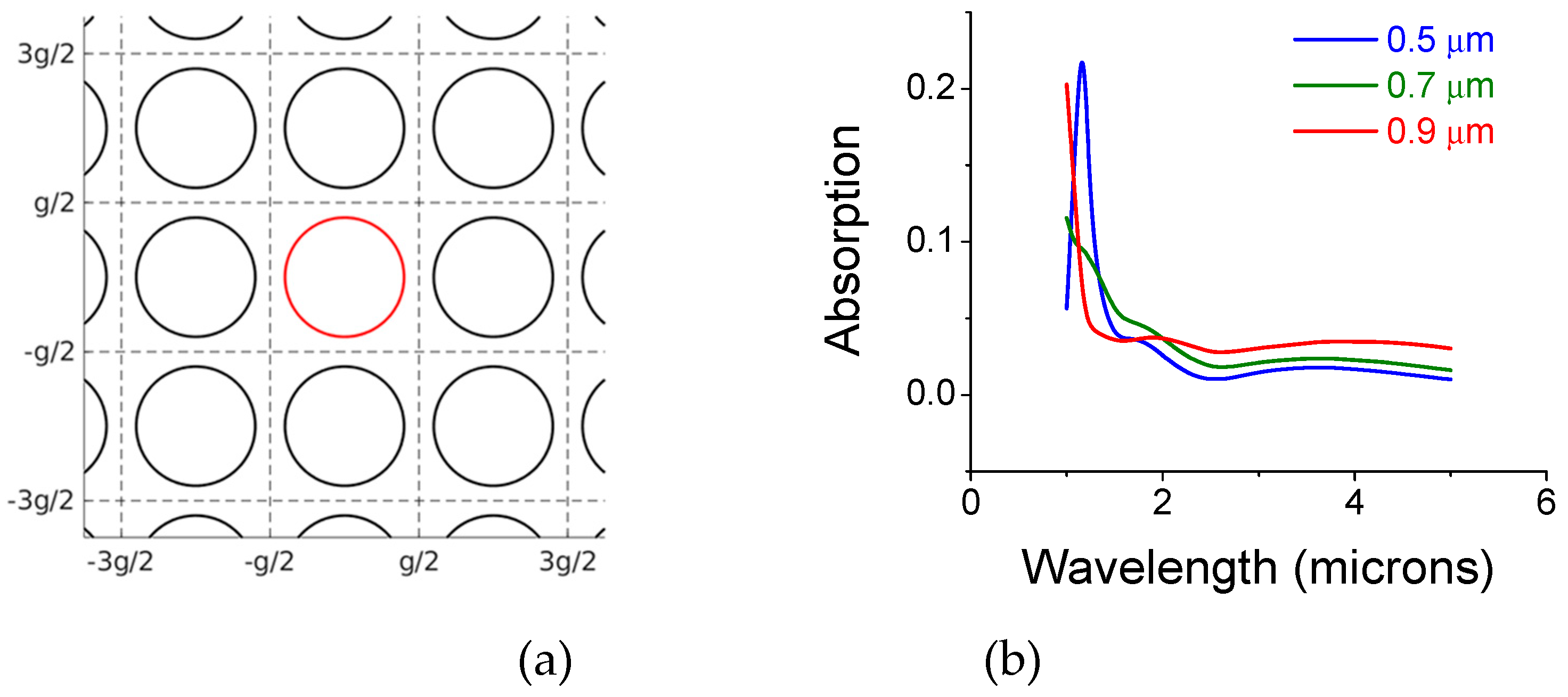
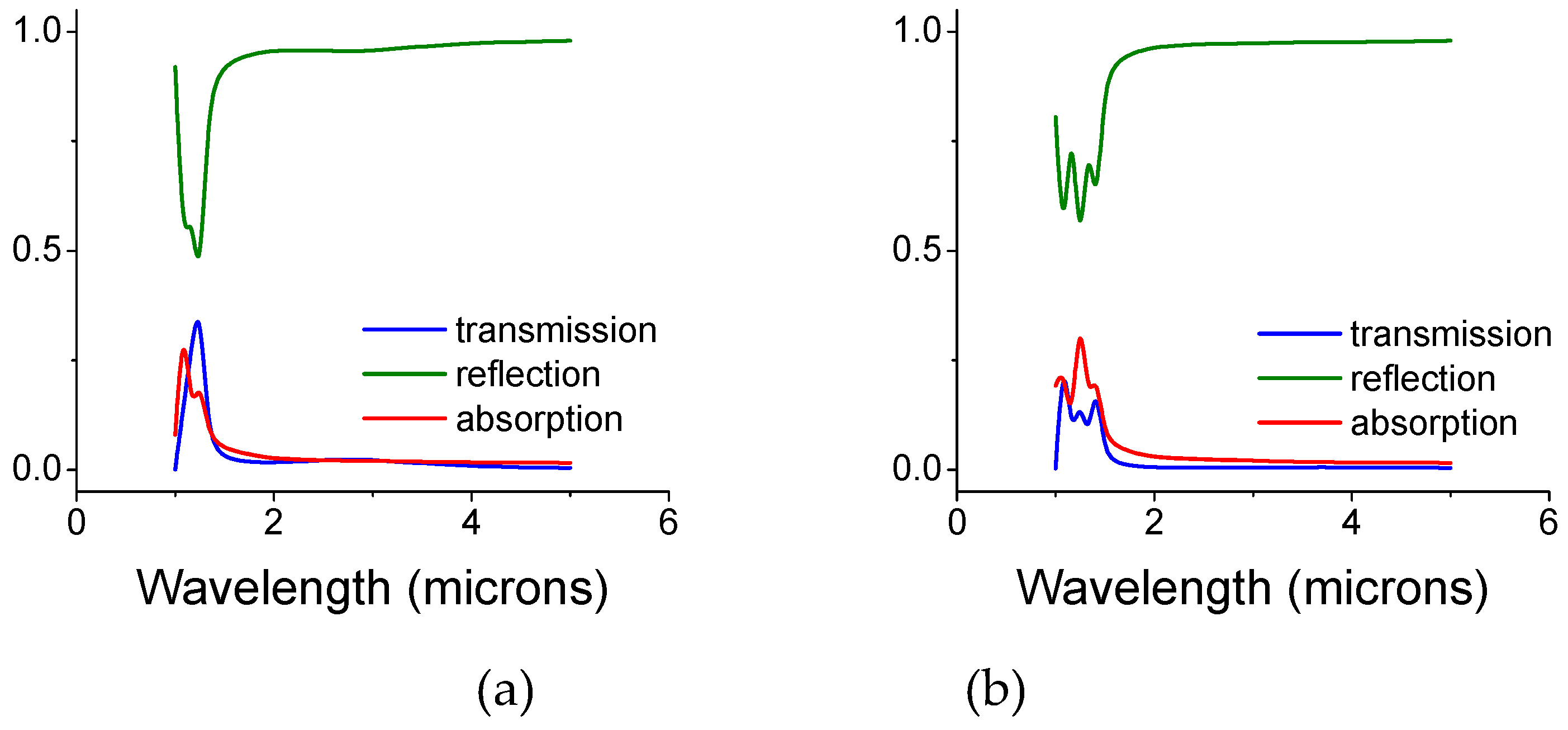
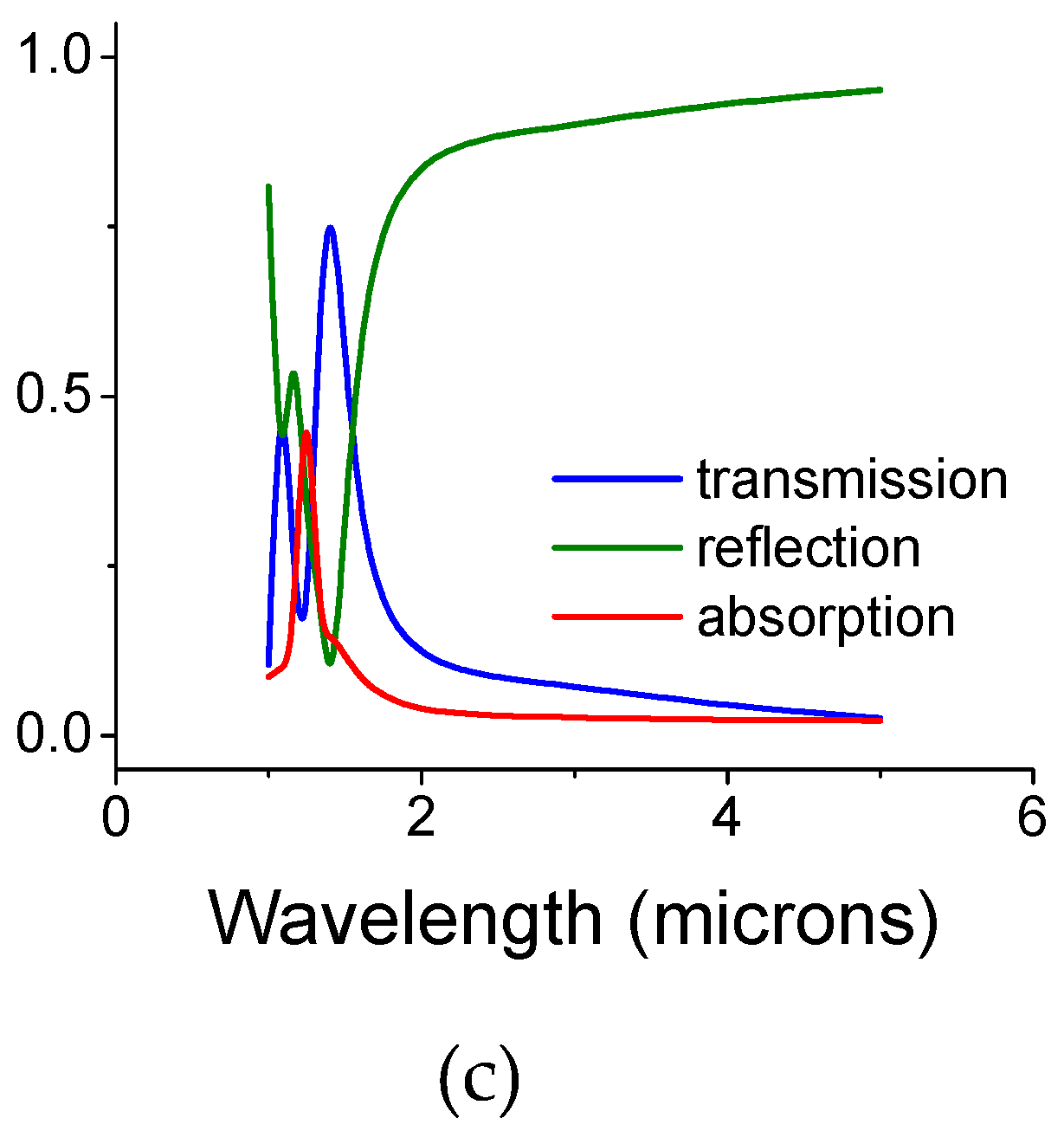
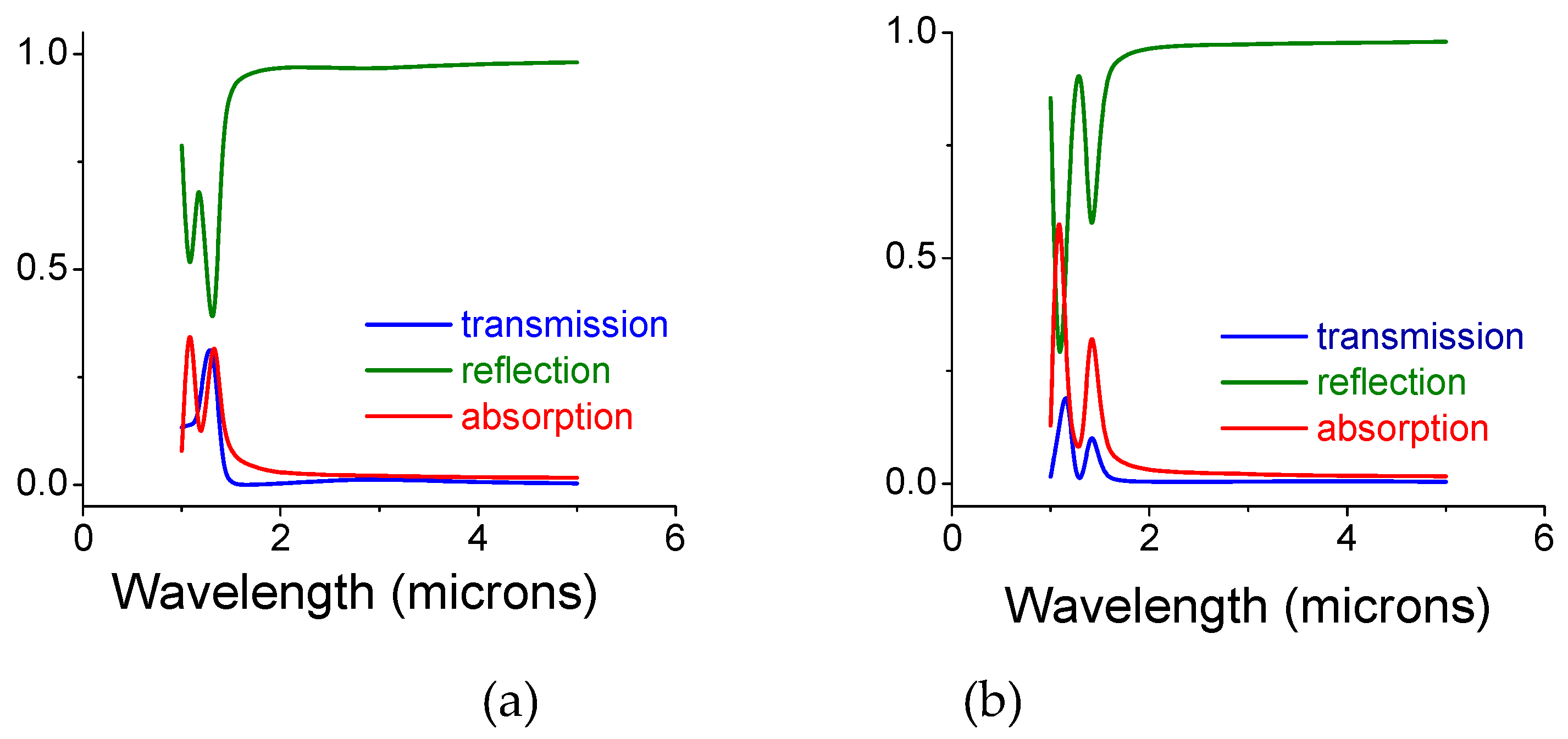
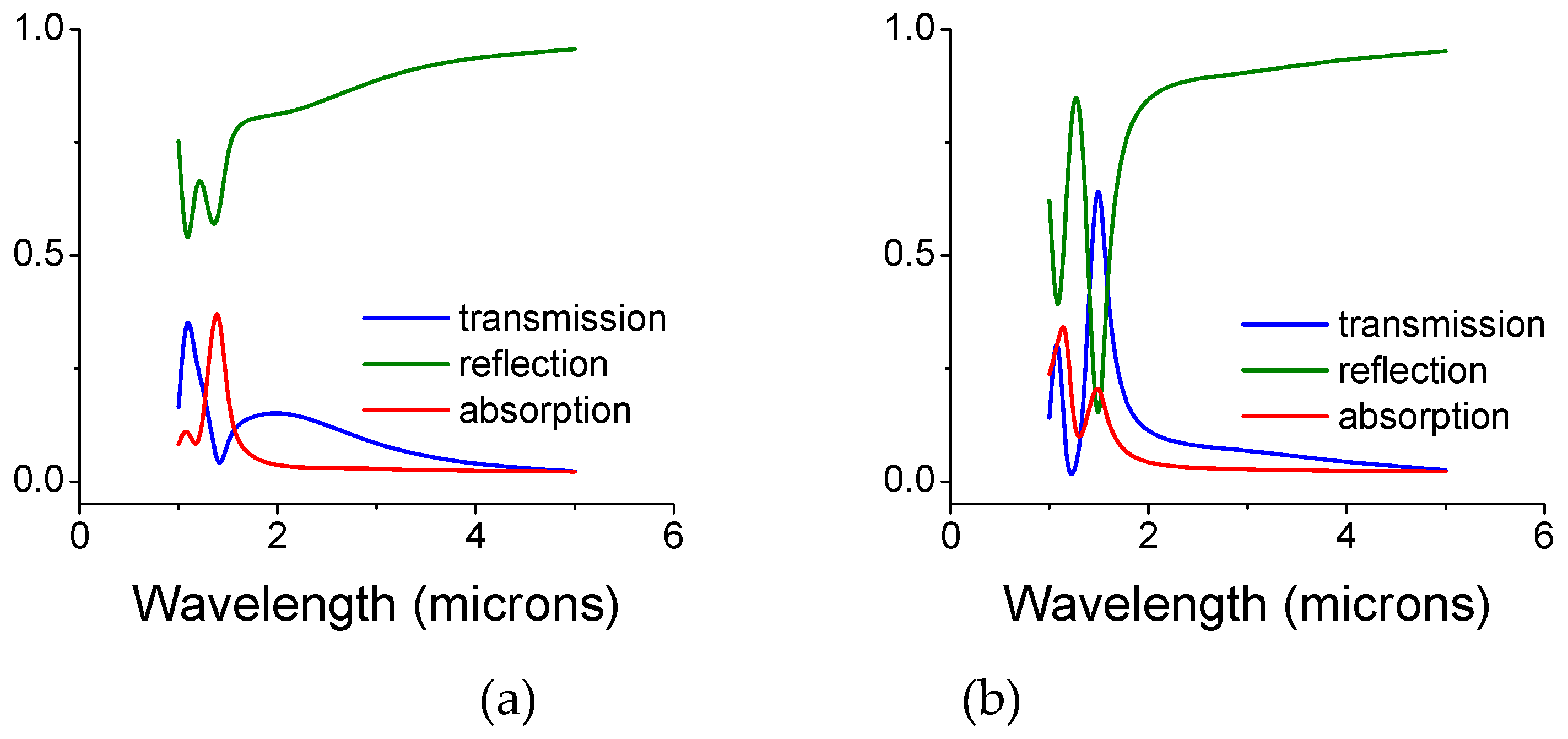
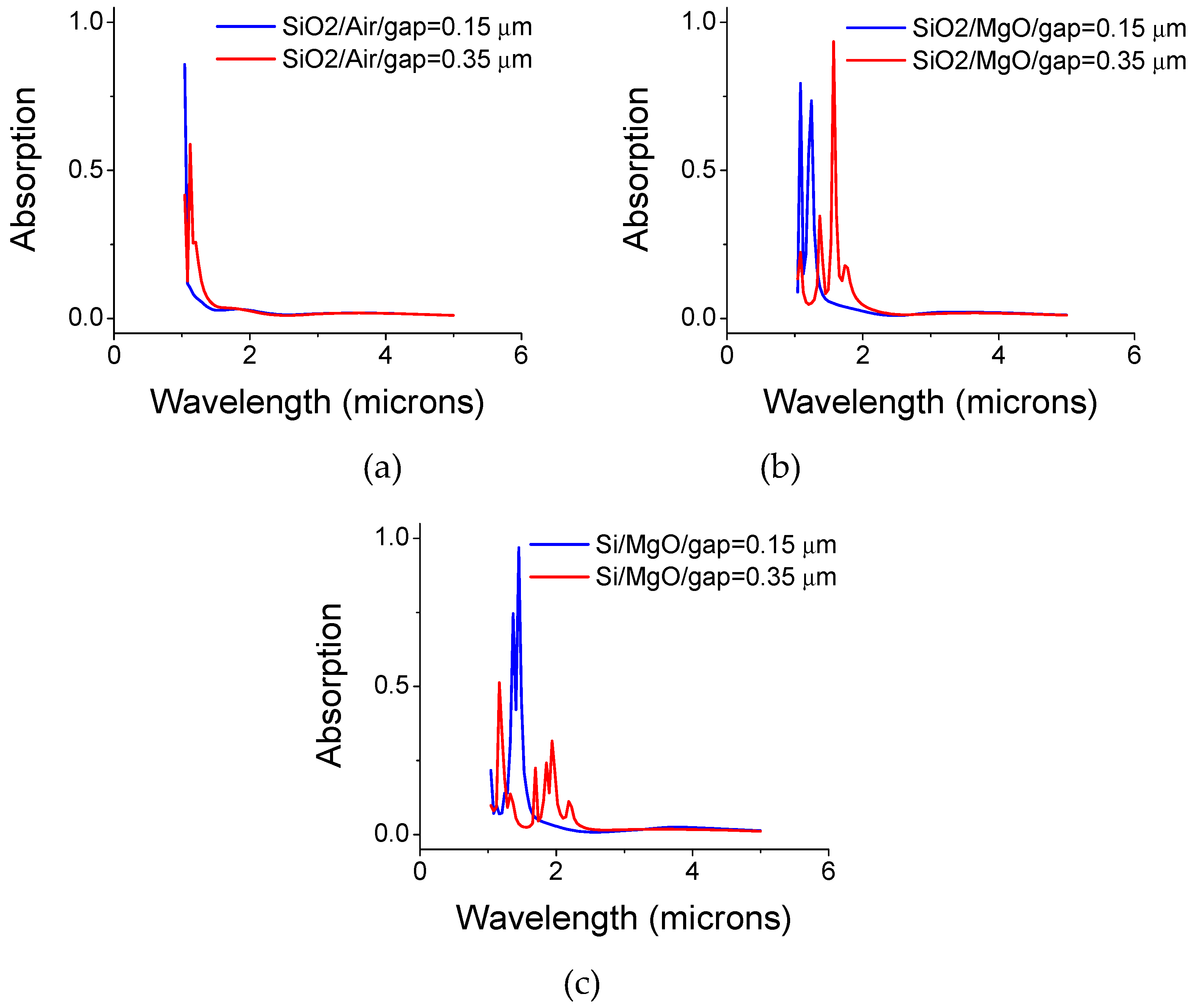
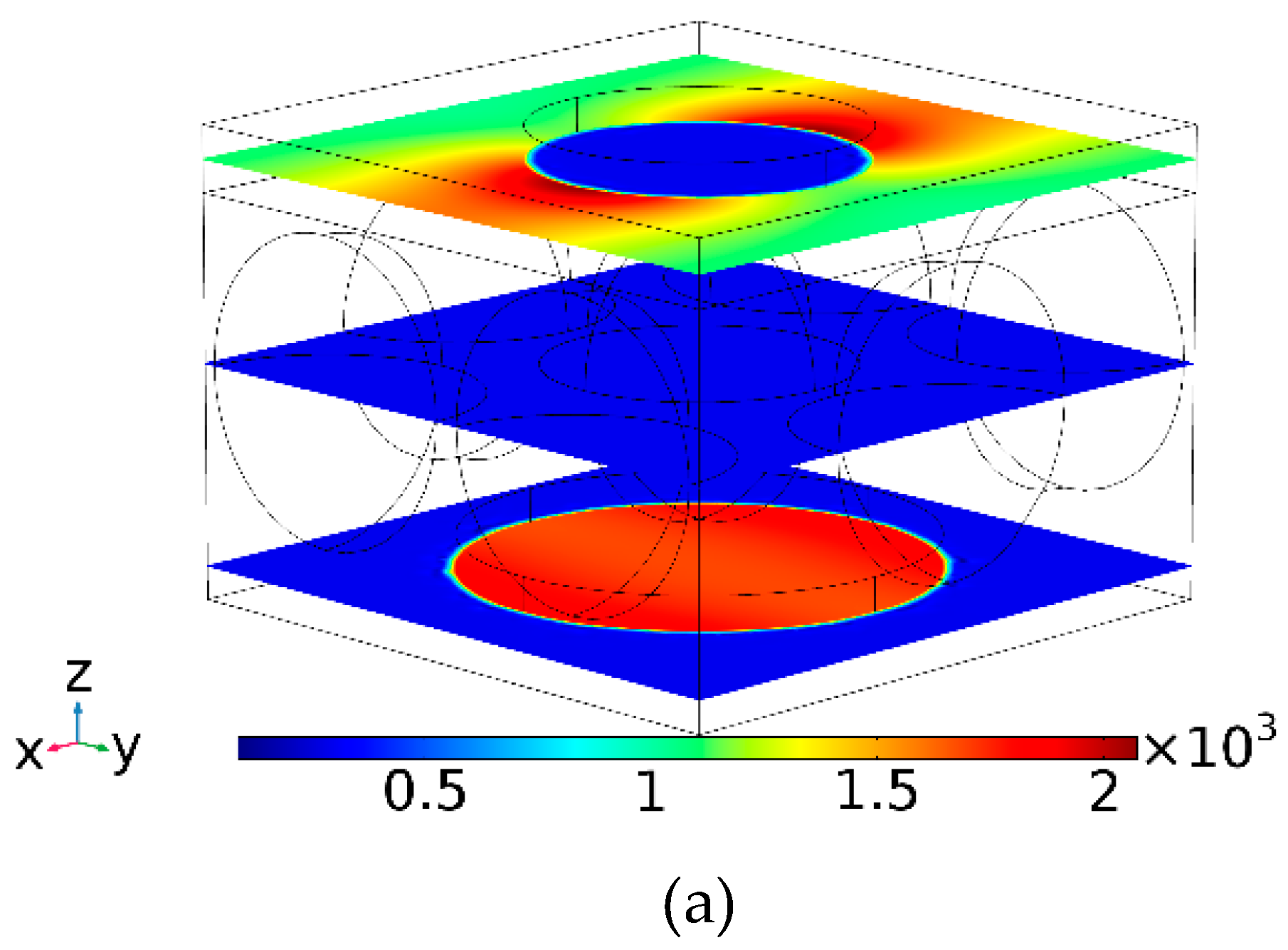
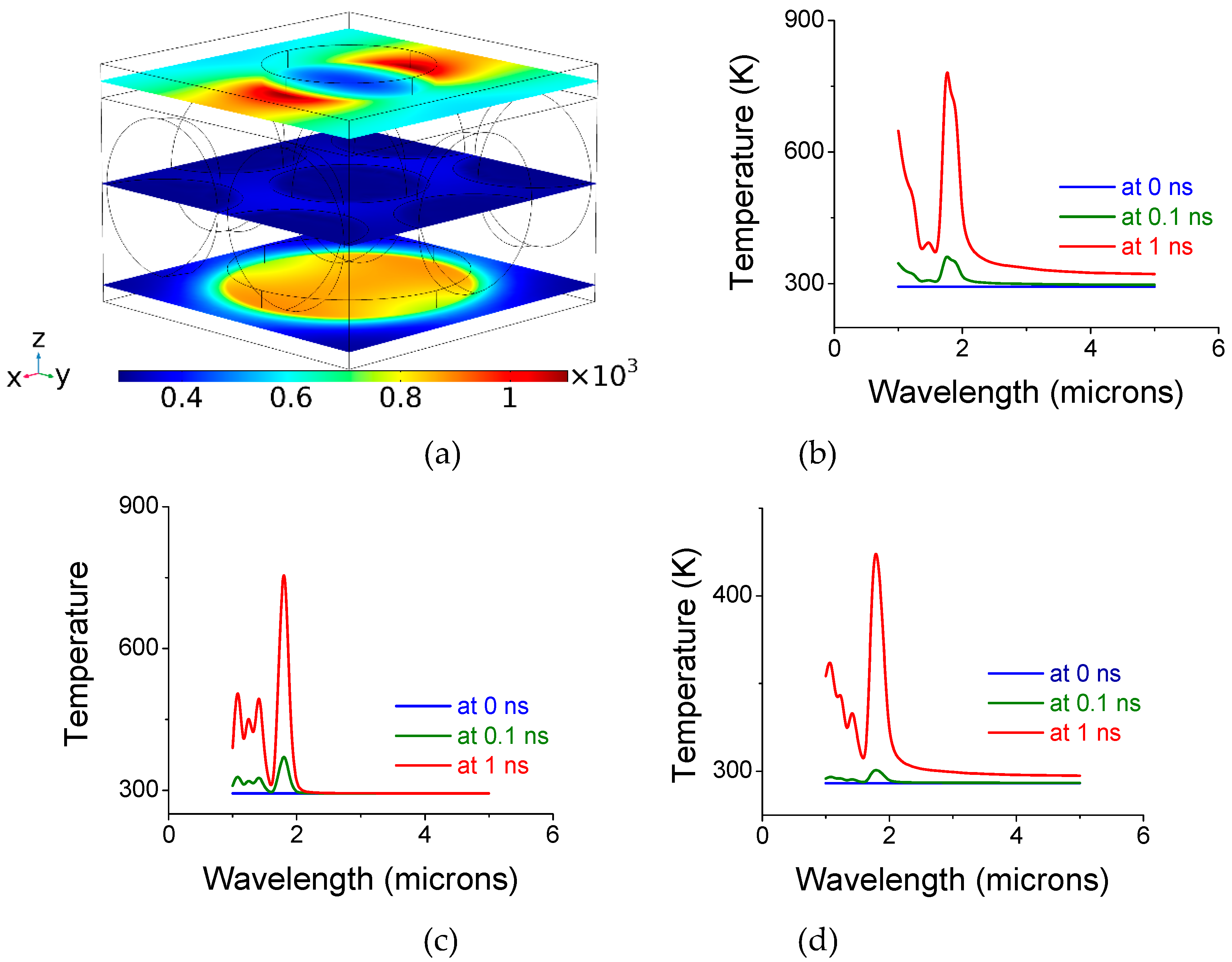
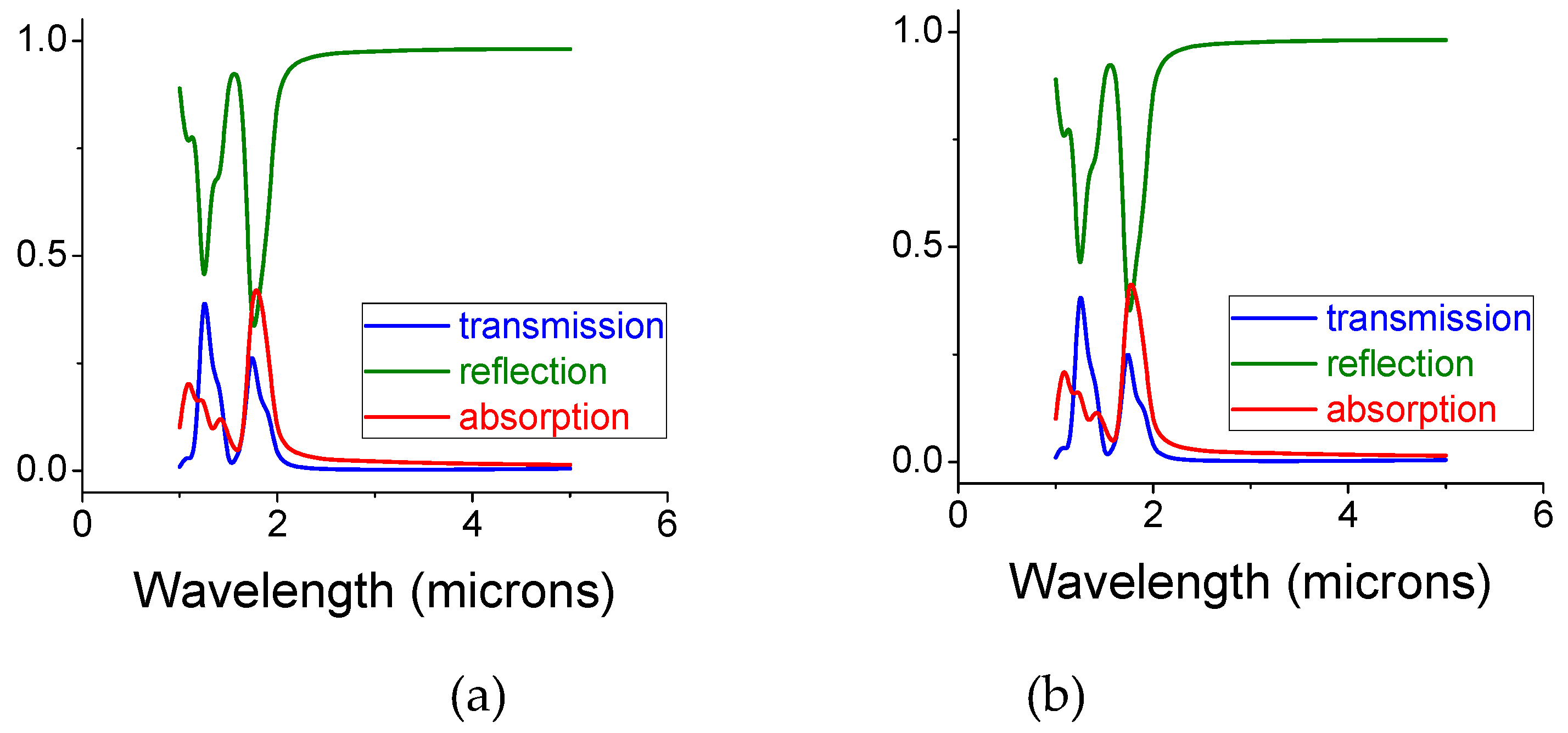
2. Simulations
3. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ulrich, R.; Renk, K.F.; Genzel, L. Tunable sub-millimeter interferometers of the Fabry-Perot type. IEEE Trans. Microw. Theory Tech. 1963, 11, 363–371. [Google Scholar] [CrossRef]
- Ressler, G.M.; Möller, K.D. Far infrared bandpass filters and measurements on a reciprocal grid. Appl. Opt. 1967, 6, 893–896. [Google Scholar] [CrossRef] [PubMed]
- Möller, K.D.; Warren, J.B.; Heaney, J.B.; Kotecki, C. Cross-shaped bandpass filters for the near- and mid-infrared wavelength region. Appl. Opt. 1996, 35, 6210–6215. [Google Scholar] [CrossRef] [PubMed]
- Munk, B.J. Frequency Sensitive Surfaces; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2000. [Google Scholar]
- Ebbesen, T.W.; Lezec, H.J.; Ghaemi, H.F.; Thio, T.; Wolff, P.A. Extraordinary optical transmission through sub-wavelength hole arrays. Nature 1998, 391, 667–669. [Google Scholar] [CrossRef]
- Lüker, A.; Hein, H.; Schulz, J.; Dambrowsky, N.; Sternberg, O.; Sweetgall, M.J.; Abdijalilov, K.; Möller, K.D.; Grebel, H. Band Pass Filters in the 1 µm Spectral Region: Thick Metal Screens. J. Infrared Tech. 2008, 51, 178–185. [Google Scholar] [CrossRef]
- Qin, F.; Ding, L.; Zhang, L.; Monticone, F.; Chum, C.C.; Deng, J.; Mei, S.; Li, Y.; Teng, J.; Hong, M.; et al. Hybrid bilayer plasmonic metasurface efficiently manipulates visible light. Sci. Adv. 2016, 2, 1–8. [Google Scholar] [CrossRef]
- Chen, C.-C. Transmission of Microwave Through Perforated Flat Plates of Finite Thickness. IEEE Trans. Microw. Theory Tech. 1973, 21, 1–7. [Google Scholar] [CrossRef]
- Moeller, K.D.; Sternberg, O.; Grebel, H.; Lalanne, P. Thick inductive cross shaped metal meshes. J. Appl. Phys. 2002, 91, 9461–9465. [Google Scholar] [CrossRef]
- Martin-Moreno, L.; Garcia-Vidal, F.J.; Lezec, H.J.; Pellerin, K.M.; Thio, T.; Pendry, J.B.; Ebbesen, T.W. Theory of Extraordinary Optical Transmission through Subwavelength Hole Arrays. Phys. Rev. Lett. 2001, 86, 1114–1117. [Google Scholar] [CrossRef] [Green Version]
- Barnes, W.L.; Murray, W.A.; Dintinger, J.; Devaux, E.; Ebbesen, T.W. Surface Plasmon Polaritons and Their Role in the Enhanced Transmission of Light through Periodic Arrays of Subwavlength Holes in a Metal Film. Phys. Rev. Lett. 2004, 92, 107401–107404. [Google Scholar] [CrossRef] [PubMed]
- Koerkamp, K.J.; Enoch, S.; Segerink, F.B.; van Hulst, N.F.; Kuipers, L. Strong Influence of Hole Shape on Extraordinary Transmssion through Periodic Arrays of Subwavelength Holes. Phys. Rev. Lett. 2004, 92, 183901–183904. [Google Scholar] [CrossRef] [PubMed]
- Fan, W.; Zhang, S.; Minhas, B.; Malloy, K.J.; Brueck, S.R.J. Enhanced Infrared Transmission through Subwavelength Coaxial Metallic Array. Phys. Rev. Lett. 2005, 94, 33902–33904. [Google Scholar] [CrossRef] [PubMed]
- Raether, H. Surface Plasmons on Smooth and RoughSurfaces and on Gratings; Springer: Berlin, Germany, 1988. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics, 2nd ed.; Wiley: New York, NY, USA, 1975. [Google Scholar]
- Rebbert, M.; Isaacson, P.; Fischer, J.; Greenhouse, M.A.; Grossman, J.; Peckerar, M.; Smith, H.A. Microstructure technology for fabrication of metal-mesh grids. Appl. Opt. 1994, 33, 1286–1292. [Google Scholar] [CrossRef] [PubMed]
- McPhedran, R.C.; Maystre, D. On the Theory and Solar Applications of Inductive Grids. Appl. Phys. 1977, 14, 1–20. [Google Scholar] [CrossRef]
- Pisano, G.; Ade, P.A.R.; Weaver, S. Polarization effects investigations in quasi-optical metal grid filters. Infrared Phys. Tech. 2006, 48, 89–100. [Google Scholar] [CrossRef]
- Banerjee, A.; Sliwinski, D.; Stewart, K.P.; Möller, K.D.; Grebel, H. Curved infrared screens. Opt. Lett. 2010, 35, 1635–1637. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- la Spada, L.; Spooner, C.; Haq, S.; Hao, Y. Curvilinear Meta Surfaces for Surface Wave Manipulation. Sci. Rep. 2019, 9, 3107. [Google Scholar] [CrossRef]
- la Spada, L.; Vegni, L. Electromagnetic Nanoparticles for Sensing and Medical Diagnostic Applications. Materials 2018, 11, 603. [Google Scholar] [CrossRef]
- Jaksic, Z.; Vukovic, S.; Matovic, J.; Tanaskovic, D. Negative Refractive Index Metasurfaces for Enhanced Biosensing. Materials 2011, 4, 1–36. [Google Scholar] [CrossRef]
- la Spada, L. Metasurfaces for Advanced Sensing and Diagnostics. Sensors 2019, 19, 355. [Google Scholar] [CrossRef]
- Liu, N.; Mesch, M.; Weiss, T.; Hentschel, M.; Giessen, H. Infrared Perfect Absorber and Its Application as Plasmonic Sensor. Nano Lett. 2010, 10, 2342–2348. [Google Scholar] [CrossRef] [PubMed]
- Kumar, V.; Walker, J.; Grebel, H. Optical Cages. Opt. Mater. X 2019, 1, 100008. [Google Scholar] [CrossRef]
- Stewart, K.P.; Hor, Y.L.; Bandyopadhyay, A.; Federici, J.; Bornefeld, M.; Mathis, Y.-L.; Sliwinski, D.; Moller, K.D.; Grebel, H. Square-Shaped Metal Screens in the IR to THz Spectral Region: Resonance Frequency, Band gap and Bandpass Filter Characteristics. J. Appl. Phys. 2008, 104, 023103. [Google Scholar]
- Moeller, K.D.; Sternberg, O.; Grebel, H.; Stewart, K.P. Near-field effects in multi-layer inductive metal meshes. Appl. Opt. 2002, 41, 1942–1948. [Google Scholar] [CrossRef]
- Shah, J.; Moeller, D.; Grebel, H.; Sternberg, O.; Tobias, J.M. Three-dimensional metallo-dielectric photonic crystals with cubic symmetry as stacks of two-dimensional screens. J. Opt. Soc. Am. JOSA A 2005, 22, 370–376. [Google Scholar] [CrossRef] [Green Version]
- Ajgaonkar, M.; Grebel, Y.Z.H.; White, C.W. Nonlinear optical properties of a coherent array of sub-micron SiO2 spheres (opal) embedded with Si nanoparticle. Appl. Phys. Lett. 1999, 75, 1532–1535. [Google Scholar] [CrossRef]
- Vijayalakshmi, S.; Grebel, H.; Yaglioglu, G.; Dorsinville, R.; White, C.W. Nonlinear dispersion properties of sub-wavelength photonic crystals. Appl. Phys. Lett. 2001, 78, 1754–1756. [Google Scholar] [CrossRef]
- Han, H.; Chen, J.; Zhang, Y.; Etienne, M.; Dorsinville, R.; Grebel, H. Distributed p–n nano-interfaces. J. Phys. D Appl. Phys. 2008, 41, 065305. [Google Scholar] [CrossRef]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Walker, J.P.; Swaminathan, V.; Haynes, A.S.; Grebel, H. Periodic Metallo-Dielectric Structures: Electromagnetic Absorption and its Related Developed Temperatures. Materials 2019, 12, 2108. https://doi.org/10.3390/ma12132108
Walker JP, Swaminathan V, Haynes AS, Grebel H. Periodic Metallo-Dielectric Structures: Electromagnetic Absorption and its Related Developed Temperatures. Materials. 2019; 12(13):2108. https://doi.org/10.3390/ma12132108
Chicago/Turabian StyleWalker, Jean Paul, Venkataraman Swaminathan, Aisha S. Haynes, and Haim Grebel. 2019. "Periodic Metallo-Dielectric Structures: Electromagnetic Absorption and its Related Developed Temperatures" Materials 12, no. 13: 2108. https://doi.org/10.3390/ma12132108
APA StyleWalker, J. P., Swaminathan, V., Haynes, A. S., & Grebel, H. (2019). Periodic Metallo-Dielectric Structures: Electromagnetic Absorption and its Related Developed Temperatures. Materials, 12(13), 2108. https://doi.org/10.3390/ma12132108