Hydrogen/Deuterium Dynamics in Hydroxyl Salts Co2(OH)3Br/Co2(OD)3Br Revealed by Muon Spin Relaxation
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Dielectric Measurement
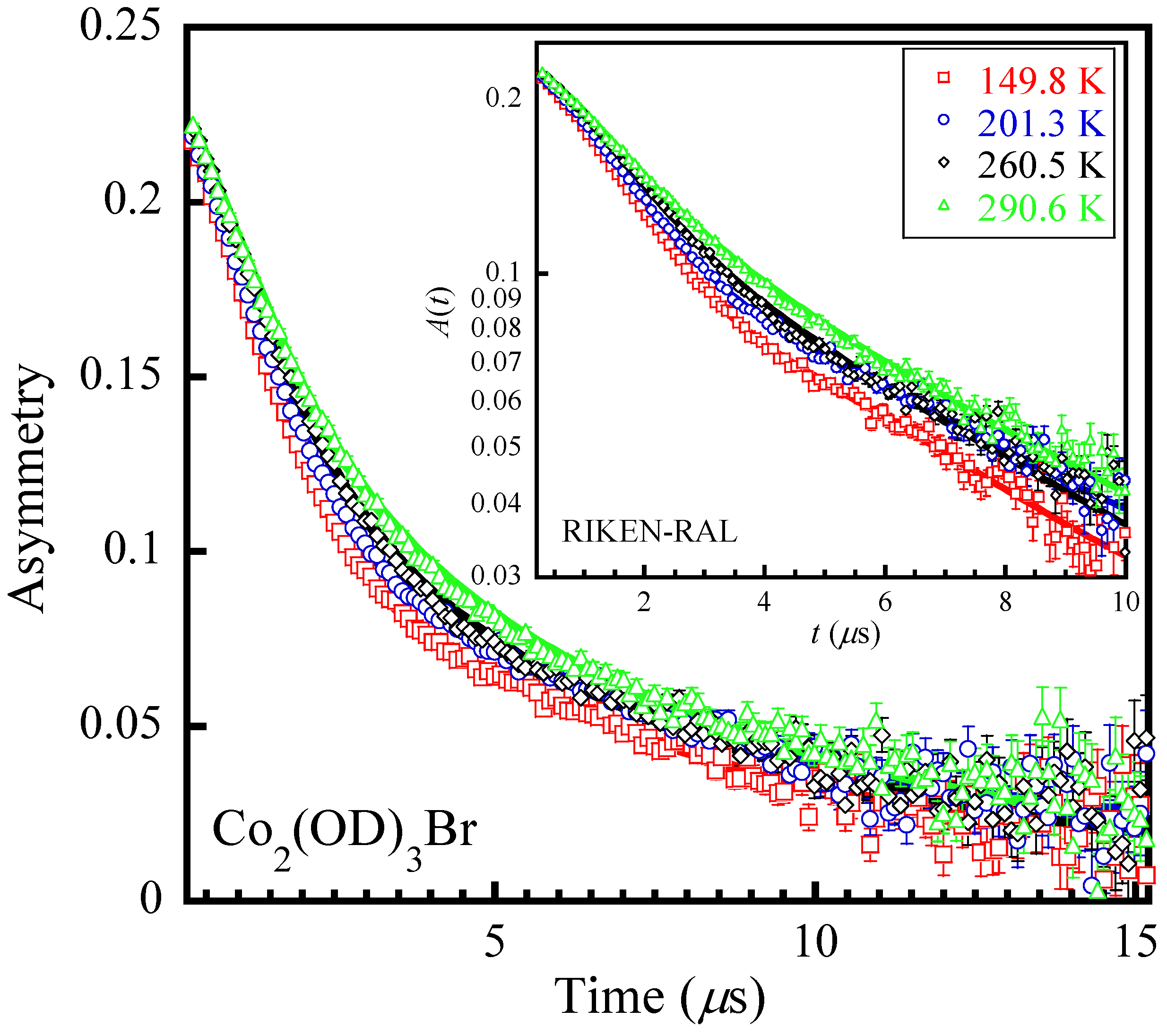
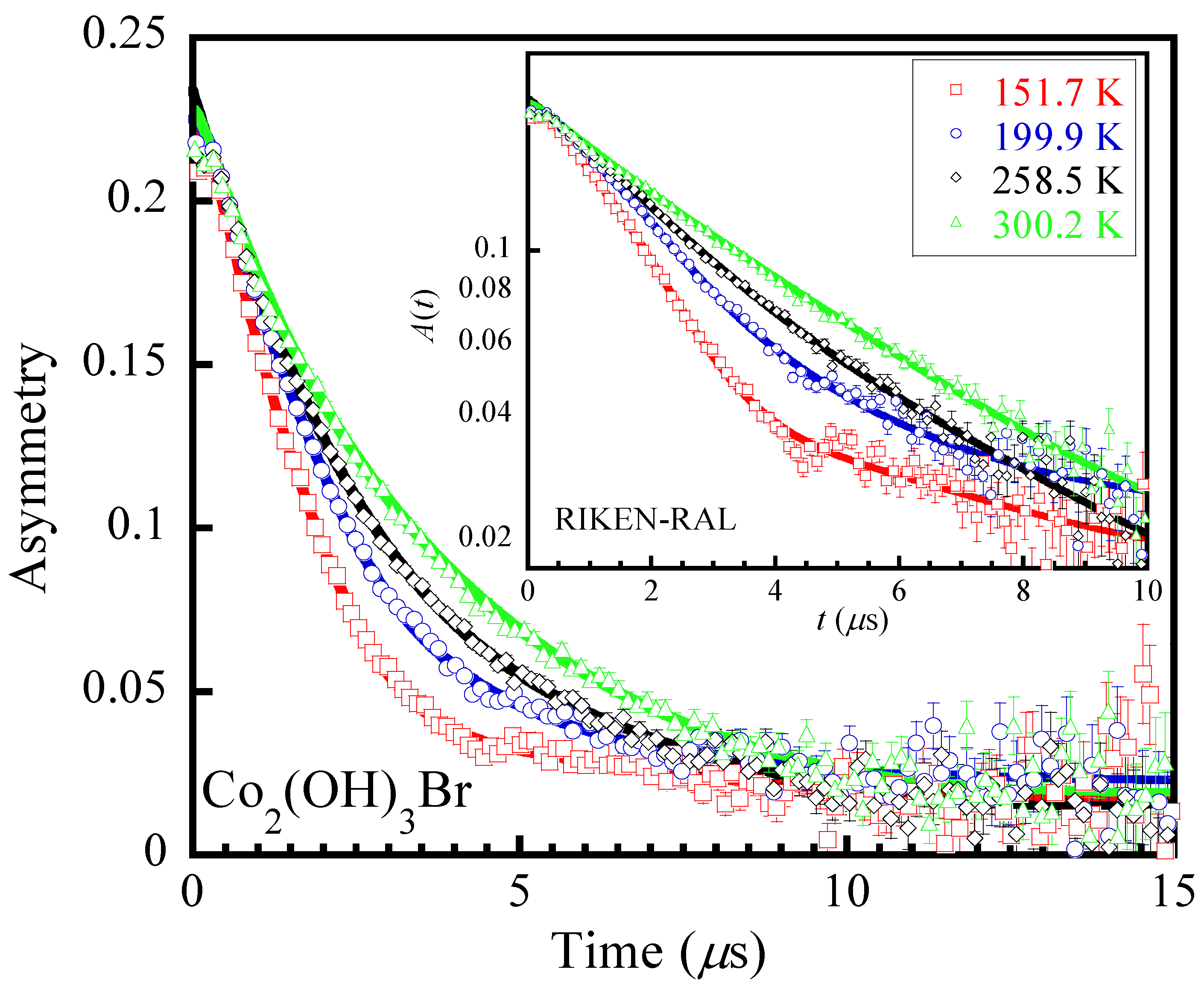
3.2. Muon Spin Relaxation (μSR)
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Valasek, J. Piezoelectric and allied phenomena in Rochelle salt. Phys. Rev. 1920, 15, 537–538. [Google Scholar]
- Cohen, R.E. Origin of ferroelectricity in perovskite oxides. Nature 1992, 358, 136. [Google Scholar] [CrossRef]
- Strukov, B.A.; Levanyuk, A.P. Ferroelectric Phenomena in Crystals: Physical Foundations; Springer: New York, NY, USA, 1998. [Google Scholar]
- Ikeda, N.; Ohsumi, H.; Ohwada, K.; Ishii, K.; Inami, T.; Kakurai, K.; Murakami, Y.; Yoshii, K.; Mori, S.; Horibe, Y.; et al. Ferroelectricity from iron valence ordering in the charge-frustrated system LuFe2O4. Nature 2005, 436, 1136. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.G.; Kubozono, H.; Nishiyama, K.; Higemoto, W.; Kawae, T.; Koda, A.; Xu, C.N. Coexistence of Long-Range Order and Spin Fluctuation in Geometrically Frustrated Clinoatacamite Cu2Cl(OH)3. Phys. Rev. Lett. 2005, 95, 057201. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.G.; Kawae, T.; Yamada, H.; Nishiyama, K.; Xu, C.N. Coexisting Ferromagnetic Order and Disorder in a Uniform System of Hydroxyhalide Co2(OH)3Cl. Phys. Rev. Lett. 2006, 97, 247204. [Google Scholar] [CrossRef] [PubMed]
- Hagihala, M.; Zheng, X.G.; Kawae, T.; Sato, T.J. Successive antiferromagnetic transitions with multi-k and noncoplanar spin order, spin fluctuations, and field-induced phases in deformed pyrochlore compound Co2(OH)3Br. Phys. Rev. B 2010, 82, 214424. [Google Scholar] [CrossRef]
- Fujihala, M.; Zheng, X.G.; Oohara, Y.; Morodomi, H.; Kawae, T.; Matsuo, A.; Kindo, K. Short-range correlations and persistent spin fluctuations in the undistorted kagome lattice Ising antiferromagnet Co3Mg(OH)6Cl2. Phys. Rev. B 2012, 85, 012402. [Google Scholar] [CrossRef]
- Zheng, X.G.; Fujihala, M.; Kitajima, S.; Maki, M.; Kato, K.; Takata, M.; Xu, C.N. Strong magnetic-dielectric-lattice coupling in transition metal hydroxyhalides and ferroelectric response in rhombohedral Co2(OD)3X (X = Cl, Br). Phys. Rev. B 2013, 87, 174102. [Google Scholar] [CrossRef]
- Kimura, T.; Goto, T.; Shintani, H.; Ishizaka, K.; Arima, T.; Tokura, Y. Magnetic control of ferroelectric polarization. Nature 2003, 426, 55. [Google Scholar] [CrossRef]
- Bhadram, V.S.; Rajeswaran, B.; Sundaresan, A.; Narayana, C. Spin-phonon coupling in multiferroic RCrO3 (R-Y, Lu, Gd, Eu, Sm): A Raman study. Eur. Phys. Lett. 2013, 101, 17008. [Google Scholar] [CrossRef]
- Xu, X.L.; Meng, D.D.; Zheng, X.G.; Yamauchi, I.; Watanabe, I.; Guo, Q.X. Critical slowing of quantum atomic deuterium/hydrogen with features of multiferroicity in the geometrically frustrated system Co2(OD)3Cl/Co2(OH)3Cl. Phys. Rev. B 2017, 95, 024111. [Google Scholar] [CrossRef]
- Meng, D.D.; Zheng, X.G.; Liu, X.D.; Xu, X.L.; Guo, Q.X. Deuterium ordering found in new ferroelectric compound Co2(OD)3Cl. Mater. Res. Express 2015, 2, 076101. [Google Scholar] [CrossRef]
- Matsuzaki, T.; Ishida, K.; Nagamine, K.; Watanabe, I.; Eaton, G.H.; Williams, W.G. The RIKEN-RAL pulsed Muon Facility. Nucl. Instrum. Methods Phys. Res. Sect. A 2001, 465, 365–383. [Google Scholar] [CrossRef]
- Garwin, R.L.; Lederman, L.M.; Weinrich, M. Observations of the Failure of Conservation of Parity and Charge Conjugation in Meson Decays: The Magnetic Moment of the Free Muon. Phys. Rev. 1957, 105, 1415–1417. [Google Scholar] [CrossRef]
- Yaouanc, A.; De Reotier, P.D. Muon Spin Rotation, Relaxation, and Resonance: Applications to Condensed Matter; International Series of Monographs on Physics; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Suter, A.; Wojek, B.M. Musrfit: A free platform-independent framework for μSR data analysis. Phys. Procedia 2012, 30, 69–73. [Google Scholar] [CrossRef]
- Cross, L.E. Relaxor Ferroelectrics. Ferroelectrics 1987, 76, 241–267. [Google Scholar] [CrossRef]
- Cross, L.E. Relaxor Ferroelectrics: An overview. Ferroelectrics 1994, 151, 305–320. [Google Scholar] [CrossRef]
- Hayano, R.S.; Uemura, Y.J.; Imazato, J.; Nishida, N.; Yamazaki, T.; Kubo, R. Zero-and low-field spin relaxation studied by positive muons. Phys. Rev. B 1979, 20, 850. [Google Scholar] [CrossRef]
- Uemura, Y.J.; Hayano, R.S.; Imazato, J.; Nishida, N.; Yamazaki, T. Non-secular part of nuclear dipolar broadening detected by zero-field spin relaxation of positive muon. Solid State Commun. 1979, 31, 731–734. [Google Scholar] [CrossRef]
- Morenzoni, E.; Luetkens, H.; Suter, A.; Eshchenko, D.; Khasanov, R.; Amato, A.; Prokscha, T.; Scheuermann, R. μSR studies of hydrogen-bonded ferroelectrics and antiferroelectrics. Phys. B 2007, 388, 274. [Google Scholar] [CrossRef]
- Khomskii, D.I. Magnetism and Ferroelectricity: Why do They so Seldom Coexist? Available online: http://adsabs.harvard.edu/abs/2001APS..MARC21002K (accessed on 2 July 2019).
- Cheong, S.W.; Mostovoy, M. Multiferroics: A magnetic twist for ferroelectricity. Nat. Mater. 2007, 6, 13–20. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.L.; Meng, D.D.; Zheng, X.G.; Guo, Q.X. Hydrogen/deuterium ordering revealed by Raman spectroscopy in a new multiferroic compounds Co2(OH)3Br/Co2(OD)3Br. unpublished.
- Khomskii, D. Classifying multiferroics: Mechanisms and effects. Physics 2009, 2, 20. [Google Scholar] [CrossRef]




© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.-L.; Zheng, X.-G.; Watanabe, I. Hydrogen/Deuterium Dynamics in Hydroxyl Salts Co2(OH)3Br/Co2(OD)3Br Revealed by Muon Spin Relaxation. Materials 2019, 12, 2135. https://doi.org/10.3390/ma12132135
Xu X-L, Zheng X-G, Watanabe I. Hydrogen/Deuterium Dynamics in Hydroxyl Salts Co2(OH)3Br/Co2(OD)3Br Revealed by Muon Spin Relaxation. Materials. 2019; 12(13):2135. https://doi.org/10.3390/ma12132135
Chicago/Turabian StyleXu, Xing-Liang, Xu-Guang Zheng, and Isao Watanabe. 2019. "Hydrogen/Deuterium Dynamics in Hydroxyl Salts Co2(OH)3Br/Co2(OD)3Br Revealed by Muon Spin Relaxation" Materials 12, no. 13: 2135. https://doi.org/10.3390/ma12132135
APA StyleXu, X.-L., Zheng, X.-G., & Watanabe, I. (2019). Hydrogen/Deuterium Dynamics in Hydroxyl Salts Co2(OH)3Br/Co2(OD)3Br Revealed by Muon Spin Relaxation. Materials, 12(13), 2135. https://doi.org/10.3390/ma12132135




