Study on Permeability Stability of Sand-Based Microporous Ceramic Filter Membrane
Abstract
:1. Introduction
2. Experimental Procedure
2.1. Sample Preparation
2.2. Sample Characterizations
2.2.1. Mechanical Performance Characterization
2.2.2. Hydraulic Performance Characterization
3. Results and Analysis
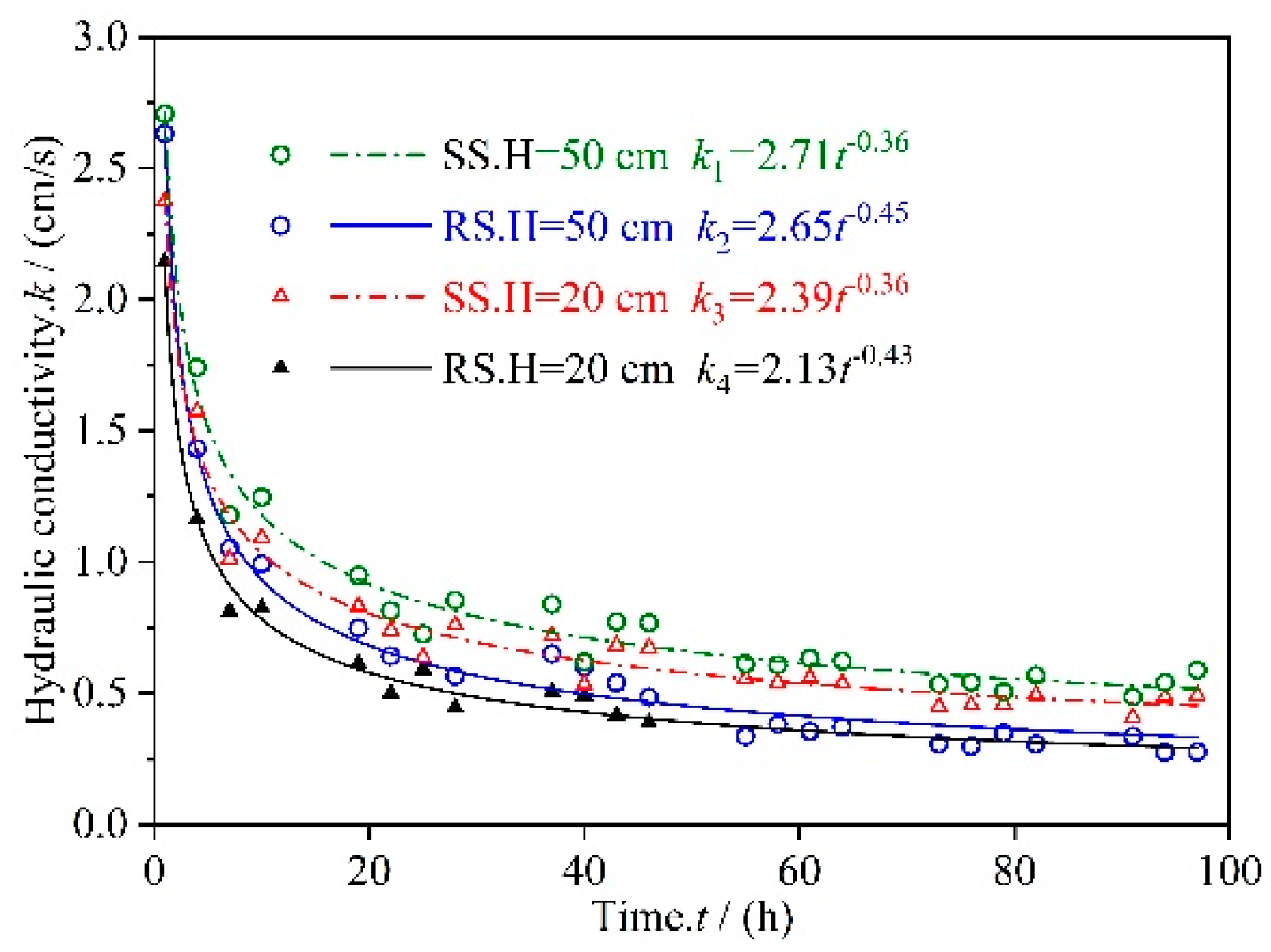
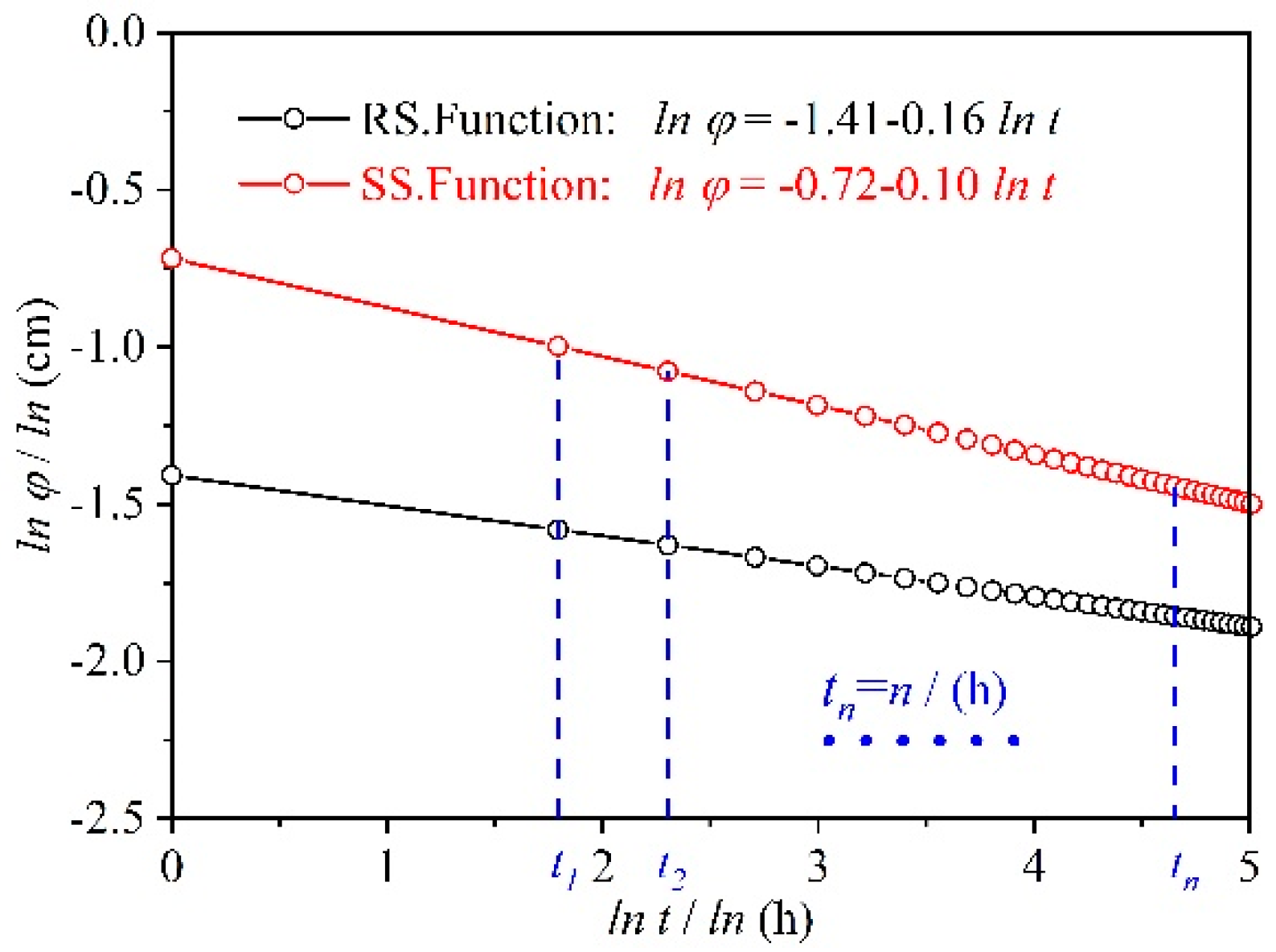
3.1. Permeate Flux Q Changes with Time t
3.2. Analysis of Factors that Affect Changes in Permeate Flux
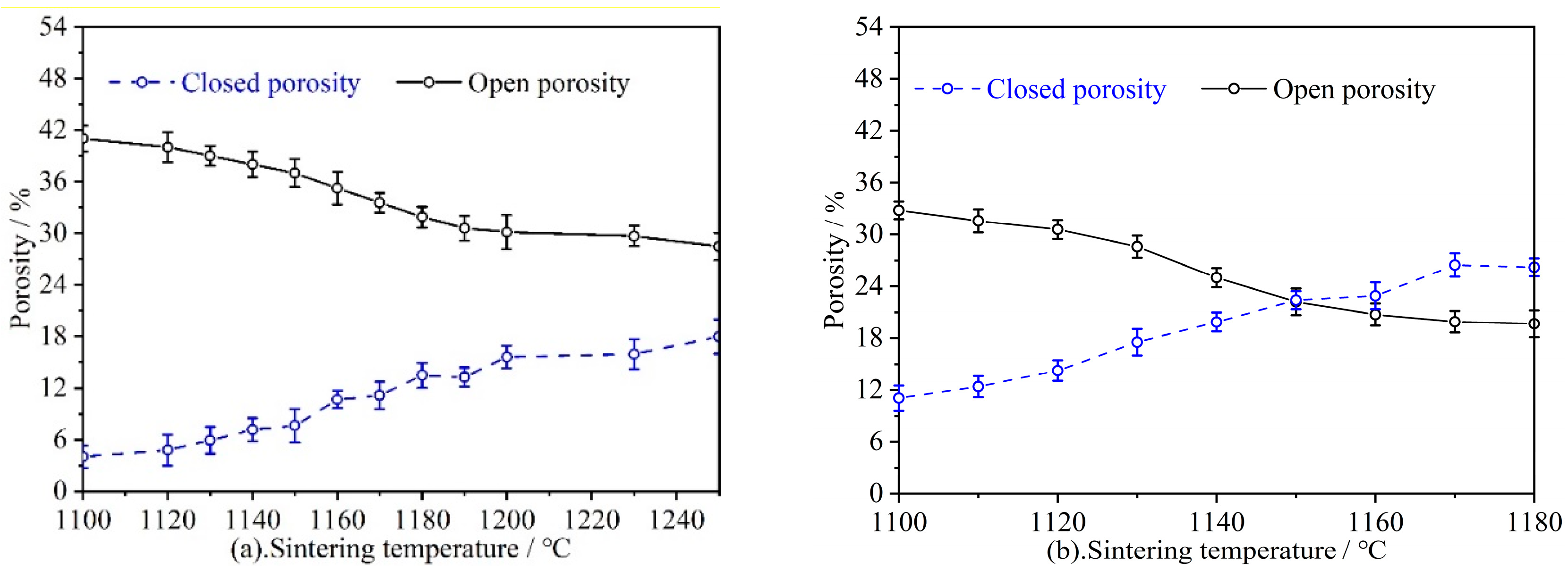
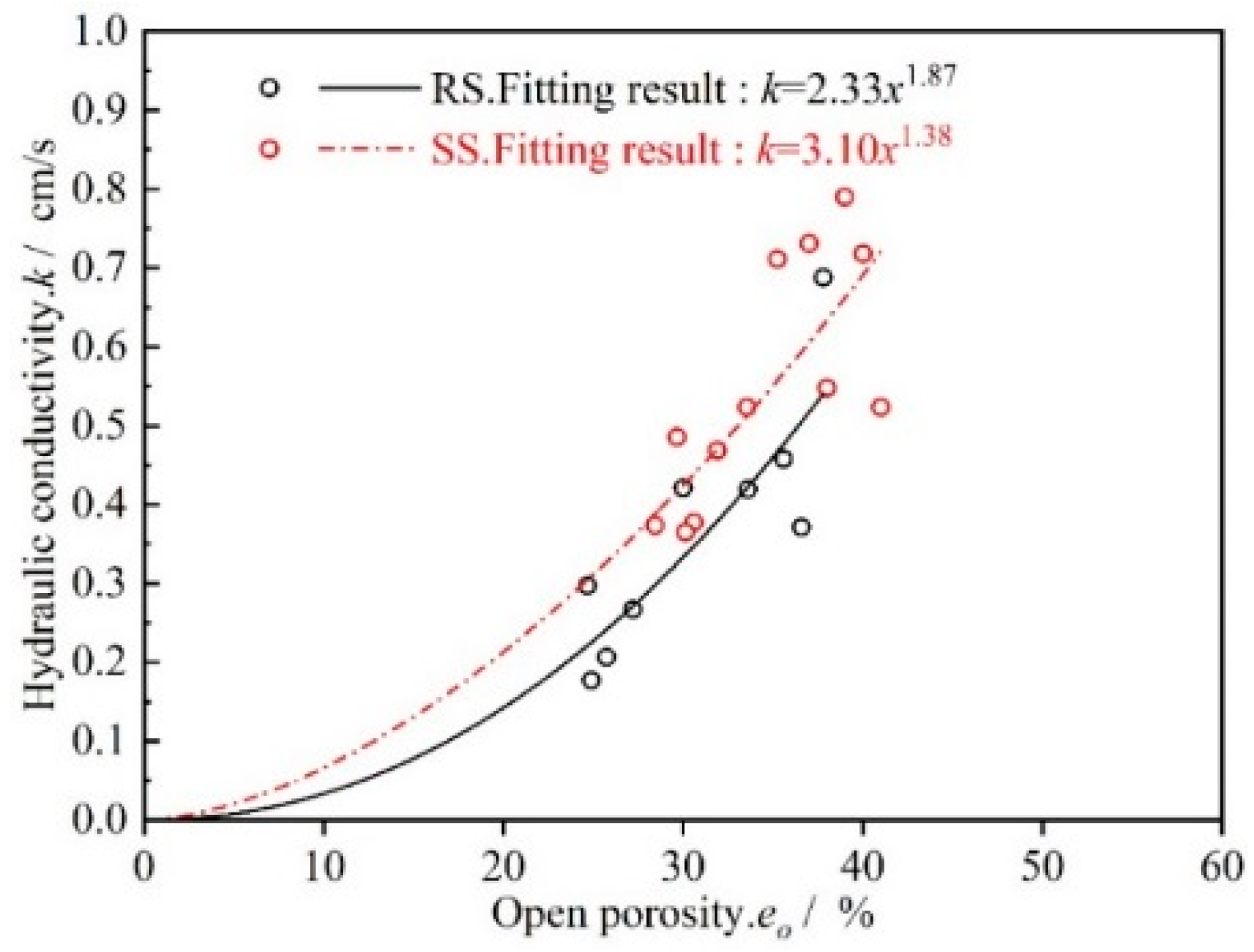
3.2.1. Porosity
3.2.2. Microstructure
3.2.3. Phase Composition
4. Approaches for Improving the Permeability of Ceramic Membranes
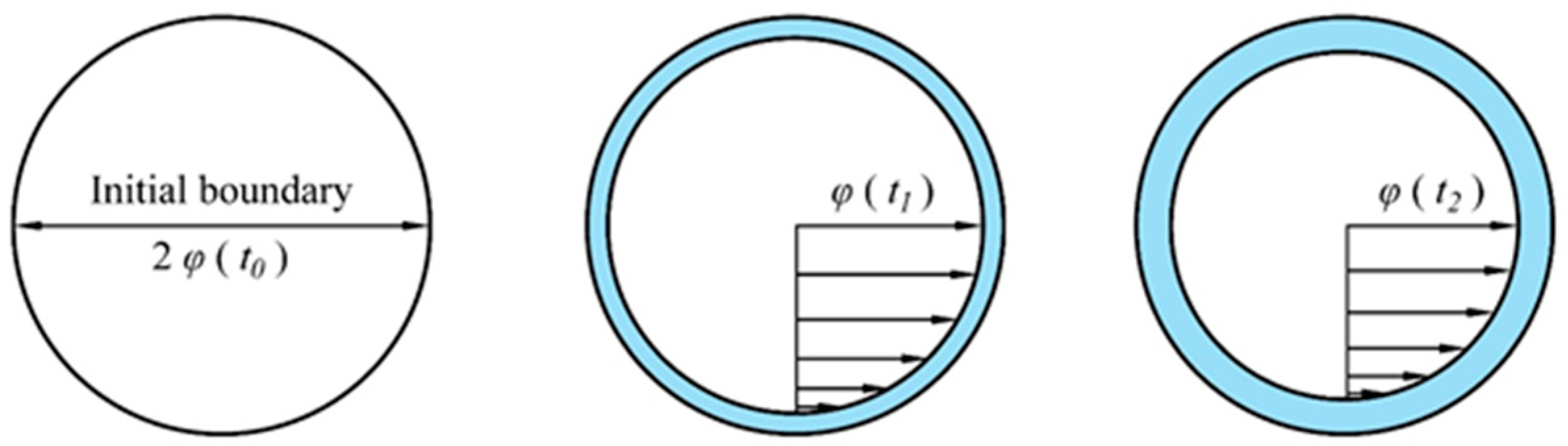
4.1. Theoretical Analysis of Permeate Flux Changes
4.2. Approaches for Improving Permeate Flux
4.2.1. Adjusting Porosity
4.2.2. Improving Surface Properties of Materials
4.2.3. Selecting an Appropriate Matrix Material and Pore Former
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Karnik, B.S.; Davies, S.H.; Chen, K.C.; Jaglowski, D.R.; Baumann, M.J.; Masten, S.J. Effects of ozonation on the permeate flux of nanocrystalline ceramic membranes. Water Res. 2005, 39, 728–734. [Google Scholar] [CrossRef] [PubMed]
- Grant, G.A.; Fisher, P.R.; Barrett, J.E.; Wilson, P.C. Removal of paclobutrazol from irrigation water using granular-activated carbon. Irrig. Sci. 2018, 36, 159–166. [Google Scholar] [CrossRef]
- Nakatsuka, S.; Nakate, I.; Miyano, T. Drinking water treatment by using ultrafiltration hollow fiber membranes. Desalination 1996, 106, 55–61. [Google Scholar] [CrossRef]
- Battistoni, P.; Cola, E.; Fatone, F.; Bolzonella, D.; Eusebi, A.L. Micropollutants Removal and Operating Strategies in Ultrafiltration Membrane Systems for Municipal Wastewater Treatment: Preliminary Results. Ind. Eng. Chem. Res. 2007, 46, 6716–6723. [Google Scholar] [CrossRef]
- Hofs, B.; Ogier, J.; Vries, D.; Beerendonk, E.F.; Cornelissen, E.R. Cornelissen, Comparison of ceramic and polymeric membrane permeability and fouling using surface water. Sep. Purif. Technol. 2011, 79, 365–374. [Google Scholar] [CrossRef]
- Sondhi, R.; Bhave, R.; Jung, G. Applications and benefits of ceramic membranes. Membr. Technol. 2003, 11, 5–8. [Google Scholar] [CrossRef]
- Processing Guide for Polymer Membranes. Available online: https://www.solvay.com/sites/g/files/srpend221/files/2018-08/Membranes-Processing-Guide_EN-v4.6_0.pdf (accessed on 10 January 2013).
- Komolikov, Y.I.; Blaginina, L.A. Technology of ceramic micro and ultrafiltration membranes (review). Refract. Ind. Ceram. 2002, 43, 181–187. [Google Scholar] [CrossRef]
- Ohji, T. Macro-porous ceramics: Processing and properties. Int. Mater. Rev. 2012, 57, 115–131. [Google Scholar] [CrossRef]
- Galassi, C. Processing of porous ceramics: Piezoelectric. J. Eur. Ceram. Soc. 2006, 26, 2951–2958. [Google Scholar] [CrossRef]
- Elomari, H.; Achiou, B.; Karim, A.; Ouammou, M.; Albizane, A.; Bennazha, J.; Alami.Younssi, S.; Elamrani, I. Influence of starch content on the properties of low cost microfiltration membranes. J. Asian Ceram. Soc. 2017, 5, 313–319. [Google Scholar] [CrossRef]
- Naito, M.; Nakahira, K.; Fukuda, Y.; Mori, H.; Tsubaki, J. Process conditions on the preparation of supported microporous SiO2 membranes by sol-gel modification techniques. J. Membr. Sci. 1997, 129, 263–269. [Google Scholar] [CrossRef]
- Song, C.L.; Liu, G. Influence of water vapor on silica membrane: Adsorption properties and seepage effect. Chin. J. Chem. Phys. 2015, 28, 345. [Google Scholar] [CrossRef]
- Sui, X.; Huang, X. The characterization and water purification behavior of gradient ceramic membranes. Sep. Purif. Technol. 2003, 32, 73–79. [Google Scholar] [CrossRef]
- Ha, J.H.; Abbas Bukhari, S.Z.; Lee, J.; Song, I.H. The preparation and characterizations of an alumina support layer as a free-standing membrane for microfiltration. Ceram. Int. 2015, 41, 13372–13380. [Google Scholar] [CrossRef]
- Lee, H.; Kim, S.G.; Choi, J.S.; Kim, S.K.; Oh, H.J.; Lee, W.T. Effects of water temperature on fouling and flux of ceramic membranes for wastewater reuse. Desalin. Water Treat. 2013, 51, 5222–5230. [Google Scholar] [CrossRef]
- Cui, Z.; Peng, W.; Fan, Y.; Xing, W.; Xu, N. Ceramic membrane filtration as seawater RO pre-treatment: Influencing factors on the ceramic membrane flux and quality. Desalin. Water Treat. 2013, 51, 2575–2583. [Google Scholar] [CrossRef]
- Li, J.; Jing, Z.; Zha, F.; Yang, Y.; Wang, Q.; Lei, Z. Facile spray-coating process for the fabrication of tunable adhesive superhydrophobic surfaces with heterogeneous chemical compositions used for selective transportation of microdroplets with different volumes. ACS Appl. Mater. Interfaces 2014, 6, 8868–8877. [Google Scholar] [CrossRef]
- Söz, C.K.; Yilgör, E.; Yilgör, I. Influence of the coating method on the formation of superhydrophobic silicone-urea surfaces modified with fumed silica nanoparticles. Prog. Org. Coat. 2015, 84, 143–152. [Google Scholar] [CrossRef]
- Li, D.; Wang, Y.; Xia, Y. Electrospinning Nanofibers as Uniaxially Aligned Arrays and Layer-by-Layer Stacked Films. Adv. Mater. 2004, 16, 361–366. [Google Scholar] [CrossRef]
- Reina, A.; Jia, X.; Ho, J.; Nezich, D.; Son, H.; Bulovic, V.; Dresselhaus, M.S.; Kong, J. Large Area, Few-Layer Graphene Films on Arbitrary Substrates by Chemical Vapor Deposition. Nano Lett. 2009, 9, 30–35. [Google Scholar] [CrossRef]
- Milenkovic, S.; Smith, A.J.; Hassel, A.W. Single Crystalline Molybdenum Nanowires, Nanowire Arrays and Nanopore Arrays in Nickel-Aluminium. J. Nanosci. Nanotechnol. 2009, 9, 3411–3417. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Zhai, J.; Liu, H.; Song, Y.; Jiang, L.; Zhu, D. Electrochemical Deposition of Conductive Superhydrophobic Zinc Oxide Thin Films. J. Phys. Chem. B 2003, 107, 9954–9957. [Google Scholar] [CrossRef] [Green Version]
- Cai, Y.; Wu, P.; Zhu, D.; Li, X.; Zhang, L.; Chen, J. Preparation technology optimization of diatomite porous ceramic irrigation emitter. Trans. Chinese Soc. Agr. Eng. 2015, 31, 70–76. [Google Scholar]
- Zhao, F.; Ge, T.; Gao, J.; Chen, L.; Liu, X. Transient liquid phase diffusion process for porous mullite ceramics with excellent mechanical properties. Ceram. Int. 2018, 44, 19123–19130. [Google Scholar] [CrossRef]
- Mattos, T.G.; Reis, F.D.A. Effects of diffusion and particle size in a kinetic model of catalyzed reactions. J. Catal. 2009, 263, 67–74. [Google Scholar] [CrossRef] [Green Version]
- Cocuzzi, D.A.; Laughner, J.W. Effects of surface abrasion and impurity levels on stress-induced Dauphine twinning in alpha quartz. In Proceedings of the 43rd Annual Symposium on Frequency Control, Denver, CO, USA, 31 May–2 June 1989. [Google Scholar]
- Hao, P.F.; Yao, Z.H.; He, F.; Zhu, K.Q. Experimental investigation of water flow in smooth and rough silicon microchannels. J. Micromech. Microeng. 2006, 16, 1397. [Google Scholar] [CrossRef]
- Zawrah, M.F.; Hamzawy, E.M.A. Effect of cristobalite formation on sinterability, microstructure and properties of glass/ceramic composites. Ceram. Int. 2002, 28, 123–130. [Google Scholar] [CrossRef]
- Spearing, D.R.; Farnan, I.; Stebbins, J.F. Dynamics of the α-β phase transitions in quartz and cristobalite as observed by in-situ high temperature 29Si and 17O NMR. Phys. Chem. Miner. 1992, 19, 307–321. [Google Scholar] [CrossRef]
- Vilaça, F.N.; de Camargo, A.P.; Frizzone, J.A.; Mateos, L.; Koech, R. Minor losses in start connectors of microirrigation laterals. Irrig. Sci. 2017, 35, 227–240. [Google Scholar] [CrossRef]
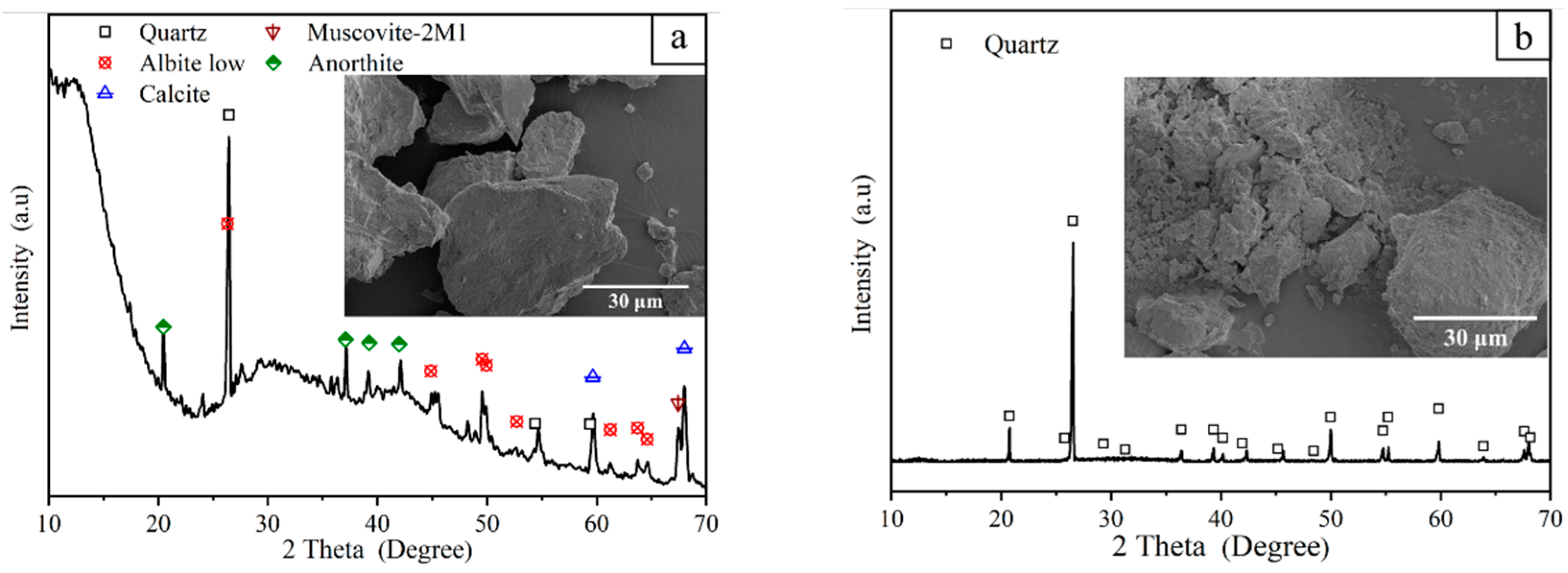
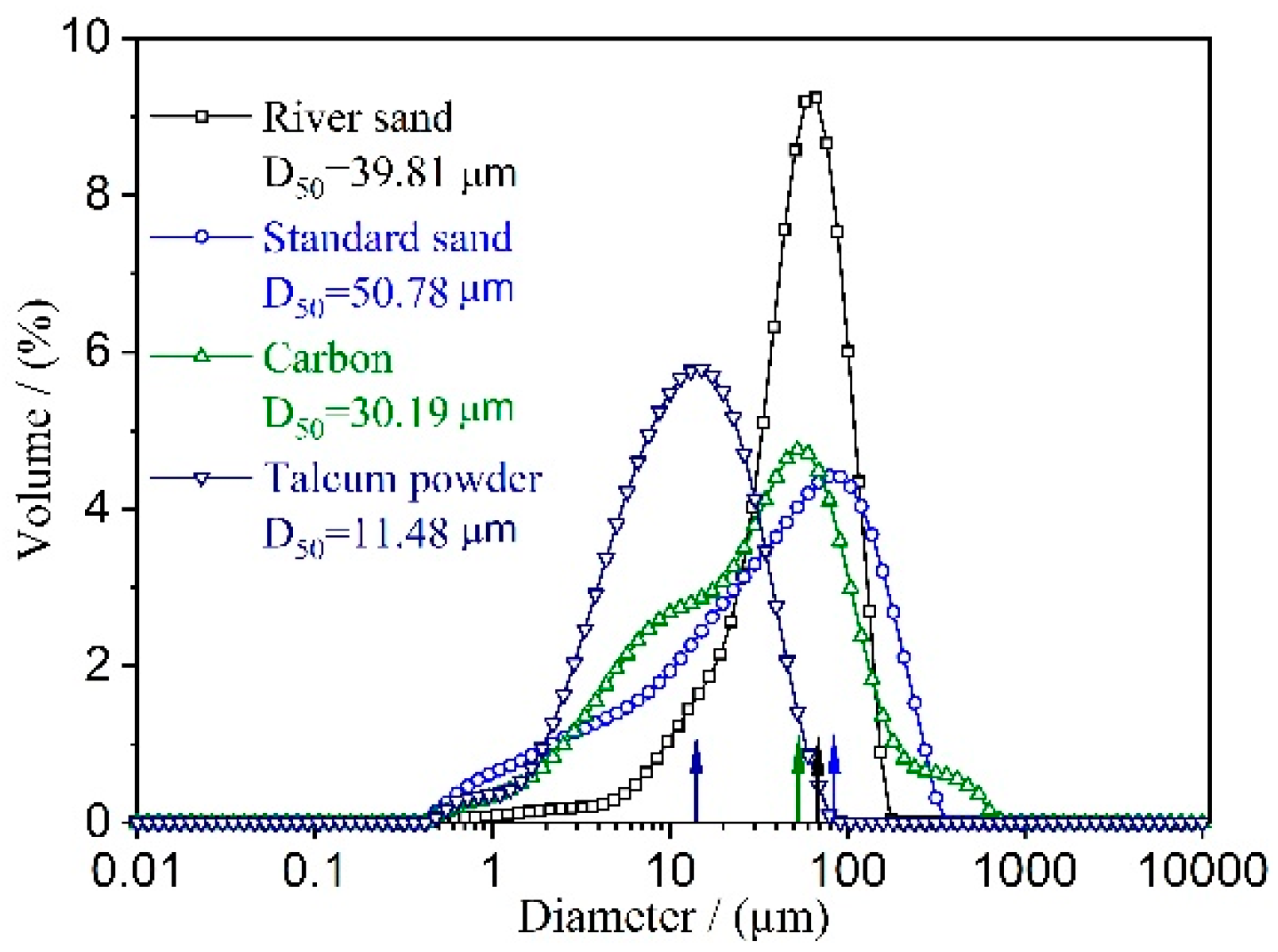
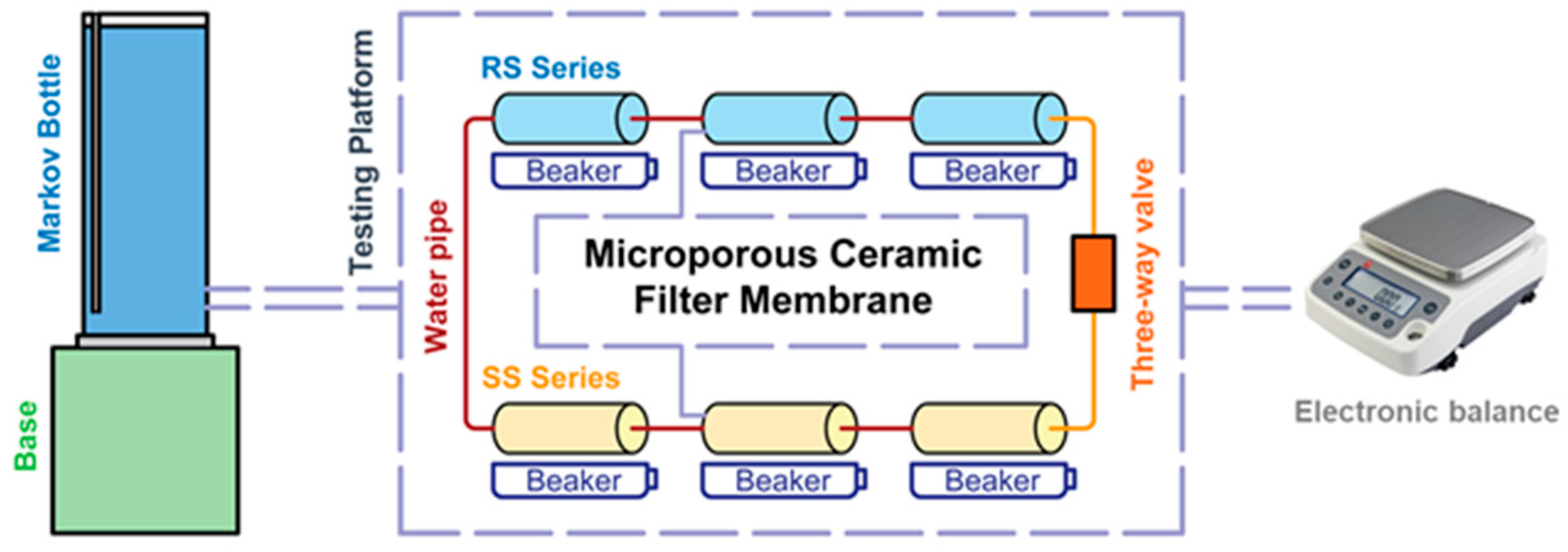
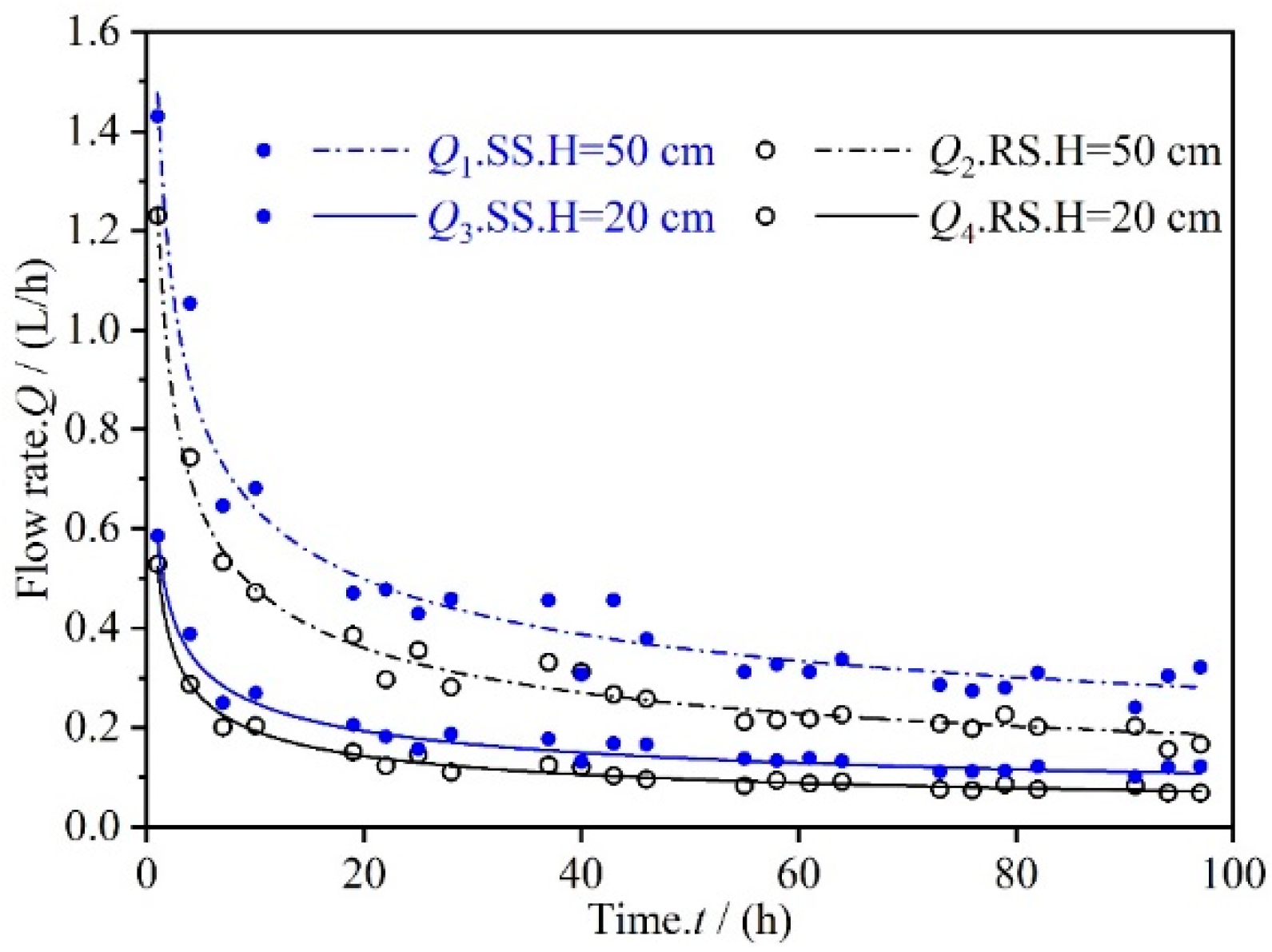


| Raw Material | Chemical Composition | |||||||
|---|---|---|---|---|---|---|---|---|
| ω(SiO2) % | ω(Al2O3) % | ω(Fe2O3) % | ω(CaO) % | ω(MgO) % | ω(K2O) % | ω(Na2O) % | Others | |
| River sand | 90.34 | 1.92 | 0.37 | 2.33 | 0.24 | 0.93 | 0.82 | 3.29 |
| Standard sand | 98.88 | - | - | - | - | - | - | 1.12 |
| Samples | ω(Standard Sand) % | ω(River Sand) % | ω(Alumina) % | ω(Slag) % | ω(Talcum) % | Total |
|---|---|---|---|---|---|---|
| RS | - | 63.17 | 7.46 | 5.83 | 25.54 | 100 |
| SS | 63.17 | - | 7.46 | 5.83 | 25.54 | 100 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, W.; Zhang, L.; Wu, P.; Cai, Y.; Zhao, X.; Yao, C. Study on Permeability Stability of Sand-Based Microporous Ceramic Filter Membrane. Materials 2019, 12, 2161. https://doi.org/10.3390/ma12132161
Zhou W, Zhang L, Wu P, Cai Y, Zhao X, Yao C. Study on Permeability Stability of Sand-Based Microporous Ceramic Filter Membrane. Materials. 2019; 12(13):2161. https://doi.org/10.3390/ma12132161
Chicago/Turabian StyleZhou, Wei, Lin Zhang, Pute Wu, Yaohui Cai, Xiao Zhao, and Chunping Yao. 2019. "Study on Permeability Stability of Sand-Based Microporous Ceramic Filter Membrane" Materials 12, no. 13: 2161. https://doi.org/10.3390/ma12132161





