Shear Behaviors of RC Beams Externally Strengthened with Engineered Cementitious Composite Layers
Abstract
1. Introduction
2. ECC Material Properties
2.1. Compressive Strength
2.2. Direct Tensile Strength
3. Four-Point Bending Experiments
3.1. Materials Properties and the Fabrication of Specimens
3.2. Experimental Setup and Instruments
3.3. Experimental Results and Discussion
3.3.1. Behaviors between Load and Mid-Span Deflection
3.3.2. Shear Strains and Stress of the Specimens
3.3.3. Failure Modes of the Specimens
4. Evaluation for the Strengthening Effect
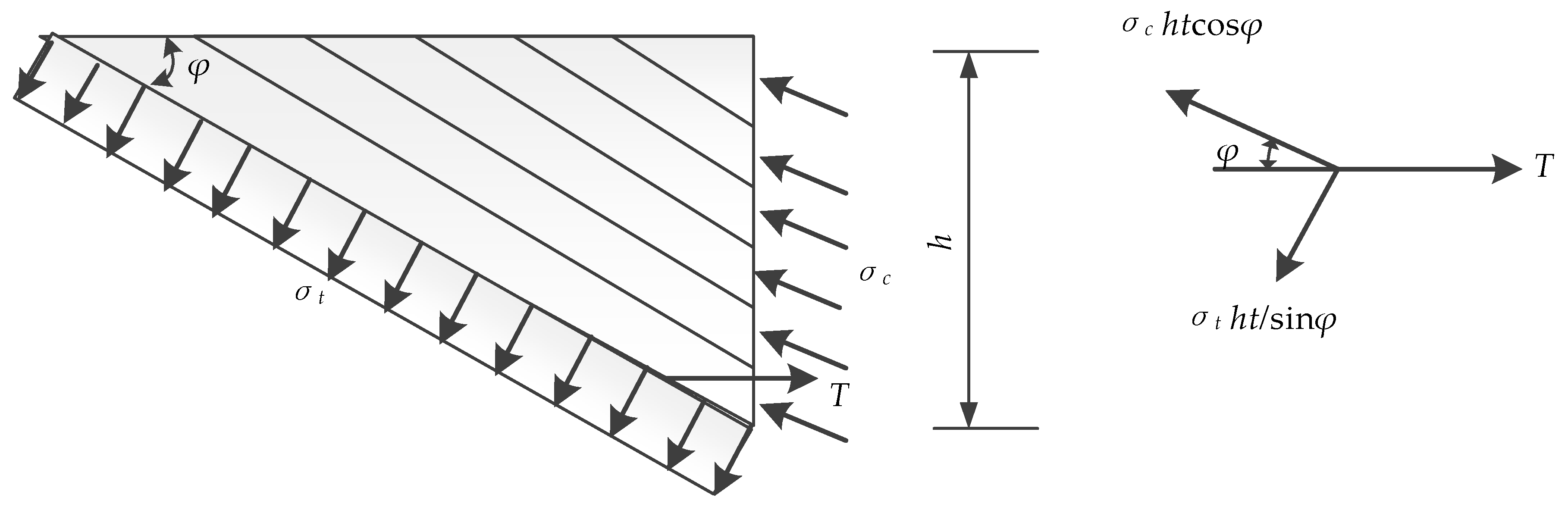
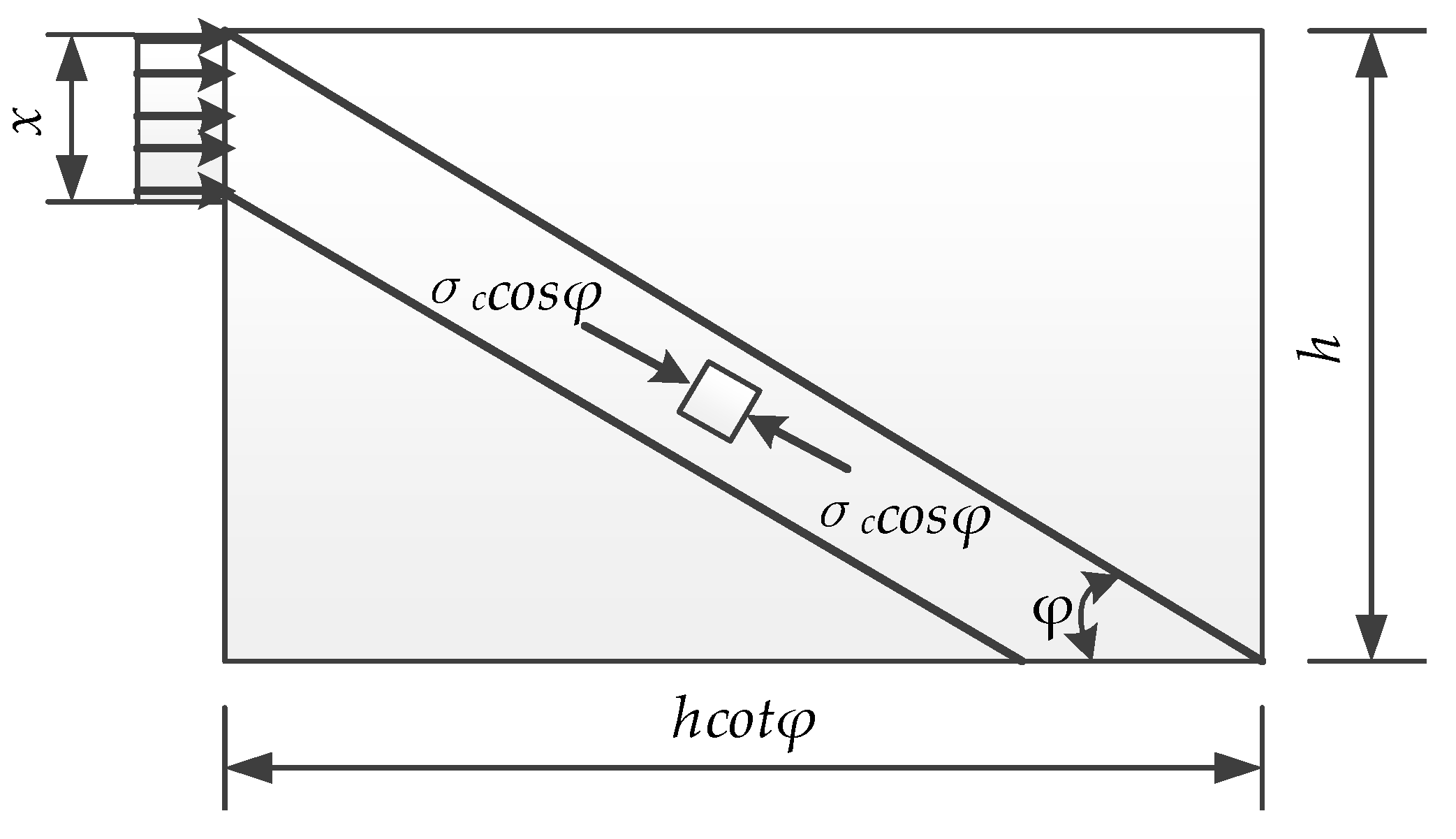
4.1. Truss Model
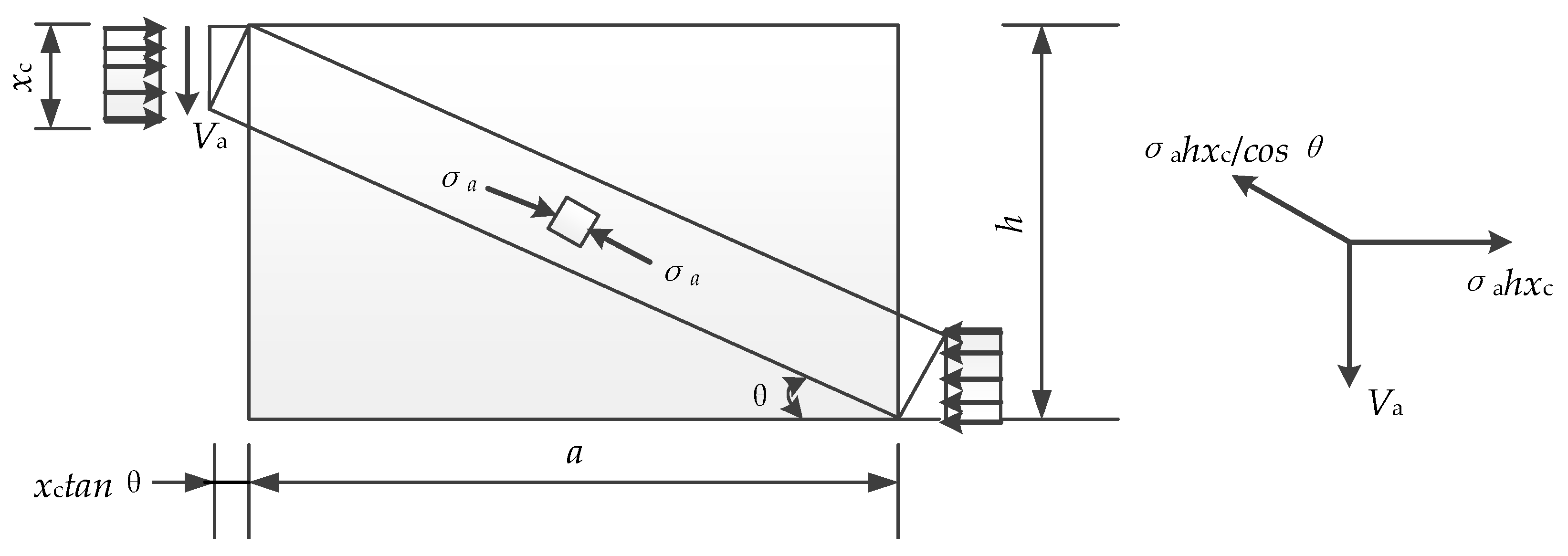
4.2. Arch Model
4.3. Values of the Correlation Coefficients in These Equations
4.3.1. Reduction Coefficient η
4.3.2. Influence Coefficient of Reinforcement Ratio β
4.3.3. Angle of the Diagonal Crack
4.3.4. Softening Coefficient of Concrete
4.4. Results and Discussions
5. Conclusions
- Shear strengthening of RC beams with side ECC layers is effective. The shear bearing capacity of the strengthened specimen can be improved by 89% over the control one.
- The ECC thickness should be eluded to override the risk of debonding failure of the concrete interface.
- The reinforcement ratio after strengthening treatment affects the shear bearing capacity. Strengthening an RC beam into an under-reinforced beam should be avoided.
- The truss and arch model is suitable for calculating the improvement of shear bearing capacity. Based on the truss and arch model, an evaluation of the shear strengthening effect of the extended ECC layers was established. It shows good agreement with experiments results and is conservative.
- Shear span-to-depth ratio affects the shear bearing capacity. When the shear span-to-depth ratio is 2, both truss and arch effects contribute to the increase of shear bearing capacity. When the shear span-to-depth ratio is 3, one can believe that only the truss effect contributes to that.
- The tensile behaviors of ECC can be taken into consideration as the tension members in Truss model when calculating the bearing capacity of the specimen. In the arch model, the softening coefficient used for the common concrete is conservative for ECC. The softening coefficient for ECC under biaxial stress conditions of tension and compression needs further study.
Author Contributions
Funding
Conflicts of Interest
References
- Li, V.C. From Micromechanics to Structural Engineering—The Design of Cementitous Composites for Civil Engineering Applications. JSCE J. Struct. Mech. Earthq. Eng. 1993, 10, 37–48. [Google Scholar]
- Li, V.C. Engineered Cementitious Composites—Tailored Composites through Micromechanical Modeling; Canadian Society for Civil Engineering: Montreal, QC, Canada, 1998; pp. 64–97. [Google Scholar]
- Li, V.C.; Wang, S.; Wu, C. Tensile strain-hardening behavior of polyvinyl alcohol engineered cementitious composite (pva-ecc). ACI Mater. J. Am. Concr. Inst. 2001, 98, 483–492. [Google Scholar]
- Li, V.C. Advances in ecc research. ACI Spec. Publ. 2002, 206, 373–400. [Google Scholar]
- Wang, S.; Li, V.C. Polyvinyl alcohol fiber reinforced engineered cementitious composites: Material design and performances. In Proc., Int’l Workshop on HPFRCC Structural Applications; Citeseer: Honolulu, HI, USA, 2005. [Google Scholar]
- Li, V.C. On engineered cementitious composites (ecc). J. Adv. Concr. Technol. 2003, 1, 215–230. [Google Scholar] [CrossRef]
- Li, V.C. Engineered Cementitious Composites (ecc)—Material, Structural, and Durability Performance. In Concrete Construction Engineering Handbook; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Zhang, J.; Maalej, M.; Quek, S.T. Performance of hybrid-fiber ecc blast/shelter panels subjected to drop weight impact. J. Mater. Civ. Eng. 2007, 19, 855–863. [Google Scholar] [CrossRef]
- Soe, K.T.; Zhang, Y.; Zhang, L. Impact resistance of hybrid-fiber engineered cementitious composite panels. Compos. Struct. 2013, 104, 320–330. [Google Scholar] [CrossRef]
- Fischer, G.; Li, V.C. Effect of matrix ductility on deformation behavior of steel-reinforced ecc flexural members under reversed cyclic loading conditions. Struct. J. 2002, 99, 781–790. [Google Scholar]
- Li, V.C.; Mishra, D.K.; Naaman, A.E.; Wight, J.K.; Lafave, J.M.; Wu, H.C.; Inada, Y. On the shear behavior of engineered cementitious composites. Adv. Cem. Based Mater. 1994, 1, 142–149. [Google Scholar] [CrossRef]
- Paegle, I.; Fischer, G. Phenomenological interpretation of the shear behavior of reinforced engineered cementitious composite beams. Cem. Concr. Compos. 2016, 73, 213–225. [Google Scholar] [CrossRef]
- Kanda, T.; Lin, Z.; Li, V.C. Application of Pseudo Strain-Hardening Cementitious Composites to Shear Resistant Structural Elements; Aedificatio Publishers: Freiburg, Germany, 1998; pp. 1477–1490. [Google Scholar]
- Shimizu, K.; Kanakubo, T.; Kanda, T.; Nagai, S. Shear behavior of steel reinforced pva-ecc beams. In Proceedings of the 2004 13th World Conference on Earthquake Engineering, Conference Proceedings DVD, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Ding, Y.; Yu, K.-Q.; Yu, J.-T.; Xu, S.-L. Structural behaviors of ultra-high performance engineered cementitious composites (uhp-ecc) beams subjected to bending-experimental study. Constr. Build. Mater. 2018, 177, 102–115. [Google Scholar] [CrossRef]
- Conforti, A.; Minelli, F. Compression field modelling of fibre reinforced concrete shear critical deep beams: A numerical study. Mater. Struct. 2016, 49, 3369–3383. [Google Scholar] [CrossRef]
- Cuenca, E.; Conforti, A.; Minelli, F.; Plizzari, G.A.; Gregori, J.N.; Serna, P. A material-performance-based database for frc and rc elements under shear loading. Mater. Struct. 2018, 51, 11. [Google Scholar] [CrossRef]
- Li, V.C.; Horii, H.; Kabele, P.; Kanda, T.; Lim, Y.M. Repair and retrofit with engineered cementitious composites. Eng. Fract. Mech. 2000, 65, 317–334. [Google Scholar] [CrossRef]
- Şahmaran, M.; Li, V.C. Engineered cementitious composites: Can composites be accepted as crack-free concrete? Transp. Res. Rec. 2010, 2164, 1–8. [Google Scholar] [CrossRef]
- Pan, Z.; Wu, C.; Liu, J.; Wang, W.; Liu, J. Study on mechanical properties of cost-effective polyvinyl alcohol engineered cementitious composites (pva-ecc). Constr. Build. Mater. 2015, 78, 397–404. [Google Scholar] [CrossRef]
- Sherir, M.A.A.; Hossain, K.M.A.; Lachemi, M. Structural performance of polymer fiber reinforced engineered cementitious composites subjected to static and fatigue flexural loading. Polymers 2015, 7, 1299–1330. [Google Scholar] [CrossRef]
- Li, V.C. Applications of engineered cementitious composites (ecc). In Engineered Cementitious Composites (ecc); Springer: Berlin, Germany, 2019; pp. 313–369. [Google Scholar]
- Kim, S.-W.; Park, W.-S.; Jang, Y.-I.; Feo, L.; Yun, H.-D. Crack damage mitigation and shear behavior of shear-dominant reinforced concrete beams repaired with strain-hardening cement-based composite. Compos. Part B Eng. 2015, 79, 6–19. [Google Scholar] [CrossRef]
- Yuan, F.; Pan, J.; Dong, L.; Leung, C. Mechanical behaviors of steel reinforced ecc or ecc/concrete composite beams under reversed cyclic loading. J. Mater. Civ. Eng. 2013, 26, 04014047. [Google Scholar] [CrossRef]
- Afefy, H.M.E.-D.; Mahmoud, M.H. Structural performance of rc slabs provided by pre-cast ecc strips in tension cover zone. Constr. Build. Mater. 2014, 65, 103–113. [Google Scholar] [CrossRef]
- Jiang, J.; Luo, J.; Yu, J.; Wang, Z. Performance improvement of a fiber-reinforced polymer bar for a reinforced sea sand and seawater concrete beam in the serviceability limit state. Sensors 2019, 19, 654. [Google Scholar] [CrossRef]
- Hung, C.-C.; Chen, Y.-S. Innovative ecc jacketing for retrofitting shear-deficient rc members. Constr. Build. Mater. 2016, 111, 408–418. [Google Scholar] [CrossRef]
- Chung, K.; Luo, J.; Yuan, L.; Zhang, C.; Qu, C. Strength correlation and prediction of engineered cementitious composites with microwave properties. Appl. Sci. 2017, 7, 35. [Google Scholar] [CrossRef]
- Wu, J.; Xu, C.; Qi, B.; Hernandez, F. Detection of impact damage on pva-ecc beam using infrared thermography. Appl. Sci. 2018, 8, 839. [Google Scholar] [CrossRef]
- Li, S.; Wu, Z. Development of distributed long-gage fiber optic sensing system for structural health monitoring. Struct. Health Monit. Int. J. 2007, 6, 133–143. [Google Scholar] [CrossRef]
- Hong, W.; Wu, Z.S.; Yang, C.Q.; Wan, C.F.; Wu, G.; Zhang, Y.F. Condition assessment of reinforced concrete beams using dynamic data measured with distributed long-gage macro-strain sensors. J. Sound Vib. 2012, 331, 2764–2782. [Google Scholar] [CrossRef]
- Ritter, W. Die Bauweise Hennebique (Hennebiques Construction Method); ETH-Bibliothek: Zurich, Switzerland, 1899. [Google Scholar]
- Mörsch, E.; Goodrich, E.P. Concrete-Steel Construction:(der Eisenbetonbau); Engineering News Publishing Company: New York, NY, USA, 1910. [Google Scholar]
- Bresler, B.; MacGregor, J.G. Review of concrete beams failing in shear. J. Struct. Div. 1967, 93, 343–372. [Google Scholar]
- Fenwick, R.; Pauley, T. Mechanism of shear resistance of concrete beams. J Struct. Div. 1968, 94, 2325–2350. [Google Scholar]
- Kani, G. A rational theory for the function of web reinforcement. J. Proc. 1969, 66, 185–197. [Google Scholar]
- Kim, W.; White, R.N. Initiation of shear cracking in reinforced concrete beams with no web reinforcement. Struct. J. 1991, 88, 301–314. [Google Scholar]
- Kim, D.; Kim, W.; White, R.N. Arch action in reinforced concrete beams—A rational prediction of shear strength. Struct. J. 1999, 96, 586–593. [Google Scholar]
- Priestley, M.N.; Verma, R.; Xiao, Y. Seismic shear strength of reinforced concrete columns. J. Struct. Eng. 1994, 120, 2310–2329. [Google Scholar] [CrossRef]
- Rebeiz, K.S. Shear strength prediction for concrete members. J. Struct. Eng. 1999, 125, 301–308. [Google Scholar] [CrossRef]
- Pansuk, W.; Sato, Y. Shear mechanism of reinforced concrete t-beams with stirrups. J. Adv. Concr. Technol. 2007, 5, 395–408. [Google Scholar] [CrossRef]
- Arslan, G. Shear strength of reinforced concrete beams with stirrups. Mater. Struct. 2008, 41, 113–122. [Google Scholar] [CrossRef]
- Zhou, J.; Qian, S.Z.; Ye, G.; Copuroglu, O.; van Breugel, K.; Li, V.C. Improved fiber distribution and mechanical properties of engineered cementitious composites by adjusting the mixing sequence. Cem. Concr. Compos. 2012, 34, 342–348. [Google Scholar] [CrossRef]
- Code for Design of Concrete Structures; GB50010-2010; Chinese Standard; China Building Industry Press: Beijing, China, 2010.
- Kim, Y.Y.; Fischer, G.; Lim, Y.M.; Li, V.C. Mechanical performance of sprayed engineered cementitious composite using wet-mix shotcreting process for repair applications. Mater. J. 2004, 101, 42–49. [Google Scholar]
- Kani, G. The riddle of shear failure and its solution. J. Proc. 1964, 61, 441–468. [Google Scholar]
- Kanakubo, T.; Shimizu, K.; Nagai, S.; Kanda, T. Shear transmission on crack surface of ecc. In Proceedings of the 7th International Conference on Fracture Mechanics of Concrete and Concrete Structures (FraMCoS-7), Jeju, Korea, 23–28 May 2010. [Google Scholar]
- Design Guidelines for Earthquake Resistant Reinforced Concrete Building Based on Ultimate Strength Concept; Architectural Institute of Japan: Tokyo, Japan, 1990.
- NISA Standrads. Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings; NISA: Dublin, Ireland, 2004. [Google Scholar]
- Code, A. Building Code Requirement for Structural Concrete and Commentary (aci 318m-05); American Concrete Institute: Farmington Hill, MI, USA, 2005. [Google Scholar]
- König, G.; Danielewicz, I. Ermüdungsfestigkeit von Stahlbeton-Und Spannbetonbauteilen Mit Erläuterungen zu den Nachweisen Gemäß Ceb-Fip Model Code 1990; Deutscher Ausschuss für Stahlbeton: Berlin, Germany, 1994. [Google Scholar]

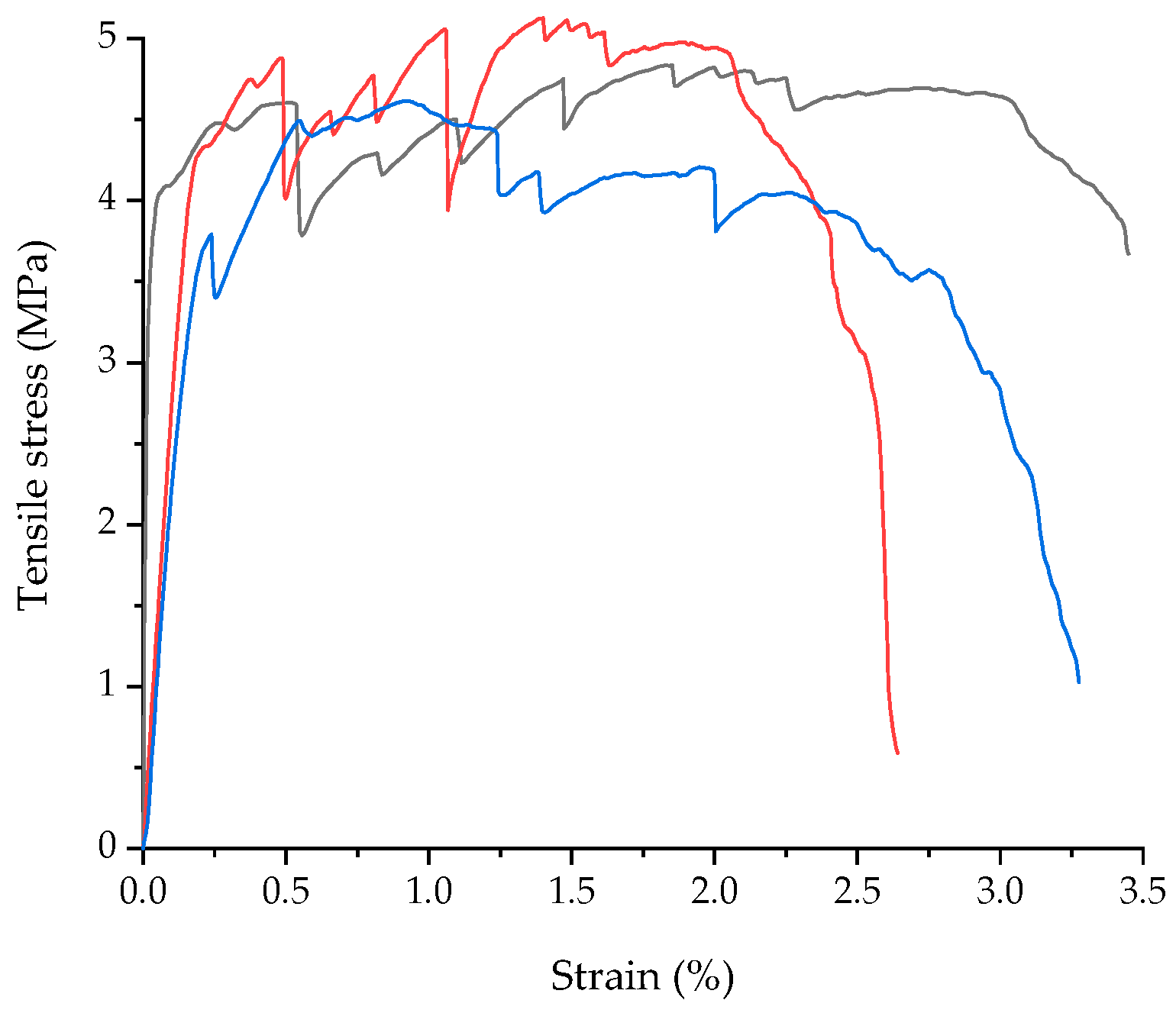

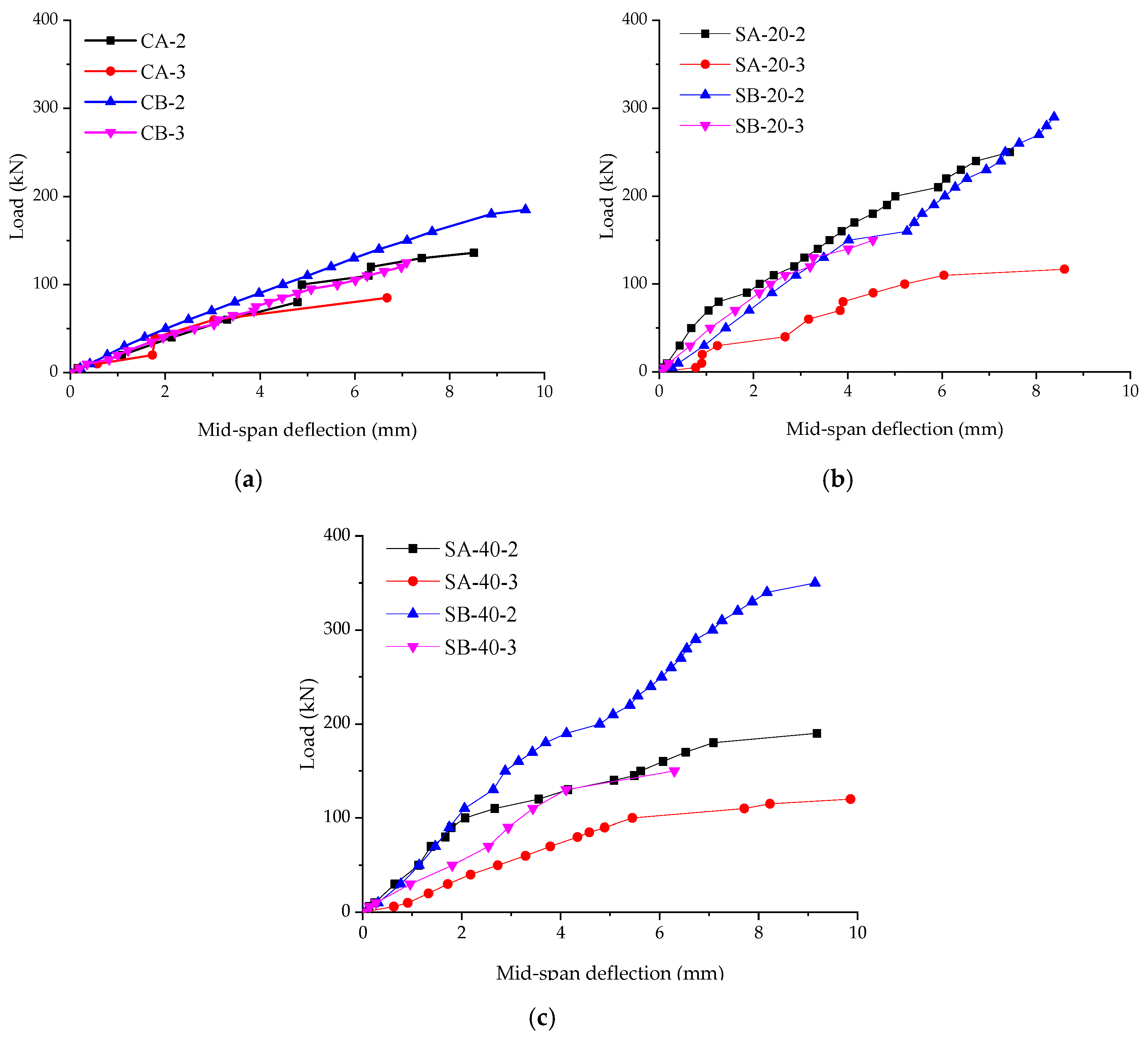
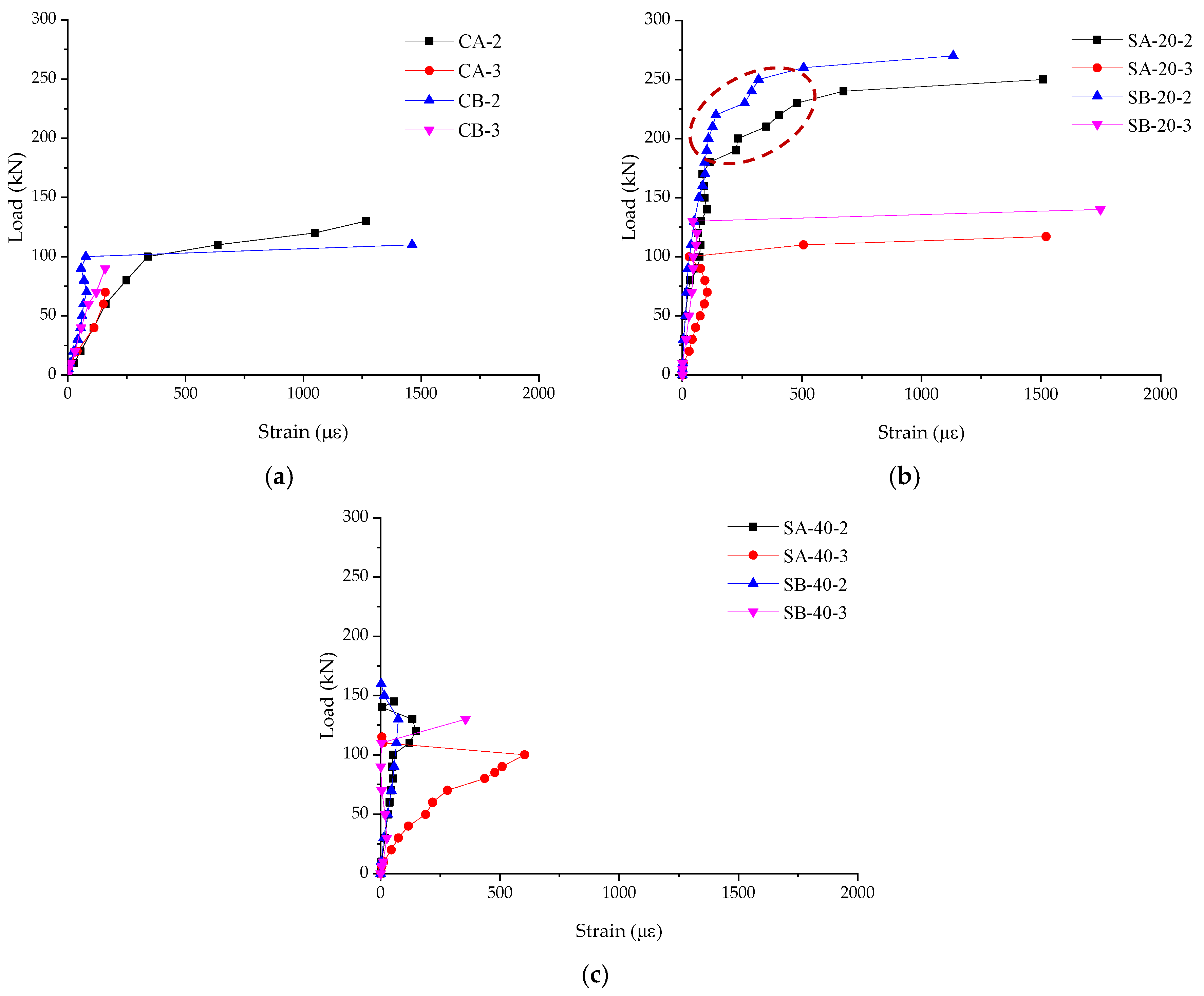


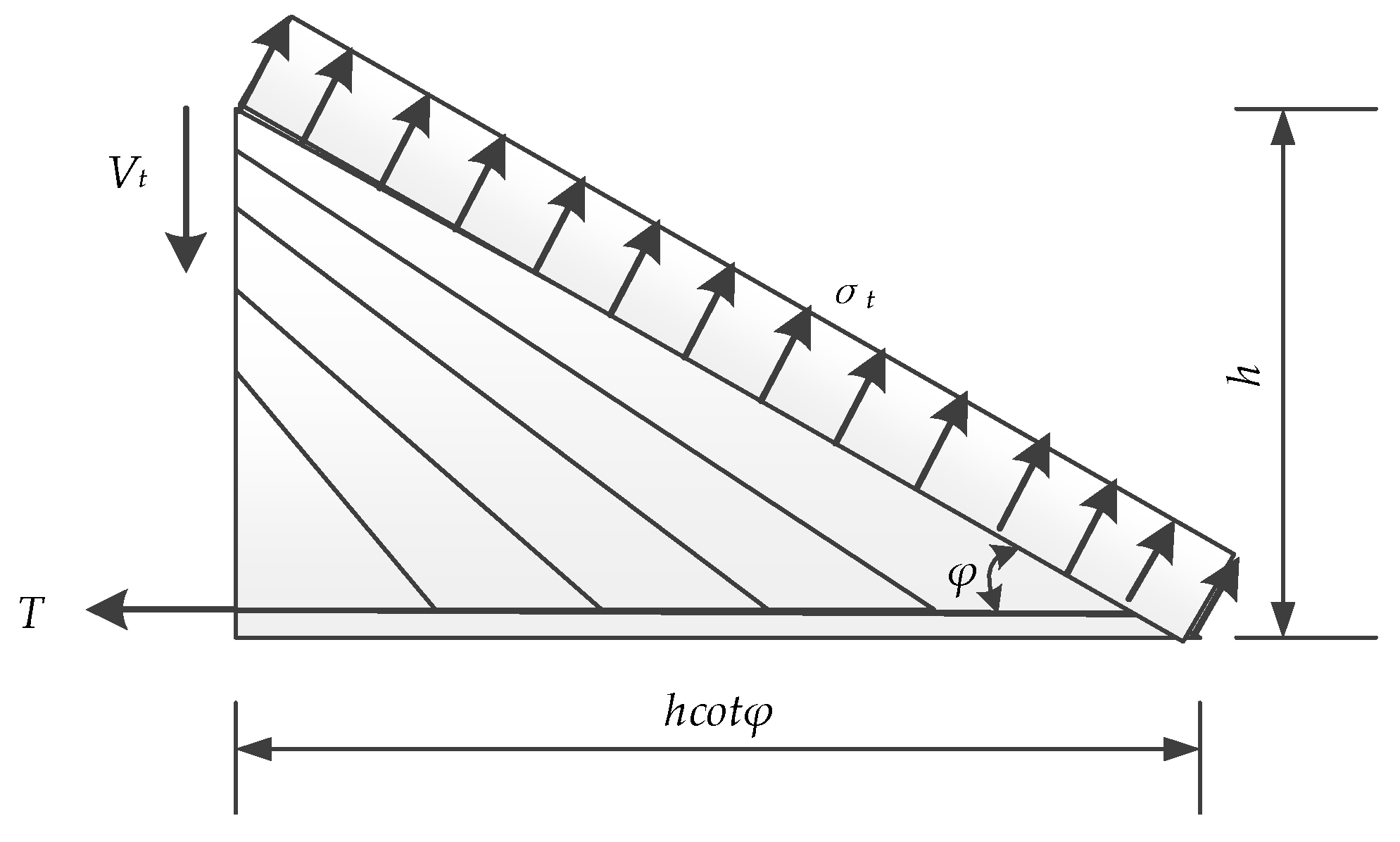
| Type | Dia. (mm) | Net Area (mm2) | fc (MPa) | ft (MPa) | fy (MPa) | εy | fu (MPa) | εu | E (GPa) |
|---|---|---|---|---|---|---|---|---|---|
| Concrete | - | - | 32 | 2.6 | - | - | - | - | 30.0 |
| ECC | - | - | 56 | 4.0 | - | - | - | - | 24.9 |
| Rebar | 10 | 50.2655 | - | - | 259 | 0.00122 | 329 | 0.012 | 212.3 |
| 16 | 201.0619 | - | - | 386 | 0.00189 | 478 | 0.013 | 203.8 | |
| 25 | 490.8738 | - | - | 374 | 0.00186 | 439 | 0.011 | 201.6 |
| Specimen ID | L (mm) | l (mm) | b × h (mm × mm) | ρ (%) | ll (mm) | t (mm) | a/d |
|---|---|---|---|---|---|---|---|
| CA-2 | 2100 | 1800 | 150 × 300 | 0.89 | 772 | 0 | 2 |
| CA-3 | 2100 | 1800 | 150 × 300 | 0.89 | 258 | 0 | 3 |
| CB-2 | 2100 | 1800 | 150 × 300 | 2.18 | 790 | 0 | 2 |
| CB-3 | 2100 | 1800 | 150 × 300 | 2.18 | 285 | 0 | 3 |
| SA-20-2 | 2100 | 1800 | ① 150 × 300 ② 190 × 300 | ① 0.89 ② 0.71 | 772 | 20 | 2 |
| SA-20-3 | 2100 | 1800 | ① 150 × 300 ② 190 × 300 | ① 0.89 ② 0.71 | 258 | 20 | 3 |
| SB-20-2 | 2100 | 1800 | ① 150 × 300 ② 190 × 300 | ① 2.18 ② 1.72 | 790 | 20 | 2 |
| SB-20-3 | 2100 | 1800 | ① 150 × 300 ② 190 × 300 | ① 2.18 ② 1.72 | 285 | 20 | 3 |
| SA-40-2 | 2100 | 1800 | ① 150 × 300 ② 230 × 300 | ① 0.89 ② 0.58 | 772 | 40 | 2 |
| SA-40-3 | 2100 | 1800 | ① 150 × 300 ② 230 × 300 | ① 0.89 ② 0.58 | 258 | 40 | 3 |
| SB-40-2 | 2100 | 1800 | ① 150 × 300 ② 230 × 300 | ① 2.18 ② 1.42 | 790 | 40 | 2 |
| SB-40-3 | 2100 | 1800 | ① 150 × 300 ② 230 × 300 | ① 2.18 ② 1.42 | 285 | 40 | 3 |
| Specimen ID | Pu (kN) | y (mm) | ΔPu (kN) | S (%) | τ (MPa) |
|---|---|---|---|---|---|
| CA-2 | 136 | 8.51 | - | - | 1.44 |
| CA-3 | 85 | 6.68 | - | - | 0.90 |
| CB-2 | 185 | 9.60 | - | - | 1.83 |
| CB-3 | 125 | 7.09 | - | - | 1.23 |
| SA-20-2 | 250 | 7.44 | 114 | 84 | 2.18 |
| SA-20-3 | 117 | 8.60 | 32 | 38 | 1.02 |
| SB-20-2 | 290 | 8.38 | 105 | 57 | 2.39 |
| SB-20-3 | 150 | 4.53 | 25 | 20 | 1.24 |
| SA-40-2 | 190 | 9.18 | 54 | 40 | 1.41 |
| SA-40-3 | 120 | 9.86 | 35 | 41 | 0.89 |
| SB-40-2 | 350 | 9.14 | 165 | 89 | 2.48 |
| SB-40-3 | 151 | 6.30 | 26 | 21 | 1.06 |
| Specimen ID | Experimental (kN) | Calculated (kN) | Calculated/Experimental (%) |
|---|---|---|---|
| SA-20-2 | 114 | 54 | 47 |
| SA-20-3 | 32 | 24 | 75 |
| SB-20-2 | 105 | 47 | 45 |
| SB-20-3 | 25 | 17 | 68 |
| SA-40-2 | 54 | 93 | 172 |
| SA-40-3 | 35 | 33 | 94 |
| SB-40-2 | 165 | 86 | 52 |
| SB-40-3 | 26 | 26 | 100 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Yang, C.; Pan, Y.; Zhu, F.; Jin, K.; Li, K.; Nanni, A. Shear Behaviors of RC Beams Externally Strengthened with Engineered Cementitious Composite Layers. Materials 2019, 12, 2163. https://doi.org/10.3390/ma12132163
Wang G, Yang C, Pan Y, Zhu F, Jin K, Li K, Nanni A. Shear Behaviors of RC Beams Externally Strengthened with Engineered Cementitious Composite Layers. Materials. 2019; 12(13):2163. https://doi.org/10.3390/ma12132163
Chicago/Turabian StyleWang, Guan, Caiqian Yang, Yong Pan, Fawang Zhu, Kai Jin, Kefeng Li, and Antonio Nanni. 2019. "Shear Behaviors of RC Beams Externally Strengthened with Engineered Cementitious Composite Layers" Materials 12, no. 13: 2163. https://doi.org/10.3390/ma12132163
APA StyleWang, G., Yang, C., Pan, Y., Zhu, F., Jin, K., Li, K., & Nanni, A. (2019). Shear Behaviors of RC Beams Externally Strengthened with Engineered Cementitious Composite Layers. Materials, 12(13), 2163. https://doi.org/10.3390/ma12132163





