Microstructure and Flux Pinning of Reacted-and-Pressed, Polycrystalline Ba0.6K0.4Fe2As2 Powders
Abstract
1. Introduction
2. Experimental Procedures
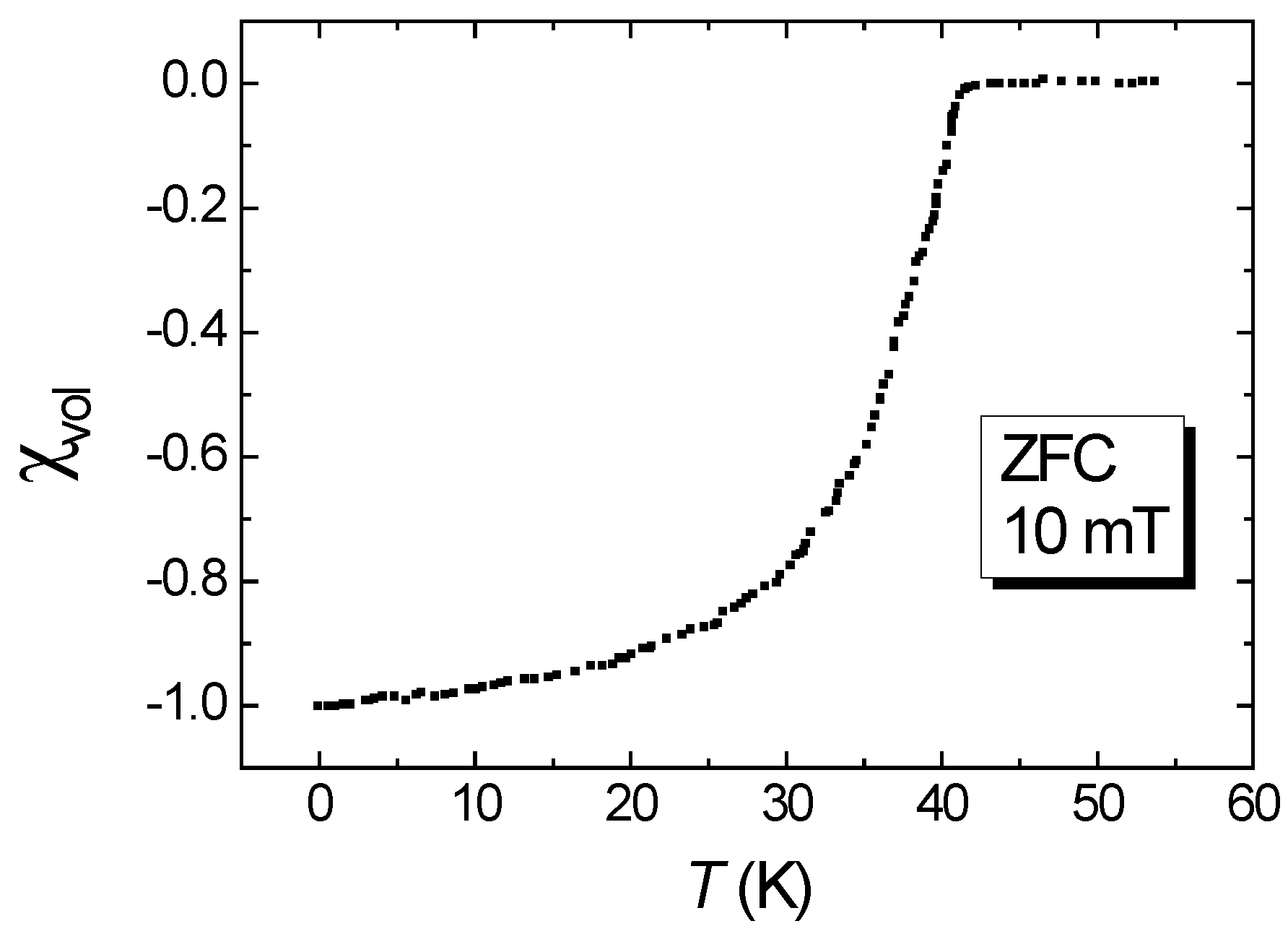
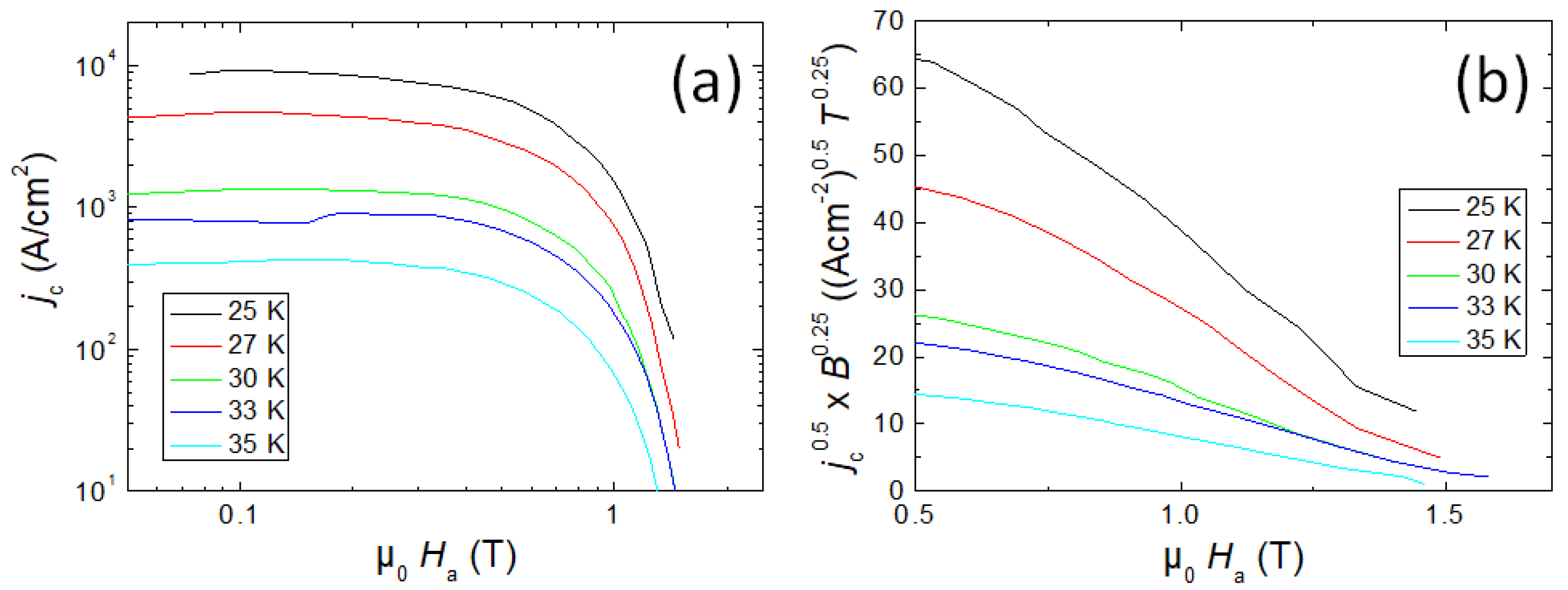
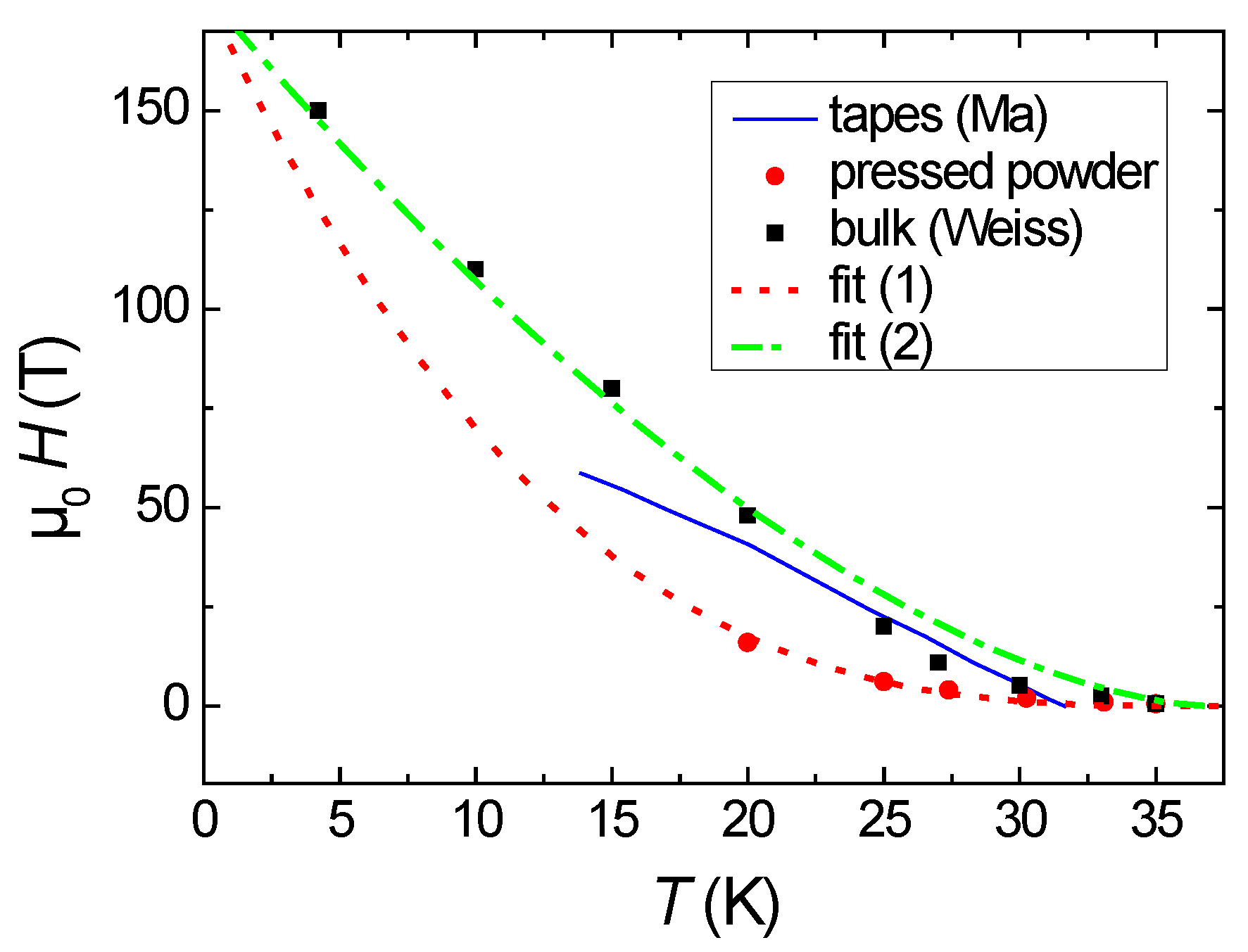
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hosono, H.; Yamamoto, A.; Hiramatsu, H.; Ma, Y. Recent advances in iron-based superconductors toward applications. Mater. Today 2018, 21, 278–302. [Google Scholar] [CrossRef]
- Gurevich, A. Iron-based superconductors at high magnetic fields. Rep. Prog. Phys. 2011, 74, 124501. [Google Scholar] [CrossRef]
- Ma, Y. Progress in wire fabrication of iron-based superconductors. Supercond. Sci. Technol. 2012, 25, 113001. [Google Scholar] [CrossRef]
- Yao, C.; Ma, Y. Recent breakthrough development in iron-based superconducting wires for practical applications. Supercond. Sci. Technol. 2019, 32, 023002. [Google Scholar] [CrossRef]
- Weiss, J.D.; Yamamoto, A.; Polyanskii, A.A.; Richardson, R.B.; Larbalestier, D.C.; Hellstrom, E.E. Demonstration of an iron-pnictide bulk superconducting magnet capable of trapping over 1 T. Supercond. Sci. Technol. 2015, 28, 112001. [Google Scholar] [CrossRef]
- Uhoya, W.; Stemshorn, A.; Tsoi, G.; Vohra, Y.K.; Sefat, A.S.; Sales, B.C.; Hope, K.M.; Weir, S.T. Collapsed tetragonal phase and superconductivity of BaFe2As2 under high pressure. Phys. Rev. B 2010, 82, 144118. [Google Scholar] [CrossRef]
- Mittal, R.; Mishra, S.K.; Chaplot, S.L.; Ovsyannikov, S.V.; Greenberg, E.; Trots, D.M.; Dubrovinsky, L.; Su, Y.; Brueckel, T.; Matsuishi, S.; et al. Ambient- and low-temperature synchrotron x-ray diffraction study of BaFe2As2 and CaFe2As2 at high pressures up to 56 GPa. Phys. Rev. B 2011, 83, 054503. [Google Scholar] [CrossRef]
- Nakajima, Y.; Wang, R.; Metz, T.; Wang, X.; Wang, L.; Cynn, H.; Weir, S.T.; Jeffries, J.R.; Paglione, J. High-temperature superconductivity stabilized by electron-hole interband coupling in collapsed tetragonal phase of KFe2As2 under high pressure. Phys. Rev. B 2015, 91, 060508. [Google Scholar] [CrossRef]
- Ptok, A.; Sternik, M.; Kapcia, K.J.; Piekarz, P. Structural, electronic, and dynamical properties of the tetragonal and collapsed tetragonal phases of KFe2As2. Phys. Rev. B 2019, 99, 134103. [Google Scholar] [CrossRef]
- Koblischka, M.R.; Muralidhar, M. Pinning force scaling analysis of Fe-based high-Tc superconductors. Int. J. Mod. Phys. B 2016, 30, 1630017. [Google Scholar] [CrossRef]
- Katase, T.; Ishimaru, Y.; Tsukamoto, A.; Hiramatsu, H.; Kamiya, T.; Tanabe, K.; Hosono, H. Advantageous grain boundaries in iron pnictide superconductors. Nat. Commun. 2011, 2, 409. [Google Scholar] [CrossRef] [PubMed]
- Kametani, F.; Li, P.; Abraimov, D.; Polyanskii, A.A.; Yamamoto, A.; Jiang, J.; Hellstrom, E.E.; Gurevich, A.; Larbalestier, D.C.; Ren, Z.A.; et al. Intergrain current flow in a randomly oriented polycrystalline SmFeAsO0.85 oxypnictide. Appl. Phys. Lett. 2009, 95, 142502. [Google Scholar] [CrossRef]
- Hecher, J.; Baumgartner, T.; Weiss, J.D.; Tarantini, C.; Yamamoto, A.; Jiang, J.; Hellstrom, E.E.; Larbalestier, D.C.; Eisterer, M. Small grains: A key to high-field applications of granular Ba-122 superconductors? Supercond. Sci. Technol. 2016, 29, 025004. [Google Scholar] [CrossRef]
- Iida, K.; Hänisch, J.; Tarantini, C. Fe-based superconducting thin films on metallic substrates: Growth, characteristics, and relevant properties. Appl. Phys. Rev. 2018, 5, 031304. [Google Scholar] [CrossRef]
- Weiss, J.D.; Tarantini, C.; Jiang, J.; Kametani, F.; Polyanskii, A.A.; Larbalestier, D.C.; Hellstrom, E.E. High intergrain critical current density in fine-grain (Ba0.6K0.4)Fe2As2 wires and bulks. Nat. Mater. 2012, 11, 682–685. [Google Scholar] [CrossRef]
- Weiss, J.D.; Jiang, J.; Polyanskii, A.A.; Hellstrom, E.E. Mechanochemical synthesis of pnictide compounds and superconducting Ba0.6K0.4Fe2As2 bulks with high critical current density. Supercond. Sci. Technol. 2013, 26, 074003. [Google Scholar] [CrossRef]
- Koblischka-Veneva, A.; Koblischka, M.R.; Qu, T.; Han, Z.; Mücklich, F. Texture analysis of monofilamentary, Ag-sheathed (Pb,Bi)2Sr2Ca2Cu3Ox tapes by electron backscatter diffraction (EBSD). Physica C 2008, 468, 174–182. [Google Scholar] [CrossRef]
- Koblischka-Veneva, A.; Koblischka, M.R.; Schmauch, J.; Inoue, K.; Muralidhar, M.; Berger, K.; Noudem, J. EBSD analysis of MgB2 bulk superconductors. Supercond. Sci. Technol. 2016, 29, 044007. [Google Scholar] [CrossRef]
- Wiesenmayer, E.; Luetkens, H.; Pascua, G.; Khasanov, R.; Amato, A.; Potts, H.; Banusch, B.; Klauss, H.-H.; Johrendt, D. Microscopic Coexistence of Superconductivity and Magnetism in Ba1−xKxFe2As2. Phys. Rev. Lett. 2011, 107, 237001. [Google Scholar] [CrossRef]
- Wiesenmayer, J.E. Dissertation LMU München, Germany. Available online: https://edoc.ub.uni-muenchen.de/18509/1/Wiesenmayer_Josef_Erwin.pdf (accessed on 20 May 2019).
- Malagoli, A.; Wiesenmayer, E.; Marchner, S.; Johrendt, D.; Genovese, A.; Putti, M. Role of heat and mechanical treatments in the fabrication of superconducting Ba0.6K0.4Fe2As2 ex situ powder-in-tube tapes. Supercond. Sci. Technol. 2015, 28, 095015. [Google Scholar] [CrossRef]
- Koblischka, M.R.; Koblischka-Veneva, A. Applications of the electron backscatter diffraction technique to ceramic materials. Phase Transit. 2013, 86, 651–660. [Google Scholar] [CrossRef]
- Koblischka, M.R.; Koblischka-Veneva, A. Advanced Characterization of Multiferroic Materials by Scanning Probe Methods and Scanning Electron Microscopy. In Nanoscale Ferroelectrics and Multiferroics; Alguero, M., Gregg, J.M., Mitoseriu, L., Eds.; Wiley and Sons Ltd.: Chichester, UK, 2016; pp. 400–434. [Google Scholar]
- Koblischka-Veneva, A.; Koblischka, M.R.; Schmauch, J.; Chen, Y.; Harris, V.G. EBSD analysis of the microtexture of Ba-hexaferrite samples. J. Phys. Conf. Ser. 2010, 200, 082014. [Google Scholar] [CrossRef]
- Koblischka-Veneva, A.; Koblischka, M.R.; Chen, Y.; Harris, V.G. Analysis of Grain Shape and Orientation in BaFe12O19-Ferrites Using Electron Backscatter Diffraction (EBSD). IEEE Trans. Magn. 2009, 45, 4219–4222. [Google Scholar] [CrossRef]
- Orientation Imaging Microscopy (OIM Analysis™); Software Version V8.1, User Manual; EDAX Inc.: Draper, UT, USA, 2018.
- Wiesinger, H.P.; Sauerzopf, F.M.; Weber, H.W. On the calculation of Jc from magnetization measurements on superconductors. Physica C 1992, 203, 121–128. [Google Scholar] [CrossRef]
- Gokhfeld, D.M.; Balaev, D.A.; Petrov, M.I.; Popkov, S.I.; Shaykhutdinov, K.A.; Val’kov, V.V. Magnetization asymmetry of type-II superconductors in high magnetic fields. J. Appl. Phys. 2011, 109, 033904. [Google Scholar] [CrossRef]
- Gokhfeld, D.M. Secondary Peak on Asymmetric Magnetization Loop of Type-II Superconductors. J. Supercond. Novel Magn. 2013, 26, 281–283. [Google Scholar] [CrossRef][Green Version]
- Gokhfeld, D.M. The circulation radius and critical current density in type-II superconductors. Tech. Phys. Lett. 2019, 45, 1–3. [Google Scholar] [CrossRef]
- Sun, Y.; Pyon, S.; Tamegai, T.; Kobayashi, R.; Watashige, T.; Kasahara, S.; Matsuda, Y.; Shibauchi, T.; Kitamura, H. Enhancement of critical current density and mechanism of vortex pinning in H+-irradiated FeSe single crystal. Appl. Phys. Exp. 2015, 8, 113102. [Google Scholar] [CrossRef]
- Karwoth, T.; Furutani, K.; Koblischka, M.R.; Zeng, X.L.; Wiederhold, A.; Muralidhar, M.; Murakami, M.; Hartmann, U. Electrotransport and magnetic measurements on bulk FeSe superconductors. J. Phys. Conf. Ser. 2018, 1054, 012018. [Google Scholar] [CrossRef]
- Koblischka-Veneva, A.; Koblischka, M.R.; Berger, K.; Nouailhetas, Q.; Douine, B.; Muralidhar, M.; Murakami, M. Comparison of Temperature and Field Dependencies of the Critical Current Densities of Bulk YBCO, MgB2, and Iron-Based Superconductors. IEEE Trans. Appl. Supercond. 2019, 29, 6801805. [Google Scholar] [CrossRef]
- Kramer, E.J. Scaling laws for flux pinning in hard superconductors. J. Appl. Phys. 1973, 44, 1360–1370. [Google Scholar] [CrossRef]
- Dew-Hughes, D. Flux pinning mechanisms in type-II superconductors. Philos. Mag. 1974, 30, 293–305. [Google Scholar] [CrossRef]
- Koblischka, M.R. Pinning in bulk high-Tc superconductors. Inst. Phys. Conf. Ser. 1997, 58, 1141–1144. [Google Scholar]
- Koblischka, M.R.; van Dalen, A.J.; Higuchi, T.; Yoo, S.I.; Murakami, M. Analysis of pinning in NdBa2Cu3O7−δ superconductors. Phys. Rev. B 1998, 58, 2863–2867. [Google Scholar] [CrossRef]
- Koblischka, M.R.; Muralidhar, M. Pinning force scaling and its analysis in the LRE-123 ternary compounds. Physica C 2014, 496, 23–27. [Google Scholar] [CrossRef]
- Huang, H.; Yao, C.; Dong, C.H.; Zhang, X.P.; Wang, D.L.; Cheng, Z.; Li, J.Q.; Awaji, S.; Wen, H.H.; Ma, Y.W. High transport current superconductivity in powder-in-tube Ba0.6K0.4Fe2As2 tapes at 27 T. Supercond. Sci. Technol. 2018, 31, 015017. [Google Scholar] [CrossRef]
- Shabbir, B.; Huang, H.; Yao, C.; Ma, Y.W.; Dou, S.X.; Johansen, T.H.; Hosono, H.; Wang, X.L. Evidence for superior current carrying capability of iron pnictide tapes under hydrostatic pressure. Phys. Rev. Mater. 2017, 1, 044805. [Google Scholar] [CrossRef]
- Altin, E.; Gokhfeld, D.M.; Demirel, S.; Oz, E.; Kurt, F.; Altin, S.; Yakinci, M.E. Vortex pinning and magnetic peak effect in Eu(Eu,Ba)2.125Cu3Ox. J. Mater. Sci. Mater. Electron. 2014, 25, 1466–1473. [Google Scholar] [CrossRef]
- Han, Z.; Skov-Hansen, P.; Freltoft, T. The mechanical deformation of superconducting BiSrCaCuO/Ag composites. Supercond. Sci. Technol. 1997, 10, 371–387. [Google Scholar] [CrossRef]

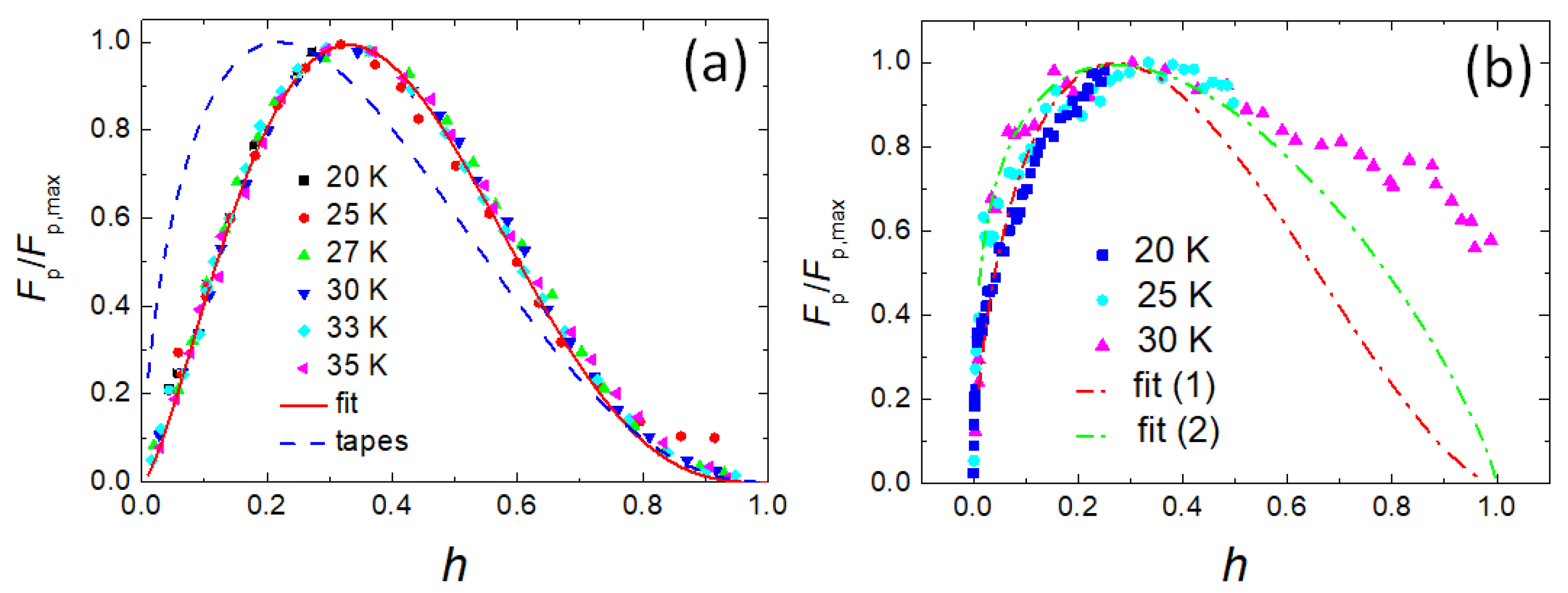


| Sample | p | q | h0 | Remarks |
|---|---|---|---|---|
| reacted-and-pressed | 1.5 | 3.05 | 0.33 | good scaling, similar to 122 crystals |
| HIP-processed bulk | ||||
| fit (1) | 0.6 | 1.62 | 0.27 | fit close to the low-field data at all T |
| fit (2) | 0.3 | 0.81 | 0.27 | steeper fit, 20 K data deviate clearly |
| tapes | ||||
| Huang | 0.64 | 2.3 | 0.22 | good scaling, 20 K ≤ T ≤ 32 K |
| Shabbir (0 GPa) | 0.65 | 1.95 | 0.25 | T = 24 K |
| Shabbir (0.7 GPa) | 0.8 | 2 | 0.29 | T = 24 K, hydrostatic pressure applied |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koblischka, M.R.; Koblischka-Veneva, A.; Schmauch, J.; Murakami, M. Microstructure and Flux Pinning of Reacted-and-Pressed, Polycrystalline Ba0.6K0.4Fe2As2 Powders. Materials 2019, 12, 2173. https://doi.org/10.3390/ma12132173
Koblischka MR, Koblischka-Veneva A, Schmauch J, Murakami M. Microstructure and Flux Pinning of Reacted-and-Pressed, Polycrystalline Ba0.6K0.4Fe2As2 Powders. Materials. 2019; 12(13):2173. https://doi.org/10.3390/ma12132173
Chicago/Turabian StyleKoblischka, Michael R., Anjela Koblischka-Veneva, Jörg Schmauch, and Masato Murakami. 2019. "Microstructure and Flux Pinning of Reacted-and-Pressed, Polycrystalline Ba0.6K0.4Fe2As2 Powders" Materials 12, no. 13: 2173. https://doi.org/10.3390/ma12132173
APA StyleKoblischka, M. R., Koblischka-Veneva, A., Schmauch, J., & Murakami, M. (2019). Microstructure and Flux Pinning of Reacted-and-Pressed, Polycrystalline Ba0.6K0.4Fe2As2 Powders. Materials, 12(13), 2173. https://doi.org/10.3390/ma12132173





