Evaluation of Interfacial Fracture Toughness and Interfacial Shear Strength of Typha Spp. Fiber/Polymer Composite by Double Shear Test Method
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Scanning Electron Microscopy (SEM)
2.3. Mode II Interfacial Fracture Toughness Test
3. Results and Discussion
3.1. Surface Morphology of Typha Spp. Fiber
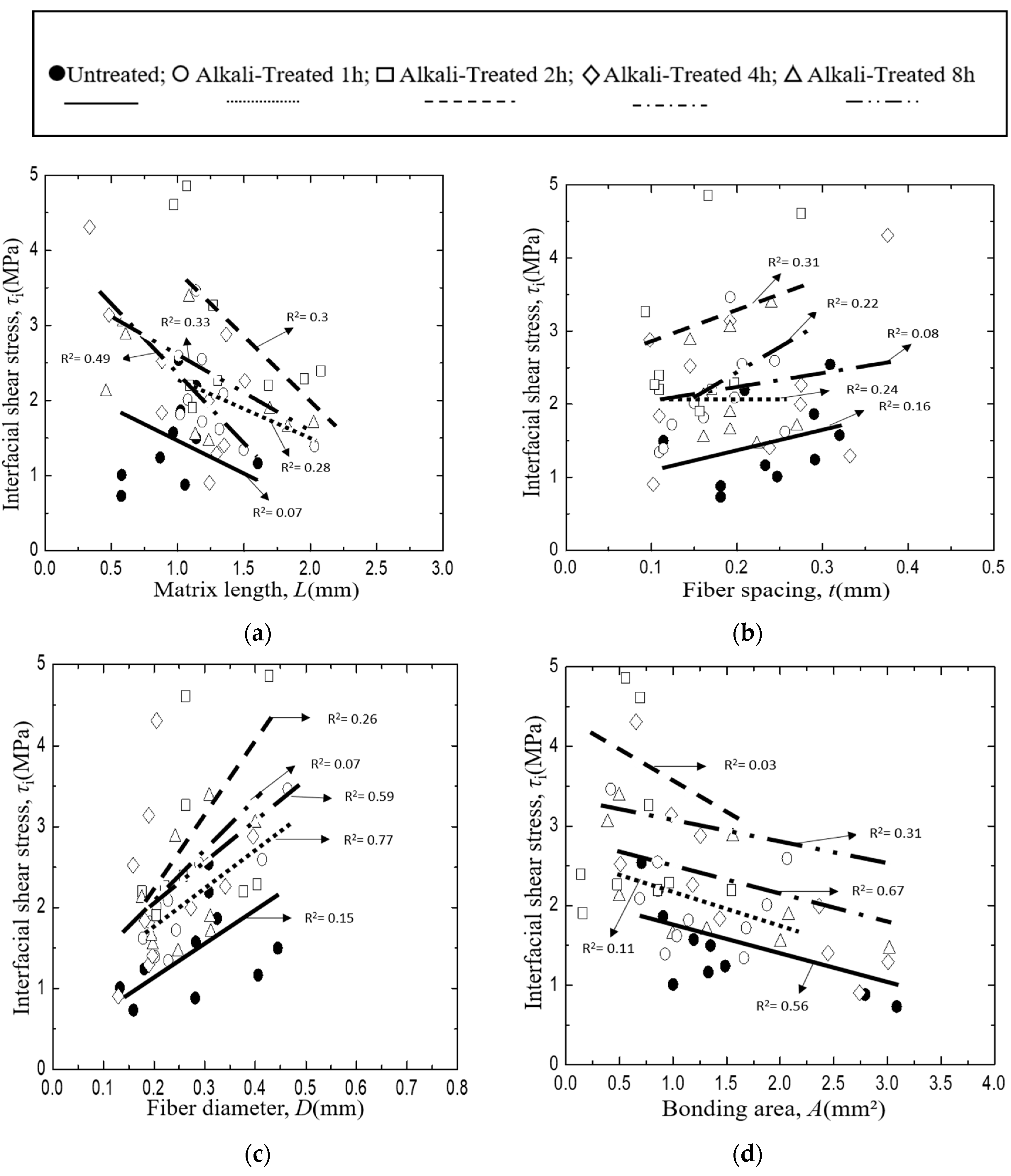
3.2. Interfacial Fracture Toughness of the Typha Spp. Fiber Model Composite
3.3. Interfacial Shear Strength of the Typha Spp. Fiber Model Composite
3.4. Effects of Geometrical Factor on Interfacial Fracture Toughness
4. Conclusions
- Alkali treatment on Typha spp. fiber can make the fiber surface coarser due to the removal of impurities, such as fatty substance from the fiber surface, thus increasing the interfacial fracture toughness and interfacial shear strength values.
- The Typha spp. fiber/epoxy has a higher interfacial fracture value than Typha spp. fiber/PLLA because the PLLA-based composite has lower mechanical properties compared to the epoxy, the PLLA has poor melt strength, brittleness and the melt viscosity of PLA has low shear sensitivity and relatively poor strength.
- Interfacial fracture toughness of Typha spp. fiber/PLLA and Typha spp. fiber/epoxy composite model specimens are influenced by the matrix length and the fiber spacing. The longer the matrix length, the higher the value of the interfacial fracture toughness. Meanwhile, the interfacial shear strength decreases with the increasing matrix length and the bonding area. Furthermore, the interfacial fracture toughness and the interfacial shear stress of the composite model increased with the increasing duration of the surface treatment.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hamidi, Y.; Yalcinkaya, M.; Guloglu, G.; Pishvar, M.; Amirkhosravi, M.; Altan, M. Silk as a Natural Reinforcement: Processing and Properties of Silk/Epoxy Composite Laminates. Materials 2018, 11, 2135. [Google Scholar] [CrossRef] [PubMed]
- Malenab, R.; Ngo, J.; Promentilla, M. Chemical treatment of waste abaca for natural fiber-reinforced geopolymer composite. Materials 2017, 10, 579. [Google Scholar] [CrossRef]
- Wu, C.-M.; Lai, W.-Y.; Wang, C.-Y. Effects of surface modification on the mechanical properties of flax/β-polypropylene composites. Materials 2016, 9, 314. [Google Scholar] [CrossRef] [PubMed]
- Golewski, G.L. Green concrete composite incorporating fly ash with high strength and fracture toughness. J. Clean. Prod. 2018, 172, 218–226. [Google Scholar] [CrossRef]
- Ray, D.; Sarkar, B.K.; Basak, R.K.; Rana, A.K. Study of the thermal behavior of alkali-treated jute fibers. J. Appl. Polym. Sci. 2002, 85, 2594–2599. [Google Scholar] [CrossRef]
- Asrofi, M.; Abral, H.; Putra, Y.K.; Sapuan, S.M.; Kim, H.-J. Effect of duration of sonication during gelatinization on properties of tapioca starch water hyacinth fiber biocomposite. Int. J. Biol. Macromol. 2018, 108, 167–176. [Google Scholar] [CrossRef]
- Golewski, G.L. Improvement of fracture toughness of green concrete as a result of addition of coal fly ash. Characterization of fly ash microstructure. Mater. Charact. 2017, 134, 335–346. [Google Scholar] [CrossRef]
- Tham, M.W.; Fazita, M.R.N.; Abdul Khalil, H.P.S.; Mahmud Zuhudi, N.Z.; Jaafar, M.; Rizal, S.; Haafiz, M.K.M. Tensile properties prediction of natural fibre composites using rule of mixtures: A review. J. Reinf. Plast. Compos. 2019, 38, 211–248. [Google Scholar] [CrossRef]
- Katogi, H.; Takemura, K.; Akiyama, M. Residual tensile property of plain woven jute fiber/poly (lactic acid) green composites during thermal cycling. Materials 2016, 9, 573. [Google Scholar] [CrossRef]
- Yuan, Y.; Guo, M.; Wang, Y. Flax fibers as reinforcement in poly (lactic acid) biodegradable composites. In Proceedings of the International Conference on Intelligent Computing and Information Science, Chongqing, China, 8–9 January 2011; Springer: Berlin, Germany, 2011; pp. 547–553. [Google Scholar]
- Ibrahim, N.A.; Yunus, W.M.Z.W.; Othman, M.; Abdan, K. Effect of chemical surface treatment on the mechanical properties of reinforced plasticized poly (lactic acid) biodegradable composites. J. Reinf. Plast. Compos. 2011, 30, 381–388. [Google Scholar] [CrossRef]
- Ikramullah; Rizal, S.; Thalib, S.; Huzni, S. Hemicellulose and lignin removal on typha fiber by alkali treatment. In Proceedings of the IOP Conference Series: Materials Science and Engineering; Banda Aceh, Indonesia, 19 October 2017, IOP Publishing: Bristol, UK, 2018; Volume 352, p. 12019. [Google Scholar]
- Beule, J.D. Control and management of cattails in southeastern Wisconsin wetlands. Wis. Dep. Nat. Resour. Tech. Bull. 1979, 112, 13–25. [Google Scholar]
- Rizal, S.; Ikramullah; Gopakumar, D.; Thalib, S.; Huzni, S.; Abdul Khalil, H. Interfacial Compatibility Evaluation on the Fiber Treatment in the Typha Fiber Reinforced Epoxy Composites and Their Effect on the Chemical and Mechanical Properties. Polymers 2018, 10, 1316. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.S.; Pickering, K.L.; Foreman, N.J. Influence of alkali treatment on the interfacial and physico-mechanical properties of industrial hemp fibre reinforced polylactic acid composites. Compos. Part A Appl. Sci. Manuf. 2010, 41, 596–603. [Google Scholar] [CrossRef]
- Song, Y.S.; Lee, J.T.; Ji, D.S.; Kim, M.W.; Lee, S.H.; Youn, J.R. Viscoelastic and thermal behavior of woven hemp fiber reinforced poly (lactic acid) composites. Compos. Part B Eng. 2012, 43, 856–860. [Google Scholar] [CrossRef]
- Peerbooms, W.; Pickering, K. Use of recycled pulped chromated copper arsenate-treated wood fibre in polymer composites. J. Compos. Sci. 2018, 2, 35. [Google Scholar] [CrossRef]
- Hao, M.; Wu, H.; Qiu, F.; Wang, X. Interface bond improvement of sisal fibre reinforced polylactide composites with added epoxy Oligomer. Materials 2018, 11, 398. [Google Scholar] [CrossRef] [PubMed]
- Nair, S.S.; Wang, S.; Hurley, D.C. Nanoscale characterization of natural fibers and their composites using contact-resonance force microscopy. Compos. Part A Appl. Sci. Manuf. 2010, 41, 624–631. [Google Scholar] [CrossRef]
- Punyamurthy, R.; Sampathkumar, D.; Srinivasa, C.V.; Bennehalli, B. Effect of alkali treatment on water absorption of single cellulosic abaca fiber. BioResources 2012, 7, 3515–3524. [Google Scholar]
- Zhou, Y.; Fan, M.; Chen, L. Interface and bonding mechanisms of plant fibre composites: An overview. Compos. Part B Eng. 2016, 101, 31–45. [Google Scholar] [CrossRef] [Green Version]
- Matthews, F.L.; Rawlings, R.D. Composite Materials: Engineering and Science; Elsevier: Amsterdam, The Netherlands, 1999; ISBN 184569855X. [Google Scholar]
- Pickering, K.L.; Efendy, M.G.A.; Le, T.M. A review of recent developments in natural fibre composites and their mechanical performance. Compos. Part A Appl. Sci. Manuf. 2016, 83, 98–112. [Google Scholar] [CrossRef] [Green Version]
- Sreekala, M.S.; Kumaran, M.G.; Thomas, S. Stress relaxation behaviour in oil palm fibres. Mater. Lett. 2001, 50, 263–273. [Google Scholar] [CrossRef]
- Gassan, J.; Bledzki, A.K. Alkali treatment of jute fibers: relationship between structure and mechanical properties. J. Appl. Polym. Sci. 1999, 71, 623–629. [Google Scholar] [CrossRef]
- Mylsamy, K.; Rajendran, I. The mechanical properties, deformation and thermomechanical properties of alkali treated and untreated Agave continuous fibre reinforced epoxy composites. Mater. Des. 2011, 32, 3076–3084. [Google Scholar] [CrossRef]
- Jacob, M.; Thomas, S.; Varughese, K.T. Mechanical properties of sisal/oil palm hybrid fiber reinforced natural rubber composites. Compos. Sci. Technol. 2004, 64, 955–965. [Google Scholar] [CrossRef]
- Mishra, S.; Mohanty, A.K.; Drzal, L.T.; Misra, M.; Parija, S.; Nayak, S.K.; Tripathy, S.S. Studies on mechanical performance of biofibre/glass reinforced polyester hybrid composites. Compos. Sci. Technol. 2003, 63, 1377–1385. [Google Scholar] [CrossRef]
- So, C.L.; Young, R.J. Interfacial failure in poly (p-phenylene benzobisoxazole)(PBO)/epoxy single fibre pull-out specimens. Compos. Part A Appl. Sci. Manuf. 2001, 32, 445–455. [Google Scholar] [CrossRef]
- Kuntz, M.; Schlapschi, K.-H.; Meier, B.; Grathwohl, G. Evaluation of interface parameters in push-out and pull-out tests. Composites 1994, 25, 476–481. [Google Scholar] [CrossRef]
- Day, R.J.; Rodrigez, J.V.C. Investigation of the micromechanics of the microbond test. Compos. Sci. Technol. 1998, 58, 907–914. [Google Scholar] [CrossRef] [Green Version]
- Chou, C.T.; Gaur, U.; Miller, B. The effect of microvise gap width on microbond pull-out test results. Compos. Sci. Technol. 1994, 51, 111–116. [Google Scholar] [CrossRef]
- Zinck, P.; Wagner, H.D.; Salmon, L.; Gerard, J.F. Are microcomposites realistic models of the fibre/matrix interface? I. Micromechanical modelling. Polymer (Guildf). 2001, 42, 5401–5413. [Google Scholar] [CrossRef]
- Broutman, L.J. Measurement of the Fiber-Polymer Matrix Interfacial Strength. In Interfaces in Composites; ASTM International: West Conshohocken, PA, USA, 1969. [Google Scholar]
- Crews, J.H., Jr.; Shivakumar, K.N.; Raju, I.S. A fibre-resin micromechanics analysis of the delamination front in a double cantilever beam specimen. Phase Interact. Compos. Mater. 1992, 396–405. [Google Scholar]
- Dubois, F.; Keunings, R. DCB testing of thermoplastic composites: a non-linear micro-macro numerical analysis. Compos. Sci. Technol. 1997, 57, 437–450. [Google Scholar] [CrossRef]
- Tanaka, H.; Nakai, Y.; Ye, L.; Mai, Y.W.; Su, Z. Three-Dimensional Micromechanics Analysis of Strain Energy Release Rate Distribution along Delamination Crack Front in FRP. In Composite Technologies for 2020; Woodhead Publishing: Cambridge, UK, 2004; pp. 439–444. ISBN 9781855738317. [Google Scholar]
- Kotaki, M.; Hojo, M.; Tsujioka, N.; Hamada, H. Effect of surface treatment on interlaminar/intralaminar crack growth behavior of CFRP laminates. In Proceedings of the Japan International Sampe Symposium, Tokyo, Japan, 24 September 1995; Japan Chapter OF Sampe: Tokyo, Japan, 1995; Volume 2, pp. 1008–1013. [Google Scholar]
- Hojo, M. Effect of interfacial strength on interlaminar and intralaminar fracture toughness of CFRP laminates. Proc. Comp. 1995, ’95, 30–36. [Google Scholar]
- KOIWA, K.; TANAKA, H.; NAKAI, Y.; ITO, S.; TUKAHARA, T. OS12F018 Fracture Mechanics Evaluation of Mode I and Mode II Fiber/Matrix Interfacial Crack by Using Real-Size Model Composite. In Proceedings of the The Abstracts of ATEM: International Conference on Advanced Technology in Experimental Mechanics: Asian Conference on Experimental Mechanics 2011.10, Osaka, Japan, 3 November 2011; The Japan Society of Mechanical Engineers: Tokyo, Japan, 2011; p. _OS12F018. [Google Scholar]
- Sangappa; Rao, B.L.; Asha, S.; Kumar, R.M.; Somashekar, R. Physical, chemical, and surface properties of alkali-treated Indian hemp fibers. Compos. Interfaces 2014, 21, 153–159. [Google Scholar] [CrossRef]
- Sia, C.V.; Nakai, Y.; Tanaka, H.; Shiozawa, D. Interfacial Fracture Toughness Evaluation of Poly ( L-lactide acid )/ Natural Fiber Composite by Using Double Shear Test Method. Open J. Compos. Mater. 2014, 4, 97–105. [Google Scholar] [CrossRef]
- Reddy, K.O.; Maheswari, C.U.; Shukla, M.; Song, J.I.; Rajulu, A.V. Tensile and structural characterization of alkali treated Borassus fruit fine fibers. Compos. Part B Eng. 2013, 44, 433–438. [Google Scholar] [CrossRef]
- Boopathi, L.; Sampath, P.S.; Mylsamy, K. Investigation of physical, chemical and mechanical properties of raw and alkali treated Borassus fruit fiber. Compos. Part B Eng. 2012, 43, 3044–3052. [Google Scholar] [CrossRef]
- Chen, J.-C.; Lin, J.-C. Manufacturing and properties of cotton and jute fabrics reinforced epoxy and PLA composites. Int. J. Mod. Phys. B 2018, 32, 1840084. [Google Scholar] [CrossRef]
- Zhao, H.; Turng, L.-S. Mechanical performance of microcellular injection molded biocomposites from green plastics: PLA and PHBV. In Biocomposites; Elsevier: Amsterdam, The Netherlands, 2015; pp. 141–160. [Google Scholar]
- Zhandarov, S.; Mäder, E. Characterization of fiber/matrix interface strength: applicability of different tests, approaches and parameters. Compos. Sci. Technol. 2005, 65, 149–160. [Google Scholar] [CrossRef]
- Gorbatkina, Y.A.; Ivanova-Mumzhieva, V.G.; Gorenberg, A.Y. Adhesive strength of bonds of polymers with carbon fibres at different loading rates. Fibre Chem. 1999, 31, 405–409. [Google Scholar] [CrossRef]
- Gorbatkina, Y.A.; Ivanova-Mumjieva, V.G. Adhesion of polymers to fibers: Further elaboration of pull-out method. Polym. Sci. Ser. D 2009, 2, 214. [Google Scholar] [CrossRef]
- Le Duigou, A.; Davies, P.; Baley, C. Interfacial bonding of Flax fibre/Poly (l-lactide) bio-composites. Compos. Sci. Technol. 2010, 70, 231–239. [Google Scholar] [CrossRef]

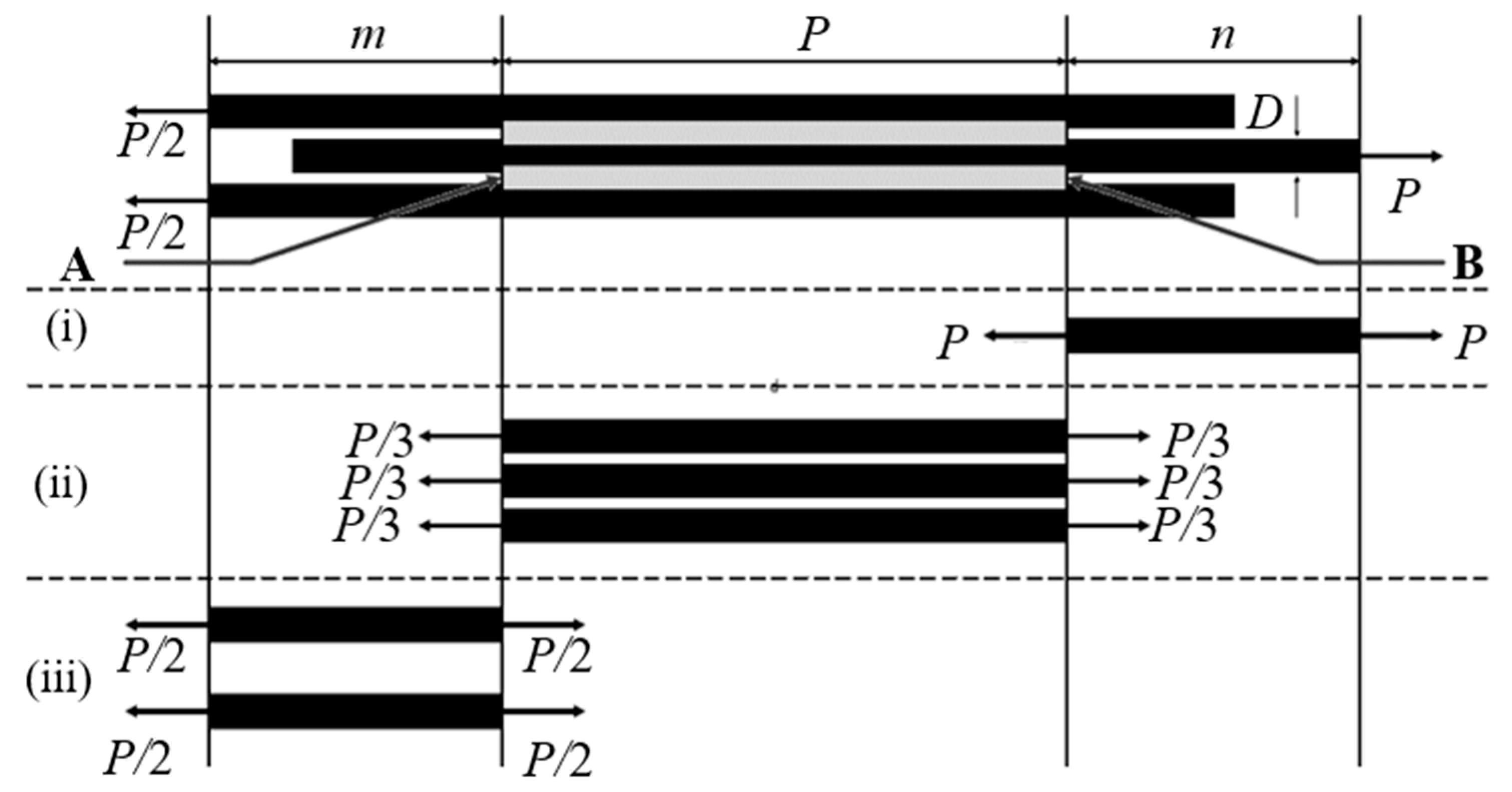

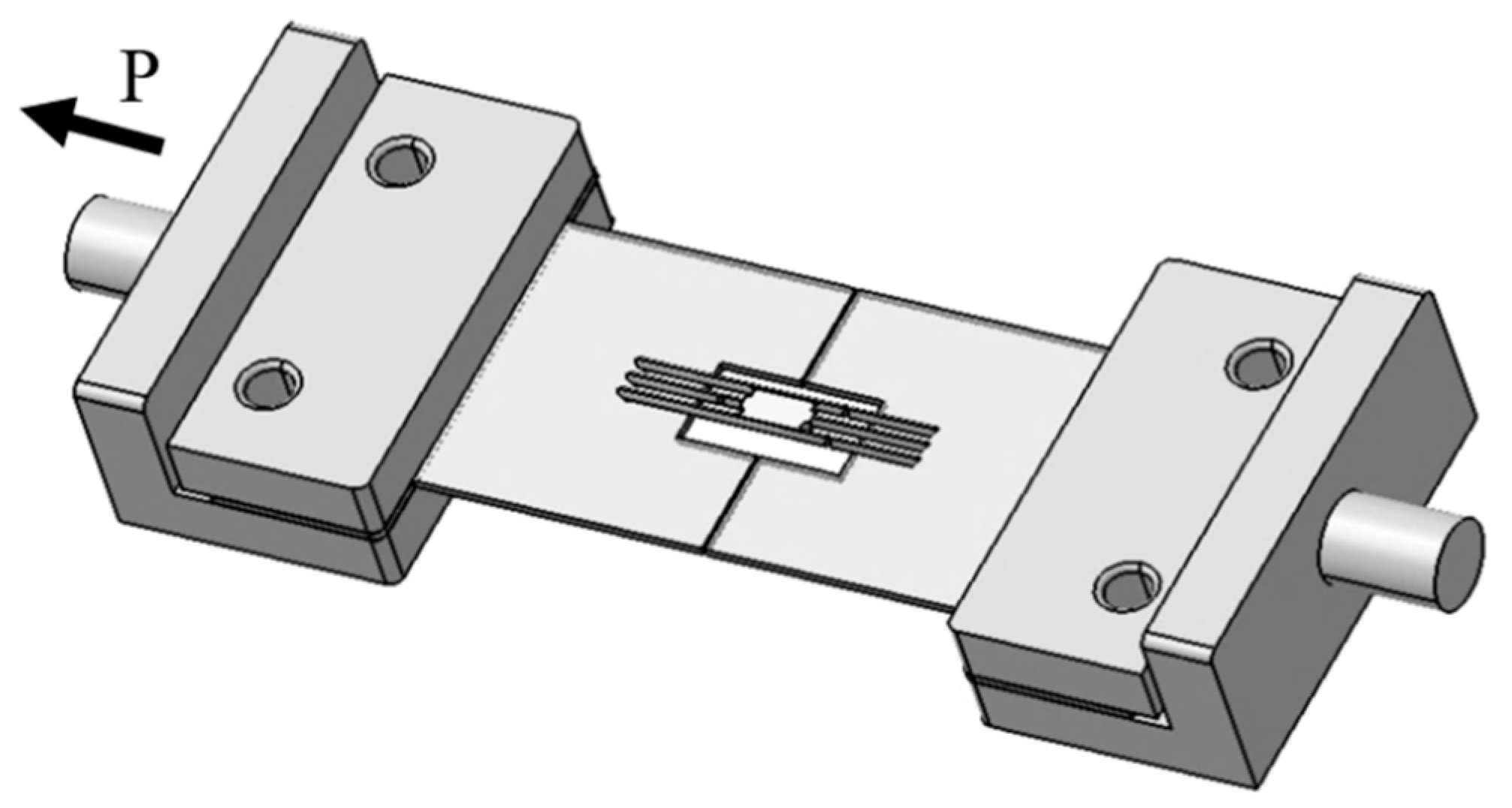












| Alkali Treatment Period | Average Diameter (μm) |
|---|---|
| 0 | 309 |
| 1 | 286 |
| 2 | 282 |
| 4 | 263 |
| 8 | 226 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ikramullah; Rizal, S.; Nakai, Y.; Shiozawa, D.; Khalil, H.P.S.A.; Huzni, S.; Thalib, S. Evaluation of Interfacial Fracture Toughness and Interfacial Shear Strength of Typha Spp. Fiber/Polymer Composite by Double Shear Test Method. Materials 2019, 12, 2225. https://doi.org/10.3390/ma12142225
Ikramullah, Rizal S, Nakai Y, Shiozawa D, Khalil HPSA, Huzni S, Thalib S. Evaluation of Interfacial Fracture Toughness and Interfacial Shear Strength of Typha Spp. Fiber/Polymer Composite by Double Shear Test Method. Materials. 2019; 12(14):2225. https://doi.org/10.3390/ma12142225
Chicago/Turabian StyleIkramullah, Samsul Rizal, Yoshikazu Nakai, Daiki Shiozawa, H.P.S. Abdul Khalil, Syifaul Huzni, and Sulaiman Thalib. 2019. "Evaluation of Interfacial Fracture Toughness and Interfacial Shear Strength of Typha Spp. Fiber/Polymer Composite by Double Shear Test Method" Materials 12, no. 14: 2225. https://doi.org/10.3390/ma12142225
APA StyleIkramullah, Rizal, S., Nakai, Y., Shiozawa, D., Khalil, H. P. S. A., Huzni, S., & Thalib, S. (2019). Evaluation of Interfacial Fracture Toughness and Interfacial Shear Strength of Typha Spp. Fiber/Polymer Composite by Double Shear Test Method. Materials, 12(14), 2225. https://doi.org/10.3390/ma12142225






