Prediction of Crack Formation for Cross Wedge Rolling of Harrow Tooth Preform
Abstract
:1. Introduction
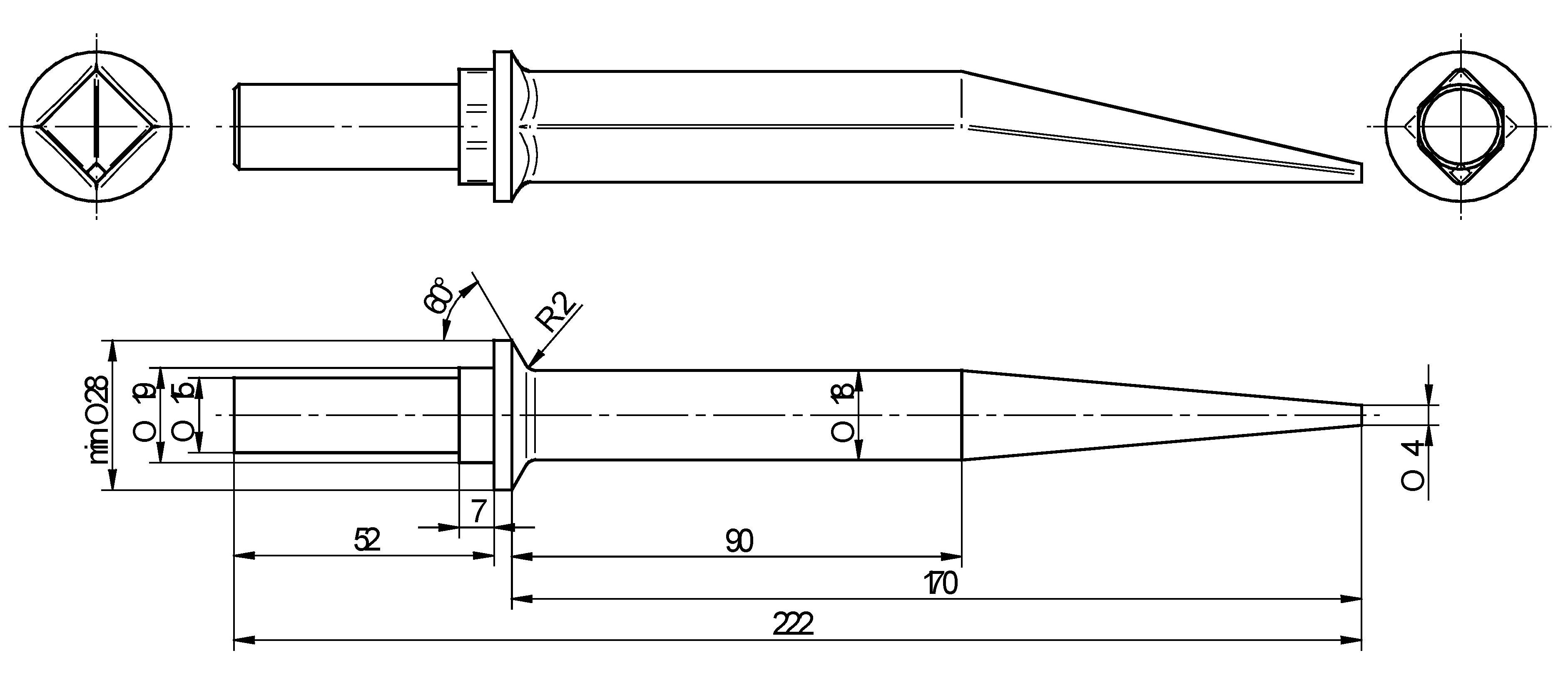
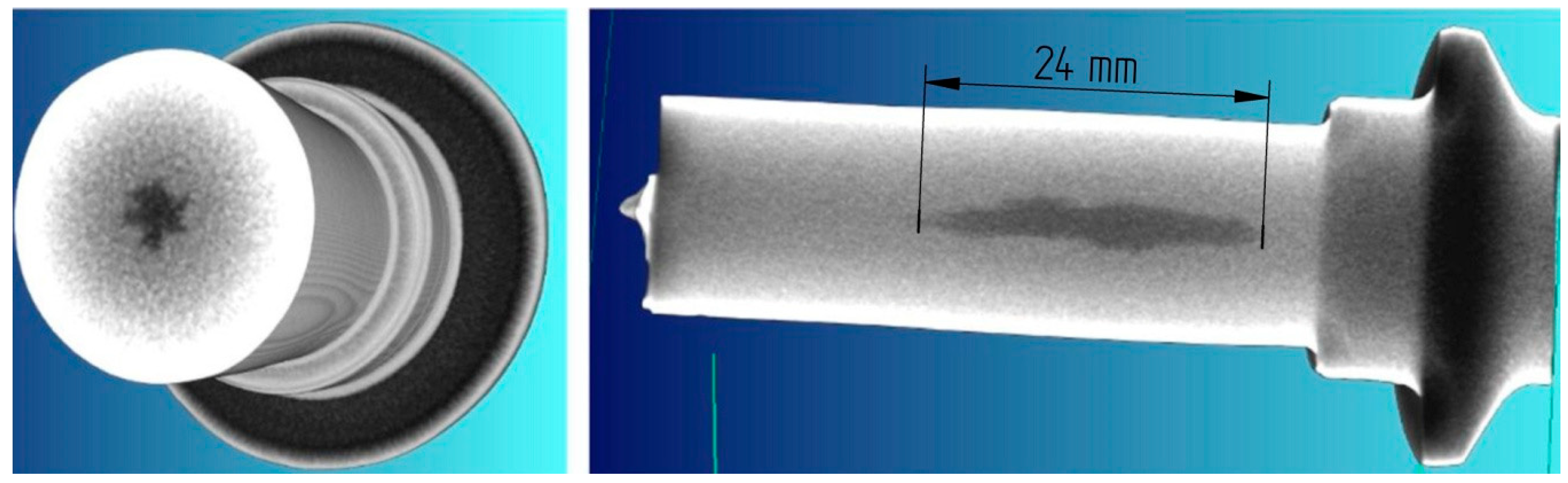
2. Subject of Research
3. Modeling of the Ductile Fracture
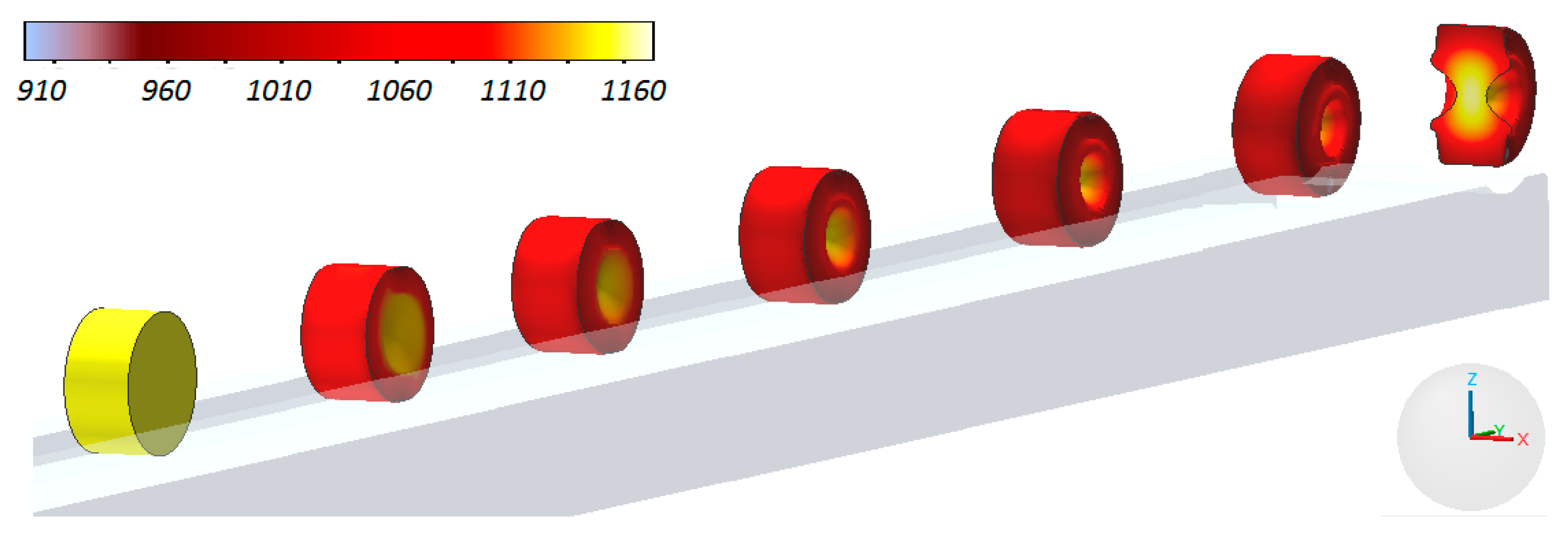
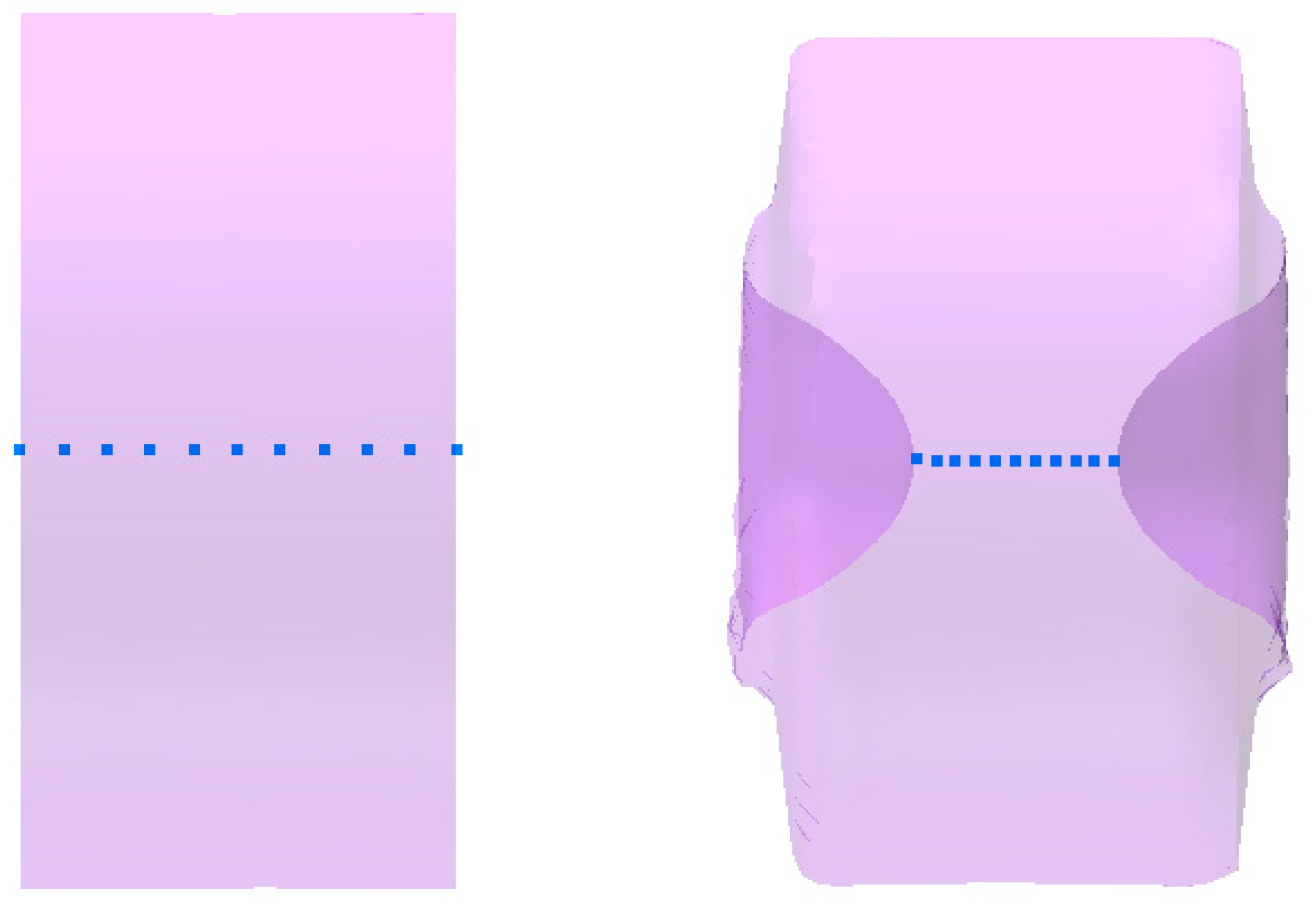
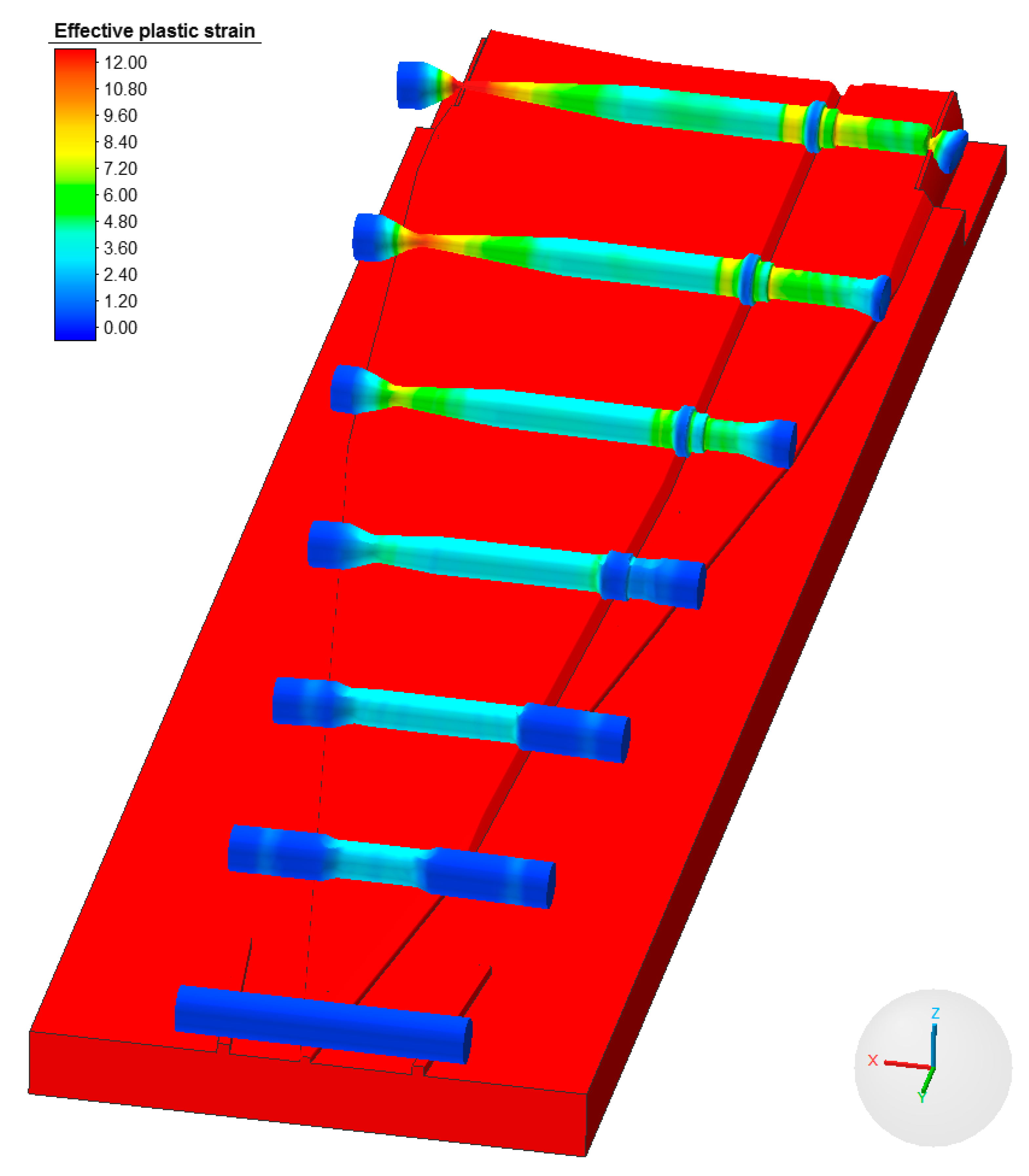
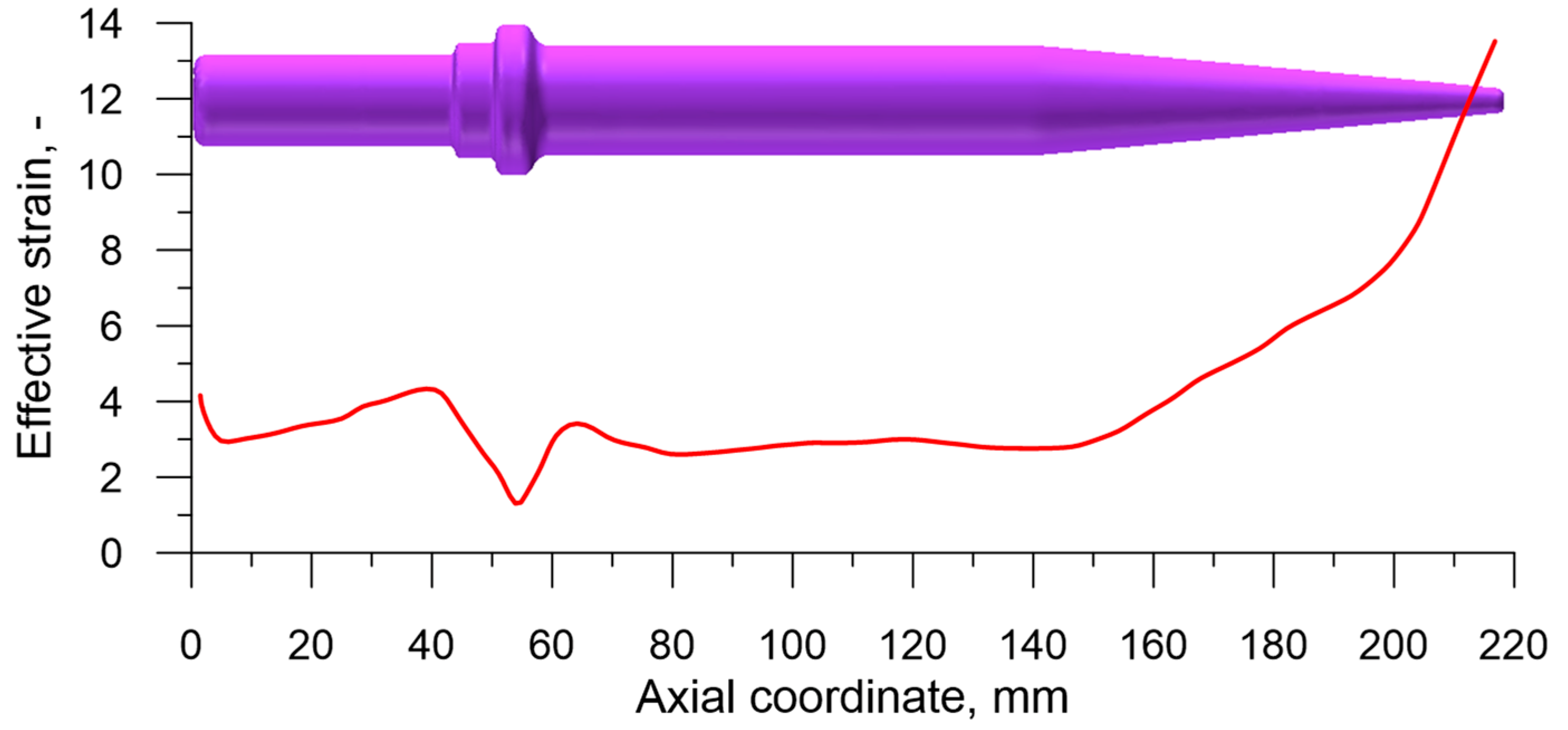
4. Numerical Modeling of the Process of Cross Wedge Rolling of the Harrow Tooth Preform
5. Conclusions
- Material cracking in the axial area of the workpiece was one of the major hindrances to the CWR process;
- In order to prognosticate the material cracking the critical damage of the material must be known. In the case of the CWR process it could be determined based on the rotational compression of a disc in a channel; in this article this method was described in detail on the example of determining the critical damage values for C45 grade steel, formed in 1150 °C;
- In prognosticating material fracture during the CWR process realized in the state of stress characterized by stress triaxiality , the widely-known damage energetic criteria could be applied; the best results were obtained using the criteria developed by Freudenthal, Cockroft and Latham and Argon et al.;
- In the case of CWR realized in the stress triaxiality applying energetic damage criteria proved unsuccessful; it is to be deemed reasonable to seek for damage criteria of a different type (e.g., stress), whose efficiency ought to be researched in other papers.
Author Contributions
Funding
Conflicts of Interest
References
- Pater, Z. Cross Wedge Rolling. In Comprehensive Materials Processing; Button, S.T., Ed.; Elsevier Ltd: New York, NY, USA, 2014; Volume 3, pp. 211–279. [Google Scholar]
- Li, Q.; Lovell, M. Cross wedge rolling failure mechanisms and industrial application. Int. J. Adv. Manuf. Technol. 2008, 37, 265–278. [Google Scholar] [CrossRef]
- Fu, X.P.; Dean, T.A. Past developments, current applications and trends in the cross wedge rolling process. Int. J. Mach. Tool. Manuf. 1993, 33, 367–400. [Google Scholar] [CrossRef]
- Pater, Z. Development of Cross-Wedge Rolling Theory and Technology. Steel Res. Int. 2010, 81, 25–32. [Google Scholar]
- Tofil, A.; Pater, Z. Overview of the research on roll forging processes. Adv. Sci. Technol. Res. J. 2017, 11, 72–86. [Google Scholar]
- Li, Q.; Lovell, M.R.; Slaughter, W.; Tagavi, K. Investigation of internal defects in cross wedge rolling. J. Mater. Process. Technol. 2002, 125–126, 248–257. [Google Scholar] [CrossRef]
- Li, Q.; Lovell, M.R. The establishment of failure criterion in cross wedge rolling. Int. J. Adv. Manuf. Technol. 2004, 24, 180–189. [Google Scholar] [CrossRef]
- Piedrahita, F.; Garcia Arana, L.; Chastel, Y. Three Dimensional Numerical Simulation of Cross-Wedge Rolling of Bars. In Proceedings of the 8th International Conference on Technology of Plasticity (ICTP 2005), Verona, Italy, 9–13 October 2005; pp. 1–6. [Google Scholar]
- Yang, C.; Zhang, K.; Hu, Z. Development of central minute cavity in the workpiece of cross wedge rolling. Appl. Mech. Mater. 2012, 215–216, 766–770. [Google Scholar] [CrossRef]
- Novella, M.F.; Ghiotti, A.; Bruschi, S.; Bariani, P.F. Ductile damage modeling at elevated temperature applied to the cross wedge rolling of AA6082-T6 bars. J. Mater. Process. Technol. 2015, 222, 259–267. [Google Scholar] [CrossRef]
- Liu, G.; Zhong, Z.; Shen, Z. Influence of reduction distribution on internal defects during cross wedge-rolling process. Procedia Eng. 2014, 81, 263–267. [Google Scholar] [CrossRef]
- Carkicrcali, M.; Kilicaslan, C.; Guden, M.; Kiranli, E.; Shchukin, V.Y.; Petronko, V.V. Cross wedge rolling of a TiAl4V (ELI) alloy: The experimental studies and the finite element simulation of the deformation and failure. Int. J. Adv. Manuf. Technol. 2013, 65, 1273–1287. [Google Scholar] [CrossRef]
- Hai, D.V.; Hue, D.T.H. Finite element simulation and experimental study on internal fracture of railway sleeper screw during cross wedge rolling process. Mater. Sci. Forum 2015, 804, 311–314. [Google Scholar]
- Silva, M.L.N.; Pires, G.H.; Button, S.T. Damage evolution during cross wedge rolling of steel DIN 38MnSiVS5. Procedia Eng. 2011, 10, 752–757. [Google Scholar] [CrossRef] [Green Version]
- Bulzak, T.; Pater, Z.; Tomczak, J. Numerical and experimental analysis of a cross wedge rolling process for producing ball studs. Arch. Civ. Mech. Eng. 2017, 17, 729–737. [Google Scholar] [CrossRef]
- Huang, X.; Wang, B.; Zhou, J.; Ji, H.; Mu, Y.; Li, J. Comparative study of warm and hot cross-wedge rolling: Numerical simulation and experimental trial. Int. J. Adv. Manuf. Technol. 2017, 92, 3541–3551. [Google Scholar] [CrossRef]
- Pater, Z.; Tomczak, J.; Bulzak, T. FEM simulation of the cross-wedge rolling process for a stepped shaft. Strength Mater. 2017, 49, 521–527. [Google Scholar] [CrossRef]
- Wierzbicki, T.; Bao, Y.; Lee, Y.W.; Bai, Y. Calibration and evaluation of seven fracture models. Int. J. Mech. Sci. 2005, 47, 719–743. [Google Scholar] [CrossRef]
- Bai, Y.; Wierzbicki, T. A new model of metal plasticity and fracture with pressure and Lode dependence. Int. J. Plast. 2008, 24, 1071–1096. [Google Scholar] [CrossRef]
- Pater, Z.; Walczuk, P.; Lis, K.; Wójcik, Ł. Preliminary Analysis of Rotary Compression Test. Adv. Sci. Technol. Res. J. 2018, 12, 77–82. [Google Scholar] [CrossRef]
- Yang, C.; Dong, H.; Hu, Z. Micro-mechanism of central damage formation during cross wedge rolling. J. Mater. Process. Technol. 2018, 252, 322–332. [Google Scholar] [CrossRef]
- Freudenthal, A.M. The Inelastic Behaviour of Engineering Materials and Structures; John Wiley & Sons: New York, NY, USA, 1950. [Google Scholar]
- Cockroft, M.G.; Latham, D.J. Ductility and the workability of metals. J. Inst. Met. 1968, 96, 33–39. [Google Scholar]
- Rice, J.R.; Tracey, D.M. On the ductile enlargement of voids in triaxial stress fields. J. Mech. Phys. Solids 1969, 17, 201–217. [Google Scholar] [CrossRef]
- Brozzo, P.; Deluca, B.; Rendina, R. A new method for the prediction of formability limits in metal sheets. In Proceedings of the 7th Biennial Conference of the International Deep Drawing Research Group, Amsterdam, The Netherlands, 9–13 October 1972. [Google Scholar]
- Oyane, M. Criteria of DF strain. Bull. JSME 1972, 15, 1507–1513. [Google Scholar] [CrossRef]
- Argon, A.I.J.; Safoglu, R. Cavity formation from inclusions in ductile fracture. Metall. Mater. Trans. A 1975, 6, 825–837. [Google Scholar] [CrossRef]
- Oh, S.I.; Chen, C.C.; Kobayashi, S. Ductile fracture in axisymmetric extrusion and drawing. Part II Workability in extrusion and drawing. J. Eng. Ind. 1979, 101, 36–44. [Google Scholar] [CrossRef]
- Ayada, M.; Higashino, T.; Mori, K. Central bursting in extrusion of inhomogeneous materials. In Proceedings of the First International Conference on Technology of Plasticity, Tokyo, Japan, 3–5 September 1984; pp. 553–558. [Google Scholar]
- Zhan, M.; Gu, C.; Jiang, Z.; Hu, L.; Yang, H. Application of ductile fracture criteria in spin-forming and tube-bending processes. Comp. Mater. Sci. 2009, 47, 353–365. [Google Scholar] [CrossRef]
- Hambli, R.; Reszka, M. Fracture criteria identification using an inverse technique method and blanking experiment. Int. J. Mech. Sci. 2002, 44, 1349–1361. [Google Scholar] [CrossRef]
- Tomczak, J.; Bulzak, T.; Pater, Z. Theoretical and experimental analysis of rotary compression of ball pins hollow forgings. Adv. Sci. Technol. Res. J. 2016, 10, 109–117. [Google Scholar] [CrossRef]
- Pater, Z. Analysis of the Helical-Wedge Rolling Process for Producing a Long Stepped Shaft. Key Eng. Mater. 2014, 622–623, 893–898. [Google Scholar] [CrossRef]
- Pater, Z. A thermomechanical analysis of the multi-wedge helical rolling (MWHR) process for producing balls. Metalurgija 2016, 55, 233–236. [Google Scholar]
- Pater, Z.; Tofil, A.; Tomczak, J.; Bulzak, T. Numerical analysis of the cross wedge rolling process (CWR) for a stepped shaft. Metalurgija 2015, 54, 177–180. [Google Scholar]
- Pater, Z.; Tomczak, J.; Bartnicki, J.; Lovell, M.R.; Menezes, P.L. Experimental and numerical analysis of helical-wedge rolling process for producing steel balls. Int. J. Mach. Tool. Manuf. 2013, 67, 1–7. [Google Scholar] [CrossRef]
- Tofil, A.; Tomczak, J.; Bulzak, T. Numerical and experimental study on producing aluminium alloy 6061 shafts by cross wedge rolling using a universal rolling mill. Arch. Metall. Mater. 2015, 60, 801–807. [Google Scholar] [CrossRef]
- Copolla, T.; Cortese, L.; Folgarait, P. The effect of stress invariants on ductile fracture limit in steels. Eng. Fract. Mech. 2009, 76, 1288–1302. [Google Scholar] [CrossRef]
- Faleskog, J.; Barsoum, I. Tension-torsion fracture experiments—Part I: Experiments and a procedure to evaluate the equivalent plastic strain. Int. J. Solids Struct. 2013, 50, 4241–4257. [Google Scholar] [CrossRef]
- Li, W.; Liao, F.; Zhou, T.; Askes, H. Ductile fracture of Q460 steel: Effects of stress triaxiality and Lode angle. J. Constr. Steel Res. 2016, 123, 1–17. [Google Scholar] [CrossRef]
- Lee, Y.W.; Wierzbicki, T. Fracture prediction of thin plates under localized impulsive loading. Part II: Discing and petalling. Int. J. Impact Eng. 2005, 31, 1277–1308. [Google Scholar] [CrossRef]
- Bao, Y.; Wierzbicki, T. On the cut-off value of negative triaxiality for fracture. Eng. Fract. Mech. 2005, 72, 1049–1069. [Google Scholar] [CrossRef]








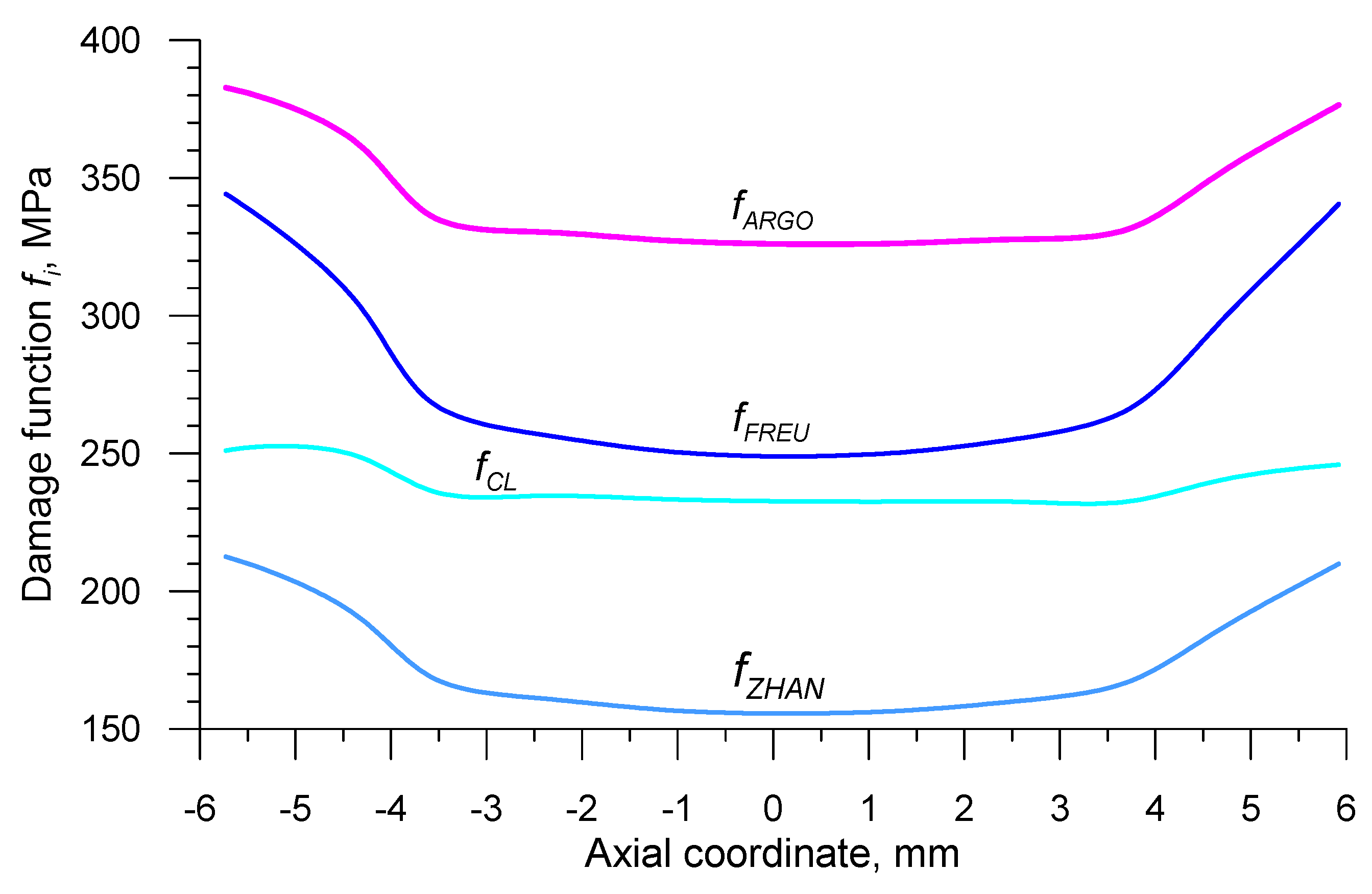
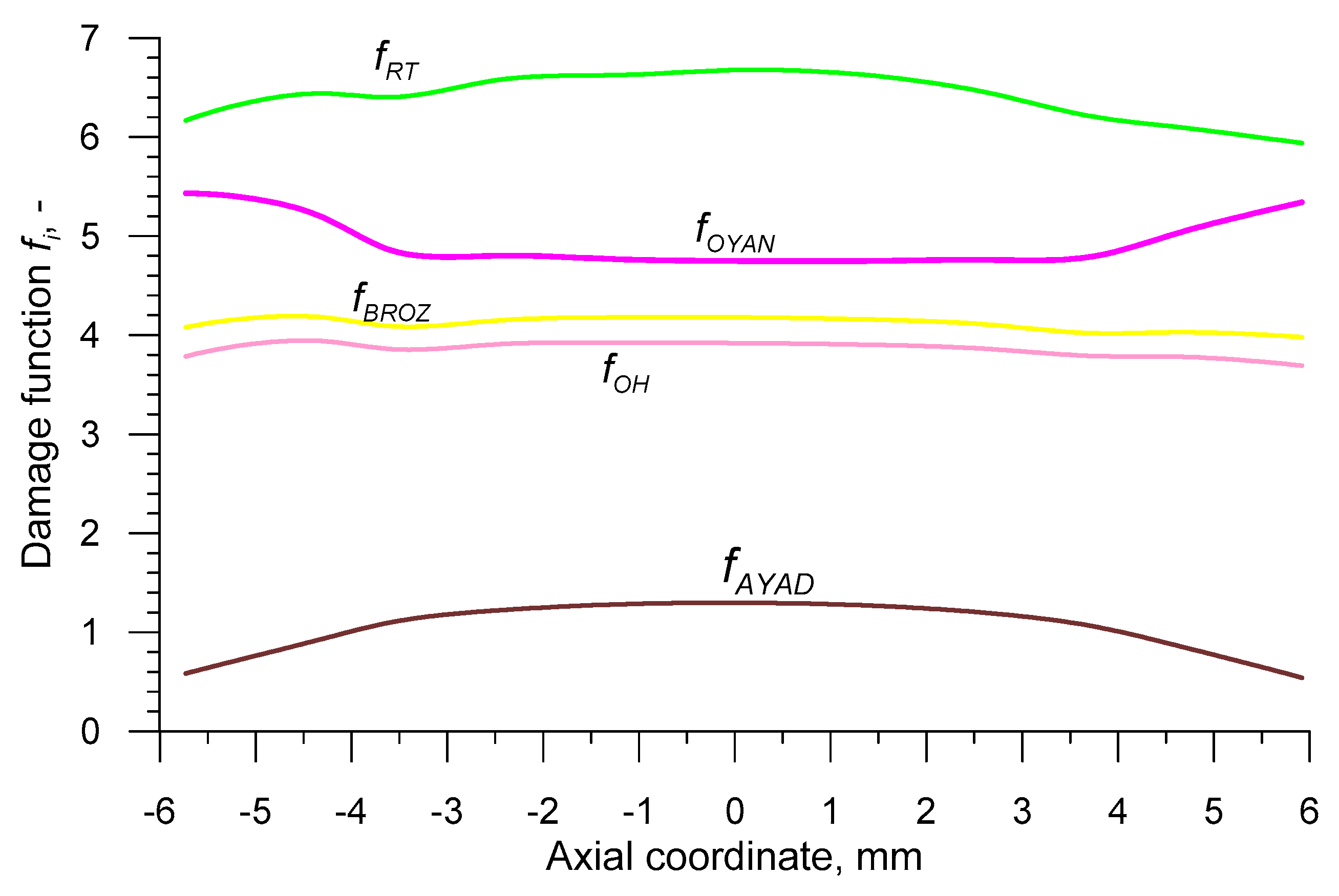


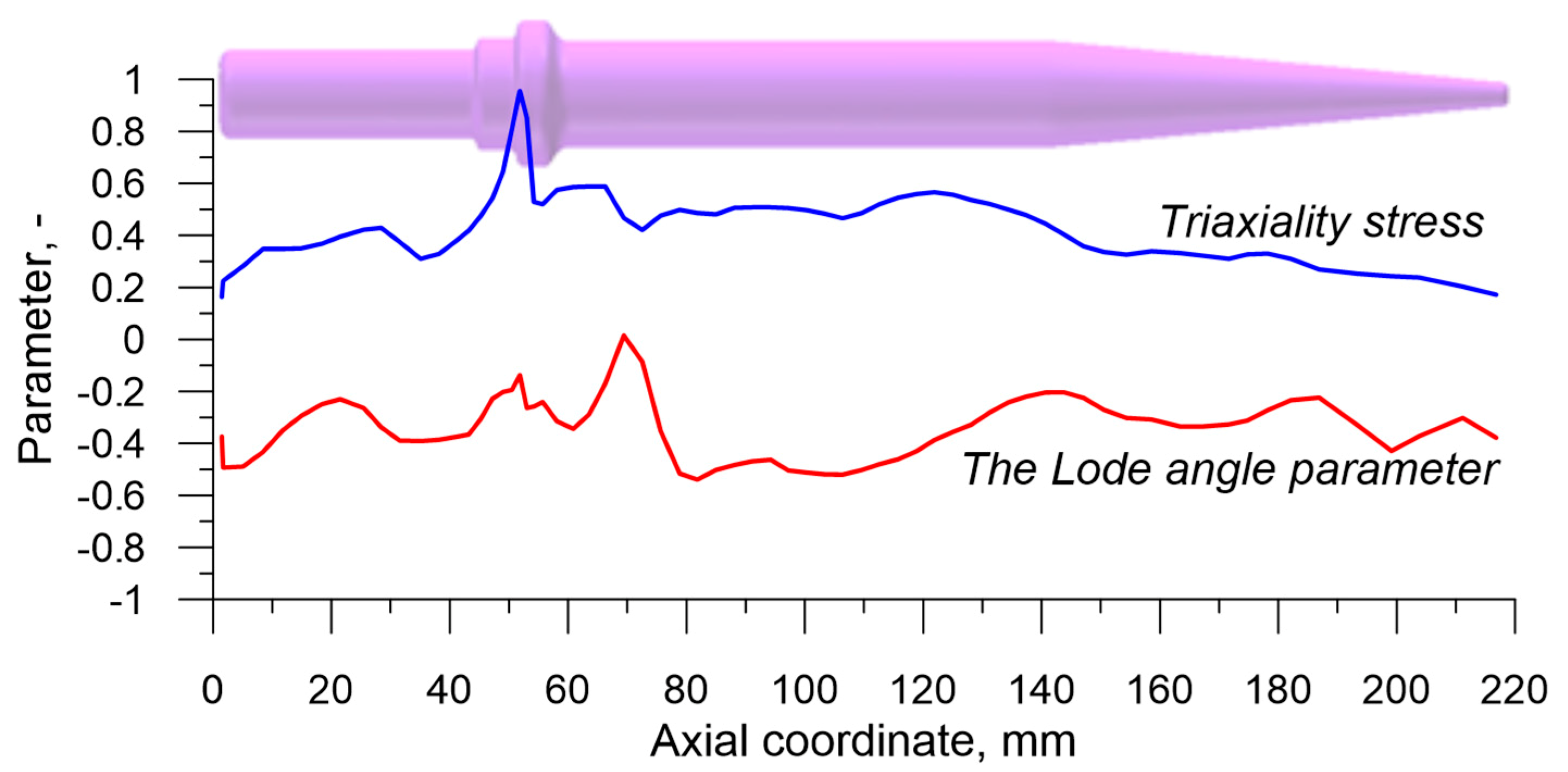

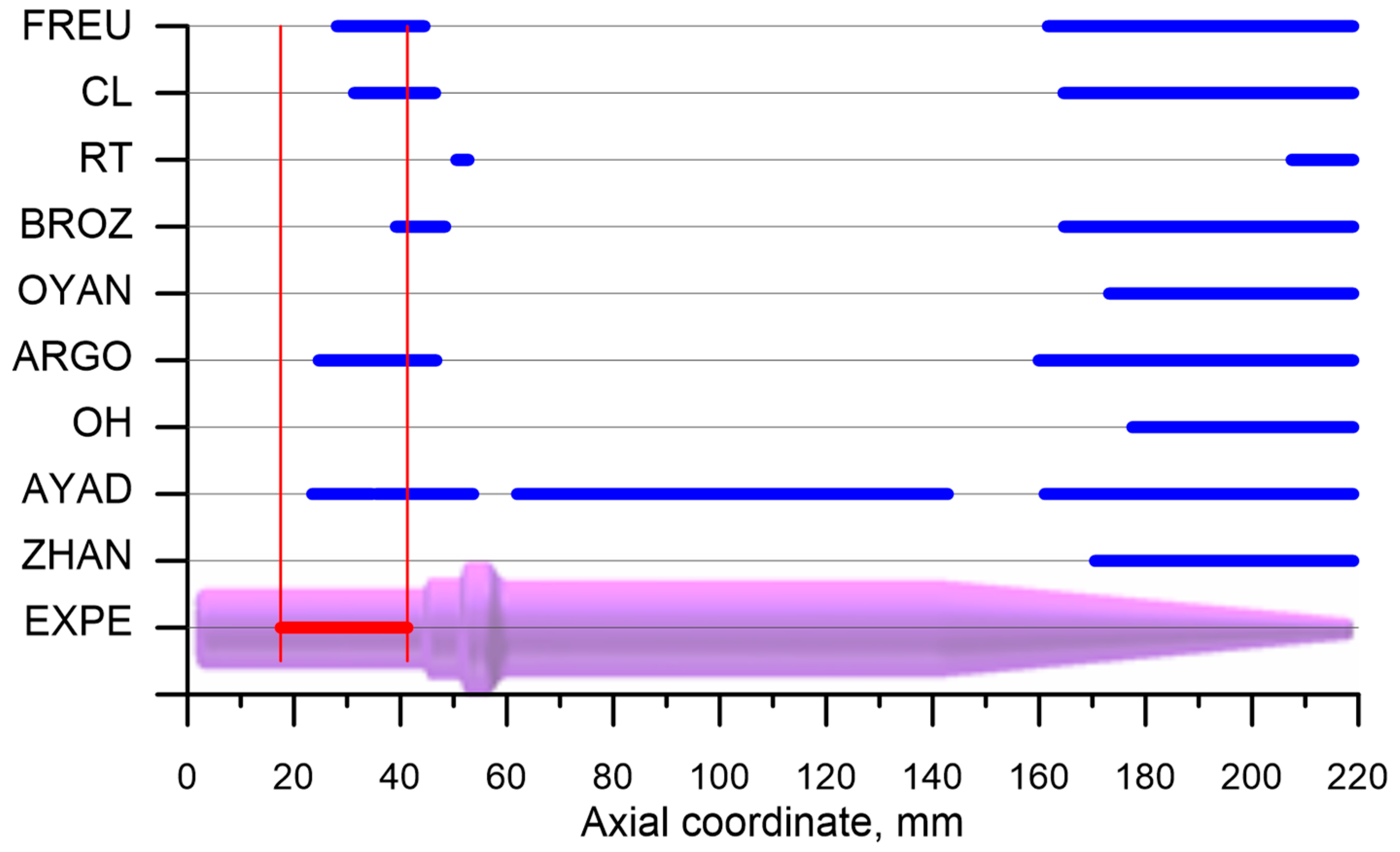
| Abbreviation | Criterion (year) | Formula |
|---|---|---|
| FREU | Freudenthal (1950) | |
| CL | Cockroft and Latham (1968) | |
| RT | Rice and Tracey (1969) | |
| BROZ | Brozzo et al. (1972) | |
| OYAN | Oyane (1972) | |
| ARGO | Argon et al. (1975) | |
| OH | Oh et al. (1979) | |
| AYAD | Ayada (1984) | |
| ZHAN | Zhan et al. (2009) |
| CFREU | CCL | CRT | CBROZ | COYAN | CARGO | COH | CAYAD | CZHAN |
|---|---|---|---|---|---|---|---|---|
| 180.1 MPa | 238.2 MPa | 6.38 | 4.11 | 4.95 | 343.3 MPa | 3.85 | 1.03 | 174.9 MPa |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pater, Z.; Tomczak, J.; Bulzak, T.; Bartnicki, J.; Tofil, A. Prediction of Crack Formation for Cross Wedge Rolling of Harrow Tooth Preform. Materials 2019, 12, 2287. https://doi.org/10.3390/ma12142287
Pater Z, Tomczak J, Bulzak T, Bartnicki J, Tofil A. Prediction of Crack Formation for Cross Wedge Rolling of Harrow Tooth Preform. Materials. 2019; 12(14):2287. https://doi.org/10.3390/ma12142287
Chicago/Turabian StylePater, Zbigniew, Janusz Tomczak, Tomasz Bulzak, Jarosław Bartnicki, and Arkadiusz Tofil. 2019. "Prediction of Crack Formation for Cross Wedge Rolling of Harrow Tooth Preform" Materials 12, no. 14: 2287. https://doi.org/10.3390/ma12142287
APA StylePater, Z., Tomczak, J., Bulzak, T., Bartnicki, J., & Tofil, A. (2019). Prediction of Crack Formation for Cross Wedge Rolling of Harrow Tooth Preform. Materials, 12(14), 2287. https://doi.org/10.3390/ma12142287







