A Different Approach to Estimate Temperature-Dependent Thermal Properties of Metallic Materials
Abstract
:1. Introduction
2. Materials and Methods
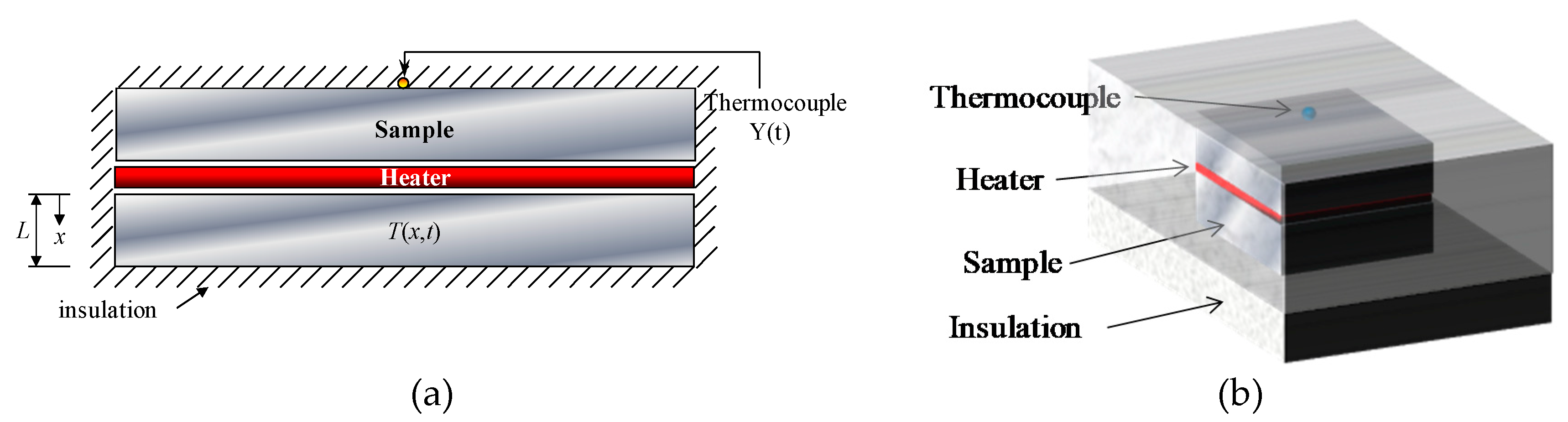
2.1. Thermal Design Model
2.2. Objective Function
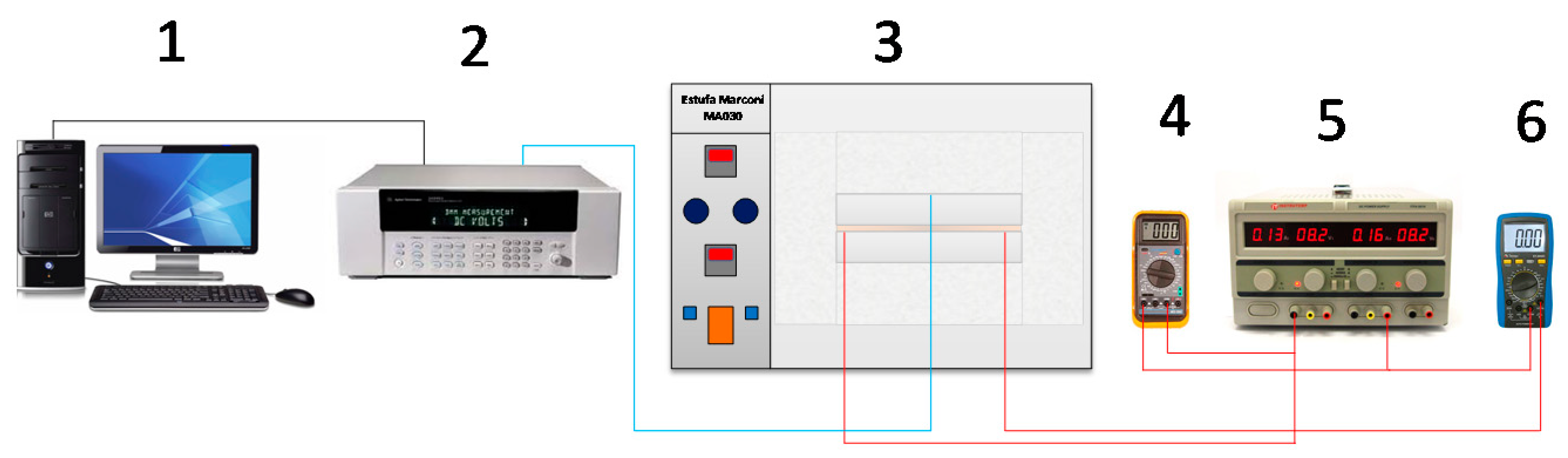
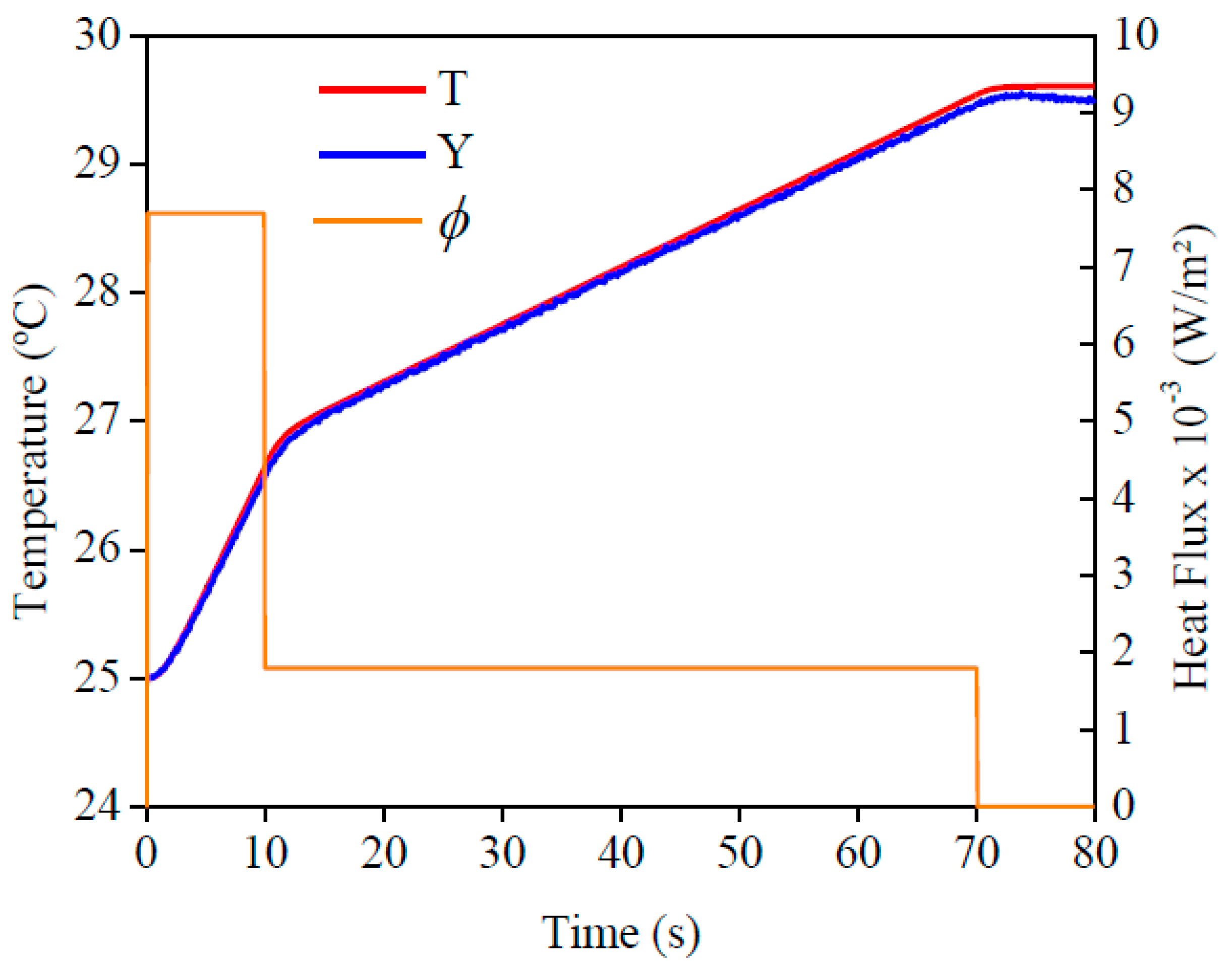
2.3. Experimental Procedure
3. Results and Discussion
3.1. AISI 1045 Steel
3.2. AISI 304 Stainless Steel
4. Uncertainty Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Santos, M.R.; Lima e Silva, S.M.M.; Machado, A.R.; Silva, M.B.; Guimarães, G.; Carvalho, S.R. Analysis of Effects of Cutting Parameters on Cutting Edge Temperature Using Inverse Heat Conduction Technique. Math. Prob. Eng. 2014, 2014, 1–11. [Google Scholar] [CrossRef]
- Brito, R.F.; Carvalho, S.R.; Lima e Silva, S.M.M. Investigation of Thermal Aspects in a Cutting Tool Using Comsol and Inverse Problem. Appl. Therm. Eng. 2015, 86, 60–68. [Google Scholar] [CrossRef]
- Jannot, Y.; Degiovanni, A.; Payet, G. Thermal conductivity measurement of insulating materials with a three layers device. Int. J. Heat Mass Transf. 2009, 52, 1105–1111. [Google Scholar] [CrossRef]
- Xamán, J.; Lira, L.; Arce, J. Analysis of the temperature distribution in a guarded hot plate apparatus for measuring thermal conductivity. Appl. Therm. Eng. 2009, 29, 617–623. [Google Scholar] [CrossRef]
- Thomas, M.; Boyard, N.; Lefèvre, N.; Jarny, Y.; Delaunay, D. An experimental device for the simultaneous estimation of the thermal conductivity 3-D tensor and the specific heat of orthotropic composite materials. Int. J. Heat Mass Transf. 2010, 53, 5487–5498. [Google Scholar] [CrossRef]
- Aksöz, S.; Ocak, Y.; Marasli, N.; Cadirli, E.; Kaya, H.; Böyük, U. Dependency of the Thermal and Electrical Conductivity on the Temperature and Composition of Cu in the Al based Al–Cu Alloys. Exp. Therm. Fluid Sci. 2010, 34, 1507–1516. [Google Scholar] [CrossRef]
- Karimi, G.; Li, X.; Teerstra, P. Measurement of Through-plane Effective Thermal Conductivity and Contact Resistance in PEM Fuel Cell Diffusion. Media Electrochim. Acta 2010, 55, 1619–1625. [Google Scholar] [CrossRef]
- Sadeghi, E.; Djilali, N.; Bahrami, M. A Novel Approach to Determine the In-plane Thermal Conductivity of Gas Diffusion Layers in Proton Exchange Membrane Fuel Cells. J. Power Sources 2011, 196, 3565–3571. [Google Scholar] [CrossRef]
- Zamel, N.; Becker, J.; Wiegmann, A. Estimating the Thermal Conductivity and Diffusion Coefficient of the Microporous Layer of Polymer Electrolyte Membrane Fuel Cells. J. Power Sources 2012, 207, 70–80. [Google Scholar] [CrossRef]
- Öztürk, E.; Aksöz, S.; Keslioglu, K.; Marasli, N. The Measurement of Thermal Conductivity variation with Temperature for Sn-20 wt.% in based Lead-free Ternary Solders. Thermochim. Acta 2013, 554, 63–70. [Google Scholar] [CrossRef]
- Zgraja, J.; Cieslak, A. Induction heating in estimation of thermal properties of conductive materials. Int. J. Comput. Math. Electr. Electron. Eng. 2017, 36, 458–468. [Google Scholar] [CrossRef]
- Somasundharam, S.; Reddy, K.S. Simultaneously estimation of thermal properties of orthotropic material with non-intrusive measurement. Int. J. Heat Mass Transf. 2018, 126, 1162–1177. [Google Scholar] [CrossRef]
- García, E.; Amaya, I.; Correa, R. Estimation of thermal properties of a solid sample during a microwave heating process. Appl. Therm. Eng. 2018, 129, 587–595. [Google Scholar] [CrossRef]
- Lembcke, L.G.M.; Roubinet, D.; Gidel, F.; Irving, J.; Pehme, P.; Parker, B.L. Analytical analysis of borehole experiments for the estimation of subsurface thermal properties. Adv. Water Resour. 2016 91, 88–103.
- Ren, Y.; Qi, H.; He, M.; Ruan, S.; Ruan, L.; Tan, H. Application of an improved firework algorithm for simultaneous estimation of temperature-dependent thermal and optical properties of molten salt. Int. Commun. Heat Mass Transf. 2016, 77, 33–42. [Google Scholar] [CrossRef]
- Udayraj; Talukdar, P.; Das, A.; Alagirusamy, R. Simultaneous estimation of thermal conductivity and specific heat of thermal protective fabrics using experimental data of high heat flux exposure. Appl. Therm. Eng. 2016, 107, 785–796. [Google Scholar] [CrossRef]
- Carollo, L.F.S.; Lima e Silva, A.L.F.; Lima e Silva, S.M.M. Applying Different Heat Flux Intensities to Simultaneously Estimate the Thermal Properties of Metallic Materials. Meas. Sci. Technol. 2012, 23, 1–10. [Google Scholar] [CrossRef]
- Özisik, M.N. Heat Conduction; John Wiley & Sons: Etobicoke, ON, Canada, 1993; p. 692. [Google Scholar]
- Tillmann, A.R.; Borges, V.L.; Guimarães, G.; Lima e Silva, A.L.F.; Lima e Silva, S.M.M. Identification of Temperature-Dependent Thermal Properties of Solid Materials. J. Braz. Soc. Mech. Sci. Eng. 2008, 30, 269–278. [Google Scholar] [CrossRef]
- Vanderplaats, G.N. Numerical Optimization Techniques for Engineering Design; McGraw: New York, NY, USA, 2005; p. 465. [Google Scholar]
- Grzesik, W.; Nieslony, P.; Bartoszuk, M. Modelling of the Cutting Process Analytical and Simulation Methods. Adv. Manuf. Sci. Technol. 2009, 33, 6–29. [Google Scholar]
- Montgomery, D.C.; Runger, G.C. Applied Statistic and Probability for Engineers; John Wiley & Sons: New York, NY, USA, 2013; p. 811. [Google Scholar]
- Abas, R.A.; Hayashi, M.; Seetharaman, S. Thermal Diffusivity Measurements of Some Industrially Important Alloys by a Laser Flash Method. Int. J. Mater. Res. 2009, 98, 1–6. [Google Scholar] [CrossRef]
- Taylor, J.R. An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements; University Science Books: Sausalito, CA, USA, 1997; p. 488. [Google Scholar]




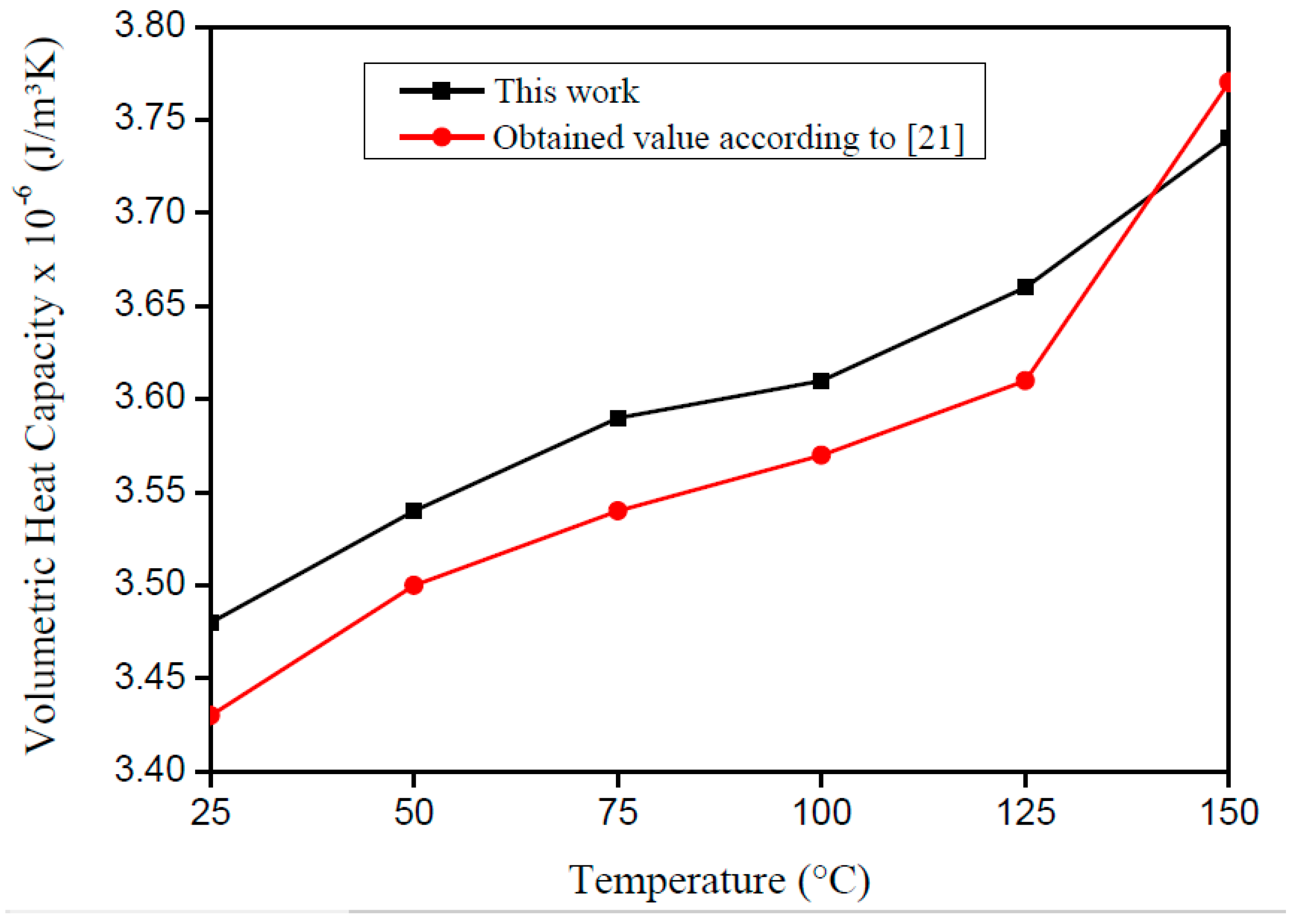
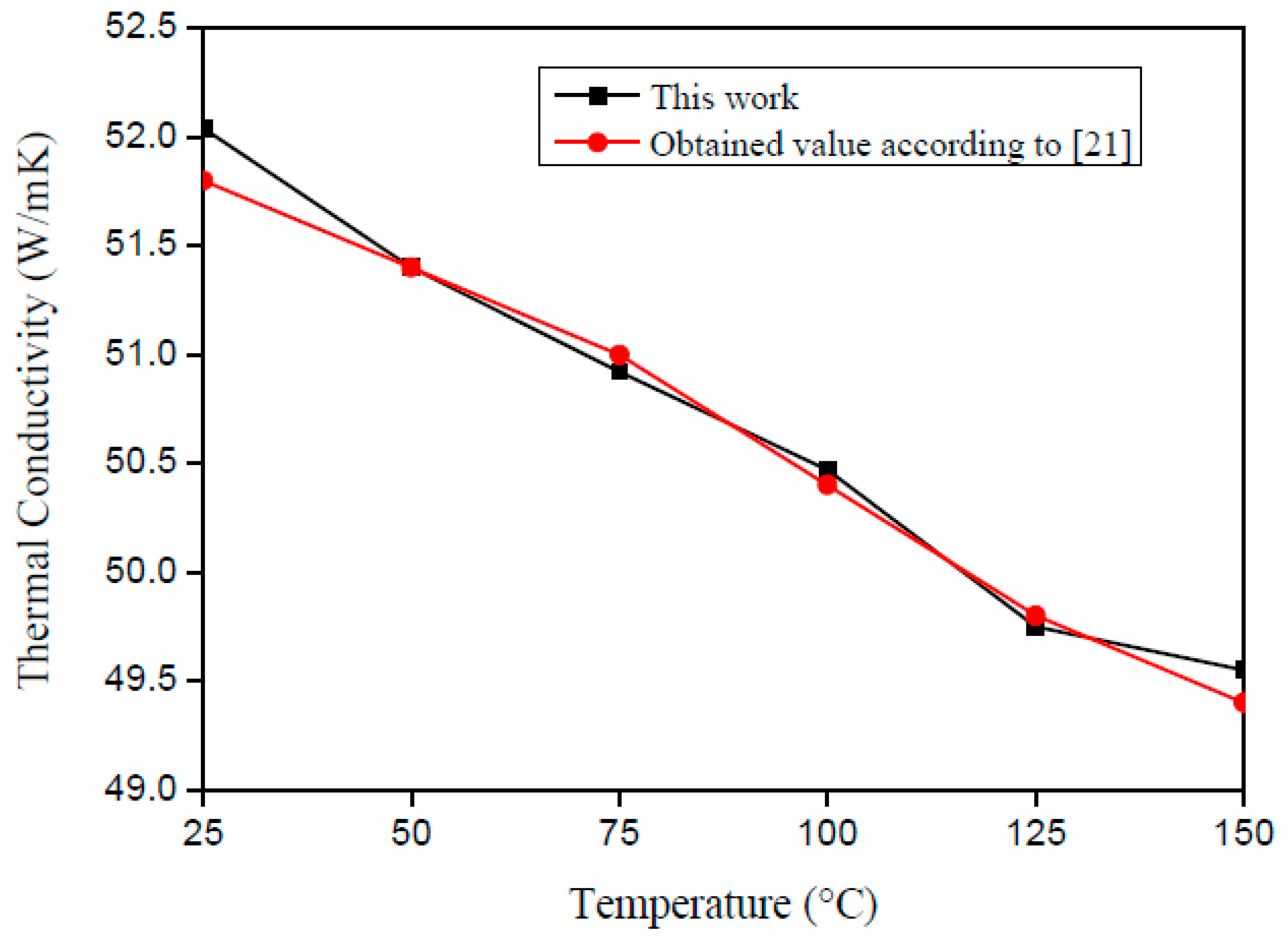





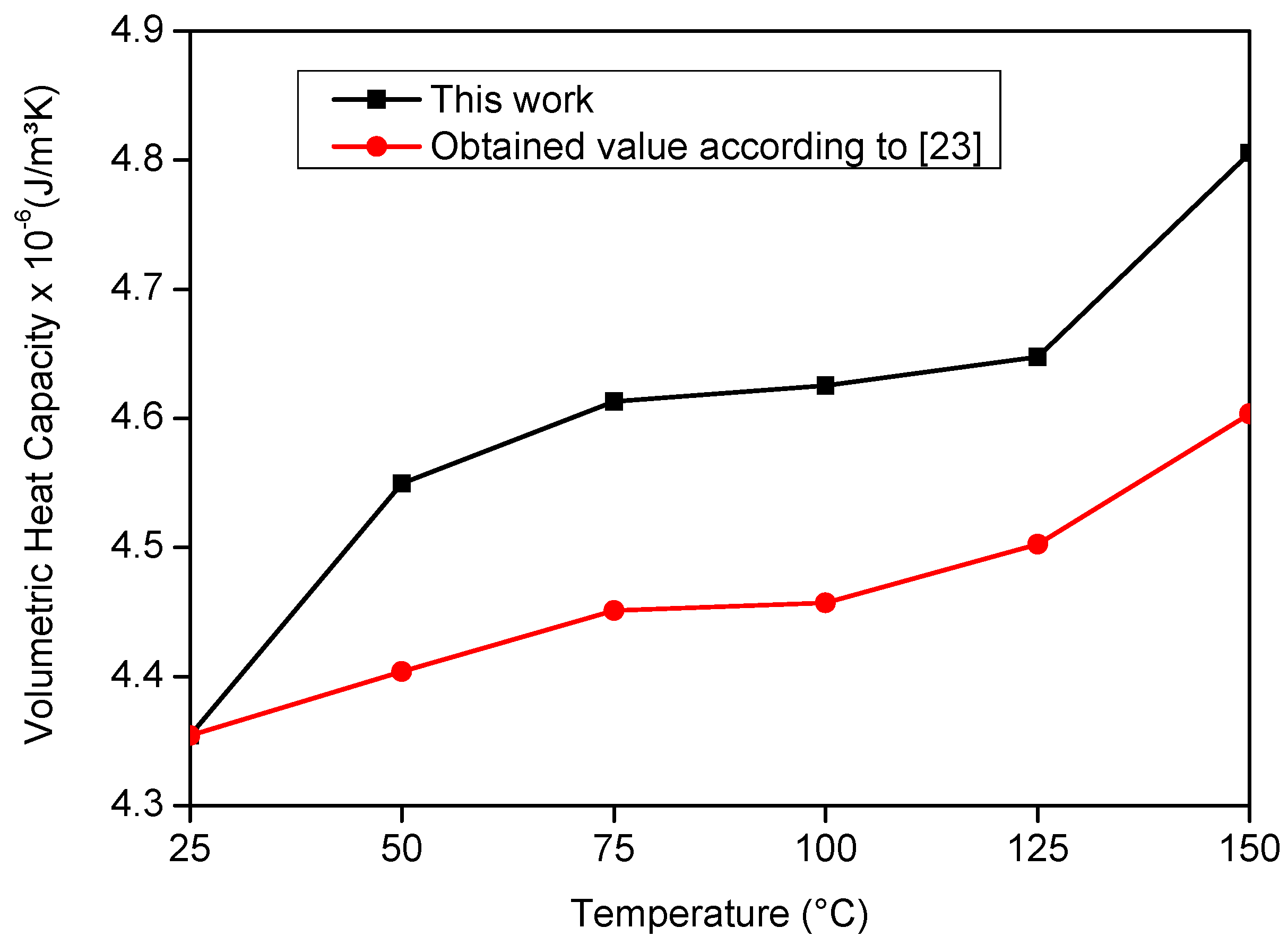
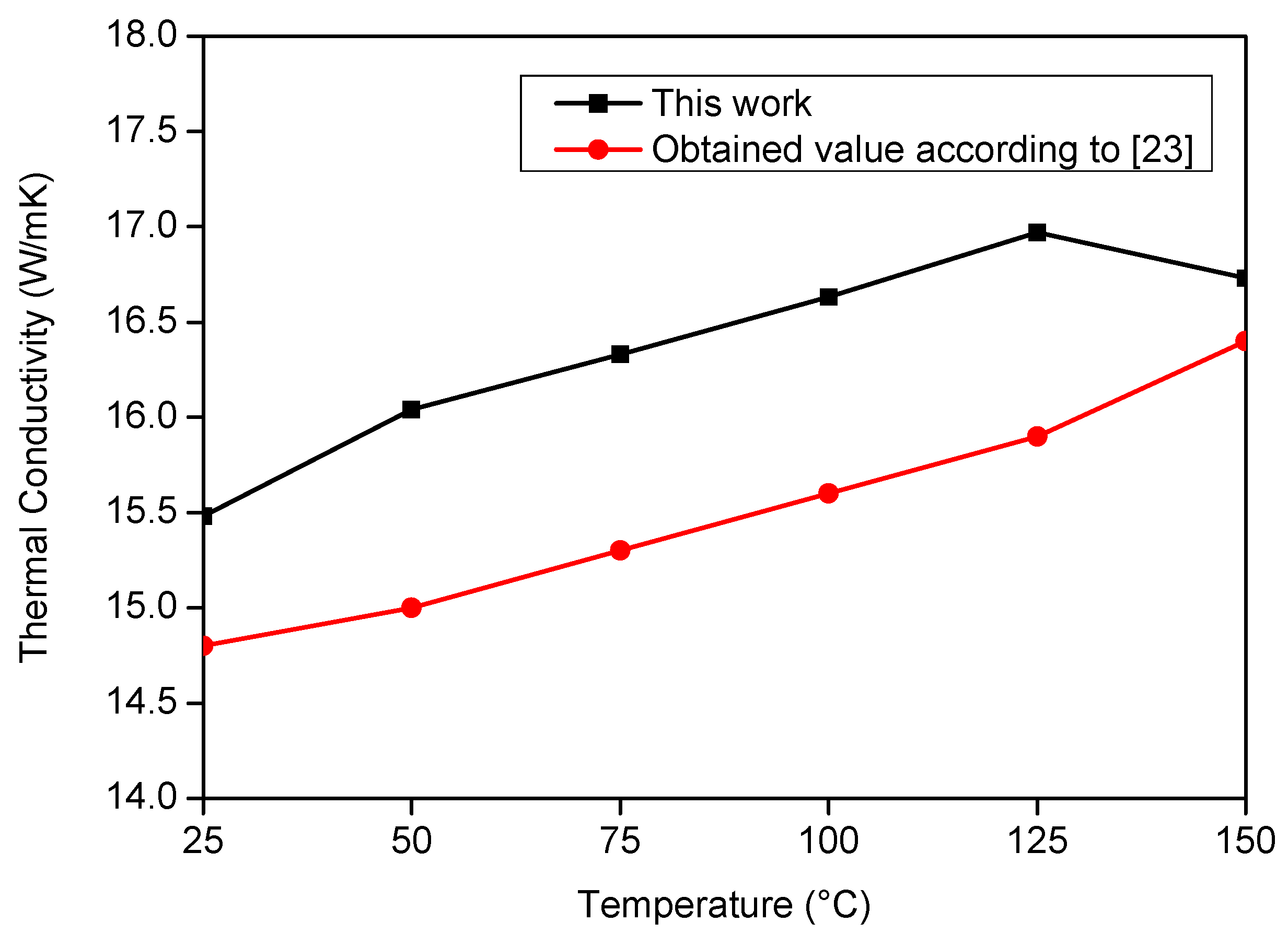
| Average T0 (°C) | Thermal Properties | Mean | Obtained value from Grzesik et al. [21] | Standard Deviation | Error (%) |
|---|---|---|---|---|---|
| 25.4 | ρcp × 10−6 (J/m³K) | 3.48 | 3.43 | ±0.02 | 1.44 |
| λ (W/mK) | 52.04 | 51.80 | ±0.49 | 0.46 | |
| 50.1 | ρcp ×10−6 (J/m³K) | 3.54 | 3.50 | ±0.05 | 1.18 |
| λ (W/mK) | 51.39 | 51.4 | ±0.25 | 0.02 | |
| 75.4 | ρcp × 10−6 (J/m³K) | 3.59 | 3.54 | ±0.04 | 1.36 |
| λ (W/mK) | 50.92 | 51.00 | ±0.37 | 0.16 | |
| 100.4 | ρcp × 10−6 (J/m³K) | 3.61 | 3.66 | ±0.03 | 0.99 |
| λ (W/mK) | 50.47 | 50.40 | ±0.28 | 0.14 | |
| 125.3 | ρcp × 10−6 (J/m³K) | 3.66 | 3.61 | ±0.05 | 1.42 |
| λ (W/mK) | 49.75 | 49.80 | ±0.38 | 0.10 | |
| 150.2 | ρcp × 10−6 (J/m³K) | 3.74 | 3.77 | ±0.02 | 0.86 |
| λ (W/mK) | 49.55 | 49.40 | ±0.36 | 0.30 |
| Average T0 (°C) | Thermal Properties | Mean | Obtained value from Abas et al. [23] | Standard Deviation | Error (%) |
|---|---|---|---|---|---|
| 24.8 | ρcp × 10−6 (J/m³K) | 4.35 | 4.35 | ±0.12 | 0.03 |
| λ (W/mK) | 15.49 | 14.8 | ±0.39 | 4.64 | |
| 49.7 | ρcp × 10−6 (J/m³K) | 4.55 | 4.40 | ±0.09 | 3.31 |
| λ (W/mK) | 16.04 | 15.0 | ±0.58 | 6.95 | |
| 74.9 | ρcp × 10−6 (J/m³K) | 4.61 | 4.45 | ±0.06 | 3.64 |
| λ (W/mK) | 16.33 | 15.3 | ±0.47 | 6.76 | |
| 99.2 | ρcp × 10−6 (J/m³K) | 4.63 | 4.46 | ±0.07 | 3.77 |
| λ (W/mK) | 16.63 | 15.6 | ±0.53 | 6.62 | |
| 124.9 | ρcp × 10−6 (J/m³K) | 4.65 | 4.50 | ±0.06 | 3.22 |
| λ (W/mK) | 16.97 | 15.9 | ±0.57 | 6.74 | |
| 149.5 | ρcp × 10−6 (J/m³K) | 4.80 | 4.60 | ±0.09 | 4.38 |
| λ (W/mK) | 16.73 | 16.4 | ±0.67 | 2.01 |
| Material | Uncertainty (%) |
|---|---|
| AISI 1045 steel | 5.45 |
| AISI 304 stainless steel | 4.79 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carollo, L.F.d.S.; Lima e Silva, A.L.F.d.; Lima e Silva, S.M.M.d. A Different Approach to Estimate Temperature-Dependent Thermal Properties of Metallic Materials. Materials 2019, 12, 2579. https://doi.org/10.3390/ma12162579
Carollo LFdS, Lima e Silva ALFd, Lima e Silva SMMd. A Different Approach to Estimate Temperature-Dependent Thermal Properties of Metallic Materials. Materials. 2019; 12(16):2579. https://doi.org/10.3390/ma12162579
Chicago/Turabian StyleCarollo, Luís Felipe dos Santos, Ana Lúcia Fernandes de Lima e Silva, and Sandro Metrevelle Marcondes de Lima e Silva. 2019. "A Different Approach to Estimate Temperature-Dependent Thermal Properties of Metallic Materials" Materials 12, no. 16: 2579. https://doi.org/10.3390/ma12162579
APA StyleCarollo, L. F. d. S., Lima e Silva, A. L. F. d., & Lima e Silva, S. M. M. d. (2019). A Different Approach to Estimate Temperature-Dependent Thermal Properties of Metallic Materials. Materials, 12(16), 2579. https://doi.org/10.3390/ma12162579





