Electrical Resistance Prediction for Functionalized Multi-Walled Carbon Nanotubes/Epoxy Resin Composite Gasket under Thermal Creep Conditions
Abstract
:1. Introduction
2. Experimental
2.1. Composite Preparation
2.2. Scanning Electron Microscope Observation
2.3. Electrical Resistance Measurement during Creep
2.4. Dynamic Thermomechanical Analysis
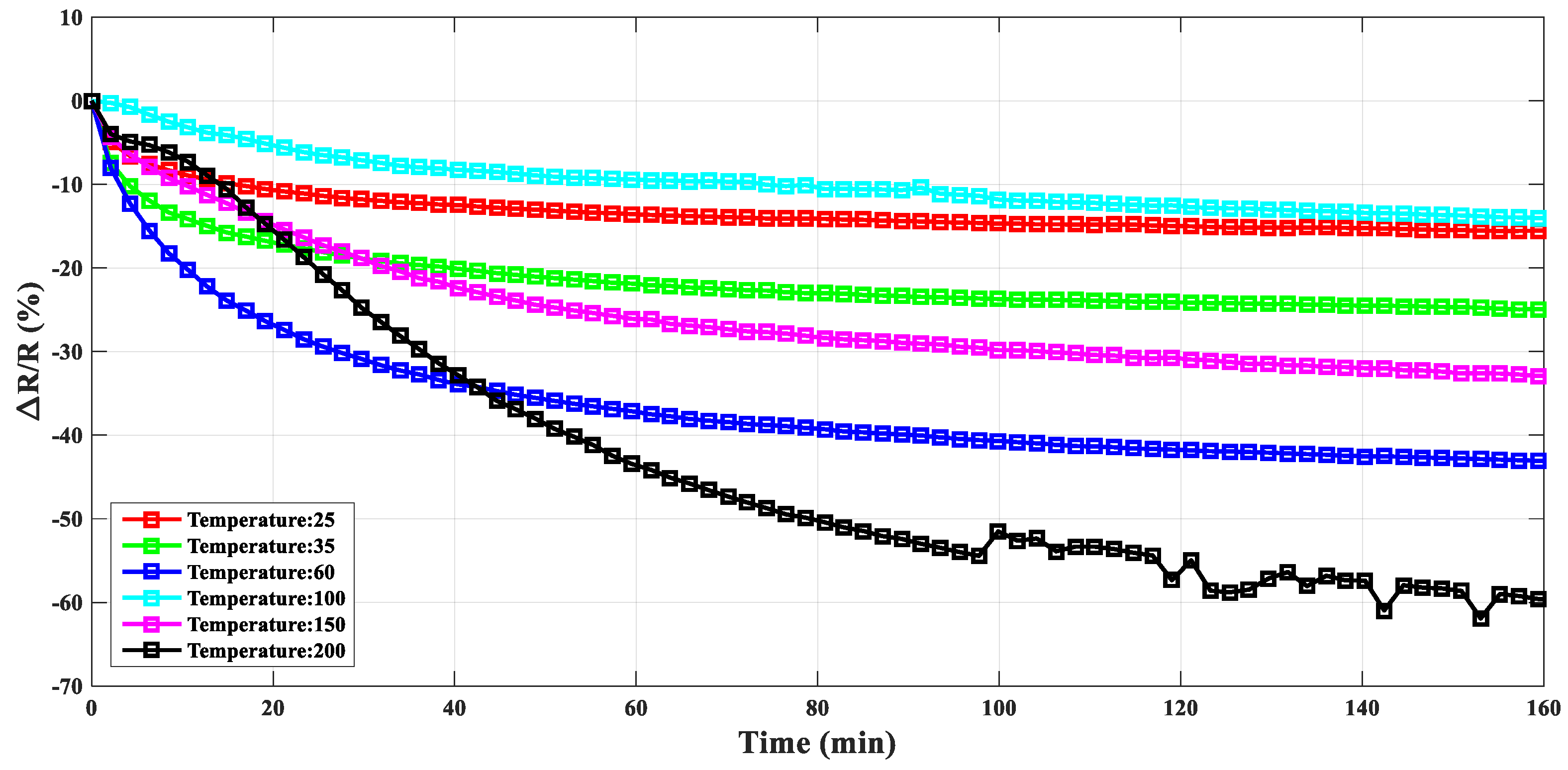
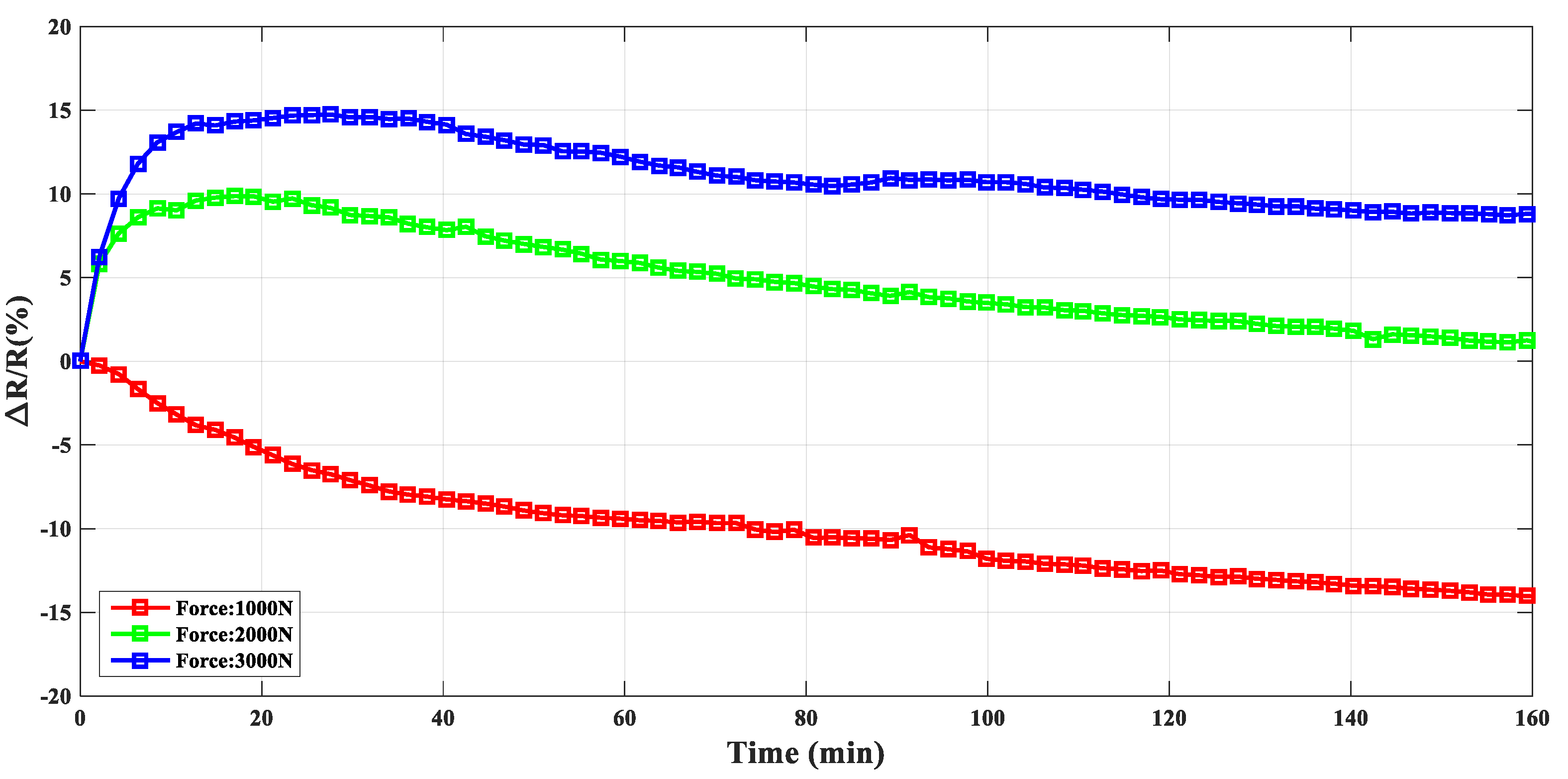
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nie, P.; Xiong, X.H. Progress on carbon nanotubes in health monitoring of polymer composites. J. Aeronaut. Mater. 2015, 35, 12–20. [Google Scholar]
- Xu, D.; Cheng, X.; Huang, S.; Jiang, M. Identifying technology for structural damage based on the impedance analysis of piezoelectric sensor. Constr. Build. Mater. 2010, 24, 2522–2527. [Google Scholar] [CrossRef]
- Thostenson, E.T.; Chou, T.W. Carbon nanotube-based health monitoring of mechanically fastened composite joints. Compos. Sci. Technol. 2008, 68, 2557–2561. [Google Scholar] [CrossRef]
- Friedrich, S.M.; Wu, A.S.; Thostenson, E.T.; Chou, T.W. Damage mode characterization of mechanically fastened composite joints using carbon nanotube networks. Compos. Part A Appl. Sci. Manuf. 2011, 42, 2003–2009. [Google Scholar] [CrossRef]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56. [Google Scholar] [CrossRef]
- Schilde, C.; Schlömann, M.; Overbeck, A.; Linke, S.; Kwade, A. Thermal, mechanical and electrical properties of highly loaded cnt-epoxy composites—A model for the electric conductivity. Compos. Sci. Technol. 2015, 117, 183–190. [Google Scholar] [CrossRef]
- Hu, L.; Hecht, D.S.; Gruner, G. Percolation in transparent and conducting carbon nanotube networks. Nano Lett. 2004, 4, 2513–2517. [Google Scholar] [CrossRef]
- Wang, W.; Wang, C.; Yue, X.; Zhang, C.; Zhou, C.; Wu, W.; Zhu, H. Raman spectroscopy and resistance-temperature studies of functionalized multiwalled carbon nanotubes/epoxy resin composite film. Microelectron. Eng. 2019, 214, 50–54. [Google Scholar] [CrossRef]
- Hu, B.; Liu, Y.; Hu, N.; Wu, L.; Ning, H.; Zhang, J.; Fu, S.; Tang, S.; Xu, C.; Liu, F.; et al. Conductive pvdf-hfp/cnt composites for strain sensing. Funct. Mater. Lett. 2016, 9, 1650024. [Google Scholar] [CrossRef]
- Gao, L.; Chou, T.W.; Thostenson, E.T.; Zhang, Z.; Coulaud, M. In situ sensing of impact damage in epoxy/glass fiber composites using percolating carbon nanotube networks. Carbon 2011, 49, 3382–3385. [Google Scholar] [CrossRef]
- Kim, K.J.; Yu, W.R.; Lee, J.S.; Gao, L.; Thostenson, E.T.; Chou, T.W.; Byun, J.H. Damage characterization of 3d braided composites using carbon nanotube-based in situ sensing. Compos. Part A Appl. Sci. Manuf. 2010, 41, 1531–1537. [Google Scholar] [CrossRef]
- Wu, A.S.; Coppola, A.M.; Sinnott, M.J.; Chou, T.W.; Thostenson, E.T.; Byun, J.H.; Kim, B.S. Sensing of damage and healing in three-dimensional braided composites with vascular channels. Compos. Sci. Technol. 2012, 72, 1618–1626. [Google Scholar] [CrossRef]
- Fiedler, B.; Gojny, F.H.; Wichmann, M.H.G.; Bauhofer, W.; Schulte, K. Can carbon nanotubes be used to sense damage in composites? Ann. De Chim. Sci. Des Mater. 2004, 29, 81–94. [Google Scholar] [CrossRef]
- Alexopoulos, N.D.; Bartholome, C.; Poulin, P.; Marioli-Riga, Z. Structural health monitoring of glass fiber reinforced composites using embedded carbon nanotube (CNT) fibers. Compos. Sci. Technol. 2010, 70, 260–271. [Google Scholar] [CrossRef]
- Dehghani, S.; Moravvej-Farshi, M.K. Temperature dependence of electrical resistance of individual carbon nanotubes and carbon nanotubes network. Mod. Phys. Lett. B 2012, 26, 1250136. [Google Scholar] [CrossRef]
- Yin, G.; Hu, N.; Karube, Y.; Liu, Y.; Li, Y.; Fukunaga, H. A carbon nanotube/polymer strain sensor with linear and anti-symmetric piezoresistivity. J. Compos. Mater. 2011, 45, 1315–1323. [Google Scholar]
- Song, X.; Liu, S.; Gan, Z.; Lv, Q.; Cao, H.; Yan, H. Controllable fabrication of carbon nanotube-polymer hybrid thin film for strain sensing. Microelectron. Eng. 2009, 86, 2330–2333. [Google Scholar] [CrossRef]
- Wang, Z.; Ye, X. A numerical investigation on piezoresistive behaviour of carbon nanotube/polymer composites: Mechanism and optimizing principle. Nanotechnology 2013, 24, 256704. [Google Scholar] [CrossRef]
- Cai, L.; Song, L.; Luan, P.; Zhang, Q.; Zhang, N.; Gao, Q.; Zhao, D.; Zhang, X.; Tu, M.; Yang, F.; et al. Super-stretchable, transparent carbon nanotube-based capacitive strain sensors for human motion detection. Sci. Rep. 2013, 3, 3048. [Google Scholar] [CrossRef]
- Liu, L.; Wang, Z.; Feng, J.; Ye, X. Benzene sensors based on multi-walled carbon nanotube networks decorated with metal nanoclusters. J. Nanosci. Nanotechnol. 2013, 13, 989–992. [Google Scholar] [CrossRef]
- Shojaei, A.K.; Wedgewood, A.R. An anisotropic cyclic plasticity, creep and fatigue predictive tool for unfilled polymers. Mech. Mater. 2017, 106, 20–34. [Google Scholar] [CrossRef]
- Wang, X.; Gong, L.X.; Tang, L.C.; Peng, K.; Pei, Y.B.; Zhao, L.; Wu, L.B.; Jiang, J.X. Temperature dependence of creep and recovery behaviors of polymer composites filled with chemically reduced graphene oxide. Compos. Part A Appl. Sci. Manuf. 2015, 69, 288–298. [Google Scholar] [CrossRef]
- Zeng, Y.; Lu, G.; Wang, H.; Du, J.; Ying, Z.; Liu, C. Positive temperature coefficient thermistors based on carbon nanotube/polymer composites. Sci. Rep. 2014, 4, 6684. [Google Scholar] [CrossRef] [PubMed]
- Tae, P.; Zhao, C.; Fernandes, G.E.; Kim, J.H.; Xu, J. Molecular weight effects on the phase-change-enhanced temperature coefficient of resistance in carbon nanotube/poly(n-isopropylacrylamide) composites. Nanotechnology 2015, 26, 215705. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.P.; Wu, Y.H.; Yang, D.D.; Wang, J.R.; Xie, H.Q. Study on theories and influence factors of ptc property in polymer-based conductive composites. Rev. Adv. Mater. Sci. 2011, 27, 173–183. [Google Scholar]
- Kaiser, A.B.; Skakalova, V. Electronic conduction in polymers, carbon nanotubes and graphene. Chem. Soc. Rev. 2011, 40, 3786–3801. [Google Scholar] [CrossRef] [PubMed]
- Alig, I.; Skipa, T.; Lellinger, D.; Pötschke, P. Destruction and formation of a carbon nanotube network in polymer melts: Rheology and conductivity spectroscopy. Polymer 2008, 49, 3524–3532. [Google Scholar] [CrossRef]
- Schawe, J.E.K. Description of thermal relaxation of polystyrene close to the thermal glass transition. J. Polym. Sci. Part B Polym. Phys. 2015, 36, 2165–2175. [Google Scholar] [CrossRef]
- Pegel, S.; Poetschke, P.; Petzold, G.; Alig, I.; Dudkin, S.M.; Lellinger, D. Dispersion, agglomeration, and network formation of multiwalled carbon nanotubes in polycarbonate melts. Polymer 2008, 49, 974–984. [Google Scholar] [CrossRef]
- Meier, J.G.; Klüppel, M. Carbon black networking in elastomers monitored by dynamic mechanical and dielectric spectroscopy. Macromol. Mater. Eng. 2010, 293, 12–38. [Google Scholar] [CrossRef]
- Alig, I.; Skipa, T.; Engel, M.; Lellinger, D.; Pegel, S.; Pötschke, P. Electrical conductivity recovery in carbon nanotube–polymer composites after transient shear. Phys. Status Solidi 2010, 244, 4223–4226. [Google Scholar] [CrossRef]
- Alig, I.; Skipa, T.; Lellinger, D.; Bierdel, M.; Meyer, H. Dynamic percolation of carbon nanotube agglomerates in a polymer matrix: Comparison of different model approaches. Phys. Status Solidi B 2010, 245, 2264–2267. [Google Scholar] [CrossRef]
- Wang, P.; Ding, T. Creep of electrical resistance under uniaxial pressures for carbon black–silicone rubber composite. J. Mater. Sci. 2010, 45, 3595–3601. [Google Scholar] [CrossRef]
- Alig, I.; Lellinger, D.; Engel, M.; Skipa, T.; Pötschke, P. Destruction and formation of a conductive carbon nanotube network in polymer melts: In-line experiments. Polymer 2008, 49, 1902–1909. [Google Scholar] [CrossRef]





© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Yue, X.; Huang, H.; Wang, C.; Mo, D.; Wu, Y.; Xu, Q.; Zhou, C.; Zhu, H.; Zhang, C. Electrical Resistance Prediction for Functionalized Multi-Walled Carbon Nanotubes/Epoxy Resin Composite Gasket under Thermal Creep Conditions. Materials 2019, 12, 2704. https://doi.org/10.3390/ma12172704
Wang W, Yue X, Huang H, Wang C, Mo D, Wu Y, Xu Q, Zhou C, Zhu H, Zhang C. Electrical Resistance Prediction for Functionalized Multi-Walled Carbon Nanotubes/Epoxy Resin Composite Gasket under Thermal Creep Conditions. Materials. 2019; 12(17):2704. https://doi.org/10.3390/ma12172704
Chicago/Turabian StyleWang, Wenlong, Xia Yue, He Huang, Chao Wang, Diwei Mo, Yuyan Wu, Qingchun Xu, Chao Zhou, Houyao Zhu, and Chunliang Zhang. 2019. "Electrical Resistance Prediction for Functionalized Multi-Walled Carbon Nanotubes/Epoxy Resin Composite Gasket under Thermal Creep Conditions" Materials 12, no. 17: 2704. https://doi.org/10.3390/ma12172704
APA StyleWang, W., Yue, X., Huang, H., Wang, C., Mo, D., Wu, Y., Xu, Q., Zhou, C., Zhu, H., & Zhang, C. (2019). Electrical Resistance Prediction for Functionalized Multi-Walled Carbon Nanotubes/Epoxy Resin Composite Gasket under Thermal Creep Conditions. Materials, 12(17), 2704. https://doi.org/10.3390/ma12172704



