Estimation of Recycled Concrete Aggregate’s Water Permeability Coefficient as Earth Construction Material with the Application of an Analytical Method
Abstract
:1. Introduction
2. Literature Review
3. Materials and Methods
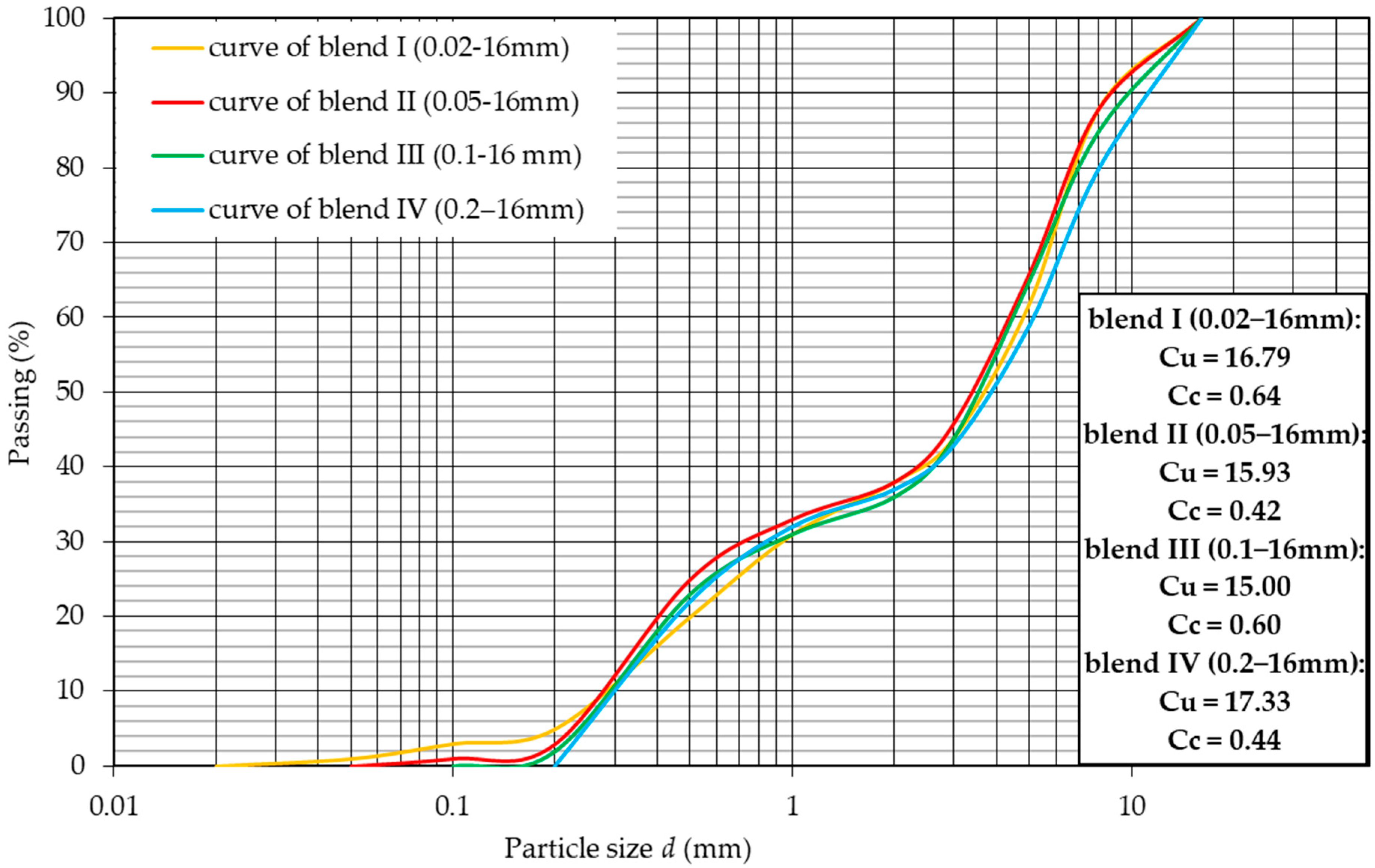
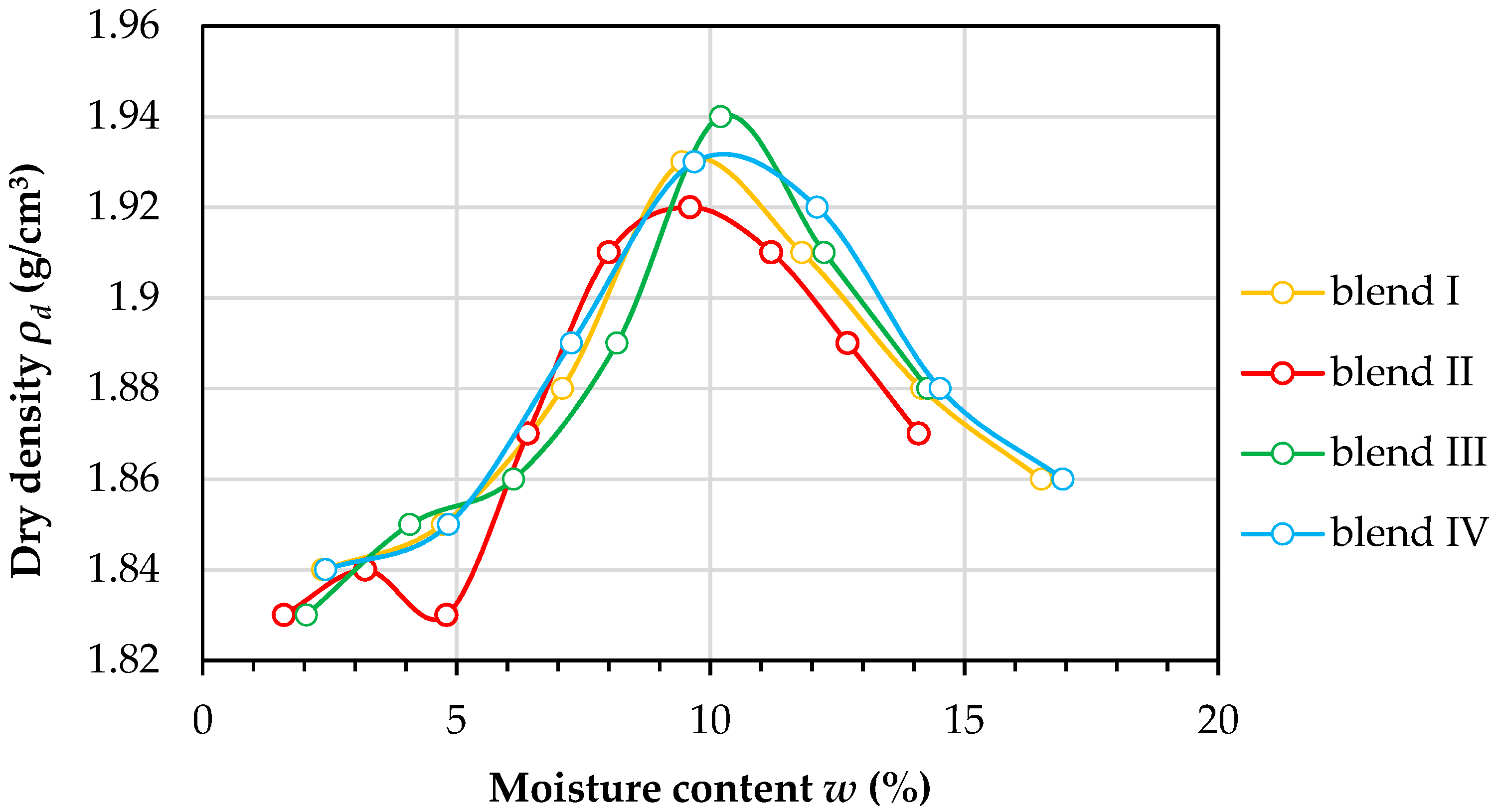
3.1. Material
3.2. Permeability Test
3.3. Estimation Theory
4. Test Results
5. Result Discussion and Conclusions
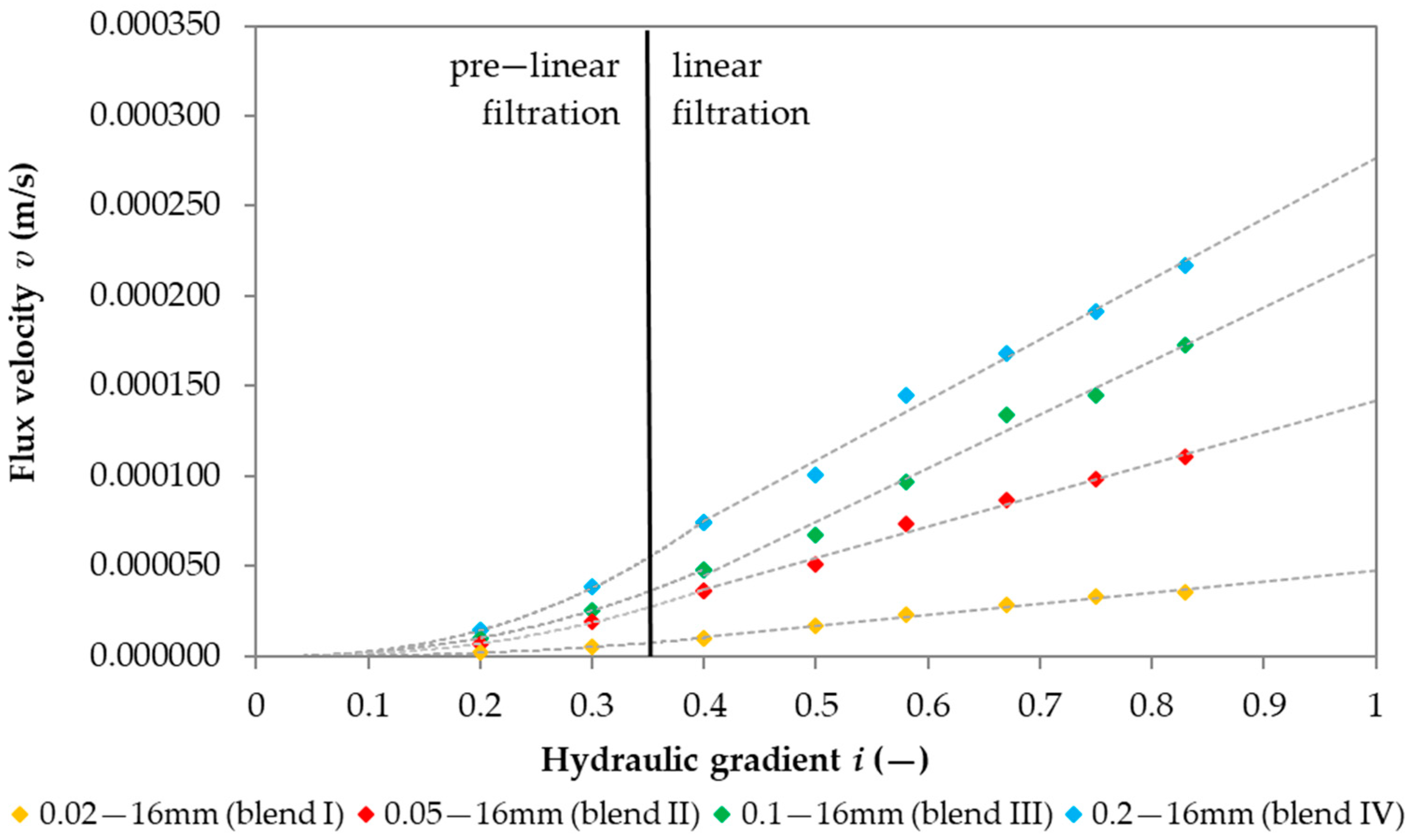
- The RCA material tested for blends with 0.02–16 mm, 0.05–16 mm, 0.1–16 mm, and 0.2–16 mm grains was characterized by good permeability from 3.1 × 10−4 to 4 × 10−6 m/s. Reported coefficients of permeability by Azram and Cameron [51] of RCAs with gradation in the range of 0–20 mm with 6 to 7% fine particles (d < 0.0063 mm) were in the range of 2 × 10−7 to 2 × 10−8 m/s. Arulrajach et al. [52], based on constant head test experiments, estimated the coefficient of permeability in range of 2.04 × 10−3 to 3.3 × 10−8 m/s, which indicates the existence of non-Darcian flow. Tests performed by McCulloch et al. [53] were conducted for RCAs with 4% fines and with fractions of 0–50 mm. The reported coefficients of permeability were in the range of 1 × 10−4 to 3 × 10−4 m/s. Tests on RCAs with poorly graded RCAs with fractions of 6–12 mm and with no fine content have proven a high water permeability of such material with a coefficient of permeability of approximately 1 × 10−3 m/s [53]. Tests performed on an RCA blend with gradation of 0−50 mm and with 5% fine contents have shown that the coefficient of permeability calculated based on a constant head permeability test is equal to 1.06 × 10−6 m/s [54]. As can be seen, the coefficient of permeability value strongly depends on the fines content. Test results presented in this article corresponds with the test results presented by other studies.
- The specific density, optimal moisture content, and particle sizes d5 and d90 had a significant influence on the determination of the permeability coefficient.
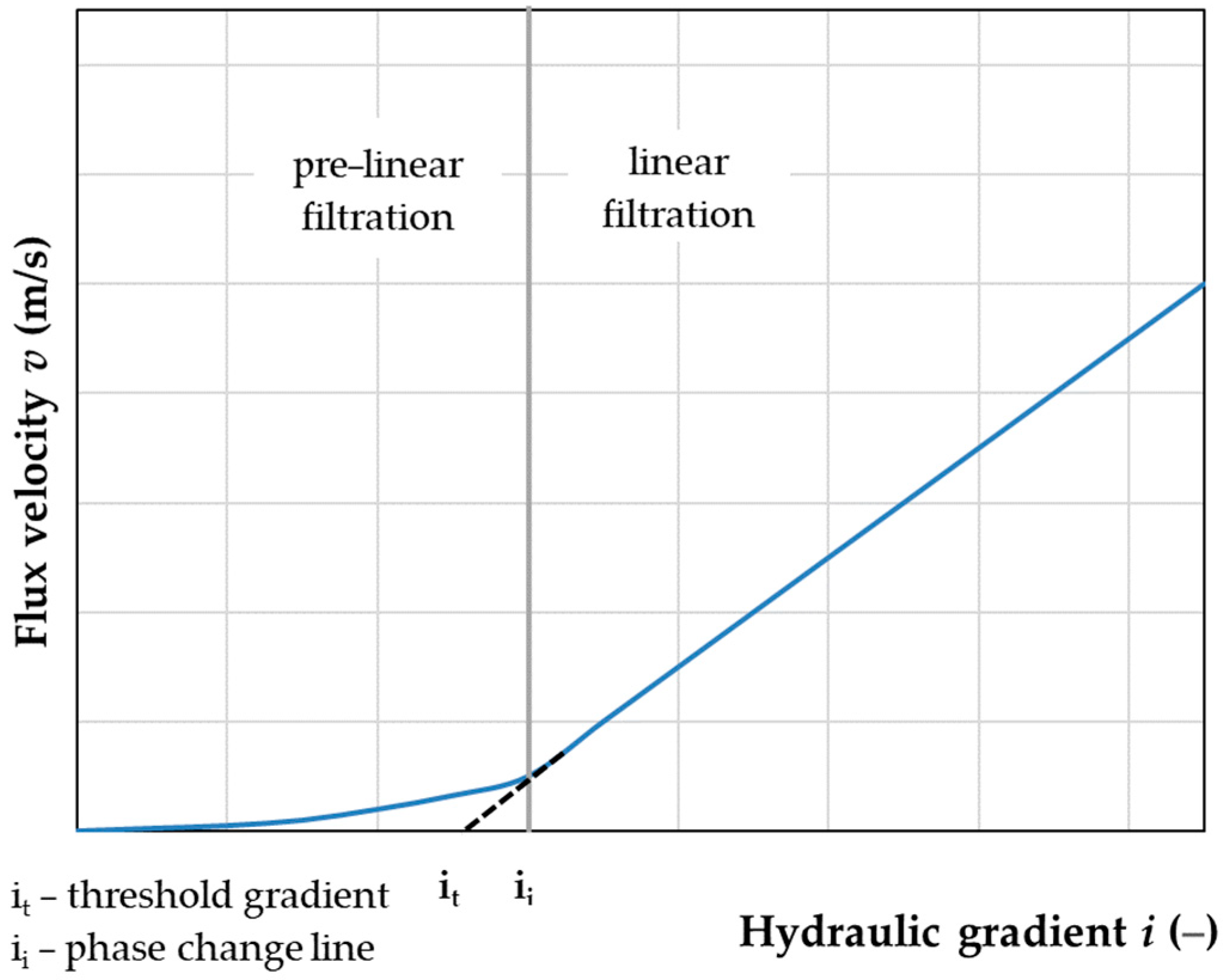
- Regarding RCAs, a relationship between the flow velocity and the hydraulic gradient showed the existence of two phases, namely pre-linear and linear.
- Models created for individual phases gave greater confidence in determining the permeability coefficient.
- The models were created on the basis of the same set of variables, which facilitated their application and implementation in practice.
- Each of the models was examined in terms of the discrepancy with the observed value in relation to the forecasted results.
- For each of the models, the limits of its applicability were estimated.
Author Contributions
Funding
Conflicts of Interest
References
- Global Construction Outlook 2022. Report ID: 4496591. Available online: https://www.researchandmarkets.com/reports/4496591/global-construction-outlook-2022 (accessed on 3 September 2019).
- Podvezko, V.; Kildienė, S.; Zavadskas, K.E. Assessing the performance of the construction sectors in the Baltic states and Poland. Panoeconomicus 2017, 64, 493–512. [Google Scholar] [CrossRef]
- Wilkinson, S.; Richards, A.Y.; Sapeciay, Z.; Costello, S.B. Improving construction sector resilience. Int. J. Disaster Resil. Built Environ. 2016, 7, 173–185. [Google Scholar] [CrossRef]
- European Aggregates Association A Sustainable Industry for a Sustainable Europe; UEPG: Brussels, Belgium, 2017.
- Cardoso, R.; Silva, R.V.; de Brito, J.; Dhir, R. Use of recycled aggregates from construction and demolition waste in geotechnical applications: A literature review. Waste Manag. 2016, 49, 131–145. [Google Scholar] [CrossRef] [PubMed]
- Yilmaz, M.; BAKIŞ, A. Sustainability in construction sector. Procedia Soc. Behav. Sci. 2015, 195, 2253–2262. [Google Scholar] [CrossRef]
- Michel, L.; Angela, B. Quantitative and Statistical Data in Education; Aix-Marseille University: Marseille, France, 2018; ISBN 9781786302281. [Google Scholar]
- Cowan, G. Statistical models with uncertain error parameters. Eur. Phys. J. C 2019, 79, 133. [Google Scholar] [CrossRef] [Green Version]
- Gnedenko, B.V. Theory of Probability; Routledge: London, UK, 2018. [Google Scholar]
- Rao, J.N.K. Interplay between sample survey theory and practice: An appraisal. Surv. Methodol. 2005, 31, 117–138. [Google Scholar]
- Kish, L. Survey Sampling; John Wily & Sons: New York, NY, USA, 1995. [Google Scholar]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Routledge: London, UK, 2018. [Google Scholar]
- Hilbe, J.; Robinson, A. Methods of Statistical Model Estimation; Chapman and Hall/CRC: Boca Raton, FL, USA, 2013. [Google Scholar]
- Li, X.R. Probability, Random Signals, and Statistics; CRC press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Brus, D.J. Statistical sampling approaches for soil monitoring. Eur. J. Soil Sci. 2014, 65, 779–791. [Google Scholar] [CrossRef]
- Speak, A.; Escobedo, F.J.; Russo, A.; Zerbe, S. Comparing convenience and probability sampling for urban ecology applications. J. Appl. Ecol. 2018, 55, 2332–2342. [Google Scholar] [CrossRef]
- Petkovic, G.; Engelsen, C.J.; Haoya, A.O.; Breedveld, G. Environmental impact from the use of recycled materials in road construction: Method for decision making in Norway. Resour. Conserv. Recycl. 2004, 42, 249–264. [Google Scholar] [CrossRef]
- Poon, C.S.; Chan, D. Feasible use of recycled concrete aggregates and crushed clay brick as unbound road sub-base. Constr. Build. Mater. 2006, 20, 578–585. [Google Scholar] [CrossRef]
- Herrador, R.; Pérez, P.; Garach, L.; Ordóñez, J. Use of recycled construction and demolition waste aggregate for road course surfacing. J. Transp. Eng. 2011, 138, 182–190. [Google Scholar] [CrossRef]
- Gabryś, K.; Sas, W.; Soból, E.; Głuchowski, A. Application of bender elements technique in testing of anthropogenic soil—recycled concrete aggregate and its mixture with rubber chips. Appl. Sci. 2017, 7, 741. [Google Scholar] [CrossRef]
- Sas, W.; Głuchowski, A.; Gabryś, K.; Soból, E.; Szymański, A. Deformation Behavior of Recycled Concrete Aggregate during Cyclic and Dynamic Loading Laboratory Tests. Materials 2016, 9, 780. [Google Scholar] [CrossRef] [PubMed]
- O’Mahony, M.M. An analysis of the shear strength of recycled aggregates. Mater. Struct. 1997, 30, 599–606. [Google Scholar] [CrossRef]
- Arm, M. Self-cementing properties of crushed demolished concrete in unbound layers: Results from triaxial tests and field tests. Waste Manag. 2001, 21, 235–239. [Google Scholar] [CrossRef]
- Chapuis, R.P. Predicting the saturated hydraulic conductivity of soils: A review. Bull. Eng. Geol. Environ. 2012, 71, 401–434. [Google Scholar] [CrossRef]
- Deshpande, Y.S.; Hiller, J.E. Pore characterization of manufactured aggregates: Recycled concrete aggregates and lightweight aggregates. Mater. Struct. 2011, 45, 67–79. [Google Scholar] [CrossRef]
- Gee, K.K. Use of recycled concrete Pavement as Aggregate in Hydraulic-Cement. 42 Concrete Pavement; FHWA Publication: Washington, DC, USA, 2007. [Google Scholar]
- Paranavithana, S.; Mohajerani, A. Effects of Recycled Concrete Aggregates on Properties of Asphalt Concrete. Resour. Conserv. Recycl. 2006, 48, 1–12. [Google Scholar] [CrossRef]
- Gómez-Soberón, J.M. Porosity of recycled concrete with substitution of recycled concrete aggregate: An experimental study. Cement Concr. Res. 2002, 32, 1301–1311. [Google Scholar] [CrossRef] [Green Version]
- Tam, V.W.Y.; Gao, X.F.; Tam, C.M.; Chan, C.H. New Approach in Measuring Water Absorption of Recycled Aggregates. Constr. Build. Mater. 2008, 22, 364–369. [Google Scholar] [CrossRef]
- ASTM D698-12e1. Standard Test Methods for Laboratory Compaction Characteristics of Soil Using Standard Effort (12 400 ft-lbf/ft3 (600 kN-m/m3)). Annual Book of ASTM Standards, USA. 2008. Available online: https://www.techstreet.com/standards/astm-d5254-d5254m-92-2010-e1?product_id=1751704 (accessed on 8 January 2010).
- Głuchowski, A.; Sas, W.; Dzięcioł, J.; Soból, E.; Szymański, A. Permeability and Leaching Properties of Recycled Concrete Aggregate as an Emerging Material in Civil Engineering. Appl. Sci. 2019, 9, 81. [Google Scholar] [CrossRef]
- EN 933-11:2009/AC:2009 Tests for geometrical properties of aggregates—Part 11: Classification test for the constituents of coarse recycled aggregate; Spanish Association for Standardisation and Certification (AENOR): Madrid, Spain, 2009.
- WT–4 Unbound Mix for National Roads; Technical Specifications; Directive No 102 of Polish General Director of National Roads and Motorways; Polish General Director of National Roads and Motorways: Warsaw, Poland, 2010.
- ISO 17892-4:2016 Geotechnical Investigation and Testing—Laboratory Testing of Soil—Part 4: Determination of Particle Size Distribution. Available online: http://sklep.pkn.pl/pn-en-iso-17892-4-2017-01e.html (accessed on 18 January 2017).
- Maia, M.B.; De Brito, J.; Martins, I.M.; Silvestre, J.D. Toxicity of recycled concrete aggregates: Review on leaching tests. Open Constr. Build. Technol. J. 2018, 12, 187–196. [Google Scholar] [CrossRef]
- Rodrigues, P.; Silvestre, J.; Flores-Colen, I.; Viegas, C.; de Brito, J.; Kurad, R.; Demertzi, M. Methodology for the assessment of the ecotoxicological potential of construction materials. Materials 2017, 10, 649. [Google Scholar] [CrossRef] [PubMed]
- Bestgen, J.O.; Cetin, B.; Tanyu, B.F. Effects of extraction methods and factors on leaching of metals from recycled concrete aggregates. Environ. Sci. Pollut. Res. 2016, 23, 12983–13002. [Google Scholar] [CrossRef] [PubMed]
- Galvín, A.P.; Ayuso, J.; Agrela, F.; Barbudo, A.; Jiménez, J.R. Analysis of leaching procedures for environmental risk assessment of recycled aggregate use in unpaved roads. Constr. Build. Mater. 2013, 40, 1207–1214. [Google Scholar] [CrossRef]
- Galvín, A.P.; Ayuso, J.; García, I.; Jiménez, J.R.; Gutiérrez, F. The effect of compaction on the leaching and pollutant emission time of recycled aggregates from construction and demolition waste. J. Clean. Prod. 2014, 83, 294–304. [Google Scholar] [CrossRef]
- Saca, N.; Dimache, A.; Radu, L.R.; Iancu, I. Leaching behavior of some demolition wastes. J. Mater. Cycles Waste Manag. 2017, 19, 623–630. [Google Scholar] [CrossRef]
- Butera, S.; Hyks, J.; Christensen, T.H.; Astrup, T.F. Construction and demolition waste: Comparison of standard up-flow column and down-flow lysimeter leaching tests. Waste Manag. 2015, 43, 386–397. [Google Scholar] [CrossRef]
- Kowalski, J. Hydrogeologia z podstawami geologii; Wydaw AR: Wrocław, Poland, 1998. (in Polish) [Google Scholar]
- Hansbo, S. Consolidation equation valid for both Darcian and non-Darcian flow. Geotechnique 2011, 51, 51–54. [Google Scholar] [CrossRef]
- Hansbo, S. Deviation from Darcy’s law observed in one-dimensional consolidation. Geotechnique 2003, 53, 601–605. [Google Scholar] [CrossRef]
- Sas, W.; Dzieciol, J. Determination of the fi ltration rate for anthropogenic soil from the recycled concrete aggregate by analytical methods. Sci. Rev. Eng. Environ. Sci. 2018, 27, 80. [Google Scholar]
- Batezini, R.; Balbo, J.T. Study on the hydraulic conductivity by constant and falling head methods for pervious concrete. Rev. IBRACON Estrut. e Mater. 2015, 8, 248–259. [Google Scholar] [CrossRef] [Green Version]
- Allen, A.O. Probability, Statistics, and Queueing Theory; Academic press: London, UK, 2014. [Google Scholar]
- Gatti, P.L. Probability Theory and Mathematical Statistics for Engineers; CRC Press: New York, NY, USA, 2004. [Google Scholar]
- Giri, N.C. Introduction to Probability and Statistics; Routledge: New York, NY, USA, 1993. [Google Scholar]
- WYWIAŁ, J. Estimation of population mean on the basis of non-simple sample when nonresponse error is present. Stat. Transit. 2001, 5, 443–450. [Google Scholar]
- Azram, A.M.; Cameron, D.A. Geotechnical properties of blends of Recycled Clay Marsony and Recycled Concrete Aggregates in Unbound Pavement Construction. J. Mater. Civ. Eng. 2013, 25, 788–798. [Google Scholar] [CrossRef]
- Arulrajah, A.; Piratheepan, J.; Ali, M.M.Y.; Bo, M.W. Geotechnical properties of recycled concrete aggregate in pavement sub-base applications. Geotech. Test. J. 2012, 35, 1–9. [Google Scholar] [CrossRef]
- McCulloch, T.; Kang, D.; Shamet, R.; Lee, S.J.; Nam, B.H. Long-Term performance of recycled concrete aggregate for subsurface drainage. J. Perform. Constr. Facil. 2017, 04017015, 1–8. [Google Scholar] [CrossRef]
- Bennert, T.; Maher, A. The Use of Recycled Concrete Aggregate in a Dense Graded Aggregate Base Course; Rutgers: Piscataway, NJ, USA, 2008. [Google Scholar]

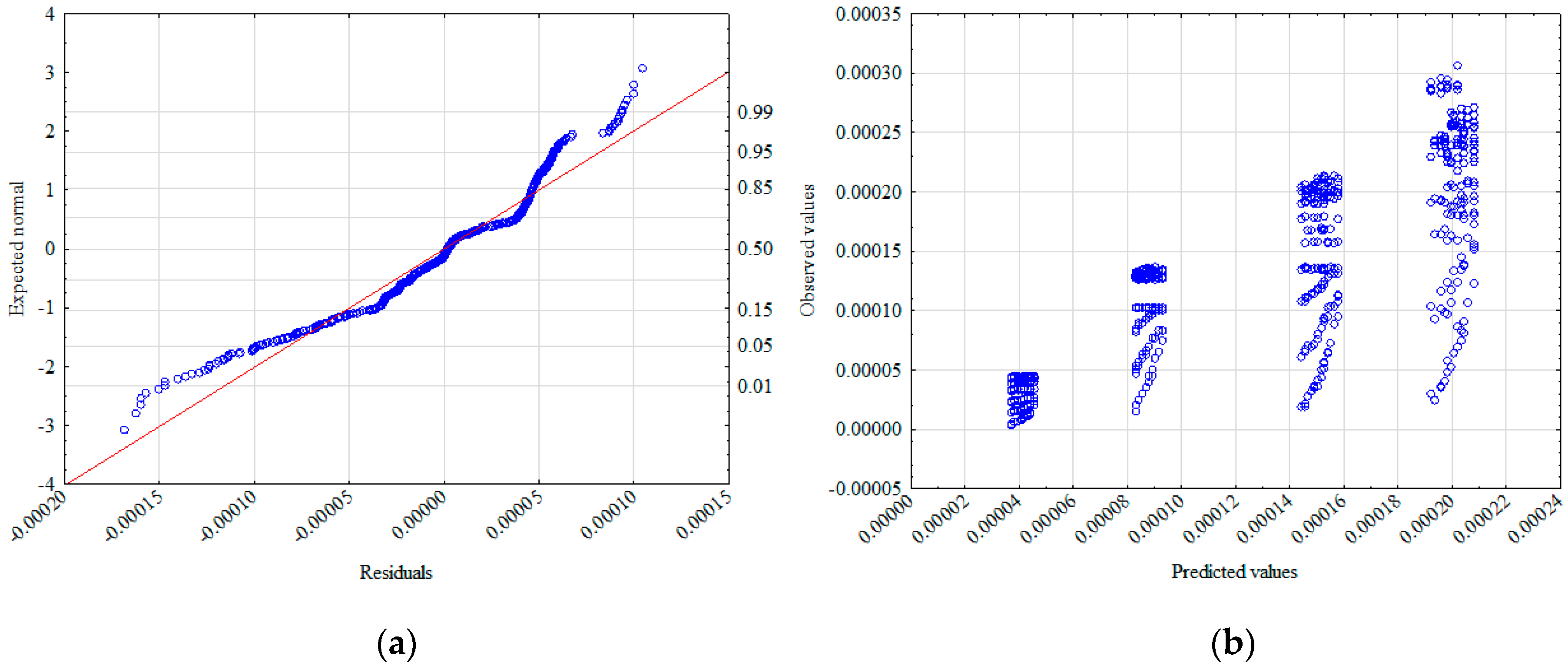
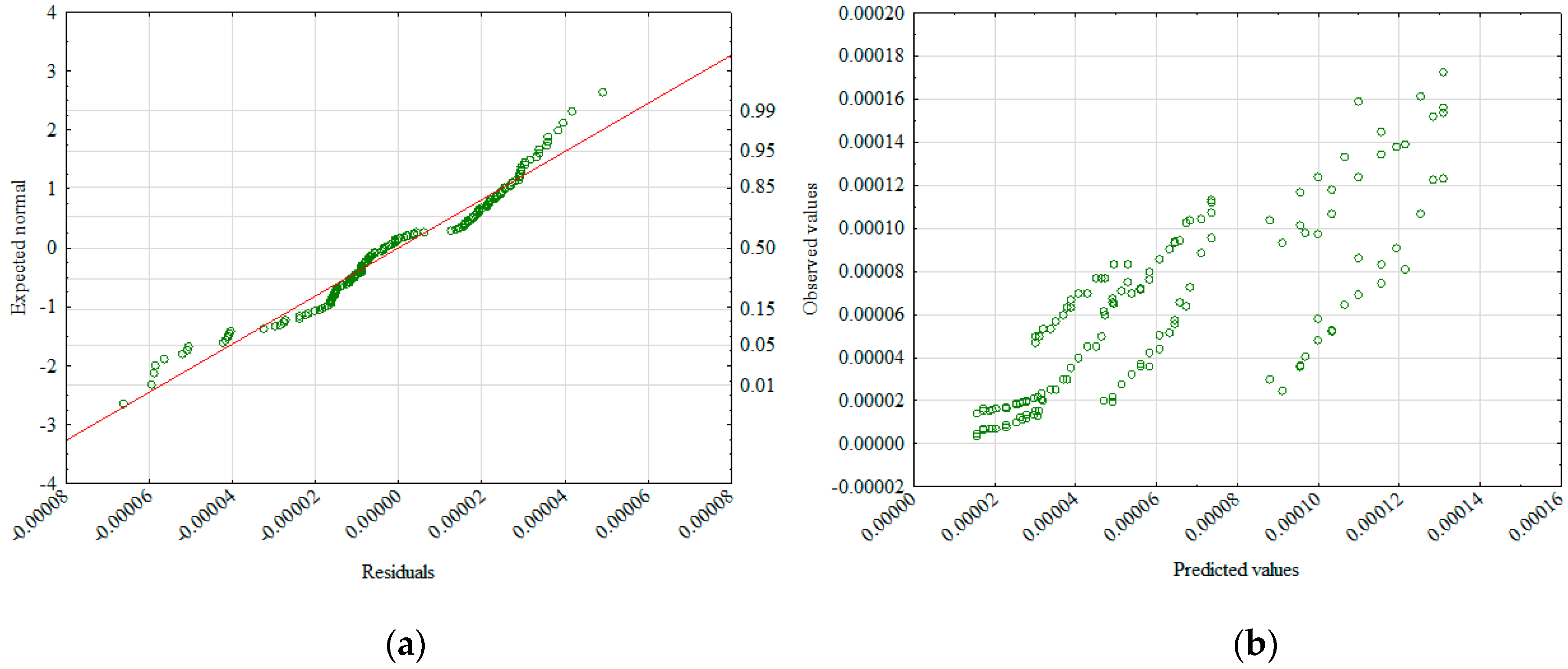

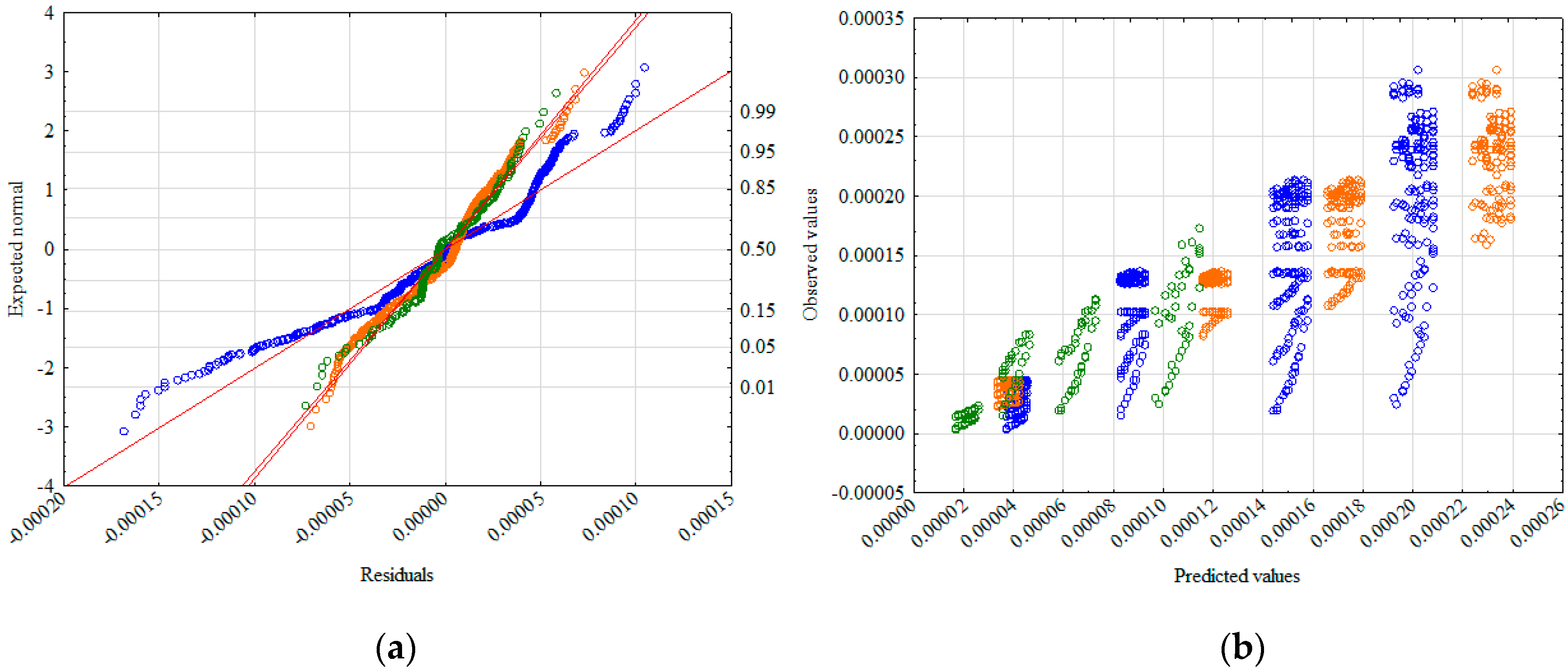
| Variable | Description | Mean | Standard Deviation | Standard Error | Test t |
|---|---|---|---|---|---|
| k | Coefficient of permeability | 0.000120 | 0.000078 | 0.000003 | 38.958 |
| v | Flux velocity | 0.000072 | 0.000061 | 0.000002 | 29.890 |
| ρ | Specific density | 1.931437 | 0.019769 | 0.000781 | 2471.586 |
| n | Porosity | 0.374610 | 0.083305 | 0.003293 | 113.762 |
| e | Void ratio | 0.611371 | 0.190529 | 0.007531 | 81.177 |
| w | Moisture content | 0.105425 | 0.009157 | 0.000362 | 291.260 |
| d5 | Particle size when passing 5% | 0.230000 | 0.018723 | 0.000740 | 310.774 |
| d10 | Particle size when passing 10% | 0.287500 | 0.013001 | 0.000514 | 559.457 |
| d30 | Particle size when passing 30% | 0.837500 | 0.086200 | 0.003407 | 245.793 |
| d60 | Particle size when passing 60% | 4.675000 | 0.334739 | 0.013232 | 353.318 |
| d90 | Particle size when passing 90% | 9.350000 | 0.753915 | 0.029801 | 313.747 |
| Variable | Value of Correlation for Coefficient of Permeability k (m/s) |
|---|---|
| i * | 0.504794 |
| ρ | −0.754960 |
| n | −0.112145 |
| e | −0.137592 |
| w | −0.737912 |
| d5 | 0.772737 |
| d10 | 0.569209 |
| d30 | −0.140365 |
| d60 | 0.408963 |
| d90 | 0.701564 |
| Independent Variable’s Label | Independent Variable’s Value | Standard Error |
|---|---|---|
| a1 | −0.001220 | 0.000231 |
| b1 | −0.002296 | 0.000464 |
| c1 | 0.099420 | 0.029056 |
| Independent Variable’s Label | Independent Variable’s Value | Standard Error |
|---|---|---|
| a2 | 0.001734 | 0.000319 |
| b2 | −0.002594 | 0.000455 |
| c2 | −0.000040 | 0.000030 |
| Independent Variable’s Label | Independent Variable’s Value | Standard Error |
|---|---|---|
| a2 | −0.001169 | 0.000150 |
| b2 | 0.00165 | 0.000256 |
| c2 | −0.163 | 0.058118 |
| d2 | 0.00185 | 0.000307 |
| Variable | Mean (m/s) | Std. Dev. | Minimum (m/s) | Maximum (m/s) |
|---|---|---|---|---|
| k | 0.000120 | 0.000078 | 0.000004 | 0.00031 |
| ρd | 1.931438 | 0.019769 | 1.895000 | 1.95600 |
| d5 | 0.230000 | 0.018723 | 0.200000 | 0.25000 |
| d90 | 9.350000 | 0.753915 | 8.600000 | 10.20000 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sas, W.; Dzięcioł, J.; Głuchowski, A. Estimation of Recycled Concrete Aggregate’s Water Permeability Coefficient as Earth Construction Material with the Application of an Analytical Method. Materials 2019, 12, 2920. https://doi.org/10.3390/ma12182920
Sas W, Dzięcioł J, Głuchowski A. Estimation of Recycled Concrete Aggregate’s Water Permeability Coefficient as Earth Construction Material with the Application of an Analytical Method. Materials. 2019; 12(18):2920. https://doi.org/10.3390/ma12182920
Chicago/Turabian StyleSas, Wojciech, Justyna Dzięcioł, and Andrzej Głuchowski. 2019. "Estimation of Recycled Concrete Aggregate’s Water Permeability Coefficient as Earth Construction Material with the Application of an Analytical Method" Materials 12, no. 18: 2920. https://doi.org/10.3390/ma12182920
APA StyleSas, W., Dzięcioł, J., & Głuchowski, A. (2019). Estimation of Recycled Concrete Aggregate’s Water Permeability Coefficient as Earth Construction Material with the Application of an Analytical Method. Materials, 12(18), 2920. https://doi.org/10.3390/ma12182920







