A Dual-Band Terahertz Absorber with Two Passbands Based on Periodic Patterned Graphene
Abstract
:1. Introduction
2. Structures and Methods
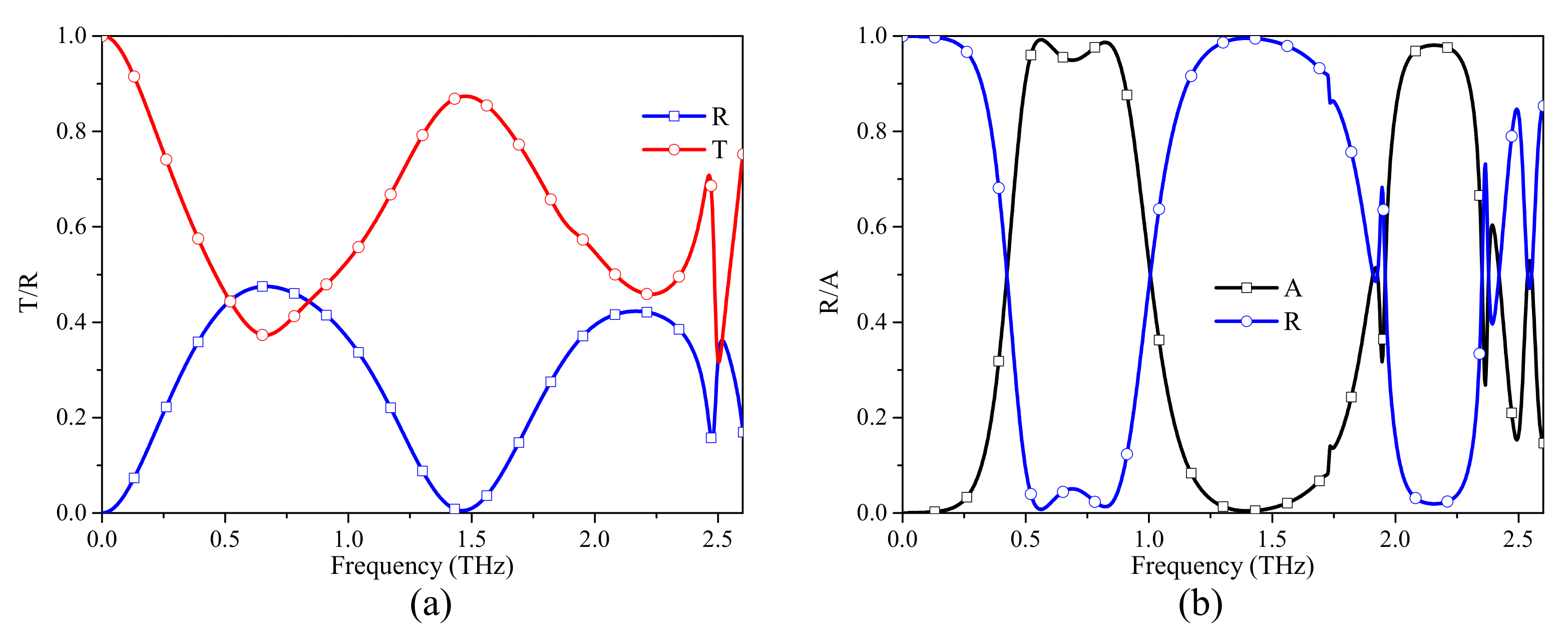
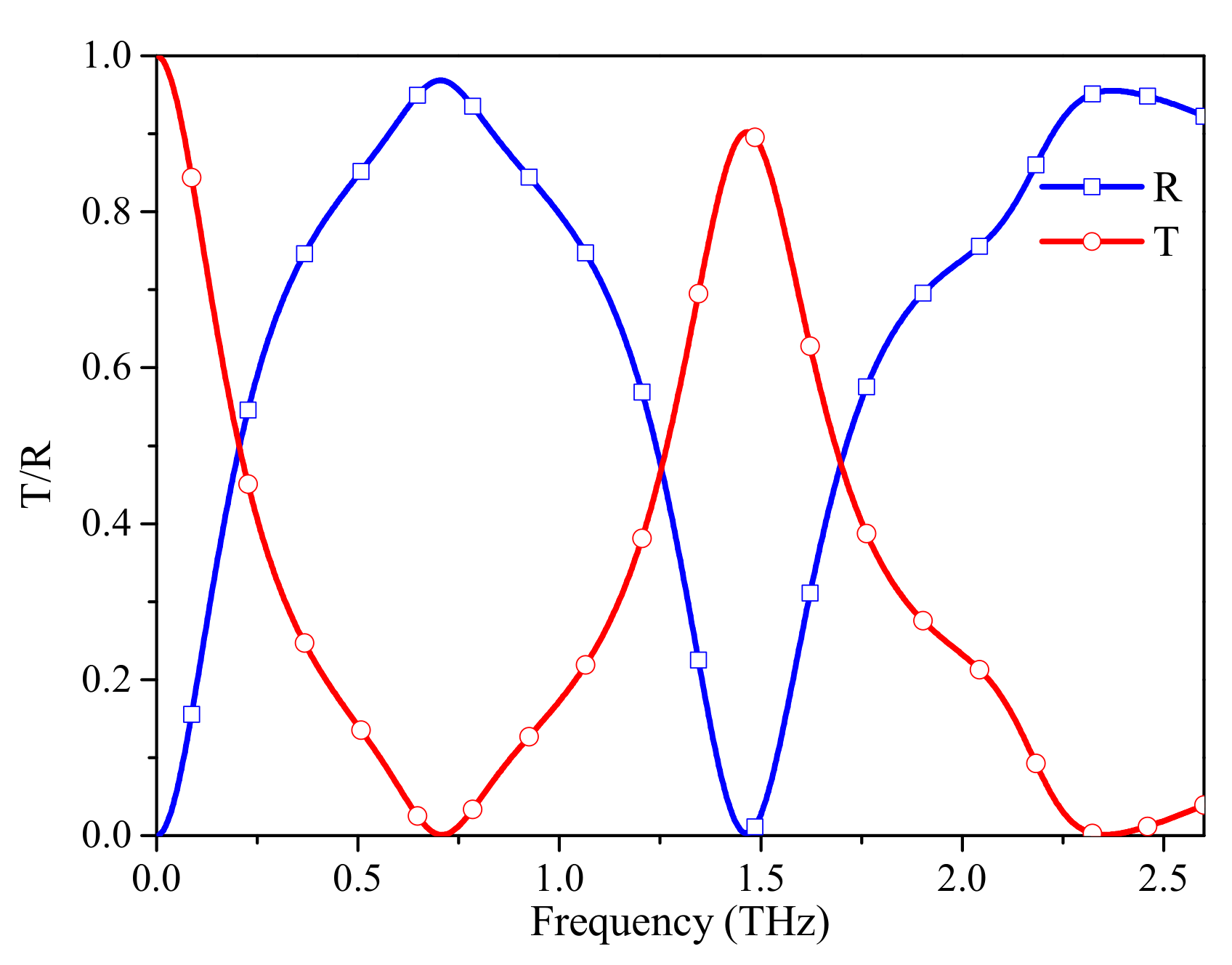
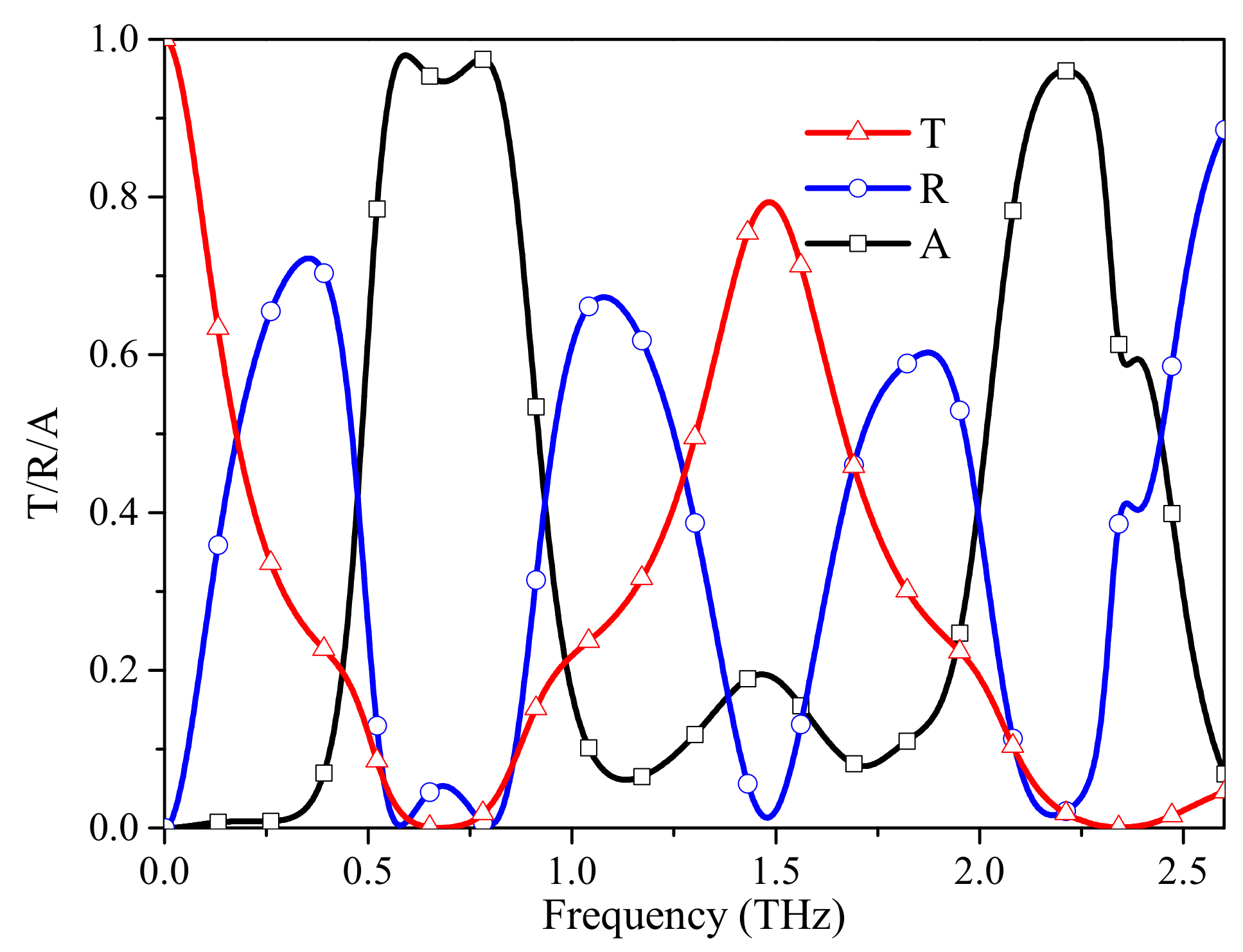
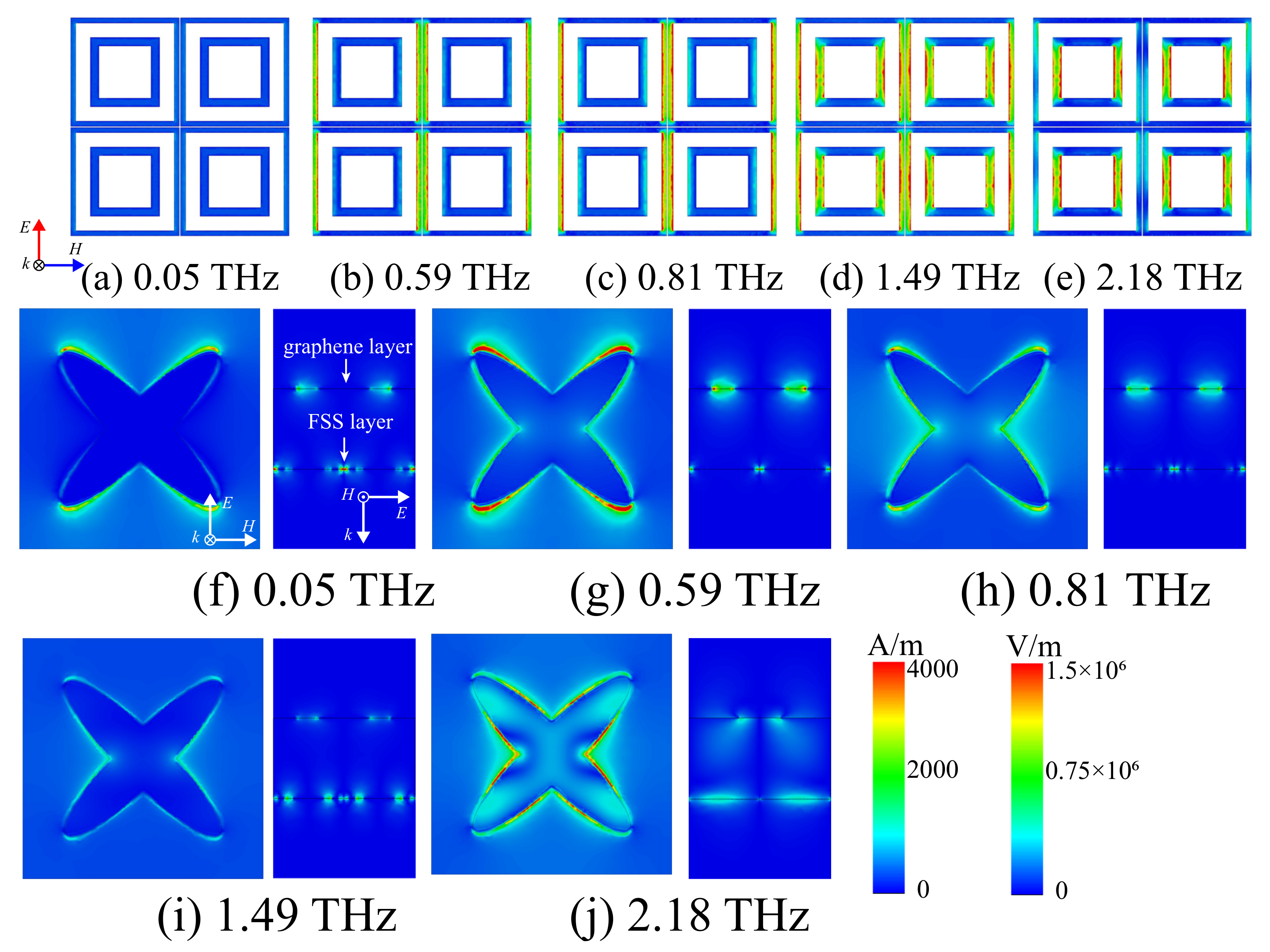
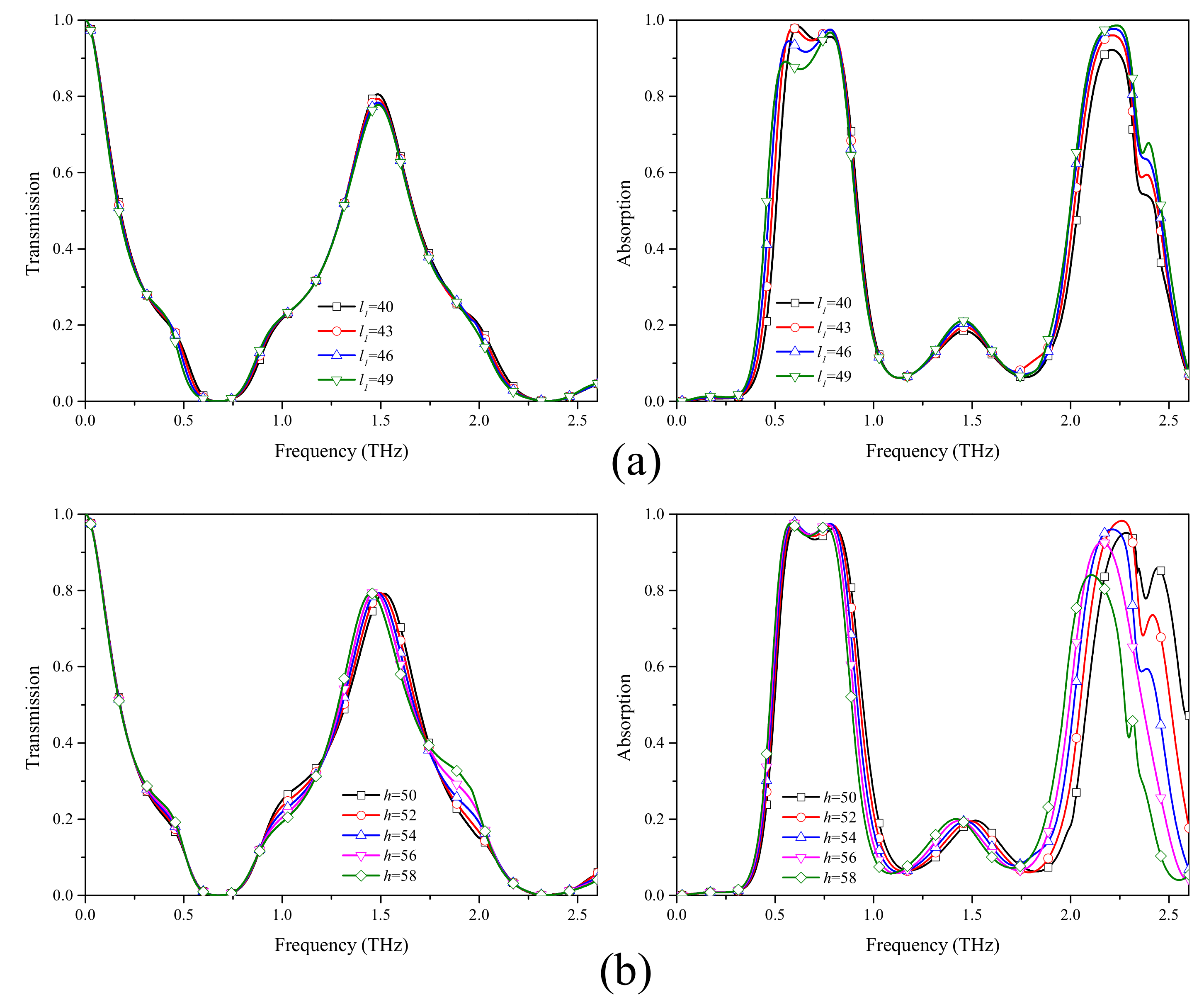
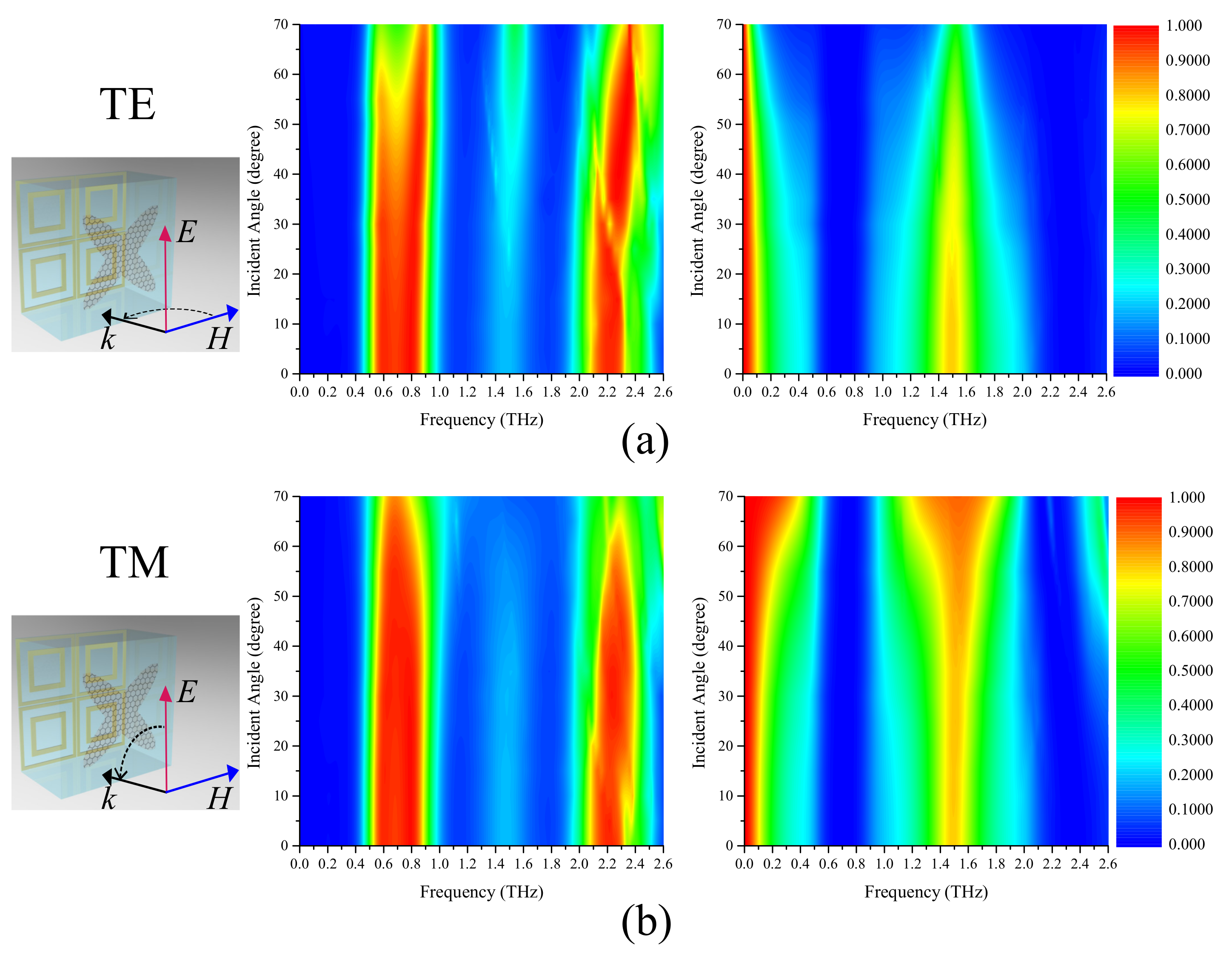
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Veselago, V.G. The electrodynamics of substances with simultaneously negative values of ϵ and μ. Sov. Phys. Uspekhi 1968, 10, 509–514. [Google Scholar] [CrossRef]
- Valentine, J.; Zhang, S.; Zentgraf, T.; Ulin-Avila, E.; Genov, D.A.; Bartal, G.; Zhang, X. Three-dimensional optical metamaterial with a negative refractive index. Nature 2008, 455, 376–379. [Google Scholar] [CrossRef] [PubMed]
- Simovski, C.R.; Belov, P.A.; He, S. Backward wave region and negative material parameters of a structure formed by lattices of wires and split-ring resonators. IEEE Trans. Antennas Propag. 2003, 51, 2582–2591. [Google Scholar] [CrossRef]
- Xiong, Z.; Cao, L. Interparticle spacing dependence of magnetic anisotropy and dipolar interaction of Ni nanocrystals embedded in epitaxial BaTiO3 matrix. Ceram. Int. 2018, 44, 8155–8160. [Google Scholar] [CrossRef]
- Caloz, C.; Itoh, T. Electromagnetic Metamaterials: Transmission Line Theory and Microwave Applications; John Wiley & Sons: New York, NY, USA, 2004. [Google Scholar]
- Landy, N.I.; Sajuyigbe, S.; Mock, J.J.; Smith, D.R.; Padilla, W.J. Perfect metamaterial absorber. Phys. Rev. Lett. 2008, 10, 207402. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Koschny, T.; Soukoulis, C.M. Wide-angle and polarization-independent chiral metamaterial absorber. Phys. Rev. B 2009, 80, 033108. [Google Scholar] [CrossRef]
- Hanson, G.W. Dyadic green’s functions and guided surface waves for a surface conductivity model of graphene. J. Appl. Phys. 2008, 103, 064302. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Fal, V.I.; Colombo, L.; Gellert, P.R.; Schwab, M.G.; Kim, K. A roadmap for graphene. Nature 2012, 490, 192–200. [Google Scholar] [CrossRef]
- Alaee, R.; Farhat, M.; Rockstuhl, C.; Lederer, F. A perfect absorber made of a graphene micro-ribbon metamaterial. Opt. Exp. 2012, 20, 28017–28024. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Feng, Y.; Zhu, B.; Zhao, J.; Jiang, T. Graphene based tunable metamaterial absorber and polarization modulation in terahertz frequency. Opt. Exp. 2014, 22, 22743–22752. [Google Scholar] [CrossRef]
- Nikitin, A.Y.; Guinea, F.; Garcia-Vidal, F.J.; Martin-Moreno, L. Surface plasmon enhanced absorption and suppressed transmission in periodic arrays of graphene ribbons. Phys. Rev. B 2012, 85, 081405. [Google Scholar] [CrossRef]
- Chen, P.Y.; Alù, A. Terahertz metamaterial devices based on graphene nanostructures. IEEE Trans. Terahertz Sci. Technol. 2013, 3, 748–756. [Google Scholar] [CrossRef]
- Thongrattanasiri, S.; Koppens, F.H.L.; De Abajo, F.J.G. Complete optical absorption in periodically patterned graphene. Phys. Rev. Lett. 2012, 108, 047401. [Google Scholar] [CrossRef]
- Fang, Z.; Thongrattanasiri, S.; Schlather, A.; Liu, Z.; Ma, L.; Wang, Y.; García de Abajo, F.J. Gated tunability and hybridization of localized plasmons in nanostructured graphene. ACS Nano 2013, 3, 2388–2395. [Google Scholar] [CrossRef]
- He, X.; Zhong, X.; Lin, F.; Shi, W. Investigation of graphene assisted tunable terahertz metamaterials absorber. Opt. Mater. Express 2016, 6, 331–342. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, Z.; Liu, W.; Yuan, X.; Qin, S. Towards photodetection with high efficiency and tunable spectral selectivity: Graphene plasmonics for light trapping and absorption engineering. Nanoscale 2015, 7, 13530–13536. [Google Scholar] [CrossRef]
- Shi, X.; Ge, L.; Wen, X.; Han, D.; Yang, Y. Broadband light absorption in graphene ribbons by canceling strong coupling at subwavelength scale. Opt. Express 2016, 24, 26357–26362. [Google Scholar] [CrossRef]
- Yi, S.; Zhou, M.; Shi, X.; Gan, Q.; Zi, J.; Yu, Z. A multiple-resonator approach for broadband light absorption in a single layer of nanostructured graphene. Opt. Express 2015, 23, 10081–10090. [Google Scholar] [CrossRef] [Green Version]
- Cai, Y.; Xu, K.D. Tunable broadband terahertz absorber based on multilayer graphene-sandwiched plasmonic structure. Opt. Express 2018, 26, 31693–31705. [Google Scholar] [CrossRef]
- Amin, M.; Farhat, M.; Bağcı, H. An ultra-broadband multilayered graphene absorber. Opt. Express 2013, 21, 29938–29948. [Google Scholar] [CrossRef]
- He, S.; Chen, T. Broadband THz absorbers with graphene-Based anisotropic metamaterial films. IEEE Trans. Terahertz Sci. Technol. 2013, 3, 757–763. [Google Scholar] [CrossRef]
- Xiao, B.; Gu, M.; Xiao, S. Broadband, wide-angle and tunable terahertz absorber based on cross-shaped graphene arrays. Appl. Opt. 2017, 56, 5458–5462. [Google Scholar] [CrossRef]
- Ye, L.; Chen, Y.; Cai, G.; Liu, N.; Zhu, J.; Song, Z.; Liu, Q.H. Broadband absorber with periodically sinusoidally-patterned graphene layer in terahertz range. Opt. Express 2017, 25, 11223–11232. [Google Scholar] [CrossRef]
- Zhu, Z.; Guo, C.; Zhang, J.; Liu, K.; Yuan, X.; Qin, S. Broadband single-layered graphene absorber using periodic arrays of graphene ribbons with gradient width. Appl. Phys. Express 2014, 8, 015102. [Google Scholar]
- Yu, W.; Luo, G.Q.; Yu, Y.; Pan, Y.; Cao, W.; Shen, Z. Dual-polarized band-absorptive frequency selective rasorber using meander-line and lumped resistors. IEEE Trans. Antennas Propag. 2019, 67, 1318–1322. [Google Scholar] [CrossRef]
- Guo, M.; Sun, Z.; Sang, D.; Jia, X.; Fu, Y. Design of frequency-selective rasorbers based on centrosymmetric bended-strip resonator. IEEE Access 2019, 7, 24964–24970. [Google Scholar] [CrossRef]
- Chen, Q.; Sang, D.; Guo, M.; Fu, Y. Miniaturized frequency-selective rasorber with a wide transmission band using circular spiral resonator. IEEE Trans. Antennas Propag. 2019, 67, 1045–1052. [Google Scholar] [CrossRef]
- Wang, Z.; Zeng, Q.; Fu, J.; Chen, W.; Lv, B.; Song, M.; Denidni, T.A. A high-transmittance frequency-selective rasorber based on dipole arrays. IEEE Access 2018, 6, 31367–31374. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, W.; Ma, Y.; Wang, C.; Li, C.; Yuan, N. Design dual-polarization frequency selective rasorber using split ring resonators. IEEE Access 2019, 7, 101139–101146. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, W.; Huang, L.; Ma, Y.; Yuan, N. Design of dual absorptive bands frequency selective rasorber with Minkowski loop arrays. IEEE Antennas Wirel. Propag. Lett. 2019, in press. [Google Scholar] [CrossRef]
- Chen, Q.; Sang, D.; Guo, M.; Fu, Y. Frequency-selective rasorber with interabsorption band transparent window and interdigital resonator. IEEE Trans. Antennas Propag. 2018, 8, 4105–4114. [Google Scholar] [CrossRef]
- Zhou, Q.; Zha, S.; Liu, P.; Liu, C.; Bian, L.A.; Zhang, J.; Liu, H.; Ding, L. Graphene based controllable broadband terahertz metamaterial absorber with transmission band. Materials 2018, 11, 2409. [Google Scholar] [CrossRef]
- Deng, X.H.; Liu, J.T.; Yuan, J.; Wang, T.B.; Liu, N.H. Tunable THz absorption in graphene-based heterostructures. Opt. Express 2014, 22, 30177–30183. [Google Scholar] [CrossRef]
- Deng, G.; Chen, P.; Yang, J.; Yin, Z.; Qiu, L. Graphene-based tunable polarization sensitive terahertz metamaterial absorber. Opt. Commun. 2016, 380, 101–107. [Google Scholar] [CrossRef]
- Mishra, R.; Panwar, R.; Singh, D. Equivalent circuit model for the design of frequency-selective, terahertz-band, graphene-based metamaterial absorbers. IEEE Magn. Lett. 2018, 9, 1–5. [Google Scholar] [CrossRef]
- Hanson, G.W. Dyadic Green’s functions for an anisotropic, non-local model of biased graphene. IEEE Trans. Antennas Propag. 2008, 56, 747–757. [Google Scholar] [CrossRef]


| Ref. | Polarization | Number of Passbands | Normalized Bandwidth | Number of Graphene Layers | |
|---|---|---|---|---|---|
| [20] | dual | 0 | 14.7% (4.8–5.56 THz) | 3 | |
| [21] | single | 0 | 84.6% (4.7–11.6 THz) | 3 | |
| [25] | single | 0 | 41.3% (2.5–3.8 THz) | 1 | |
| [33] | dual | 1 | 66.7% (0.5–1 THz) | 1 | |
| This work | dual | 2 | 43.5%/7.2% (0.54–0.84 THz, 2.13–2.29 THz) | 1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Wu, W.; Li, C.; Wang, C.; Ma, Y.; Yang, Z.; Sun, G.; Yuan, N. A Dual-Band Terahertz Absorber with Two Passbands Based on Periodic Patterned Graphene. Materials 2019, 12, 3016. https://doi.org/10.3390/ma12183016
Zhang X, Wu W, Li C, Wang C, Ma Y, Yang Z, Sun G, Yuan N. A Dual-Band Terahertz Absorber with Two Passbands Based on Periodic Patterned Graphene. Materials. 2019; 12(18):3016. https://doi.org/10.3390/ma12183016
Chicago/Turabian StyleZhang, Ximeng, Weiwei Wu, Chenxin Li, Chang Wang, Yuhong Ma, Zhangbiao Yang, Guang Sun, and Naichang Yuan. 2019. "A Dual-Band Terahertz Absorber with Two Passbands Based on Periodic Patterned Graphene" Materials 12, no. 18: 3016. https://doi.org/10.3390/ma12183016
APA StyleZhang, X., Wu, W., Li, C., Wang, C., Ma, Y., Yang, Z., Sun, G., & Yuan, N. (2019). A Dual-Band Terahertz Absorber with Two Passbands Based on Periodic Patterned Graphene. Materials, 12(18), 3016. https://doi.org/10.3390/ma12183016





