Initial Crack Propagation and the Influence Factors of Aircraft Pipe Pressure
Abstract
:1. Introduction
2. The Extended Finite Element Method
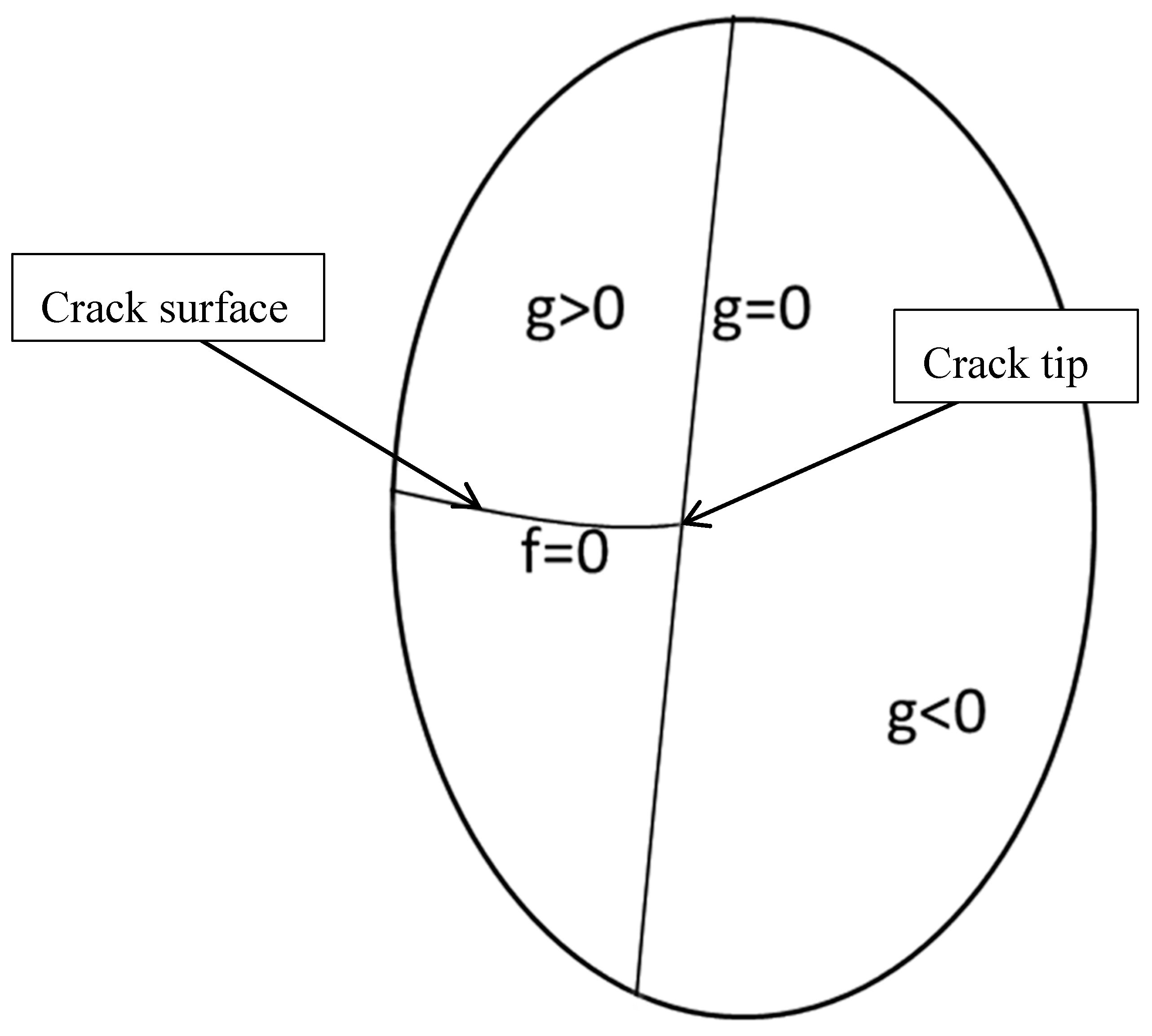
2.1. Level Set Method and Unit Decomposition Method
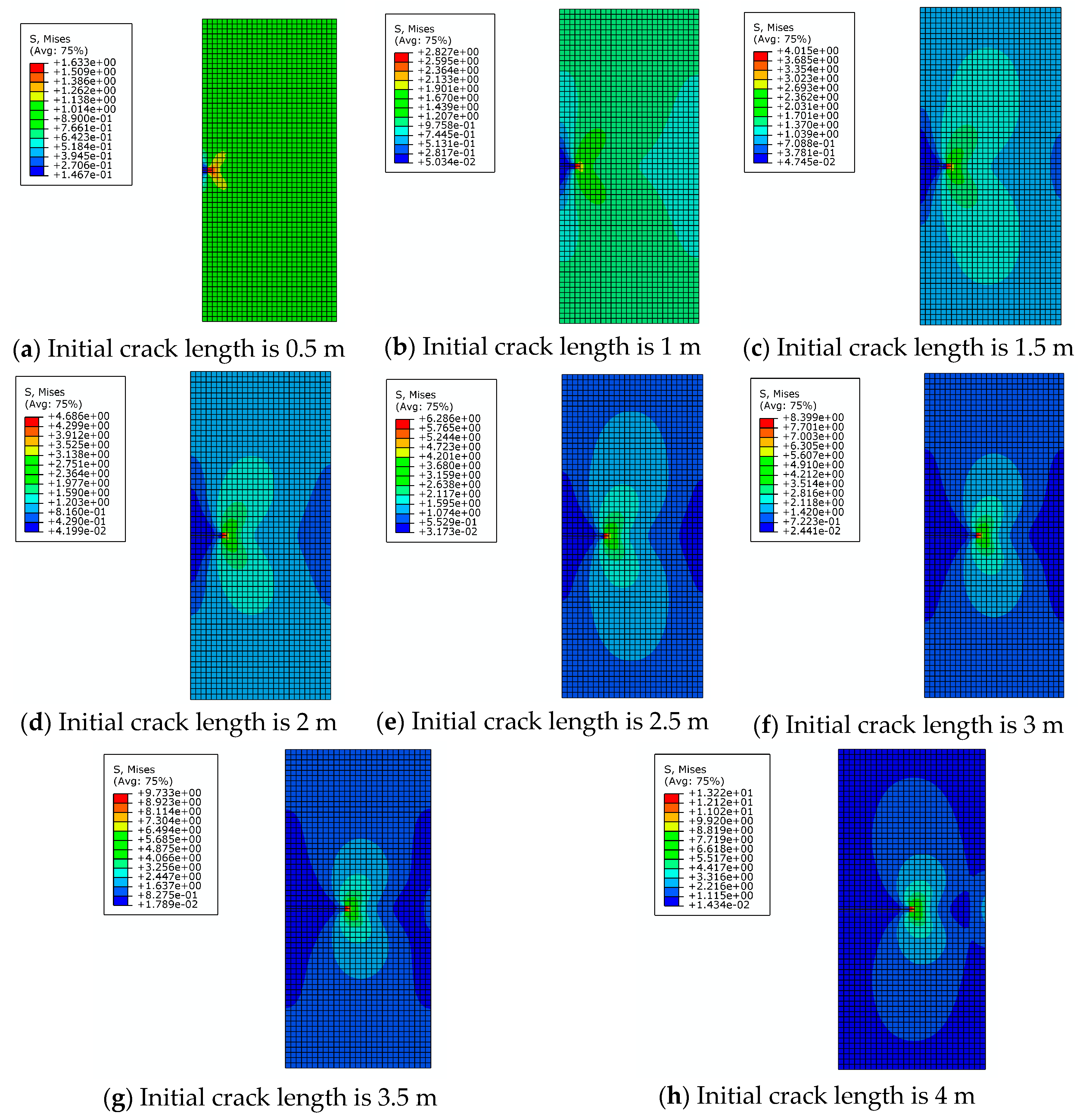
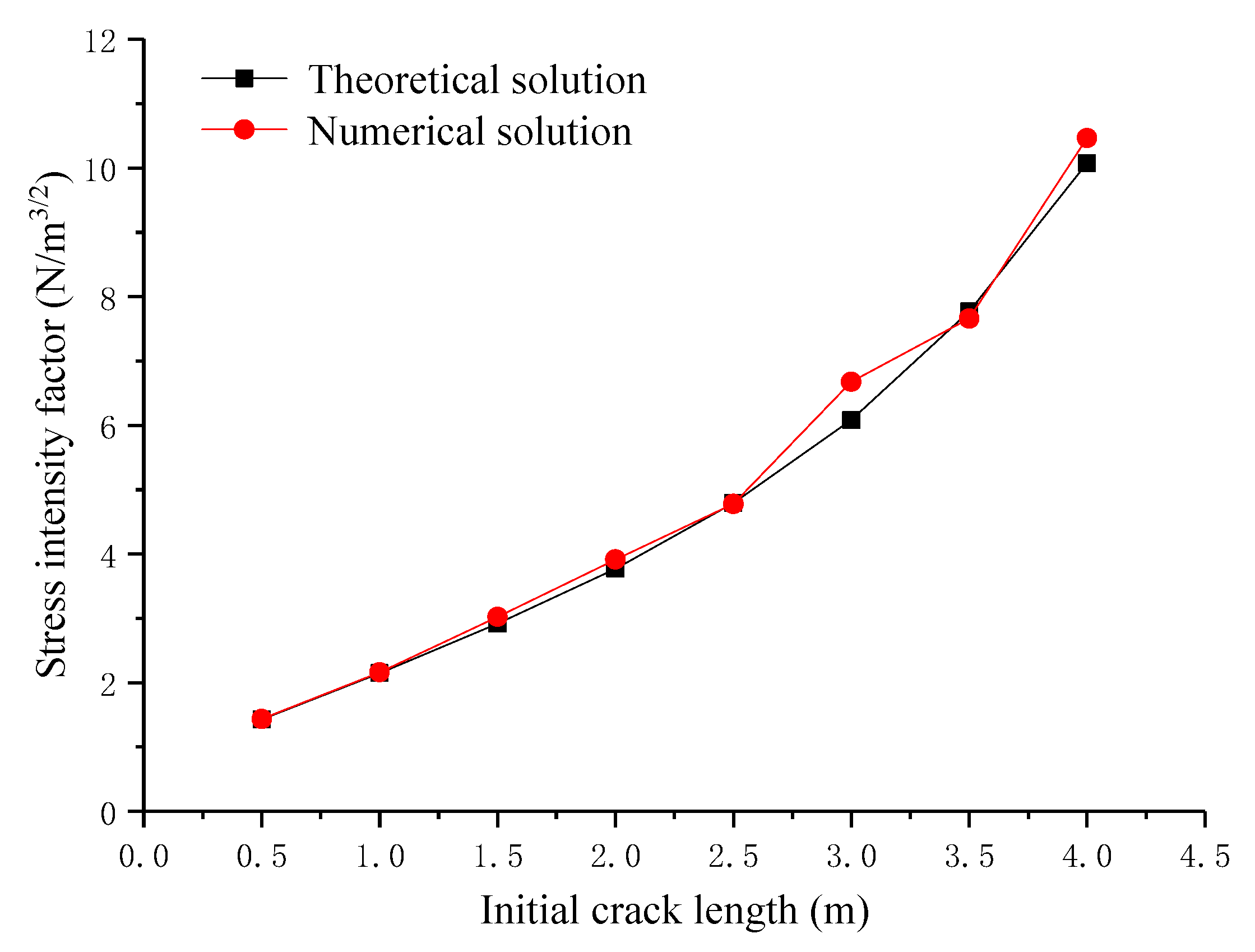
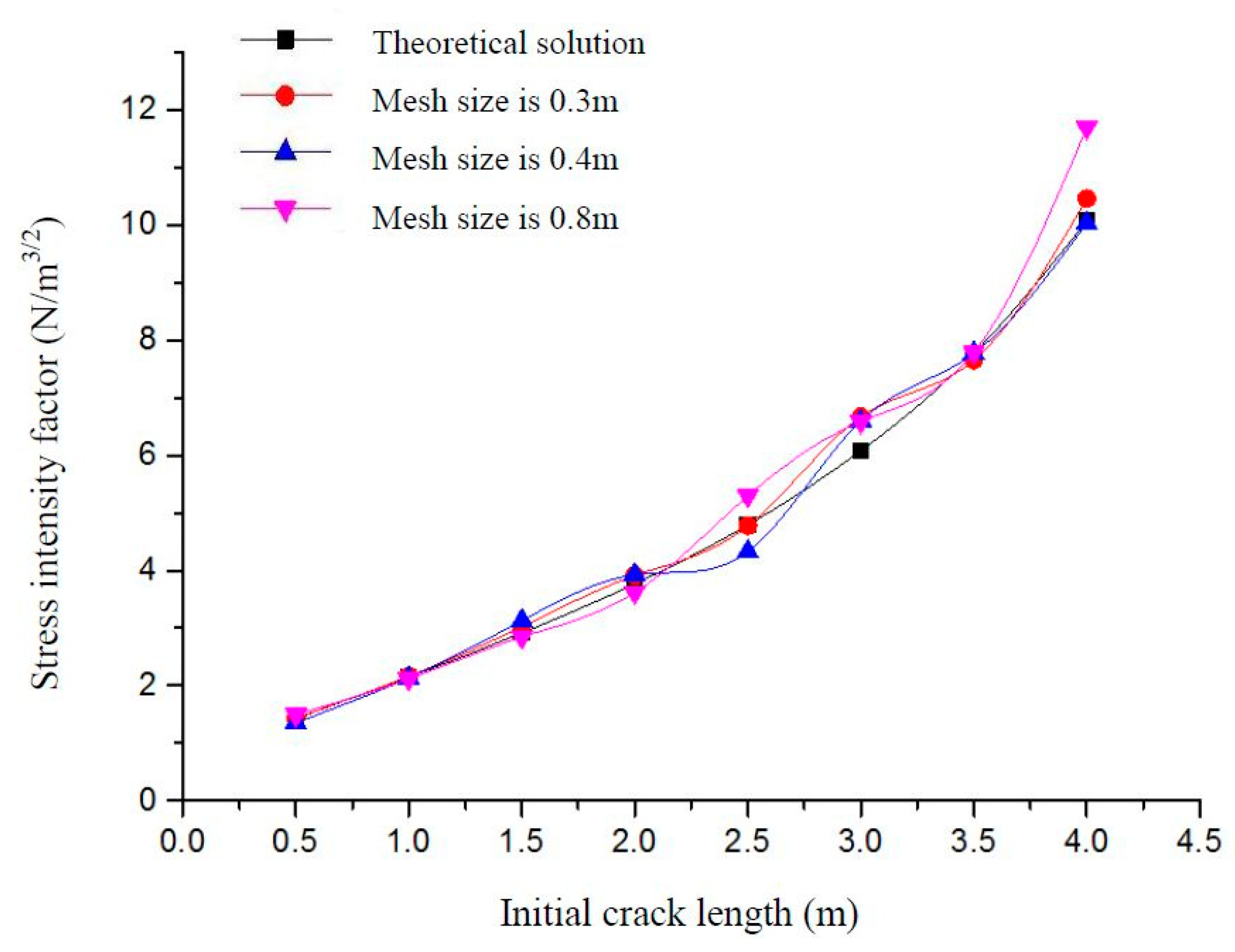
2.2. Correctness and Mesh Independence Verification of the XFEM
3. Crack Propagation in Aircraft Pipes
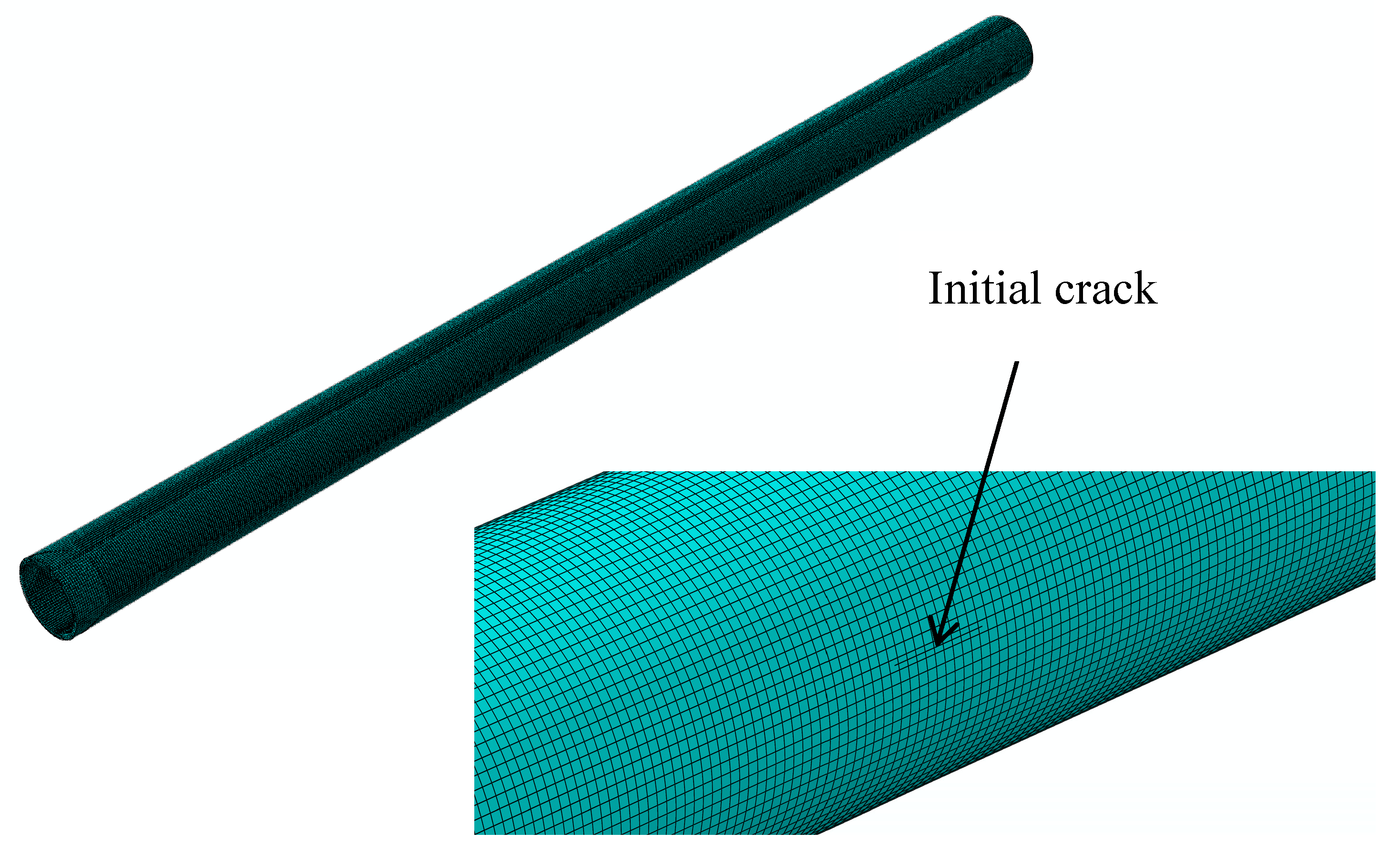
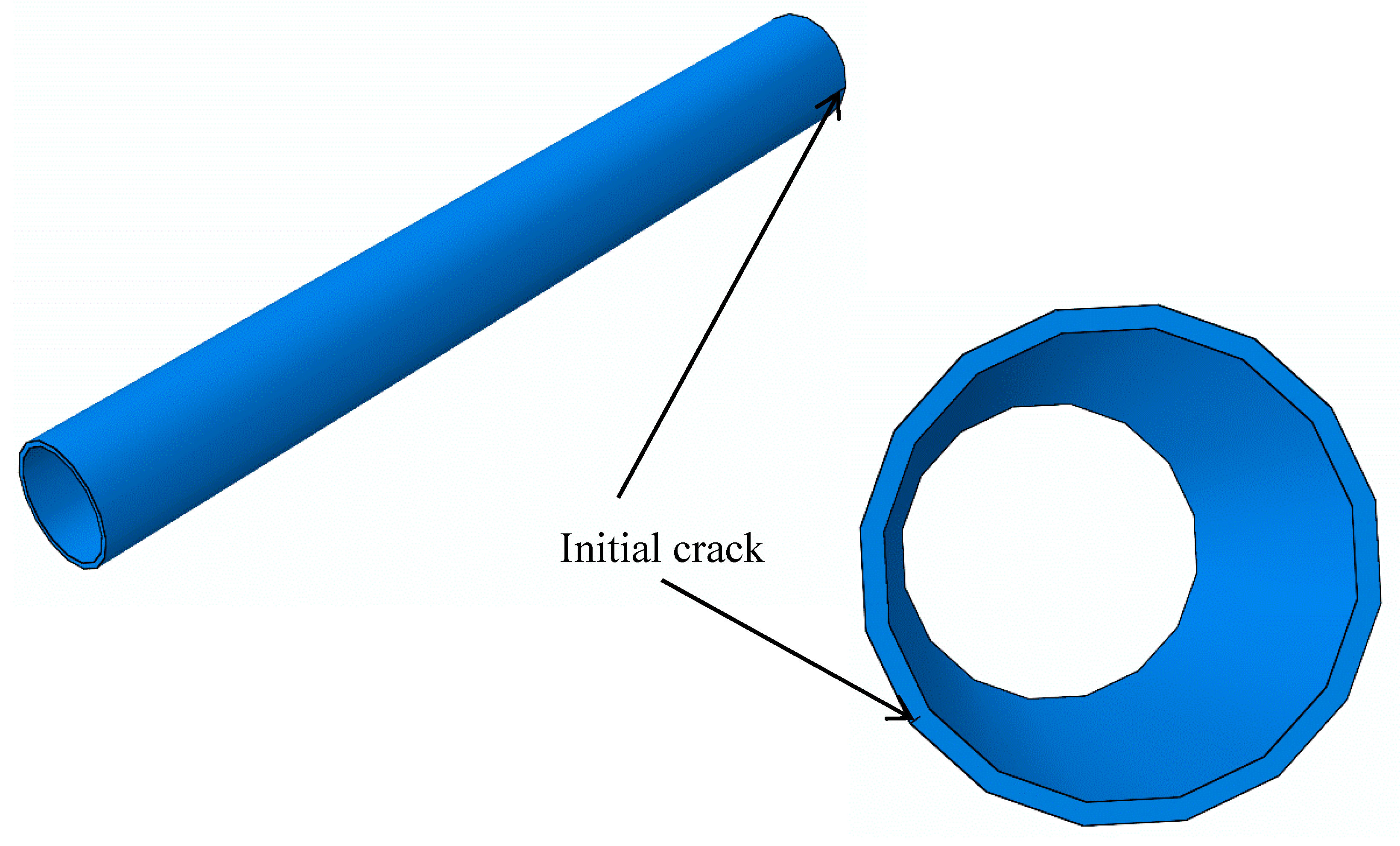
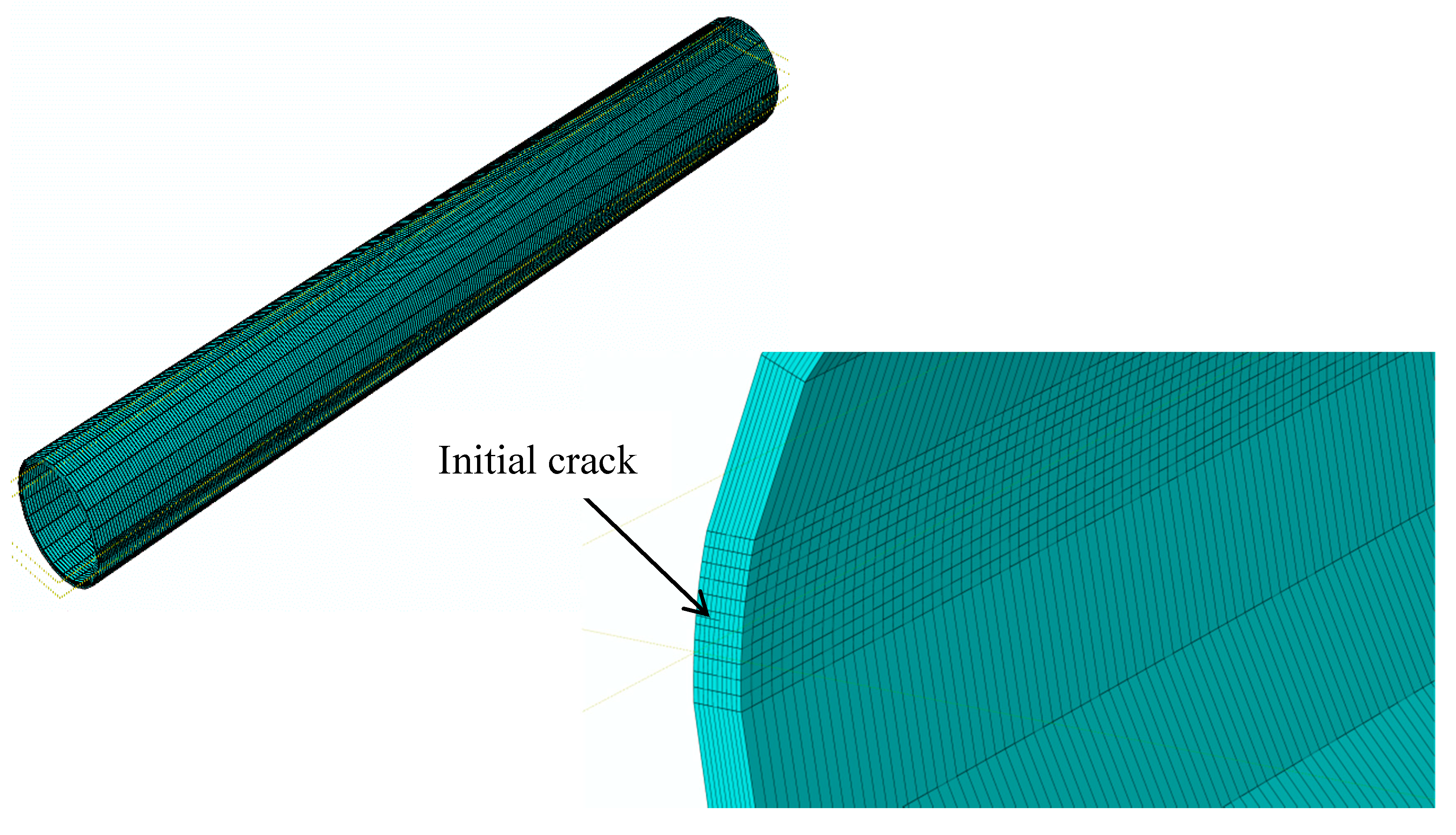
3.1. Geometric and Numerical Models
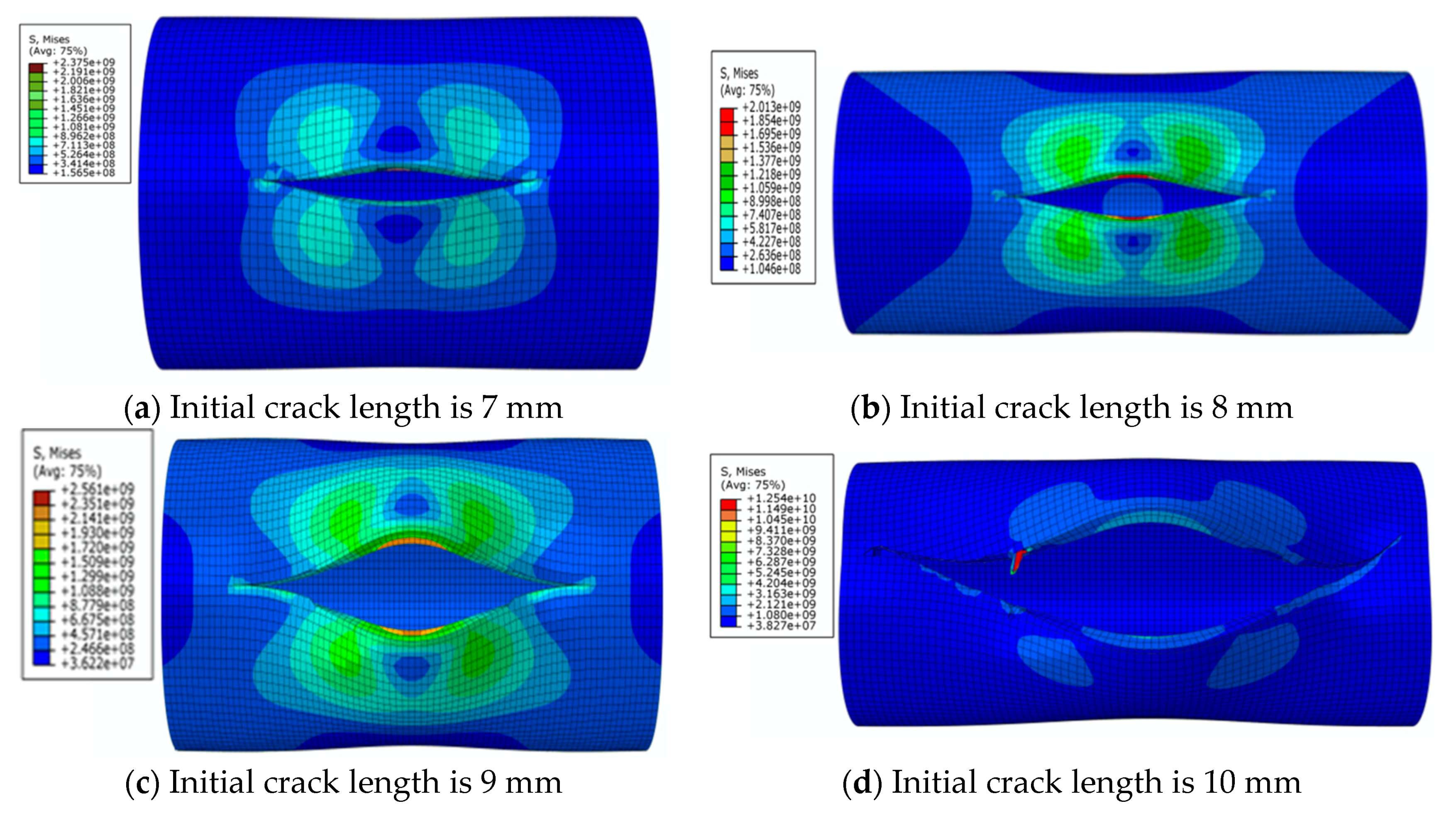
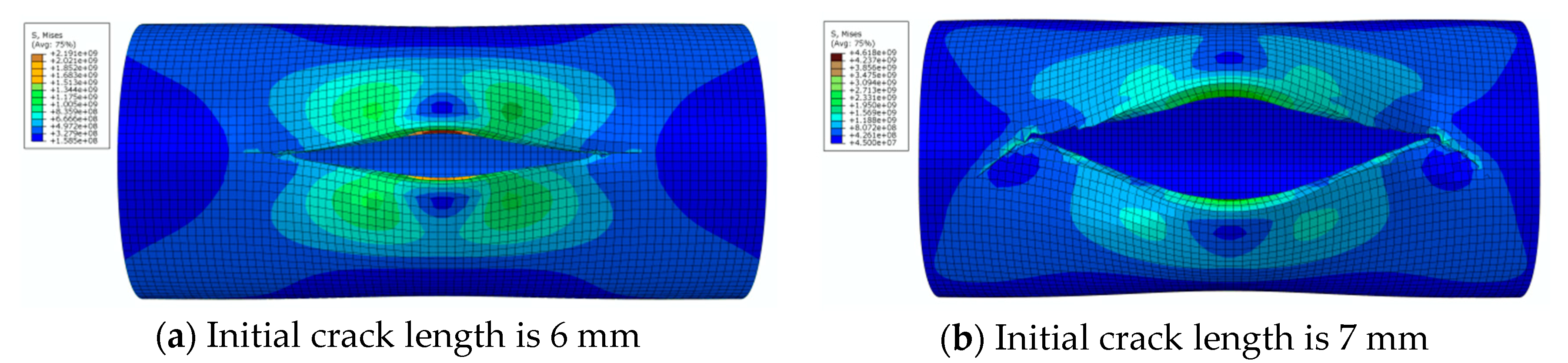
3.2. Results and Discussion
4. Factors Affecting Crack Propagation
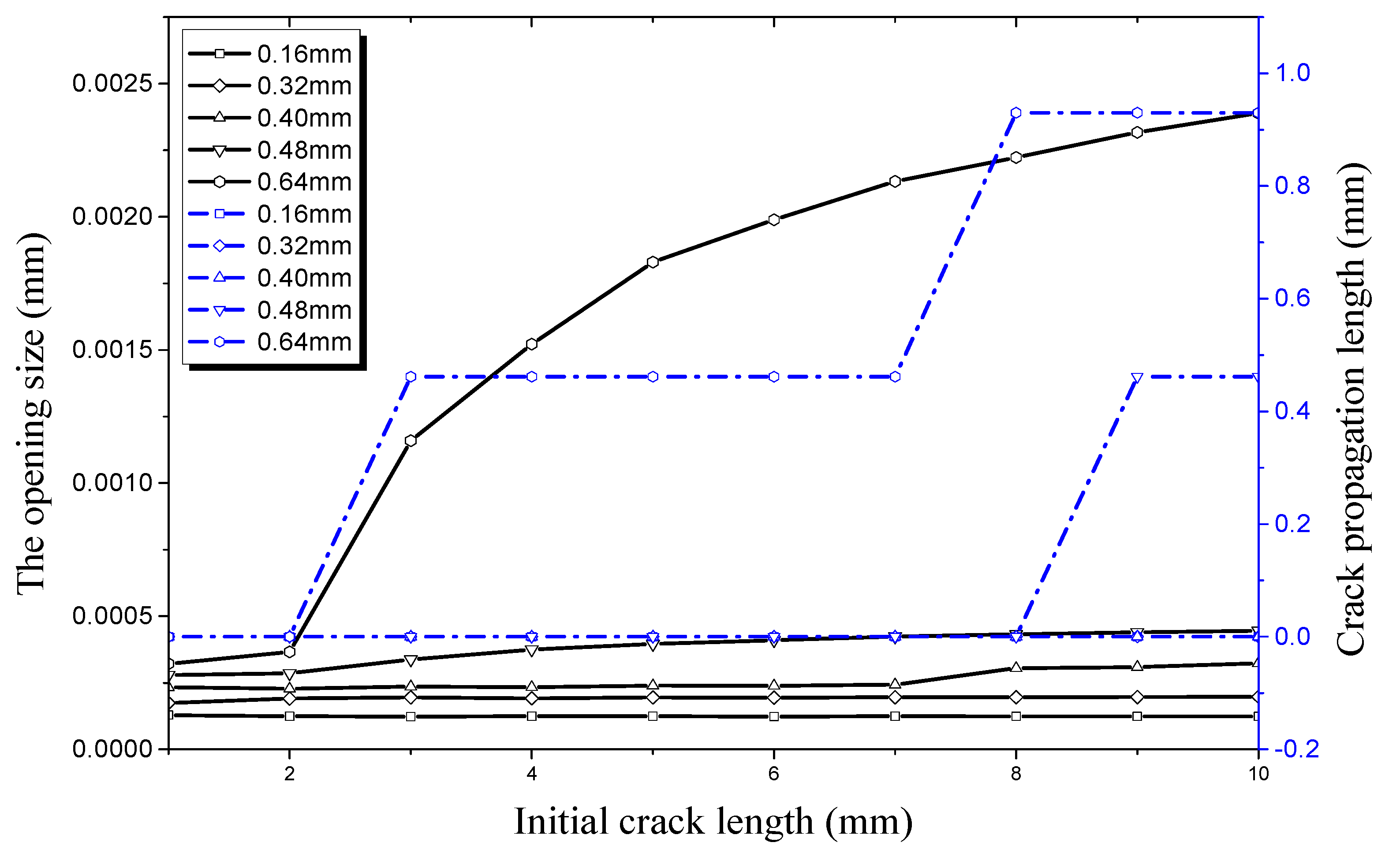
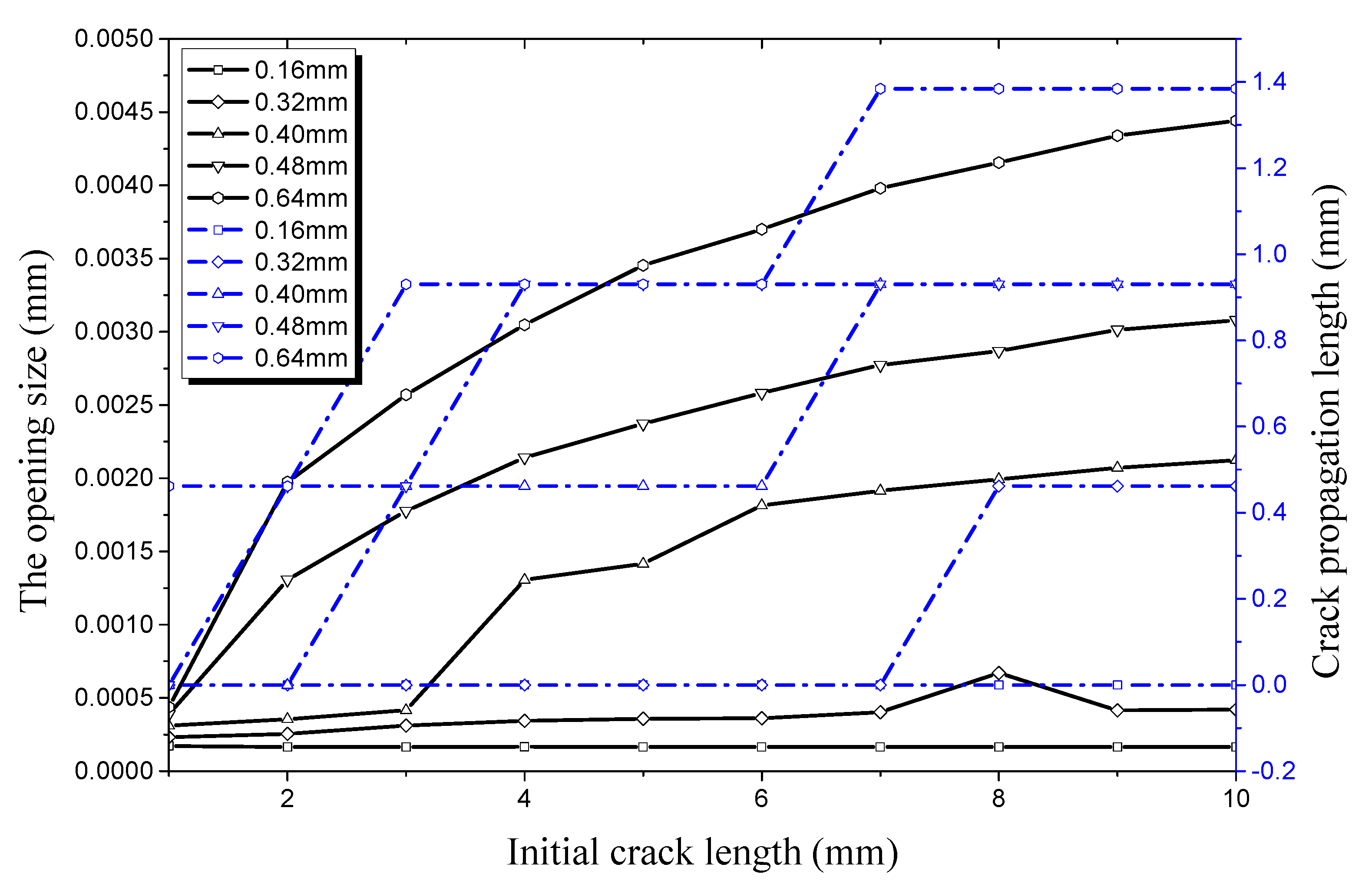
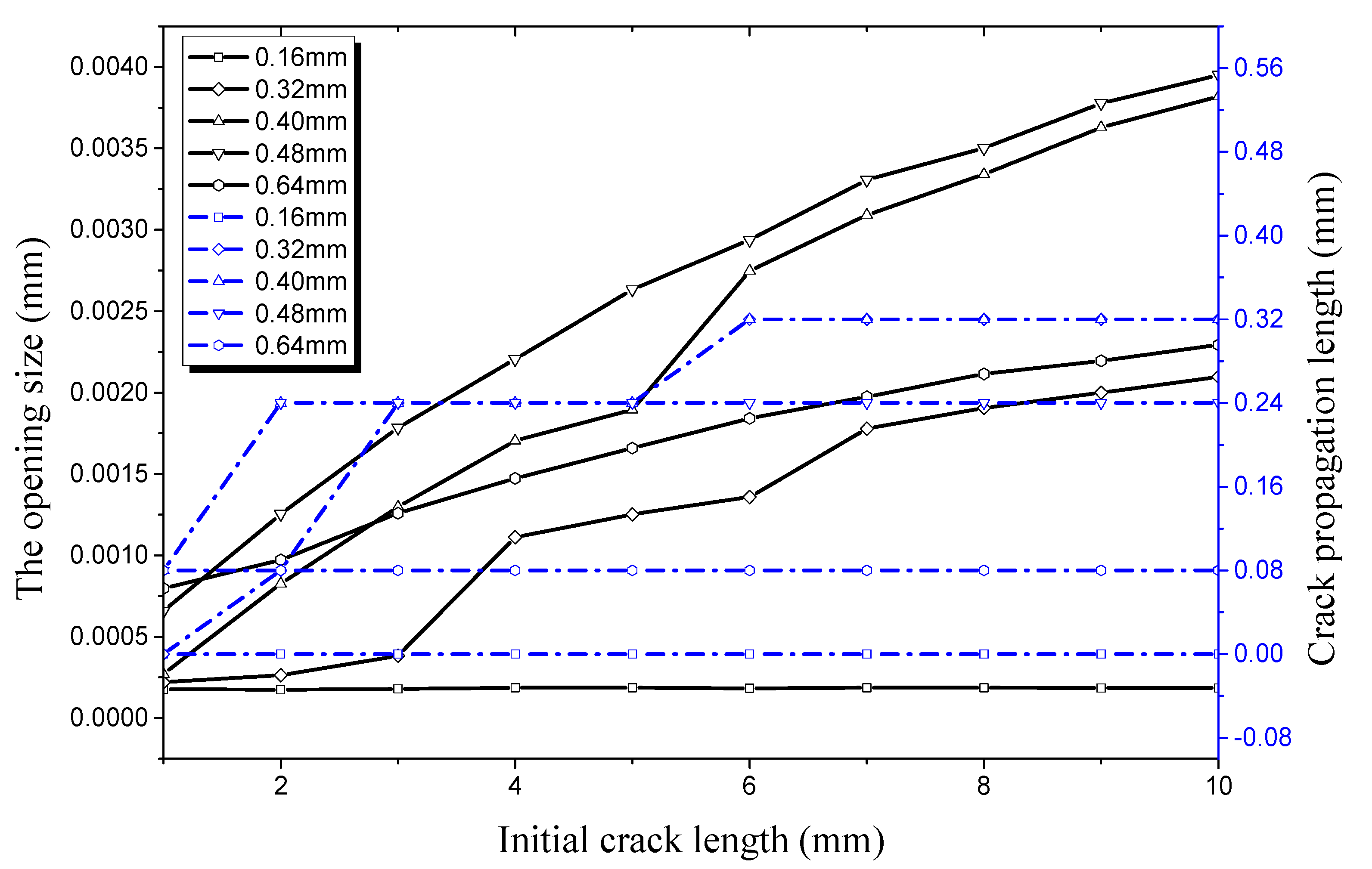
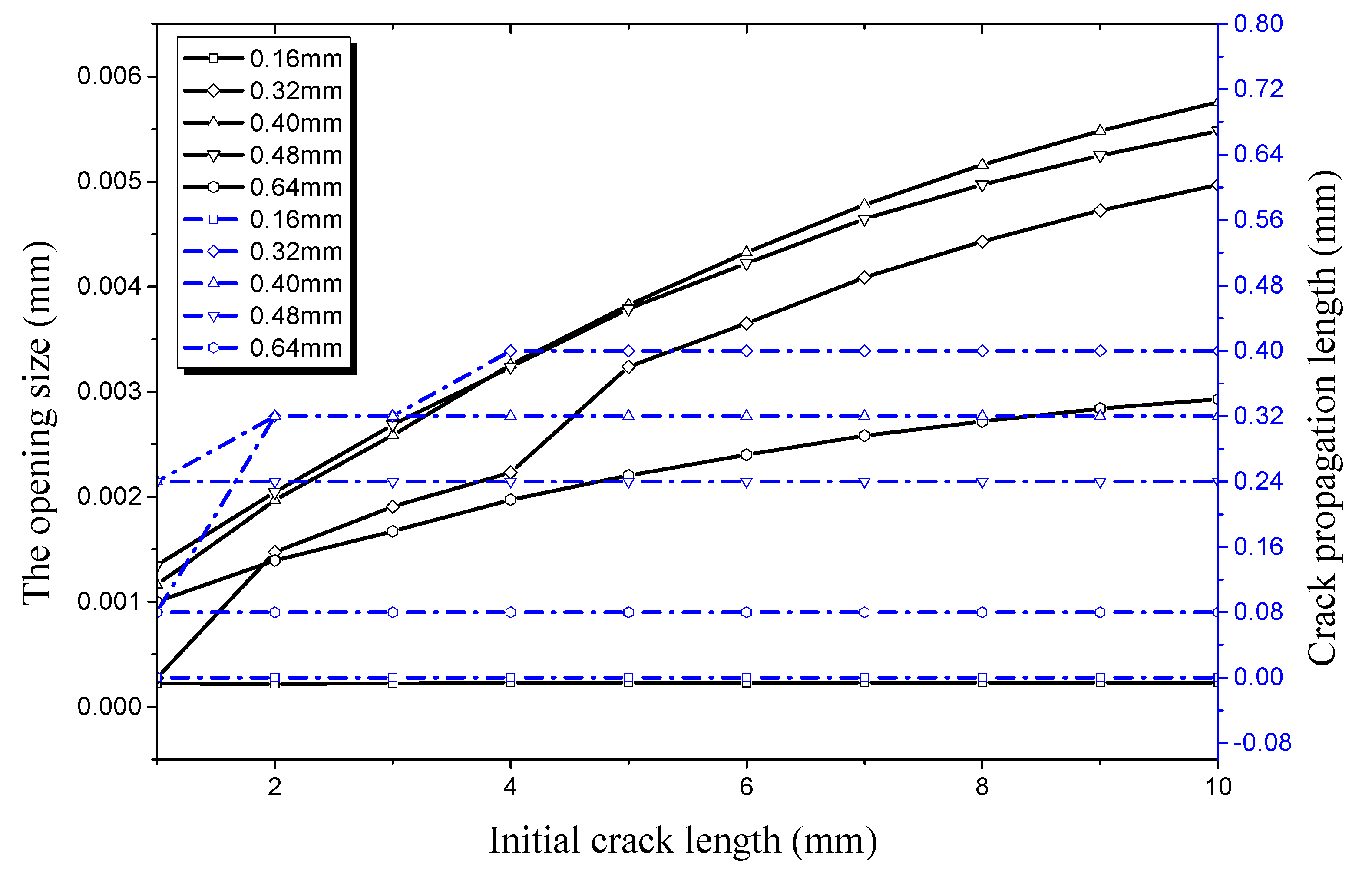
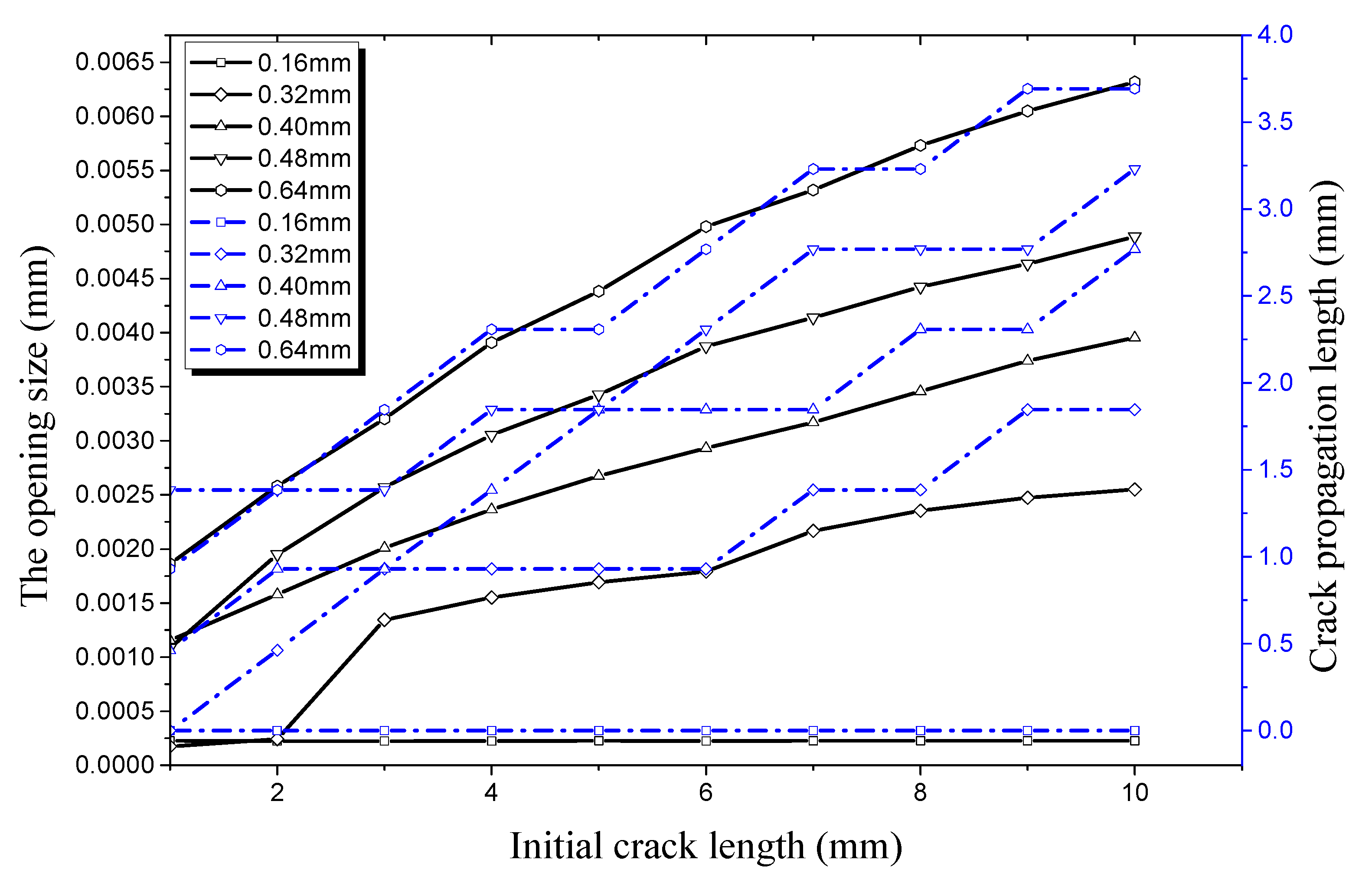
4.1. Factors Affecting Initial Crack Propagation on the Outer Surface
4.1.1. Crack Propagation in the Longitudinal Direction
4.1.2. Crack Propagation in the Radial Direction
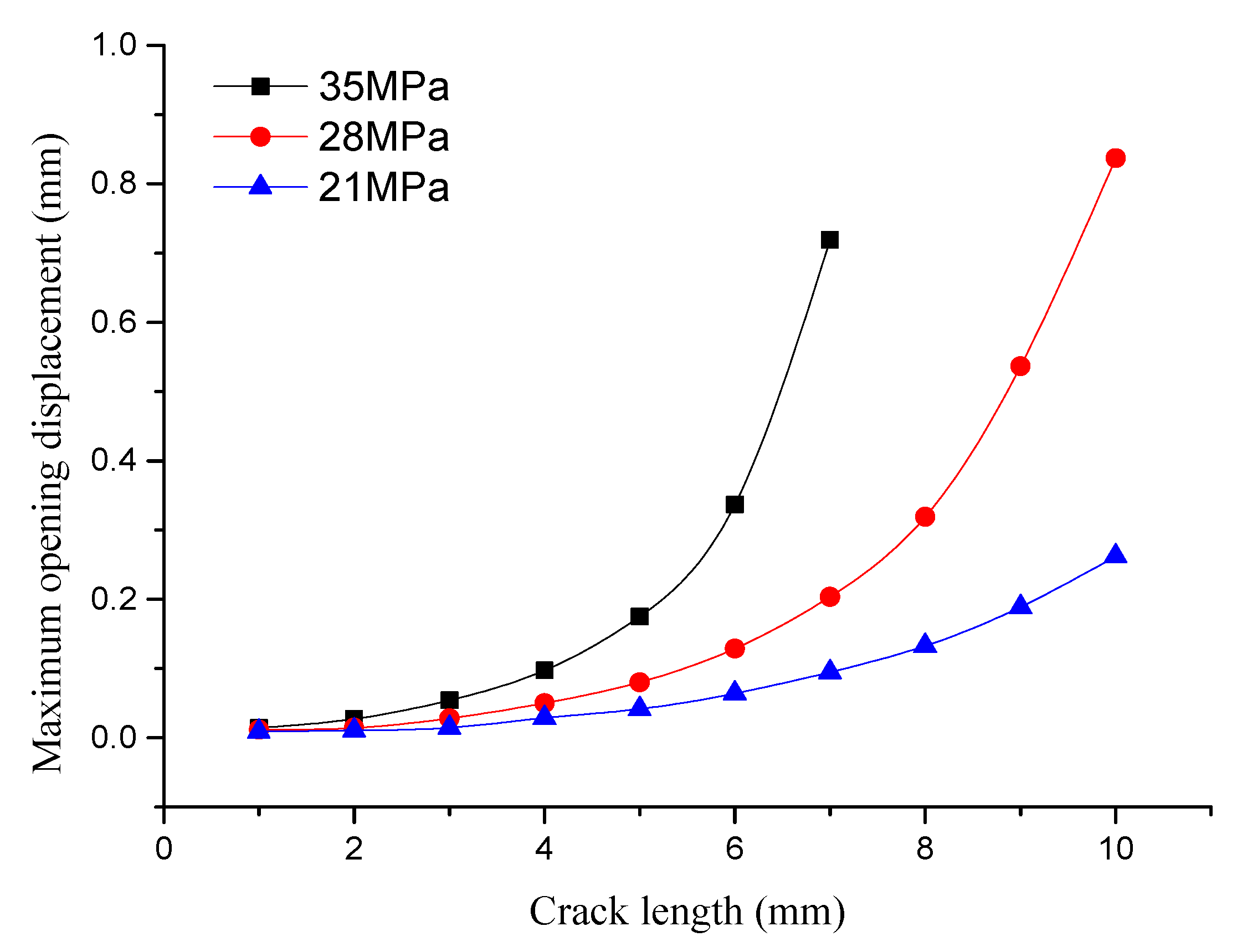
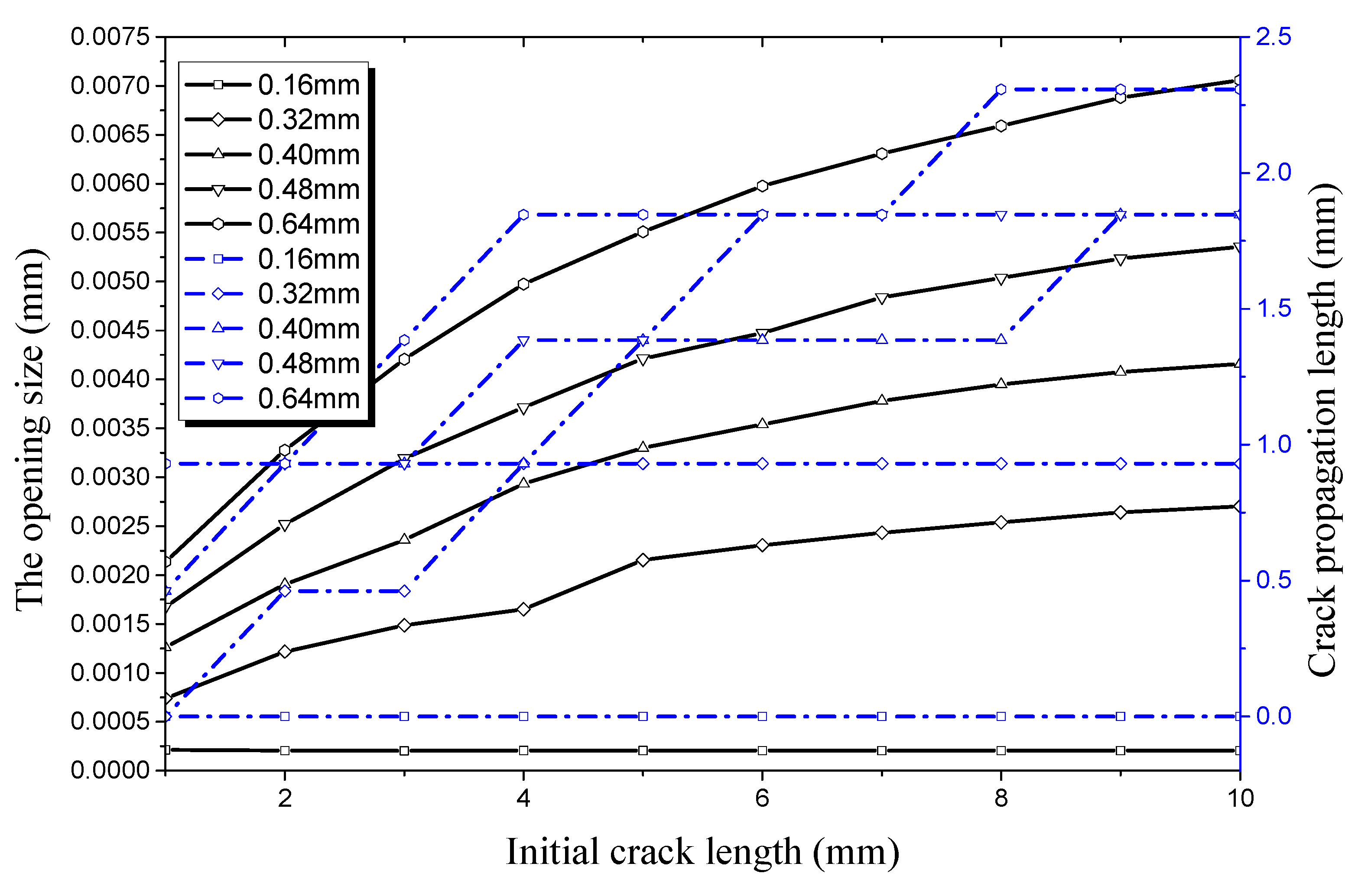
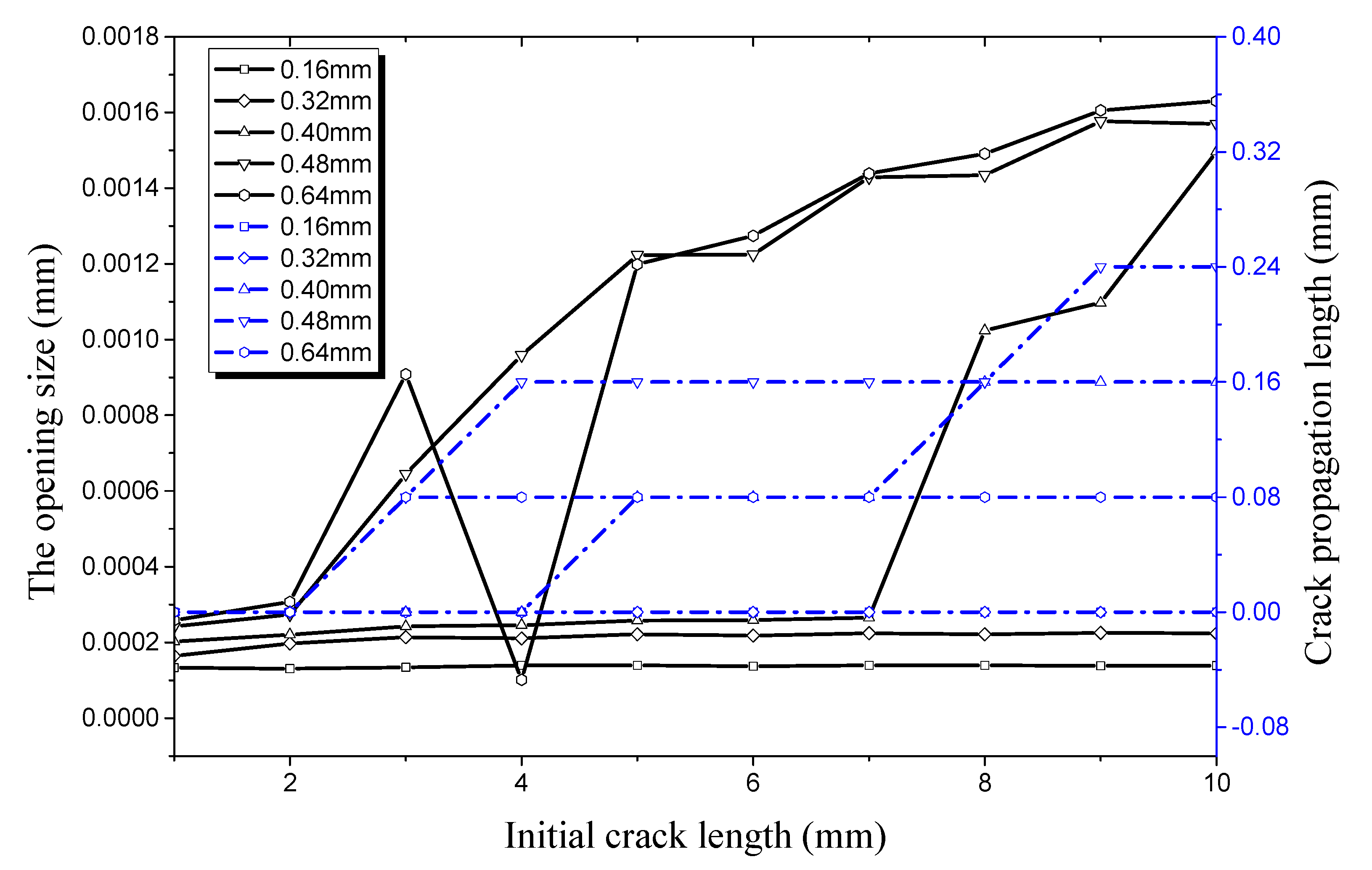
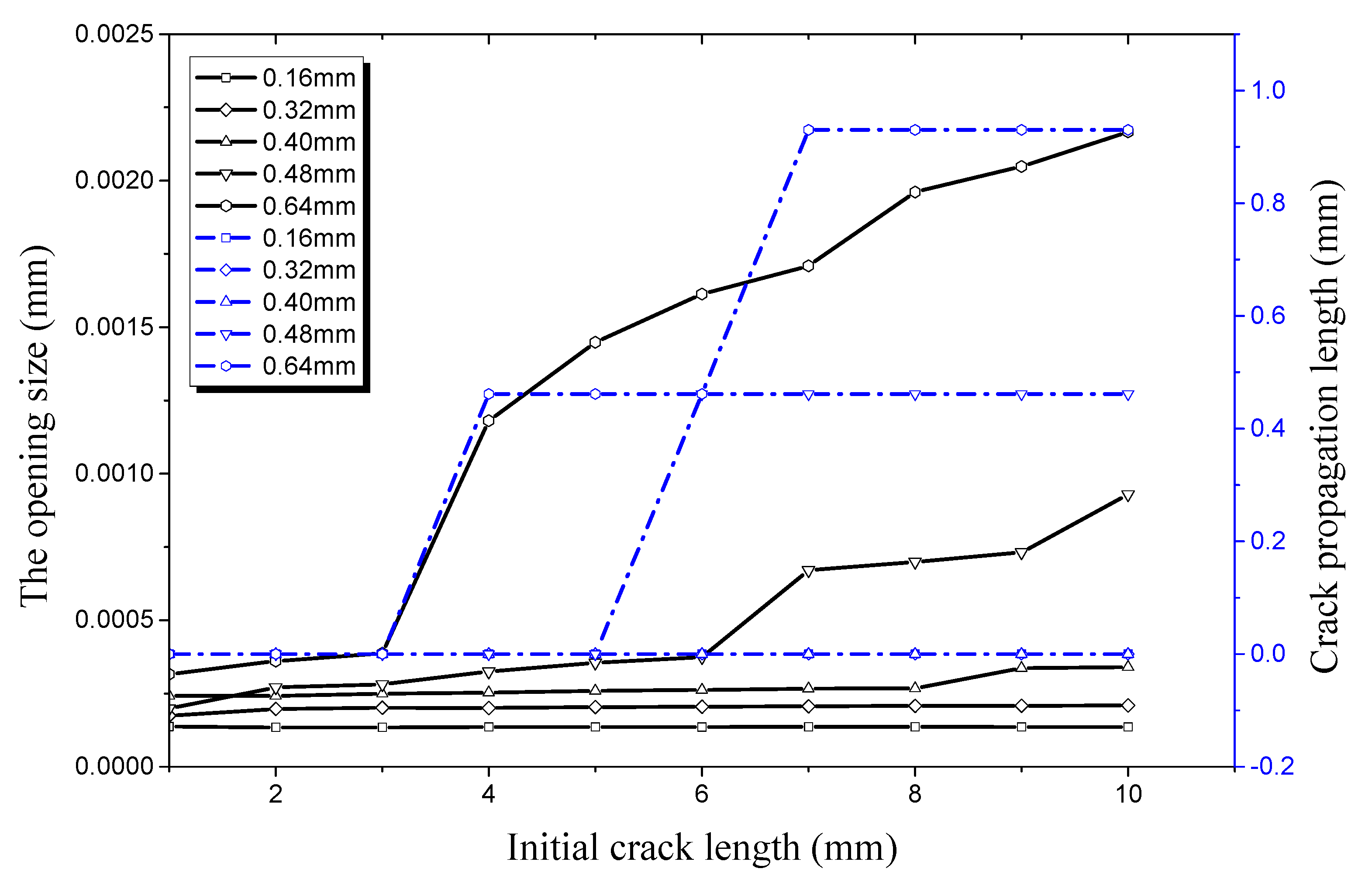
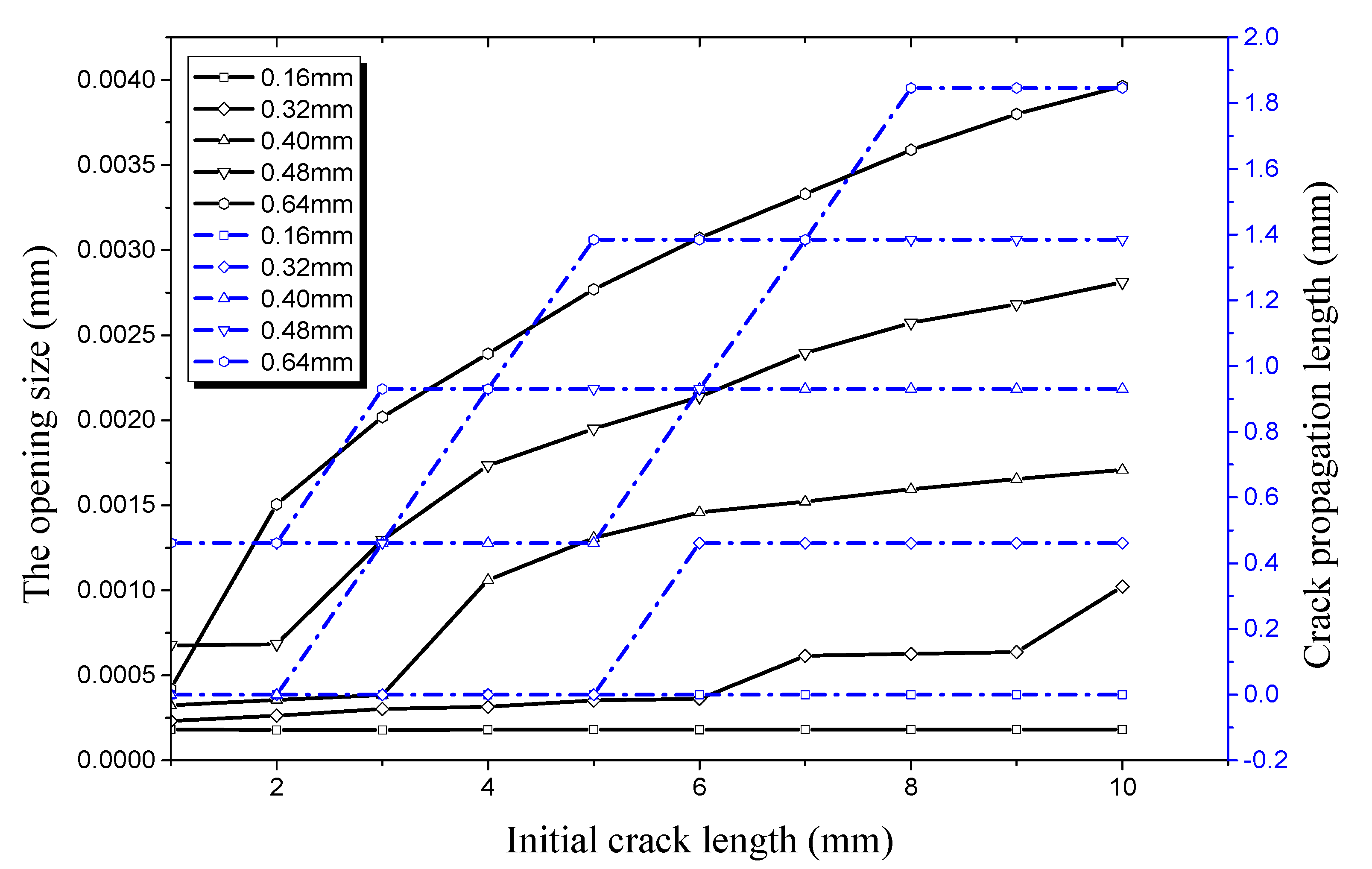
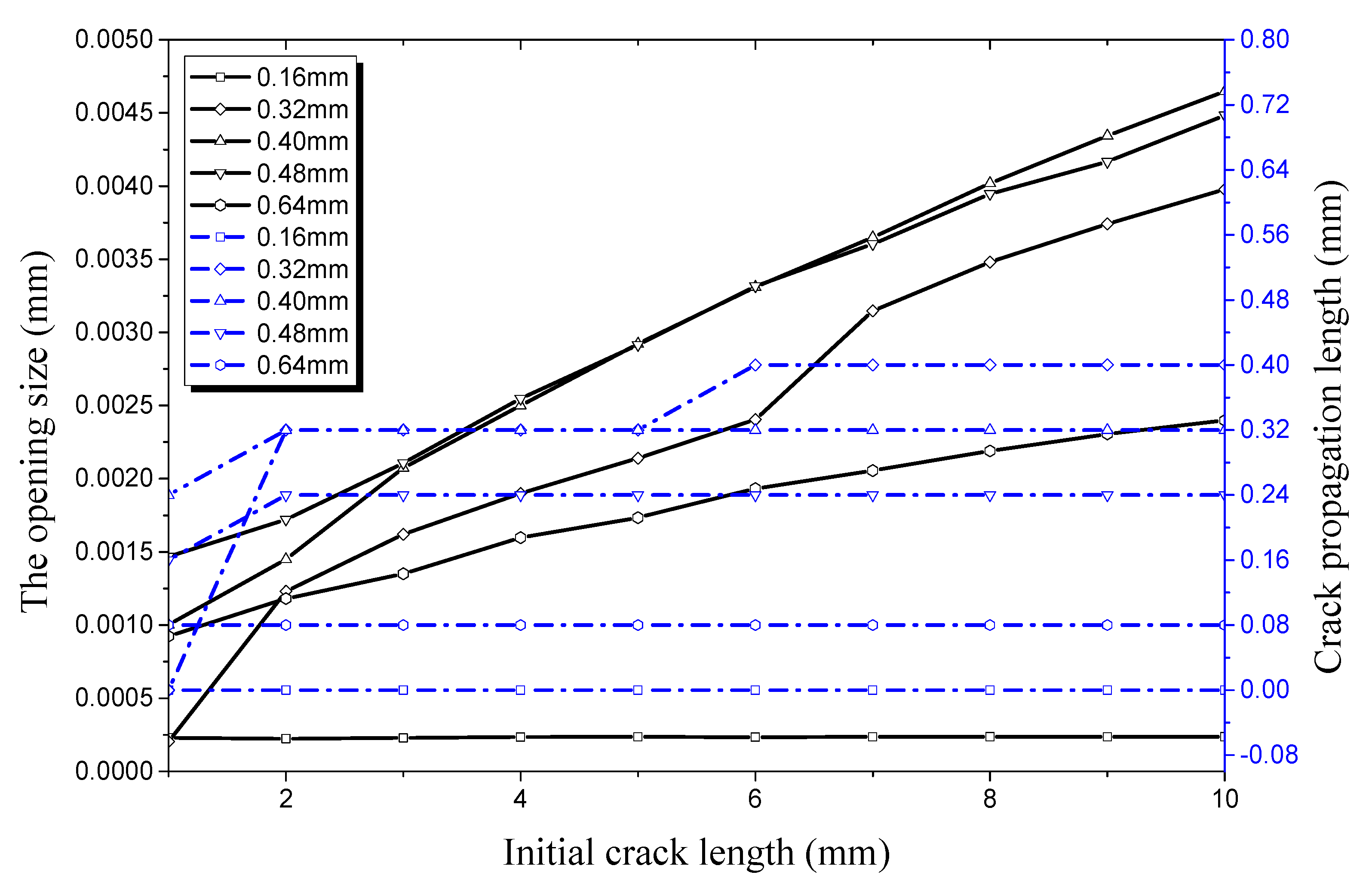
4.2. Factors Affecting Initial Crack Propagation on the Inner Surface
4.2.1. Crack Propagation along the Longitudinal Direction
4.2.2. Crack Propagation along the Radial Direction
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Atamturktur, S.; Li, T.; Ramage, M.H.; Farajpour, I. Load carrying capacity assessment of a scaled masonry dome: Simulations validated with non–destructive and destructive measurements. Constr. Build. Mater. 2012, 34, 418–429. [Google Scholar] [CrossRef]
- Chakherlou, T.N.; Mirzajanzadeh, M.; Vogwell, J.; Abazadeh, B. Investigation of the fatigue life and crack growth in torque tightened bolted joints. Aerosp. Sci. Technol. 2011, 15, 304–313. [Google Scholar] [CrossRef]
- Laiarinandrasana, L.; Devilliers, C.; Lucatelli, J.M.; Gaudichet–Maurin, E.; Brossard, J.M. Experimental study of the crack depth ratio threshold to analyze the slow crack growth by creep of high density polyethylene pipes. Int. J. Press. Vessels Pip. 2014, 122, 22–30. [Google Scholar] [CrossRef]
- Toribio, J.; Matos, J.C.; González, B. Corrosion–Fatigue Crack Growth in Plates: A Model Based on the Paris Law. Materials 2017, 10, 439. [Google Scholar]
- Oh, C.K.; Kim, Y.J.; Baek, J.H. Ductile failure analysis of API X65 pipes with notch–type defects using a local fracture criterion. Int. J. Press. Vessels Pip. 2007, 84, 512–525. [Google Scholar] [CrossRef]
- Oh, C.S.; Kim, N.H.; Kim, Y.J.; Baek, J.H.; Kim, Y.P.; Kim, W.S. A finite element ductile failure simulation method using stress–modified fracture strain model. Eng. Fract. Mech. 2011, 78, 124–137. [Google Scholar] [CrossRef]
- Kikuchi, M.; Wada, Y.; Shimizu, Y.; Li, Y. Crack growth analysis in a weld–heat–affected zone using S–version FEM. Int. J. Press. Vessels Pip. 2012, 90–91, 2–8. [Google Scholar] [CrossRef]
- Daimon, R.; Okada, H. Mixed–mode stress intensity factor evaluation by interaction integral method for quadratic tetrahedral finite element with correction terms. Eng. Fract. Mech. 2014, 115, 22–42. [Google Scholar] [CrossRef]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Sukumar, N.; Huang, Z.Y.; Prévost, J.H.; Suo, Z. Partition of unity enrichment for bimaterial interface cracks. Int. J. Numer. Methods Eng. 2004, 59, 1075–1102. [Google Scholar] [CrossRef]
- Moës, N.; Dolbow, J.; Belytschko, T. A finite element method for crack growth without remeshing. Int. J. Numer. Methods Eng. 1999, 46, 131–150. [Google Scholar] [CrossRef]
- Moës, N.; Belytschko, T. Extended finite element method for cohesive crack growth. Eng. Fract. Mech. 2002, 69, 813–833. [Google Scholar] [CrossRef] [Green Version]
- Sukumar, N.; Prévost, J.H. Modeling quasi–static crack growth with the extended finite element method Part I: Computer implementation. Int. J. Solids Struct. 2003, 40, 7513–7537. [Google Scholar] [CrossRef]
- Huang, R.; Sukumar, N.; Prévost, J.H. Modeling quasi–static crack growth with the extended finite element method Part II: Numerical applications. Int. J. Solids Struct. 2003, 40, 7539–7552. [Google Scholar] [CrossRef]
- Shi, J.; Chopp, D.; Lua, J.; Sukumar, N.; Belytschko, T. Abaqus implementation of extended finite element method using a level set representation for three–dimensional fatigue crack growth and life predictions. Eng. Fract. Mech. 2010, 77, 2840–2863. [Google Scholar] [CrossRef]
- Zhang, Y.M.; Fan, M.; Xiao, Z.M.; Zhang, W.G. Fatigue analysis on offshore pipelines with embedded cracks. Ocean Eng. 2016, 117, 45–56. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, J.; Zuo, Z. Numerical Study of the Effects of Residual Stress on Fretting Fatigue Using XFEM. Materials 2015, 8, 7094–7105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- González–Albuixech, V.F.; Qian, G.; Niffenegger, M. Integrity analysis of reactor pressure vessels subjected to pressurized thermal shocks by XFEM. Nucl. Eng. Des. 2014, 275, 336–343. [Google Scholar]
- Zhang, B.; Ye, C.; Liang, B.; Zhang, Z.; Zhi, Y. Ductile failure analysis and crack behavior of X65 buried pipes using extended finite element method. Eng. Fail. Anal. 2014, 45, 26–40. [Google Scholar] [CrossRef]
- Zarrinzadeh, H.; Kabir, M.Z.; Deylami, A. Crack growth and debonding analysis of an aluminum pipe repaired by composite patch under fatigue loading. Thin–Wall Struct. 2017, 112, 140–148. [Google Scholar] [CrossRef]
- Taheri, S.; Julan, E.; Tran, X.V.; Robert, N. Impacts of weld residual stresses and fatigue crack growth threshold on crack arrest under high–cycle thermal fluctuations. Nucl. Eng. Des. 2017, 311, 16–27. [Google Scholar] [CrossRef]
- Na, S.; Spatari, S.; Hsuan, Y.G. Fracture characterization of pristine/post–consumer HDPE blends using the essential work of fracture (EWF) concept and extended finite element method (XFEM). Eng. Fract. Mech. 2015, 139, 1–17. [Google Scholar] [CrossRef]
- Zarrinzadeh, H.; Kabir, M.Z.; Deylami, A. Experimental and numerical fatigue crack growth of an aluminium pipe repaired by composite patch. Eng. Struct. 2017, 133, 24–32. [Google Scholar] [CrossRef]
- Geniaut, S.; Galenne, E. A simple method for crack growth in mixed mode with X–FEM. Int. J. Solids Struct. 2012, 49, 2094–2106. [Google Scholar] [CrossRef]
- Bayesteh, H.; Mohammadi, S. XFEM fracture analysis of shells: The effect of crack tip enrichments. Comput. Mater. Sci. 2011, 50, 2793–2813. [Google Scholar] [CrossRef]
- Lin, Z.; Zhuang, Z.; You, X.; Wang, H.; Xu, D. Enriched goal–oriented error estimation applied to fracture mechanics problems solved by XFEM. Acta Mech. Solida Sin. 2012, 25, 393–403. [Google Scholar] [CrossRef]
- Loehnert, S.; Belytschko, T. A multiscale projection method for macro/microcrack simulations. Int. J. Numer. Methods Eng. 2007, 71, 1466–1482. [Google Scholar] [CrossRef]
- Duarte, C.A.; Kim, D.J. Analysis and applications of a generalized finite element method with global–local enrichment functions. Comput. Methods Appl. Mech. Eng. 2008, 197, 487–504. [Google Scholar] [CrossRef]
- Malekan, M.; Barros, F.B.; Pitangueira, R.L.S. Fracture analysis in plane structures with the two–scale G/XFEM method. Int J. Solids Struct. 2018, 155, 65–80. [Google Scholar] [CrossRef]
- Zhuang, Z.; Liu, Z.L.; Cheng, B.B.; Liao, J.H. The Extended Finite Element Method, Computational Mechanics; Tsinghua University Press: Beijing, China, 2012. [Google Scholar]
- Chinese Aeronautical Establishment. Stress Intensity Factor Manual; Science Press: Beijing, China, 1981. [Google Scholar]
- Sukumar, N.; Moës, N.; Moran, B.; Belytschko, T. Extended finite element method for three–dimensional crack modeling. Int. J. Numer. Methods Eng. 2000, 48, 1549–1570. [Google Scholar] [CrossRef]



| E (GPa) | μ | Maximum Principal Stress (MPa) | GI (N/m) | GII (N/m) | GIII (N/m) |
|---|---|---|---|---|---|
| 210 | 0.3 | 84.4 | 42,200 | 42,200 | 42,200 |
| Ratio of Initial Crack a/b | 0.0625 | 0.125 | 0.1875 | 0.25 | 0.3125 | 0.375 | 0.4375 | 0.5 |
| F | 1.142 | 1.222 | 1.344 | 1.505 | 1.711 | 1.981 | 2.345 | 2.843 |
| Crack Length | 0.5 m | 2 m | 4 m | |
|---|---|---|---|---|
| Mesh Size | ||||
| 0.3 m | 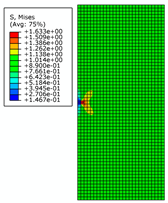 | 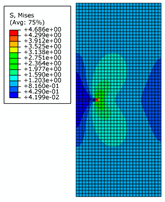 |  | |
| 0.4 m |  | 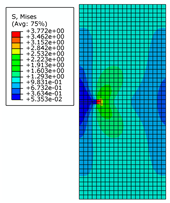 | 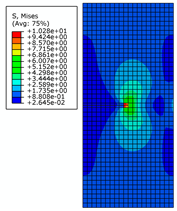 | |
| 0.8 m |  | 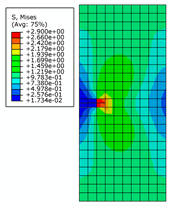 | 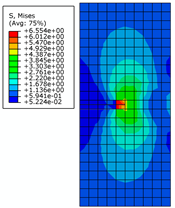 | |
| E (GPa) | μ | Maximum Principal Stress (MPa) | GI (N/m) | GII (N/m) | GIII (N/m) |
|---|---|---|---|---|---|
| 210 | 0.3 | 540 | 643,000 | 643,000 | 643,000 |
| l0/mm | 1 mm | 2 mm | 3 mm | 4 mm | 5 mm | 6 mm | 7 mm | 8 mm | 9 mm | 10 mm | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Internal Pressure/MPa | |||||||||||
| 21 | l1/mm | 0 | 0 | 0 | 1.015 | 1.015 | 1.523 | 2.03 | 3.045 | 3.553 | 4.823 |
| /mm | 0 | 0 | 0 | 50.75 | 40.6 | 50.77 | 58 | 76.125 | 78.96 | 96.46 | |
| 28 | l1/mm | 0 | 0 | 1.015 | 2.03 | 2.5375 | 3.5525 | 4.5675 | 7.105 | 10.6575 | 13.195 |
| /mm | 0 | 0 | 67.67 | 101.5 | 101.5 | 118.42 | 130.5 | 177.625 | 236.83 | 263.9 | |
| 35 | l1/mm | 0 | 1.523 | 3.046 | 4.1615 | 5.5825 | 9.138 | 15.23 | — | — | — |
| /mm | 0 | 152.3 | 203.07 | 208.075 | 223.3 | 304.6 | 435.14 | — | — | — |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Wei, Z.; Li, P.; Yu, L.; Huang, W. Initial Crack Propagation and the Influence Factors of Aircraft Pipe Pressure. Materials 2019, 12, 3098. https://doi.org/10.3390/ma12193098
Wang F, Wei Z, Li P, Yu L, Huang W. Initial Crack Propagation and the Influence Factors of Aircraft Pipe Pressure. Materials. 2019; 12(19):3098. https://doi.org/10.3390/ma12193098
Chicago/Turabian StyleWang, Fusheng, Zheng Wei, Pu Li, Lingjun Yu, and Weichao Huang. 2019. "Initial Crack Propagation and the Influence Factors of Aircraft Pipe Pressure" Materials 12, no. 19: 3098. https://doi.org/10.3390/ma12193098
APA StyleWang, F., Wei, Z., Li, P., Yu, L., & Huang, W. (2019). Initial Crack Propagation and the Influence Factors of Aircraft Pipe Pressure. Materials, 12(19), 3098. https://doi.org/10.3390/ma12193098





