Experimental and Theoretical Investigations of the Constitutive Relations of Artificial Frozen Silty Clay
Abstract
:1. Introduction
2. Experimental Conditions
2.1. Experimental Material
2.2. Sample Preparation and Test Apparatus
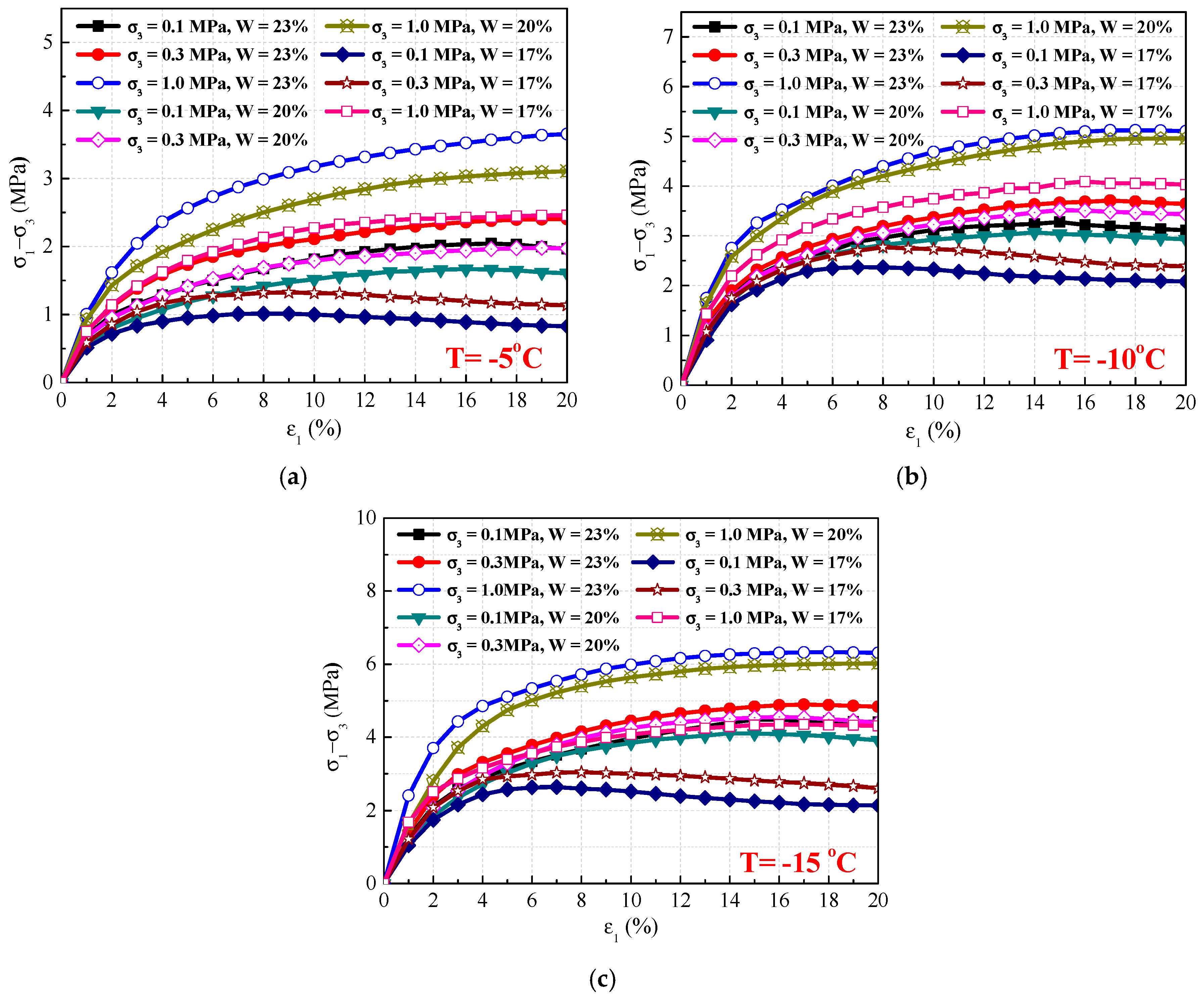
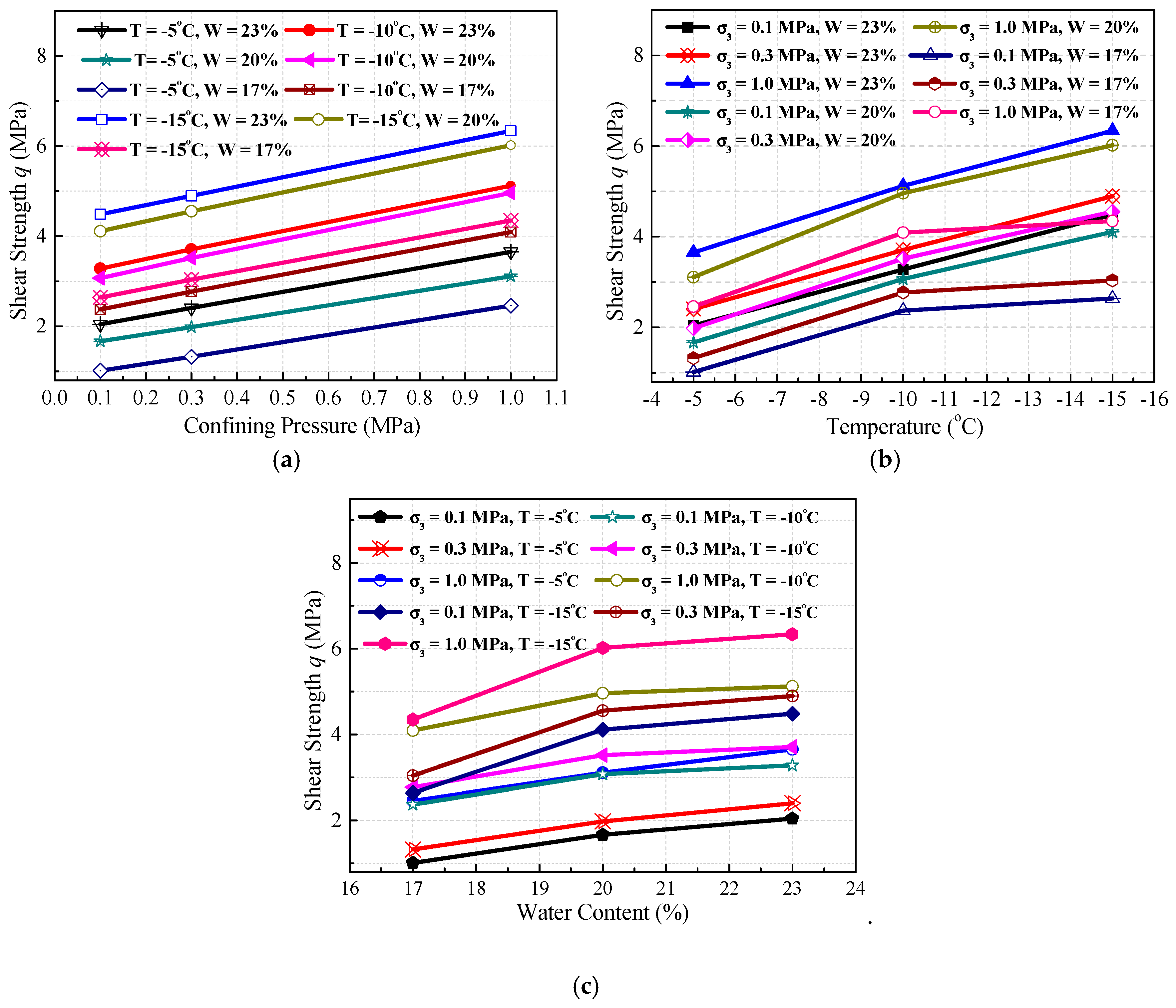
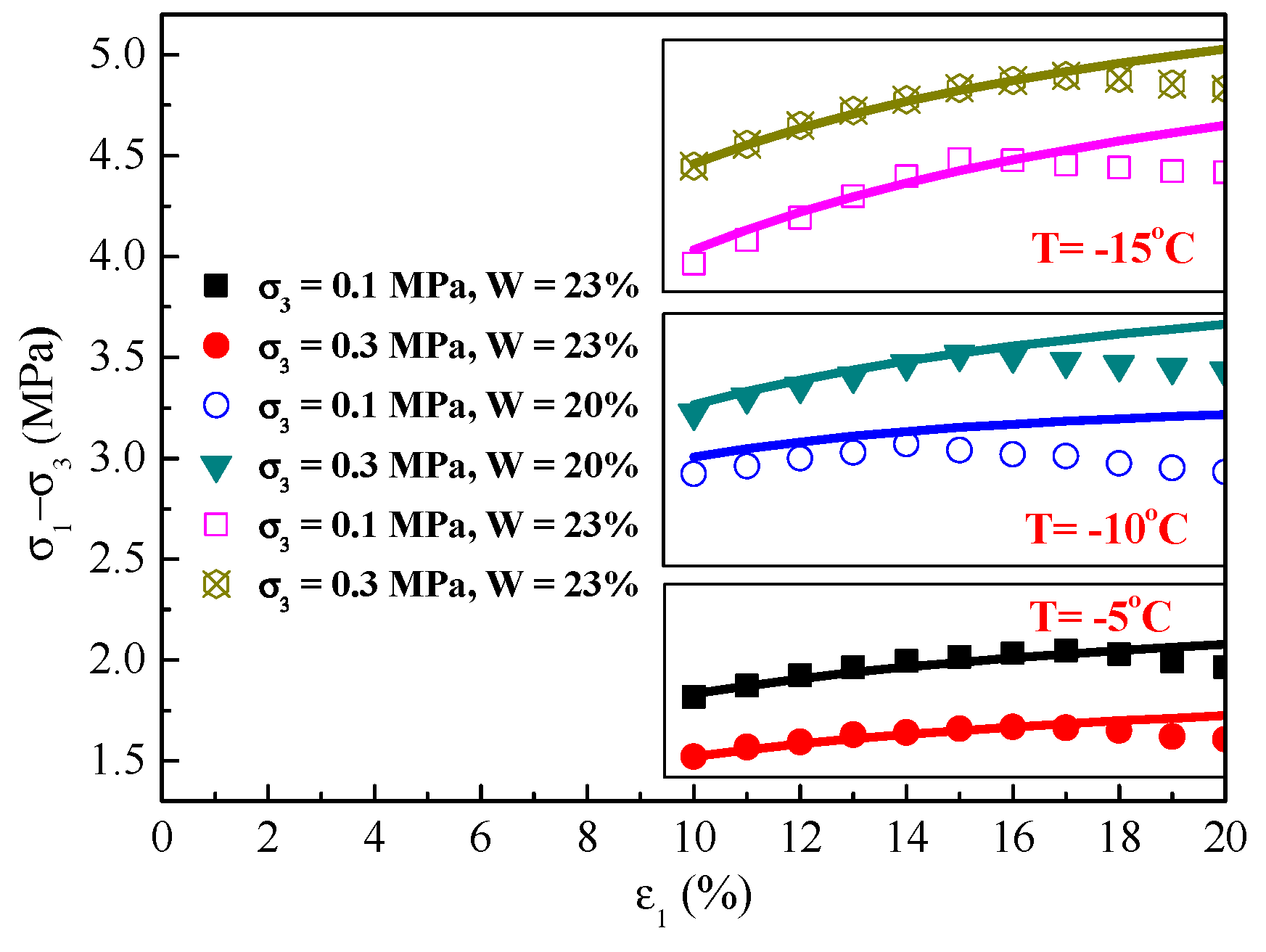
2.3. Experimental Results and Analysis
3. MDC Model for Frozen Silty Clay
3.1. Constitutive Model and Parameter Determination
3.2. STRAIN-Softening Criterion of the MDC Model
4. SD Model for Frozen Soil
4.1. SD Constitutive Model
- Set the initial value of x = [m, F0] and threshold ε;
- Calculate fi(x) and obtain the vector fk;
- Calculate fi’(x) and obtain the Jacobian matrix Jk;
- Calculate xk+1 by using the iteration form of the Gauss-Newton method;
- Judge the condition ‖xk+1 − xk‖ < ε, if it is not satisfied, repeat step (2) until the condition is satisfied.
4.2. Strain-Softening Criterion of the SD Model
4.3. Model Verification and Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Notation List
| Symbol | Description |
| σ1−σ3 | Deviatoric stress |
| εa | Axial strain |
| a | Parameter related to initial elastic modulus |
| b | Parameter related to residual and ultimate strengths |
| c | Parameter related to residual and ultimate strengths |
| Et | Tangent modulus |
| Ei | Initial elastic modulus |
| εrs | Calculated initial softening strain |
| q | Shear strength |
| δe | Positive error correction term |
| δb | Length of the confidence interval for parameter b |
| δc | Length of the confidence interval for parameter c |
| α | Significance level |
| Z | Random variable that satisfies normal distribution |
| n | Number of samples |
| σb | Standard deviation of parameter b |
| σc | Standard deviation of parameter c |
| δt | Length of the confidence interval of b-c |
| εre | Experimental initial softening strain |
| σ1ʹ-σ3ʹ | Effective deviatoric stress |
| D | Damage variable |
| N | Total number of elements |
| N(εa) | Number of damaged elements |
| f(εa) | Probability density function of the Weibull distribution |
| m | Scale parameter of the Weibull distribution |
| F0 | Shape parameter of the Weibull distribution |
| fi(x) | Residuals between test and simulation results |
| x | Parameter set |
| xk | Parameter value at k-th iteration |
| A | Predicted results calculated by the MDC model |
| gi(x) | First order Taylor expansion of fi(x) |
| F(x) | Objective function |
| Jk | Jacobian matrix |
| ε | Error threshold |
| εrep | Reference strain |
References
- Li, S.Y.; Lai, Y.M.; Zhang, M.Y.; Zhang, S.J. Minimum ground pre-freezing time before excavation of Guangzhou subway tunnel. Cold Reg. Sci. Technol. 2006, 46, 181–191. [Google Scholar] [CrossRef]
- Zhou, M.M.; Meschke, G. A three-phase thermo-hydro-mechanical finite element model for freezing soils. Int. J. Numer. Anal. Meth. Geomech. 2013, 37, 3173–3193. [Google Scholar] [CrossRef]
- Zhou, J.; Tang, Y.Q. Centrifuge experimental study of thaw settlement characteristics of mucky clay after artificial ground freezing. Eng. Geol. 2015, 190, 98–108. [Google Scholar] [CrossRef]
- Marwan, A.; Zhou, M.M.; Abdelrehim, M.Z.; Meschke, G. Optimization of artificial ground freezing in tunneling in the presence of seepage flow. Comput. Geotech. 2016, 75, 112–125. [Google Scholar] [CrossRef]
- Lai, Y.M.; Li, S.Y.; Qi, J.L.; Gao, Z.H.; Chang, X.X. Strength distributions of warm frozen clay and its stochastic damage constitutive model. Cold Reg. Sci. Technol. 2008, 53, 200–215. [Google Scholar] [CrossRef]
- Yang, Y.G.; Lai, Y.M.; Chang, X.X. Laboratory and theoretical investigations on the deformation and strength behaviors of artificial frozen soil. Cold Reg. Sci. Technol. 2010, 64, 39–45. [Google Scholar] [CrossRef]
- Lai, Y.M.; Xu, X.T.; Yu, W.B.; Qi, J.L. An experimental investigation of the mechanical behavior and a hyperplastic constitutive model of frozen loess. Int. J. Eng. Sci. 2014, 84, 29–53. [Google Scholar] [CrossRef]
- Zhu, Z.W.; Kang, G.Z.; Ma, Y.; Xie, Q.J.; Zhang, D.; Ning, J.G. Temperature damage and constitutive model of frozen soil under dynamic loading. Mech. Mater. 2016, 102, 108–116. [Google Scholar] [CrossRef]
- Xu, X.T.; Wang, Y.B.; Yin, Z.H.; Zhang, H.W. Effect of temperature and strain rate on mechanical characteristics and constitutive model of frozen Helin loess. Cold Reg. Sci. Technol. 2017, 136, 44–51. [Google Scholar] [CrossRef]
- Lu, J.G.; Zhang, M.Y.; Zhang, X.Y.; Pei, W.S.; Bi, J. Experimental study on the freezing–thawing deformation of a silty clay. Cold Reg. Sci. Technol. 2018, 151, 19–27. [Google Scholar] [CrossRef]
- Tsytovich, N.A.; Sumgin, M.I. Fundamentals of the Mechanics of Frozen Ground; Union of Soviet Socialist Republics, USSR Academy of Sciences Press: Moscow, Russia, 1937. [Google Scholar]
- Andersen, G.R.; Swan, C.W.; Ladd, C.C.; Germaine, J.T. Small-strain behavior of frozen sand in triaxial compression. Can. Geotech. J. 1995, 32, 428–451. [Google Scholar] [CrossRef]
- Ma, W.; Wu, Z.W.; Zhang, L.X.; Chang, X.X. Analyses of process on the strength decrease in frozen soils under high confining pressures. Cold Reg. Sci. Technol. 1999, 29, 1–7. [Google Scholar] [CrossRef]
- Arenson, L.U.; Springman, S.M. Triaxial constant stress and constant strain rate tests on ice-rich permafrost samples. Can. Geotech. J. 2005, 42, 412–430. [Google Scholar] [CrossRef]
- Lai, Y.M.; Jin, L.; Chang, X.X. Yield criterion and elasto-plastic damage constitutive model for frozen sandy soil. Int. J. Plast. 2009, 25, 1177–1205. [Google Scholar] [CrossRef]
- Roustaei, M.; Eslami, A.; Ghazavi, M. Effects of freeze–thaw cycles on a fiber reinforced fine grained soil in relation to geotechnical parameters. Cold Reg. Sci. Technol. 2015, 120, 127–137. [Google Scholar] [CrossRef]
- Yang, Z.H.; Still, B.; Ge, X.X. Mechanical properties of seasonally frozen and permafrost soils at high strain rate. Cold Reg. Sci. Technol. 2015, 113, 12–19. [Google Scholar] [CrossRef]
- Xu, G.F.; Wu, W.; Qi, J.L. An extended hyperplastic constitutive model for frozen sand. Soils Found. 2016, 56, 704–711. [Google Scholar] [CrossRef]
- Ma, L.; Qi, J.L.; Yu, F.; Yao, X.L. Experimental study on variability in mechanical properties of a frozen sand as determined in triaxial compression tests. Acta Geotech. 2016, 11, 61–70. [Google Scholar] [CrossRef]
- Hou, F.; Lai, Y.M.; Liu, E.L.; Liu, X.Y. A creep constitutive model for frozen soils with different contents of coarse grains. Cold Reg. Sci. Technol. 2018, 145, 119–126. [Google Scholar] [CrossRef]
- Lai, Y.M.; Xu, X.T.; Dong, Y.H.; Li, S.Y. Present situation and prospect of mechanical research on frozen soils in China. Cold Reg. Sci. Technol. 2013, 87, 6–18. [Google Scholar] [CrossRef]
- Lai, Y.M.; Zhang, Y.; Zhang, S.J.; Jin, L.; Chang, X.X. Experimental study of strength of frozen sandy soil under different water contents and temperatures. Rock Soil Mech. 2009, 30, 3665–3670. (In Chinese) [Google Scholar]
- Chen, Y.L.; Wang, M.; Xu, S.; Chang, L.Q.; Yin, Z.Z. Tensile and compressive strength tests on artificial frozen soft clay in Shanghai. Chin. J. Geotech. Eng. 2009, 31, 1046–1051. (In Chinese) [Google Scholar]
- Xu, X.T.; Lai, Y.M.; Dong, Y.H.; Qi, J.L. Laboratory investigation on strength and deformation characteristics of ice-saturated frozen sandy soil. Cold Reg. Sci. Technol. 2011, 69, 98–104. [Google Scholar] [CrossRef]
- Zhao, X.D.; Zhou, G.Q.; Wang, J.Z. Deformation and strength behaviors of frozen clay with thermal gradient under uniaxial compression. Tunn. Undergr. Space Technol. 2013, 38, 550–558. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, E.L.; Liu, Y.X.; Zhang, G.; Song, B.T. A new strength criterion for frozen soils considering the influence of temperature and coarse-grained contents. Cold Reg. Sci. Technol. 2017, 143, 1–12. [Google Scholar] [CrossRef]
- Wu, Z.W.; Zhang, J.Y.; Zhu, Y.L. Strength and Failure Characteristics of Frozen Soil. J. Glaciol. Geocryol. 1983, 275–280. (In Chinese) [Google Scholar]
- Wu, Z.W.; Ma, W.; Zhang, C.Q.; Shen, Z.Y. Strength characteristics of frozen sandy soil. J. Glaciol. Geocryol. 1994, 16, 15–20. (In Chinese) [Google Scholar]
- Ma, W.; Wu, Z.W.; Sheng, Y. Effect of confining pressure on strength behavior of frozen soil. Chin. J. Geotech. Eng. 1995, 17, 7–11. (In Chinese) [Google Scholar]
- Shen, Z.J. A nonlinear dilatant stress-strain model for soil and rock material. Hydro. Sci. Eng. 1986, 4, 1–14. (In Chinese) [Google Scholar]
- Li, S.Y.; Lai, Y.M.; Zhang, S.J.; Liu, D.R. An improved statistical damage constitutive model for warm frozen clay based on Mohr–Coulomb criterion. Cold Reg. Sci. Technol. 2009, 57, 154–159. [Google Scholar] [CrossRef]
- Cao, W.G.; Zhao, H.; Li, X.; Zhang, Y.J. Statistical damage model with strain softening and hardening for rocks under the influence of voids and volume changes. Can. Geotech. J. 2010, 47, 857–871. [Google Scholar] [CrossRef]
- Yang, Y.G.; Lai, Y.M.; Chang, X.X. Experimental and theoretical studies on the creep behavior of warm ice-rich frozen sand. Cold Reg. Sci. Technol. 2010, 63, 61–67. [Google Scholar] [CrossRef]
- Lai, Y.M.; Li, J.B.; Li, Q.Z. Study on damage statistical constitutive model and stochastic simulation for warm ice-rich frozen silt. Cold Reg. Sci. Technol. 2012, 71, 102–110. [Google Scholar] [CrossRef]
- Fu, H.L.; Zhang, J.B.; Huang, Z.; Shi, Y.; Chen, W. A statistical model for predicting the triaxial compressive strength of transversely isotropic rocks subjected to freeze–thaw cycling. Cold Reg. Sci. Technol. 2018, 145, 237–248. [Google Scholar] [CrossRef]
- Lemaitre, J.; Chaboche, J.L. Mechanics of Solid Materials; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Yang, Y.G.; Gao, F.; Lai, Y.M.; Cheng, H.M. Experimental and theoretical investigations on the mechanical behavior of frozen silt. Cold Reg. Sci. Technol. 2016, 130, 59–65. [Google Scholar]

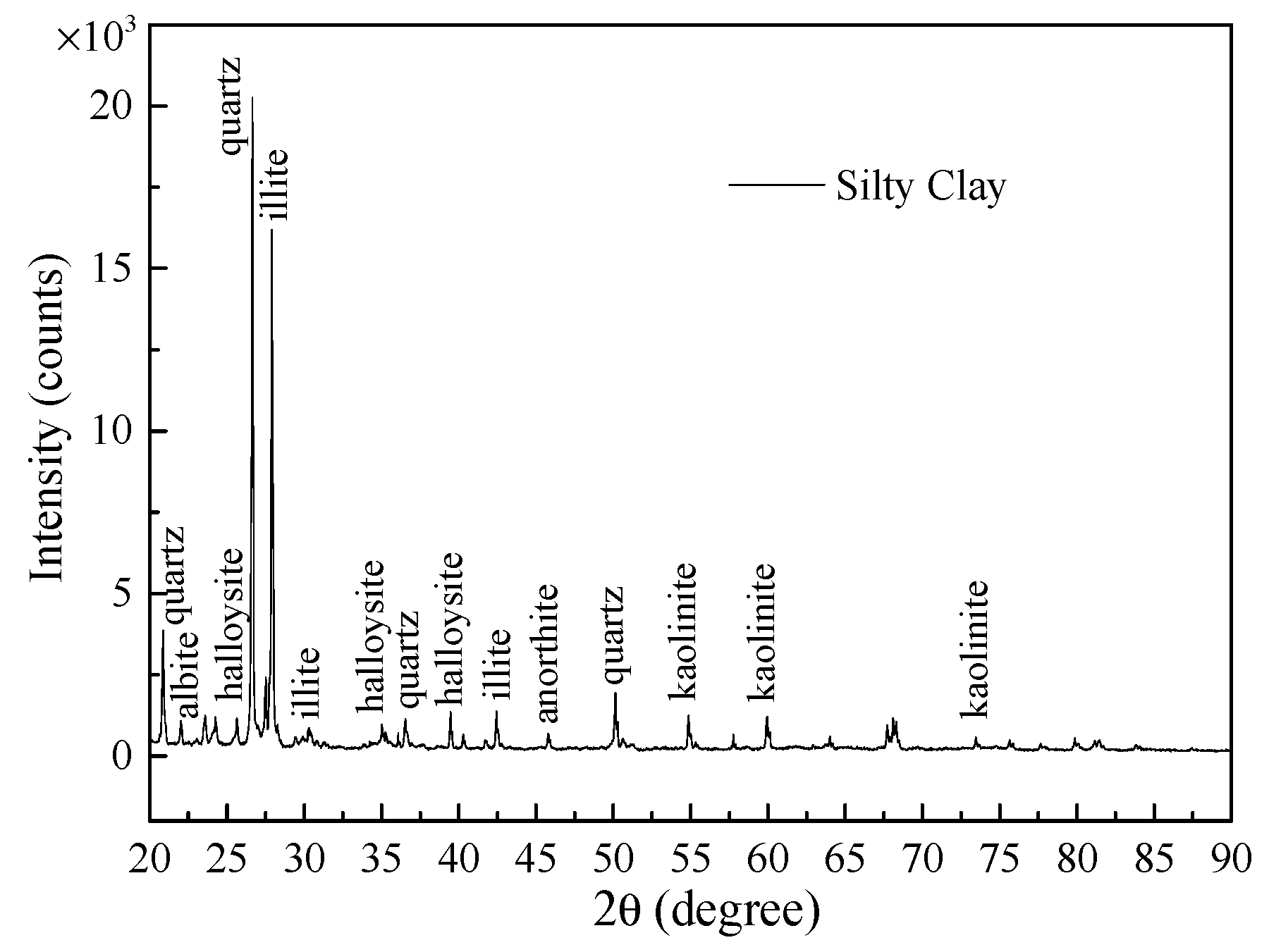

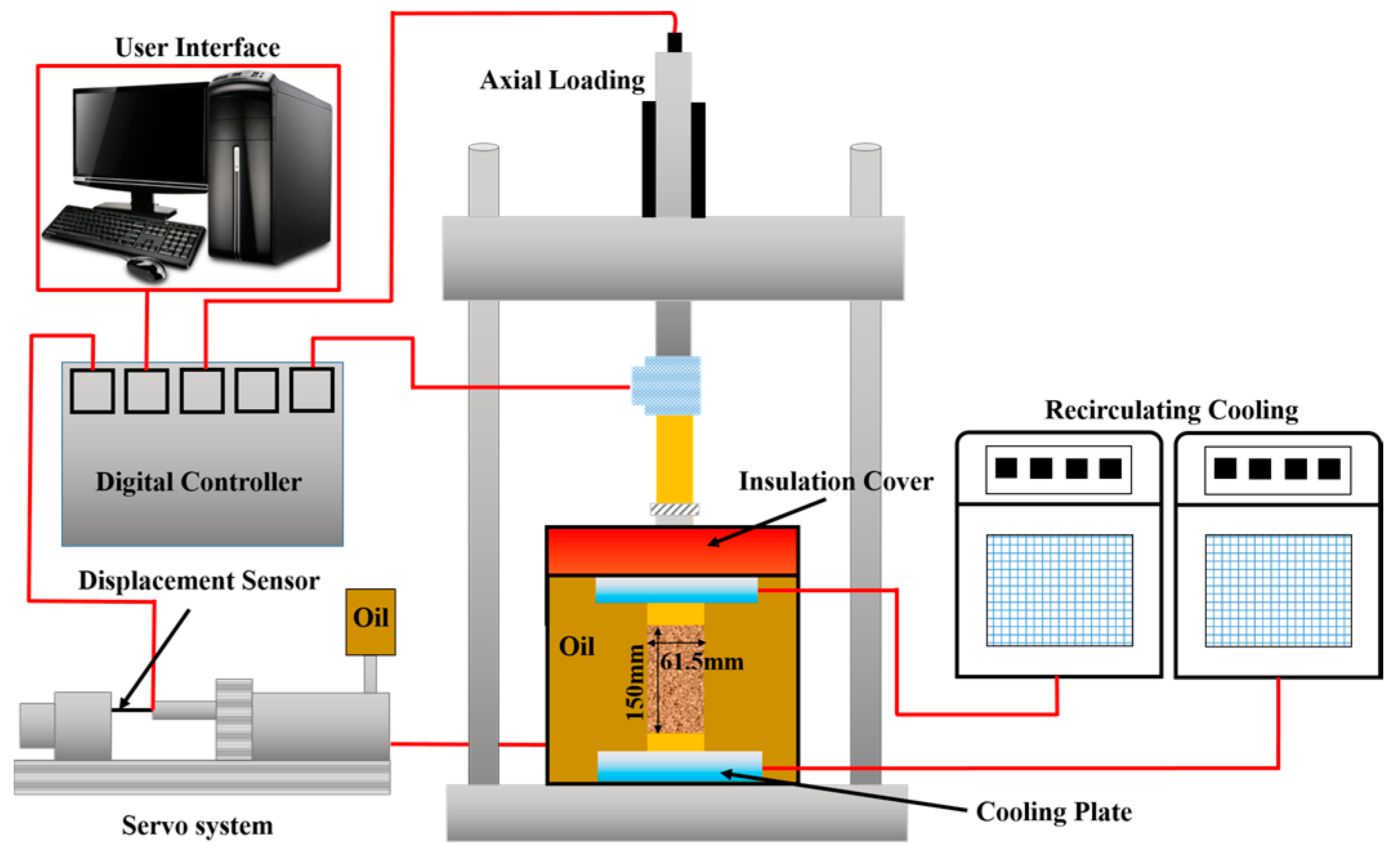



| Mineral Composition | Quartz | Illite | Halloysite | Kaolinite | Albite | Anorthite | Unknown |
|---|---|---|---|---|---|---|---|
| Relative content (%) | 39.9 | 10.2 | 14.7 | 5.6 | 13.2 | 12.4 | 4.0 |
| No. | Fitting Parameters | No. | Fitting Parameters | ||||||
|---|---|---|---|---|---|---|---|---|---|
| a | b | c | R2 | a | b | c | R2 | ||
| 1 | 1.292 | 0.416 | 0.415 | 0.9885 | 15 | 0.421 | 0.191 | 0.191 | 0.9972 |
| 2 | 0.960 | 0.371 | 0.372 | 0.9939 | 16 | 0.756 | 0.120 | 0.011 | 0.9942 |
| 3 | 0.690 | 0.244 | 0.244 | 0.9988 | 17 | 0.709 | 0.101 | 0.009 | 0.9976 |
| 4 | 1.537 | 0.502 | 0.501 | 0.9898 | 18 | 0.486 | 0.238 | 0.260 | 0.9989 |
| 5 | 1.124 | 0.448 | 0.447 | 0.9970 | 19 | 0.660 | 0.191 | 0.189 | 0.9943 |
| 6 | 0.796 | 0.288 | 0.288 | 0.9911 | 20 | 0.507 | 0.174 | 0.174 | 0.9976 |
| 7 | 1.662 | 0.265 | 0.017 | 0.9919 | 21 | 0.279 | 0.097 | 0.065 | 0.9988 |
| 8 | 1.440 | 0.204 | 0.015 | 0.9859 | 22 | 0.636 | 0.314 | 0.450 | 0.9898 |
| 9 | 1.139 | 0.565 | 0.914 | 0.9983 | 23 | 0.545 | 0.198 | 0.198 | 0.9907 |
| 10 | 0.707 | 0.123 | 0.045 | 0.9956 | 24 | 0.481 | 0.152 | 0.152 | 0.9919 |
| 11 | 0.534 | 0.265 | 0.278 | 0.9963 | 25 | 0.681 | 0.098 | 0.002 | 0.9995 |
| 12 | 0.368 | 0.179 | 0.181 | 0.9946 | 26 | 0.580 | 0.090 | 0.008 | 0.9983 |
| 13 | 0.727 | 0.143 | 0.066 | 0.9974 | 27 | 0.386 | 0.209 | 0.209 | 0.9959 |
| 14 | 0.669 | 0.239 | 0.239 | 0.9973 | – | – | – | – | – |
| No. | q(b–c) | δb | δc | 0.5δt | δe | εrs (%) | εre (%) |
|---|---|---|---|---|---|---|---|
| 7 | 0.2514 | 0.0346 | 0.0284 | 0.0315 | 0.0014 | 7.20 | 7~9 |
| 8 | 0.2504 | 0.0322 | 0.0266 | 0.0294 | 0.0004 | 8.28 | 8~10 |
| 16 | 0.2514 | 0.0098 | 0.0080 | 0.0089 | 0.0014 | 7.95 | 6~8 |
| 17 | 0.2550 | 0.0092 | 0.0078 | 0.0087 | 0.0050 | 8.54 | 7~9 |
| 25 | 0.2533 | 0.0074 | 0.0058 | 0.0071 | 0.0033 | 6.75 | 6~8 |
| 26 | 0.2492 | 0.0064 | 0.0054 | 0.0059 | 0.0008 | 7.84 | 7~9 |
| Fitting Parameters | ||||||||
|---|---|---|---|---|---|---|---|---|
| a | b | c | F0 | m | εrs (%) | εre (%) | R2 | |
| 1 | 1.292 | 0.416 | 0.415 | 28.61 | 8.322 | 17.63 | 16~18 | 0.9916 |
| 4 | 1.537 | 0.502 | 0.501 | 28.20 | 8.012 | 17.17 | 16~18 | 0.9952 |
| 13 | 0.727 | 0.143 | 0.067 | 27.12 | 7.306 | 14.61 | 14~16 | 0.9986 |
| 14 | 0.669 | 0.239 | 0.239 | 27.86 | 7.967 | 16.81 | 15~17 | 0.9988 |
| 19 | 0.660 | 0.182 | 0.181 | 28.01 | 8.043 | 17.36 | 15~17 | 0.9961 |
| 20 | 0.507 | 0.174 | 0.174 | 28.91 | 8.643 | 17.92 | 16~18 | 0.9982 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Chen, J.; Mao, C. Experimental and Theoretical Investigations of the Constitutive Relations of Artificial Frozen Silty Clay. Materials 2019, 12, 3159. https://doi.org/10.3390/ma12193159
Li Z, Chen J, Mao C. Experimental and Theoretical Investigations of the Constitutive Relations of Artificial Frozen Silty Clay. Materials. 2019; 12(19):3159. https://doi.org/10.3390/ma12193159
Chicago/Turabian StyleLi, Zhiming, Jian Chen, and Chaojun Mao. 2019. "Experimental and Theoretical Investigations of the Constitutive Relations of Artificial Frozen Silty Clay" Materials 12, no. 19: 3159. https://doi.org/10.3390/ma12193159




