Topological Design of a Lightweight Sandwich Aircraft Spoiler
Abstract
1. Introduction
2. Materials and Methods
2.1. Topology Optimization Method
2.2. Design Problem Definition
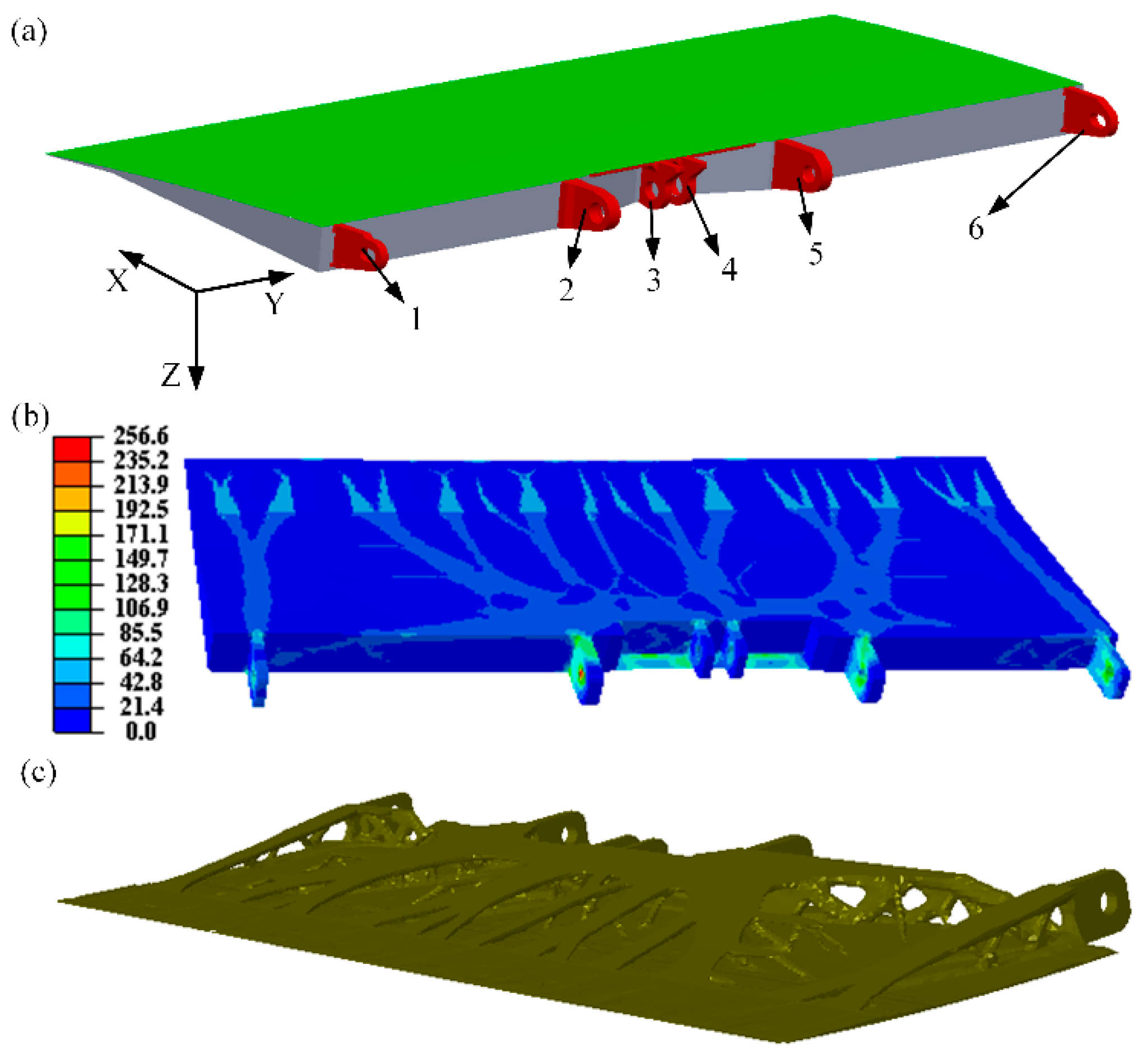
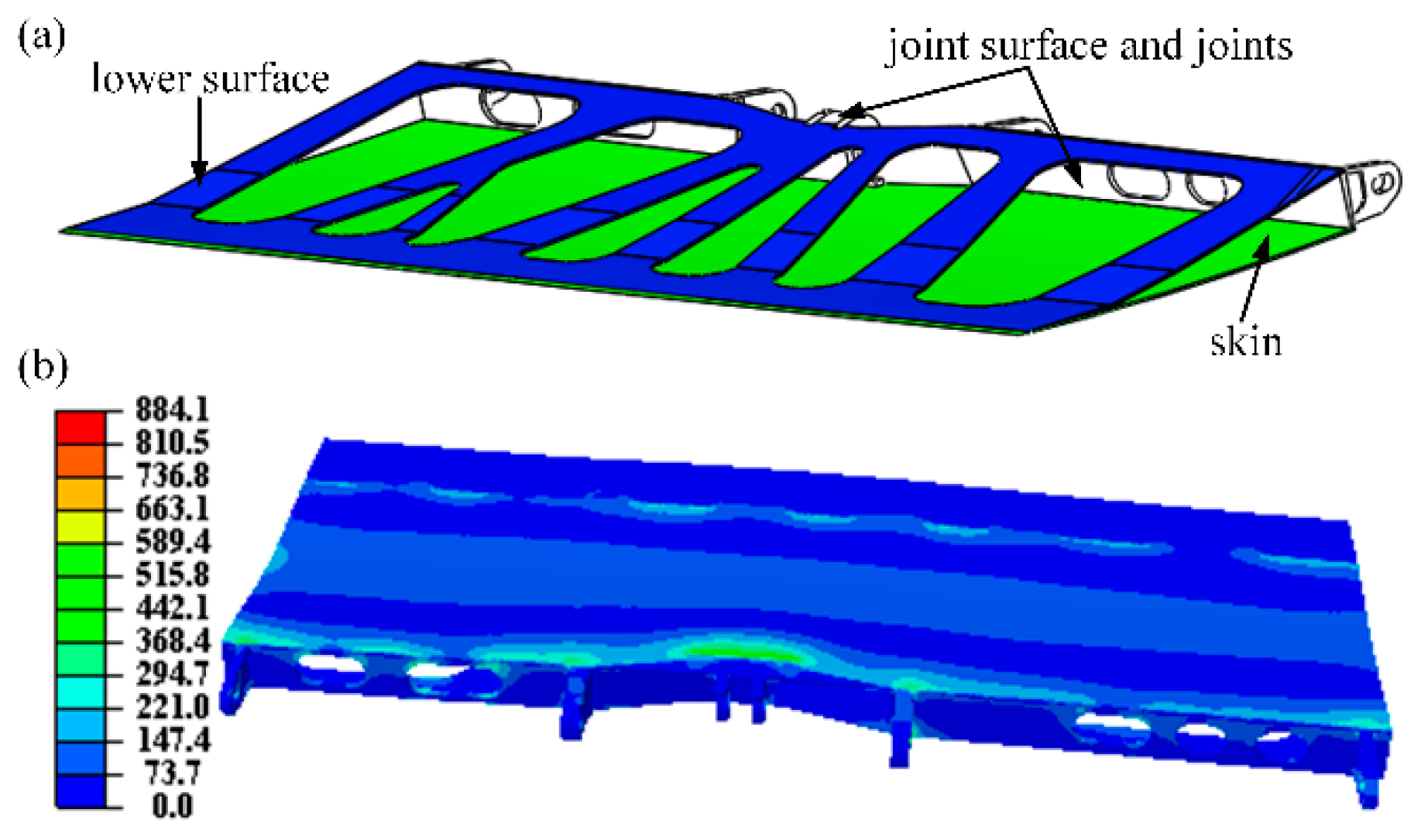
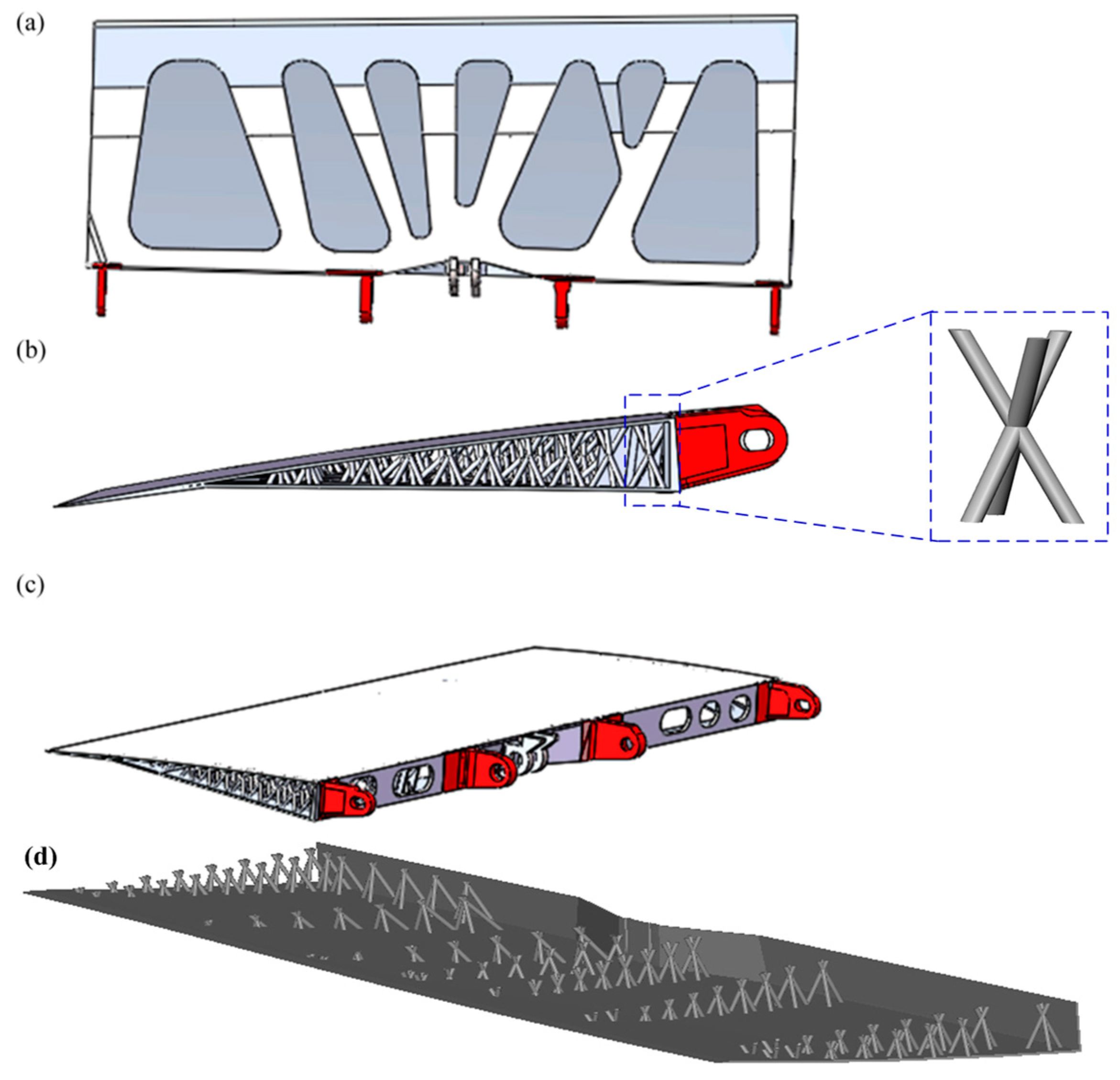
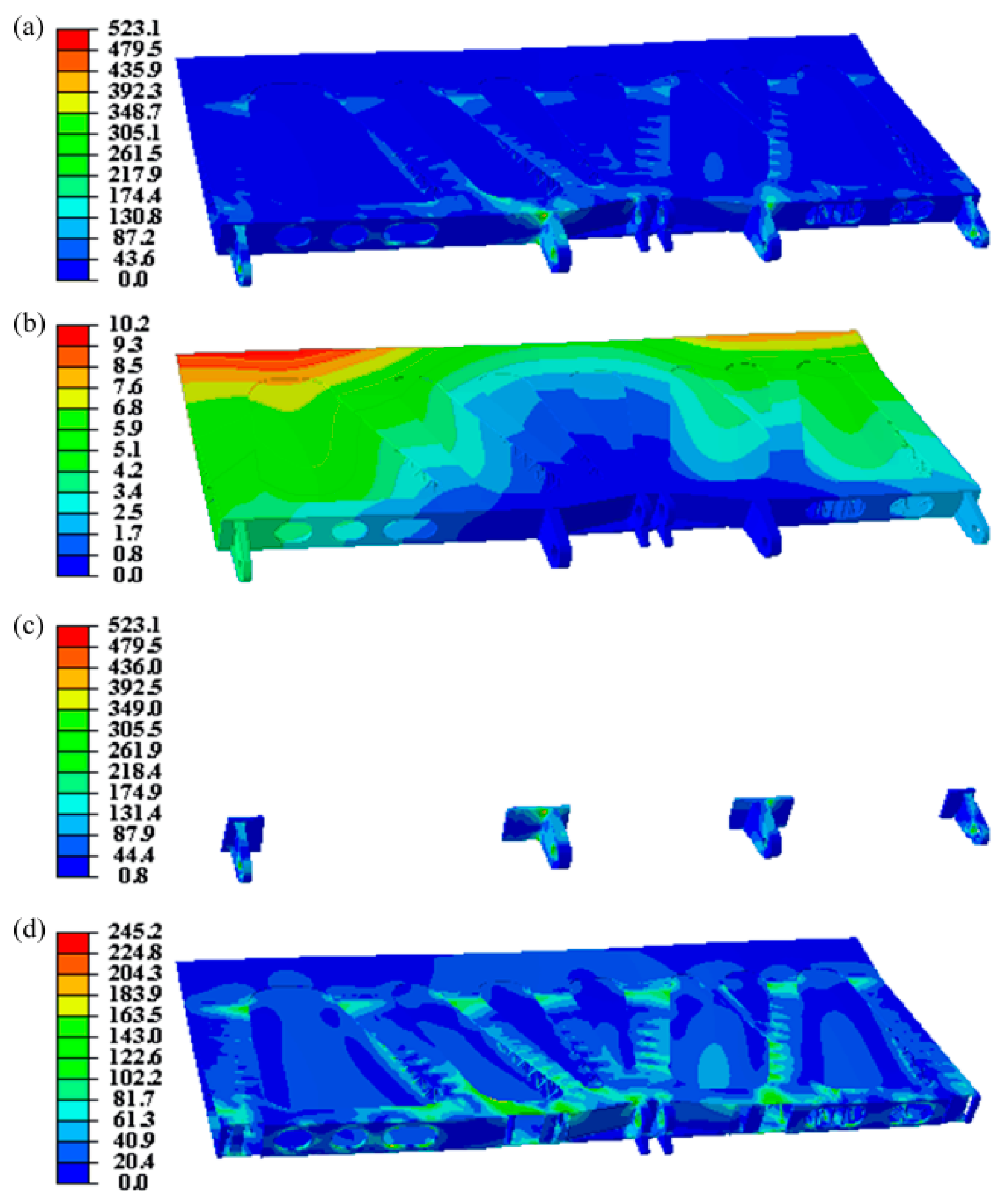
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, X.L.; Wang, F.X.; Li, Y.L. Aerodynamic characteristics of high-lift devices with downward deflection of spoiler. J. Aircr. 2011, 48, 730–735. [Google Scholar] [CrossRef]
- Zhu, J.H.; Zhang, W.H.; Xia, L. Topology optimization in aircraft and aerospace structures design. Arch. Comput. Methods Eng. 2016, 23, 595–622. [Google Scholar] [CrossRef]
- Sigmund, O.; Maute, K. Topology optimization approaches. Struct. Multidiscip. Optim. 2013, 48, 1031–1055. [Google Scholar] [CrossRef]
- Huang, X.; Xie, Y.M. A further review of ESO type methods for topology optimization. Struct. Multidiscip. Optim. 2010, 41, 671–683. [Google Scholar] [CrossRef]
- Zhu, B.; Chen, Q.; Li, H.; Zhang, H.; Zhang, X. Design of planar large-deflection compliant mechanisms with decoupled multi-input-output using topology optimization. J. Mech. Robot. 2019, 11, 031015. [Google Scholar] [CrossRef]
- Liu, J.; Ma, Y. A survey of manufacturing oriented topology optimization methods. Adv. Eng. Softw. 2016, 100, 161–175. [Google Scholar] [CrossRef]
- Zegard, T.; Paulino, G.H. Bridging topology optimization and additive manufacturing. Struct. Multidiscip. Optim. 2016, 53, 175–192. [Google Scholar] [CrossRef]
- Guo, X.; Zhou, J.; Zhang, W.; Du, Z.; Liu, C.; Liu, Y. Self-supporting structure design in additive manufacturing through explicit topology optimization. Comput. Methods Appl. Mech. Eng. 2017, 323, 27–63. [Google Scholar] [CrossRef]
- Zhang, K.; Cheng, G.; Xu, L. Topology optimization considering overhang constraint in additive manufacturing. Comput. Struct. 2019, 212, 86–100. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Z.; Wei, P.; Chen, S. Generating support structures for additive manufacturing with continuum topology optimization methods. Rapid Prototyp. J. 2019, 25, 232–246. [Google Scholar] [CrossRef]
- Mei, J.; Liu, J.; Liu, J. A novel fabrication method and mechanical behavior of all-composite tetrahedral truss core sandwich panel. Compos. Part A Appl. Sci. Manuf. 2017, 102, 28–39. [Google Scholar] [CrossRef]
- Wei, K.; Yang, Q.; Ling, B.; Xie, H.; Qu, Z.; Fang, D. Mechanical responses of titanium 3D kagome lattice structure manufactured by selective laser melting. Extrem. Mech. Lett. 2018, 23, 41–48. [Google Scholar] [CrossRef]
- Liu, J.; Chen, T.; Zhang, Y.; Wen, G.; Qing, Q.; Wang, H.; Sedaghati, R.; Xie, Y.M. On sound insulation of pyramidal lattice sandwich structure. Compos. Struct. 2019, 208, 385–394. [Google Scholar] [CrossRef]
- Yin, H.; Huang, X.; Scarpa, F.; Wen, G.; Chen, Y.; Zhang, C. In-plane crashworthiness of bio-inspired hierarchical honeycombs. Compos. Struct. 2018, 192, 516–527. [Google Scholar] [CrossRef]
- Liu, J.; Fan, X.; Wen, G.; Qing, Q.; Wang, H.; Zhao, G. A novel design framework for structures/materials with enhanced mechanical performance. Materials 2018, 11, 576. [Google Scholar] [CrossRef] [PubMed]
- Birman, V.; Kardomateas, G.A. Review of current trends in research and applications of sandwich structures. Compos. Part B Eng. 2018, 142, 221–240. [Google Scholar] [CrossRef]
- Caliri, M.F., Jr.; Ferreira, A.J.; Tita, V. A review on plate and shell theories for laminated and sandwich structures highlighting the Finite Element Method. Compos. Struct. 2016, 156, 63–77. [Google Scholar] [CrossRef]
- Remouchamps, A.; Bruyneel, M.; Fleury, C.; Grihon, S. Application of a bi-level scheme including topology optimization to the design of an aircraft pylon. Struct. Multidiscip. Optim. 2011, 44, 739–750. [Google Scholar] [CrossRef]
- Zhu, J.H.; Gu, X.J.; Zhang, W.H.; Beckers, P. Structural design of aircraft skin stretch-forming die using topology optimization. J. Comput. Appl. Math. 2013, 246, 278–288. [Google Scholar] [CrossRef]
- Liu, S.; Li, Q.; Chen, W.; Hu, R.; Tong, L. H-DGTP—A Heaviside-function based directional growth topology parameterization for design optimization of stiffener layout and height of thin-walled structures. Struct. Multidiscip. Optim. 2015, 52, 903–913. [Google Scholar] [CrossRef]
- Krog, L.; Tucker, A.; Kemp, M.; Boyd, R. Topology optimisation of aircraft wing box ribs. In Proceedings of the 10th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Albany, NY, USA, 30 August–1 September 2004. [Google Scholar]
- Maute, K.K.; Reich, G.W. Integrated multidisciplinary topology optimization approach to adaptive wing design. J. Aircr. 2006, 43, 253–263. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, W.; Beckers, P. Integrated layout design of multi-component system. Int. J. Numer. Methods Eng. 2009, 78, 631–651. [Google Scholar] [CrossRef]
- Xia, L.; Zhu, J.; Zhang, W. Sensitivity analysis with the modified Heaviside function for the optimal layout design of multi-component systems. Comput. Methods Appl. Mech. Eng. 2012, 241, 142–154. [Google Scholar] [CrossRef]
- Yang, K.; Zhu, J.; Wu, M.; Zhang, W. Integrated optimization of actuators and structural topology of piezoelectric composite structures for static shape control. Comput. Methods Appl. Mech. Eng. 2018, 334, 440–469. [Google Scholar] [CrossRef]
- Roy, S.; Crossley, W.A.; Stanford, B.; Moore, K.T.; Gray, J.S. A Mixed Integer Efficient Global Optimization Algorithm with Multiple Infill Strategy-Applied to a Wing Topology Optimization Problem. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; p. 2356. [Google Scholar]
- Dubois, A.; Farhat, C.; Abukhwejah, A.H.; Shageer, H.M. Parameterization Framework for the MDAO of Wing Structural Layouts. AIAA J. 2018, 56, 1627–1638. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Conlan-Smith, C.; James, K.A. Design of a Bi-stable Airfoil with Tailored Snap-through Response Using Topology Optimization. Comput. Aided Des. 2019, 108, 42–55. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, W.; Zhong, W. Doing topology optimization explicitly and geometrically—A new moving morphable components based framework. J. Appl. Mech. 2014, 81, 081009. [Google Scholar] [CrossRef]
- Zhang, W.; Yuan, J.; Zhang, J.; Guo, X. A new topology optimization approach based on Moving Morphable Components (MMC) and the ersatz material model. Struct. Multidiscip. Optim. 2016, 53, 1243–1260. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, J.; Zhu, X.; Zhou, J.; Xue, D.; Lei, X.; Guo, X. Explicit three dimensional topology optimization via Moving Morphable Void (MMV) approach. Comput. Methods Appl. Mech. Eng. 2017, 322, 590–614. [Google Scholar] [CrossRef]
- Costa, J.C.A., Jr.; Alves, M.K. Layout optimization with h-adaptivity of structures. Int. J. Numer. Methods Eng. 2003, 58, 83–102. [Google Scholar] [CrossRef]
- Stainko, R. An adaptive multilevel approach to the minimal compliance problem in topology optimization. Commun. Numer. Methods Eng. 2006, 22, 109–118. [Google Scholar] [CrossRef]
- Wang, Y.; Kang, Z.; He, Q. An adaptive refinement approach for topology optimization based on separated density field description. Comput. Struct. 2013, 117, 10–22. [Google Scholar] [CrossRef]
- Wang, H.; Liu, J.; Wen, G. An efficient evolutionary structural optimization method with smooth edges based on the game of building blocks. Eng. Optim. 2019. [Google Scholar] [CrossRef]
- Wang, H.; Liu, J.; Wen, G. An adaptive mesh-adjustment strategy for continuum topology optimization to achieve manufacturable structural layout. Int. J. Numer. Methods Eng. 2019, 117, 1304–1322. [Google Scholar] [CrossRef]
- Liu, C.; Zhu, Y.; Sun, Z.; Li, D.; Du, Z.; Zhang, W.; Guo, X. An efficient moving morphable component (MMC)-based approach for multi-resolution topology optimization. Struct. Multidiscip. Optim. 2018, 58, 2455–2479. [Google Scholar] [CrossRef]
- Leader, M.K.; Chin, T.W.; Kennedy, G.J. High-resolution topology optimization with stress and natural frequency constraints. AIAA J. 2019. [Google Scholar] [CrossRef]
- Wei, P.; Li, Z.; Li, X.; Wang, M.Y. An 88-line MATLAB code for the parameterized level set method based topology optimization using radial basis functions. Struct. Multidiscip. Optim. 2018, 58, 831–849. [Google Scholar] [CrossRef]
- Zhu, B.; Zhang, X.; Liu, M.; Chen, Q.; Li, H. Topological and shape optimization of flexure hinges for designing compliant mechanisms using the level set method. Chin. J. Mech. Eng. 2019, 32, 13. [Google Scholar] [CrossRef]
- ABAQUS User’s Manual, version 6.14; Dassault Systèmes Simulia Corp.: Providence, RI, USA, 2014.
- SolidWorks User’s Guide, version 2014; SolidWorks Corp.: Waltham, MA, USA, 2014.
- Svanberg, K. The method of moving asymptotes—A new method for structural optimization. Int. J. Numer. Methods Eng. 1987, 24, 359–373. [Google Scholar] [CrossRef]
- Zuo, W.; Saitou, K. Multi-material topology optimization using ordered SIMP interpolation. Struct. Multidiscip. Optim. 2017, 55, 477–491. [Google Scholar] [CrossRef]
- Rong, J.H.; Tang, Z.L.; Xie, Y.M.; Li, F.Y. Topological optimization design of structures under random excitations using SQP method. Eng. Struct. 2013, 56, 2098–2106. [Google Scholar] [CrossRef]
- Long, K.; Wang, X.; Liu, H. Stress-constrained topology optimization of continuum structures subjected to harmonic force excitation using sequential quadratic programming. Struct. Multidiscip. Optim. 2019, 59, 1747–1759. [Google Scholar] [CrossRef]
- Liu, J.; Wen, G.; Xie, Y.M. Layout optimization of continuum structures considering the probabilistic and fuzzy directional uncertainty of applied loads based on the cloud model. Struct. Multidiscip. Optim. 2016, 53, 81–100. [Google Scholar] [CrossRef]
- Xie, Y.M.; Steven, G.P. A simple evolutionary procedure for structural optimization. Comput. Struct. 1993, 49, 885–896. [Google Scholar] [CrossRef]
- Hu, Z.; Gadipudi, V.K.; Salem, D.R. Topology optimization of lightweight lattice structural composites inspired by cuttlefish bone. Appl. Compos. Mater. 2019, 26, 15–27. [Google Scholar] [CrossRef]
- Aage, N.; Andreassen, E.; Lazarov, B.S.; Sigmund, O. Giga-voxel computational morphogenesis for structural design. Nature 2017, 550, 84. [Google Scholar] [CrossRef]
- Xue, X.; Pereira, A.; Vincze, G.; Wu, X.; Liao, J. Interfacial Characteristics of Dissimilar Ti6Al4V/AA6060 Lap Joint by Pulsed Nd: YAG Laser Welding. Metals 2019, 9, 71. [Google Scholar] [CrossRef]

| Material | Titanium Alloy | Aluminum Alloy |
|---|---|---|
| Density (kg/m3) | 4500 | 2760 |
| Tensile strength (MPa) | 900 | 450 |
| Compressive strength (MPa) | 880 | 270 |
| Modulus of elasticity (GPa) | 108 | 68 |
| Poisson’s ratio | 0.33 | 0.33 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Ou, H.; He, J.; Wen, G. Topological Design of a Lightweight Sandwich Aircraft Spoiler. Materials 2019, 12, 3225. https://doi.org/10.3390/ma12193225
Liu J, Ou H, He J, Wen G. Topological Design of a Lightweight Sandwich Aircraft Spoiler. Materials. 2019; 12(19):3225. https://doi.org/10.3390/ma12193225
Chicago/Turabian StyleLiu, Jie, Haifeng Ou, Junfeng He, and Guilin Wen. 2019. "Topological Design of a Lightweight Sandwich Aircraft Spoiler" Materials 12, no. 19: 3225. https://doi.org/10.3390/ma12193225
APA StyleLiu, J., Ou, H., He, J., & Wen, G. (2019). Topological Design of a Lightweight Sandwich Aircraft Spoiler. Materials, 12(19), 3225. https://doi.org/10.3390/ma12193225






