Semi-Empirical Force-Field Model for the Ti1−xAlxN (0 ≤ x ≤ 1) System
Abstract
:1. Introduction
2. Potential Parametrization and Validation Methodology
2.1. Potential Parametrization Methodology
2.2. Potential Validation Methodology
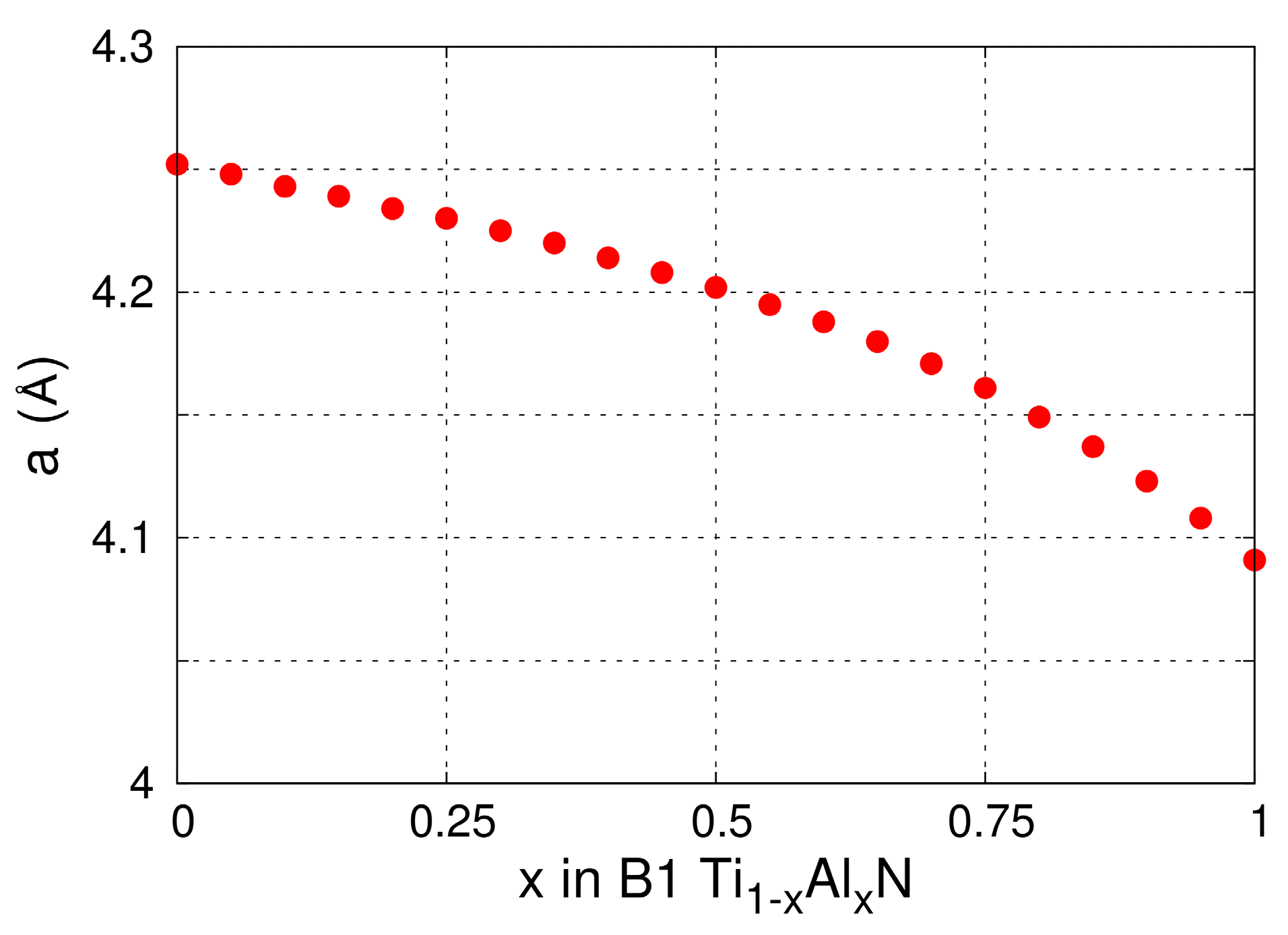
3. Potential Parametrization Results
4. Potential Validation Results
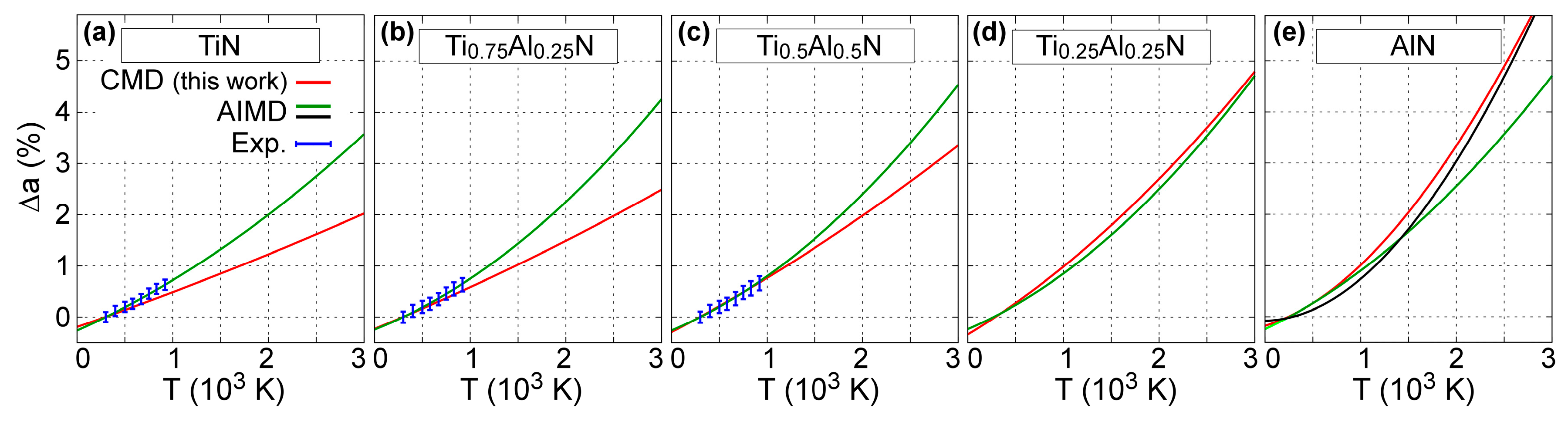
4.1. Lattice Thermal Expansion
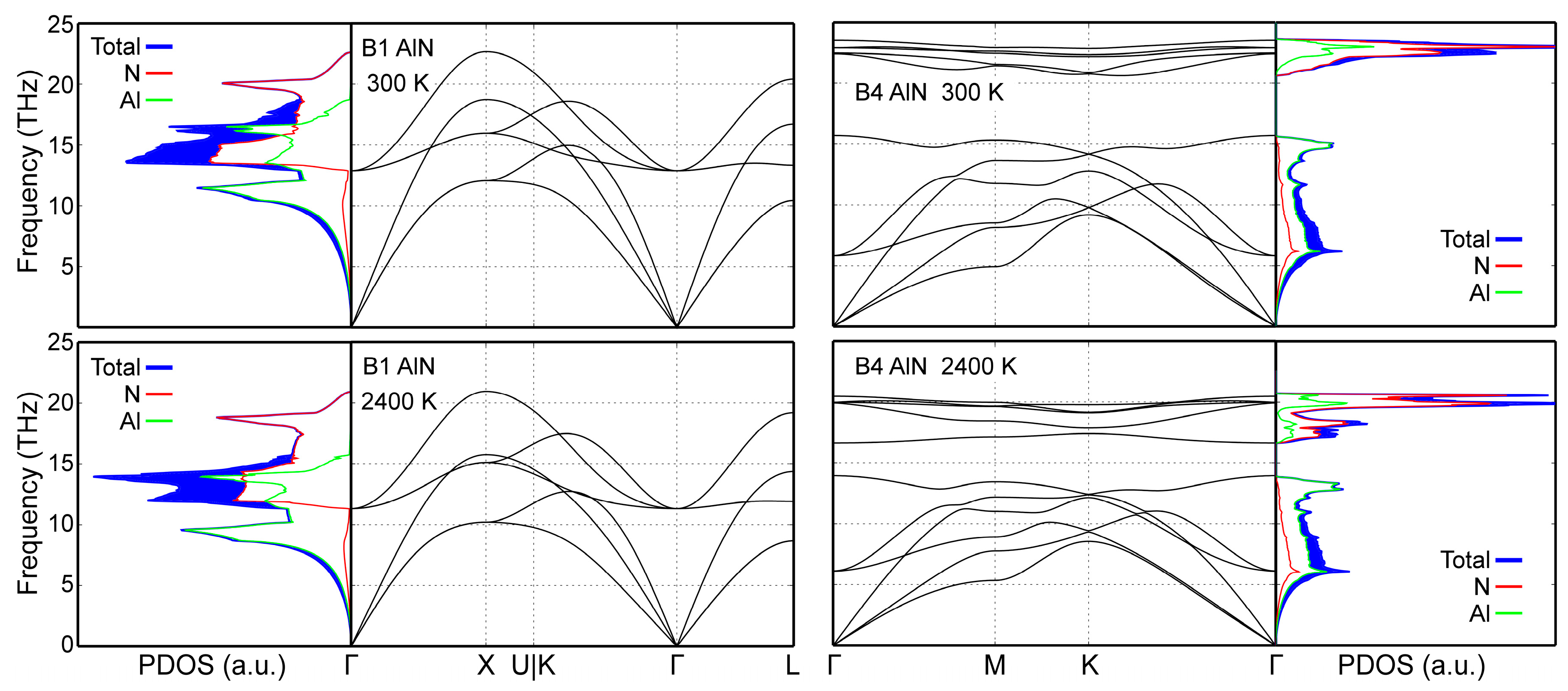
4.2. Lattice Dynamics
4.3. Point-Defect Migration Energies
4.4. Equilibrium Volumes and Elastic Properties of B1-TiNy, B2-TiN, and bct-Ti2N
4.5. Phase Stability and Transitions
4.5.1. Ti-N
4.5.2. Al-N
4.5.3. Ti-Al-N
5. Summary and Outlook
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Münz, W.D. Titanium aluminum nitride films: A new alternative to TiN coatings. J. Vac. Sci. Technol. A 1986, 4, 2717–2725. [Google Scholar] [CrossRef]
- Matthes, B.; Herr, W.; Broszeit, E.; Kloos, K.H.; Nurnberger, G.; Schmoeckel, D.; Hohl, F.; Stock, H.R.; Mayr, P. Tribological properties and wear behavior of sputtered titanium-based hard coatings under sheet metal forming conditions. Mater. Sci. Eng. A 1991, 140, 593–601. [Google Scholar] [CrossRef]
- Alling, B.; Oden, M.; Hultman, L.; Abrikosov, I.A. Pressure enhancement of the isostructural cubic decomposition in Ti1−xAlxN. Appl. Phys. Lett. 2009, 95, 181906. [Google Scholar] [CrossRef]
- Petrov, I.; Barna, P.B.; Hultman, L.; Greene, J.E. Microstructural evolution during film growth. J. Vac. Sci. Technol. A 2003, 21, S117–S128. [Google Scholar] [CrossRef]
- Johnson, L.J.S.; Thuvander, M.; Stiller, K.; Oden, M.; Hultman, L. Spinodal decomposition of Ti0.33Al0.67N thin films studied by atom probe tomography. Thin Solid Films 2012, 520, 4362–4368. [Google Scholar] [CrossRef]
- Mayrhofer, P.H.; Hörling, A.; Karlsson, L.; Sjölen, J.; Larsson, T.; Mitterer, C.; Hultman, L. Self-organized nanostructures in the Ti-Al-N system. Appl. Phys. Lett. 2003, 83, 2049–2051. [Google Scholar] [CrossRef]
- Abrikosov, I.A.; Knutsson, A.; Alling, B.; Tasnadi, F.; Lind, H.; Hultman, L.; Oden, M. Phase Stability and Elasticity of TiAlN. Materials 2011, 4, 1599–1618. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Horling, A.; Hultman, L.; Oden, M.; Sjolen, J.; Karlsson, L. Thermal stability of arc evaporated high aluminum-content Ti1−xAlxN thin films. J. Vac. Sci. Technol. A 2002, 20, 1815–1823. [Google Scholar] [CrossRef]
- Kutschej, K.; Mayrhofer, P.H.; Kathrein, M.; Polcik, P.; Tessadri, R.; Mitterer, C. Structure, mechanical and tribological properties of sputtered Ti1−xAlxN coatings with 0.5 ≤ x ≤ 0.75. Surf. Coat. Technol. 2005, 200, 2358–2365. [Google Scholar] [CrossRef]
- Music, D.; Geyer, R.W.; Schneider, J.M. Recent progress and new directions in density functional theory based design of hard coatings. Surf. Coat. Technol. 2016, 286, 178–190. [Google Scholar] [CrossRef]
- Alling, B.; Steneteg, P.; Tholander, C.; Tasnadi, F.; Petrov, I.; Greene, J.E.; Hultman, L. Configurational disorder effects on adatom mobilities on Ti1−xAlxN(001) surfaces from first principles. Phys. Rev. B 2012, 85, 245422. [Google Scholar] [CrossRef]
- Music, D.; Schneider, J.M. Ab initio study of Ti0.5Al0.5N(001)-residual and environmental gas interactions. New J. Phys. 2013, 15, 073004. [Google Scholar] [CrossRef]
- Kunze, C.; Music, D.; Baben, M.T.; Schneider, J.M.; Grundmeier, G. Temporal evolution of oxygen chemisorption on TiAlN. Appl. Surf. Sci. 2014, 290, 504–508. [Google Scholar] [CrossRef]
- Lennard-Jones, J.E. On the Determination of Molecular Fields: II: From the Equation of State of a Gas. Proc. R. Soc. Lond. A 1924, 106, 463–477. [Google Scholar] [CrossRef]
- Lennard-Jones, J.E. On the Determination of Molecular Fields: I: From the Variation of the Viscosity of a Gas with Temperature. Proc. R. Soc. Lond. A 1924, 106, 441–462. [Google Scholar] [CrossRef]
- Finnis, M.W.; Sinclair, J.E. A simple empirical N-body potential for transition-metals. Philos. Mag. A 1984, 50, 45–55. [Google Scholar] [CrossRef]
- Drautz, R.; Pettifor, D.G. Valence-dependent analytic bond-order potential for transition metals. Phys. Rev. B 2006, 74, 174177. [Google Scholar] [CrossRef]
- Pettifor, D.G.; Oleinik, I.I.; Nguyen-Manh, D.; Vitek, V. Bond-order potentials: Bridging the electronic to atomistic modelling hierarchies. Comput. Mater. Sci. 2002, 23, 33–37. [Google Scholar] [CrossRef]
- Stillinger, F.H.; Weber, T.A. Computer simulation of local order in condensed phases of silicon. Phys. Rev. B 1985, 31, 5262. [Google Scholar] [CrossRef]
- Sangiovanni, D.G.; Chirita, V.; Hultman, L. Toughness enhancement in TiAlN-based quarternary alloys. Thin Solid Films 2012, 520, 4080–4088. [Google Scholar] [CrossRef] [Green Version]
- Lee, B.J.; Baskes, M.I. Second nearest-neighbor modified embedded-atom-method potential. Phys. Rev. B 2000, 62, 8564. [Google Scholar] [CrossRef]
- Jelinek, B.; Houze, J.; Kim, S.; Horstemeyer, M.F.; Baskes, M.I.; Kim, S.G. Modified embedded-atom method interatomic potentials for the Mg-Al alloy system. Phys. Rev. B 2007, 75, 054106. [Google Scholar] [CrossRef]
- Kim, Y.M.; Lee, B.J. Modified embedded-atom method interatomic potentials for the Ti-C and Ti-N binary systems. Acta Mater. 2008, 56, 3481–3489. [Google Scholar] [CrossRef]
- Kim, H.K.; Jung, W.S.; Lee, B.J. Modified embedded-atom method interatomic potentials for the Fe-Ti-C and Fe-Ti-N ternary systems. Acta Mater. 2009, 57, 3140–3147. [Google Scholar] [CrossRef]
- Lee, B.J.; Baskes, M.I.; Kim, H.; Cho, Y.K. Second nearest-neighbor modified embedded atom method potentials for bcc transition metals. Phys. Rev. B 2001, 64, 184102. [Google Scholar] [CrossRef]
- Lee, B.J.; Shim, J.H.; Baskes, M.I. Semiempirical atomic potentials for the fcc metals Cu, Ag, Au, Ni, Pd, Pt, Al, and Pb based on first and second nearest-neighbor modified embedded atom method. Phys. Rev. B 2003, 68, 144112. [Google Scholar] [CrossRef]
- Lee, B.J.; Lee, T.H.; Kim, S.J. A modified embedded-atom method interatomic potential for the Fe-N system: A comparative study with the Fe-C system. Acta Mater. 2006, 54, 4597–4607. [Google Scholar] [CrossRef]
- Do, E.C.; Shin, Y.-H.; Lee, B.-J. Atomistic modeling of III-V nitrides: Modified embedded-atom method interatomic potentials for GaN, InN and Ga1−xInxN. J. Phys.-Condens. Matter 2009, 21, 325801. [Google Scholar] [CrossRef] [PubMed]
- Maisel, S.B.; Ko, W.S.; Zhang, J.L.; Grabowski, B.; Neugebauer, J. Thermomechanical response of NiTi shape-memory nanoprecipitates in TiV alloys. Phys. Rev. Mater. 2017, 1, 033610. [Google Scholar] [CrossRef]
- Kang, K.H.; Sa, I.; Lee, J.C.; Fleury, E.; Lee, B.J. Atomistic modeling of the Cu-Zr-Ag bulk metallic glass system. Scr. Mater. 2009, 61, 801–804. [Google Scholar] [CrossRef]
- Sangiovanni, D.G.; Edström, D.; Hultman, L.; Chirita, V.; Petrov, I.; Greene, J.E. Dynamics of Ti, N, and TiNx (x = 1–3) admolecule transport on TiN(001) surfaces. Phys. Rev. B 2012, 86, 155443. [Google Scholar] [CrossRef]
- Jelinek, B.; Groh, S.; Horstemeyer, M.F.; Houze, J.; Kim, S.G.; Wagner, G.J.; Moitra, A.; Baskes, M.I. Modified embedded atom method potential for Al, Si, Mg, Cu, and Fe alloys. Phys. Rev. B 2012, 85, 245102. [Google Scholar] [CrossRef]
- Kim, Y.M.; Lee, B.J.; Baskes, M.I. Modified embedded-atom method interatomic potentials for Ti and Zr. Phys. Rev. B 2006, 74, 014101. [Google Scholar] [CrossRef]
- Ko, W.-S.; Grabowski, B.; Neugebauer, J. Development and application of a Ni-Ti interatomic potential with high predictive accuracy of the martensitic phase transition. Phys. Rev. B 2015, 92, 134107. [Google Scholar] [CrossRef]
- Baskes, M.I. Modified embedded atom potentials for cubic materials and impurities. Phys. Rev. B 1992, 46, 2727. [Google Scholar] [CrossRef]
- Sangiovanni, D.G.; Alling, B.; Steneteg, P.; Hultman, L.; Abrikosov, I.A. Nitrogen vacancy, self-interstitial diffusion, and Frenkel-pair formation/dissociation in B1 TiN studied by ab initio and classical molecular dynamics with optimized potentials. Phys. Rev. B 2015, 91, 054301. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef]
- Freitas, R.; Asta, M.; de Koning, M. Nonequilibrium free-energy calculation of solids using LAMMPS. Comput. Mater. Sci. 2016, 112A, 333–341. [Google Scholar] [CrossRef]
- de Koning, M.; Antonelli, A. Einstein crystal as a reference system in free energy estimation using adiabatic switching. Phys. Rev. E 1996, 53, 465. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single-crystals—A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Hellman, O.; Abrikosov, I.A.; Simak, S.I. Lattice dynamics of anharmonic solids from first principles. Phys. Rev. B 2011, 84, 180301. [Google Scholar] [CrossRef]
- Hellman, O.; Steneteg, P.; Abrikosov, I.A.; Simak, S.I. Temperature dependent effective potential method for accurate free energy calculations of solids. Phys. Rev. B 2013, 87, 104111. [Google Scholar] [CrossRef]
- Hellman, O.; Abrikosov, I.A. Temperature-dependent effective third-order interatomic force constants from first principles. Phys. Rev. B 2013, 88, 144301. [Google Scholar] [CrossRef]
- Mei, A.B.; Hellman, O.; Wireklint, N.; Schlepuetz, C.M.; Sangiovanni, D.G.; Alling, B.; Rockett, A.; Hultman, L.; Petrov, I.; Greene, J.E. Dynamic and structural stability of cubic vanadium nitride. Phys. Rev. B 2015, 91, 054101. [Google Scholar] [CrossRef] [Green Version]
- Budai, J.D.; Hong, J.W.; Manley, M.E.; Specht, E.D.; Li, C.W.; Tischler, J.Z.; Abernathy, D.L.; Said, A.H.; Leu, B.M.; Boatner, L.A.; et al. Metallization of vanadium dioxide driven by large phonon entropy. Nature 2014, 515, 535. [Google Scholar] [CrossRef] [PubMed]
- Car, R.; Parrinello, M. Unified approach for molecular dynamics and density-functional theory. Phys. Rev. Lett. 1985, 55, 2471. [Google Scholar] [CrossRef] [PubMed]
- Shulumba, N.; Raza, Z.; Hellman, O.; Janzen, E.; Abrikosov, I.A.; Oden, M. Impact of anharmonic effects on the phase stability, thermal transport, and electronic properties of AlN. Phys. Rev. B 2016, 94, 104305. [Google Scholar] [CrossRef]
- Wang, Y.; Zacherl, C.L.; Shang, S.; Chen, L.-Q.; Liu, Z.-K. Phonon dispersions in random alloys: A method based on special quasi-random structure force constants. J. Phys.-Condens. Matter 2011, 23, 485403. [Google Scholar] [CrossRef] [PubMed]
- Porter, D.A.; Easterling, K.E.; Sherif, M.Y. Phase Transformations in Metals and Alloys, 3rd ed.; CRC Press, Taylor & Francis: London, UK, 2009; p. 304, Figure 5.38. [Google Scholar]
- Henkelman, G.; Uberuaga, B.P.; Jonsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 2000, 113, 9901–9904. [Google Scholar] [CrossRef]
- Henkelman, G.; Jonsson, H. Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points. J. Chem. Phys. 2000, 113, 9978–9985. [Google Scholar] [CrossRef]
- Tasnadi, F.; Oden, M.; Abrikosov, I.A. Ab initio elastic tensor of cubic Ti0.5Al0.5N alloys: Dependence of elastic constants on size and shape of the supercell model and their convergence. Phys. Rev. B 2012, 85, 144112. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. Model. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- National Institute of Standard and Technology. Available online: https://www.ctcms.nist.gov/potentials/ (accessed on 8 January 2019).
- OpenKIM – Knowledge of Interatomic Models. Available online: https://openkim.org/ (accessed on 8 January 2019).
- Siegel, A.; Parlinski, K.; Wdowik, U.D. Ab initio calculation of structural phase transitions in AlN crystal. Phys. Rev. B 2006, 74, 104116. [Google Scholar] [CrossRef]
- Materials Project. Available online: https://materialsproject.org/materials/mp-1700/ (accessed on 8 January 2019).
- Materials Project. Available online: https://materialsproject.org/materials/mp-1330/ (accessed on 8 January 2019).
- Edgar, J.H. (Ed.) Properties of Group-III Nitrides; EMIS Data reviews Series; IEE: London, UK, 1994. [Google Scholar]
- Stampfl, C.; van de Walle, C.G. Density-functional calculations for III-V nitrides using the local-density approximation and the generalized gradient approximation. Phys. Rev. B 1999, 59, 5521. [Google Scholar] [CrossRef]
- Paulus, B.; Shi, E.J.; Stoll, H. A correlated ab initio treatment of the zinc-blende wurtzite polytypism of SIC and III-V nitrides. J. Phys.-Condens. Matter 1997, 9, 2745. [Google Scholar] [CrossRef]
- Harrison, W.A. Electronic Structure and the Properties of Solids; Dover: New York, NY, USA, 1989. [Google Scholar]
- Ueno, M.; Onodera, A.; Shimomura, O.; Takemura, K. X-ray observation of the structural phase transition of aluminum nitride under high pressure. Phys. Rev. B 1992, 45, 10123. [Google Scholar] [CrossRef]
- McNeil, L.E.; Grimsditch, M.; French, R.H. Vibrational spectroscopy of aluminum nitride. J. Am. Ceram. Soc. 1993, 76, 1132–1136. [Google Scholar] [CrossRef]
- Materials Project. Available online: https://materialsproject.org/materials/mp-8282/ (accessed on 8 January 2019).
- Materials Project. Available online: https://materialsproject.org/materials/mp-661/ (accessed on 8 January 2019).
- Shulumba, N.; Hellman, O.; Rogström, L.; Raza, Z.; Tasnadi, F.; Abrikosov, I.A.; Oden, M. Temperature-dependent elastic properties of Ti1−xAlxN alloys. Appl. Phys. Lett. 2015, 107, 231901. [Google Scholar] [CrossRef]
- Gall, D.; Stoehr, M.; Greene, J.E. Vibrational modes in epitaxial Ti1−xScxN(001) layers: An ab initio calculation and Raman spectroscopy study. Phys. Rev. B 2001, 64, 174302. [Google Scholar] [CrossRef]
- Wriedt, H.A.; Murray, J.L. The N-Ti (Nitrogen-Titanium) system. Bull. Alloy Phase Diagr. 1987, 8, 378–388. [Google Scholar] [CrossRef]
- Xia, Q.; Xia, H.; Ruoff, A.L. Pressure-induced rock-salt phase of aluminum nitride—A metastable structure at ambient condition. J. Appl. Phys. 1993, 73, 8198–8200. [Google Scholar] [CrossRef]
- Vashishta, P.; Kalia, R.K.; Nakano, A.; Rino, J.P.; Simulation Collaboratory Advanced Computing. Interaction potential for aluminum nitride: A molecular dynamics study of mechanical and thermal properties of crystalline and amorphous aluminum nitride. J. Appl. Phys. 2011, 109, 033514. [Google Scholar] [CrossRef]
- Sherwin, M.E.; Drummond, T.J. Predicted elastic constants and critical layer thicknesses for cubic-phase AlN, GaN, and InN on β-SiC. J. Appl. Phys. 1991, 69, 8423–8425. [Google Scholar] [CrossRef]
- Christensen, N.E.; Gorczyca, I. Calculated structural phase transitions of aluminum nitride under pressure. Phys. Rev. B 1993, 47, 4307. [Google Scholar] [CrossRef]
- Ruiz, E.; Alvarez, S.; Alemany, P. Electronic structure and properties of AlN. Phys. Rev. B 1994, 49, 7115. [Google Scholar] [CrossRef]
- Uehara, S.; Masamoto, T.; Onodera, A.; Ueno, M.; Shimomura, O.; Takemura, K. Equation of state of the rocksalt phase of III–V nitrides to 72 GPa or higher. J. Phys. Chem. Solids 1997, 58, 2093–2099. [Google Scholar] [CrossRef]
- Mastail, C.; David, M.; Nita, F.; Michel, A.; Abadias, G. Ti, Al and N adatom adsorption and diffusion on rocksalt cubic AlN (001) and (011) surfaces: Ab initio calculations. Appl. Surf. Sci. 2017, 423, 354–364. [Google Scholar] [CrossRef]
- Shen, L.H.; Li, X.F.; Ma, Y.M.; Yang, K.F.; Lei, W.W.; Cui, Q.L.; Zou, G.T. Pressure-induced structural transition in AlN nanowires. Appl. Phys. Lett. 2006, 89, 141903. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.; Lambrecht, W.R.L.; Segall, B. Erratum: Elastic constants and related properties of tetrahedrally bonded BN, AlN, GaN, and InN. Phys. Rev. B 1997, 56, 16310. [Google Scholar] [CrossRef]
- Merad, A.E.; Kanoun, M.B.; Cibert, J.; Aourag, H.; Merad, G. Ab initio study of electronic properties of zincblende AlN and deformation potentials under hydrostatic stress. Mater. Chem. Phys. 2003, 82, 471–477. [Google Scholar] [CrossRef]
- Lee, T.; Ohmori, K.; Shin, C.S.; Cahill, D.G.; Petrov, I.; Greene, J.E. Elastic constants of single-crystal TiNx(001) (0.67 ≤ x ≤ 1.0) determined as a function of x by picosecond ultrasonic measurements. Phys. Rev. B 2005, 71, 144106. [Google Scholar] [CrossRef]
- Lee, Y.-C.; Kim, J.O.; Achenbach, J.D. Acoustic microscopy measurement of elastic constants and mass density. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1995, 42, 253–264. [Google Scholar] [CrossRef]
- Iwanaga, H.; Kunishige, A.; Takeuchi, S. Anisotropic thermal expansion in wurtzite-type crystals. J. Mater. Sci. 2000, 35, 2451–2454. [Google Scholar] [CrossRef]
- Zhang, R.F.; Sheng, S.H.; Veprek, S. First principles studies of ideal strength and bonding nature of AIN polymorphs in comparison to TiN. Appl. Phys. Lett. 2007, 91, 031906. [Google Scholar] [CrossRef]
- Haglund, J.; Grimvall, G.; Jarlborg, T.; Guillermet, A.F. Band structure and cohesive properties of 3d transition-metal carbides and nitrides with the NaCl-type structure. Phys. Rev. B 1991, 43, 14400. [Google Scholar] [CrossRef]
- Dudiy, S.V.; Lundqvist, B.I. First-principles density-functional study of metal-carbonitride interface adhesion: Co/TiC(001) and Co/TiN(001). Phys. Rev. B 2001, 64, 045403. [Google Scholar] [CrossRef]
- Alling, B.; Karimi, A.; Hultman, L.; Abrikosov, I.A. First-principles study of the effect of nitrogen vacancies on the decomposition pattern in cubic Ti1−xAlxN1−y. Appl. Phys. Lett. 2008, 92, 071903. [Google Scholar] [CrossRef]
- Alling, B.; Ruban, A.V.; Karimi, A.; Hultman, L.; Abrikosov, I.A. Unified cluster expansion method applied to the configurational thermodynamics of cubic Ti1−xAlxN. Phys. Rev. B 2011, 83, 104203. [Google Scholar] [CrossRef]
- Alling, B.; Ruban, A.V.; Karimi, A.; Peil, O.E.; Simak, S.I.; Hultman, L.; Abrikosov, I.A. Mixing and decomposition thermodynamics of c- Ti1−xAlxN from first-principles calculations. Phys. Rev. B 2007, 75, 045123. [Google Scholar] [CrossRef]
- Wang, A.; Shang, S.-L.; Du, Y.; Chen, L.; Wang, J.; Liu, Z.-K. Effects of pressure and vibration on the thermal decomposition of cubic Ti1−xAlxN, Ti1−xZrxN, and Zr1−xAlxN coatings: A first-principles study. J. Mater. Sci. 2012, 47, 7621–7627. [Google Scholar] [CrossRef]
- Mayrhofer, P.H.; Music, D.; Schneider, J.M. Ab initio calculated binodal and spinodal of cubic Ti1−xAlxN. Appl. Phys. Lett. 2006, 88, 071922. [Google Scholar] [CrossRef]
- Tsetseris, L.; Kalfagiannis, N.; Logothetidis, S.; Pantelides, S.T. Structure and interaction of point defects in transition-metal nitrides. Phys. Rev. B 2007, 76, 224107. [Google Scholar] [CrossRef]
- Mei, Z.-G.; Yacout, A.M.; Kim, Y.S.; Hofman, G.; Stan, M. First-principles study of transition-metal nitrides as diffusion barriers against Al. J. Nuclear Mater. 2016, 471, 208–213. [Google Scholar] [CrossRef] [Green Version]
- Gambino, D.; Sangiovanni, D.G.; Alling, B.; Abrikosov, I.A. Nonequilibrium ab initio molecular dynamics determination of Ti monovacancy migration rates in B1 TiN. Phys. Rev. B 2017, 96, 104306. [Google Scholar] [CrossRef]
- Mattila, T.; Nieminen, R.M. Point-defect complexes and broadband luminescence in GaN and AlN. Phys. Rev. B 1997, 55, 9571. [Google Scholar] [CrossRef]
- Stampfl, C.; van de Walle, C.G. Doping of AlxGa1−xN. Appl. Phys. Lett. 1998, 72, 459. [Google Scholar] [CrossRef]
- Alling, B.; Karimi, A.; Abrikosov, I.A. Electronic origin of the isostructural decomposition in cubic M1−xAlxN (M = Ti, Cr, Sc, Hf): A first-principles study. Surf. Coat. Technol. 2008, 203, 883–886. [Google Scholar] [CrossRef]
- Tasnadi, F.; Abrikosov, I.A.; Rogström, L.; Almer, J.; Johansson, M.P.; Oden, M. Significant elastic anisotropy in Ti1−xAlxN alloys. Appl. Phys. Lett. 2010, 97, 231902. [Google Scholar] [CrossRef]
- Blackman, M. On anomalous vibrational spectra. Proc. R. Soc. Lond. A 1938, 164, 62–79. [Google Scholar] [CrossRef] [Green Version]
- Pettifor, D.G. Theoretical predictions of structure and related properties of intermetallics. Mater. Sci. Technol. 1992, 8, 345–349. [Google Scholar] [CrossRef]
- Toth, L.E. Transition Metal Carbides and Nitrides; Academic Press: New York, NY, USA, 1971. [Google Scholar]
- Zhu, L.-F.; Grabowski, B.; Neugebauer, J. Efficient approach to compute melting properties fully from ab initio with application to Cu. Phys. Rev. B 2017, 96, 224202. [Google Scholar] [CrossRef]
- Shin, C.S.; Rudenja, S.; Gall, D.; Hellgren, N.; Lee, T.Y.; Petrov, I.; Greene, J.E. Growth, surface morphology, and electrical resistivity of fully strained substoichiometric epitaxial TiNx (0.67 ≤ x < 1.0) layers on MgO(001). J. Appl. Phys. 2004, 95, 356–362. [Google Scholar] [CrossRef]
- Aigner, K.; Lengauer, W.; Rafaja, D.; Ettmayer, P. Lattice parameters and thermal expansion of TiCxN1−x, ZrCxN1−x, HfCxN1−x, and TiN1−x from 298 K to 1473 K as investigated by high-temperature X-ray diffraction. J. Alloys Compd. 1994, 215, 121–126. [Google Scholar] [CrossRef]
- Rickerby, D.S.; Bull, S.J.; Jones, A.M.; Cullen, F.L.; Bellamy, B.A. High-temperature X-ray diffraction studies on physical vapour deposited TiN. Surf. Coat. Technol. 1989, 39, 397–408. [Google Scholar] [CrossRef]
- Bartosik, M.; Holec, D.; Apel, D.; Klaus, M.; Genzel, C.; Keckes, J.; Arndt, M.; Polcik, P.; Koller, C.M.; Mayrhofer, P.H. Thermal expansion of Ti-Al-N and Cr-Al-N coatings. Scr. Mater. 2017, 127, 182–185. [Google Scholar] [CrossRef] [Green Version]
- Bartosik, M.; Todt, M.; Holec, D.; Todt, J.; Zhou, L.; Riedl, H.; Boehm, H.J.; Rammerstorfer, F.G.; Mayrhofer, P.H. Thermal expansion of rock-salt cubic AlN. Appl. Phys. Lett. 2015, 107, 071602. [Google Scholar] [CrossRef] [Green Version]
- Kress, W.; Roedhammer, P.; Bilz, H.; Teuchert, W.D.; Christensen, A.N. Phonon anomalies in transition-metal nitrides—TiN. Phys. Rev. B 1978, 17, 111. [Google Scholar] [CrossRef]
- Baroni, S.; Giannozzi, P.; Testa, A. Green-function approach to linear response in solids. Phys. Rev. Lett. 1987, 58, 1861. [Google Scholar] [CrossRef]
- Höglund, C.; Alling, B.; Birch, J.; Beckers, M.; Persson, P.O.A.; Baehtz, C.; Czigany, Z.; Jensen, J.; Hultman, L. Effects of volume mismatch and electronic structure on the decomposition of ScAlN and TiAlN solid solutions. Phys. Rev. B 2010, 81, 224101. [Google Scholar] [CrossRef] [Green Version]
- Tsetseris, L.; Kalfagiannis, N.; Logothetidis, S.; Pantelides, S.T. Role of N defects on thermally induced atomic-scale structural changes in transition-metal nitrides. Phys. Rev. Lett. 2007, 99, 125503. [Google Scholar] [CrossRef] [PubMed]
- Kodambaka, S.; Khare, S.V.; Swiech, W.; Ohmori, K.; Petrov, I.; Greene, J.E. Dislocation-driven surface dynamics on solids. Nature 2004, 429, 49. [Google Scholar] [CrossRef]
- Hultman, L.; Engstrom, C.; Oden, M. Mechanical and thermal stability of TiN/NbN superlattice thin films. Surf. Coat. Technol. 2000, 133, 227–233. [Google Scholar] [CrossRef]
- Wood, F.W.; Paasche, O.G. Dubious details of nitrogen diffusion in nitrided titanium. Thin Solid Films 1977, 40, 131–137. [Google Scholar] [CrossRef]
- Anglezioabautret, F.; Pellissier, B.; Miloche, M.; Eveno, P.; S.O.C. European Ceram. Nitrogen self-diffusion in titanium nitride single-crystals and polycrystals. J. Eur. Ceram. Soc. 1991, 8, 299–304. [Google Scholar] [CrossRef]
- Sternitzke, M.; Muller, G. EELS study of oxygen diffusion in aluminum nitride. J. Am. Ceram. Soc. 1994, 77, 737–742. [Google Scholar] [CrossRef]
- Norrby, N.; Rogström, L.; Johansson-Joesaar, M.P.; Schell, N.; Oden, M. In situ X-ray scattering study of the cubic to hexagonal transformation of AlN in Ti1−xAlxN. Acta Mater. 2014, 73, 205–214. [Google Scholar] [CrossRef]
- Tasnadi, F.; Lugovskoy, A.V.; Oden, M.; Abrikosov, I.A. Non-equilibrium vacancy formation energies in metastable alloys—A case study of Ti0.5Al0.5N. Mater. Des. 2017, 114, 484–493. [Google Scholar] [CrossRef]
- Sundgren, J.E.; Johansson, B.O.; Rockett, A.; Barnett, S.A.; Greene, J.E. TiNx (0.6 < x < 1.2): Atomic Arrangements, Electronic Structure, and Recent Results on Crystal Growth and Physical Properties of Epitaxial Layers. AIP Conf. Proc. 1986, 149, 95–115. [Google Scholar] [CrossRef]
- Lengauer, W. Properties of bulk δ-TiN1−x prepared by nitrogen diffusion into titanium metal. J. Alloys Compd. 1992, 186, 293–307. [Google Scholar] [CrossRef]
- Porte, L.; Roux, L.; Hanus, J. Vacancy effects in the X-ray photoelectron spectra of TiNx. Phys. Rev. B 1983, 28, 3214. [Google Scholar] [CrossRef]
- Shin, C.S.; Gall, D.; Hellgren, N.; Patscheider, J.; Petrov, I.; Greene, J.E. Vacancy hardening in single-crystal TiNx(001) layers. J. Appl. Phys. 2003, 93, 6025–6028. [Google Scholar] [CrossRef]
- Jhi, S.H.; Louie, S.G.; Cohen, M.L.; Ihm, J. Vacancy hardening and softening in transition metal carbides and nitrides. Phys. Rev. Lett. 2001, 86, 3348. [Google Scholar] [CrossRef] [PubMed]
- Hu, Q.-M.; Kadas, K.; Hogmark, S.; Yang, R.; Johansson, B.; Vitos, L. Hardness and elastic properties of covalent/ionic solid solutions from first-principles theory. J. Appl. Phys. 2008, 103, 083505. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, M.; Schmidt, K.; Dunlop, E.; Haupt, J.; Gissler, W. Elastic constants and hardness of ion-beam sputtered TiNx films measured by Brillouin scattering and depth-sensing indentation. J. Appl. Phys. 1991, 69, 3053. [Google Scholar] [CrossRef]
- Materials Project. Available online: https://materialsproject.org/materials/mp-7790/ (accessed on 8 January 2019).
- Schwarz, M.R.; Antlauf, M.; Schmerler, S.; Keller, K.; Schlothauer, T.; Kortus, J.; Heide, G.; Kroke, E. Formation and properties of rocksalt-type AlN and implications for high pressure phase relations in the system Si-Al-O-N. High Press. Res. 2014, 34, 22–38. [Google Scholar] [CrossRef]
- van Camp, P.E.; van Doren, V.E.; Devreese, J.T. High-pressure properties of wurtzite-type and rocksalt type aluminum nitride. Phys. Rev. B 1991, 44, 9056. [Google Scholar] [CrossRef]
- Schmerler, S.; Kortus, J. Ab initio study of AlN: Anisotropic thermal expansion, phase diagram, and high-temperature rocksalt to wurtzite phase transition. Phys. Rev. B 2014, 89, 064109. [Google Scholar] [CrossRef]
- Durandurdu, M. Pressure-induced phase transition in AIN: An ab initio molecular dynamics study. J. Alloys Compd. 2009, 480, 917–921. [Google Scholar] [CrossRef]
- Harris, S.G.; Doyle, E.D.; Vlasveld, A.C.; Audy, J.; Long, J.M.; Quick, D. Influence of chromium content on the dry machining performance of cathodic arc evaporated TiAlN coatings. Wear 2003, 254, 185–194. [Google Scholar] [CrossRef]
- Hörling, A.; Hultman, L.; Oden, M.; Sjölen, J.; Karlsson, L. Mechanical properties and machining performance of Ti1−xAlxN-coated cutting tools. Surf. Coat. Technol. 2005, 191, 384–392. [Google Scholar] [CrossRef]
- Zhang, Y.; Franke, P.; Seifert, H.J. CALPHAD modeling of metastable phases and ternary compounds in Ti-Al-N system. Calphad 2017, 59, 142–153. [Google Scholar] [CrossRef]
- Shulumba, N.; Hellman, O.; Raza, Z.; Alling, B.; Barrirero, J.; Muecklich, F.; Abrikosov, I.A.; Oden, M. Lattice Vibrations Change the Solid Solubility of an Alloy at High Temperatures. Phys. Rev. Lett. 2016, 117, 205502. [Google Scholar] [CrossRef]
- Zhou, J.; Zhong, J.; Chen, L.; Zhang, L.; Du, Y.; Liu, Z.-K.; Mayrhofer, P.H. Phase equilibria, thermodynamics and microstructure simulation of metastable spinodal decomposition in c-Ti1−xAlxN coatings. Calphad 2017, 56, 92–101. [Google Scholar] [CrossRef]
- Hultman, L. Thermal stability of nitride thin films. Vacuum 2000, 57, 1–30. [Google Scholar] [CrossRef]
- Petrov, I.; Mojab, E.; Adibi, F.; Greene, J.E.; Hultman, L.; Sundgren, J.E. Interfacial reactions in epitaxial Al/Ti1−xAlxN (0 ≤ x ≤ 0.2) model diffusion barrier structures. J. Vac. Sci. Technol. A 1993, 11, 11–17. [Google Scholar] [CrossRef]
- Chun, J.S.; Desjardins, P.; Petrov, I.; Greene, J.E.; Lavoie, C.; Cabral, C. Interfacial reaction pathways and kinetics during annealing of epitaxial Al/TiN(001) model diffusion barrier systems. Thin Solid Films 2001, 391, 69–80. [Google Scholar] [CrossRef]
- Chun, J.S.; Petrov, I.; Greene, J.E. Dense fully 111-textured TiN diffusion barriers: Enhanced lifetime through microstructure control during layer growth. J. Appl. Phys. 1999, 86, 3633–3641. [Google Scholar] [CrossRef]
- Mikula, M.; Plašienka, D.; Sangiovanni, D.G.; Sahul, M.; Roch, T.; Truchlý, M.; Gregor, M.; Caplovic, L.U.; Plecenik, A.; Kus, P. Toughness enhancement in highly NbN-alloyed Ti-Al-N hard coatings. Acta Mater. 2016, 121, 59–67. [Google Scholar] [CrossRef]
- Mikula, M.; Truchlý, M.; Sangiovanni, D.G.; Plašienka, D.; Roch, T.; Gregor, M.; Ďurina, P.; Janík, M.; Kúš, P. Experimental and computational studies on toughness enhancement in Ti-Al-Ta-N quaternaries. J. Vac. Sci. Technol. A 2017, 35, 060602. [Google Scholar] [CrossRef]
- Fager, H.; Tengstrand, O.; Lu, J.; Bolz, S.; Mesic, B.; Koelker, W.; Schiffers, C.; Lemmer, O.; Greene, J.E.; Hultman, L.; et al. Low-temperature growth of dense and hard Ti0.41Al0.51Ta0.08N films via hybrid HIPIMS/DC magnetron co-sputtering with synchronized metal-ion irradiation. J. Appl. Phys. 2017, 121, 171902. [Google Scholar] [CrossRef]
- Mayrhofer, P.H.; Rachbauer, R.; Holec, D. Influence of Nb on the phase stability of Ti-Al-N. Scr. Mater. 2010, 63, 807–810. [Google Scholar] [CrossRef]
- Rachbauer, R.; Holec, D.; Mayrhofer, P.H. Phase stability and decomposition products of Ti-Al-Ta-N thin films. Appl. Phys. Lett. 2010, 97, 151901. [Google Scholar] [CrossRef]
- Rachbauer, R.; Holec, D.; Lattemann, M.; Hultman, L.; Mayrhofer, P.H. Electronic origin of structure and mechanical properties in Y and Nb alloyed Ti-Al-N thin films. Int. J. Mater. Res. 2011, 102, 735–742. [Google Scholar] [CrossRef]
- Kim, S.K.; Vinh, P.V.; Kim, J.H.; Ngoc, T. Deposition of superhard TiAlSiN thin films by cathodic arc plasma deposition. Surf. Coat. Technol. 2005, 200, 1391–1394. [Google Scholar] [CrossRef]
- Chen, Y.H.; Roa, J.J.; Yu, C.H.; Johansson-Joesaar, M.P.; Andersson, J.M.; Anglada, M.J.; Oden, M.; Rogström, L. Enhanced thermal stability and fracture toughness of TiAlN coatings by Cr, Nb and V-alloying. Surf. Coat. Technol. 2018, 342, 85–93. [Google Scholar] [CrossRef] [Green Version]








| B1-TiN | ε-Ti2N | B1-AlN | B3-AlN | B4-AlN | ||
|---|---|---|---|---|---|---|
| Ec | 6.613 | 6.180 | 5.690 | 5.728 | 5.758 | |
| (eV/at.) | [6.69 ± 0.07c1] (6.8d1, 8.708c1) | (5.597e1) | (6.621e, 5.681e, 5.44f) | [5.76g, 5.76o] (5.701e, 5.779e1, 6.643e, 5.055r, 5.545r) | ||
| Energy above hull (meV/at.) | 68 | 30 | 0 | |||
| - | - | (147q, 204a, 172c, 182e1) | (43q, 23a, 21b, 21e, 22e, 41f) | |||
| a | 4.252 | 4.939 | 4.090 | 4.366 | 3.112 | |
| (Å) | [4.240z] (4.188–4.254s) | [4.938–4.946l] (4.955*, 4.960j) | [4.046u, 4.064w] (4.014–4.070v, 4.06a, 4.069c, 4.071*) | [4.37d, 4.38p] (4,349y, 4.39a, 4.320x, 4.401b, 4.310e, 4.394e, 4.374f) | [3.111d, 3.111b1, 3.110–3.113f] (3.12a, 3.06x, 3.100f, 3.113e, 3.057e, 3.129k, 3.101r, 3.117r) | |
| c/a | 0.616 | 1.600 | ||||
| - | [0.613–0.614l] (0.612j, 0.613*) | - | - | [1.601d, 1.600b1, 1.602h, 1.600–1.602f] (1.596q, 1.603a, 1.60x, 1.619e, 1.617e, 1.609f, 1.603k, 1.598r, 1.604r) | ||
| B | 298 | 208 | 277 | 237 | 236 | |
| (GPa) | [298–324a1] (277n, 303t, 290–350s) | (204j, 214*) | [221 ± 5m, 295 ± 17u, 319 ± 8w] (253–277v, 270q, 207n, 265t, 255c, 261*) | [202p] (213y, 216q, 195b, 206e, 209x, 191e, 218f, 228r) | [208 ± 6h, 211b1, 185 ± 5m, 185–212f, 185–237o, 303 ± 4w] (205q, 202x, 209e, 192e, 194k, 228–243r) | |
| C11 | 613 | 309 | 480 | 289 | 432 | |
| (GPa) | [626z, 605–649a1] (590n, 610t, 640–710s) | (429j, 434*) | (340n, 425t, 428c, 432*) | [328p] (309y, 284b, 298x, 348r) | [395p, 411b1, 410 ± 10i, 345–411o] (458x, 376k, 389–464r) | |
| C12 | 140 | 153 | 175 | 213 | 203 | |
| (GPa) | [145–165a1] (120n, 150t, 115–125s) | (105j, 127*) | (140n, 185t, 168c, 175*) | [139p] (164y, 150b, 164x, 168r) | [125p, 149b1, 148 ± 10i, 125–149o] (154x, 129k, 149–158r) | |
| C44 | 165 | 130 | 271 | 100 | 70 | |
| (GPa) | [156z, 162–171a1] (160n, 165t, 159–169s) | (151j,169*) | (260n, 298t, 307c, 296*) | [133p] (78y, 179b, 187x,135r) | [118p, 125b1, 125 ± 5i, 118–125o] (85x, 113k) | |
| C13 | 163 | 153 | ||||
| (GPa) | - | (194j, 205*) | - | - | [120p, 99b1, 99 ± 4i, 95–120o] (84x, 98k, 116–138r) | |
| C33 | 296 | 337 | ||||
| (GPa) | - | (300j, 337*) | - | - | [345p, 389b1, 388 ± 10i, 394–402o] (388x, 353k, 408–409r) | |
| C66 | 121 | 115 | ||||
| (GPa) | - | (138j, 136*) | - | - | [135p, 131b1, 131 ± 10i, 130–131o] (152x, 124k, 115–157r) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almyras, G.A.; Sangiovanni, D.G.; Sarakinos, K. Semi-Empirical Force-Field Model for the Ti1−xAlxN (0 ≤ x ≤ 1) System. Materials 2019, 12, 215. https://doi.org/10.3390/ma12020215
Almyras GA, Sangiovanni DG, Sarakinos K. Semi-Empirical Force-Field Model for the Ti1−xAlxN (0 ≤ x ≤ 1) System. Materials. 2019; 12(2):215. https://doi.org/10.3390/ma12020215
Chicago/Turabian StyleAlmyras, G. A., D. G. Sangiovanni, and K. Sarakinos. 2019. "Semi-Empirical Force-Field Model for the Ti1−xAlxN (0 ≤ x ≤ 1) System" Materials 12, no. 2: 215. https://doi.org/10.3390/ma12020215