1. Introduction
Directed energy deposition (DED) is based on a laser process in which a laser beam generates a melt pool on a substrate. An additional metallic powder material is transported to the melt pool, where it becomes molten. Due to a feed movement, the molten material cools down and welding tracks are formed. By placing a couple of single tracks side by side, a planar coating can be obtained. Furthermore, it is possible to generate whole three-dimensional structures by depositing one layer or track at the top of another already welded layer or track [
1].
This technique can be used to coat or repair already existing parts, as well as to create completely new components. Many advantages, like a much higher deposition rate or no longer need of support structures compared to powder bed techniques, lead to a growing importance for industrial applications [
2]. On the other hand, the variety of parameters leads to a high complexity and requires a deep understanding of the process [
1].
A great deal of research has been done to analyse the effect on the cladding track according to a systematic variation of process parameters [
3,
4,
5,
6]. For example, de Oliveira et al. [
4] showed that the clad width
increases as the energy per unit length (given as
, with the laser power
and scanning speed
) increases. On the other hand, the authors determined an increasing clad height
, with an increasing powder mass per length
, with the powder feed rate
and scanning speed
.
In current practice, most suitable measurement systems work contactless and using optical technology [
7]. Several studies [
8,
9,
10,
11] have shown that temperature distribution inside a melt pool, as well as its shape, contain information about process parameters. Meriaudeau et al. [
9] determined a decreasing melt pool surface temperature as an indicator for an increasing powder feed rate
. Walter [
10] uses melt pool size
as an input for a closed-loop control to adjust the laser power
. Ocylok et al. [
8] showed the influence of the laser power
, scanning speed
, powder feed rate
and temperature of the base plate
on melt pool size
, where the laser power
had the biggest influence (a
larger melt pool size by doubling the laser power from
up to
).
The previously cited references mostly focus on single tracks. There, the heat transfer situation can be assumed as constant, which is not the case when complex 3D geometries are built up. Furthermore, the aforementioned publications predominantly analyse experiments performed in specially developed test stations under laboratory conditions.
This article examines the influence of the process parameters laser power , scanning speed , powder feed rate and substrate plate–nozzle distance on the melt intensity distribution of the melt pool surface while building up a single-track multilayer fillet.
3. Results
3.1. Steady State and Reproducibility
Because of the changing heat transfer situation, it is important not to consider all frames of an experiment, but to consider just the frames during steady state (
Figure 5). In this case, we recognised a significant difference between the first-layer signal (
), the transient behaviour (
) and the steady-state signal (
).
The first experiments were conducted to ensure reproducibility. Therefore, three cylinders were built up using the standard parameters (, , and ). The temporal average of the NOP showed a maximum deviation of , while the temporal standard deviation of the NOP showed a deviation of . Based on this result we concluded that one execution of each experiment was representative enough to derive meaningful results.
3.2. Variation of the Laser Power
Within the experiments, the laser power was varied from to in increments of . This range was chosen because the process became unstable (“unstable“ denotes a process that leads to dilution problems or porosity problems) at a power range of .
The temporally averaged NOP showed a maximum value of
at a power of
(
Figure 6). From that point, increasing laser power led to a local minimum (
) at
before increasing again. The maximum of the temporal standard derivation (
) appeared at
. It could be observed in the experiments that the welding process showed a behaviour with increased stochasticity for laser powers
. This was reflected by the higher standard deviation for
and
. Detailed analysis revealed that at
and
the distribution of observed NOPs was bimodal.
3.3. Variation of the Scanning Speed
Motivated by common industrial applications, the variation range of the scanning speed was chosen as .
Considering the scanning speed variation (
Figure 7), the maximum temporally averaged NOP (
) occurred at a scanning speed of
. By increasing the scanning speed, the temporally averaged NOP decreased, reaching its minimum at
, while at higher scanning speeds it rose again to
at a scanning speed of
. Throughout the whole variation, a standard deviation between
and
could be seen, which became maximal at a scanning speed of
(
).
3.4. Variation of the Powder Feed Rate
As with the range of the scanning speed variation, the powder mass flow variation range was set to base on common industrial applications.
The graph of the temporally averaged NOP over the powder feed rate variation (
Figure 8) starts with
at a powder feed rate of
. With an increasing powder feed rate, the temporally averaged NOP decreased so that it reached its minimum of
at a powder feed rate of
. The temporally averaged NOP then increased up to a value of
at a powder feed rate of
.
The relative temporal standard deviation increased with the growing powder feed rates until . With a further increasing powder feed rate, it stayed almost constant at about .
3.5. Variation of the Substrate Plate–Nozzle Distance
The range of the substrate plate–nozzle distance variation was chosen as . Distances of resulted in a growing nozzle temperature and thus to a growing number of nozzle adhesions, which disturbed the process. At distances of , no welding tracks could be formed.
Figure 9 shows the temporally averaged NOP over the variation of the substrate plate–nozzle distance. The temporally averaged NOP remained almost constant at about
from the substrate plate–nozzle distance of
up to
.
a significant increase was recognisable from a distance of
, so the temporally averaged NOP at a distance of
was
. The absolute temporal standard deviation followed a similar characteristic. It amounted to about
at a substrate plate–nozzle distance of
but increased up to
at a distance of
.
4. Discussion
4.1. Oscillation of the Process at Lower Specific Energies
By analysing the histograms of the steady-state time interval (
Figure 10), we recognised a bimodal behaviour in the laser power values of
and
, which explains the high standard deviation in this range. The bimodality was caused by a change of the NOP between two value ranges. The time increment in which the NOP fluctuated around one mode lasted several seconds and depended on the laser power. At the laser power of
, the NOP remained in the upper-value range (
Figure 11a) for longer, while staying longer in the lower-value range (
Figure 11b) at a power of
. This behaviour was also recognisable through visual inspections of the welding process as an alternative of the weld pool brightness.
The same bimodal behaviour was observed during the experiments in which the scanning speed was varied. It appeared at and .
In order to compare the experiments of power variation with those of the scanning speed variation, the specific energy
[
13] was used to build an applicable characteristic value. The specific energy combined the absorbed laser power
with the scanning speed
and laser spot diameter
, according to
.
To calculate the absorbed laser power
, the laser power had to be multiplied by the absorptance
(or emissivity
) of the melt pool surface in accordance with
. Devesse et al. [
7] showed that emissivity was approximately constant over the melt pool surface for the stainless steel LPW 316L. Furthermore, they determined the emissivity to lie in between
and
. According to this, an absorptance of
was assumed.
Table 1 shows the experiments, during which the process was pulsating, and their respective specific energies. As one can see, the specific energy values during laser power variation correlated with those of the scanning speed variation.
Steen et al. [
13] determined a minimum specific energy of
, which was required to achieve a stable process in the case of NiCr20Ti. At this point it can only be assumed that—due to a different heat transfer situation, the higher temperature of the base material and the different materials during the present analysis—lower specific energies were capable of achieving a stable process. This point should be examined in detail and might be a subject for further investigations.
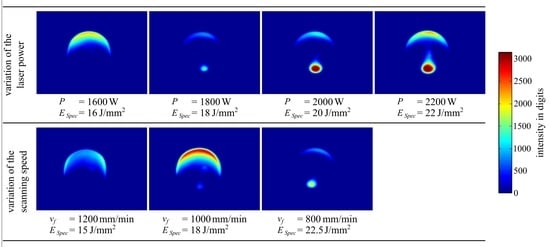
4.2. Expression of the Plasma Plume
In addition, a further effect was observed regarding intensity distribution. An increasing laser power, as well as a decreasing scanning speed, resulted in a larger plasma plume. Again the specific energy is capable to compare the experimental series of varying the laser power and varying the scanning speed.
Figure 12 shows no plasma plume at the specific energies
.
The expression of a plasma plume is a known phenomenon when the carrier and shielding gas argon is used in combination with higher specific energy values. For example, Ruiz et al. [
11] varied the specific energy in the range of
while building up single tracks of NiCr19NbMo. They suspected the argon to form an ionised gas because of its first ionisation energy of
.
4.3. Variation of the Powder Feed Rate
The introduced powder mass flow of was insufficient to reach the required welding track height. This led to a growing distance between the base material and the nozzle tip. Therefore, the high temporally averaged NOP at this point was not an indicator of a low powder mass flow, but a result of the distance between the base material and nozzle tip being too large. Consequently, the powder mass flow affected the NOP indirectly, but the NOP only allowed limited conclusions about the powder mass flow to be drawn.
4.4. Variation of the Substrate Plate–Nozzle Distance
The behaviour of the NOPs over the variation of the substrate plate–nozzle distance can be explained by considering the self-curing effect. In order to prevent process errors according to a misestimated welding track height in the NC code, the powder focus was placed 2 mm below the laser focus (and the usual working distance). If the welding tracks were calculated too small, the process ran increasingly out of the powder focus and less powder reached the melt pool. If the welding tracks were calculated too high, the process drifted increasingly inside the powder focus, which led to higher powder efficacy and a higher welding track.
Figure 9 shows that the process was able to “cure” itself until a substrate plate–nozzle distance of
. At higher distances, the self-curing effect was no longer able to compensate for it and the process drifted away. The high temporally averaged NOP at
was caused by the fact that powder that could not reach the melt pool. In that case, power was ignited by the laser beam and burned brightly below the nozzle, emitting radiation that was not representative of the melt pool intensity.
4.5. Stochasticity of the Process
During the whole variation of the different process parameters, we recognise that the temporal standard deviation of the NOP was low at a stable process where the process parameter combination led to a well build-up, while it increased as the process became unstable. An exception can be seen at the high substrate plate–nozzle distance of which is explained above.