A Comprehensive Numerical Approach for Analyzing the Residual Stresses in AISI 301LN Stainless Steel Induced by Shot Peening
Abstract
:1. Introduction
2. Proposed Constitutive Model
2.1. Mechanical Behavior Law
2.2. Yield Surface
2.3. Kinematic Hardening Law
2.4. Isotropic Hardening Law
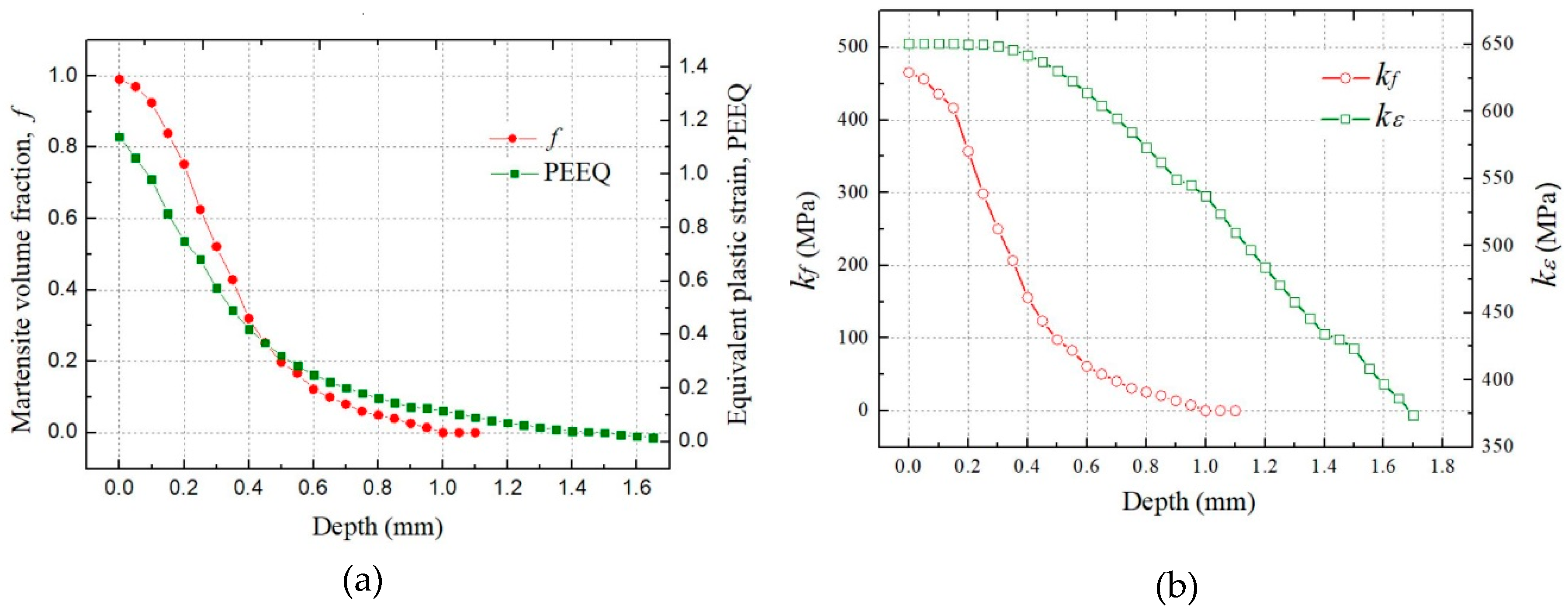
2.5. Martensitic Transformation Kinetics Law
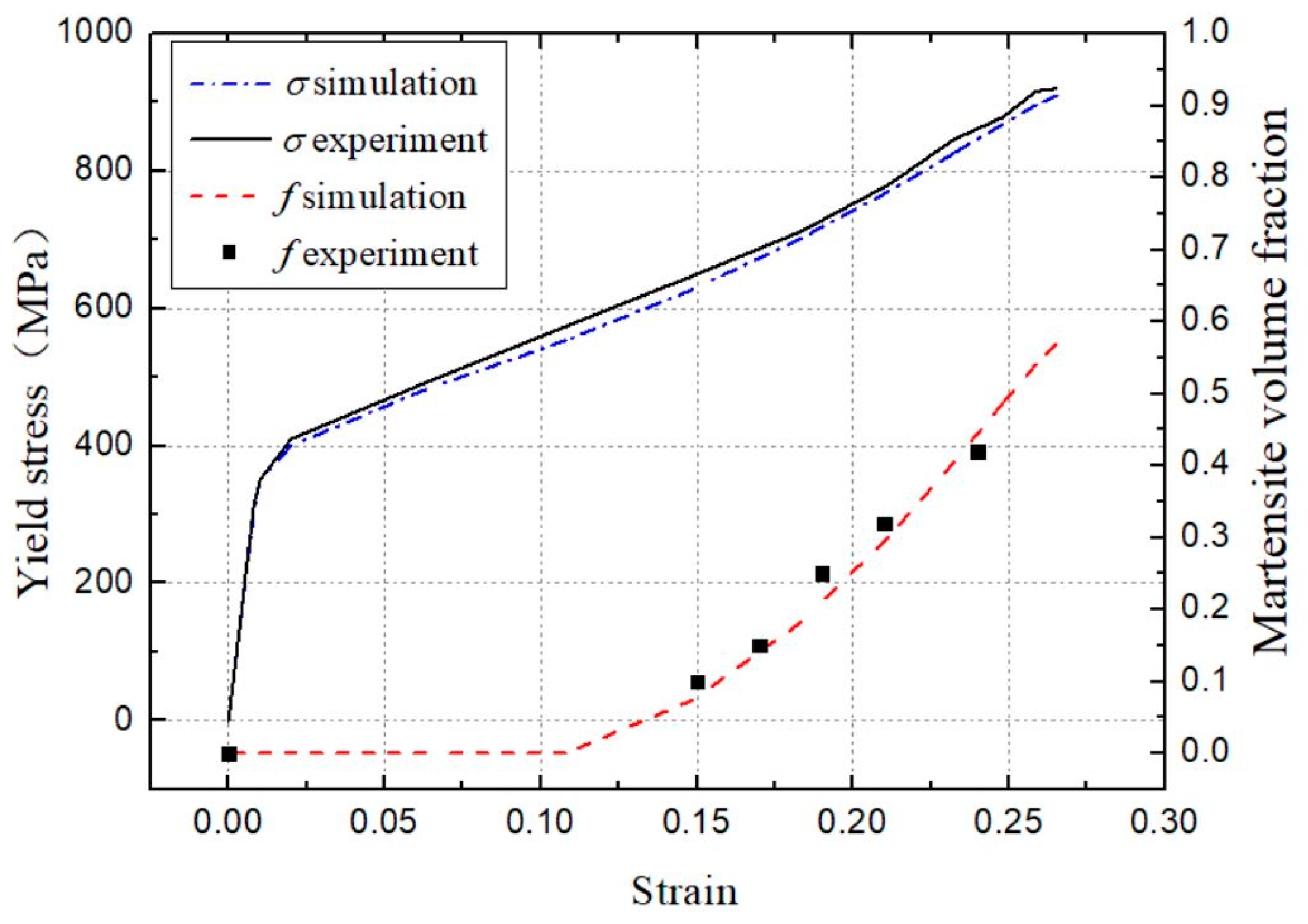
2.6. Identification of the Constitutive Model Parameters
3. Finite Element Modelling
4. Results and Discussions
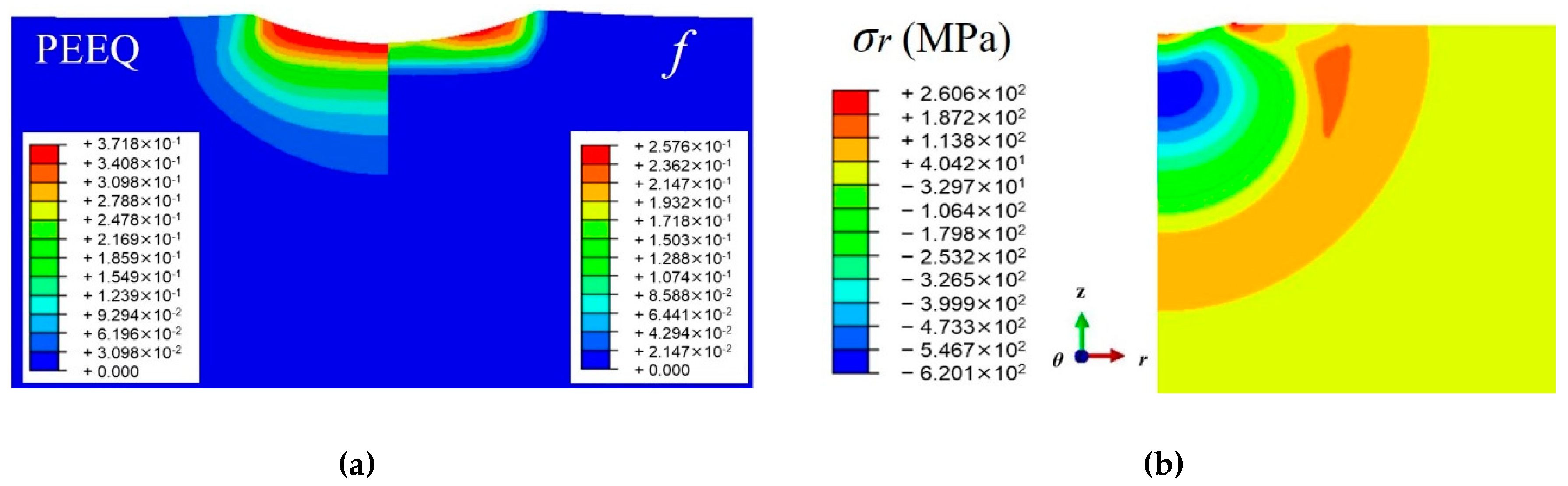
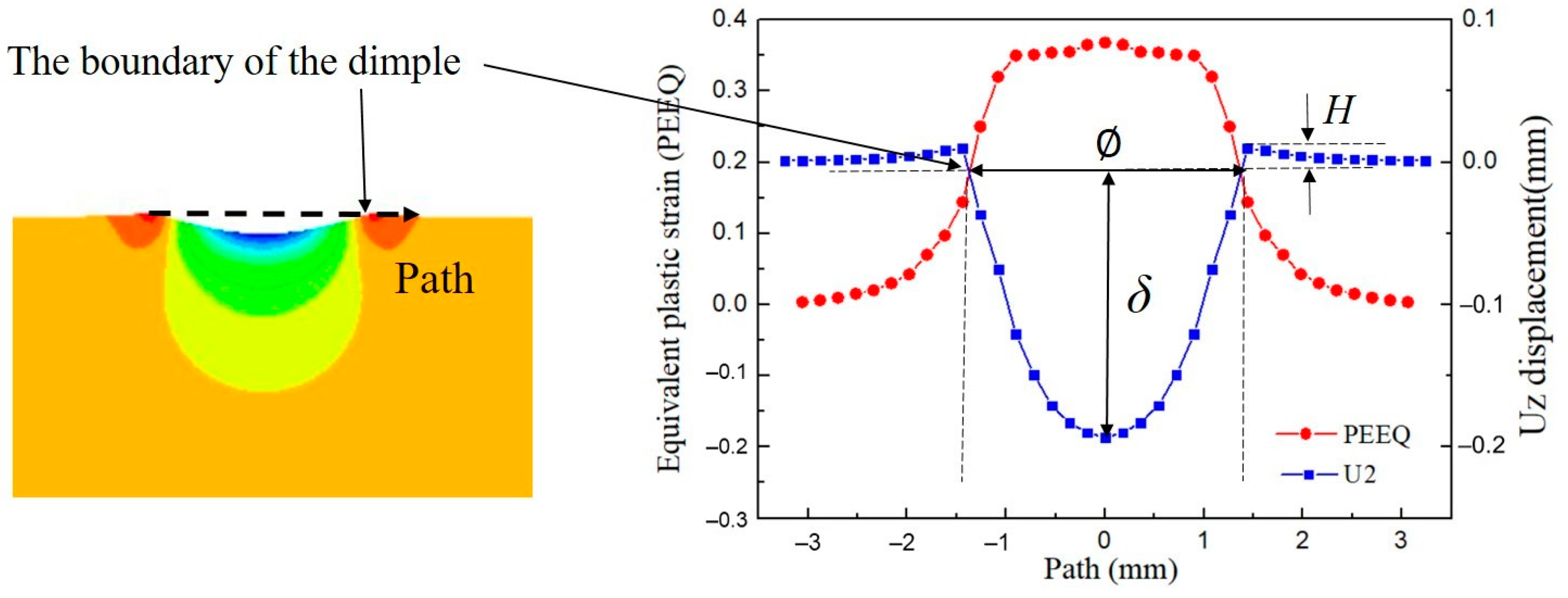
4.1. Single Shot-Peening Simulation
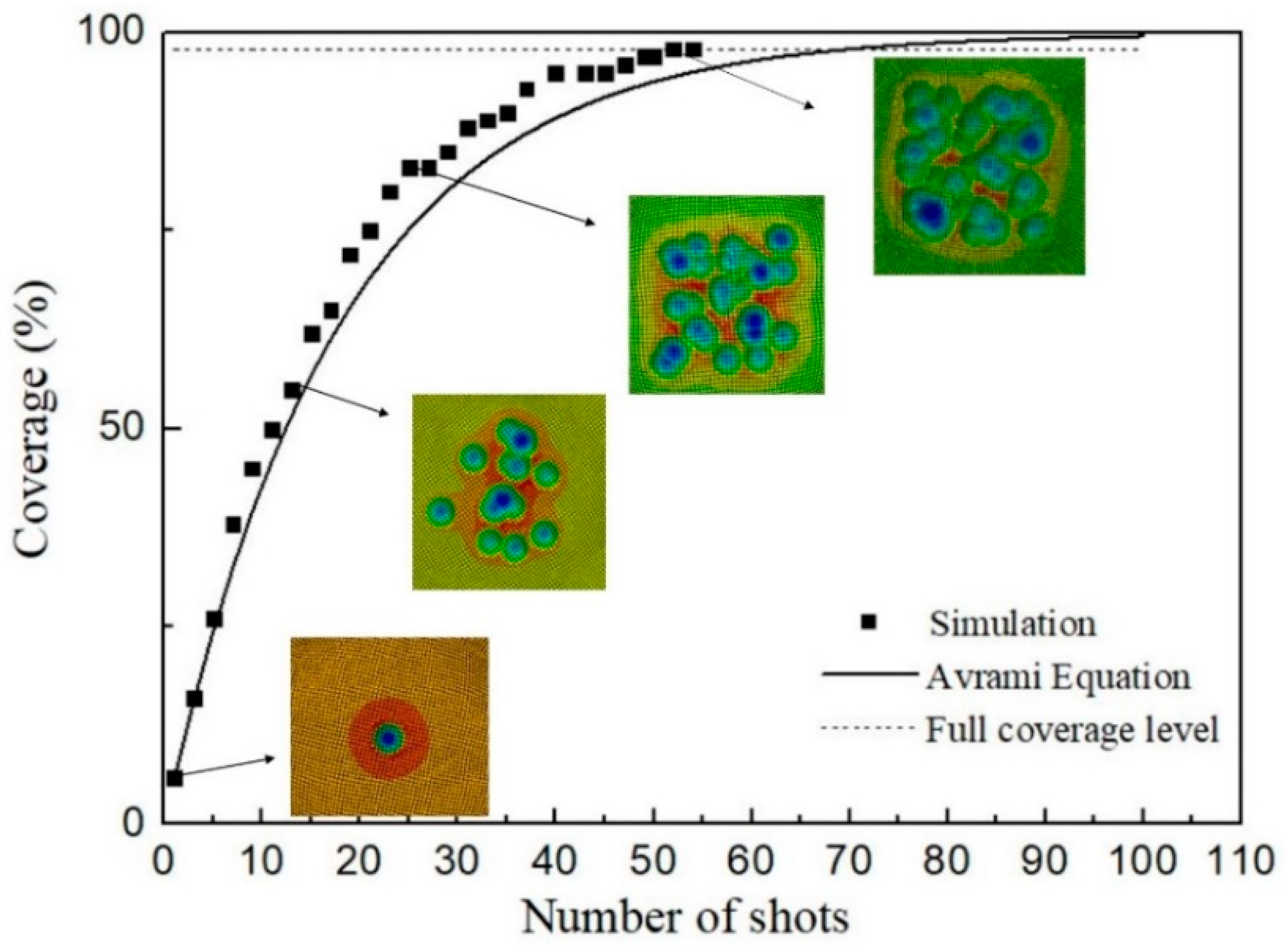
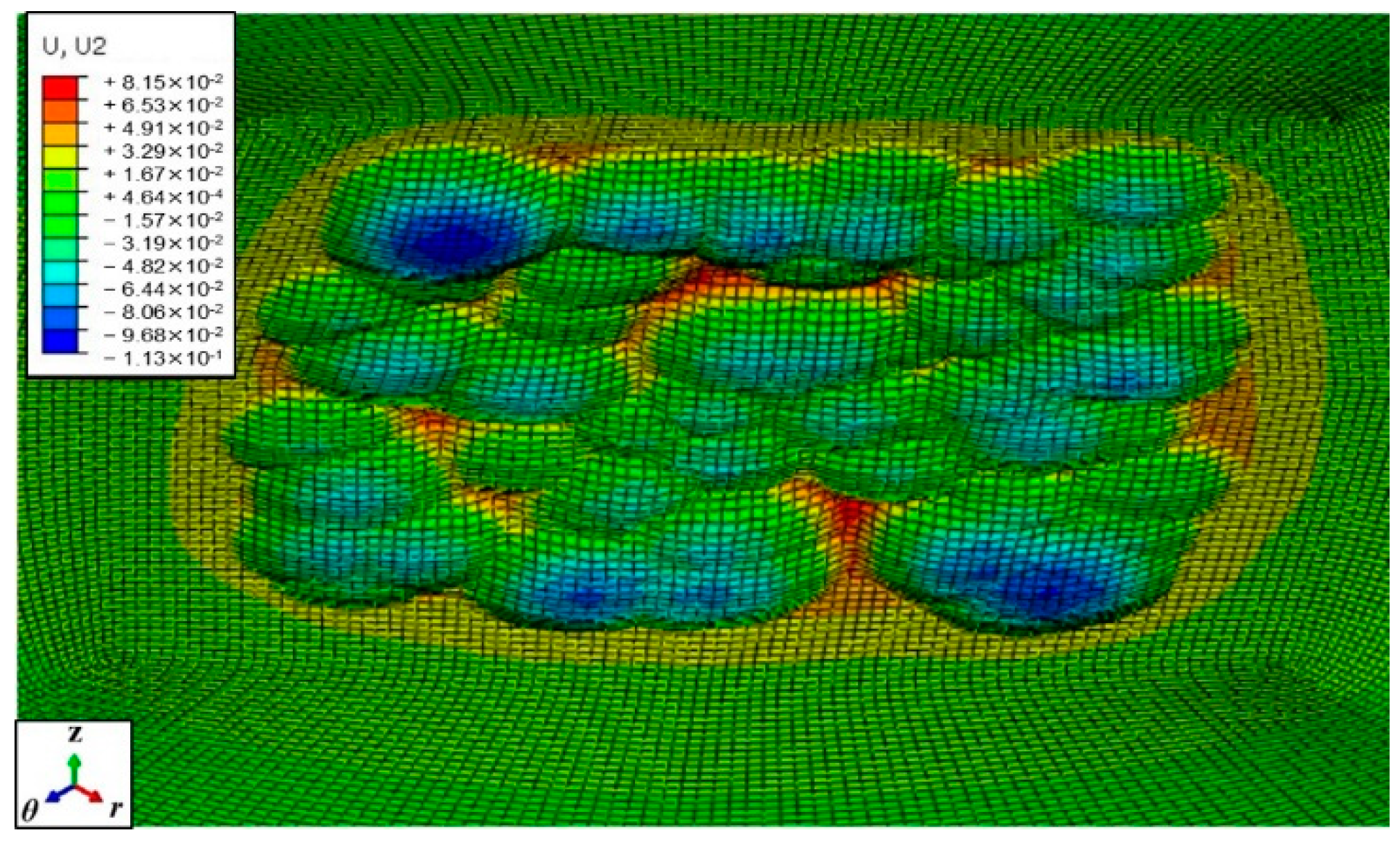
4.2. Surface Coverage by Random Multiple Shots Simulation
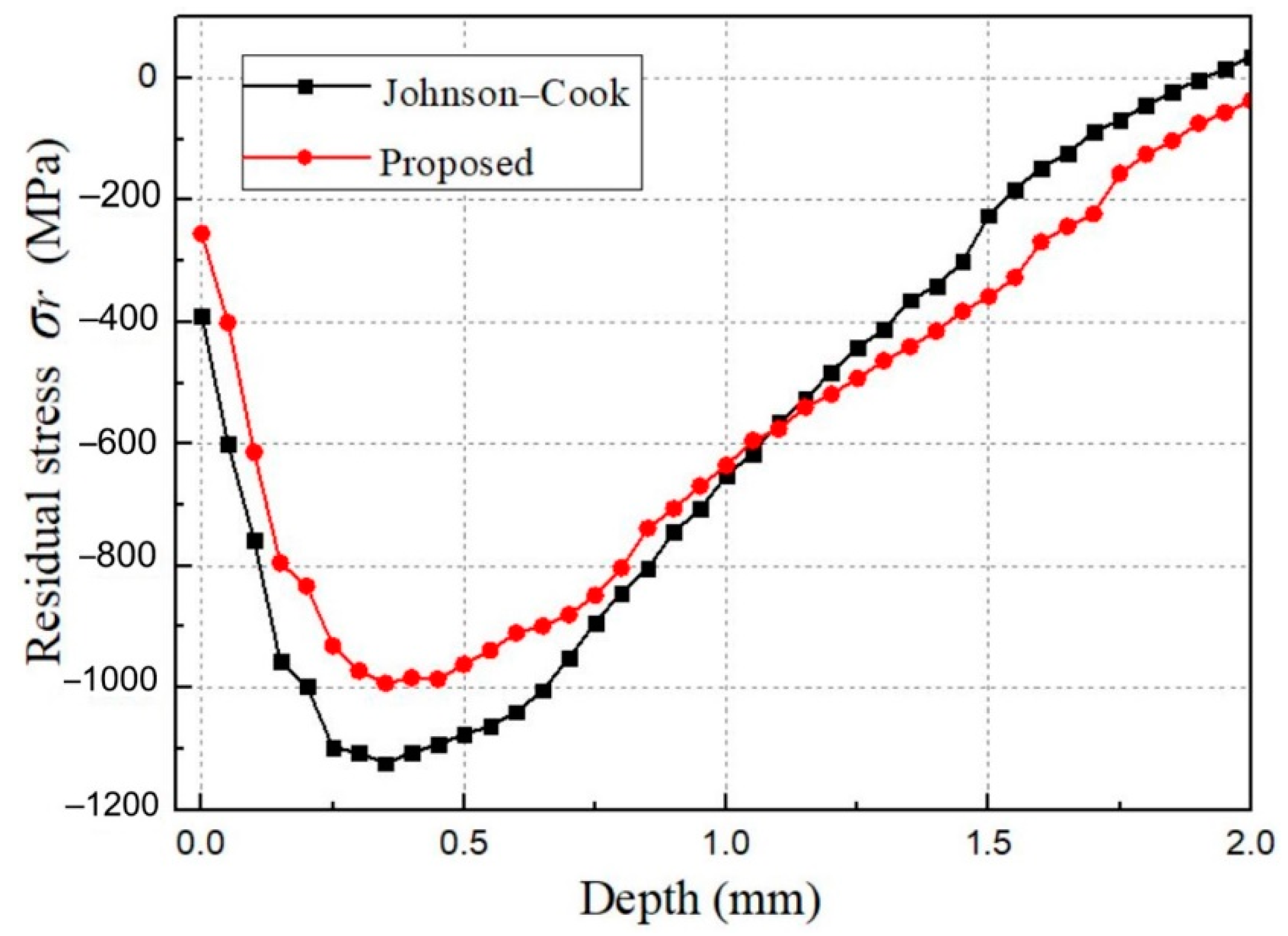
4.3. Residual Stress Field by Random Multiple Shots Simulation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Computational Model
References
- Lv, Y.; Lei, L.; Sun, L. Influence of different combined severe shot peening and laser surface melting treatments on the fatigue performance of 20CrMnTi steel gear. Mat. Sci. Eng. A 2016, 658, 77–85. [Google Scholar] [CrossRef]
- Ciuffini, A.F.; Barella, S.; Peral Martínez, L.B.; Mapelli, C.; Fernández Pariente, I. Influence of Microstructure and Shot Peening Treatment on Corrosion Resistance of AISI F55-UNS S32760 Super Duplex Stainless Steel. Materials 2018, 11, 1038. [Google Scholar] [CrossRef] [PubMed]
- González, J.; Bagherifard, S.; Guagliano, M.; Fernández Pariente, I. Influence of different shot peening treatments on surface state and fatigue behaviour of Al 6063 alloy. Eng. Fract. Mech. 2017, 185, 72–81. [Google Scholar] [CrossRef]
- Bhuvaraghan, B.; Srinivasan, S.M.; Maffeo, B.; Mcclain, R.D.; Potdar, Y.; Prakash, O. Shot peening simulation using discrete and finite element methods. Adv. Eng. Softw. 2010, 41, 1266–1276. [Google Scholar] [CrossRef]
- Fargas, G.; Roa, J.J.; Mateo, A. Effect of shot peening on metastable austenitic stainless steels. Mat. Sci. Eng. A 2015, 641, 290–296. [Google Scholar] [CrossRef] [Green Version]
- Kang, J.Y.; Kim, H.; Kyung-Il, K.; Lee, C.H.; Han, H.N.; Oh, K.H.; Lee, T.H. Effect of austenitic texture on tensile behavior of lean duplex stainless steel with transformation induced plasticity (TRIP). Mat. Sci. Eng. A 2016, 681, 114–120. [Google Scholar] [CrossRef]
- Olson, G.B.; Cohen, M. Kinetics of strain-induced martensitic nucleation. Metall. Trans. A 1975, 6, 791–795. [Google Scholar] [CrossRef]
- Greenwood, G.W.; Johnson, R.H. The Deformation of Metals under Small Stresses during Phase Transformations. Proc. R. Soc. Lond. 1965, 283, 403–422. [Google Scholar] [CrossRef]
- Magee, C. Transformation Kinetics, Microplasticity and Ageing of Martensite in fe-3lni. Ph.D. Thesis, Carnegie Institute of Technologie University, Pittsburgh, PA, USA, 1966. [Google Scholar]
- Bobbili, R.; Madhu, V. A Modified Johnson-Cook Model for FeCoNiCr high entropy alloy over a wide range of strain rates. Mater. Lett. 2018, 218, 103–105. [Google Scholar] [CrossRef]
- Hernandez, C.; Maranon, A.; Ashcroft, I.A.; Cacas-Rodriguez, J.P. A computational determination of the Cowper–Symonds parameters from a single Taylor test. Appl. Math. Model. 2013, 37, 4698–4708. [Google Scholar] [CrossRef]
- Wolff, M.; Suhr, B.; Şimşir, C. Parameter identification for an Armstrong–Frederick hardening law for supercooled austenite of SAE 52100 steel. Comp. Mater. Sci. 2011, 50, 487–495. [Google Scholar] [CrossRef]
- Li, J.; Li, Q.; Jiang, J.; Dai, J. Particle swarm optimization procedure in determining parameters in Chaboche kinematic hardening model to assess ratcheting under uniaxial and biaxial loading cycles. Fatigue Fract. Eng. Mater. 2018, 41, 1637–1645. [Google Scholar] [CrossRef]
- Zaera, R.; Rodríguez-Martínez, J.A.; Casado, A.; Fernández-Sáez, J.; Rusinek, A.; Pesci, R. A constitutive model for analyzing martensite formation in austenitic steels deforming at high strain rates. Int. J. Plast. 2012, 29, 77–101. [Google Scholar] [CrossRef] [Green Version]
- Post, J.; Datta, K.; Beyer, J. A macroscopic constitutive model for a metastable austenitic stainless steel. Mater. Sci. Eng. A 2008, 485, 290–298. [Google Scholar] [CrossRef]
- Papatriantafillou, I.; Agoras, M.; Aravas, N.; Haidemenopoulos, G. Constitutive modeling and finite element methods for TRIP steels. Comput. Methods Appl. Mech. Eng. 2006, 195, 5094–5114. [Google Scholar] [CrossRef]
- Beese, A.M.; Mohr, D. Anisotropic plasticity model coupled with Lode angle dependent strain-induced transformation kinetics law. J. Mech. Phys. Solids 2012, 60, 1922–1940. [Google Scholar] [CrossRef]
- Santacreu, P.O.; Glez, J.C.; Chinouilh, G.; Froehlich, T. Behaviour Model of Austenitic Stainless Steels for Automotive Structural Parts. Steel Res. Int. 2006, 77, 686–691. [Google Scholar] [CrossRef]
- Sanjurjo, P.; Rodríguez, C.; Peñuelas, I.; García, T.E.; Belzunce, F.J. Influence of the target material constitutive model on the numerical simulation of a shot peening process. Surf. Coat. Technol. 2014, 258, 822–831. [Google Scholar] [CrossRef]
- Guiheux, R.; Berveiller, S.; Kubler, R.; Bouscaud, D.; Patoor, E.; Patoor, Q. Martensitic transformation induced by single shot peening in a metastable austenitic stainless steel 301LN: Experiments and numerical simulation. J. Mater. Process. Technol. 2017, 249, 339–349. [Google Scholar] [CrossRef] [Green Version]
- Mori, K.; Osakada, K.; Matsuoka, N. Finite element analysis of peening process with plastically deforming shot. J. Mater. Process. Technol. 1994, 45, 607–612. [Google Scholar] [CrossRef]
- Meguid, S.A.; Shagal, G.; Stranart, J.C. 3D FE analysis of peening of strain-rate sensitive materials using multiple impingement model. Int. J. Impact Eng. 2002, 27, 119–134. [Google Scholar] [CrossRef]
- Schiffner, K.K.; Helling, C.D.G. Simulation of residual stresses by shot peening. Comput. Struct. 1999, 72, 329–340. [Google Scholar] [CrossRef]
- Guagliano, M. Relating Almen intensity to residual stresses induced by shot peening: A numerical approach. J. Mater. Process. Technol. 2001, 110, 277–286. [Google Scholar] [CrossRef]
- Baragetti, S. Three-dimensional finite element procedures for shot peening residual stress field prediction. Int. J. Comput. Appl. Technol. 2001, 14, 51–63. [Google Scholar] [CrossRef]
- Schwarzer, J.; Schulze, V.; Vöringer, O. Evaluation of the influence of shot peening parameters on residual stress profiles using finite element simulation. Mater. Sci. Forum 2003, 426, 3951–3956. [Google Scholar] [CrossRef]
- Miao, H.Y.; Larose, S.; Perron, C.; Lévesque, M. On the potential applications of a 3D random finite element model for the simulation of shot peening. Adv. Eng. Softw. 2009, 40, 1023–1038. [Google Scholar] [CrossRef]
- Gangaraj, S.M.H.; Guagliano, M.; Farrahi, G.H. An approach to relate shot peening finite element simulation to the actual coverage. Surf. Coat. Technol. 2014, 243, 39–45. [Google Scholar] [CrossRef]
- Wang, X.; Li, F.; Yang, Q.; He, A. FEM analysis for residual stress prediction in hot rolled steel strip during the run-out table cooling. Appl. Math. Model. 2013, 37, 586–609. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of Phase Change. I General Theory. J. Chem. Phys. 1939, 7, 1103–1112. [Google Scholar] [CrossRef]
- Frija, M.; Hassine, T.; Fathallah, R.; Bouraoui, C.; Dogui, A.; Mécanique, L.G. Finite element modelling of shot peening process: Prediction of the compressive residual stresses, the plastic deformations and the surface integrity. Mat. Sci. Eng. A 2006, 426, 173–180. [Google Scholar] [CrossRef]
- Klemenz, M.; Schulze, V.; Vöhringer, O.; Löhe, D. Finite Element Simulation of the Residual Stress States after Shot Peening. Mater. Sci. Forum 2006, 524, 349–354. [Google Scholar] [CrossRef]
- Bagherifard, S.; Ghelichi, R.; Guagliano, M. A numerical model of severe shot peening (SSP) to predict the generation of a nanostructured surface layer of material. Surf. Coat. Technol. 2010, 204, 4081–4090. [Google Scholar] [CrossRef]
- Hribernik, A.; Bombek, G.; Markocic, I. Velocity measurements in a shotblasting machine. Flow Meas. Instrum. 2003, 14, 225–231. [Google Scholar] [CrossRef]
- Bombek, G.; Hribernik, A. Measuring the velocities of particles in a shot-blasting chamber. Meas. Sci. Technol. 2010, 21, 085101. [Google Scholar] [CrossRef]
- Miao, H.Y.; Demers, D.; Larose, S.; Perron, C.; Lévesque, M. Experimental study of shot peening and stress peen forming. J. Mater. Process. Technol. 2010, 210, 2089–2102. [Google Scholar] [CrossRef]
- Karuppanan, S. A theoretical and experimental investigation into the development of coverage in shot peening. J. Polym. Sci. A 2000, 49, 3863–3873. [Google Scholar] [CrossRef]
- Pour-Ali, S.; Kiani-Rashid, A.R.; Babakhani, A.; Virtanen, S.; Allieta, M. Correlation between the surface coverage of severe shot peening and surface microstructural evolutions in AISI 321: A TEM, FE-SEM and GI-XRD study. Surf. Coat. Technol. 2018, 334, 461–470. [Google Scholar] [CrossRef]
- SAE Standard J2277. Shot Peening Coverage; Surface Enhancement Committee: Warrendale, PA, USA, 2003. [Google Scholar]





| r/MPa | θ | σ0/MPa | hε/MPa | a | hf/MPa | D0 | D1 | fmax | m |
|---|---|---|---|---|---|---|---|---|---|
| 2 | 767 | 963 | 103 | 5.6 | 396 | 6.0 | 3.0 | 1.0 | 1.5 |
| r/MPa | θ | σ0/MPa | hε/MPa | C | a | hf/MPa |
|---|---|---|---|---|---|---|
| 2.5 | 300 | 350 | 301 | 0.013 | 8.37 | 470 |
| n | D0 | D1 | fmax | m | βx | M |
| 0.97 | 2.62 | 0.6 | 0.99 | 2.22 | 1.0 | 5.9 × 10−11 |
| A/MPa | B/MPa | C | n |
|---|---|---|---|
| 350 | 420 | 0.015 | 0.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, F.; Jiang, W.; Du, Y.; Xiao, C. A Comprehensive Numerical Approach for Analyzing the Residual Stresses in AISI 301LN Stainless Steel Induced by Shot Peening. Materials 2019, 12, 3338. https://doi.org/10.3390/ma12203338
Zhou F, Jiang W, Du Y, Xiao C. A Comprehensive Numerical Approach for Analyzing the Residual Stresses in AISI 301LN Stainless Steel Induced by Shot Peening. Materials. 2019; 12(20):3338. https://doi.org/10.3390/ma12203338
Chicago/Turabian StyleZhou, Fan, Wenchun Jiang, Yang Du, and Chengran Xiao. 2019. "A Comprehensive Numerical Approach for Analyzing the Residual Stresses in AISI 301LN Stainless Steel Induced by Shot Peening" Materials 12, no. 20: 3338. https://doi.org/10.3390/ma12203338
APA StyleZhou, F., Jiang, W., Du, Y., & Xiao, C. (2019). A Comprehensive Numerical Approach for Analyzing the Residual Stresses in AISI 301LN Stainless Steel Induced by Shot Peening. Materials, 12(20), 3338. https://doi.org/10.3390/ma12203338





