A Finite Element Model for the Vibration Analysis of Sandwich Beam with Frequency-Dependent Viscoelastic Material Core
Abstract
:1. Introduction
2. Finite Element Methods for a Sandwich Beam with a Frequency-Dependent Viscoelastic Material
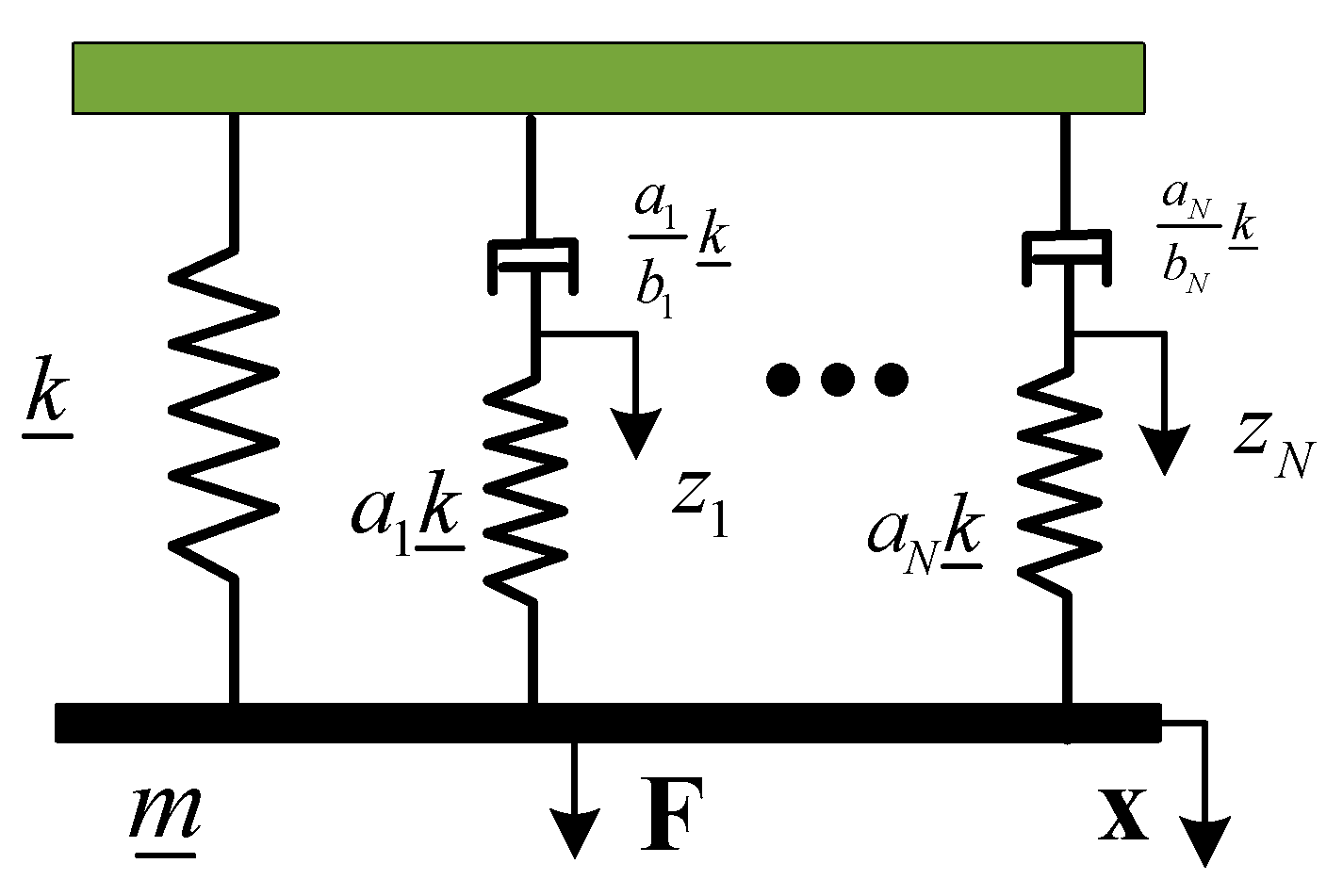
2.1. Viscoelastic Models Using Biot Methods
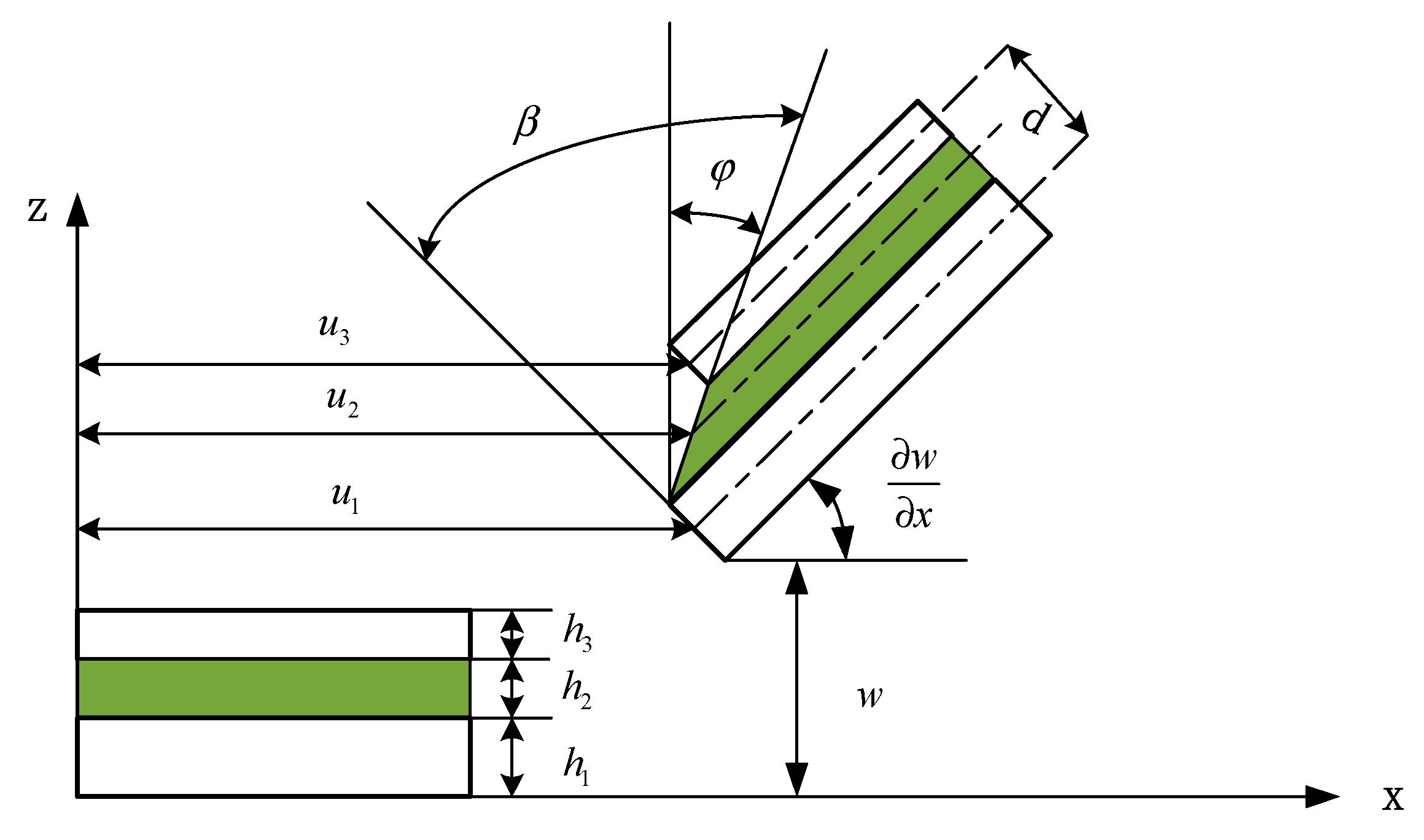
2.2. Assumptions of a Sandwich Beam
- (1)
- The constraining layer and the base beam satisfy two hypotheses of the Euler–Bernoulli beam theory, that is, the section perpendicular to the centerline of the beam is still planar after deformation (assumption of rigid cross section) and after deformation, the plane of the cross section is still perpendicular to the deformed axis.
- (2)
- Regardless of the vertical transverse compression deformation, the base beam layer, the damping layer, and the constraining layer is considered to have the same deflection.
- (3)
- The influence of moment of inertia is negligible relative to bending and tensile deformation of the elastic layers and the shear deformation of the viscoelastic layer. Therefore, in order to simplify the modeling process, the moment of inertia is ignored.
- (4)
- The layers of the materials are firmly bonded and there is no relative sliding between the layers.
2.3. Kinematics
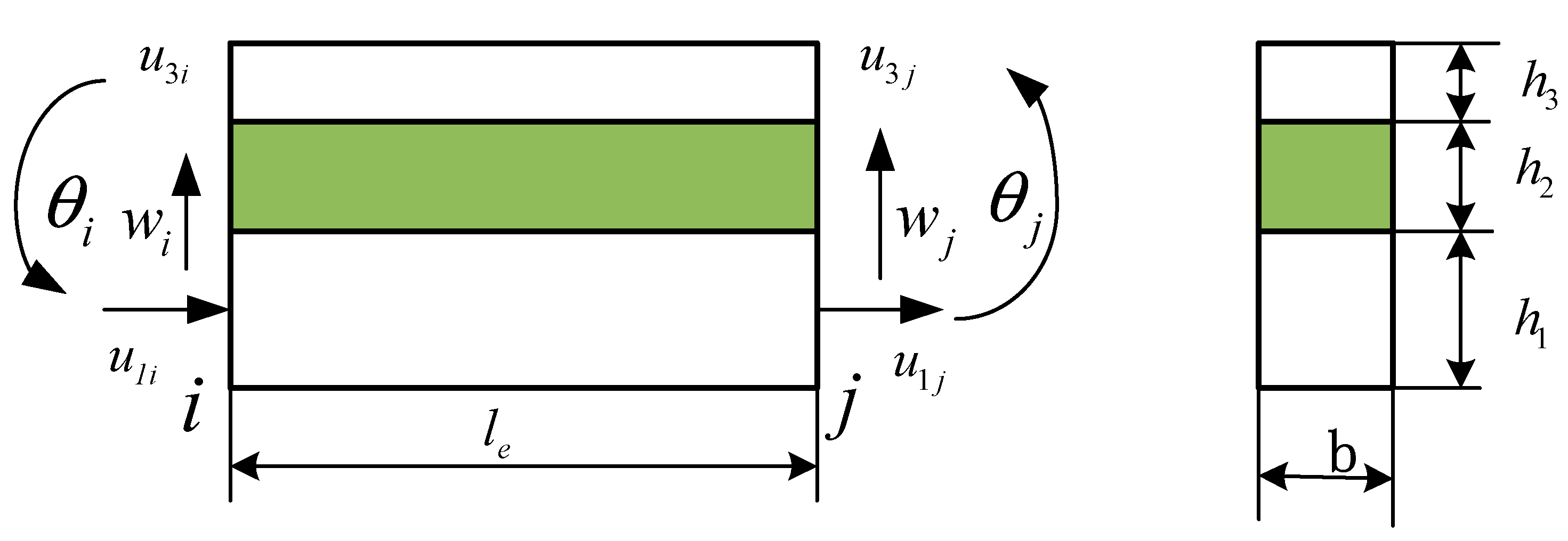
2.4. Degrees of Freedom and Shape Functions
2.5. Energy Terms
2.5.1. The Strain Energy
2.5.2. The Kinetic Energy
2.6. Equation of Motion with Viscoelastic Damping
3. Numerical Simulation and Experimental Validation
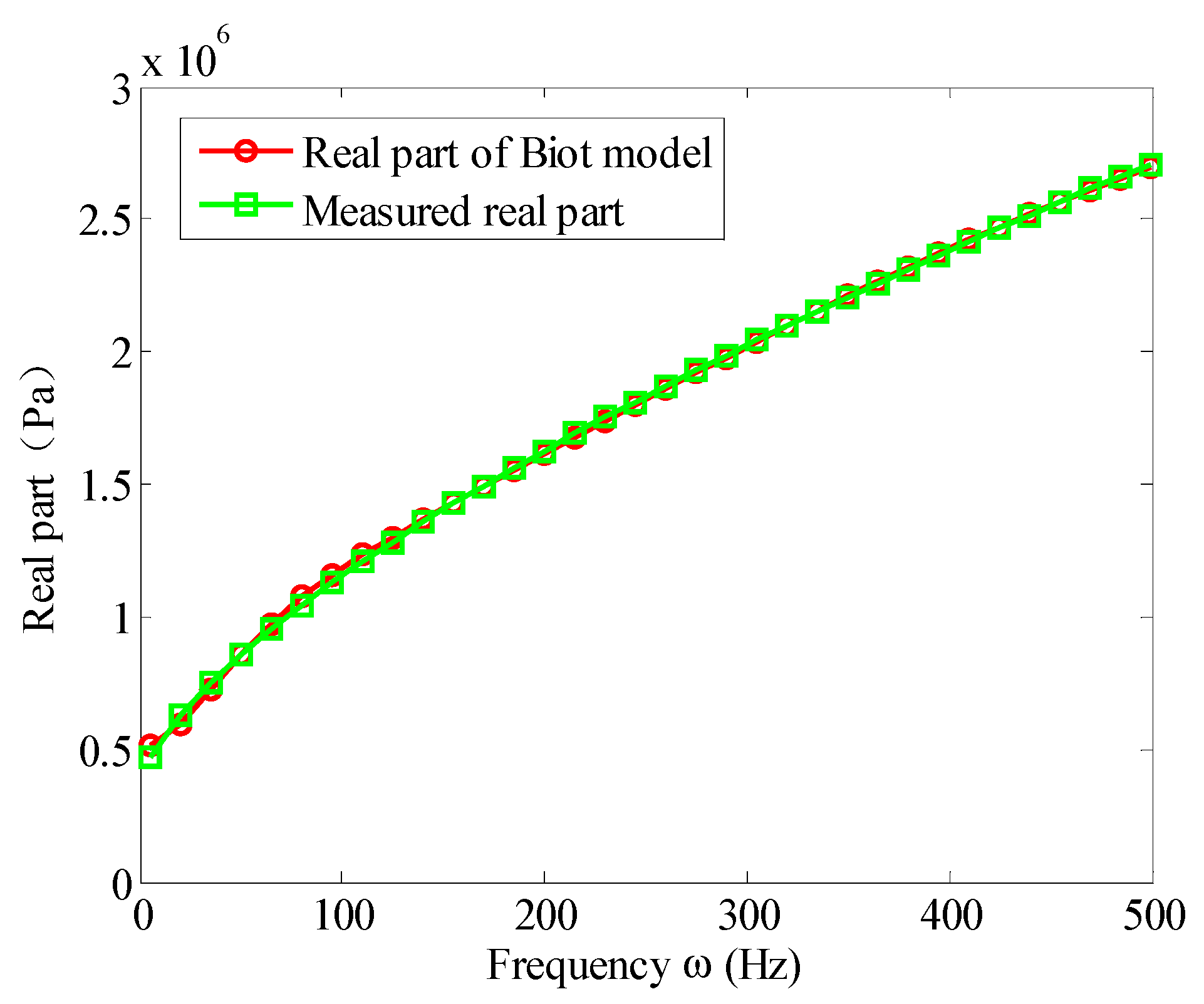
3.1. Curve Fits for Biot Model Parameter
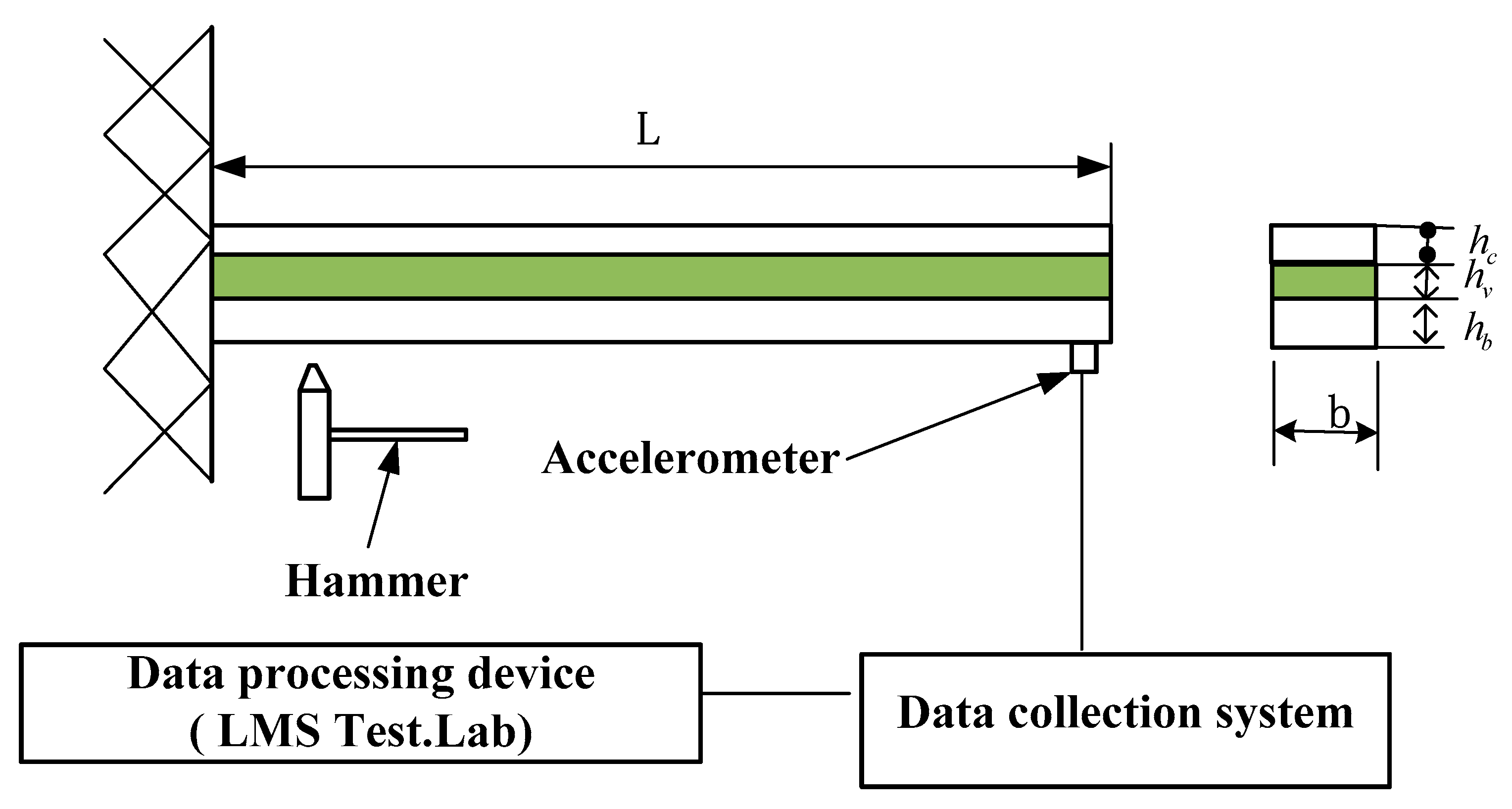
3.2. Experimental Validation of the Sandwich Composite Cantilever Beam
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Qin, Z.; Pang, X.; Safaei, B.; Chu, F. Free vibration analysis of rotating functionally graded CNT reinforced composite cylindrical shells with arbitrary boundary conditions. Compos. Struct. 2019, 220, 847–860. [Google Scholar] [CrossRef]
- Du, S.; An, F.; Liu, B. On the sound transmission loss of finite plates with constrained viscoelastic layer. Appl. Acoust. 2019, 149, 32–38. [Google Scholar] [CrossRef]
- Deepak, K.B.; Sukesh, C.M. Free vibration study of multilayer sandwich spherical shell panels with viscoelastic core and isotropic/laminated face layers. Compos. Part B Eng. 2019, 159, 72–85. [Google Scholar]
- Nashif, A.D.; Jones, D.I.G.; Henderson, J.P. Vibration Damping; John Wiley & Sons: New York, NY, USA, 1985. [Google Scholar]
- Jones, D.I.G. Handbook of Viscoelastic Vibration Damping; John Wiley & Sons: Chichester, UK, 2001. [Google Scholar]
- Jones, D.I.G. On temperature-frequency analysis of polymer dynamic mechanical behavior. J. Sound Vib. 1990, 140, 85–102. [Google Scholar] [CrossRef]
- Kerwin, E.M., Jr. Damping of flexural waves by a constrained viscoelastic layer. J. Acoust. Soc. Am. 1959, 31, 952–962. [Google Scholar] [CrossRef]
- DiTaranto, R.A. Theory of vibratory bending for elastic and viscoelastic layered finite-length beams. J. Appl. Mech. 1965, 32, 881–886. [Google Scholar] [CrossRef]
- Mead, D.J.; Markus, S. The forced vibration of a three-layer, damped sandwich beam with arbitrary boundary conditions. J. Sound Vib. 1969, 10, 163–175. [Google Scholar] [CrossRef]
- Yan, M.J.; Dowell, E.H. Governing equations for vibrating constrained-layer damping sandwich plates and beams. J. Appl. Mech. Trans. ASME 1972, 39, 1041–1046. [Google Scholar] [CrossRef]
- Park, S.W. Analytical modeling of viscoelastic dampers for structure and vibration control. Int. J. Solids Struct. 2001, 38, 8065–8092. [Google Scholar] [CrossRef]
- Zhai, Y.C.; Li, Y.; Lian, S. Free vibration analysis of five-layered composite sandwich plates with two layered viscoelastic cores. Compos. Struct. 2018, 200, 346–357. [Google Scholar] [CrossRef]
- Rezvani, S.S.; Kiasat, M.S. Analytical and experimental investigation on the free vibration of a floating composite sandwich plate having viscoelastic core. Arch. Civ. Mech. Eng. 2018, 18, 1241–1258. [Google Scholar] [CrossRef]
- Manex, M.A.; Elejabarrieta, M.J. Dynamic characterization of high damping viscoelastic materials from vibration test data. J. Sound Vib. 2011, 330, 3930–3943. [Google Scholar]
- Liu, Q.; Xu, Y.; Kurths, J. Active vibration suppression of a novel airfoil model with fractional order viscoelastic constitutive relationship. J. Sound Vib. 2018, 432, 50–64. [Google Scholar] [CrossRef]
- Lewandowski, R.; Wielentejczyk, P. Nonlinear vibration of viscoelastic beams described using fractional order derivatives. J. Sound Vib. 2017, 399, 228–243. [Google Scholar] [CrossRef]
- Lin, R.M. Comments on “Nonlinear vibration of viscoelastic beams described using fractional order derivatives”. J. Sound Vib. 2018, 428, 195–204. [Google Scholar] [CrossRef]
- Johnson, C.D.; Kienholz, D.A. Finite element prediction of damping in structures with constrained viscoelastic layers. AIAA J. 1982, 20, 1284–1290. [Google Scholar]
- Mace, M. Damping of beam vibrations by means of a thin constrained viscoelastic layer: Evaluation of a new theory. J. Sound Vib. 1994, 172, 577–591. [Google Scholar] [CrossRef]
- Baber, T.T.; Maddox, R.A.; Orozco, C.E. A finite element model for harmonically excited viscoelastic sandwich beams. Comput. Struct. 1998, 66, 105–113. [Google Scholar] [CrossRef]
- Chen, Q.; Chan, Y.W. Integral finite element method for dynamical analysis of elastic-viscoelastic composite structures. Comput. Struct. 2000, 74, 51–64. [Google Scholar] [CrossRef]
- Park, C.H.; Baz, A. Comparison between finite element formulations of active constrained layer damping using classical and layer-wise laminate theory. Finite Elem. Anal. Des. 2001, 37, 35–56. [Google Scholar] [CrossRef]
- Daya, E.M.; Potier-Ferry, M. A shell finite element for viscoelastically damped sandwich structures. Rev. Eur. Élém. 2002, 11, 39–56. [Google Scholar] [CrossRef]
- Adhikari, S.; Manohar, C. Transient dynamics of stochastically parametered beams. J. Eng. Mech. 2000, 126, 1131–1140. [Google Scholar] [CrossRef]
- Druesne, F.; Hamdaoui, M.; Lardeur, P.; Daya, E.M. Variability of dynamic responses of frequency dependent viscoelastic sandwich beams with material and physical properties modeled by spatial random fields. Compos. Struct. 2016, 152, 316–323. [Google Scholar] [CrossRef]
- Golla, D.F.; Hughes, P.C. Dynamics of viscoelastic structure- a time-domain, finite element formulation. J. Appl. Mech. 1985, 52, 897–906. [Google Scholar] [CrossRef]
- Mctavish, J.; Hughes, P.C. Prediction and Measurement of Modal Damping Factors for Viscoelastic Space Structures. AIAA J. 1992, 30, 1392–1399. [Google Scholar] [CrossRef]
- McTavish, D.J.; Hughes, P.C. Modeling of linear viscoelastic space structures. J. Vib. Acoust. 1993, 115, 103–110. [Google Scholar] [CrossRef]
- Park, C.H.; Inman, D.J.; Lam, M.J. Model reduction of viscoelastic finite element models. J. Sound Vib. 1999, 219, 619–637. [Google Scholar] [CrossRef]
- Trindade, M.A.; Benjeddou, A.; Ohayon, R. Piezoelectric active vibration control of damped sandwich beams. J. Sound Vib. 2001, 246, 653–677. [Google Scholar] [CrossRef]
- Barbosa, F.S.; Farage, M. A finite element model for sandwich viscoelastic beams: Experimental and numerical assessment. J. Sound Vib. 2008, 317, 91–111. [Google Scholar] [CrossRef]
- Lesieutre, G.A.; Lee, U. Finite element for beams having segmented active constrained layers with frequency-dependent viscoelastics. Smart Mater. Struct. 1996, 5, 615–627. [Google Scholar] [CrossRef]
- Lesieutre, G.A.; Bianchini, E.; Maiani, A. Finite element modeling of one-dimensional viscoelastic structures using anelastic displacement fields. J. Guid. Control Dynam. 1996, 19, 520–527. [Google Scholar] [CrossRef]
- Wang, Y.; Inman, D.J. Finite element analysis and experimental study on dynamic properties of a composite beam with viscoelastic damping. J. Sound Vib. 2013, 332, 6177–6191. [Google Scholar] [CrossRef]
- Biot, M.A. Variational principles in irreversible thermodynamics with application to viscoelasticity. Phys. Rev. 1955, 97, 1463–1469. [Google Scholar] [CrossRef]




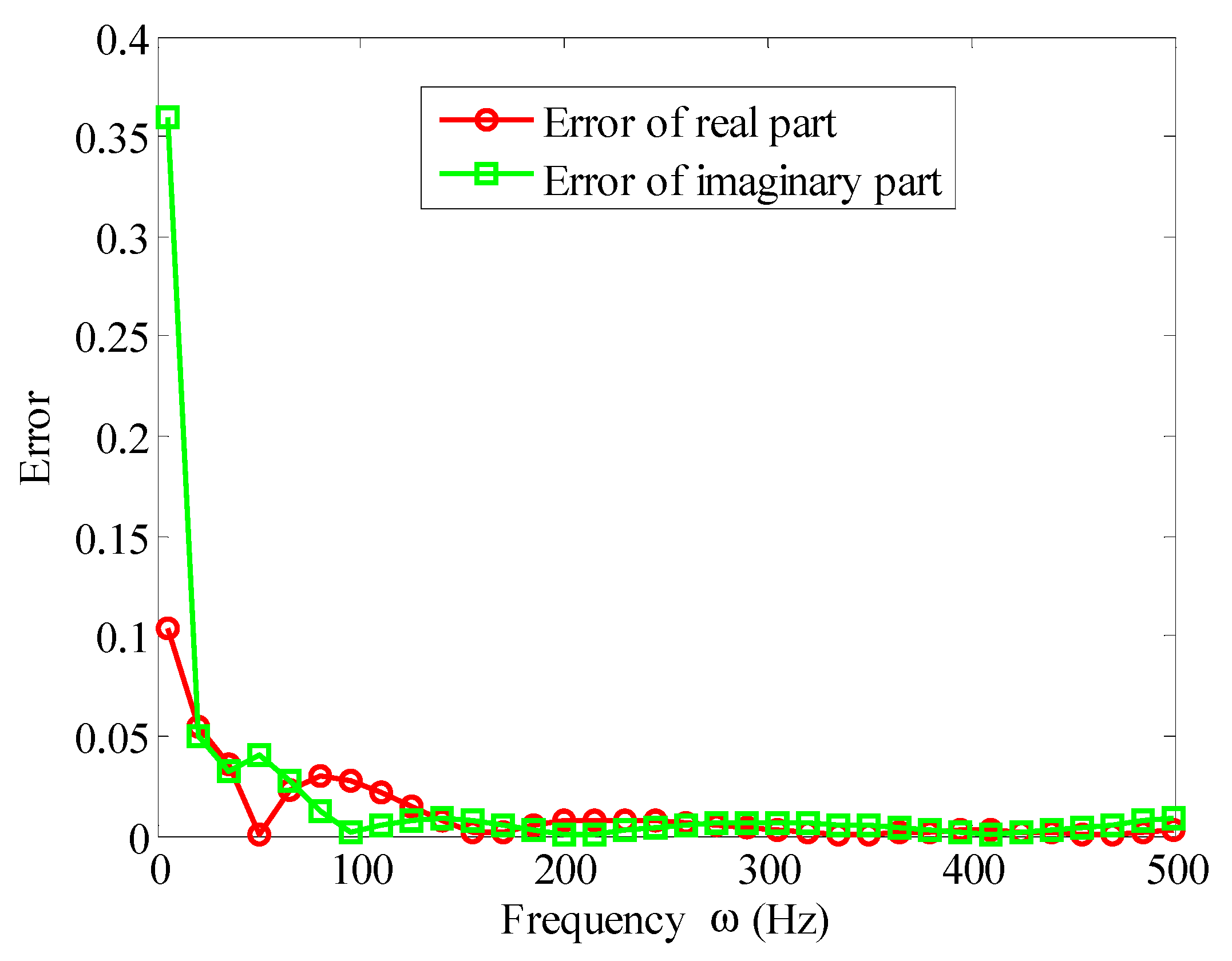
| Frequency (Hz) | 5 | 10 | 30 | 60 | 100 | 150 | 200 | 220 | 240 |
| The storage modulus (MPa) | 0.51 | 0.62 | 0.91 | 1.1 | 1.43 | 1.71 | 1.92 | 1.73 | 1.76 |
| Loss factor | 0.63 | 0.75 | 0.9 | 1.03 | 1.12 | 1.18 | 1.2 | 1.2 | 1.21 |
| Frequency (Hz) | 270 | 300 | 340 | 360 | 400 | 440 | 460 | 500 | 600 |
| The storage modulus (MPa) | 1.79 | 1.82 | 1.84 | 1.88 | 1.92 | 2.1 | 2.15 | 2.27 | 3.23 |
| Loss factor | 1.2 | 1.22 | 1.21 | 1.21 | 1.21 | 1.21 | 1.22 | 1.22 | 1.23 |
| Parameters | |||
|---|---|---|---|
| G∞ | 5.1e5 | ||
| ak | 1.4406 | 4.9338 | 202.3130 |
| bk | 359.5605 | 2834.2208 | 114811.7290 |
| Material Properties | Constraining Layer (Aluminum) | Base Beam(Aluminum) | Viscoelastic Layer (ZN-1 ) |
|---|---|---|---|
| Elastic Modulus (GPa ) | 69 | 69 | Table 2 |
| density (kg/m3 ) | 2700 | 2700 | 1010 |
| Poisson’s ratio | 0.3 | 0.3 | 0.3 |
| Thickness (mm) | 0.78 | 1.91 | 0.40 |
| Length (mm) | 290 | 290 | 290 |
| Width (mm) | 25 | 25 | 25 |
| Order | Experimental Result | Finite Element Model This Paper | ||||
|---|---|---|---|---|---|---|
| Natural Frequency (Hz) | Natural Frequency (Hz) | Error (%) | Error (%) | |||
| 1 | 24.3 | 0.1123 | 25.1 | 3.29 | 0.1152 | 2.58 |
| 2 | 151.5 | 0.2784 | 145.8 | 3.78 | 0.2910 | 4.53 |
| 3 | 390.5 | 0.3212 | 375.7 | 3.79 | 0.3362 | 3.87 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Wang, X.; Wu, N.; Chu, F.; Luo, J. A Finite Element Model for the Vibration Analysis of Sandwich Beam with Frequency-Dependent Viscoelastic Material Core. Materials 2019, 12, 3390. https://doi.org/10.3390/ma12203390
Huang Z, Wang X, Wu N, Chu F, Luo J. A Finite Element Model for the Vibration Analysis of Sandwich Beam with Frequency-Dependent Viscoelastic Material Core. Materials. 2019; 12(20):3390. https://doi.org/10.3390/ma12203390
Chicago/Turabian StyleHuang, Zhicheng, Xingguo Wang, Nanxing Wu, Fulei Chu, and Jing Luo. 2019. "A Finite Element Model for the Vibration Analysis of Sandwich Beam with Frequency-Dependent Viscoelastic Material Core" Materials 12, no. 20: 3390. https://doi.org/10.3390/ma12203390




