Bending Fatigue Behaviors Analysis and Fatigue Life Prediction of 20Cr2Ni4 Gear Steel with Different Stress Concentrations near Non-metallic Inclusions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials and Specimens
2.2. Experimental Procedures
3. Experimental Results
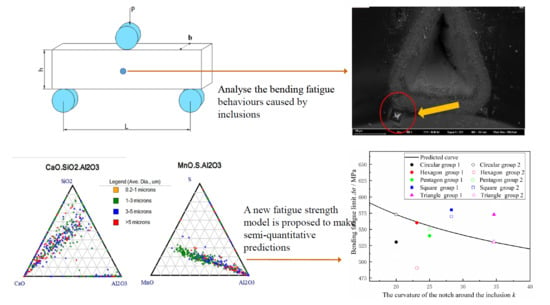
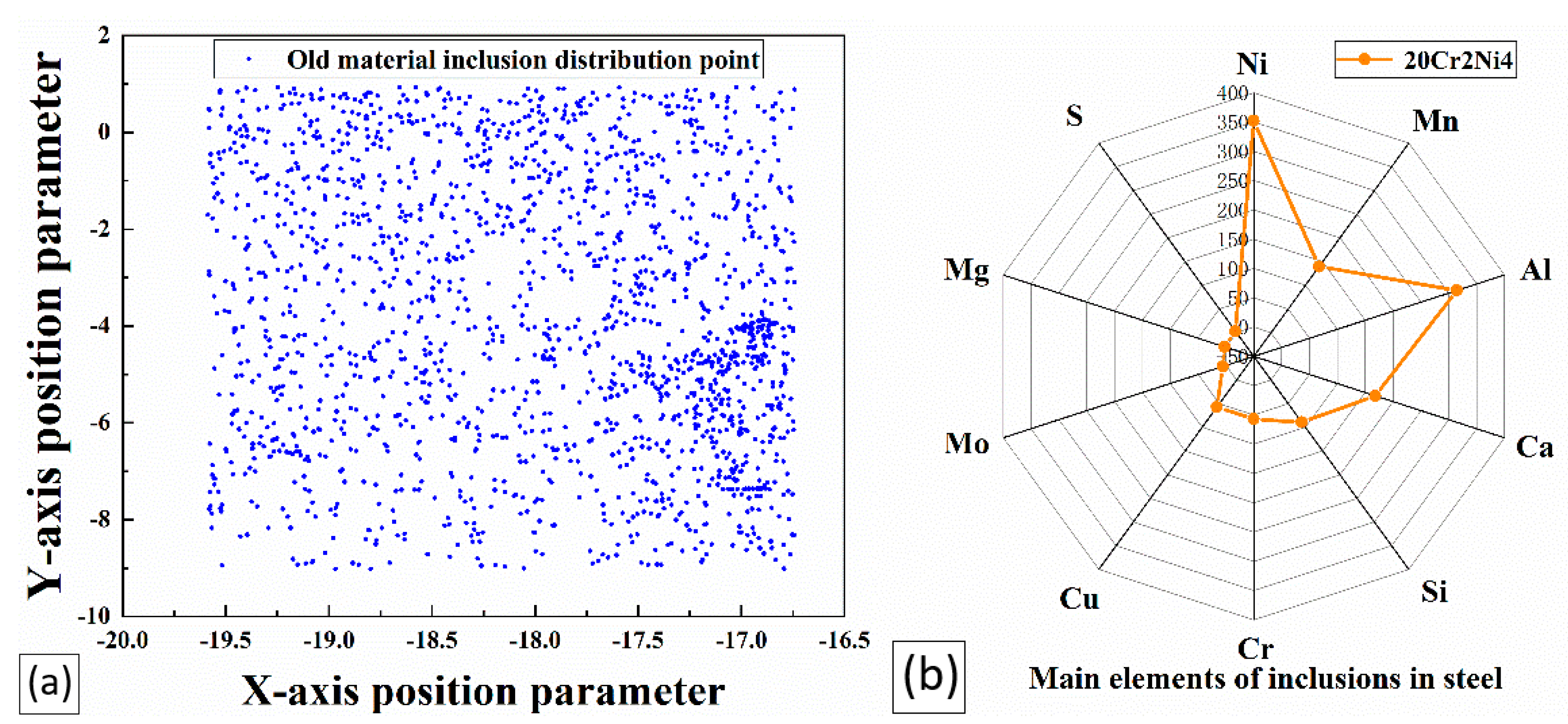
3.1. Analysis of the Inclusions in Steel
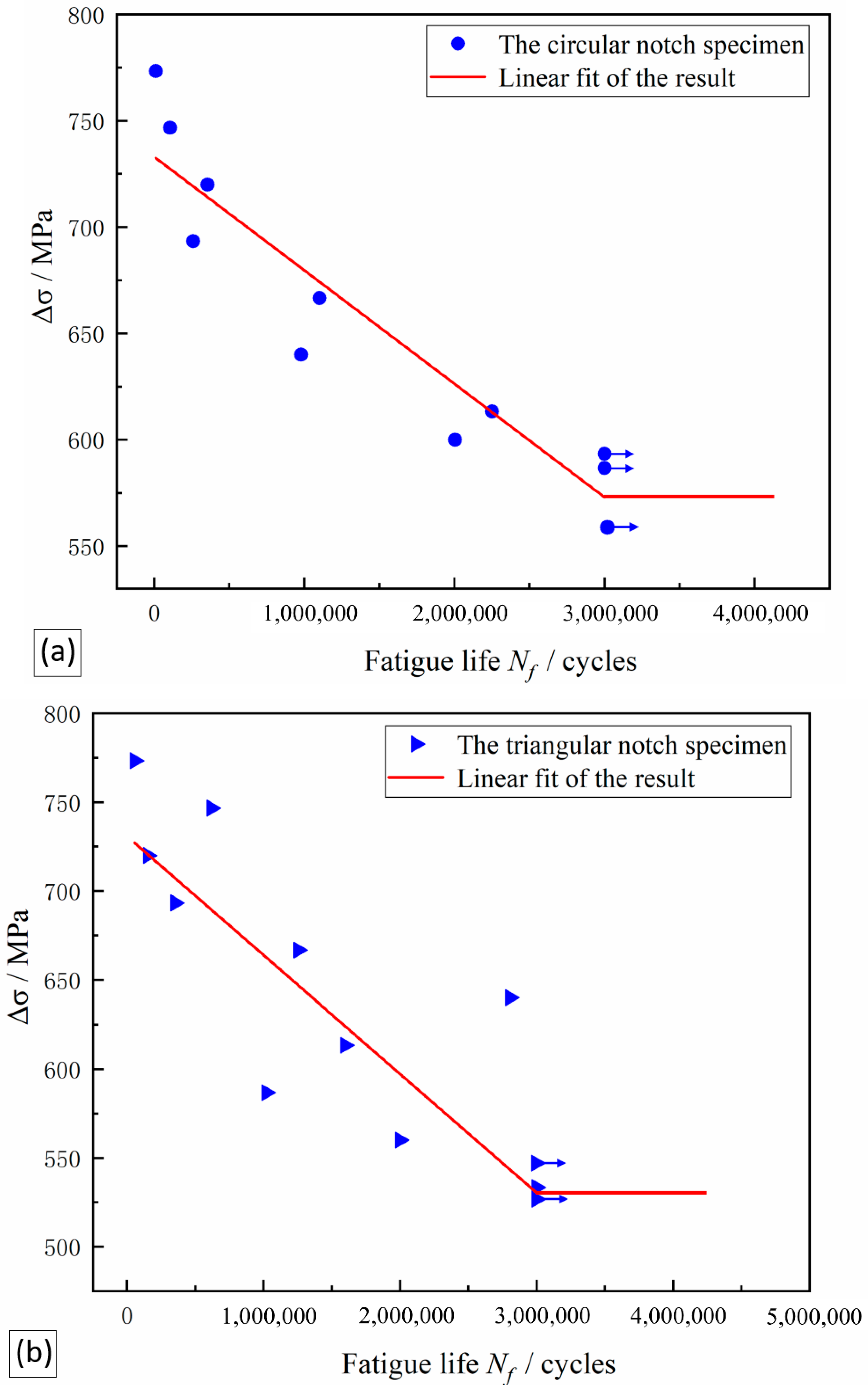
3.2. Fatigue Behavior Analysis
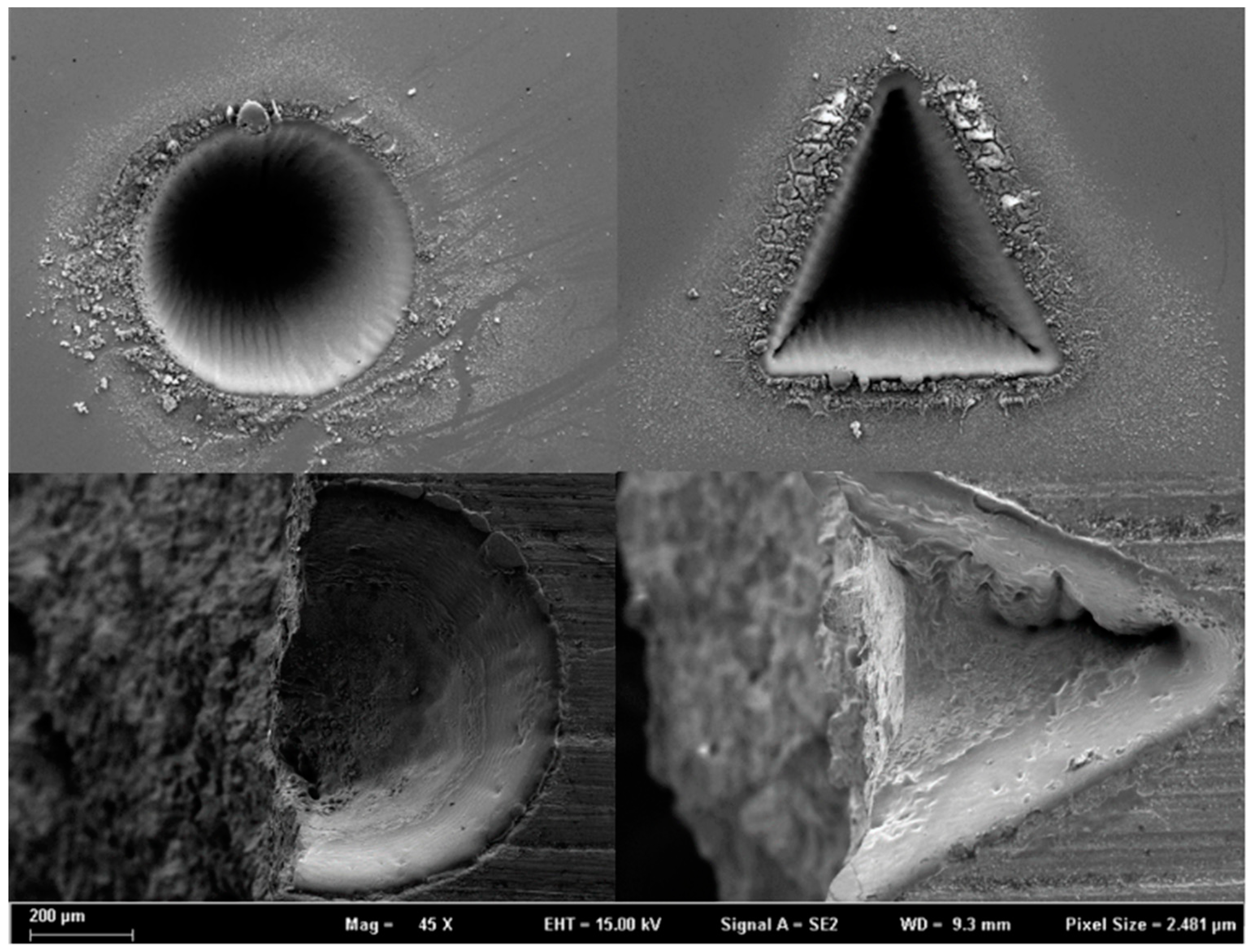
3.3. Fractography Morphology
4. Discussion
4.1. Mechanism of Laser Etching to Predict Fatigue Performance
- The microhardness tester results can be seen by the naked eye with three regular indentations.
- The observation of inclusions must be ultimately supplemented by energy spectra for final confirmation, which requires multiple experiments to ensure the effects.
- The parameters of the laser etching equipment are set in the diameter of 0.2 mm–1mm to ensure full coverage of the indentation, and the power of 50 W and 200 cycles can reach the desired depth.
4.2. Influence Mechanisms of the Inclusions and Prefabricated Stress on the Fatigue Properties
4.3. Fatigue Strength Prediction of 20Cr2Ni4 Steel Notch Shape and Inclusion Size
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gao, M.; Bai, S.; Wang, H.; Sun, J. Study on Heavy-duty Gears Materials for Mining. Foundry Technol. 2013, 1, 34–35. [Google Scholar]
- Zhang, W.H.; Wang, M.Q.; Shi, J.; Hui, W.; Dong, H.; Wu, R. Effect of Vanadium-niobium Microalloying on Properties of Cr-Ni-Mo Heavy-duty Gear Steel. Mater. Mech. Eng. 2007, 31, 31. [Google Scholar]
- Cantó, J.S.; Winwood, S.; Rhodes, K.; Birosca, S. A Study of Low Cycle Fatigue Life and its correlation with Microstructural Parameters in IN713C Nickel Based Superalloy. Mater. Sci. Eng. A 2018, 718, 19–32. [Google Scholar]
- Zhang, Y.; Wang, J.; Sun, Q.; Zhang, H.; Jiang, P. Fatigue life prediction of FV520B with internal inclusions. Mater. Des. 2015, 69, 241–246. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Q.; Xu, Z.Z.; Shin, G.-S.; Lyu, S.K. A study on the evaluation of bending fatigue strength for 20CrMoH gear. Int. J. Precis. Eng. Manuf. 2013, 14, 1339–1343. [Google Scholar] [CrossRef]
- Dengo, C.; Meneghetti, G.; Dabalà, M. Experimental analysis of bending fatigue strength of plain and notched case-hardened gear steels. Int. J. Fatigue 2015, 80, 145–161. [Google Scholar] [CrossRef]
- Tong, J.; Alshammrei, S.; Wigger, T.; Lupton, C.; Yates, J.R. Full-field characterization of a fatigue crack: Crack closure revisited. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 2130–2139. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Y.; Liu, S.; Sun, Q.; Lu, H. Competitive giga-fatigue life analysis owing to surface defect and internal inclusion for FV520B-I. Int. J. Fatigue 2016, 87, 203–209. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, P.; Duan, Q.Q.; Zhang, Z.J.; Yang, H.J.; Pang, J.C.; Tian, Y.Z.; Li, X.W.; Zhang, Z.F. Synchronously improved fatigue strength and fatigue crack growth resistance in twinning-induced plasticity steels. Mater. Sci. Eng. A 2018, 711, 533–542. [Google Scholar] [CrossRef]
- Krewerth, D.; Lippmann, T.; Weidner, A.; Biermann, H. Influence of non-metallic inclusions on fatigue life in the very high cycle fatigue regime. Int. J. Fatigue 2016, 84, 40–52. [Google Scholar] [CrossRef]
- Tang, J.; Hu, W.; Meng, Q.; Sun, L.; Zhan, Z. A novel two-scale damage model for fatigue damage analysis of transition region between high- and low-cycle fatigue. Int. J. Fatigue 2017, 105, 208–218. [Google Scholar] [CrossRef]
- Chen, Y.Q. Experimental research on crack length measurement method of three point bending specimen. Master’s Thesis, Dalian University of Technology, Dalian, China, May 2015. [Google Scholar]
- Roiko, A.; Solin, J.; Hänninen, H. Behavior of small cracks under negative stress ratio fatigue loading. Int. J. Fatigue 2017, 104, 379–388. [Google Scholar] [CrossRef]
- Goyal, S.; Mariappan, K.; Shankar, V.; Sandhya, R.; Laha, K.; Bhaduri, A.K. Studies on creep-fatigue interaction behaviour of Alloy 617M. Mater. Sci. Eng. A 2018, 730, 16–23. [Google Scholar] [CrossRef]
- Cyril, N.S.; Fatemi, A. Experimental evaluation and modeling of sulfur content and anisotropy of sulfide inclusions on fatigue behavior of steels. Mater. Sci. Eng. A 2009, 31, 526–537. [Google Scholar] [CrossRef]
- Xie, B.B.; Yuan, G.F. Study of the surface morphology of laser etching on engineering ceramics. Mater. Res. Innovations 2016, 19, S10-420–S10-423. [Google Scholar] [CrossRef]
- Fauchais, P.; Fukumoto, M.; Vardelle, A.; Vardelle, M. Knowledge concerning splat formation. J. Thermal Spray Technol. 2004, 13, 337–360. [Google Scholar] [CrossRef]
- Tanaka, K.; Akiniwa, Y. Modeling of Fatigue Crack Growth: Mechanistic Models. Compre. Struct. Integrity 2003, 4, 165–189. [Google Scholar]
- Murakami, Y.; Takahashi, K.; Kusumoto, R. Threshold and growth mechanism of fatigue cracks under mode II and III loadings. Fatigue Fract. Eng. Mater. Struct. 2010, 26, 523–531. [Google Scholar] [CrossRef]
- Li, S.X.; Zhang, P.Y.; Yu, S.R. Experimental study on very high cycle fatigue of martensitic steel of 2Cr13 under corrosive environment. Fatigue Fract. Eng. Mater. Struct. 2014, 37, 1146–1152. [Google Scholar] [CrossRef]













| Process Standard | Alloy Element (wt%) | |||||||
|---|---|---|---|---|---|---|---|---|
| C | Cr | Ni | Mn | Si | Al | S | O | |
| National standard | 0.17 ~ 0.23 | 1.25 ~ 1.65 | 3.25 ~ 3.65 | 0.30 ~ 0.60 | 0.24 | ≤0.03 | ≤0.03 | ≤0.0025 |
| Steel Grade | Tensile Strength (MPa) | Elastic Modulus (MPa) | Yield Strength (MPa) | Section Elongation (%) | Section Shrinkage (%) | Hardness (HB) |
|---|---|---|---|---|---|---|
| 20Cr2Ni4 | 1483 | 211 | 1292 | 13 | 57 | 434 |
| Steel | Heat Treatment Process | ||||
|---|---|---|---|---|---|
| 20Cr2Ni4 | Normalizing Temperature /°C | Carburizing temperature /°C | High-temperature Tempering/°C | Quenching Temperature /°C | Low-temperature Tempering/°C |
| 950 | 920 | 640 | 800 | 150 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, Z.; Wang, Z.; Wang, H.; Shan, D. Bending Fatigue Behaviors Analysis and Fatigue Life Prediction of 20Cr2Ni4 Gear Steel with Different Stress Concentrations near Non-metallic Inclusions. Materials 2019, 12, 3443. https://doi.org/10.3390/ma12203443
Xing Z, Wang Z, Wang H, Shan D. Bending Fatigue Behaviors Analysis and Fatigue Life Prediction of 20Cr2Ni4 Gear Steel with Different Stress Concentrations near Non-metallic Inclusions. Materials. 2019; 12(20):3443. https://doi.org/10.3390/ma12203443
Chicago/Turabian StyleXing, Zhiguo, Zhiyuan Wang, Haidou Wang, and Debin Shan. 2019. "Bending Fatigue Behaviors Analysis and Fatigue Life Prediction of 20Cr2Ni4 Gear Steel with Different Stress Concentrations near Non-metallic Inclusions" Materials 12, no. 20: 3443. https://doi.org/10.3390/ma12203443
APA StyleXing, Z., Wang, Z., Wang, H., & Shan, D. (2019). Bending Fatigue Behaviors Analysis and Fatigue Life Prediction of 20Cr2Ni4 Gear Steel with Different Stress Concentrations near Non-metallic Inclusions. Materials, 12(20), 3443. https://doi.org/10.3390/ma12203443