Characterizing the Complex Modulus of Asphalt Concrete Using a Scanning Laser Doppler Vibrometer
Abstract
:1. Introduction
2. Materials and Methods
2.1. Theoretical Background
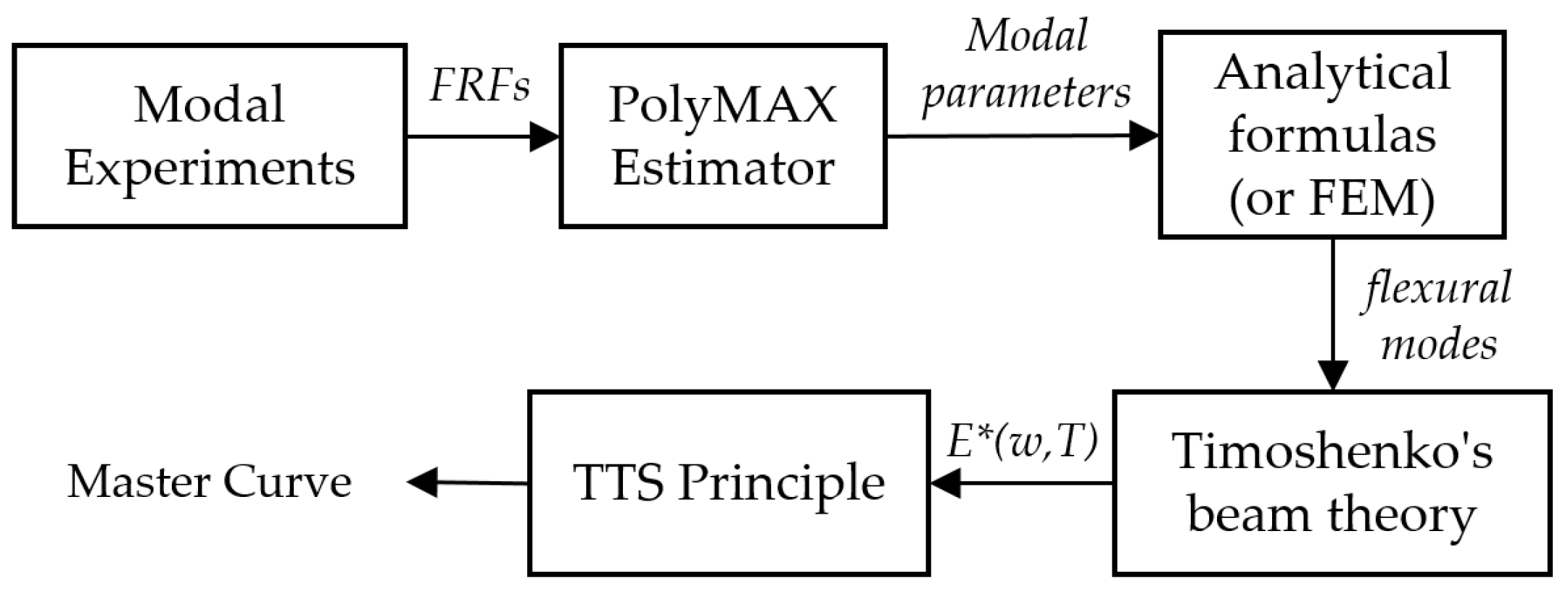
2.1.1. Modal Analysis
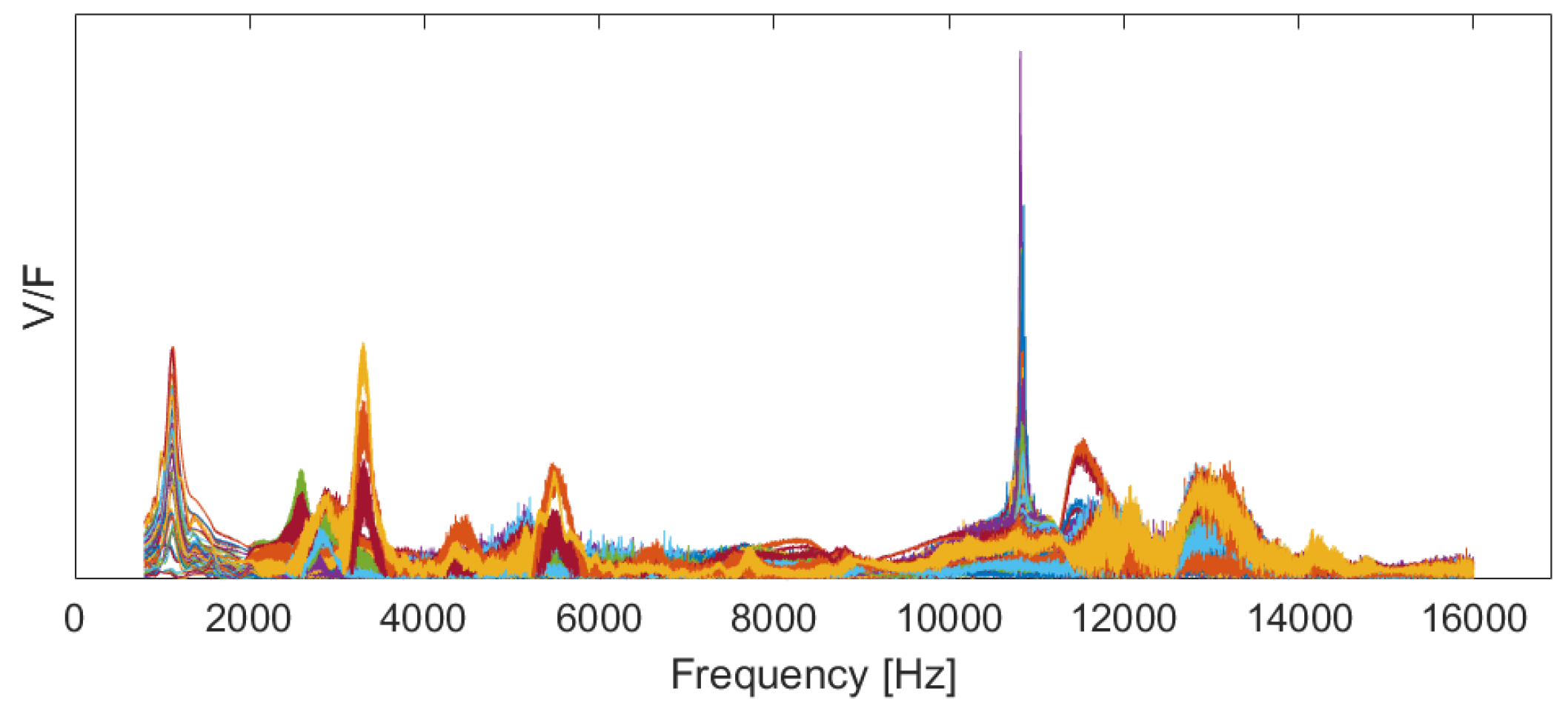
2.1.2. Laser Doppler Vibrometry
2.1.3. Classical Beam Theories
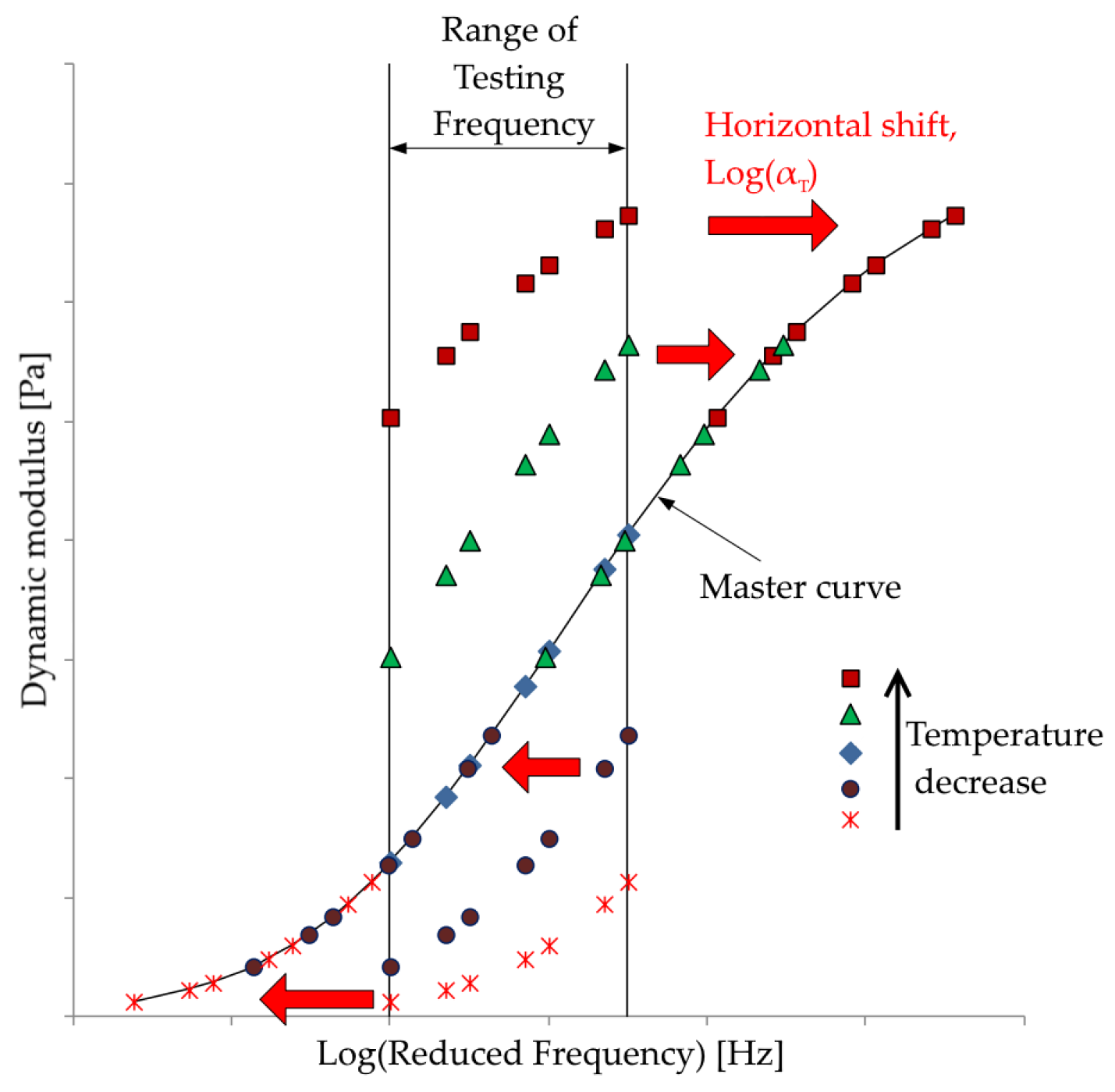
2.1.4. Master Curve of Complex Modulus
2.2. Practical Implementation
2.2.1. Material Production
- The specimens are beam shaped to follow the classical beam theories (stated in Section 2.1.3).
- According to NBN EN 12697-26:2018 [4], for the asphalt specimens to represent their true material properties, it is recommended that their width and height be at least three times the maximum grain size of the mixture. Therefore, the width and height of the beam for this mixture are higher than 42 mm.
- The samples should fit in the available climate chamber, so in this study, their length L should be less than 45 cm, which is the width of the frame built to be placed inside the climate chamber (see Figure 4b).
2.2.2. Experimental Setup
2.2.3. Data Processing
3. Results and Discussion
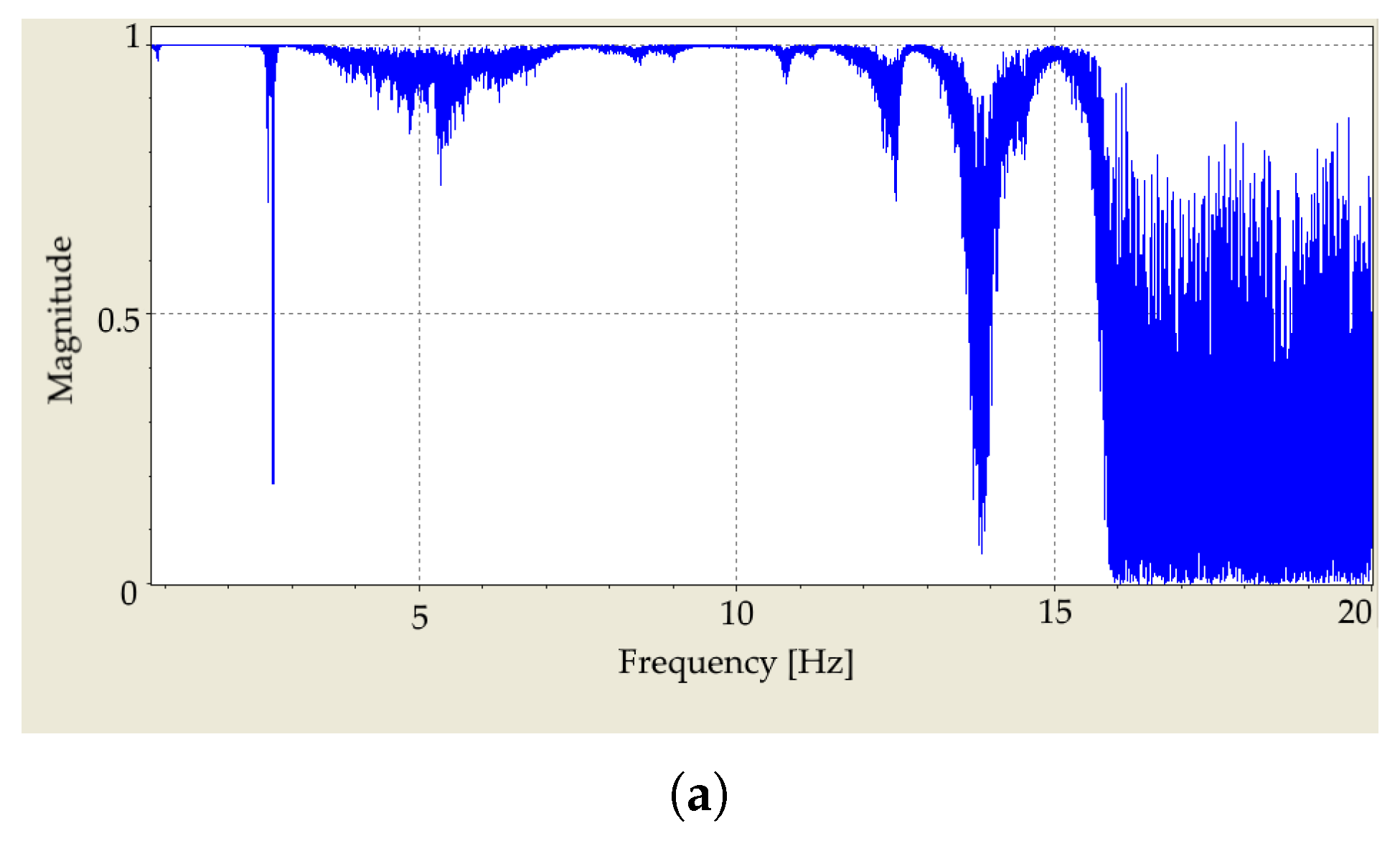
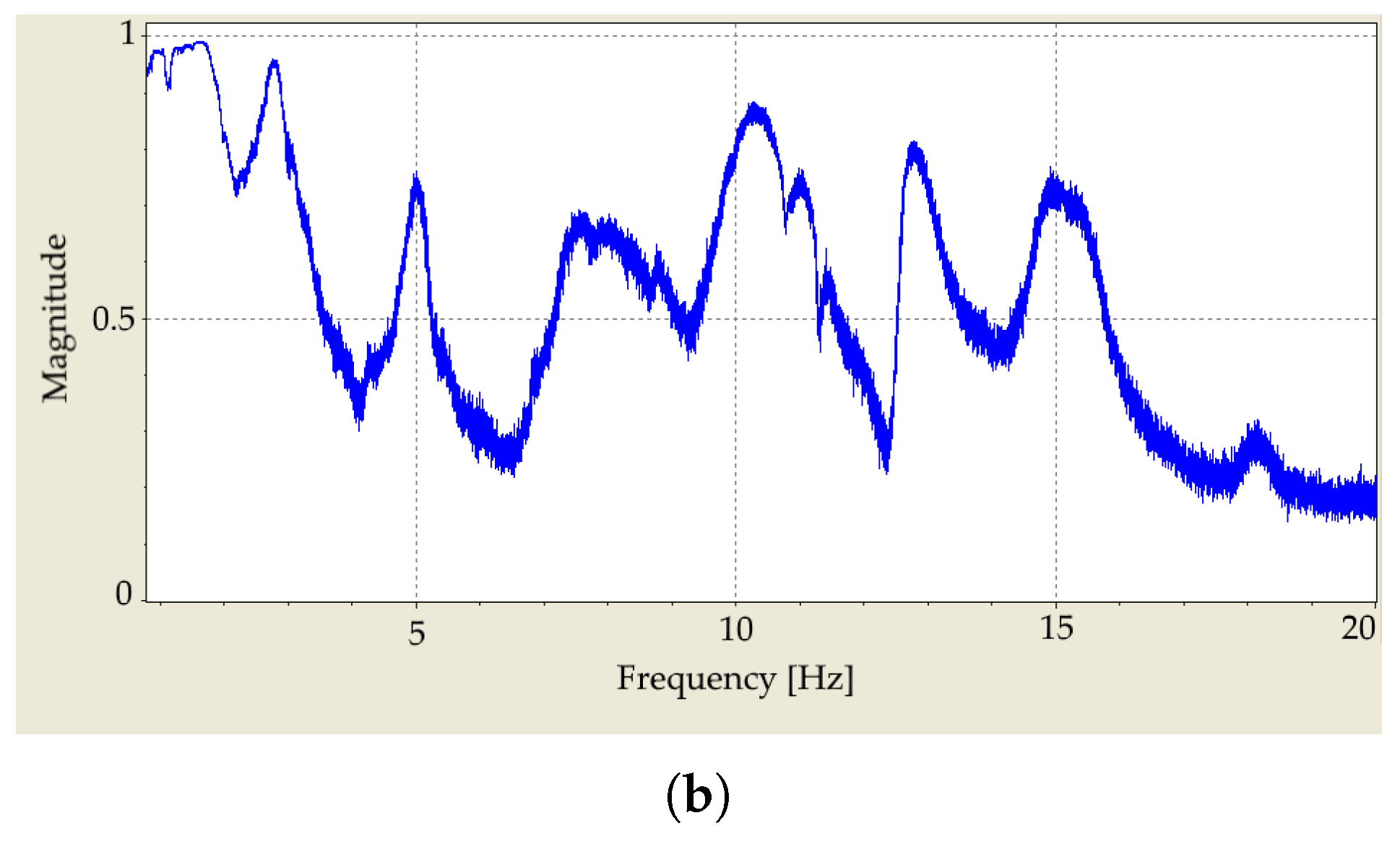
3.1. Repeatability of the Measurements
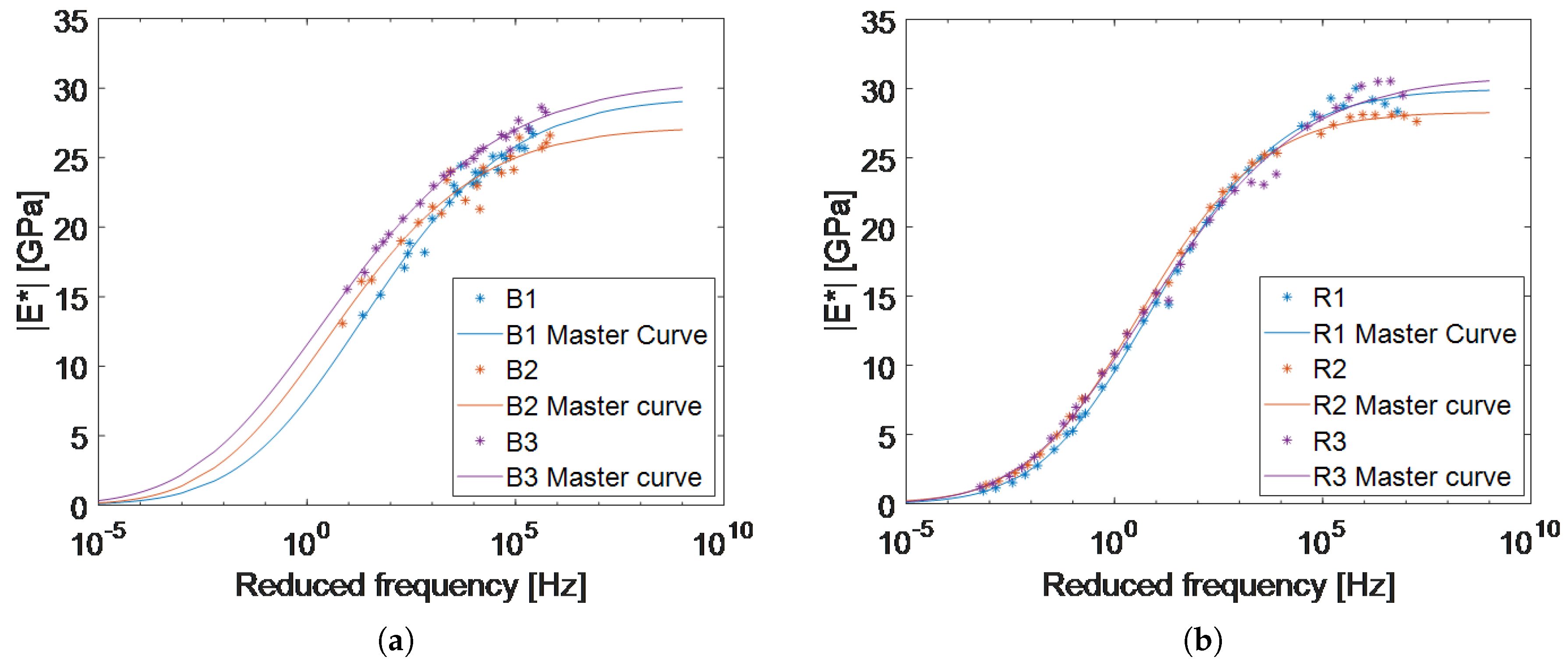
3.2. Complex Modulus of Elasticity
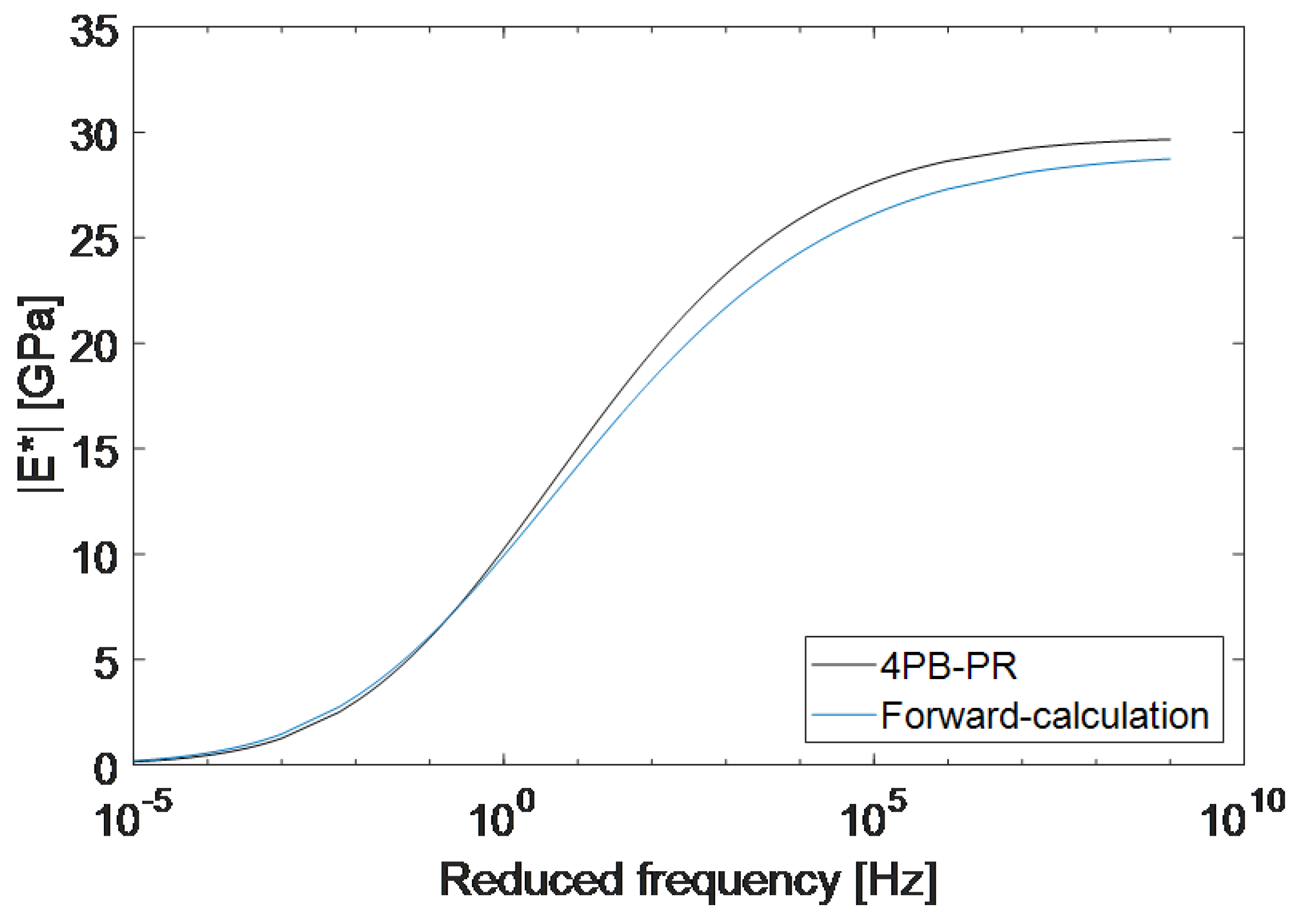
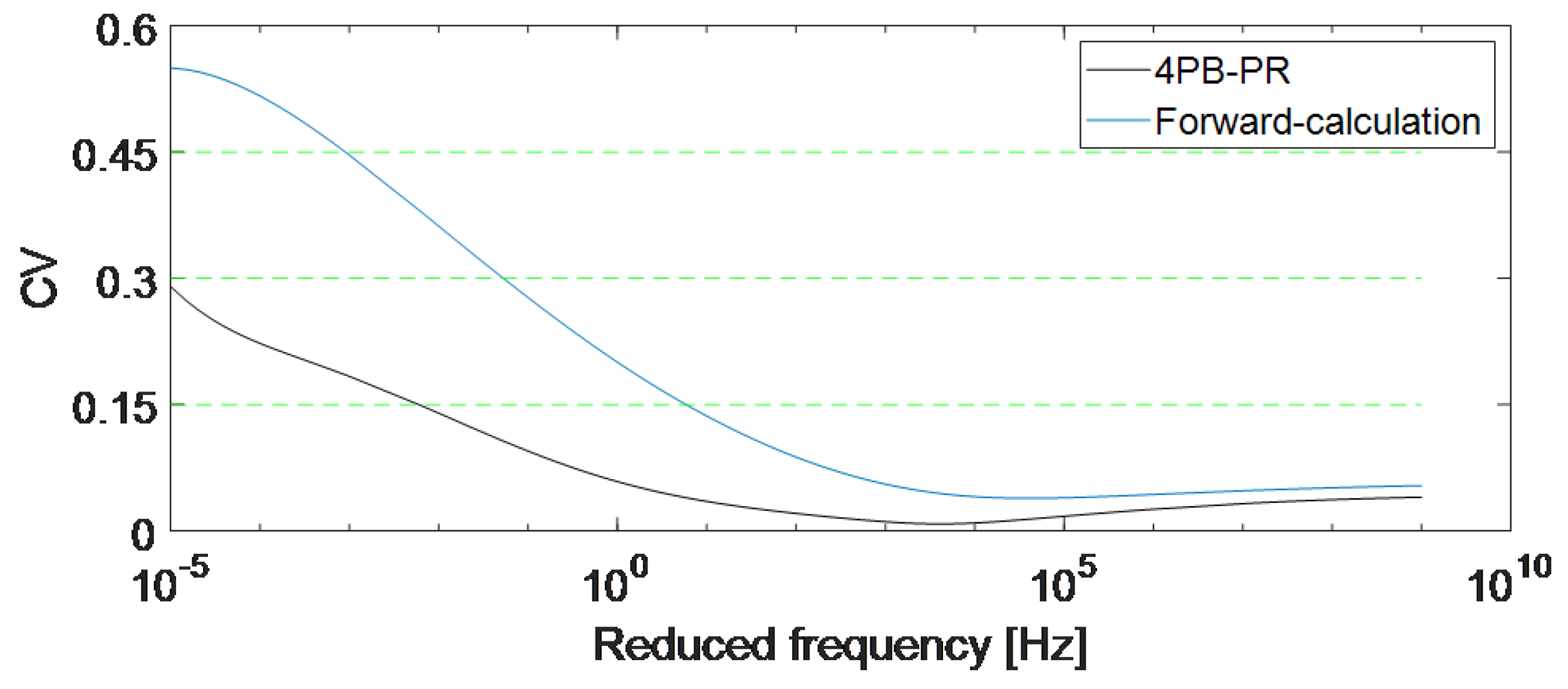
3.3. Master Curves Estimated by the Proposed Forward-Calculation Method
3.4. Advantages and Limitations of the Proposed Method
- The operational temperature of the shaker used in this research was between 0 to 40 °C. Therefore, the testing temperatures were selected based on this limitation. By using a shaker with a wider operational temperature range or designing a climate chamber in a way that the shaker can be placed outside of the chamber, it is possible to conduct measurements in a wider temperature range. This leads to more data for master curve creation and therefore, more accurate master curves.
- The first natural frequency of the beam in this study was relatively high. Therefore the first point of the master curve in 15 °C was located at 7 Hz, and the master curve was extrapolated for lower frequencies. This could cause a less accurate result in low frequencies. This problem can be solved by increasing the length of the beam or decreasing the cross-section dimensions. As explained before, the cross-section of the sample cannot be smaller than three times the biggest aggregate in the mixture. Therefore for this base layer mixture, the lowest cross-section could be 4.2 mm. Furthermore, the length of the beam was selected based on the dimensions of the available climate chambers. By using a larger climate chamber, it is possible to produce longer specimens with a lower first natural frequency. In that case, more data will be available at lower frequencies which is beneficial for the formation of a more accurate master curve. For instance, according to the analysis done by FEM, the first natural frequency of the asphalt mixture used in this research with dimensions of m m m is 193 Hz, which considering the shifting parameters, means a data point at 0.5 Hz for the master curve plotted in a reference temperature of 15 °C. Producing specimens with this dimension is convenient in the asphalt lab since the asphalt plates are normally produced with m m m dimension and the beams with the proper cross-section can be cut from them.
- According to the datasheets of the shaker used in this research, the frequency range of the shaker is 10 Hz to 20 kHz. However, in these experiments, the shaker was not able to sufficiently excite the specimen in high frequencies, which led to noisy data at some frequencies. Therefore, the mode shapes plotted at high frequencies did not match very well with the FEM model causing low MAC values, so they were removed from the calculations. Having a more powerful shaker can lead to acquiring more mode shapes of the system and therefore, estimation of more complex moduli and more accurate master curves. However, it is also essential to be careful not to increase the load too much, to keep the strain under the level in which the material can be considered as linear viscoelastic.
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, H.; Zhan, S.; Liu, G. The Effects of Asphalt Migration on the Dynamic Modulus of Asphalt Mixture. Appl. Sci. 2019, 9, 2747. [Google Scholar] [CrossRef]
- Gu, L.; Chen, L.; Zhang, W.; Ma, H.; Ma, T. Mesostructural Modeling of Dynamic Modulus and Phase Angle Master Curves of Rubber Modified Asphalt Mixture. Materials 2019, 12, 1667. [Google Scholar] [CrossRef] [PubMed]
- Gudmarsson, A. Resonance Testing of Asphalt Concrete. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2014. [Google Scholar]
- NBN EN 12697-26:2018 Bituminous Mixtures—Test Methods—Part 26: Stiffness; Technical Report; Bureau voor Normalisatie: Brussels, Belgium, 2018.
- Whitmoyer, S.; Kim, Y. Determining Asphalt Concrete Properties via the Impact Resonant Method. J. Test. Eval. 1994, 22, 139–148. [Google Scholar] [CrossRef]
- LaCroix, A.; Kim, Y.R.; Sadat, M.; Far, S. Constructing the Dynamic Modulus Mastercurve Using Impact Resonance Testing; Association of Asphalt Paving Technologists: Lino Lakes, MN, USA, 2009; Volume 78. [Google Scholar]
- Mun, S. Determining the Dynamic Modulus of a Viscoelastic Asphalt Mixture Using an Impact Resonance Test with Damping Effect. Res. Nondestruct. Eval. 2015, 26, 189–207. [Google Scholar] [CrossRef]
- Ryden, N. Resonant frequency testing of cylindrical asphalt samples. Eur. J. Environ. Civ. Eng. 2011, 15, 587–600. [Google Scholar] [CrossRef]
- Gudmarsson, A.; Ryden, N.; Birgisson, B. Application of resonant acoustic spectroscopy to asphalt concrete beams for determination of the dynamic modulus. Mater. Struct. 2012, 45, 1903–1913. [Google Scholar] [CrossRef]
- Gudmarsson, A.; Ryden, N.; Birgisson, B. Characterizing the low strain complex modulus of asphalt concrete specimens through optimization of frequency response functions. J. Acoust. Soc. Am. 2012, 132, 2304–2312. [Google Scholar] [CrossRef]
- Gudmarsson, A.; Ryden, N.; Di Benedetto, H.; Sauzeat, C. Complex modulus and complex Poisson’s ratio from cyclic and dynamic modal testing of asphalt concrete. Constr. Build. Mater. 2015, 88, 20–31. [Google Scholar] [CrossRef]
- Gudmarsson, A.; Ryden, N.; Di Benedetto, H.; Sauzeat, C.; Tapsoba, N.; Birgisson, B. Comparing Linear Viscoelastic Properties of Asphalt Concrete Measured by Laboratory Seismic and Tension-Compression Tests. J. Nondestruct. Eval. 2014, 33, 571–582. [Google Scholar] [CrossRef]
- He, J.; Fu, Z.F. Modal Analysis; Elsevier: Oxford, UK, 2001. [Google Scholar]
- Castellini, P.; Martarelli, M.; Tomasini, E.P. Laser Doppler Vibrometry: Development of advanced solutions answering to technology’s needs. Mech. Syst. Signal Process. 2006, 20, 1265–1285. [Google Scholar] [CrossRef]
- Rothberg, S.; Allen, M.; Castellini, P.; Di Maio, D.; Dirckx, J.; Ewins, D.; Halkon, B.; Muyshondt, P.; Paone, N.; Ryan, T.; et al. An international review of laser Doppler vibrometry: Making light work of vibration measurement. Opt. Lasers Eng. 2016, 99, 11–22. [Google Scholar] [CrossRef] [Green Version]
- Martatelli, M.; Revel, G.; Santolini, C. Automated Modal Analysis By Scanning Laser Vibrometry: Problems and Uncertainties Associated With the Scanning System Calibration. Mech. Syst. Signal Process. 2001, 15, 581–601. [Google Scholar] [CrossRef]
- Stanbridge, A.B.; Ewins, D.J. Modal Testing Using a Scanning laser Doppler vibrometer. Mech. Syst. Signal Process. 1999, 13, 255–270. [Google Scholar] [CrossRef]
- Pedersen, L.; Hjorth, P.G.; Knudsen, K. Viscoelastic Modellling of Road Deflections for use with the Traffic Speed Deflectometer. Ph.D. Thesis, Technical University of Denmark, Lyngby, Denmark, 2013. [Google Scholar]
- Hasheminejad, N.; Vuye, C.; Van den bergh, W.; Dirckx, J.; Vanlanduit, S. A Comparative Study of laser Doppler vibrometers for Vibration Measurements on Pavement Materials. Infrastructures 2018, 3, 47. [Google Scholar] [CrossRef]
- Carrera, E.; Giunta, G.; Petrolo, M. Beam Structures: Classical and Advanced Theories, 1st ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2011; pp. 9–22. [Google Scholar] [CrossRef]
- Euler, L. Methodus Inveniendi Lineas Curvas Maximi Minimive Proprietate Gaudentes; apud Marcum-Michaelem Bousquet: Lausanne, Switzerland; Geneva, Switzerland, 1744. [Google Scholar]
- Timoshenko, S. On the transverse vibrations of bars of uniform cross-section. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1922, 43, 125–131. [Google Scholar] [CrossRef]
- Timoshenko, S. On the correction for shear of the differential equation for transverse vibrations of prismatic bars. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1921, 41, 744–746. [Google Scholar] [CrossRef]
- Inman, D.J. Engineering Vibration; Pearson Education, Inc.: Upper Saddle River, NJ, USA, 2014. [Google Scholar]
- Labuschagne, A.; van Rensburg, N.F.; van der Merwe, A.J. Comparison of linear beam theories. Math. Comput. Model. 2009, 49, 20–30. [Google Scholar] [CrossRef]
- Pintelon, R.; Guillaume, P.; Vanlanduit, S.; De Belder, K.; Rolain, Y. Identification of Young’s modulus from broadband modal analysis experiments. Mech. Syst. Signal Process. 2004, 18, 699–726. [Google Scholar] [CrossRef]
- Ypma, T.J. Historical Development of the Newton–Raphson Method. Soc. Ind. Appl. Math. 1995, 37, 531–551. [Google Scholar] [CrossRef]
- Wineman, A.S.; Rajagopal, K.R. Mechanical Response of Polymers: An Introduction; Cambridge University Press: Cambridge, UK, 2000; p. 317. [Google Scholar]
- Nguyen, H.M.; Pouget, S.; Di Benedetto, H.; Sauzéat, C. time–temperature superposition principle for bituminous mixtures. Eur. J. Environ. Civ. Eng. 2009, 13, 1095–1107. [Google Scholar] [CrossRef]
- Lee, H.S. Development of a New Solution for Viscoelastic Wave Propagation of Pavements Structures and Its Use in Dynamic Backcalculations. Ph.D. Thesis, Michigan State University, East Lansing, MI, USA, 2013. [Google Scholar]
- Rowe, G.M.; Sharrock, M.J. Alternate shift factor relationship for describing temperature dependency of viscoelastic behavior of asphalt materials. Transp. Res. Rec. 2011, 2207, 125–135. [Google Scholar] [CrossRef]
- Walubita, L.F.; Alvarez, A.E.; Simate, G.S. Evaluating and comparing different methods and models for generating relaxation modulus master-curves for asphalt mixes. Constr. Build. Mater. 2011, 25, 2619–2626. [Google Scholar] [CrossRef]
- Williams, M.L.; Landel, R.F.; Ferry, J.D. The temperature dependence of relaxation mechanisms in amorphous polymers and other glass-forming liquids. J. Am. Chem. Soc. 1955, 77, 3701–3707. [Google Scholar] [CrossRef]
- Pellinen, T.K.; Witczak, M.W.; Bonaquist, R.F. Asphalt Mix Master Curve Construction Using Sigmoidal Fitting Function with Non-Linear Least Squares Optimization. In Proceedings of the 15th Engineering Mechanics Division Conference, New York, NY, USA, 2–5 June 2002; pp. 83–101. [Google Scholar] [CrossRef]
- Medani, T.O.; Huurman, M. Constructing the Stiffness Master Curves for Asphaltic Mixes; Technical Report; Delft University of Technology: Delft, The Netherlands, 2003. [Google Scholar]
- NBN EN 1426:2015 Bitumen and Bituminous Binders—Determination of Needle Penetration; Technical Report; Bureau voor Normalisatie: Brussels, Belgium, 2015.
- NBN EN 1427:2015 Bitumen and Bituminous Binders—Determination of the Softening Point—Ring and Ball Method; Technical Report; Bureau voor Normalisatie: Brussels, Belgium, 2015.
- NBN EN 12593:2015 Bitumen and Bituminous Binders—Determination of the Fraass Breaking Point; Technical Report; Bureau voor Normalisatie: Brussels, Belgium, 2015.
- NBN EN 12697-35:2016 Bituminous Mixtures—Test Methods—Part 35: Laboratory Mixing; Technical Report; Bureau voor Normalisatie: Brussels, Belgium, 2016.
- NBN EN 12697-31:2007 Bituminous Mixtures—Test Methods for Hot Mix Asphalt—Part 31: Specimen Preparation by Gyratory Compactor; Technical Report; Bureau voor Normalisatie: Brussels, Belgium, 2007.
- Peeters, B.; Auweraer, H.V.D.; Guillaume, P.; Leuridan, J. The PolyMAX frequency-domain method: A new standard for modal parameter estimation? Shock Vib. 2004, 11, 395–409. [Google Scholar] [CrossRef]
- Peeters, B.; Lowet, G.; Van der Auweraer, H.; Leuridan, J. A new procedure for modal parameter estimation. Sound Vib. 2004, 38, 24–29. [Google Scholar]
- Roylance, D. Engineering Viscoelasticity; Department of Materials Science and Engineering-Massachusetts Institute of Technology: Cambridge, MA, USA, 2001; pp. 1–37. [Google Scholar] [CrossRef]
- Molenaar, A. Lecture Notes: Design of Flexible Pavements; Delft University of Technology: Delft, The Netherlands, 2018. [Google Scholar]



| Property (Unit) | Penetration ( mm) | Softening Point (°C) | Fraass Breaking Point (°C) |
|---|---|---|---|
| Value | 37 | 54.3 | −10 |
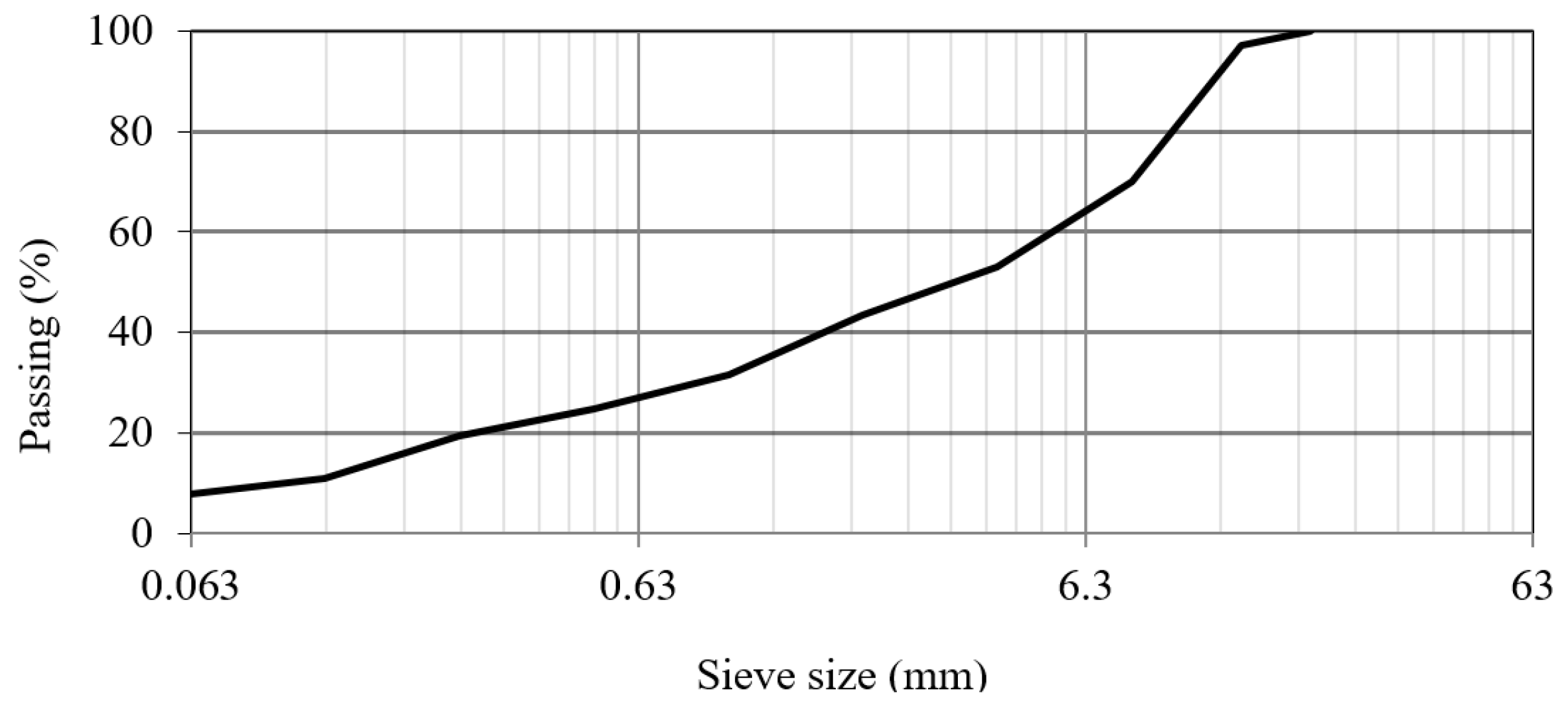
| Limestone 6.3/14 | 39.8% |
| Limestone 2/6.3 | 14.0% |
| Limestone 0/2 | 30.0% |
| River sand 0/1 | 7.5% |
| Filler (filler 15) | 8.7% |
| Total | 100% |
| Bitumen 35/50 | 4.3% |
| Specimen | Height (H, cm) | Width (W, cm) | Length (L, cm) |
|---|---|---|---|
| B1 | 5.23 | 5.40 | 40.0 |
| B2 | 5.27 | 5.37 | 39.9 |
| B3 | 5.26 | 5.51 | 40.0 |
| R1 | 5.02 | 5.07 | 44.8 |
| R2 | 4.95 | 5.07 | 44.8 |
| R3 | 4.34 | 5.00 | 44.7 |
| T (°C) | Mode Shape # | B1 | B2 | B3 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| freq. (Hz) | D (%) | |E*| (GPa) | freq. (Hz) | D (%) | |E*| (GPa) | freq. (Hz) | D (%) | |E*| (GPa) | ||
| 5 | 1 | 1080.2 | 4.7 | 23.91 | 1077.4 | 3.8 | 23.90 | 1160.6 | 3.6 | 26.64 |
| 3 | 2809.4 | 3.2 | 25.17 | 2875.2 | 4.0 | 26.45 | 2990.7 | 3.3 | 27.68 | |
| 4 | 5224.9 | 4.5 | 27.08 | |||||||
| 6 | 7460.6 | 4.2 | 25.72 | |||||||
| 8 | 10,013.5 | 2.3 | 25.68 | 10,023.8 | 2.5 | 25.71 | 10,662.5 | 1.8 | 28.61 | |
| 10 | 12,974.6 | 2.5 | 27.07 | 12,741.2 | 3.0 | 26.06 | 13,360.1 | 2.6 | 28.28 | |
| 12 | 15,610.2 | 3.4 | 26.72 | 15,594.0 | 1.7 | 26.60 | ||||
| 10 | 1 | 1041.6 | 4.7 | 22.50 | 1031.9 | 5.1 | 21.93 | 1114.0 | 4.7 | 24.55 |
| 3 | 2775.2 | 5.9 | 23.94 | 2754.0 | 4.3 | 24.26 | 2880.8 | 4.2 | 25.68 | |
| 6 | 7369.1 | 6.0 | 25.09 | |||||||
| 8 | 9706.1 | 3.4 | 24.13 | 10,256.3 | 3.6 | 26.48 | ||||
| 10 | 12,503.6 | 2.6 | 25.09 | 12,699.7 | 1.2 | 25.55 | ||||
| 12 | 15,080.7 | 4.1 | 24.94 | 14,848.8 | 3.2 | 24.12 | 15,775.2 | 3.4 | 26.93 | |
| 15 | 1 | 1003.2 | 5.5 | 20.62 | 1020.9 | 5.2 | 21.46 | 1077.8 | 6.2 | 22.97 |
| 3 | 2613.9 | 5.8 | 21.79 | 2740.6 | 4.6 | 24.03 | 2782.5 | 5.0 | 23.96 | |
| 4 | 4899.1 | 5.7 | 24.41 | 4225.6 | 1.6 | |||||
| 8 | 9500.6 | 3.6 | 23.11 | 9953.8 | 3.6 | 24.94 | ||||
| 10 | 12,026.9 | 3.8 | 23.26 | 11,964.0 | 6.7 | 22.97 | 12,674.5 | 3.1 | 25.45 | |
| 12 | 14,763.7 | 4.9 | 23.90 | |||||||
| 20 | 1 | 939.7 | 10.1 | 18.09 | 960.8 | 10.9 | 19.01 | 1020.9 | 8.6 | 20.61 |
| 3 | 2388.3 | 9.1 | 18.19 | 2520.9 | 7.5 | 20.33 | 2649.2 | 6.4 | 21.72 | |
| 8 | 9055.9 | 5.7 | 20.98 | 9704.6 | 6.3 | 23.70 | ||||
| 10 | 11,963.4 | 6.1 | 23.01 | 12,072.6 | 5.5 | 23.39 | ||||
| 12 | 14,352.7 | 5.7 | 22.59 | |||||||
| 30 | 1 | 816.6 | 15.2 | 13.66 | 796.8 | 13.6 | 13.07 | 886.2 | 14.1 | 15.53 |
| 3 | 2177.9 | 10.0 | 15.12 | 2244.2 | 11.3 | 16.11 | 2325.8 | 14.2 | 16.74 | |
| 6 | 6469.7 | 9.7 | 18.94 | |||||||
| 8 | 8169.3 | 5.3 | 17.09 | 8798.3 | 8.4 | 19.48 | ||||
| 10 | 10,829.9 | 7.9 | 18.86 | |||||||
| Sample | C1 | C2 | Smin (MPa) | Smax (MPa) | ||
|---|---|---|---|---|---|---|
| R1 | 7.17 | 2.15 | 29.47 | 190.88 | 4.49 | 29,960.97 |
| R2 | 7.34 | 2.29 | 20.76 | 134.53 | 16.95 | 28,291.33 |
| R3 | 6.34 | 1.77 | 31.88 | 199.93 | 1.21 | 30,868.85 |
| Average | 6.95 | 2.07 | 27.37 | 175.11 | 7.55 | 29,707.05 |
| std | 0.44 | 0.22 | 4.78 | 28.93 | 6.78 | 1067.48 |
| Ave. R1–3 measurements | 6.81 | 1.98 | 26.97 | 172.35 | 3.39 | 29,793.11 |
| B1 | 7.28 | 2.00 | 19.12 | 167.06 | 4.35 | 29,329.50 |
| B2 | 6.35 | 1.82 | 20.91 | 138.11 | 1.53 | 27,186.87 |
| B3 | 5.87 | 1.57 | 19.25 | 130.58 | 1.63 | 30,554.48 |
| Average | 6.50 | 1.80 | 19.76 | 145.25 | 2.50 | 29,023.62 |
| std | 0.59 | 0.17 | 0.82 | 15.73 | 1.30 | 1391.73 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hasheminejad, N.; Vuye, C.; Margaritis, A.; Van den bergh, W.; Dirckx, J.; Vanlanduit, S. Characterizing the Complex Modulus of Asphalt Concrete Using a Scanning Laser Doppler Vibrometer. Materials 2019, 12, 3542. https://doi.org/10.3390/ma12213542
Hasheminejad N, Vuye C, Margaritis A, Van den bergh W, Dirckx J, Vanlanduit S. Characterizing the Complex Modulus of Asphalt Concrete Using a Scanning Laser Doppler Vibrometer. Materials. 2019; 12(21):3542. https://doi.org/10.3390/ma12213542
Chicago/Turabian StyleHasheminejad, Navid, Cedric Vuye, Alexandros Margaritis, Wim Van den bergh, Joris Dirckx, and Steve Vanlanduit. 2019. "Characterizing the Complex Modulus of Asphalt Concrete Using a Scanning Laser Doppler Vibrometer" Materials 12, no. 21: 3542. https://doi.org/10.3390/ma12213542





