Microstructure and Formation Mechanism of Ultrasound-Assisted Transient Liquid Phase Bonded Magnesium Alloys with Ni Interlayer
Abstract
1. Introduction
2. Experimental
3. Results
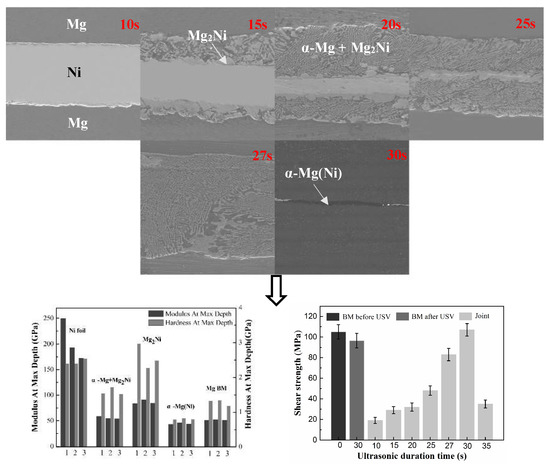
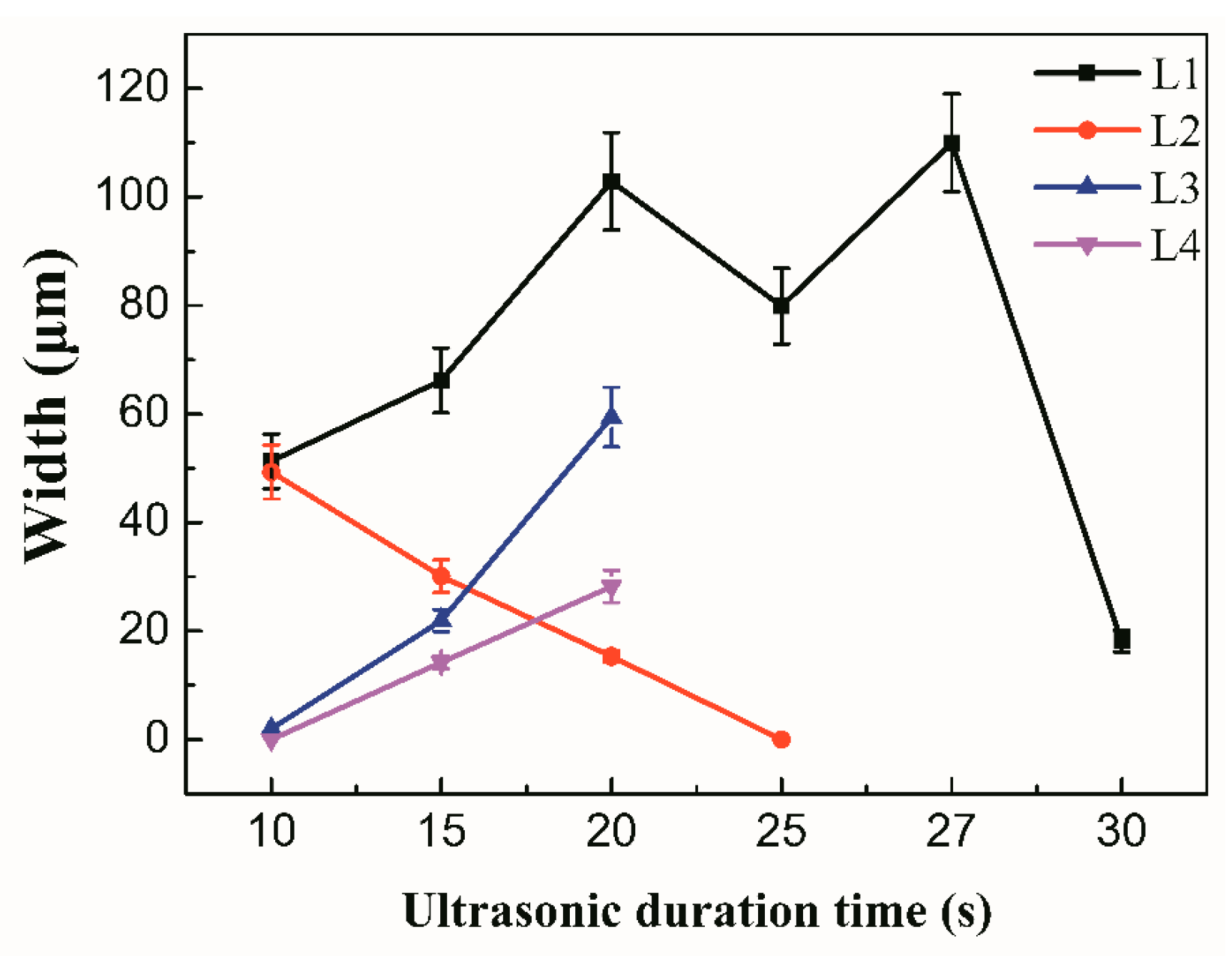
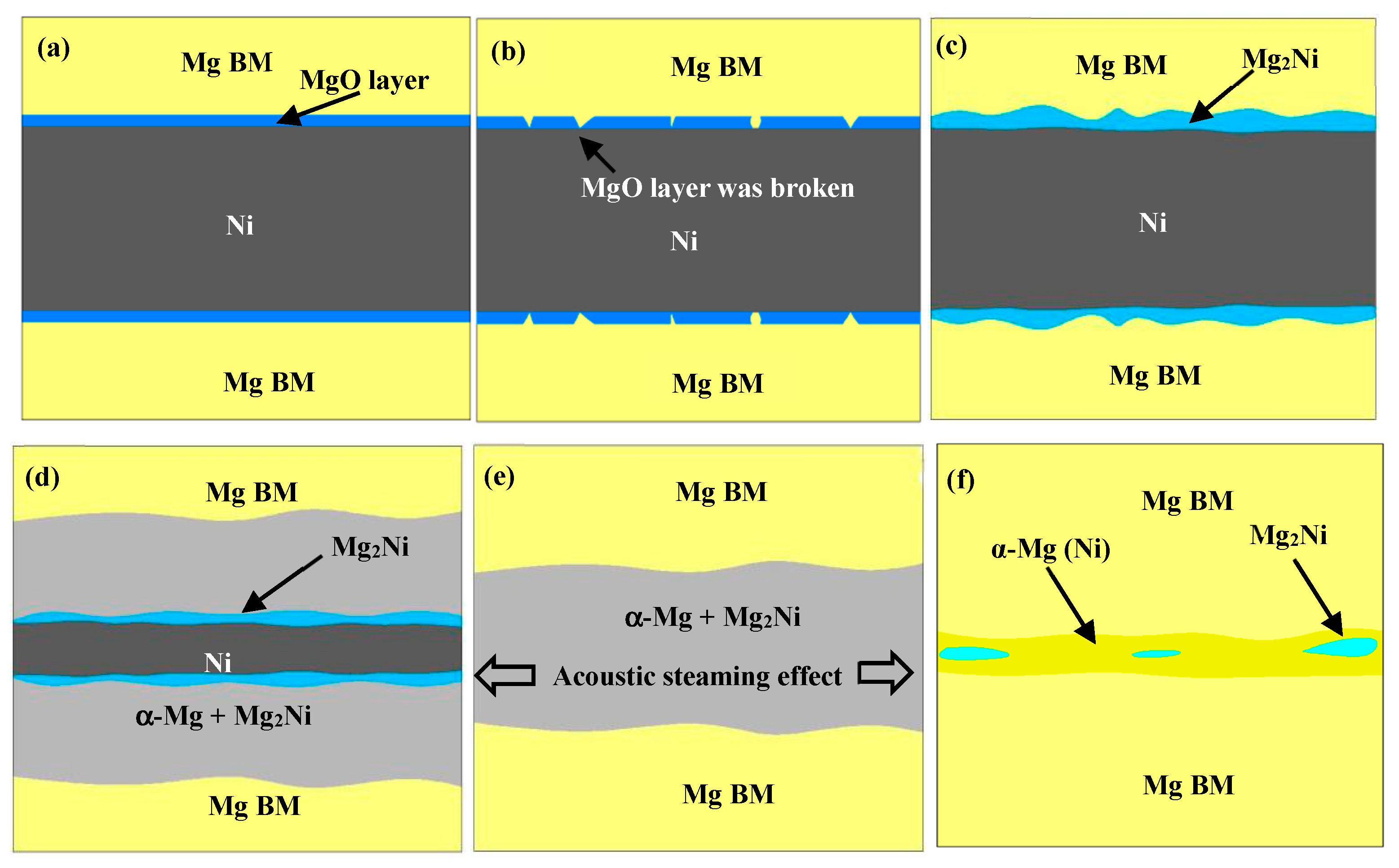
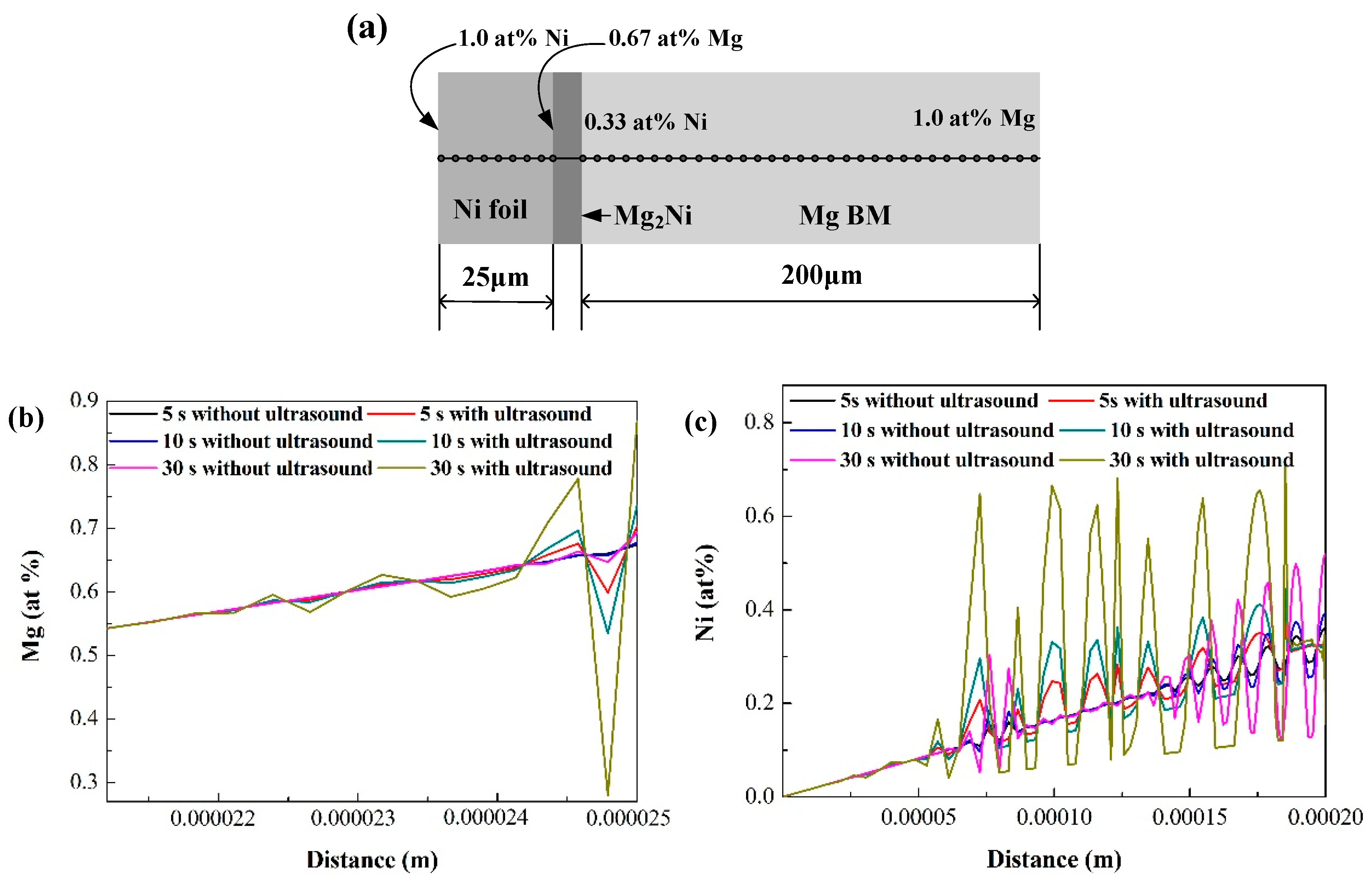
3.1. The Microstructure of Mg/Ni/Mg Joints
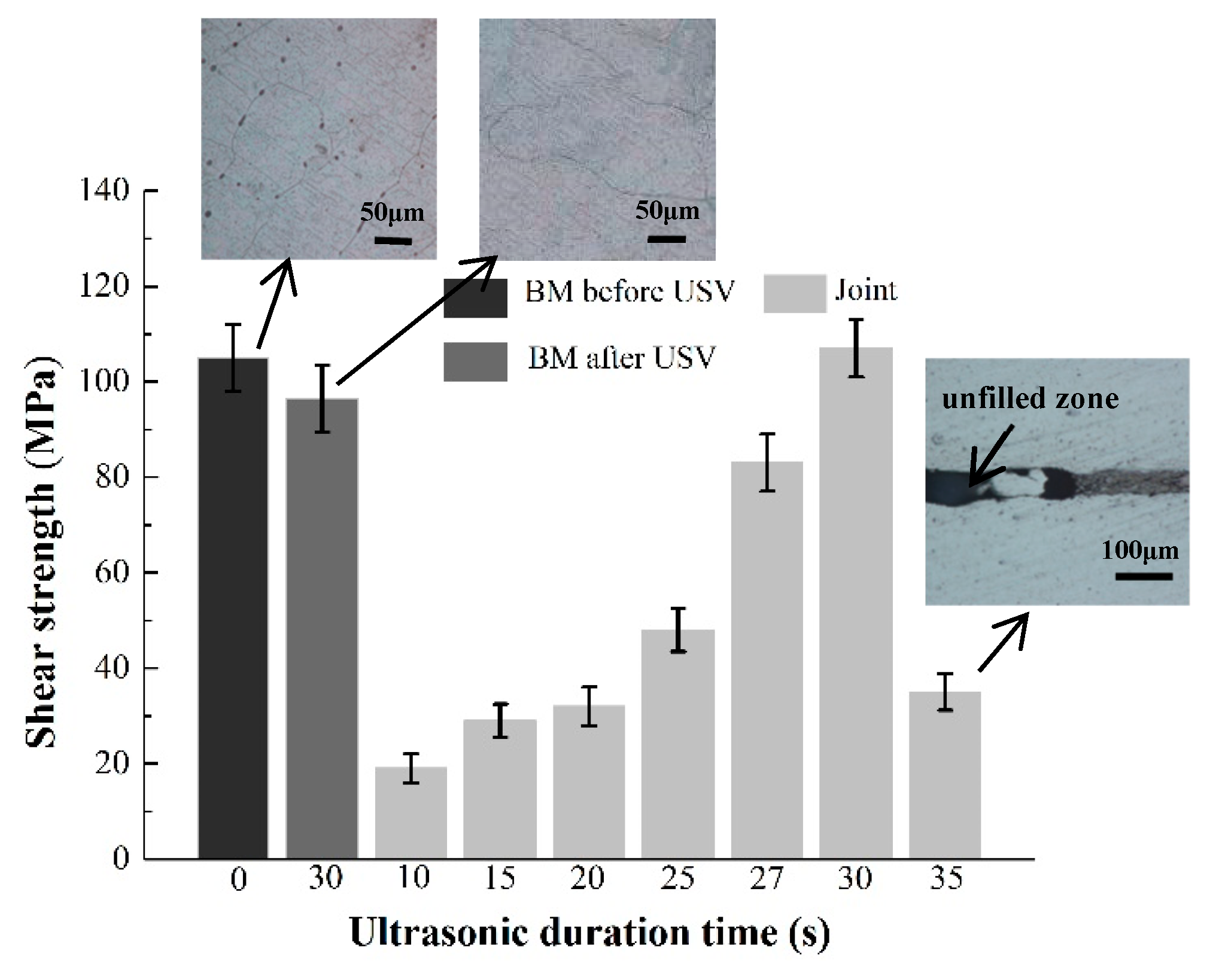
3.2. Mechanical Performance of the Mg/Ni/Mg Joints
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mordlike, B.L.; Ebert, T. Magnesium: Properties-applications-potential. Mater. Sci. Eng. A 2001, 301, 37–45. [Google Scholar] [CrossRef]
- Liu, L.M.; Ren, D.X.; Liu, F. A Review of Dissimilar Weld Techniques for Magnesium Alloys to Aluminum alloys. Materials 2014, 7, 3735–3757. [Google Scholar] [CrossRef] [PubMed]
- Xie, X.; Shen, J.; Cheng, L. Effects of nano-particles strengthening activating flux on the microstructures and mechanical properties of TIG welded AZ31 magnesium alloy joints. Mater. Des. 2015, 81, 31–38. [Google Scholar] [CrossRef]
- Wang, H.Y.; Li, N.; Liu, L.M. Investigation of the Joining Technology of FRP/AZ31B Magnesium Alloy by Welding and Riveting Hybrid Bonding Method. Materials 2019, 12, 2167. [Google Scholar] [CrossRef] [PubMed]
- Wahba, M.; Mizutani, M.; Kawahito, Y. Laser welding of die-cast AZ91D magnesium alloy. Mater. Des. 2012, 33, 569–576. [Google Scholar] [CrossRef]
- Li, T.T.; Song, G.; Zhang, Z.D. Mechanical Properties and Microstructures of Laser-TIG Welded ME21 Rare Earth Mg Alloy. Materials 2019, 12, 2188. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Qu, W.Q.; Zhuang, H.S. Development of Mg-Al filler metal for brazing magnesium alloy AZ31B. Mater. Lett. 2016, 182, 75–77. [Google Scholar] [CrossRef]
- Xu, N.; Song, Q.N. Mechanical properties’ modification of large load friction stir welded AZ31B Mg alloy joint. Mater. Lett. 2018, 219, 93–96. [Google Scholar] [CrossRef]
- Zheng, Y.; Pan, X.M.; Ma, Y.L. Microstructure and Corrosion Behavior of Friction Stir-Welded 6061 Al/AZ31 Mg Joints with a Zr Interlayer. Materials 2019, 12, 1115. [Google Scholar] [CrossRef] [PubMed]
- AlHazaa, A.; Alhoweml, I.; Shar, M.A. Transient Liquid Phase Bonding of Ti-6Al-4V and Mg-AZ31 Alloys Using Zn Coatings. Materials 2019, 12, 769. [Google Scholar] [CrossRef] [PubMed]
- Chowdhury, S.M.; Chen, D.L.; Bhole, S.D. Microstructure and mechanical properties of fiber-laser-welded and diode-laser-welded AZ31 magnesium. Metall. Mater. Trans. A 2011, 42, 1974–1989. [Google Scholar] [CrossRef]
- Munitz, A.; Cotler, C.; Stern, A. Mechanical properties and microstructure of gas tungsten arc welded magnesium AZ91D plates. Mater. Sci. Eng. A 2001, 302, 68–73. [Google Scholar] [CrossRef]
- Harooni, M.; Carlson, B.; Strohmeier, B.R. Pore formation mechanism and its mitigation in laser welding of AZ31B magnesium alloy in lap joint configuration. Mater. Des. 2014, 58, 265–276. [Google Scholar] [CrossRef]
- Shao, H.K.; Wu, A.P.; Bao, Y.D. Rapid Ag/Sn/Ag transient liquid phase bonding for high-temperature power devices packaging by assistance of ultrasound. Ultrason. Sonochem. 2017, 37, 561–570. [Google Scholar] [CrossRef] [PubMed]
- Guo, W.B.; Leng, X.S.; Luan, T.M. Ultrasonic-promoted rapid TLP bonding of fine-grained 7034 high strength aluminum alloys. Ultrason. Sonochem. 2017, 36, 354–361. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.W.; Li, Z.W.; Li, L.Q. Control Al/Mg intermetallic compound formation during ultrasonic-assisted soldering Mg to Al. Ultrason. Sonochem. 2018, 46, 48–88. [Google Scholar] [CrossRef] [PubMed]
- Lai, Z.W.; Pan, C.; Du, H.D. Ultrasonic-assisted fluxless reactive bonding of Mg/Al dissimilar alloy using Zn–Al solder in air. Sci. Technol. Weld. Join. 2018, 23, 19–27. [Google Scholar] [CrossRef]
- Li, Z.W.; Xu, Z.W.; Zhu, D.W. Control of Mg2Sn formation through ultrasonic-assisted transient liquid phase bonding of Mg to Al. J. Mater. Process. Technol. 2018, 255, 524–529. [Google Scholar] [CrossRef]
- Xu, Z.; Li, Z.; Peng, L.; Yan, J. Ultra-rapid transient liquid phase bonding of Mg alloys within 1 s in air by ultrasonic assistance. Mater. Des. 2019, 161, 72–79. [Google Scholar] [CrossRef]
- Lai, Z.W.; Chen, X.G.; Pan, C. Joining Mg alloys with Zn interlayer by novel ultrasonic-assisted transient liquid phase bonding method in air. Mater. Lett. 2016, 166, 219–222. [Google Scholar] [CrossRef]
- Wang, Q.; Fu, Y.; Liang, Q. Microstructure and mechanical properties of magnesium alloys joints with Ag-Cu interlayer by ultrasonic-induced transient liquid phase bonding in air for structure lightweight design. Mater. Lett. 2019, 237, 37–40. [Google Scholar] [CrossRef]
- Khodabakhshi, F.; Shah, L.H.; Gerlich, A.P. Dissimilar laser welding of an AA6022-AZ31 lap-joining by using Ni-interlayer: Novel beam-wobbing technique, processing parameters, and metallurgical characterization. Opt. Laser Technol. 2019, 112, 349–362. [Google Scholar] [CrossRef]
- Shah, L.H.; Gerlich, A.; Zhou, Y. Design guideline for intermetallic compound mitigation in Al-Mg dissimilar welding through addition of interlayer. Int. J. Adv. Manuf. Technol. 2018, 94, 2667–2678. [Google Scholar] [CrossRef]
- Wang, H.Y.; Liu, L.M.; Liu, F. The characterization investigation of laser-arc-adhesive hybrid welding of Mg to Al joint using Ni interlayer. Mater. Des. 2013, 50, 463–466. [Google Scholar] [CrossRef]
- Xie, R.S.; Chen, X.G.; Lai, Z.W. Microstructure, mechanical properties and mechanism of ultrasound-assisted rapid transient liquid phase bonding of magnesium alloy in air. Mater. Des. 2016, 91, 19–27. [Google Scholar] [CrossRef]
- Cui, W.; Wang, C.W.; Yan, J.C. Wetting and reaction promoted by ultrasound between sapphire and liquid Al-12Si alloy. Ultrason. Sonochem. 2013, 20, 196–201. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.G.; Yan, J.C.; Ren, S.C. Microstructure and mechanical properties of Ti-6Al-4V/Al1060 joints by ultrasonic-assisted brazing in air. Mater. Lett. 2013, 95, 197–200. [Google Scholar] [CrossRef]
- Gu, J.; Fan, F.; Li, Y.; Yang, H.; Su, M.; Cai, X. Modeling and prediction of ultrasonic attenuation in liquid-solid dispersions containing mixed particles with Monte Carlo method. Particuology 2019, 43, 84–91. [Google Scholar] [CrossRef]
- Grosjean, V.; Julcour, C.; Louisnard, O.; Barthe, L. Axial acoustic field along a solid-liquid fluidized bed under power ultrasound. Ultrason. Sonochem. 2019, 56, 273–283. [Google Scholar] [CrossRef] [PubMed]
- Hutchinson, B.; Lundin, P.; Lindh-Ulmgren, E.; Lévesque, D. Anomalous ultrasonic attenuation in ferritic steels at elevated temperatures. Ultrasonics 2016, 69, 268–272. [Google Scholar] [CrossRef] [PubMed]
- Robson, J.D.; Henry, D.T. Particle effects on recrystallization in magnesium-manganese alloys: Particle pining. Mater. Sci. Eng. A 2011, 528, 4239–4247. [Google Scholar] [CrossRef]
- Wang, J.; Lu, R.; Qin, D.; Huang, X.; Pan, F. A study of the ultrahigh damping capacities in Mg-Mn alloys. Mater. Sci. Eng. A 2013, 560, 667–671. [Google Scholar] [CrossRef]
- Rusinko, A. Analytical description of ultrasonic hardening and softening. Ultrasonics 2011, 51, 709–714. [Google Scholar] [CrossRef] [PubMed]
- Kelly, G.S.; Advani, S.G.; Gillespie, J.W., Jr.; Bogetti, T.A. A model to characterize acoustic softening during ultrasonic consolidation. J. Mater. Process. Technol. 2013, 213, 1835–1845. [Google Scholar] [CrossRef]
- Hu, J.; Shimizu, T.; Yang, M. Investigation on ultrasonic volume effects: Stress superposition, acoustic softening and dynamic impact. Ultrason. Sonochem. 2018, 48, 240–248. [Google Scholar] [CrossRef] [PubMed]
- Ramamurty, U.; Jang, J. Nanoindentation for probing the mechanical behavior of molecular crystals—A review of the technique and how to use it. Cryst. Eng. Comm. 2014, 16, 12–23. [Google Scholar] [CrossRef]
- Wang, Y.K.; Liu, W.S.; Ma, Y.Z. Indentation depth dependent micromechanical properties and rate dependent pop-in events of (Au, Cu)5Sn. Mater. Lett. 2014, 131, 57–60. [Google Scholar] [CrossRef]
- Jin, Y.J.; Khan, T.I. Effect of bonding time on microstructure and mechanical properties of transient liquid phase bonded magnesium AZ31 alloy. Mater. Des. 2012, 38, 32–37. [Google Scholar] [CrossRef]
- Siddiq, A.; Sayed, T.E. Acoustic softening in metals during ultrasonic assisted deformation via CP-FEM. Mater. Lett. 2011, 65, 356–359. [Google Scholar] [CrossRef]
- Siddiq, A.; Sayed, T.E. A thermomechanical crystal plasticity constitutive model for ultrasonic consolidation. Comput. Mater. Sci. 2012, 51, 241–251. [Google Scholar] [CrossRef]
- Huang, H.; Pequegnat, A.; Chang, B.H. Influence of superimposed ultrasound on deformability of Cu. J. Appl. Phys. 2009, 6, 113514. [Google Scholar] [CrossRef]
- Yao, Z.H.; Kim, G.Y.; Wang, Z.H. Acoustic softening and residual hardening in aluminum: Modeling and experiments. Int. J. Plast. 2012, 39, 75–87. [Google Scholar] [CrossRef]
- Yao, Z.; Mei, D.; Chen, Z. Modeling of metallic surface topography modification by high-frequency vibration. J. Sound Vibr. 2016, 363, 258–271. [Google Scholar] [CrossRef]
- Frost, H.J.; Ashby, M.F. Deformation-Mechanism Maps: The Plasticity and Creep of Metals and Ceramics, Firsted; Pergamon Press: Oxford, UK, 1982. [Google Scholar]
- Kocks, U.F. Constitutive Behavior Based on Crystal Plasticity, Unified Constitutive Equations for Creep and Plasticity; Springer: Dordrecht, The Netherlands, 1987; pp. 1–88. [Google Scholar]
- Barlat, F.; Glazov, M.V.; Brem, J.C.; Lege, D.J. A simple model for dislocation behavior, strain and strain rate hardening evolution in deforming aluminum alloys. Int. J. Plast. 2002, 18, 919–939. [Google Scholar] [CrossRef]
- Li, Q.Z.; Jiao, X. Recrystallization mechanism and activation energies of severely-deformed magnesium during annealing process. Materialia 2019, 5, 100188. [Google Scholar] [CrossRef]
- Tang, X.J.; Nie, Y.X.; Jin, Q. Kinetics and mechanism of ultrasonic-assisted magnesium oxide hydration. Ultrason. Sonochem. 2018, 40, 995–1002. [Google Scholar] [CrossRef] [PubMed]
- Sandlöbes, S.; Friák, M.; Neugebauer, J. Basal and non-basal dislocation slip in Mg-Y. Mater. Sci. Eng. A 2013, 576, 61–68. [Google Scholar] [CrossRef]
- Higashida, K.; Okazaki, S.; Morikawa, T. Burgers vector of crack tip dislocation in magnesium oxide crystals. Mater. Trans. 1998, 39, 967–974. [Google Scholar] [CrossRef]
- Garlea, E.; Radovic, M.; Liaw, P.K. High-temperature dependency of elastic mechanical behavior of two wrought magnesium alloys AS31B and ZK60A studied by resonant ultrasound spectroscopy. Mater. Sci. Eng. A 2019, 758, 86–95. [Google Scholar] [CrossRef]
- Fu, X.Q.; Liang, L.H.; Wei, Y.G. Atomistic simulation study on the shear behavior of Ag/MgO interface. Comput. Mater. Sci. 2018, 155, 116–128. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, Y.; Zhang, J.; Ma, R.; Liu, Y.; Wang, Y.; Zhang, Q.; Li, W.; Zhang, Y. Quantitative analysis on friction stress of hot-extruded AZ31magnesium alloy at room temperature. J. Mater. Sci. Technol. 2018, 34, 1765–1772. [Google Scholar] [CrossRef]
- Wachtman, J.B. Mechanical and Thermal Properties of Ceramics; National Bureau of Standards Special Publication: Washington, DC, USA, 1969; p. 231. [Google Scholar]
- Larche, F.C.; Voorhees, P.W. Diffusion and stresses, basic thermodynamics. Defect Diffus. 1996, 129, 31–36. [Google Scholar] [CrossRef]
- Fischer, F.D.; Svoboda, J. Deformation and diffusion interactions in solids-A simulation study. J. Mech. Phys. Solids 2015, 78, 427–442. [Google Scholar] [CrossRef]
- Larcht’e, F.C.; Cahn, J. The effect of self-stress on diffusion in solids. Acta Metall. 1982, 30, 1835–1845. [Google Scholar] [CrossRef]
- Balluffi, R.W. Kinetics of Materials; Wiley-Interscience: Hoboken, NJ, USA, 2005. [Google Scholar]
- Liu, Y.; Yu, W.; Liu, Y.Z. Effect of ultrasound on dissolution of Al in Sn. Ultrason. Sonochem. 2019, 50, 67–73. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Yan, J.; Zhang, B.; Kong, X.; Yang, S. Behaviors of oxide film at the ultrasonic aided interaction interface of Zn-Al alloys and Al2O3/6061Al composites in air. Mater. Sci. Eng. A 2006, 45, 80–86. [Google Scholar] [CrossRef]
- Tzanakis, I.; Xu, W.W.; Lebon, G.S.B.; Eskin, D.G. In Situ synchrotron radiography and spectrum analysis of transient cavitation bubbles in molten aluminum alloy. Phys. Procedia 2015, 70, 841–845. [Google Scholar] [CrossRef]
- Li, Z.; Xu, Z.; Ma, L.; Wang, S.; Liu, X.; Yan, J. Cavitation at filler metal/substrate interface during ultrasonic-assisted soldering. Part I: Cavitation characteristics. Ultrason. Sonochem. 2018, 49, 249–259. [Google Scholar] [CrossRef] [PubMed]






| Point | Mg (at %) | Ni (at %) | Possible Phase |
|---|---|---|---|
| A | 68.23 | 31.77 | Mg2Ni |
| B | 66.89 | 33.11 | Mg2Ni |
| C | 4.10 | 95.90 | Ni |
| D | 66.92 | 33.08 | Mg2Ni |
| E | 98.85 | 1.15 | α-Mg(Ni) |
| F | 67.04 | 32.96 | Mg2Ni |
| G | 97.80 | 2.20 | α-Mg(Ni) |
| H | 78.76 | 21.24 | Mg2Ni + α-Mg(Ni) |
| I | 98.90 | 1.10 | α-Mg(Ni) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Yang, C.; Peng, Z.; Wu, Z.; Cui, Z. Microstructure and Formation Mechanism of Ultrasound-Assisted Transient Liquid Phase Bonded Magnesium Alloys with Ni Interlayer. Materials 2019, 12, 3732. https://doi.org/10.3390/ma12223732
Li Y, Yang C, Peng Z, Wu Z, Cui Z. Microstructure and Formation Mechanism of Ultrasound-Assisted Transient Liquid Phase Bonded Magnesium Alloys with Ni Interlayer. Materials. 2019; 12(22):3732. https://doi.org/10.3390/ma12223732
Chicago/Turabian StyleLi, Yinan, Chengfei Yang, Zilong Peng, Zhiyuan Wu, and Zhuang Cui. 2019. "Microstructure and Formation Mechanism of Ultrasound-Assisted Transient Liquid Phase Bonded Magnesium Alloys with Ni Interlayer" Materials 12, no. 22: 3732. https://doi.org/10.3390/ma12223732
APA StyleLi, Y., Yang, C., Peng, Z., Wu, Z., & Cui, Z. (2019). Microstructure and Formation Mechanism of Ultrasound-Assisted Transient Liquid Phase Bonded Magnesium Alloys with Ni Interlayer. Materials, 12(22), 3732. https://doi.org/10.3390/ma12223732