A New Approach of Mathematical Analysis of Structure of Graphene as a Potential Material for Composites
Abstract
:1. Introduction
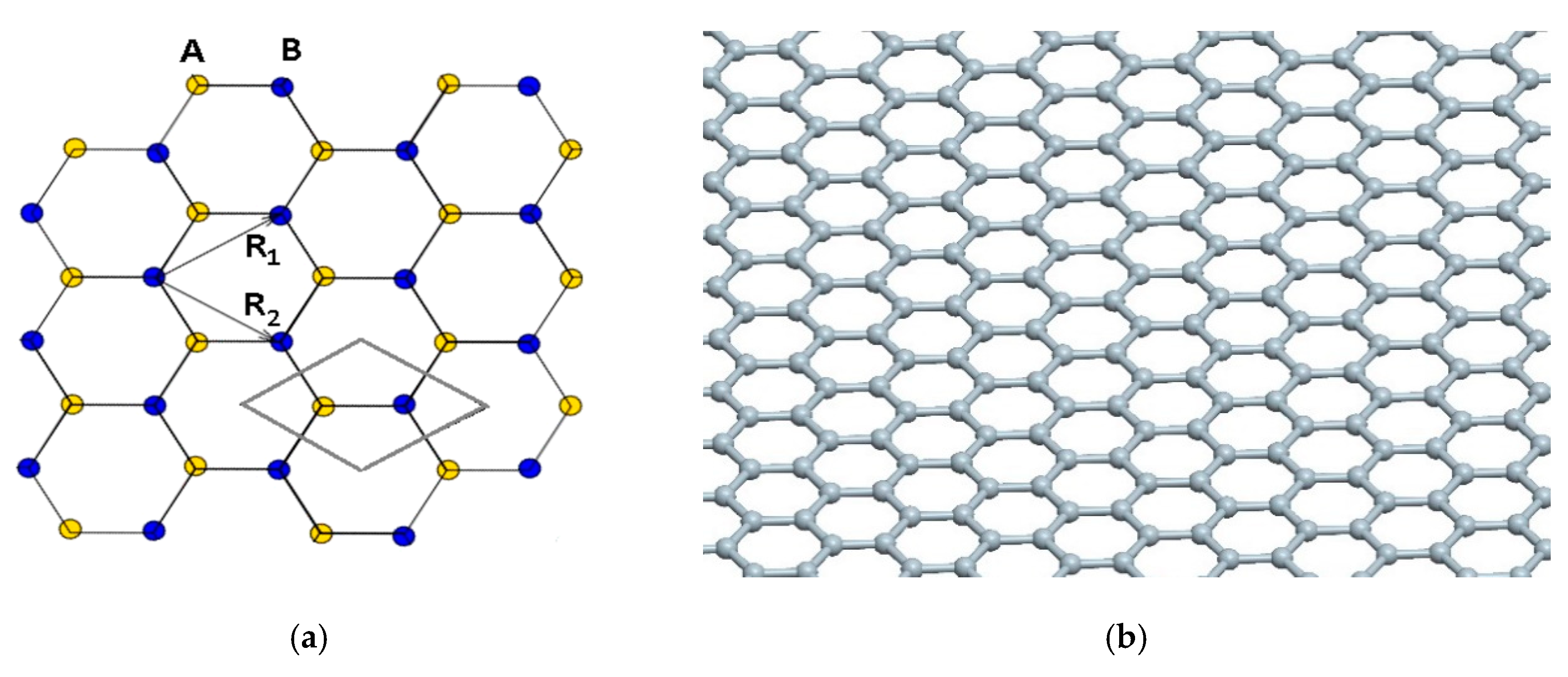
2. Assumptions for Modeling the Graphene Structure
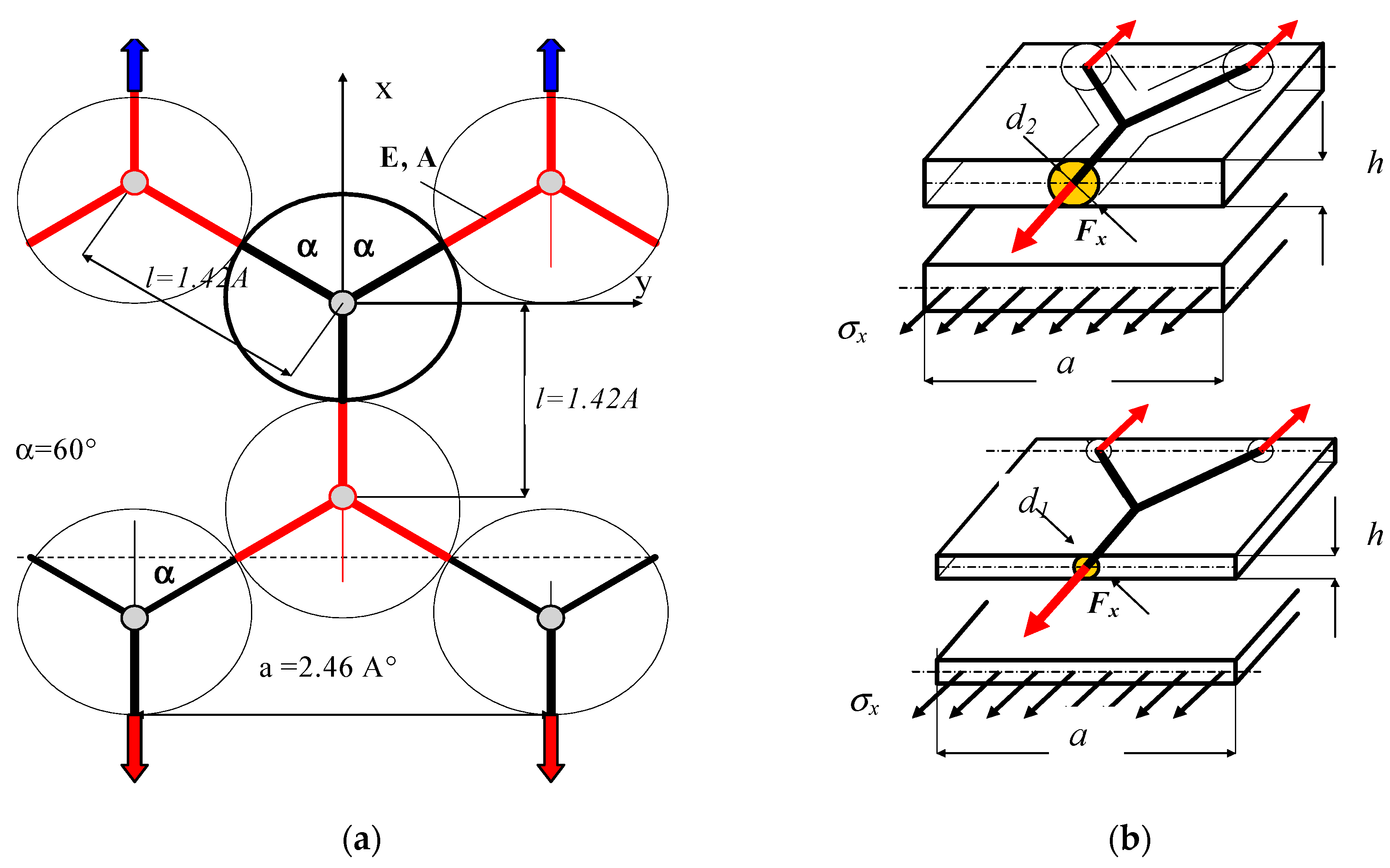
3. Basic Model of Graphene Cell (Calculations of Strains)
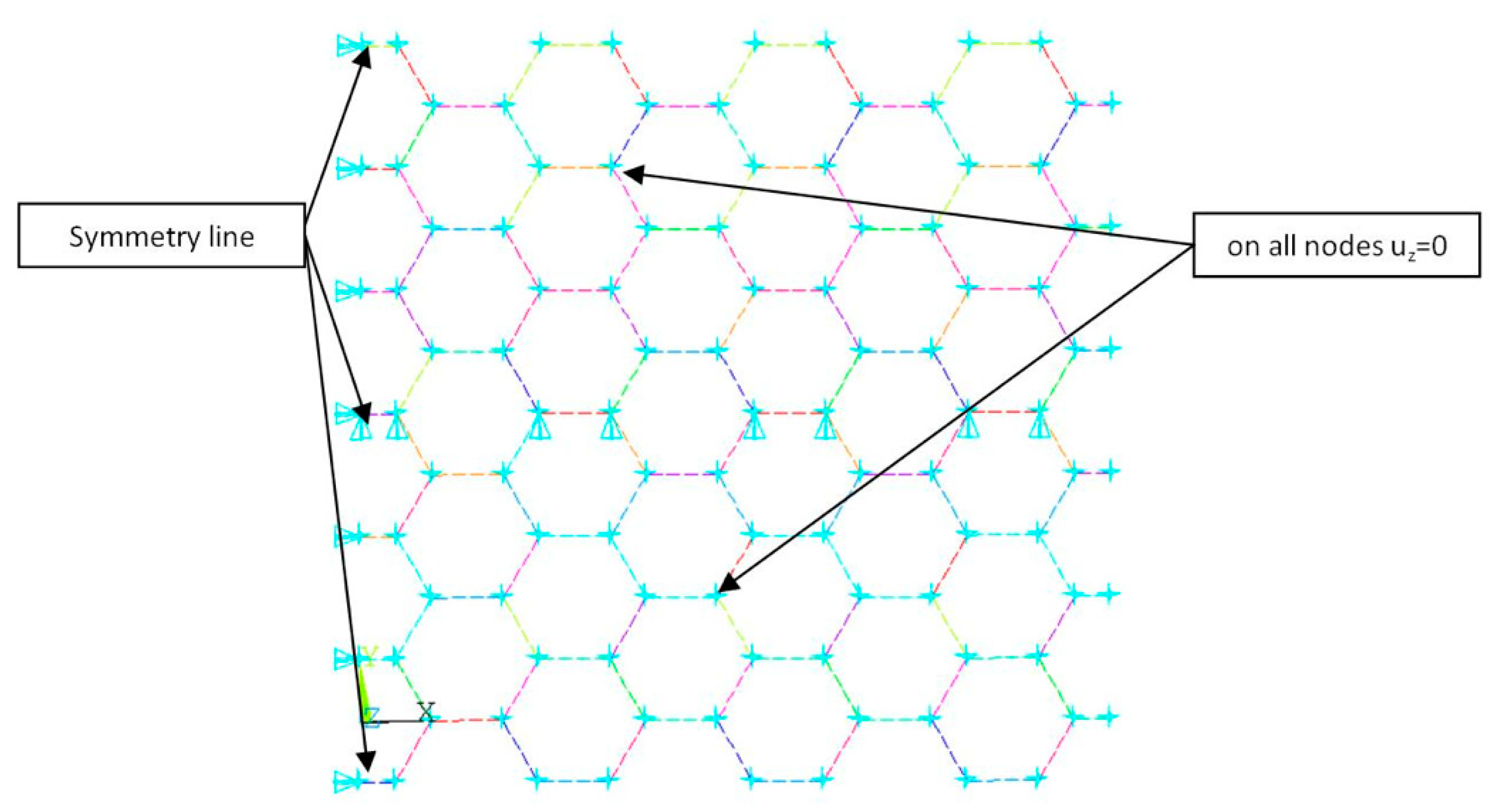
4. Numerical Model of Graphene Band
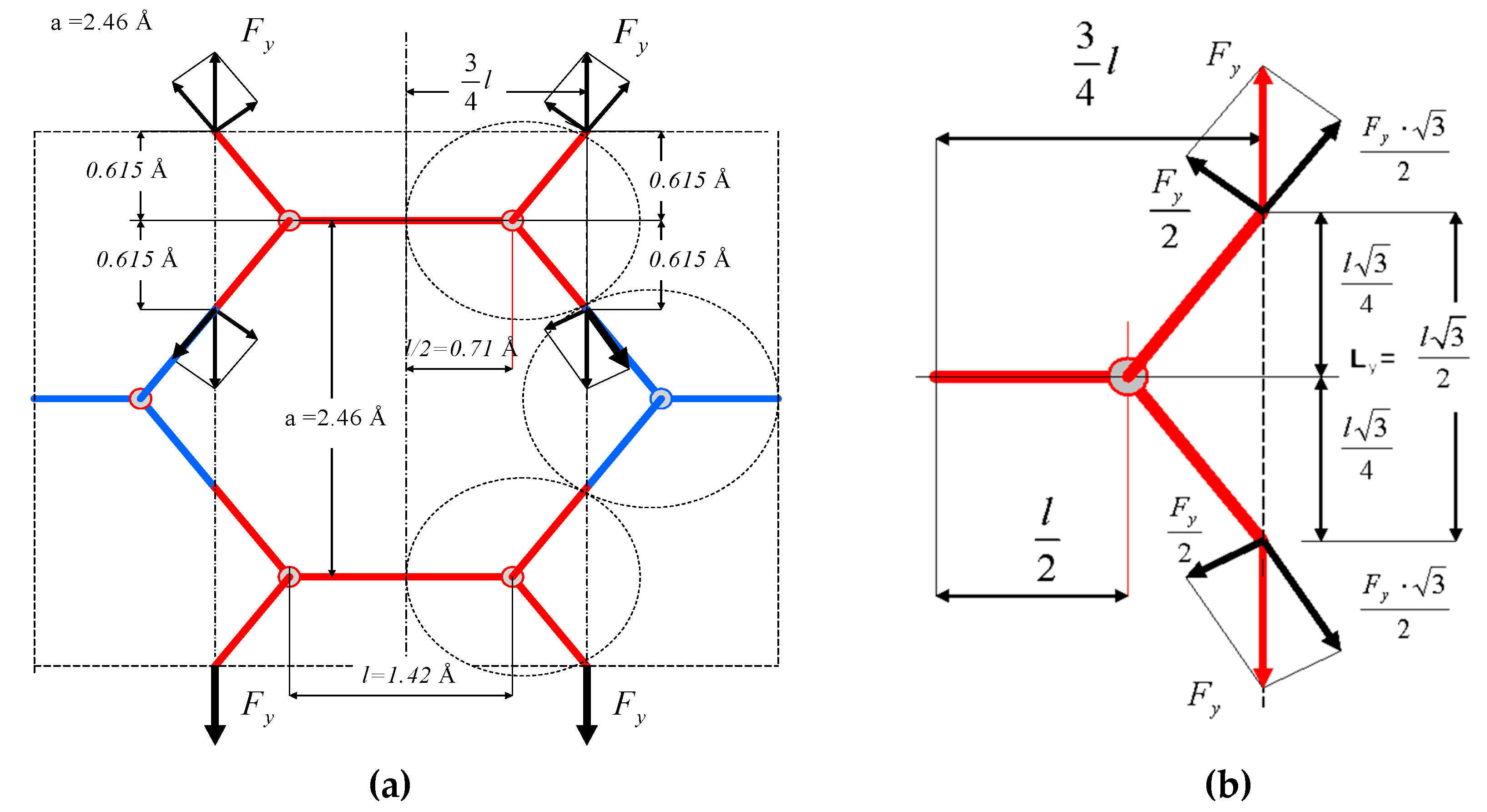
5. The Strain in y-Direction
6. Results
7. Strains in Both Directions
8. Summary
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Dimension between atoms bond | |
| Length of graphene bar | |
| Diameter of graphene bar | |
| Thickness of single graphene sheet for one layer | |
| Length of segment | |
| Tension force for armchair edge (x-direction) | |
| Tension force for zigzag edge (y-direction) | |
| Angle between graphene bar | |
| Increment of elongation of segment caused by tension | |
| Increment of elongation of bar | |
| Total elongation caused by bending | |
| Young’s modulus of segment of graphene sheet | |
| Young’s modulus of graphene bar | |
| Moment of inertia of graphene bar | |
| Cross-section area | |
| Total increment of elongation due to bending and tension | |
| Length of graphene segment | |
| Poisson’s ratio for graphene bar | |
| Poisson’s ratio for graphene cut-out for x-direction | |
| Poisson’s ratio for graphene cut-out for y-direction | |
| Strain of segment in x-direction caused by tension and bending in x-direction | |
| Strain of segment in y-direction caused by tension and bending in x-direction | |
| Strain in x-direction of alternative segment in x-direction | |
| Strain of segment in y-direction caused by tension and bending in y-direction | |
| Strain of segment in x-direction caused by tension and bending in y-direction | |
| Strain in y-direction of alternative segment in y-direction | |
| νxy | Poisson’s ratio of graphene calculated for two perpendicular forces |
| kxy | Ratio of forces |
References
- Zhou, B.L.; Zhou, B.H.; Chen, X.W.; Zhou, G.H.; Zhou, G. Electronic transport for impurity-doped armchair-edge graphene nanoribbons. Eur. Phys. J. B 2012, 85, 85–121. [Google Scholar] [CrossRef]
- Shin, S.; Kim, J.; Kim, J.H.; Kim, S.I. Enhanced performance of organic light-emitting diodes by using hybrid anodes composed of graphene and conducting polimer. Curr. Appl. Phys. 2013, 13, 144–147. [Google Scholar] [CrossRef]
- Atabaki, M.M.; Kovacevic, R. Graphene composites as anode materials in lithium-ion batteries. Electron. Mater. Lett. 2013, 9, 133–153. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, X.; Yan, X.; Chen, Y.; Tian, J. Nonlinear optical properties of graphene-based materials. Chin. Sci. Bull. 2012, 57, 2971–2982. [Google Scholar] [CrossRef]
- Yamuna, R.; Ramakrishnan, S.; Dhara, K.; Devi, R.; Kothurkar, N.K.; Kirubha, E.; Palanisamy, P.K. Synthesis, characterization, and nonlinear optical properties of graphene oxide functionalized with tetra-amino porphyrin. J. Nanopart. Res. 2013, 15, 1399. [Google Scholar] [CrossRef]
- Yang, Y.E.; Yang, Y.R.; Yan, X.H. Universal optical properties of graphene nanoribbons: A first-principles study. Phys. E Low Dimens. Syst. Nano Struct. 2012, 44, 1406–1409. [Google Scholar] [CrossRef]
- Gao, Y.; Hao, P. Mechanical properties of monolayer graphene under tensile and compressive loading. Phys. E Low Dimens. Syst. Nanostruct. 2009, 41, 1561–1566. [Google Scholar] [CrossRef]
- Ferralis, N. Probing mechanical properties of graphene with Raman spectroscopy. J. Mater. Sci. 2010, 45, 5135–5149. [Google Scholar] [CrossRef]
- Xiao, J.R.; Staniszewski, J.; Gillespie, J.W., Jr. Tensile behaviors of graphene sheets and carbon nanotubes with multiple Stone–Wales defects. Mater. Sci. Eng. A 2010, 527, 715–723. [Google Scholar] [CrossRef]
- Park, H.J.; Meyer, J.; Roth, S.; Skákalová, V. Growth and properties of few-layer graphene prepared by chemical vapor deposition. Carbon 2010, 48, 1088–1094. [Google Scholar] [CrossRef]
- Georgantzinos, S.; Giannopoulos, G.; Anifantis, N.; Georgantzinos, S. Numerical investigation of elastic mechanical properties of graphene structures. Mater. Des. 2010, 31, 4646–4654. [Google Scholar] [CrossRef]
- Ni, Z.; Bu, H.; Zou, M.; Yi, H.; Bi, K.; Chen, Y. Anisotropic mechanical properties of graphene sheets from molecular dynamics. Phys. B Condens. Matter 2010, 405, 1301–1306. [Google Scholar] [CrossRef]
- Soldano, C.; Mahmood, A.; Dujardin, E. Production, properties and potential of graphene. Carbon 2010, 48, 2127–2150. [Google Scholar] [CrossRef]
- Kula, P.; Szymanski, W.; Kolodziejczyk, L.; Atraszkiewicz, R.; Grabarczyk, J.; Clapa, M.; Kaczmarek, L.; Jedrzejczak, A.; Niedzielski, P. High strength metallurgical graphene for hydrogen storage nanocomposites. Vacuum 2016, 129, 79–85. [Google Scholar] [CrossRef]
- Kula, P.; Kaczmarek, L.; Zawadzki, P.; Kołodziejczyk, L.; Szymanski, W.; Niedzielski, P.; Pietrasik, R.; Dybowski, K.; Kazimierski, D.; Nowak, D. Functionality of graphene as a result of its heterogenic growth on SiC nanoparticles on the basis of reversible hydrogen storage. Int. J. Hydrogen Energy 2014, 39, 19662–19671. [Google Scholar] [CrossRef]
- Tu, Z.C.; Ou-Yang, Z.C. Single-walled and multi-walled carbon nanotubes viewed as elastic tubes with the effective Young’s moduli dependent on layer number. Phys. Rev. B 2002, 65, 233407. [Google Scholar] [CrossRef]
- Meguid, S.; Wernik, J.; Cheng, Z. Atomistic-based continuum representation of the effective properties of nano-reinforced epoxies. Int. J. Solids Struct. 2010, 47, 1723–1736. [Google Scholar] [CrossRef]
- Zhao, P.; Shi, G. Study of poisson’s ratios of graphene and single-walled carbon nanotubes based on an improved molecular structural mechanics model. SL 2011, 5, 49–58. [Google Scholar]
- Zhao, H.; Min, K.; Aluru, N.R. Size and Chirality Dependent Elastic Properties of Graphene Nanoribbons under Uniaxial Tension. Nano Lett. 2009, 9, 3012–3015. [Google Scholar] [CrossRef]
- Baykasoglu, C.; Kirca, M.; Mugan, A. Nonlinear failure analysis of carbon nanotubes by using molecular-mechanics based models. Compos. Part B Eng. 2013, 50, 150–157. [Google Scholar] [CrossRef]
- Frank, I.W.; Tanenbaum, D.M.; Van Der Zande, A.M.; McEuen, P.L. Mechanical properties of suspended graphene sheets. J. Vac. Sci. Technol. B. 2007, 25, 2558–2561. [Google Scholar] [CrossRef]
- Cao, G. Atomistic Studies of Mechanical Properties of Graphene. Polymers 2014, 6, 2404–2432. [Google Scholar] [CrossRef]
- Akinwande, D.; Brennan, C.J.; Bunch, J.S.; Egberts, P.; Felts, J.R.; Gao, H.; Huang, R.; Kim, J.S.; Li, T.; Li, Y.; et al. A review on mechanics and mechanical properties of 2D materials—Graphene and beyond. Extrem. Mech. Lett. 2017, 13, 42–77. [Google Scholar] [CrossRef]
- Tian, W.; Li, W.; Yu, W.; Liu, X. A Review on Lattice Defects in Graphene: Types, Generation, Effects and Regulation. Micromachines 2017, 8, 163. [Google Scholar] [CrossRef]
- Peng, Q.; Chen, Z.; De, S. A Density Functional Theory Study of the Mechanical Properties of Graphane with van der Waals Corrections. Mech. Adv. Mater. Struct. 2015, 22, 717–721. [Google Scholar] [CrossRef]
- Kvashnin, A.G.; Sorokin, P.B.D.; Kvashnin, G. The Theoretical Study of Mechanical Properties of Graphene Membranes. Fuller. Nanotub. Carbon Nanostruct. 2010, 18, 497–500. [Google Scholar] [CrossRef]
- Meo, M.; Rossi, M. A molecular-mechanics based finite element model for strength prediction of single wall carbon nanotubes. Mater. Sci. Eng. A 2007, 454, 170–177. [Google Scholar] [CrossRef]
- Liu, B.; Huang, Y.; Jiang, H.; Qu, S.; Hwang, K.C. The atomic-scale finite element method. Comput. Methods Appl. Mech. Eng. 2004, 193, 1849–1864. [Google Scholar] [CrossRef]
- Wernik, J.M.; Meguid, S.A. Recent Developments in Multifunctional Nanocomposites Using Carbon Nanotubes. Appl. Mech. Rev. 2010, 63, 050801. [Google Scholar] [CrossRef]
- Liu, B.; Jiang, H.; Huang, Y.; Qu, S.; Yu, M.F.; Hwang, K.C. Atomic-scale finite element method in multiscale computation with applications to carbon nanotubes. Phys. Rev. B 2005, 72, 035435. [Google Scholar] [CrossRef]
- Song, Y.S.; Youn, J.R. Modeling of effective elastic properties for polymer based carbon nanotube composites. Polymer 2006, 47, 1741–1748. [Google Scholar] [CrossRef]
- Meo, M.; Rossi, M. Prediction of Young’s modulus of single wall carbon nanotubes by molecular-mechanics based finite element modelling. Compos. Sci. Technol. 2006, 66, 1597–1605. [Google Scholar] [CrossRef]
- Lei, X.; Natsuki, T.; Shi, J.; Ni, Q.Q. Analysis of Carbon Nanotubes on the Mechanical Properties at Atomic Scale. J. Nanomater. 2011, 2011, 805313. [Google Scholar] [CrossRef] [Green Version]
- Parvaneh, V.; Shariati, M.; Torabi, H. Bending buckling behavior of perfect and defective single-walled carbon nanotubes via a structural mechanics model. Acta Mech. 2012, 223, 2369–2378. [Google Scholar] [CrossRef]
- Tserpes, K.; Papanikos, P.; Labeas, G.; Pantelakis, S. Multi-scale modeling of tensile behavior of carbon nanotube-reinforced composites. Theor. Appl. Fract. Mech. 2008, 49, 51–60. [Google Scholar] [CrossRef]
- Tserpes, K.; Papanikos, P. The effect of Stone–Wales defect on the tensile behavior and fracture of single-walled carbon nanotubes. Compos. Struct. 2007, 79, 581–589. [Google Scholar] [CrossRef]
- Mohammadpour, E.; Awang, M. Predicting the nonlinear tensile behavior of carbon nanotubes using finite element simulation. Appl. Phys. A 2011, 104, 609–614. [Google Scholar] [CrossRef]
- Wernik, J.M.; Meguid, S.A. Atomistic-based continuum modeling of the nonlinear behaviour of carbon nanotubes. Acta Mech. 2010, 212, 167–179. [Google Scholar] [CrossRef]
- Xiao, J.R.; Staniszewski, J.; Gillespie, J.W. Fracture and progressive failure of defective graphene sheets and carbon nanotubes. Compos. Struct. 2009, 88, 602–609. [Google Scholar] [CrossRef]
- Rao, P.S.; Anandatheertha, S.; Naik, G.N.; Gopalakrishnan, S. Estimation of mechanical properties of single wall carbon nanotubes using molecular mechanics approach. Sadhana 2015, 40, 1301–1311. [Google Scholar] [CrossRef]
- Bernholc, J.; Brabec, C.J.; Yakobson, B.I. Nanomechanics of Carbon Tubes: Instabilities beyond Linear Response. Phys. Rev. Lett. 1996, 76, 2511–2514. [Google Scholar]
- Chen, X.; Cao, G. A structural mechanics study of single-walled carbon nanotubes generalized from atomistic simulation. Nanotechnology 2006, 17, 1004–1015. [Google Scholar] [CrossRef] [PubMed]
- Tserpes, K.I.; Papanikos, P. Finite element modeling of single-walled carbon nanotubes. Compos. Part B 2005, 36, 468–477. [Google Scholar] [CrossRef]
- Nahas, M.N.; Abd-Rabou, M. Finite Element Modeling of Carbon Nanotubes. Int. J. Mech. Mechatron. Eng. 2010, 10, 19–24. [Google Scholar]
- Gupta, S.S.; Bosco, F.G.; Batra, R.C. Wall thickness and elastic moduli of single-walled carbon nanotubes from frequencies of axial, torsional and inextensional modes of vibration. Comput. Mater. Sci. 2010, 47, 1049–1059. [Google Scholar] [CrossRef]
- Belytschko, T.; Xiao, S.P.; Schatz, G.C.; Ruoff, R.S. Atomistic simulations of nanotube fracture. Phys. Rev. B 2002, 65, 235430. [Google Scholar] [CrossRef] [Green Version]
- Fan, N.; Ren, Z.; Jing, G.; Guo, J.; Peng, B.; Jiang, H. Numerical Investigation of the Fracture Mechanism of Defective Graphene Sheets. Materials 2017, 10, 164. [Google Scholar] [CrossRef] [Green Version]
- Tserpes, K.; Papanikos, P.; Tsirkas, S. A progressive fracture model for carbon nanotubes. Compos. Part B Eng. 2006, 37, 662–669. [Google Scholar] [CrossRef]
- Kim, J.; Lee, N.; Min, Y.H.; Noh, S.; Kim, N.K.; Jung, S.; Joo, M.; Yamada, Y. Distinguishing Zigzag and Armchair Edges on Graphene Nanoribbons by X-ray Photoelectron and Raman Spectroscopies. ACS Omega 2018, 3, 17789–17796. [Google Scholar] [CrossRef] [Green Version]
- Geim, A.; Novoselov, K. Graphene: Scientific Background on the Nobel Prize in Physics 2010; The Royal Swedish Academy of Sciences: Stockholm, Sweden, 2010. [Google Scholar]
- Timoshenko, S.; Gere, J.M. Theory of Elastic Stability, 2nd ed.; Dover Publications: Mineola, NY, USA, 2009. [Google Scholar]




| Number of Calculation Variant | Direction of Tension | l (Å) | a (Å) | h (Å) | d (Å) | Y (Tpa) | (-) | EGr (TPa) (Equation (10)) | (-) (Equation (12)) (Equation (17)) | (-) FEM |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | x | 1.42 | 2.46 | 0.44 | 0.44 | 1.15 | 0.3 | 40.95 | 0.800 | 0.812 |
| 2 | x | 1.42 | 2.46 | 0.75 | 0.75 | 1.15 | 0.3 | 13.09 | 0.663 | 0.666 |
| 3 | x | 1.42 | 2.46 | 0.89 | 0.89 | 1.15 | 0.3 | 9.630 | 0.580 | 0.620 |
| 4 | x | 1.42 | 2.46 | 1.00 | 1.00 | 1.15 | 0.3 | 7.932 | 0.546 | 0.59 |
| 5 | x | 1.42 | 2.46 | 1.42 | 1.42 | 1.15 | 0.3 | 4.727 | 0.463 | 0.515 |
| 6 | x | 1.42 | 2.46 | 2.00 | 2.00 | 1.15 | 0.3 | 3.058 | 0.411 | 0.471 |
| 7 | x | 1.42 | 2.46 | 2.42 | 2.42 | 1.15 | 0.3 | 2.448 | 0.392 | 0.453 |
| 8 | y | 1.42 | 2.46 | 0.44 | 0.44 | 1.15 | 0.3 | 40.94 | 0.800 | 0.791 |
| 9 | y | 1.42 | 2.46 | 0.75 | 0.75 | 1.15 | 0.3 | 13.08 | 0.633 | 0.618 |
| 10 | y | 1.42 | 2.46 | 0.89 | 0.89 | 1.15 | 0.3 | 9.620 | 0.580 | 0.564 |
| 11 | y | 1.42 | 2.46 | 1.00 | 1.00 | 1.15 | 0.3 | 7.930 | 0.546 | 0.527 |
| 12 | y | 1.42 | 2.46 | 1.42 | 1.42 | 1.15 | 0.3 | 4.726 | 0.463 | 0.445 |
| 13 | y | 1.42 | 2.46 | 2.00 | 2.00 | 1.15 | 0.3 | 3.057 | 0.411 | 0.394 |
| 14 | y | 1.42 | 2.46 | 2.42 | 2.42 | 1.15 | 0.3 | 2.448 | 0.392 | 0.373 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jaroniek, M.; Czechowski, L.; Kaczmarek, Ł.; Warga, T.; Kubiak, T. A New Approach of Mathematical Analysis of Structure of Graphene as a Potential Material for Composites. Materials 2019, 12, 3918. https://doi.org/10.3390/ma12233918
Jaroniek M, Czechowski L, Kaczmarek Ł, Warga T, Kubiak T. A New Approach of Mathematical Analysis of Structure of Graphene as a Potential Material for Composites. Materials. 2019; 12(23):3918. https://doi.org/10.3390/ma12233918
Chicago/Turabian StyleJaroniek, Mieczysław, Leszek Czechowski, Łukasz Kaczmarek, Tomasz Warga, and Tomasz Kubiak. 2019. "A New Approach of Mathematical Analysis of Structure of Graphene as a Potential Material for Composites" Materials 12, no. 23: 3918. https://doi.org/10.3390/ma12233918
APA StyleJaroniek, M., Czechowski, L., Kaczmarek, Ł., Warga, T., & Kubiak, T. (2019). A New Approach of Mathematical Analysis of Structure of Graphene as a Potential Material for Composites. Materials, 12(23), 3918. https://doi.org/10.3390/ma12233918







