Chain Model for Carbon Nanotube Bundle under Plane Strain Conditions
Abstract
1. Introduction
2. Materials and Methods
3. Results
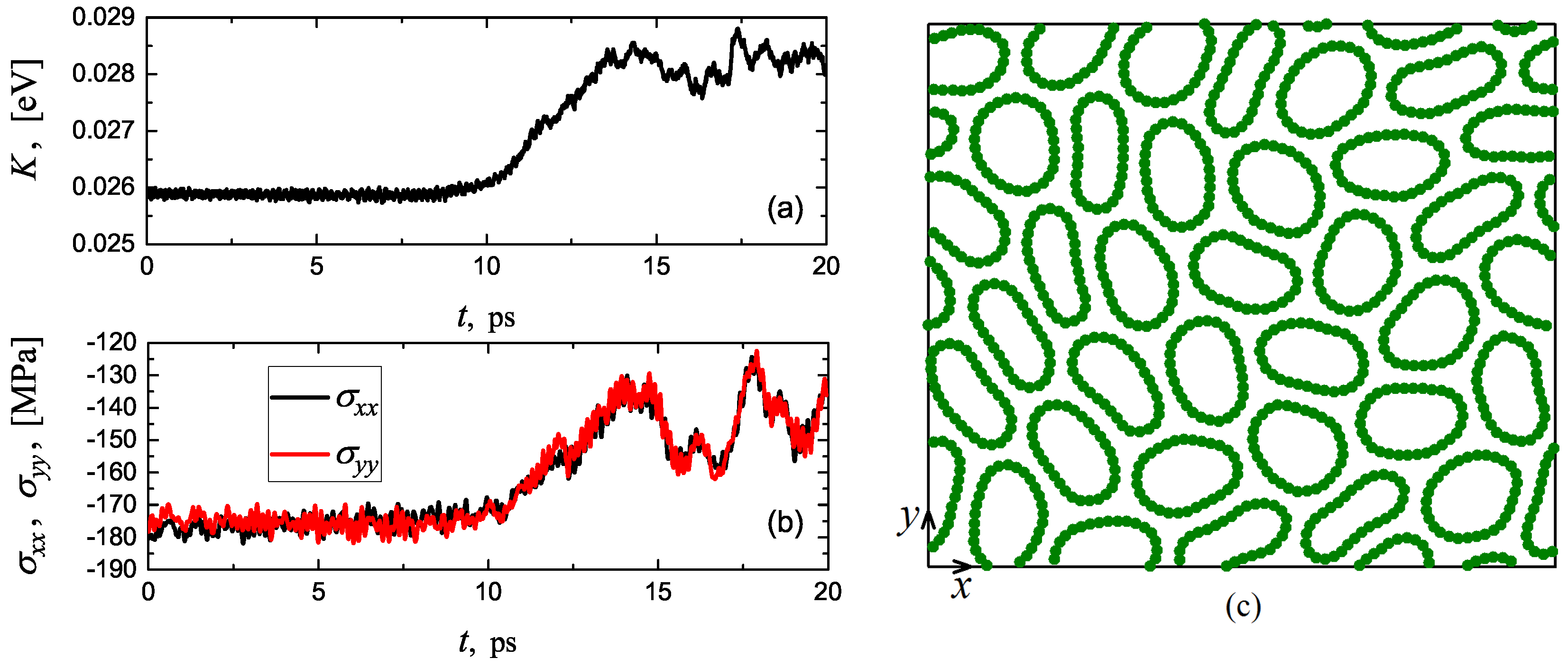
3.1. Energy and Stress in the System
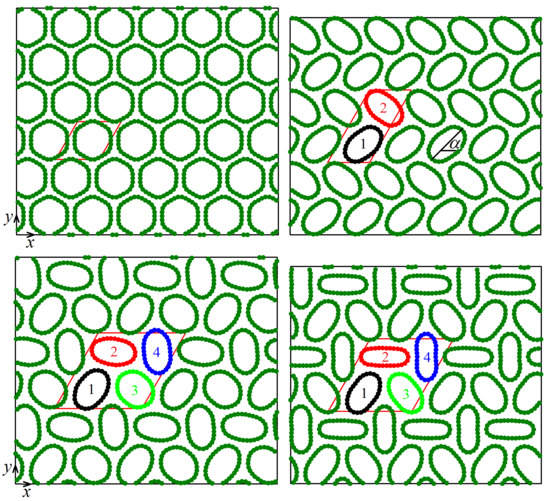
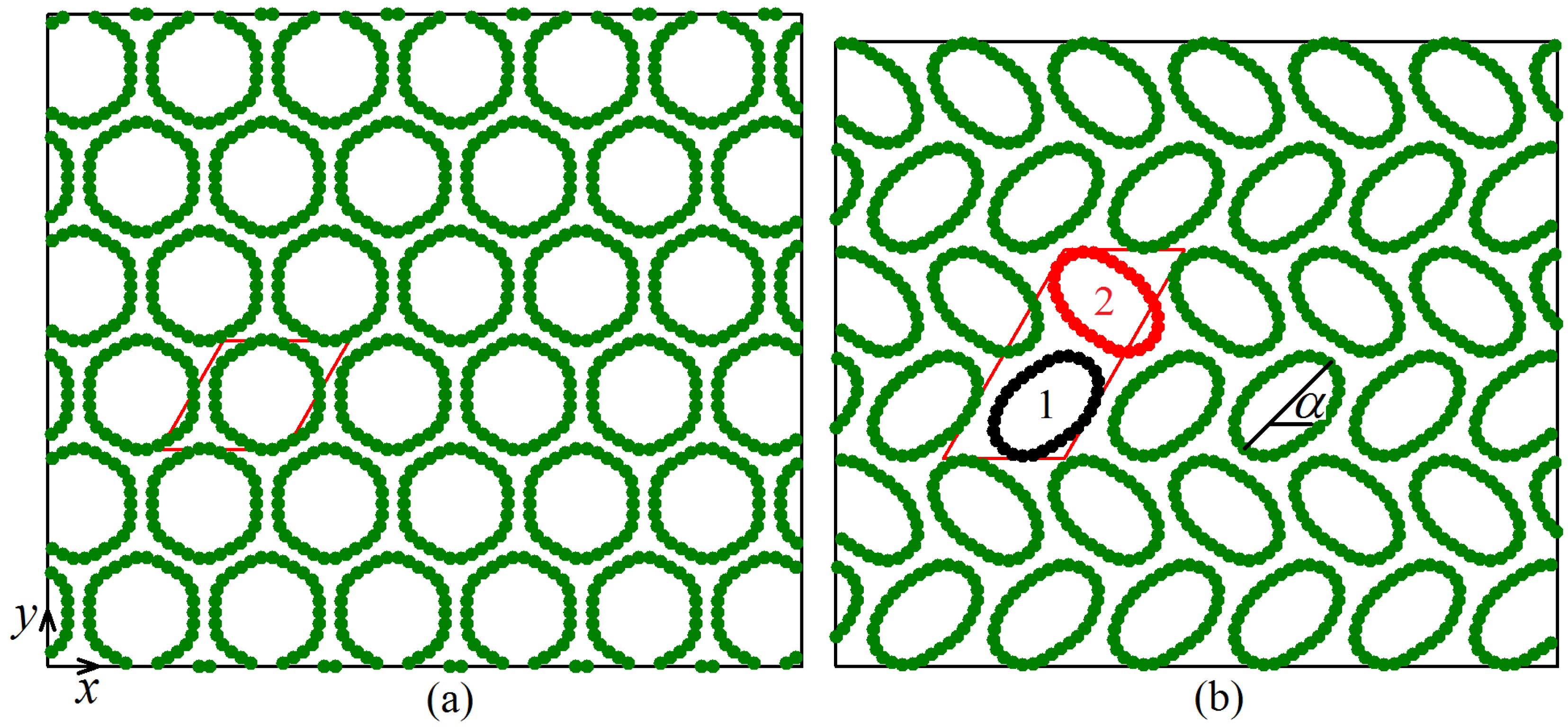
3.2. Geometry of CNTs
3.3. Temperature Effect
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pérez, E.M.; Martín, N. Curves ahead: Molecular receptors for fullerenes based on concave-convex complementarity. Chem. Soc. Rev. 2008, 37, 1512–1519. [Google Scholar] [CrossRef] [PubMed]
- Lyapin, A.G.; Brazhkin, V.V.; Lyapin, S.G.; Popova, S.V.; Varfolomeeva, T.D.; Voloshin, R.A.; Pronin, A.A.; Sluchanko, N.E.; Gavrilyuk, A.G.; Trojan, I.A. Non-traditional carbon semiconductors prepared from fullerite C60 and carbyne under high pressure. Phys. Status Solidi B 1999, 211, 401–412. [Google Scholar] [CrossRef]
- Popov, M.; Koga, Y.; Fujiwara, S.; Mavrin, B.N.; Blank, V.D. Carbon nanocluster-based superhard materials. New Diam. Front. Carbon Technol. 2002, 12, 229–260. [Google Scholar]
- Ferrari, A.C. Raman spectroscopy of graphene and graphite: Disorder, electron-phonon coupling, doping and nonadiabatic effects. Solid State Commun. 2007, 143, 47–57. [Google Scholar] [CrossRef]
- Ghosh, S.; Nika, D.L.; Pokatilov, E.P.; Balandin, A.A. Heat conduction in graphene: Experimental study and theoretical interpretation. New J. Phys. 2009, 11, 095012. [Google Scholar] [CrossRef]
- Tersoff, J.; Ruoff, R.S. Structural properties of a carbon-nanotube crystal. Phys. Rev. Lett. 1994, 73, 676–679. [Google Scholar] [CrossRef]
- Thess, A.; Lee, R.; Nikolaev, P.; Dai, H.; Petit, P.; Robert, J.; Xu, C.; Lee, Y.H.; Kim, S.G.; Rinzler, A.G.; et al. Crystalline ropes of metallic carbon nanotubes. Science 1996, 273, 483–487. [Google Scholar] [CrossRef]
- Saether, E.; Frankland, S.J.V.; Pipes, R.B. Transverse mechanical properties of single-walled carbon nanotube crystals. Part I: Determination of elastic moduli. Compos. Sci. Technol. 2003, 63, 1543–1550. [Google Scholar] [CrossRef]
- Rakov, E.G. Materials made of carbon nanotubes. The carbon nanotube forest. Russ. Chem. Rev. 2013, 82, 538–566. [Google Scholar] [CrossRef]
- Chen, H.; Roy, A.; Baek, J.-B.; Zhu, L.; Qu, J.; Dai, L. Controlled growth and modification of vertically-aligned carbon nanotubes for multifunctional applications. Mater. Sci. Eng. R Rep. 2010, 70, 63–91. [Google Scholar] [CrossRef]
- Bedewy, M.; Meshot, E.R.; Guo, H.; Verploegen, E.A.; Lu, W.; Hart, A.J. Collective mechanism for the evolution and self-termination of vertically aligned carbon nanotube growth. J. Phys. Chem. C 2009, 113, 20576–20582. [Google Scholar] [CrossRef]
- Lan, Y.; Wang, Y.; Ren, Z.F. Physics and applications of aligned carbon nanotubes. Adv. Phys. 2011, 60, 553–678. [Google Scholar] [CrossRef]
- Yu, M.-F.; Files, B.S.; Arepalli, S.; Ruoff, R.S. Tensile loading of ropes of single wall carbon nanotubes and their mechanical properties. Phys. Rev. Lett. 2000, 84, 5552–5555. [Google Scholar] [CrossRef] [PubMed]
- Dhanabalan, S.C.; Dhanabalan, B.; Chen, X.; Ponraj, J.S.; Zhang, H. Hybrid carbon nanostructured fibers: Stepping stone for intelligent textile-based electronics. Nanoscale 2019, 11, 3046–3101. [Google Scholar] [CrossRef] [PubMed]
- Bai, Y.; Zhang, R.; Ye, X.; Zhu, Z.; Xie, H.; Shen, B.; Cai, D.; Liu, B.; Zhang, C.; Jia, Z.; et al. Carbon nanotube bundles with tensile strength over 80 GPa. Nat. Nanotechnol. 2018, 13, 589–595. [Google Scholar] [CrossRef] [PubMed]
- Qiu, L.; Wang, X.; Tang, D.; Zheng, X.; Norris, P.M.; Wen, D.; Zhao, J.; Zhang, X.; Li, Q. Functionalization and densification of inter-bundle interfaces for improvement in electrical and thermal transport of carbon nanotube fibers. Carbon 2016, 105, 248–259. [Google Scholar] [CrossRef]
- Cho, H.; Lee, H.; Oh, E.; Lee, S.-H.; Park, J.; Park, H.J.; Yoon, S.-B.; Lee, C.-H.; Kwak, G.-H.; Lee, W.J.; et al. Hierarchical structure of carbon nanotube fibers, and the change of structure during densification by wet stretching. Carbon 2018, 136, 409–416. [Google Scholar] [CrossRef]
- Fernández-Toribio, J.C.; Alemán, B.; Ridruejo, Á.; Vilatela, J.J. Tensile properties of carbon nanotube fibres described by the fibrillar crystallite model. Carbon 2018, 133, 44–52. [Google Scholar] [CrossRef]
- Dang, Z.-M.; Yuan, J.-K.; Zha, J.-W.; Zhou, T.; Li, S.-T.; Hu, G.-H. Fundamentals, processes and applications of high-permittivity polymer-matrix composites. Prog. Mater. Sci. 2012, 57, 660–723. [Google Scholar] [CrossRef]
- Bakshi, S.R.; Lahiri, D.; Agarwal, A. Carbon nanotube reinforced metal matrix composites—A review. Int. Mater. Rev. 2010, 55, 41–64. [Google Scholar] [CrossRef]
- Dorri Moghadam, A.; Omrani, E.; Menezes, P.L.; Rohatgi, P.K. Mechanical and tribological properties of self-lubricating metal matrix nanocomposites reinforced by carbon nanotubes (CNTs) and graphene—A review. Compos. Part B Eng. 2015, 77, 402–420. [Google Scholar] [CrossRef]
- Reinert, L.; Lasserre, F.; Gachot, C.; Grützmacher, P.; Maclucas, T.; Souza, N.; Mücklich, F.; Suarez, S. Long-lasting solid lubrication by CNT-coated patterned surfaces. Sci. Rep. 2017, 7, 42873. [Google Scholar] [CrossRef] [PubMed]
- Samsonidze, G.G.; Samsonidze, G.G.; Yakobson, B.I. Kinetic theory of symmetry-dependent strength in carbon nanotubes. Phys. Rev. Lett. 2002, 88, 065501:1–065501:4. [Google Scholar] [CrossRef] [PubMed]
- Shenderova, O.A.; Zhirnov, V.V.; Brenner, D.W. Carbon nanostructures. Crit. Rev. Solid State 2002, 27, 227–356. [Google Scholar] [CrossRef]
- Yu, M.-F. Fundamental mechanical properties of carbon nanotubes: Current understanding and the related experimental studies. J. Eng. Mater. Trans. ASME 2004, 126, 271–278. [Google Scholar] [CrossRef]
- Yu, M.-F.; Lourie, O.; Dyer, M.J.; Moloni, K.; Kelly, T.F.; Ruoff, R.S. Strength and breaking mechanism of multiwalled carbon nanotubes under tensile load. Science 2000, 287, 637–640. [Google Scholar] [CrossRef]
- Truong, T.K.; Lee, Y.; Suh, D. Multifunctional characterization of carbon nanotube sheets, yarns, and their composites. Curr. Appl. Phys. 2016, 16, 1250–1258. [Google Scholar] [CrossRef]
- Yao, S.; Yuan, J.; Mehedi, H.-A.; Gheeraert, E.; Sylvestre, A. Carbon nanotube forest based electrostatic capacitor with excellent dielectric performances. Carbon 2017, 116, 648–654. [Google Scholar] [CrossRef]
- Yao, X.; Hawkins, S.C.; Falzon, B.G. An advanced anti-icing/de-icing system utilizing highly aligned carbon nanotube webs. Carbon 2018, 136, 130–138. [Google Scholar] [CrossRef]
- Yao, X.; Falzon, B.G.; Hawkins, S.C.; Tsantzalis, S. Aligned carbon nanotube webs embedded in a composite laminate: A route towards a highly tunable electro-thermal system. Carbon 2018, 129, 486–494. [Google Scholar] [CrossRef]
- Cao, A.Y.; Dickrell, P.L.; Sawyer, W.G.; Ghasemi-Nejhad, M.N.; Ajayan, P.M. Super-compressible foamlike carbon nanotube films. Science 2005, 310, 1307–1310. [Google Scholar] [CrossRef] [PubMed]
- Pathak, S.; Kalidindi, S.R. Spherical nanoindentation stress-strain curves. Mater. Sci. Eng. R Rep. 2015, 91, 1–36. [Google Scholar] [CrossRef]
- Pathak, S.; Cambaz, Z.G.; Kalidindi, S.R.; Swadener, J.G.; Gogotsi, Y. Viscoelasticity and high buckling stress of dense carbon nanotube brushes. Carbon 2009, 47, 1969–1976. [Google Scholar] [CrossRef]
- Maschmann, M.R.; Zhang, Q.; Du, F.; Dai, L.; Baur, J. Length dependent foam-like mechanical response of axially indented vertically oriented carbon nanotube arrays. Carbon 2011, 49, 386–397. [Google Scholar] [CrossRef]
- Cao, C.; Reiner, A.; Chung, C.; Chang, S.-H.; Kao, I.; Kukta, R.V.; Korach, C.S. Buckling initiation and displacement dependence in compression of vertically aligned carbon nanotube arrays. Carbon 2011, 49, 3190–3199. [Google Scholar] [CrossRef]
- Liang, X.; Shin, J.; Magagnosc, D.; Jiang, Y.; Jin Park, S.; John Hart, A.; Turner, K.; Gianola, D.S.; Purohit, P.K. Compression and recovery of carbon nanotube forests described as a phase transition. Int. J. Solids Struct. 2017, 122–123, 196–209. [Google Scholar] [CrossRef]
- Koumoulos, E.P.; Charitidis, C.A. Surface analysis and mechanical behaviour mapping of vertically aligned CNT forest array through nanoindentation. Appl. Surf. Sci. 2017, 396, 681–687. [Google Scholar] [CrossRef]
- Parisa Pour Shahid Saeed Abadi; Hutchens, S.B.; Greer, J.R.; Cola, B.A.; Graham, S. Buckling-driven delamination of carbon nanotube forests. Appl. Phys. Lett. 2013, 102, 223103. [Google Scholar]
- Silva-Santos, S.D.; Alencar, R.S.; Aguiar, A.L.; Kim, Y.A.; Muramatsu, H.; Endo, M.; Blanchard, N.P.; San-Miguel, A.; Souza Filho, A.G. From high pressure radial collapse to graphene ribbon formation in triple-wall carbon nanotubes. Carbon 2019, 141, 568–579. [Google Scholar] [CrossRef]
- Tangney, P.; Capaz, R.B.; Spataru, C.D.; Cohen, M.L.; Louie, S.G. Structural transformations of carbon nanotubes under hydrostatic pressure. Nano Lett. 2005, 5, 2268–2273. [Google Scholar] [CrossRef]
- Zhang, S.; Khare, R.; Belytschko, T.; Hsia, K.J.; Mielke, S.L.; Schatz, G.C. Transition states and minimum energy pathways for the collapse of carbon nanotubes. Phys. Rev. B 2006, 73, 075423. [Google Scholar] [CrossRef]
- Shima, H.; Sato, M. Multiple radial corrugations in multiwalled carbon nanotubes under pressure. Nanotechnology 2008, 19, 495705. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.S.; Zhou, X.-F.; Hu, M.; Yu, D.L.; He, J.L.; Wang, H.-T.; Tian, Y.J.; Xu, B. High-pressure behaviors of carbon nanotubes. J. Superhard Mater. 2012, 34, 371–385. [Google Scholar] [CrossRef]
- Islam, S.; Saleh, T.; Asyraf, M.R.M.; Mohamed Ali, M.S. An ex-situ method to convert vertically aligned carbon nanotubes array to horizontally aligned carbon nanotubes mat. Mater. Res. Express 2019, 6, 025019. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, Y.; Wei, F. Horizontally aligned carbon nanotube arrays: Growth mechanism, controlled synthesis, characterization, properties and applications. Chem. Soc. Rev. 2017, 46, 3661–3715. [Google Scholar] [CrossRef] [PubMed]
- Nam, T.H.; Goto, K.; Yamaguchi, Y.; Premalal, E.V.A.; Shimamura, Y.; Inoue, Y.; Naito, K.; Ogihara, S. Effects of CNT diameter on mechanical properties of aligned CNT sheets and composites. Compos. Part A Appl. Sci. Manuf. 2015, 76, 289–298. [Google Scholar] [CrossRef]
- Qiu, L.; Wang, X.; Su, G.; Tang, D.; Zheng, X.; Zhu, J.; Wang, Z.; Norris, P.M.; Bradford, P.D.; Zhu, Y. Remarkably enhanced thermal transport based on a flexible horizontally-aligned carbon nanotube array film. Sci. Rep. 2016, 6, 21014. [Google Scholar] [CrossRef]
- Qian, D.; Wagner, G.J.; Liu, W.K.; Yu, M.-F.; Ruoff, R.S. Mechanics of carbon nanotubes. Appl. Mech. Rev. 2002, 55, 495–532. [Google Scholar] [CrossRef]
- Tang, J.; Sasaki, T.; Yudasaka, M.; Matsushita, A.; Iijima, S. Compressibility and polygonization of single-walled carbon nanotubes under hydrostatic pressure. Phys. Rev. Lett. 2000, 85, 1887–1889. [Google Scholar] [CrossRef]
- Karmakar, S.; Sharma, S.M.; Teredesai, P.V.; Muthu, D.V.S.; Govindaraj, A.; Sikka, S.K.; Sood, A.K. Structural changes in single-walled carbon nanotubes under non-hydrostatic pressures: X-ray and Raman studies. New J. Phys. 2003, 5, 143.1–143.11. [Google Scholar] [CrossRef]
- Wittmaack, B.K.; Volkov, A.N.; Zhigilei, L.V. Phase transformation as the mechanism of mechanical deformation of vertically aligned carbon nanotube arrays: Insights from mesoscopic modeling. Carbon 2019, 143, 587–597. [Google Scholar] [CrossRef]
- Wittmaack, B.K.; Volkov, A.N.; Zhigilei, L.V. Mesoscopic modeling of the uniaxial compression and recovery of vertically aligned carbon. Compos. Sci. Technol. 2018, 166, 66–85. [Google Scholar] [CrossRef]
- Yakobson, B.I.; Brabec, C.J.; Bernholc, J. Nanomechanics of carbon tubes: Instabilities beyond linear response. Phys. Rev. Lett. 1996, 76, 2511–2514. [Google Scholar] [CrossRef] [PubMed]
- Rafii-Tabar, H.; Ghavanloo, E.; Fazelzadeh, S.A. Nonlocal continuum-based modeling of mechanical characteristics of nanoscopic structures. Phys. Rep. 2016, 638, 1–97. [Google Scholar] [CrossRef]
- Harik, V.M. Ranges of applicability for the continuum beam model in the mechanics of carbon nanotubes and nanorods. Solid State Commun. 2001, 120, 331–335. [Google Scholar] [CrossRef]
- Impellizzeri, A.; Briddon, P.; Ewels, C.P. Stacking- and chirality-dependent collapse of single-walled carbon nanotubes: A large-scale density-functional study. Phys. Rev. B 2019, 100, 115410. [Google Scholar] [CrossRef]
- Chopra, N.G.; Benedict, L.X.; Crespi, V.H.; Cohen, M.L.; Louie, S.G.; Zettl, A. Fully collapsed carbon nanotubes. Nature 1995, 377, 135–138. [Google Scholar] [CrossRef]
- Chang, T. Dominoes in carbon nanotubes. Phys. Rev. Lett. 2008, 101, 175501. [Google Scholar] [CrossRef]
- Ji, J.; Zhao, J.; Guo, W. Novel nonlinear coarse-grained potentials of carbon nanotubes. J. Mech. Phys. Solids 2019, 128, 79–104. [Google Scholar] [CrossRef]
- Savin, A.V.; Korznikova, E.A.; Dmitriev, S.V. Scroll configurations of carbon nanoribbons. Phys. Rev. B 2015, 92, 035412. [Google Scholar] [CrossRef]
- Savin, A.V.; Korznikova, E.A.; Dmitriev, S.V. Simulation of folded and scrolled packings of carbon nanoribbons. Phys. Solid State 2015, 57, 2348–2355. [Google Scholar] [CrossRef]
- Savin, A.V.; Korznikova, E.A.; Lobzenko, I.P.; Baimova, Y.A.; Dmitriev, S.V. Symmetric scrolled packings of multilayered carbon nanoribbons. Phys. Solid State 2016, 58, 1278–1284. [Google Scholar] [CrossRef]
- Savin, A.V.; Korznikova, E.A.; Dmitriev, S.V.; Soboleva, E.G. Graphene nanoribbon winding around carbon nanotube. Comp. Mater. Sci. 2017, 135, 99–108. [Google Scholar] [CrossRef]
- Savin, A.V.; Mazo, M.A. 2D chain models of nanoribbon scrolls. Adv. Struct. Mater. 2019, 94, 241–262. [Google Scholar]
- Savin, A.V.; Korznikova, E.A.; Dmitriev, S.V. Dynamics of surface graphene ripplocations on a flat graphite substrate. Phys. Rev. B 2019, 99, 235411. [Google Scholar] [CrossRef]
- Dmitriev, S.V.; Abe, K.; Shigenari, T. One-dimensional crystal model for incommensurate phase. I. Small displacement limit. J. Phys. Soc. Jpn. 1996, 65, 3938–3944. [Google Scholar] [CrossRef]
- Dmitriev, S.; Shigenari, T.; Abe, K. Mechanisms of transition between and incommensurate phases in a two-dimensional crystal model. Phys. Rev. B 1998, 58, 2513–2522. [Google Scholar] [CrossRef]
- Brenner, W.; Shenderova, O.A.; Harrison, J.A.; Stuart, S.J.; Ni, B.; Sinnott, S.B. A second-generation reactive empirical bond order (rebo) potential energy expression for hydrocarbons. J. Phys. Condens. Matter 2002, 14, 783. [Google Scholar] [CrossRef]
- Evazzade, I.; Lobzenko, I.P.; Saadatmand, D.; Korznikova, E.A.; Zhou, K.; Liu, B.; Dmitriev, S.V. Graphene nanoribbon as an elastic damper. Nanotechnology 2018, 29, 215704. [Google Scholar] [CrossRef]
- Liu, B.; Zhou, K. Recent progress on graphene-analogous 2D nanomaterials: Properties, modeling and applications. Progr. Mater. Sci. 2019, 100, 99–169. [Google Scholar] [CrossRef]




© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Korznikova, E.A.; Rysaeva, L.K.; Savin, A.V.; Soboleva, E.G.; Ekomasov, E.G.; Ilgamov, M.A.; Dmitriev, S.V. Chain Model for Carbon Nanotube Bundle under Plane Strain Conditions. Materials 2019, 12, 3951. https://doi.org/10.3390/ma12233951
Korznikova EA, Rysaeva LK, Savin AV, Soboleva EG, Ekomasov EG, Ilgamov MA, Dmitriev SV. Chain Model for Carbon Nanotube Bundle under Plane Strain Conditions. Materials. 2019; 12(23):3951. https://doi.org/10.3390/ma12233951
Chicago/Turabian StyleKorznikova, Elena A., Leysan Kh. Rysaeva, Alexander V. Savin, Elvira G. Soboleva, Evgenii G. Ekomasov, Marat A. Ilgamov, and Sergey V. Dmitriev. 2019. "Chain Model for Carbon Nanotube Bundle under Plane Strain Conditions" Materials 12, no. 23: 3951. https://doi.org/10.3390/ma12233951
APA StyleKorznikova, E. A., Rysaeva, L. K., Savin, A. V., Soboleva, E. G., Ekomasov, E. G., Ilgamov, M. A., & Dmitriev, S. V. (2019). Chain Model for Carbon Nanotube Bundle under Plane Strain Conditions. Materials, 12(23), 3951. https://doi.org/10.3390/ma12233951