Influence of Mixed Valence on the Formation of Oxygen Vacancy in Cerium Oxides
Abstract
:1. Introduction
2. Computational Method
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Kharton, V.V.; Figueiredo, F.M.; Navarro, L.; Naumovich, E.N.; Kovalevsky, A.V.; Yaremchenko, A.A.; Viskup, A.P.; Carneiro, A.; Marques, F.M.B.; Frade, J.R. Ceria-based materials for solid oxide fuel cells. J. Mater. Sci. 2001, 36, 1105–1117. [Google Scholar] [CrossRef]
- Kašpar, J.; Fornasiero, P.; Graziani, M. Use of CeO2-based oxides in the three-way catalysis. Catal. Today 1999, 50, 285–298. [Google Scholar] [CrossRef]
- Skorodumova, N.V.; Simak, S.I.; Lundqvist, B.I.; Abrikosov, I.A.; Johansson, B. Quantum origin of the oxygen storage capability of ceria. Phys. Rev. Lett. 2002, 89, 166601. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Adams, J.B.; Schilfgaarde, M.V. Theoretical study of environmental dependence of oxygen vacancy formation in CeO2. Appl. Phys. Lett. 2005, 87, 141915. [Google Scholar] [CrossRef]
- Wuilloud, E.; Delley, B.; Schneider, W.D.; Baer, Y. Spectroscopic evidence for localized and extended f-symmetry states in CeO2. Phys. Rev. Lett. 1984, 53, 202–205. [Google Scholar] [CrossRef]
- Fujimori, A. 4f- and core-level photoemission satellites in cerium compounds. Phys. Rev. B 1983, 27, 3992–4001. [Google Scholar] [CrossRef]
- Le Normand, F.; El Fallah, J.; Hilaire, L.; Legare, P.; Kotani, A.; Parlebas, J.C. Photoemission on 3d core levels of cerium: An experimental and theoretical investigation of the reduction of the cerium dioxide. Solid State Commun. 1989, 71, 885–889. [Google Scholar] [CrossRef]
- Marabelli, F.; Wachter, P. Covalent insulator CeO2: Optical reflectivity measurements. Phys. Rev. B 1987, 36, 1238–1243. [Google Scholar] [CrossRef]
- Koelling, D.D.; Boring, A.M.; Wood, J.H. The electronic structure of CeO2 and PrO2. Solid State Commun. 1983, 47, 227–232. [Google Scholar] [CrossRef]
- Skorodumova, N.V.; Ahuja, R.; Simak, S.I.; Abrikosov, A.; Johansson, B.; Lundqvist, B.I. Electronic, bonding, and optical properties of CeO2 and Ce2O3 from first principles. Phys. Rev. B 2001, 64, 115108. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Bader, R.F.W. A quantum theory of molecular structure and its applications. Chem. Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
- Zhang, L.; Ying, F.; Wu, W.; Hiberty, P.C.; Shaik, S. Topology of electron charge density for chemical bonds from valence bond theory: A probe of bonding types. Chem. Eur. J. 2009, 15, 2979–2989. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, T.; Momida, H.; Hamada, T.; Uda, T.; Ohno, T. First-principles study of dielectric properties of cerium oxide. Thin Solid Films 2005, 486, 136–140. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11173. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultra-soft pseudo-potentials to the projector augmented—Wave method. Phys. Rev. B 1999, 59, 1758–1762. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Ma, D.W.; Lu, Z.S.; Tang, Y.N.; Li, T.X.; Tang, Z.J.; Yang, Z.X. Effect of lattice strain on the oxygen vacancy formation and hydrogen adsorption at CeO2(111) surface. Phys. Lett. A 2014, 378, 2570–2575. [Google Scholar] [CrossRef]
- Aidhy, S.D.; Liu, B.; Zhang, Y.W.; Weber, W.J. Chemical expansion affected oxygen vacancy stability in different oxide structures from first principles calculations. Comput. Mater. Sci. 2015, 99, 298–305. [Google Scholar] [CrossRef] [Green Version]
- Gerward, L.; Staun Olsen, J.; Petit, L.; Vaitheeswaran, G.; Kanchana, V.; Svane, A. Bulk modulus of CeO2 and PrO2-An experimental and theoretical study. J. Alloy. Compd. 2005, 400, 56–61. [Google Scholar] [CrossRef]
- Sun, L.; Huang, X.W.; Wang, L.G.; Janotti, A. Disentangling the role of small polarons and oxygen vacancies in CeO2. Phys. Rev. B 2017, 95, 245101–245106. [Google Scholar] [CrossRef] [Green Version]
- Kanchana, V.; Vaitheeswaran, G.; Svane, A.; Delin, A. First-principles study of elastic properties of CeO2 ThO2 and PoO2. J. Phys. Condens. Matter 2006, 18, 9615–9624. [Google Scholar] [CrossRef]
- Pinto, H.; Mintz, M.H.; Melamud, M.; Shaked, H. Neutron diffraction study of Ce2O3. Phys. Lett. A 1982, 88, 81–83. [Google Scholar] [CrossRef]
- Matz, O.; Calatayud, M. H2 Dissociation and oxygen vacancy formation on Ce2O3 surfaces. Top. Catal. 2019, 62, 956–967. [Google Scholar] [CrossRef] [Green Version]
- Da Silva, J.L.F. Stability of the Ce2O3 phases: A DFT + U investigation. Phys. Rev. B 2007, 76, 193108–193115. [Google Scholar] [CrossRef]
- Panhans, M.A.; Blumenthal, R.N. A thermodynamic and electrical conductivity study of nonstoichiometric cerium dioxide. Solid State Ionics 1993, 60, 279–298. [Google Scholar] [CrossRef]
- Paier, J.; Penschke, C.; Sauer, J. Oxygen defects and surface chemistry of ceria: Quantum chemical studies compared to experiment. Chem. Rev. 2013, 113, 3949–3985. [Google Scholar] [CrossRef]
- Li, K.Y.; Xue, D.F. Estimation of electronegativity values of elements in different valence states. J. Phys. Chem. A 2006, 110, 11332–11337. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Xiao, W.; Hao, X.M.; Meng, Q.L.; Zhou, M. A first-principles study on the structural, thermal and electronic properties of cerium oxides by using different functionals. Electron. Struct. 2019, 1, 015003. [Google Scholar] [CrossRef]
- Sun, L.; Hao, X.; Meng, Q.; Wang, L.G.; Liu, F.; Zhou, M. Polaronic resistive switching in ceria-based memory devices. Adv. Electron. Mater. 2019, 5, 1900271. [Google Scholar] [CrossRef]
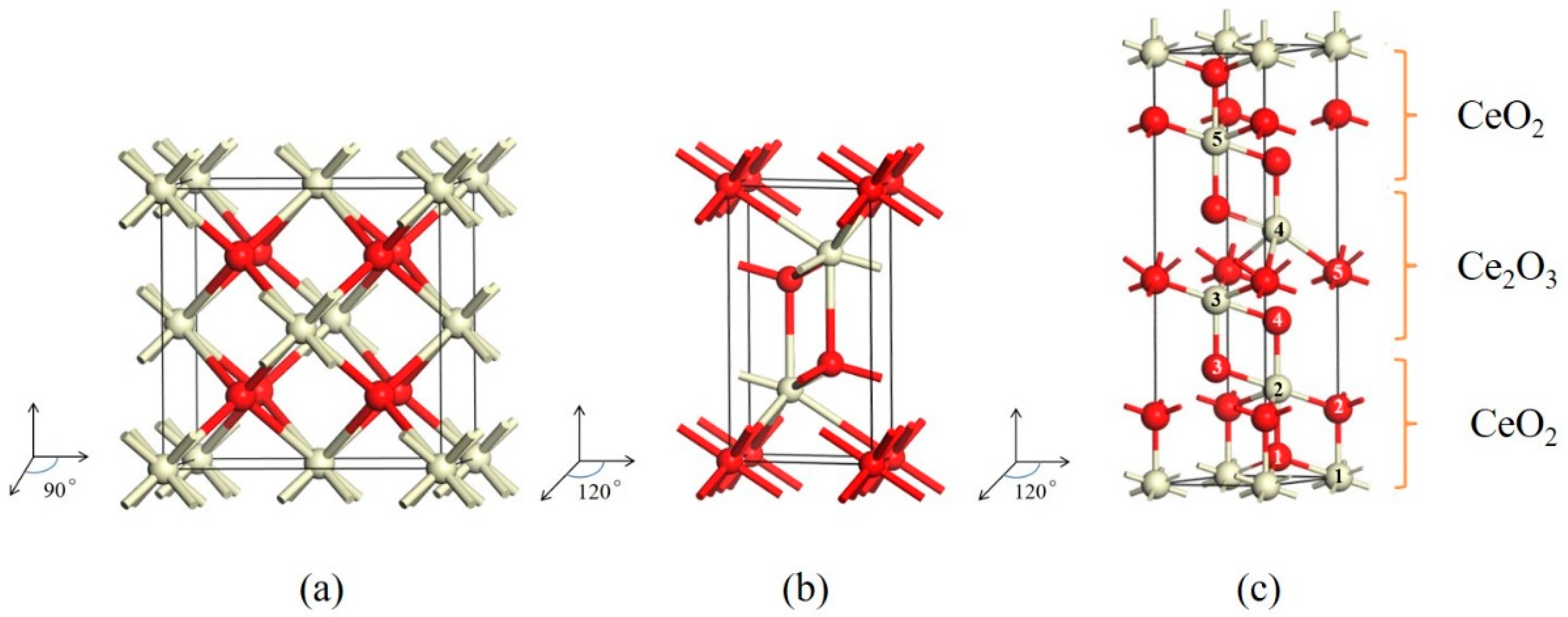

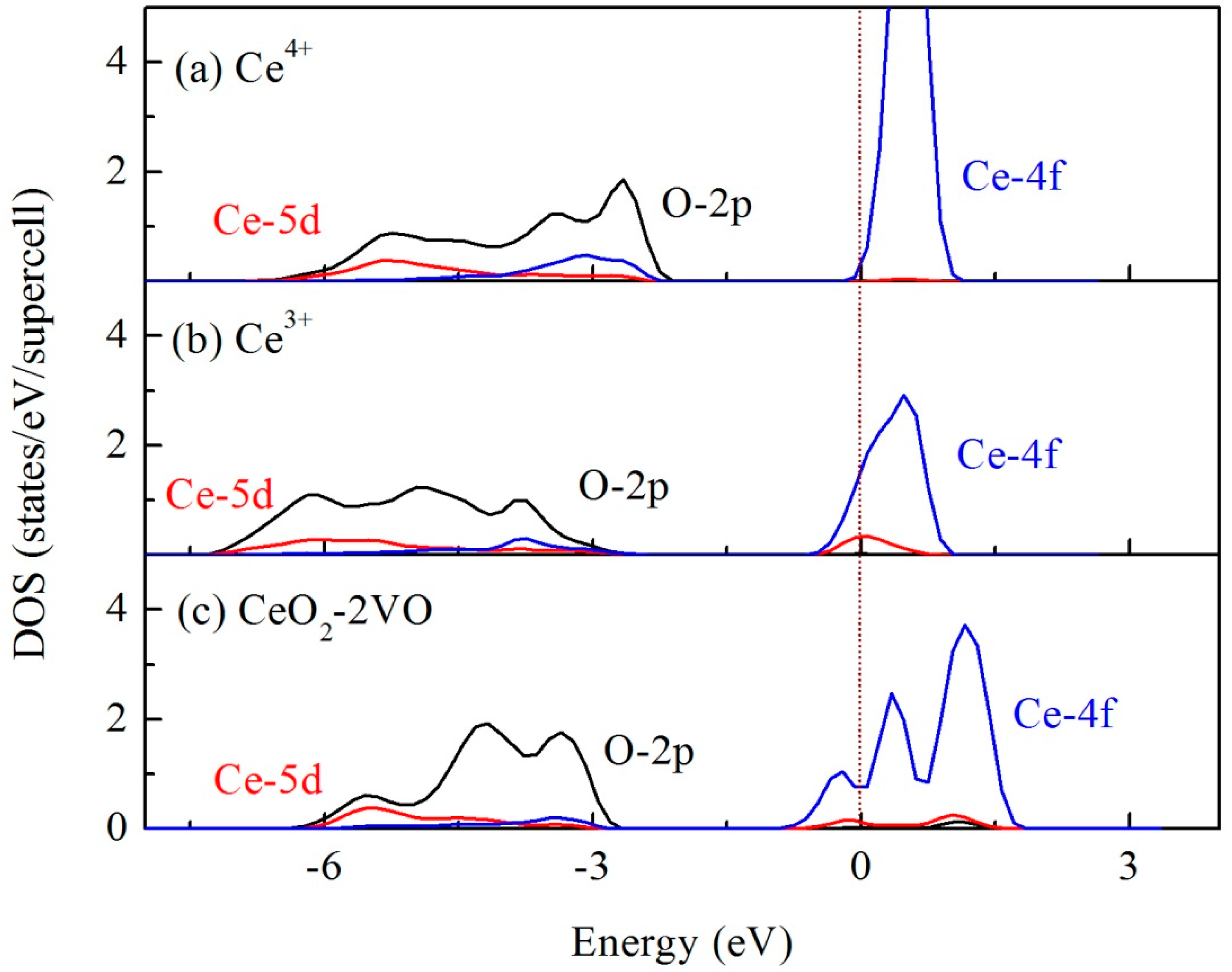
| This Work | Experiment | Theory | ||
|---|---|---|---|---|
| CeO2 | a | 5.48 | 5.41 [20] | 5.48 [21] 5.43 [22] |
| h-Ce2O3 | a | 3.89 | 3.89 [23] | 3.94 [24] 3.92 [25] |
| c | 6.18 | 6.07 [23] | 6.19 [24] 6.18 [25] | |
| CeO2/Ce2O3 | a | 3.826 | 3.822 [14] | |
| c | 15.546 | 15.351 [14] |
| CeO2/Ce2O3 | |||||
|---|---|---|---|---|---|
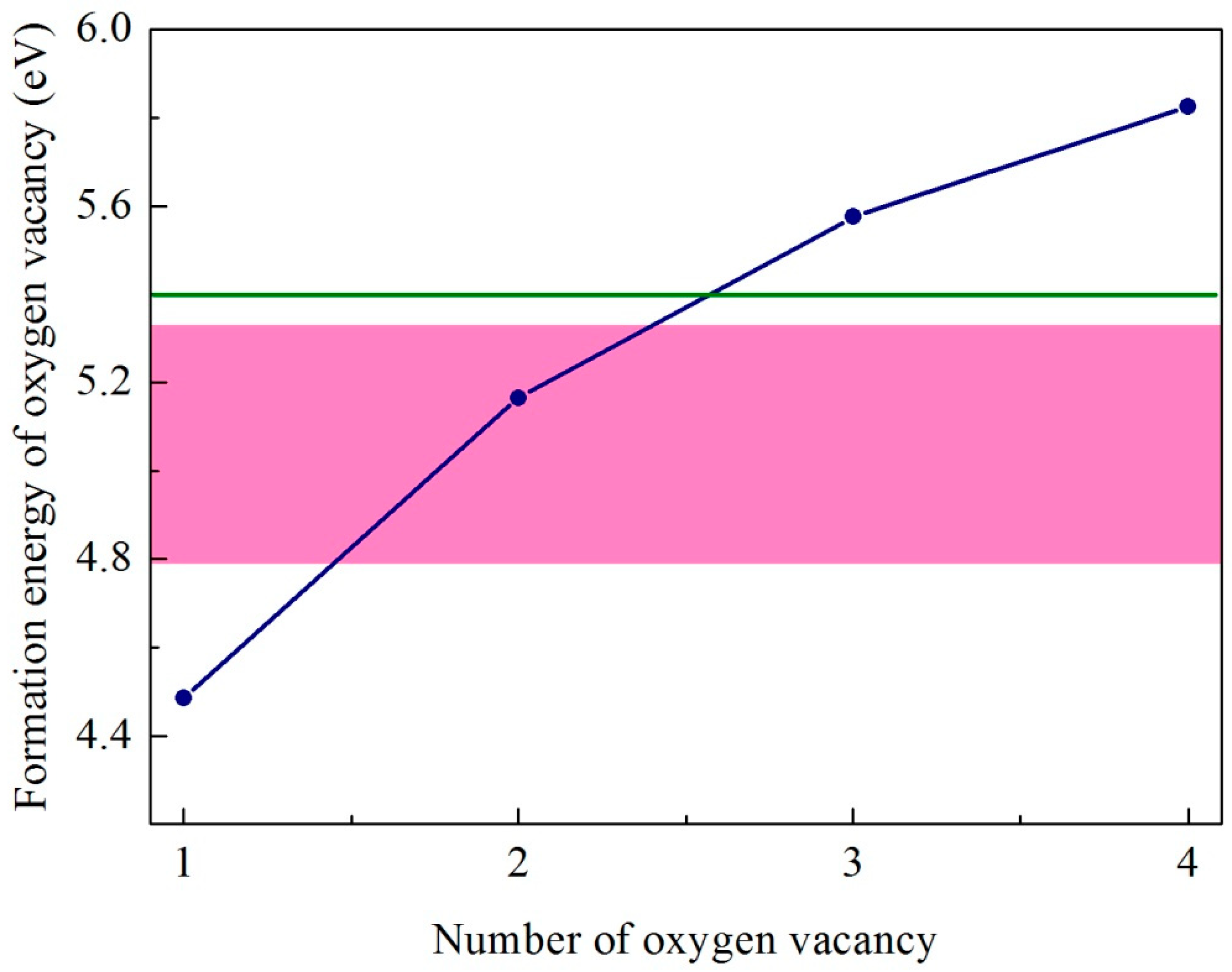
| Ef (eV) | 4.79 | 4.91 | 5.25 | 5.27 | 5.32 |
| CeO2 | |||||
| Ef (eV) | 4.49 | 5.17 | 5.57 | 5.82 |
| System | Atom | Bader Charge |
|---|---|---|
| CeO2 | O | 7.19 |
| Ce | 9.60 | |
| CeO2-Ce2O3 | O1 | 7.21 |
| O2 | 7.22 | |
| O3 | 7.22 | |
| O4 | 7.31 | |
| O5 | 7.40 | |
| Ce1 | 9.56 | |
| Ce2 | 9.58 | |
| Ce3 | 9.97 | |
| Ce4 | 9.99 | |
| Ce5 | 9.63 | |
| Ce2O3 | O1 | 7.39 |
| O2 | 7.31 | |
| Ce | 9.99 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, G.; Geng, W.; Sun, L.; Wang, X.; Xiao, W.; Wang, J.; Wang, L. Influence of Mixed Valence on the Formation of Oxygen Vacancy in Cerium Oxides. Materials 2019, 12, 4041. https://doi.org/10.3390/ma12244041
Zhou G, Geng W, Sun L, Wang X, Xiao W, Wang J, Wang L. Influence of Mixed Valence on the Formation of Oxygen Vacancy in Cerium Oxides. Materials. 2019; 12(24):4041. https://doi.org/10.3390/ma12244041
Chicago/Turabian StyleZhou, Gege, Wentong Geng, Lu Sun, Xue Wang, Wei Xiao, Jianwei Wang, and Ligen Wang. 2019. "Influence of Mixed Valence on the Formation of Oxygen Vacancy in Cerium Oxides" Materials 12, no. 24: 4041. https://doi.org/10.3390/ma12244041
APA StyleZhou, G., Geng, W., Sun, L., Wang, X., Xiao, W., Wang, J., & Wang, L. (2019). Influence of Mixed Valence on the Formation of Oxygen Vacancy in Cerium Oxides. Materials, 12(24), 4041. https://doi.org/10.3390/ma12244041





