Microstructural and Mechanical Properties of Binary Ti-Rich Fe–Ti, Al-Rich Fe–Al, and Ti–Al Alloys
Abstract
:1. Introduction
2. Materials and Methods
3. Preparation of Disc Surfaces for Mechanical Characterization
Configuration with Piezoelectric Discs
4. Ingredients for Estimating Alloy-Disc-Sample Elastic Modulus
4.1. First Model for Solving Direct Problem
4.2. Second Model for Solving Direct Problem
4.3. Solving the Inverse Problem of Vibrational Spectroscopy
4.4. Identification and Classification of Vibration Modes in the Response Spectrum
5. Results
5.1. XRF Analysis
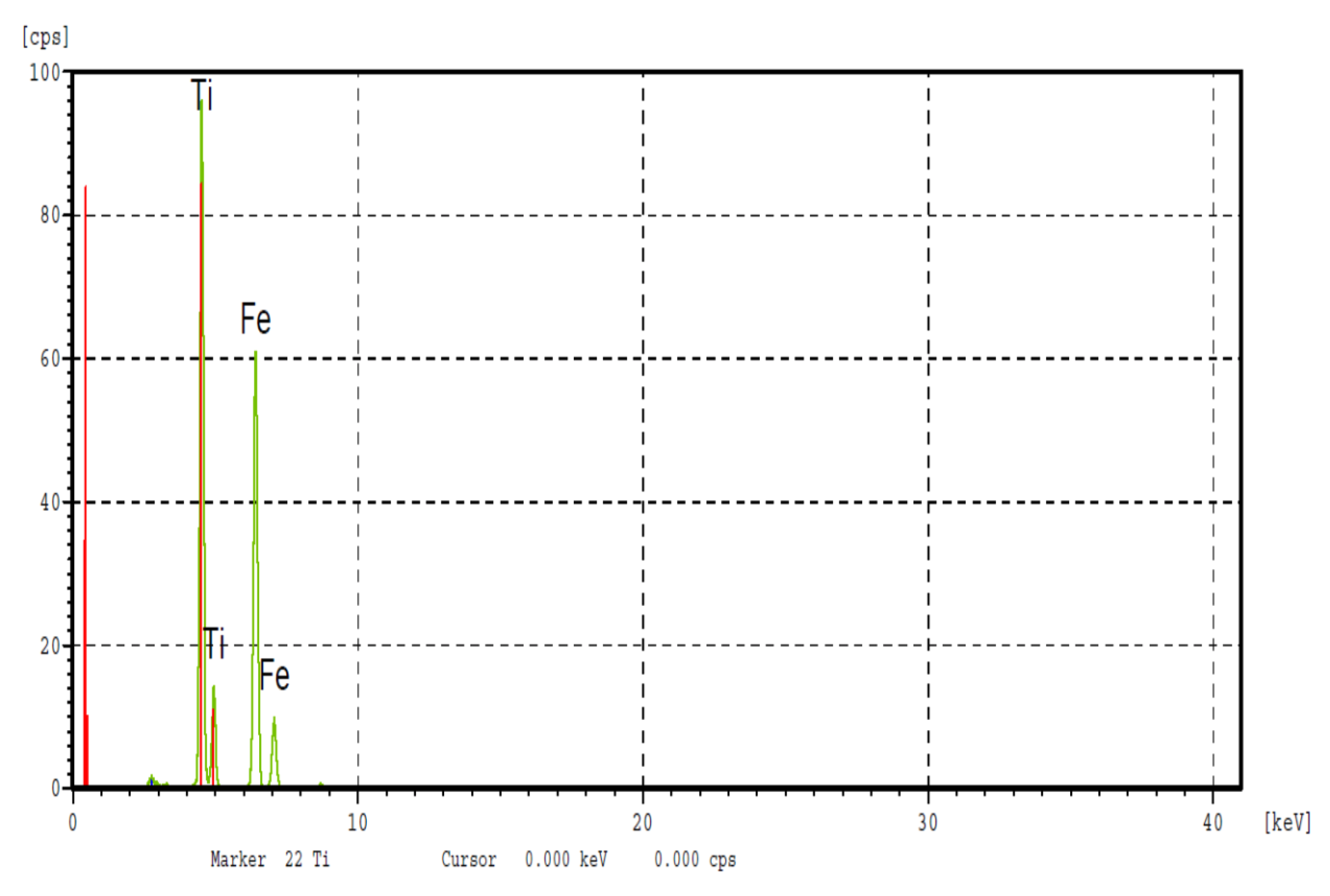
5.2. Energy Dispersive Spectrometer (EDS) Analysis
5.3. Phase Identification
5.4. Metallography
5.5. Vibration Modes
6. Discussion
6.1. Fe–Ti Binary Alloys
6.2. Fe–Al Binary Alloys
6.3. Ti–Al Binary Alloys
6.4. Retrieved Young’s Modulus Values
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zamanzade, M.; Barnoush, A.; Motz, C. A Review on the Properties of Iron Aluminide Intermetallics. Crystals 2016, 6, 10. [Google Scholar] [CrossRef]
- Moret, F.; Baccino, R.; Martel, P.; Guetaz, L. Propriétés et applications des alliages intermétalliques B2-FeAl. J. Phys. IV Fr. 1996, 06, C2-281–C2-289. [Google Scholar] [CrossRef]
- Meshram, S.; Mohandas, T.; Reddy, G.M. Friction welding of dissimilar pure metals. J. Mater. Process. Technol. 2007, 184, 330–337. [Google Scholar] [CrossRef]
- He, W.W.; Tang, H.P.; Liu, H.Y.; Jia, W.P.; Liu, Y.; Yang, X. Microstructure and tensile properties of containerless near-isothermally forged TiAl alloys. Trans. Nonferrous Met. Soc. China 2011, 21, 2605–2609. [Google Scholar] [CrossRef]
- Kim, Y.W. Intermetallic alloys based on gamma titanium aluminide. JOM 1989, 41, 24–30. [Google Scholar] [CrossRef]
- Barbier, D.; Huang, M.; Bouaziz, O. A novel eutectic Fe-15 wt.% Ti alloy with an ultrafine lamellar structure for high temperature applications. Intermetallics 2013, 35, 41–44. [Google Scholar] [CrossRef]
- Stoloff, N. Iron aluminides: Present status and future prospects. Mater. Sci. Eng. A 1998, 258, 1–14. [Google Scholar] [CrossRef]
- Hartig, C.; Yoo, M.H.; Koeppe, M.; Mecking, H. Effect of temperature on elastic constants and deformation behavior in shear tests of Fe-30%Al single crystals. Mater. Sci. Eng. A 1998, 258, 59–64. [Google Scholar] [CrossRef]
- Skrotzki, W.; Kegler, K.; Tamm, R.; Oertel, C.G. Grain structure and texture of cast iron aluminides. Cryst. Res.Technol. 2005, 40, 90–94. [Google Scholar] [CrossRef]
- Ikeda, O.; Ohnuma, I.; Kainuma, R.; Ishida, K. Phase equilibria and stability of ordered BCC phases in the Fe-rich portion of the Fe-Al system. Intermetallics 2001, 9, 755–761. [Google Scholar] [CrossRef]
- Cebulski, J.; Lalik, S. Changes in the structure of alloy on the matrix of FeAl intermetallic phase after primary crystallization and homogenizing treatment. J. Mater. Process. Technol. 2005, 162–163, 4–8. [Google Scholar] [CrossRef]
- Engelier, C.; Béchet, J. Transformations structurales dans l’alliage de titane, β-CEZ études des mécanismes de précipitation après traitement de mise en solution. J. Phys. IV Fr. 1994, 04, 111–116. [Google Scholar] [CrossRef]
- Palm, M.; Sauthoff, G. Deformation Behaviour and Oxidation Resistance of Single-Phase and Two-Phase L21 Fe-Al-Ti Alloys. Intermetallics 2004, 12, 1345–1359. [Google Scholar] [CrossRef]
- Ruan, Y.; Mohajerani, A.; Dao, M. Microstructural and Mechanical-Property Manipulation through Rapid Dendrite Growth and Undercooling in an Fe-based Multinary Alloy. Sci. Rep. 2016, 6, 31684. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bendjeddou, L.; Debili, M. Structure and Hardness of Al-Fe-Ti Alloys. In Defects and Diffusion in Metals XII; Defect and Diffusion Forum; Trans Tech Publications: Zürich, Switzerland, 2010; Volume 305, pp. 23–32. [Google Scholar]
- Brotzu, A.; Felli, F.; Marra, F.; Pilone, D.; Pulci, G. Mechanical properties of a TiAl-based alloy at room and high temperatures. Mater. Sci. Technol. 2018, 34, 1847–1853. [Google Scholar] [CrossRef]
- He, Y.; Schwarz, R.; Migliori, A.; Whang, S. Elastic constants of single crystal γ–TiAl. J. Mater. Res. 1995, 10, 1187–1195. [Google Scholar] [CrossRef]
- Wen, Y.; Wang, L.; Liu, H.; Song, L. Ab Initio Study of the Elastic and Mechanical Properties of B19 TiAl. Crystals 2017, 7, 39. [Google Scholar] [CrossRef]
- Liebertz, J.; Stähr, S.; Haussühl, S. Growth and properties of single crystals of FeTi. Krist. Tech. 1980, 15, 1257–1260. [Google Scholar] [CrossRef]
- Harmouche, M.R.; Wolfenden, A. Temperature and Composition Dependence of Young’s Modulus for Ordered B2 Polycrystalline CoAl and FeAI. Mater. Sci. Eng. 1986, 84, 35–42. [Google Scholar] [CrossRef]
- Zhang, C.H.; Huang, S.; Shen, J.; Chen, N.X. Structural and mechanical properties of Fe-Al compounds: An atomistic study by EAM simulation. Intermetallics 2014, 52, 86–91. [Google Scholar] [CrossRef]
- Migliori, A.; Sarrao, J.L.; Visscher, W.M.; Bell, T.; Lei, M.; Fisk, Z.; Leisure, R.G. Resonant ultrasound spectroscopic techniques for measurement of the elastic moduli of solids. Phys. B Condens. Matter 1993, 183, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Migliori, A.; Maynard, J.D. Implementation of a modern resonant ultrasound spectroscopy system for the measurement of the elastic moduli of small solid specimens. Rev. Sci. Instrum. 2005, 76, 121301. [Google Scholar] [CrossRef] [Green Version]
- Bernard, S.; Grimal, Q.; Laugier, P. Resonant ultrasound spectroscopy for viscoelastic characterization of anisotropic attenuative solid materials. J. Acoust. Soc. Am. 2014, 135, 2601. [Google Scholar] [CrossRef] [PubMed]
- Hughes, T.J.R. The Finite Element Method: Linear Static and Dynamic Finite Element Analysis; Dover Civil and Mechanical Engineering, Dover Publications: New York, NY, USA, 2012. [Google Scholar]
- Ogam, E.; Fellah, Z.; Ogam, G. Identification of the mechanical moduli of closed-cell porous foams using transmitted acoustic waves in air and the transfer matrix method. Compos. Struct. 2016, 135, 205–216. [Google Scholar] [CrossRef]
- ABAQUS Theory Manual, v6.14 ed.; Hibbitt, Karlsson, Sorensen: Pawtucket, RI, USA, 2014.
- Martinček, G. The determination of poisson’s ratio and the dynamic modulus of elasticity from the frequencies of natural vibration in thick circular plates. J. Sound Vib. 1965, 2, 116–127. [Google Scholar] [CrossRef]
- ASTM E1876-01(2006). Standard Test Method for Dynamic Young’s Modulus, Shear Modulus, and Poisson’s Ratio by Impulse Excitation of Vibration; ASTM International: West Conshohocken, PA, USA, 2006. [Google Scholar]
- Gulans, A.; Kontur, S.; Meisenbichler, C.; Nabok, D.; Pavone, P.; Rigamonti, S.; Sagmeister, S.; Werner, U.; Draxl, C. Exciting: A full-potential all-electron package implementing density-functional theory and many-body perturbation theory. J. Phys. Condens. Matter 2014, 26, 363202. [Google Scholar] [CrossRef] [PubMed]
- Golesorkhtabar, R.; Pavone, P.; Spitaler, J.; Puschnig, P.; Draxl, C. ElaStic: A tool for calculating second-order elastic constants from first principles. Comput. Phys. Commun. 2013, 184, 1861–1873. [Google Scholar] [CrossRef]
- Ogam, E.; Wirgin, A.; Schneider, S.; Fellah, Z.; Xu, Y. Recovery of elastic parameters of cellular materials by inversion of vibrational data. J. Sound Vib. 2008, 313, 525–543. [Google Scholar] [CrossRef]
- Chanbi, D.; Ogam, E.; Amara, S.E.; Fellah, Z.E. Synthesis and Mechanical Characterization of Binary and Ternary Intermetallic Alloys Based on Fe-Ti-Al by Resonant Ultrasound Vibrational Methods. Materials 2018, 11, 746. [Google Scholar] [CrossRef]
- Palm, M.; Lacaze, J. Assessment of the Al-Fe-Ti system. Intermetallics 2006, 14, 1291–1303. [Google Scholar] [CrossRef]
- Rigaud, V. Contribution à L’étude De La Solidification Et à La Description Thermodynamique des éQuilibres de Phases du Système Quaternaire Fe-Al-Ti-Zr. Ph.D. Thesis, Université de Lorraine, Vandoeuvre-les-Nancy, France, 2009. [Google Scholar]
- Kwiatkowska, M.; Zasada, D.; Bystrzycki, J.; Polański, M. Synthesis of Fe-Al-Ti Based Intermetallics with the Use of Laser Engineered Net Shaping (LENS). Materials 2015, 8, 2311–2331. [Google Scholar] [CrossRef] [Green Version]
- Agote, I.; Coleto, J.; Gutiérrez, M.; Sargsyan, A.; de Cortazar, M.G.; Lagos, M.; Borovinskaya, I.; Sytschev, A.; Kvanin, V.; Balikhina, N.; et al. Microstructure and mechanical properties of gamma TiAl based alloys produced by combustion synthesis+compaction route. Intermetallics 2008, 16, 1310–1316. [Google Scholar] [CrossRef]
- Connétable, D.; Maugis, P. First principle calculations of the k-Fe3AlC perovskite and iron aluminium intermetallics. Intermetallics 2008, 16, 345–352. [Google Scholar] [CrossRef]
- Friàk, M.; Hickel, T.; Körmann, F.; Udyansky, A.; Dick, A.; von Pezold, J.; Ma, D.; Kim, O.; Counts, W.; Šob, M.; et al. Determining the Elasticity of Materials Employing Quantum-mechanical Approaches: From the Electronic Ground State to the Limits of Materials Stability. Steel Res. Int. 2011, 82, 86–100. [Google Scholar] [CrossRef]
- Zhu, L.F.; Friák, M.; Udyansky, A.; Ma, D.; Schlieter, A.; Kühn, U.; Eckert, J.; Neugebauer, J. Ab initio based study of finite-temperature structural, elastic and thermodynamic properties of FeTi. Intermetallics 2014, 45, 11–17. [Google Scholar] [CrossRef]
- Friák, M.; Counts, W.; Ma, D.; Sander, B.; Holec, D.; Raabe, D.; Neugebauer, J. Theory-Guided Materials Design of Multi-Phase Ti-Nb Alloys with Bone-Matching Elastic Properties. Materials 2012, 5, 1853–1872. [Google Scholar] [CrossRef] [Green Version]
- Sai, S.V.; Satyanarayana, R.S.M.; Murthy, B.K.V.; Rao, S.G.; Prasad, S.A. An Experimental Simulation to Validate FEM to Predict Transverse Young’s Modulus of FRP Composites. Adv. Mater. Sci. Eng. 2013, 2013, 648527. [Google Scholar] [CrossRef]
- Pande, M.M.; Guo, M.; Blanpain, B. Inclusion Formation and Interfacial Reactions between FeTi Alloys and Liquid Steel at an Early Stage. ISIJ Int. 2013, 53, 629–638. [Google Scholar] [CrossRef] [Green Version]
- Nagai, H.; Kitagaki, K.; Shoji, K. Microstructure and hydriding characteristics of FeTi alloys containing manganese. J. Less Common Met. 1987, 134, 275–286. [Google Scholar] [CrossRef]
- Sarreal, J.; Koch, C. Metastable microstructures of rapidly solidified and undercooled Fe-Al-C and Fe-(Ni,Mn)-Al-C alloys. Mater. Sci. Eng. A 1991, 136, 141–149. [Google Scholar] [CrossRef]
- Bednarczyk, I.; Kuc, D.; Niewielski, G. Influence of Cumulative Plastic Deformation on Microstructure of the Fe-Al Intermetallic Phase Base Alloy. Arch. Metall. Mater. 2014, 59, 987–991. [Google Scholar] [CrossRef] [Green Version]
- Guo, F. Influence of Microstructure on the Mechanical Properties And Internal Stresses of a Two-Phase TiAl-Based Alloy. Ph.D. Thesis, Arts et Métiers ParisTech, Paris, France, 2001. [Google Scholar]
- Kartavykh, A.; Asnis, E.; Piskun, N.; Statkevich, I.; Stepashkin, A.; Gorshenkov, M.; Akopyan, T. Complementary thermodynamic and dilatometric assessment of phase transformation pathway in new β-stabilized TiAl intermetallics. Mater. Lett. 2017, 189, 217–220. [Google Scholar] [CrossRef]
- Kelm, K.; Irsen, S.; Paninski, M.; Drevermann, A.; Schmitz, G.J.; Palm, M.; Stein, F.; Engberding, N.; Heilmaier, M.; Saage, H.; et al. Characterization of the Microstructure of Al-rich TiAl-Alloys by Combined TEM Imaging Techniques. Microsc. Microanal. 2007, 13, 294–295. [Google Scholar] [CrossRef]
- Matysik, P.; Jóźwiak, S.; Czujko, T. Characterization of Low-Symmetry Structures from Phase Equilibrium of Fe-Al System–Microstructures and Mechanical Properties. Materials 2015, 8, 914–931. [Google Scholar] [CrossRef] [PubMed]
- Nazarova, T.; Imayev, V.; Imayev, R.; Fecht, H.J. Study of microstructure and mechanical properties of Ti-45Al-(Fe,Nb) (at.%) alloys. Intermetallics 2017, 82, 26–31. [Google Scholar] [CrossRef]
- Acharyan, N.; Fatima, B.; Chouhan, S.S.; Sanyal, S.P. First Principles Study on Structural, Electronic, Elastic and Thermal Properties of Equiatomic MTi (M = Fe, Co, Ni). Chem. Mater. Res. 2013, 3, 22–30. [Google Scholar]





| Alloy | Composition (at. %) | Young’s Modulus (GPa) | Characterization Method | Reference |
|---|---|---|---|---|
| TiAl | 154 | dynamic indentation | [16] | |
| 160–176 | [5] | |||
| TiAl | 182 | Resonant ultrasound spectroscopy Rectangular parallelepiped sample, sides (a, b, c) → (4.173, 3.993, 3.260) mm | [17] | |
| B19 TiAl | 161.99 159.24 | (DFT) Strain–stress method (DFT) Energy density method | [18] | |
| FeTi | (310, 86, 74.9)- > (, , ) Elastic constants | Ultrasonic measurement method Acoustic Resonance and velocity | [19] | |
| FeAl | Fe | 205 | Tensile test | [2] |
| FeAl | 48.71Al-50.87Fe | 261 | PZT ultrasonic composite oscillator-cylindrical specimens 3 mm diameter, 44 mm length | [20] |
| Fe | 204.5 | Embedded-atom method simulation | [21] |
| The Studied Alloys (w%) | ||||||
|---|---|---|---|---|---|---|
| Effective composition (Fe, Al, Ti) | 51.12–48.88 | 58.71–41.29 | 54.67–45.33 | 46.25–53.75 | 58.64–41.36 | 81.71–18.29 |
| Studied Alloys (w%) | ||||||
|---|---|---|---|---|---|---|
| Effective composition (Fe, Al, Ti) | 50.60–49.40 | 61.96–38.04 | 55.29–44.71 | 45.75–54.25 | 58.64–41.36 | 79.66–20.34 |
| Alloy Studied (w%) | Phases Formed | Crystal Structure | Prototype | Space Group | Reference |
|---|---|---|---|---|---|
| FeTi | B2 | CsCl | Pm-3m | [34,35,36,37] | |
| Ti | C14 | Mg | /mmc | ||
| FeTi | B2 | CsCl | Pm-3m | ||
| Ti | Mg | /mmc | |||
| TiAl | AuCu | P4/mmm | [34,35,36,37] | ||
| Ti | - | Hf | /amd | ||
| TiAl | AuCu | P4/mmm | |||
| Ti | - | Hf | /amd | ||
| FeAl | B2 | CsCl | Pm-3m | [34] | |
| Fe | - | Fe | P1 | ||
| FeAl | B2 | CsCl | Pm-3m |
| Element | Density (kg/m) | Young’s Modulus (GPa) | Poisson Ratio () | (Hz) | (Hz) | (GPa) | (GPa) |
|---|---|---|---|---|---|---|---|
| Fe | 7874 Ref. [38] | 212 Ref. [39] | 0.27 | 70,480 | 110,577 | 213.27 | 210.05 |
| Ti | 4500 Ref. [40] | 114.6 Ref. [38,41] | 0.3 | 67,932 | 109,053 | 111.14 | 114.60 |
| Al | 2707 Ref. [38] | 69.3 Ref. [38,42] | 0.3 | 68,230 | 109,530 | 67.27 | 69.36 |
| Composition (wt.%) | Composition (at.%) | (Hz) | (Hz) | Density (kg/m) | (GPa) | (Gpa) | E (Gpa) 3D FEM | (Hz) 3D FEM | (Hz) 3D FEM | Difference Percentage -E (%) | Previous Studies—Ref. E (GPa), |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 70,400 | 110,200 | 7412 | 200.03 | 196.30 | 200.03 | 70,650 | 110,800 | 1.86 | 200 Ref. [2] | ||
| 82,400 | 130,200 | 5330 | 197.30 | 197.10 | 197.30 | 82,840 | 130,000 | 0.10 | |||
| 70,400 | 111,400 | 7050 | 190.50 | 190.80 | 190.50 | 70,740 | 111,000 | 0.16 | 191.66, = 0.287 Ref. [40] | ||
| 69,200 | 10,800 | 6950 | 181.47 | 179.16 | 181.47 | 69,174 | 108,700 | 1.27 | 182.38, = 0.28 Ref. [52] | ||
| 88,700 | 139,800 | 3880 | 166.45 | 165.40 | 166.45 | 88,521 | 139,270 | 0.63 | 160–176 Ref. [5] | ||
| 90,800 | 145,700 | 3609 | 162.60 | 166.90 | 162.60 | 91,460 | 143,000 | 2.64 | 161.99, = 0.265 Ref. [18] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chanbi, D.; Adnane Amara, L.; Ogam, E.; Amara, S.E.; Fellah, Z.E.A. Microstructural and Mechanical Properties of Binary Ti-Rich Fe–Ti, Al-Rich Fe–Al, and Ti–Al Alloys. Materials 2019, 12, 433. https://doi.org/10.3390/ma12030433
Chanbi D, Adnane Amara L, Ogam E, Amara SE, Fellah ZEA. Microstructural and Mechanical Properties of Binary Ti-Rich Fe–Ti, Al-Rich Fe–Al, and Ti–Al Alloys. Materials. 2019; 12(3):433. https://doi.org/10.3390/ma12030433
Chicago/Turabian StyleChanbi, Daoud, Leïla Adnane Amara, Erick Ogam, Sif Eddine Amara, and Zine El Abiddine Fellah. 2019. "Microstructural and Mechanical Properties of Binary Ti-Rich Fe–Ti, Al-Rich Fe–Al, and Ti–Al Alloys" Materials 12, no. 3: 433. https://doi.org/10.3390/ma12030433
APA StyleChanbi, D., Adnane Amara, L., Ogam, E., Amara, S. E., & Fellah, Z. E. A. (2019). Microstructural and Mechanical Properties of Binary Ti-Rich Fe–Ti, Al-Rich Fe–Al, and Ti–Al Alloys. Materials, 12(3), 433. https://doi.org/10.3390/ma12030433







