Mathematical Models as Tools to Predict the Release Kinetic of Fluorescein from Lyotropic Colloidal Liquid Crystals
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Lyotropic Colloidal Liquid Crystals
2.3. Physicochemical Characterization of Lyotropic Colloidal Liquid Crystals
2.4. Release Experiments
2.5. Statistical Criteria and Information on Selection of Mathematical Models
2.5.1. Akaike and Schwarz criteria
2.5.2. Imbimbo Criterion
2.5.3. Fisher (F) Test Criterion
2.6. Applied Mathematical Models
2.6.1. Zero Order Model
2.6.2. Noyes–Whitney Model
2.6.3. Weibull Model
2.6.4. Power Law Equation (Siepman–Peppas) Model
2.6.5. Construction of Diffusion Models by using Fick’s Second Law
2.6.6. Higuchi Square Root Law
2.6.7. Square Root Laws
2.7. Graphical Representation of Data
3. Results and Discussion
3.1. Analysis of the Physicochemical and Technological Properties of Lyotropic Colloidal Liquid Crystals
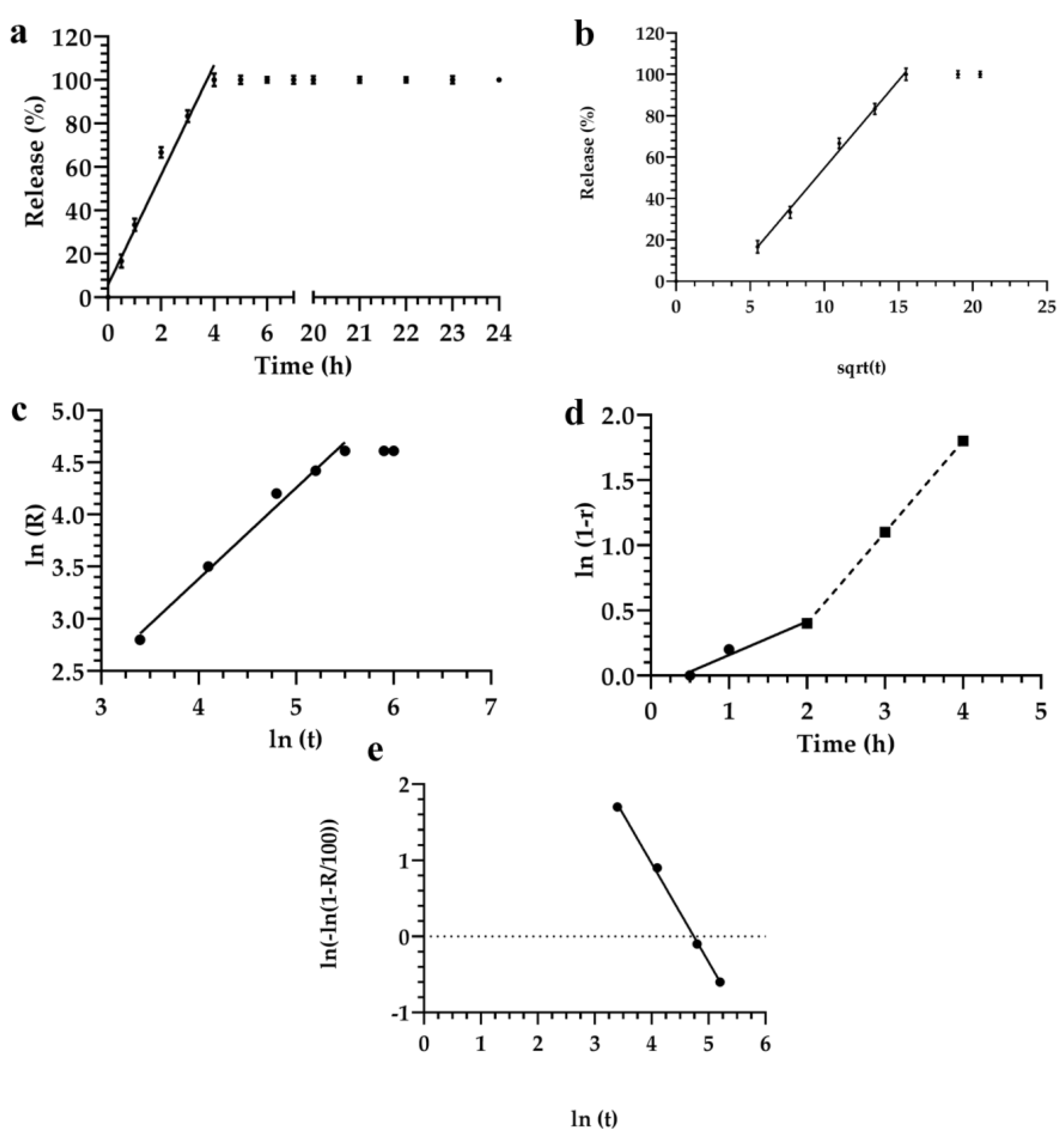
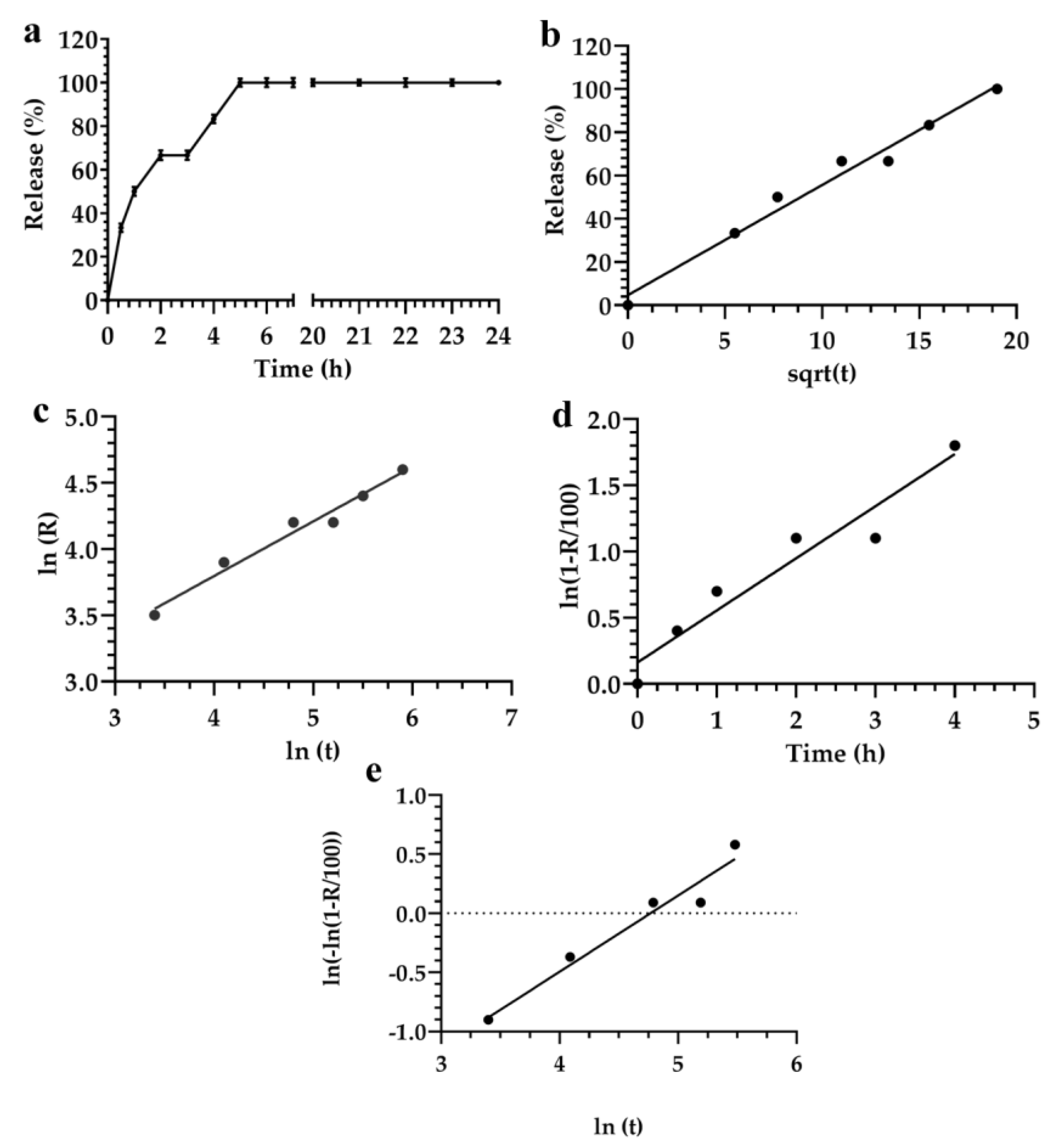
3.2. Description and Analysis of the Obtained Release Kinetics
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| (Brij® 92 or Brij O2) | Polyethylene glycol oleyl ether |
| (Brij® 72) | Polyoxyethylene stearyl ether |
| (Symperonic® PE/F127) | Polyoxyethylene-polyoxypropylene block copolymer 127 |
| (Pluronic® PE 6800) | Polyethylene glycol-polypropylene glycol-polyethylene glycol block copolymer 6800 |
| (Pluronic® PE 10500) | Polyethylene glycol block copolymer 10500 |
| (Monomuls® 90-O18) | Glyceryl mono-oleate |
| (NaCl 0.9 % w/v) | Isotonic sterile saline solution |
| FL | (Fluorescein) |
| PDI | (Polydispersity index) |
| Z.P. | (Z-potential) |
| E.M. | (Electrophoretic mobility) |
| E.E. (%) | (Entrapment efficiency (%)). |
References
- Larsen, C.; Larsen, S.W.; Jensen, H.; Yaghmur, A.; Ostergaard, J. Role of in vitro release models in formulation development and quality control of parenteral depots. Expert Opin. Drug Deliv. 2009, 6, 1283–1295. [Google Scholar] [CrossRef] [PubMed]
- Karalis, V.; Macheras, P.; Van Peer, A.; Shah, V.P. Bioavailability and bioequivalence: Focus on physiological factors and variability. Pharm. Res. 2008, 25, 1956–1962. [Google Scholar] [CrossRef] [PubMed]
- Dokoumetzidis, A.; Macheras, P. A century of dissolution research: From Noyes and Whitney to the biopharmaceutics classification system. Int. J. Pharm. 2006, 321, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Abdul, S.; Poddar, S.S. A flexible technology for modified release of drugs: Multi layered tablets. J. Control. Release 2004, 97, 393–405. [Google Scholar] [CrossRef]
- Siepmann, J.; Siepmann, F. Mathematical modeling of drug delivery. Int. J. Pharm. 2008, 364, 328–348. [Google Scholar] [CrossRef] [PubMed]
- Chountoulesi, M.; Pippa, N.; Pispas, S.; Chrysina, E.D.; Forys, A.; Trzebicka, B.; Demetzos, C. Cubic lyotropic liquid crystals as drug delivery carriers: Physicochemical and morphological studies. Int. J. Pharm. 2018, 550, 57–70. [Google Scholar] [CrossRef] [PubMed]
- Woltman, S.J.; Jay, G.D.; Crawford, G.P. Liquid-crystal materials find a new order in biomedical applications. Nat. Mater. 2007, 6, 929–938. [Google Scholar] [CrossRef] [PubMed]
- Fong, W.K.; Hanley, T.; Boyd, B.J. Stimuli responsive liquid crystals provide ’on-demand’ drug delivery in vitro and in vivo. J. Control. Release 2009, 135, 218–226. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.W.; Nguyen, T.H.; Hanley, T.; Boyd, B.J. Nanostructure of liquid crystalline matrix determines in vitro sustained release and in vivo oral absorption kinetics for hydrophilic model drugs. Int. J. Pharm. 2009, 365, 190–199. [Google Scholar] [CrossRef] [PubMed]
- Papadopoulou, V.; Kosmidis, K.; Vlachou, M.; Macheras, P. On the use of the Weibull function for the discernment of drug release mechanisms. Int. J. Pharm. 2006, 309, 44–50. [Google Scholar] [CrossRef] [PubMed]
- Dokoumetzidis, A.; Valsami, G.; Macheras, P. Modelling and simulation in drug absorption processes. Xenobiotica 2007, 37, 1052–1065. [Google Scholar] [CrossRef] [PubMed]
- Dokoumetzidis, A.; Kosmidis, K.; Macheras, P. Monte Carlo simulations and fractional kinetics considerations for the Higuchi equation. Int. J. Pharm. 2011, 418, 100–103. [Google Scholar] [CrossRef] [PubMed]
- Dokoumetzidis, A.; Magin, R.; Macheras, P. Fractional kinetics in multi-compartmental systems. J. Pharmacokinet. Pharmacodyn. 2010, 37, 507–524. [Google Scholar] [CrossRef] [PubMed]
- Noyes, A.A.; Whitney, W.R. The rate of solution of solid substances in their own solutions. J. Am. Chem. Soc. 1987, 19, 930–934. [Google Scholar] [CrossRef]
- Higuchi, T. Rate of release of medicaments from ointment bases containing drugs in suspension. J. Pharm. Sci. 1961, 50, 874–875. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, S.; Govender, T.; Khan, I.; Rehman, N.U.; Ali, W.; Shah, S.M.H.; Khan, S.; Hussain, Z.; Ullah, R.; Alsaid, M.S. Experimental and molecular modeling approach to optimize suitable polymers for fabrication of stable fluticasone nanoparticles with enhanced dissolution and antimicrobial activity. Drug Des. Dev. Ther. 2018, 12, 255–269. [Google Scholar] [CrossRef] [PubMed]
- Langerbucher, F. Linearization of dissolution rate curves by the Weibull distribution. J. Pharm. Pharmacol. 1972, 24, 979–981. [Google Scholar] [CrossRef]
- Kirui, D.K.; Celia, C.; Molinaro, R.; Bansal, S.S.; Cosco, D.; Fresta, M.; Shen, H.; Ferrari, M. Mild hyperthermia enhances transport of liposomal gemcitabine and improves in vivo therapeutic response. Adv. Healthc. Mater. 2015, 4, 1092–1103. [Google Scholar] [CrossRef] [PubMed]
- Celia, C.; Ferrati, S.; Bansal, S.; van de Ven, A.L.; Ruozi, B.; Zabre, E.; Hosali, S.; Paolino, D.; Sarpietro, M.G.; Fine, D.; et al. Sustained zero-order release of intact ultra-stable drug-loaded liposomes from an implantable nanochannel delivery system. Adv. Healthc. Mater. 2014, 3, 230–238. [Google Scholar] [CrossRef] [PubMed]
- Harrold, J.M.; Eiseman, J.L.; Joseph, E.; Strychor, S.; Zamboni, W.C.; Parker, R.S. Control-relevant modeling of the antitumor effects of 9-nitrocamptothecin in SCID mice bearing HT29 human colon xenografts. J. Pharmacokinet. Pharmacodyn. 2005, 32, 65–83. [Google Scholar] [CrossRef] [PubMed]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Sandulovici, R.; Prasacu, I.; Mircioiu, C.; Voicu, V.; Medvedovici, A.; Anuţa, V. Mathematical and phenomenological criteria in selection of pharmacokinetic model for M1 metabolite of pentoxyphylline. Farmacia 2009, 57, 235–246. [Google Scholar]
- Imbibo, B.P.; Imbibo, E.; Daniotti, S.; Verotta, D.; Bassotti, G. A new criterion for selection of pharmacokinetic multiexponential equations. J. Pharm. Sci. 1988, 77, 784–789. [Google Scholar] [CrossRef]
- Kosmidis, K.; Argyrakis, P.; Macheras, P. A reappraisal of drug release laws using Monte Carlo simulations: The prevalence of the Weibull function. Pharm. Res. 2003, 20, 988–995. [Google Scholar] [CrossRef] [PubMed]
- Passot, C.; Pouw, M.F.; Mulleman, D.; Bejan-Angoulvant, T.; Paintaud, G.; Dreesen, E.; Ternant, D. Therapeutic Drug Monitoring of Biopharmaceuticals May Benefit From Pharmacokinetic and Pharmacokinetic-Pharmacodynamic Modeling. Ther. Drug Monit. 2017, 39, 322–326. [Google Scholar] [CrossRef] [PubMed]
- Mircioiu, C.; Mircioiu, I.; Voicu, V.; Miron, D. Dissolution-bioequivalence non-correlations. Basic Clin. Pharmacol. Toxicol. 2005, 96, 262–264. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.C.; Chungt, Y.I.; Kim, Y.H.; Tae, G. The modulation of the permeability and the cellular uptake of liposome by stable anchoring of lipid-conjugated pluronic on liposome. J. Biomed. Nanotechnol. 2014, 10, 100–108. [Google Scholar] [CrossRef] [PubMed]
- Kosmidis, K.; Macheras, P. On the dilemma of fractal or fractional kinetics in drug release studies: A comparison between Weibull and Mittag-Leffler functions. Int. J. Pharm. 2018, 543, 269–273. [Google Scholar] [CrossRef] [PubMed]
- Barmpalexis, P.; Kachrimanis, K.; Malamataris, S. Statistical moments in modelling of swelling, erosion and drug release of hydrophilic matrix-tablets. Int. J. Pharm. 2018, 540, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Zarmpi, P.; Flanagan, T.; Meehan, E.; Mann, J.; Fotaki, N. Biopharmaceutical aspects and implications of excipient variability in drug product performance. Eur. J. Pharm. Biopharm. 2017, 111, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Siepmann, J.; Göpferich, A. Mathematical modeling of bioerodible, polymeric drug delivery systems. Adv. Drug Deliv. Rev. 2001, 48, 229–247. [Google Scholar] [CrossRef]
- Sackett, C.K.; Narasimhan, B. Mathematical modeling of polymer erosion: Consequences for drug delivery. Int. J. Pharm. 2011, 418, 104–114. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.M.; Wu, Z.F.; Sun, H.H.; Wu, H.; Xin, S.N.; Wang, Q.T.; Dong, G.Y.; Ma, Z.W.; Huang, S.; Zhang, Y.J.; et al. Release of bioactive BMP from dextran-derived microspheres: A novel delivery concept. Int. J. Pharm. 2006, 307, 23–32. [Google Scholar] [CrossRef] [PubMed]
- Nascimento, M.H.M.; Franco, M.K.K.D.; Yokaichyia, F.; de Paula, E.; Lombello, C.B.; de Araujo, D.R. Hyaluronic acid in Pluronic F-127/F-108 hydrogels for postoperative pain in arthroplasties: Influence on physico-chemical properties and structural requirements for sustained drug-release. Int. J. Biol. Macromol. 2018, 111, 1245–1254. [Google Scholar] [CrossRef] [PubMed]
- Martínez, L.; Villalobos, R.; Sánchez, M.; Cruz, J.; Ganem, A.; Melgoza, L.M. Monte Carlo simulations for the study of drug release from cylindrical matrix systems with an inert nucleus. Int. J. Pharm. 2009, 369, 38–46. [Google Scholar] [CrossRef] [PubMed]
- Lánský, P.; Lánská, V.; Weiss, M. A stochastic differential equation model for drug dissolution and its parameters. J. Control. Release 2004, 100, 267–274. [Google Scholar] [CrossRef] [PubMed]
- Kytariolos, J.; Dokoumetzidis, A.; Macheras, P. Power law IVIVC: An application of fractional kinetics for drug release and absorption. Eur. J. Pharm. Sci. 2010, 41, 299–304. [Google Scholar] [CrossRef] [PubMed]
- Gazga-Urioste, C.; Rivera-Becerril, E.; Pérez-Hernández, G.; Noguez-Méndez, N.A.; Faustino-Vega, A.; Quirino-Barreda, C.T. Physicochemical Characterization and Thermal Behavior of Hexosomes Containing Ketoconazole as Potential Topical Antifungal Delivery System. Drug Dev. Ind. Pharm. 2018, 20, 1–38. [Google Scholar] [CrossRef] [PubMed]
- McNaught, A.D.; Wilkinson, A. (Eds.) Definition of Electrokinetic Potential in IUPAC. Compendium of Chemical Terminology, 2nd ed.; Gold Book; Blackwell Scientific Publications: Oxford, UK, 1997; ISBN 0-9678550-9-8. [Google Scholar]
- Kirby, B.J. Micro- and Nanoscale Fluid Mechanics: Transport in Microfluidic Devices; Cambridge University Press: Cambridge, UK, 2010; ISBN 978-0-521-11903-0. [Google Scholar]
- Fernandes, C.; Martins, C.; Fonseca, A.; Nunes, R.; Matos, M.J.; Silva, R.; Garrido, J.; Sarmento, B.; Remião, F.; Otero-Espinar, F.J.; et al. PEGylated PLGA nanoparticles as a smart carrier to increase the cellular uptake of a coumarin-based monoamine oxidase B inhibitor. ACS Appl. Mater. Interfaces 2018. [Google Scholar] [CrossRef] [PubMed]
- Bozuyuk, U.; Dogan, N.O.; Kizilel, S. Deep insight into PEGylation of bioadhesive chitosan nanoparticles: Sensitivity study for the key parameters through artificial neural network model. ACS Appl. Mater. Interfaces 2018, 10, 33945–33955. [Google Scholar] [CrossRef] [PubMed]
- Toro-Cordova, A.; Flores-Cruz, M.; Santoyo-Salazar, J.; Carrillo-Nava, E.; Jurado, R.; Figueroa-Rodriguez, P.A.; Lopez-Sanchez, P.; Medina, L.A.; Garcia-Lopez, P. Liposomes loaded with cisplatin and magnetic nanoparticles: Physicochemical characterization, pharmacokinetics, and in-vitro efficacy. Molecules 2018, 23, 2272. [Google Scholar] [CrossRef] [PubMed]
- Ganipineni, L.P.; Ucakar, B.; Joudiou, N.; Bianco, J.; Danhier, P.; Zhao, M.; Bastiancich, C.; Gallez, B.; Danhier, F.; Préat, V. Magnetic targeting of paclitaxel-loaded poly(lactic-co-glycolic acid)-based nanoparticles for the treatment of glioblastoma. Int. J. Nanomed. 2018, 13, 4509–4521. [Google Scholar] [CrossRef] [PubMed]
- Conte, C.; Mastrotto, F.; Taresco, V.; Tchoryk, A.; Quaglia, F.; Stolnik, S.; Alexander, C. Enhanced uptake in 2D- and 3D- lung cancer cell models of redox responsive PEGylated nanoparticles with sensitivity to reducing extra- and intracellular environments. J. Control. Release 2018, 277, 126–141. [Google Scholar] [CrossRef] [PubMed]
- Balasubramanian, V.; Poillucci, A.; Correia, A.; Zhang, H.; Celia, C.; Santos, H.A. Cell membrane-based nanoreactor to mimic the bio-compartmentalization strategy of a cell. ACS Biomater. Sci. Eng. 2018, 4, 1471–1478. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.C.; Yu, H.P.; Lin, C.Y.; Elzoghby, A.O.; Hwang, T.L.; Fang, J.Y. Use of cilomilast-loaded phosphatiosomes to suppress neutrophilic inflammation for attenuating acute lung injury: The effect of nanovesicular surface charge. J. Nanobiotechnol. 2018, 16, 35. [Google Scholar] [CrossRef] [PubMed]
- Porsio, B.; Craparo, E.F.; Mauro, N.; Giammona, G.; Cavallaro, G. Mucus and cell-penetrating nanoparticles embedded in nano-into-micro formulations for pulmonary delivery of ivacaftor in patients with cystic fibrosis. ACS Appl. Mater. Interfaces 2018, 10, 165–181. [Google Scholar] [CrossRef] [PubMed]
- Amin, H.H.; Meghani, N.M.; Park, C.; Nguyen, V.H.; Tran, T.T.; Tran, P.H.; Lee, B.J. Fattigation-platform nanoparticles using apo-transferrin stearic acid as a core for receptor-oriented cancer targeting. Colloids Surf. B Biointerfaces 2017, 159, 571–579. [Google Scholar] [CrossRef] [PubMed]
- Sieber, S.; Grossen, P.; Detampel, P.; Siegfried, S.; Witzigmann, D.; Huwyler, J. Zebrafish as an early stage screening tool to study the systemic circulation of nanoparticulate drug delivery systems in vivo. J. Control. Release 2017, 264, 180–191. [Google Scholar] [CrossRef] [PubMed]
- Primavera, R.; Palumbo, P.; Celia, C.; Cilurzo, F.; Cinque, B.; Carata, E.; Carafa, M.; Paolino, D.; Cifone, M.G.; Di Marzio, L. Corrigendum to “An insight of in vitro transport of PEGylated non-ionic surfactant vesicles (NSVs) across the intestinal polarized enterocyte monolayers”. Eur. J. Pharm. Biopharm. 2018, 127, 432–442. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Li, Y.; Liu, Z.; Kerdsakundee, N.; Zhang, M.; Zhang, F.; Liu, X.; Bauleth-Ramos, T.; Lian, W.; Mäkilä, E.; et al. Hierarchical structured and programmed vehicles deliver drugs locally to inflamed sites of intestine. Biomaterials 2018, 185, 322–332. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Lipponen, K.; Quan, P.; Wan, X.; Zhang, H.; Mäkilä, E.; Salonen, J.; Kostiainen, R.; Hirvonen, J.; Kotiaho, T.; et al. Impact of pore size and surface chemistry of porous silicon particles and structure of phospholipids on their interactions. ACS Biomater. Sci. Eng. 2018, 4, 2308–2313. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Li, Y.; Li, W.; Xiao, C.; Liu, D.; Dong, C.; Zhang, M.; Mäkilä, E.; Kemell, M.; Salonen, J.; et al. Multifunctional nanohybrid based on porous silicon nanoparticles, gold nanoparticles, and acetalated dextran for liver regeneration and acute liver failure theranostics. Adv. Mater. 2018, 30, e1703393. [Google Scholar] [CrossRef] [PubMed]
- Khramtsov, P.; Kropaneva, M.; Kalashnikova, T.; Bochkova, M.; Timganova, V.; Zamorina, S.; Rayev, M. Highly Stable Conjugates of Carbon Nanoparticles with DNA Aptamers. Langmuir 2018, 34, 10321–10332. [Google Scholar] [CrossRef] [PubMed]
- Avachat, A.M.; Parpani, S.S. Formulation and development of bicontinuous nanostructured liquid crystalline particles of efavirenz. Colloids Surf. B Biointerfaces 2015, 126, 87–97. [Google Scholar] [CrossRef] [PubMed]
- Marianecci, C.; Paolino, D.; Celia, C.; Fresta, M.; Carafa, M.; Alhaique, F. Non-ionic surfactant vesicles in pulmonary glucocorticoid delivery: Characterization and interaction with human lung fibroblasts. J. Control. Release 2010, 147, 127–135. [Google Scholar] [CrossRef] [PubMed]
- Lopes, I.; Oliveira, C.N.A.; Sárria, P.M.; Neves Silva, P.J.; Gonçalves, O.; Gomes, A.C.; Real Oliveira, M.E. Monoolein-based nanocarriers for enhanced folate receptor-mediated RNA delivery to cancer cells. J. Liposome Res. 2016, 26, 199–210. [Google Scholar] [CrossRef] [PubMed]
- Torrisi, V.; Graillot, A.; Vitorazi, L.; Crouzet, Q.; Marletta, G.; Loubat, C.; Berret, J.F. Preventing corona effects: Multiphosphonic acid poly(ethylene glycol) copolymers for stable stealth iron oxide nanoparticles. Biomacromolecules 2014, 15, 3171–3179. [Google Scholar] [CrossRef] [PubMed]
- Pasut, G.; Paolino, D.; Celia, C.; Mero, A.; Joseph, A.S.; Wolfram, J.; Cosco, D.; Schiavon, O.; Shen, H.; Fresta, M. Polyethylene glycol (PEG)-dendron phospholipids as innovative constructs for the preparation of super stealth liposomes for anticancer therapy. J. Control. Release 2015, 199, 106–113. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Berns, A.E.; Willbold, S.; Buitenhuis, J. Synthesis of poly(ethylene glycol) (PEG)-grafted colloidal silica particles with improved stability in aqueous solvents. J. Colloid Interface Sci. 2007, 310, 446–455. [Google Scholar] [CrossRef] [PubMed]
- Sheng, Y.; Yuan, Y.; Liu, C.; Tao, X.; Shan, X.; Xu, F. In vitro macrophage uptake and in vivo biodistribution of PLA-PEG nanoparticles loaded with hemoglobin as blood substitutes: Effect of PEG content. J. Mater. Sci. Mater. Med. 2009, 20, 1881–1891. [Google Scholar] [CrossRef] [PubMed]
- Fontana, G.; Licciardi, M.; Mansueto, S.; Schillaci, D.; Giammona, G. Amoxicillin-loaded polyethylcyanoacrylate nanoparticles: Influence of PEG coating on the particle size, drug release rate and phagocytic uptake. Biomaterials 2001, 22, 2857–2865. [Google Scholar] [CrossRef]
- Croce, F.; Appetecchi, G.B.; Persi, L.; Scrosati, B. Nanocomposite polymer electrolytes for lithium batteries. Nature 1998, 394, 456–458. [Google Scholar] [CrossRef]
- Kapoor, Y.; Dixon, P.; Sekar, P.; Chauhan, A. Incorporation of drug particles for extended release of Cyclosporine A from poly-hydroxyethyl methacrylate hydrogels. Eur. J. Pharm. Biopharm. 2017, 120, 73–79. [Google Scholar] [CrossRef] [PubMed]
- Koester, L.S.; Ortega, G.G.; Mayorga, P.; Bassani, V.L. Mathematical evaluation of in vitro release profiles of hydroxypropylmethylcellulose matrix tablets containing carbamazepine associated to beta-cyclodextrin. Eur. J. Pharm. Biopharm. 2004, 58, 177–179. [Google Scholar] [CrossRef] [PubMed]
- Bhaskar, K.; Krishna-Mohan, C.; Lingam, M.; Prabhakar-Reddy, V.; Venkateswarlu, V.; Madhusudan-Rao, Y. Development of nitrendipine controlled release formulations based on SLN and NLC for topical delivery: In vitro and ex vivo characterization. Drug Dev. Ind. Pharm. 2008, 34, 719–725. [Google Scholar] [CrossRef] [PubMed]
- Campbell, P.J.; Patel, M.; Martin, J.R.; Hincapie, A.L.; Axon, D.R.; Warholak, T.L.; Slack, M. Systematic review and meta-analysis of community pharmacy error rates in the USA: 1993–2015. BMJ Open Qual. 2018, 7, e000193. [Google Scholar] [CrossRef] [PubMed]
- Verma, P.; Ahuja, M. Cubic liquid crystalline nanoparticles: Optimization and evaluation for ocular delivery of tropicamide. Drug Deliv. 2016, 23, 3043–3054. [Google Scholar] [CrossRef] [PubMed]
- Boyd, B.J. Characterisation of drug release from cubosomes using the pressure ultrafiltration method. Int. J. Pharm. 2003, 260, 239–247. [Google Scholar] [CrossRef]
- Yepuri, N.R.; Clulow, A.J.; Prentice, R.N.; Gilbert, E.P.; Hawley, A.; Rizwan, S.B.; Boyd, B.J.; Darwish, T.A. Deuterated phytantriol—A versatile compound for probing material distribution in liquid crystalline lipid phases using neutron scattering. J. Colloid Interface Sci. 2018, 534, 399–407. [Google Scholar] [CrossRef] [PubMed]
- Boyd, B.J.; Whittaker, D.V.; Khoo, S.M.; Davey, G. Lyotropic liquid crystalline phases formed from glycerate surfactants as sustained release drug delivery systems. Int. J. Pharm. 2006, 309, 218–226. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Angelova, A.; Liu, J.; Garamus, V.M.; Li, N.; Drechsler, M.; Gong, Y.; Zou, A. In situ phase transition of microemulsions for parenteral injection yielding lyotropic liquid crystalline carriers of the antitumor drug bufalin. Colloids Surf. B Biointerfaces 2018, 173, 217–225. [Google Scholar] [CrossRef] [PubMed]
- Negrini, R.; Sánchez-Ferrer, A.; Mezzenga, R. Influence of electrostatic interactions on the release of charged molecules from lipid cubic phases. Langmuir 2014, 30, 4280–4288. [Google Scholar] [CrossRef] [PubMed]
- Nazaruk, E.; Szlęzak, M.; Górecka, E.; Bilewicz, R.; Osornio, Y.M.; Uebelhart, P.; Landau, E.M. Design and assembly of pH-sensitive lipidic cubic phase matrices for drug release. Langmuir 2014, 30, 1383–1390. [Google Scholar] [CrossRef] [PubMed]
- Martiel, I.; Baumann, N.; Vallooran, J.J.; Bergfreund, J.; Sagalowicz, L.; Mezzenga, R. Oil and drug control the release rate from lyotropic liquid crystals. J. Control. Release 2015, 204, 78–84. [Google Scholar] [CrossRef] [PubMed]
- Thakkar, V.; Korat, V.; Baldaniya, L.; Gohel, M.; Gandhi, T.; Patel, N. Development and characterization of novel hydrogel containing antimicrobial drug for treatment of burns. Int. J. Pharm. Investig. 2016, 6, 158–168. [Google Scholar] [CrossRef] [PubMed]
- Oana-Purcaru, S.; Ionescu, M.; Raneti, C.; Anuta, V.; Mircioiu, I.; Belu, I. Study of nimesulide release from solid pharmaceutical formulations in tween 80 solutions. Curr. Health Sci. J. 2010, 36, 42–49. [Google Scholar]
- Pahomi, G.; Corlan, G.; Anuta, V.; Sandulovici, R.; Mircioiu, I. Study of tile influence of bile salts and lecithin on distribution of ketoconazole between plasma and methylene chloride. Farmacia 2012, 60, 809–821. [Google Scholar]
- Mircioiu, I.; Anuta, V.; Oana-Purcaru, S.; Radulescu, F.; Miron, D.; Dumitrescu, I.B.; Ibrahim, N.; Mircioiu, C. In vitro dissolution of poorly soluble drugs in the presence of surface active agents—In vivo pharmacokinetics correlations. II. Nimesulide. Farmacia 2013, 61, 88–102. [Google Scholar]




| Formulations | Monomuls | Brij 72 | Brij 92 | Pluronic 10500 | Pluronic F68 | Symperonic |
|---|---|---|---|---|---|---|
| 1 | — | — | 90 mg | — | 50 mg | — |
| 2 | 90 mg | 50 mg | — | — | — | — |
| 3 | 90 mg | — | — | — | — | 50 mg |
| 4 | 90 mg | — | — | 50 mg | — | — |
| 5 | — | — | 90 mg | — | — | 50 mg |
| Formulations | Size (nm) | PDI 2 | Z.P. (mV) 3 | E.M. (μm × cm/Vs) 4 | E.E (%) 5 |
|---|---|---|---|---|---|
| 1 | 162.4 ± 1.3 | 0.16 ± 0.05 | −29.3 ± 1.5 | −2.1 ± 0.2 | − |
| 1 + FL 1 | 163.5 ± 2.1 | 0.18 ± 0.03 | −30.3 ± 0.5 | −2.1 ± 0.3 | 85.2 ± 3.1 |
| 2 | 548.2 ± 0.9 | 0.35 ± 0.09 | −15.4 ± 0.7 | −1.79 ± 0.1 | − |
| 2 + FL 1 | 550.4 ± 1.5 | 0.37 ± 0.06 | −16.3 ± 0.4 | −1.82 ± 0.1 | 87.1 ± 2.9 |
| 3 | 187.3 ± 1.5 | 0.24 ± 0.07 | −30.2 ± 1.4 | −2.39 ± 0.18 | − |
| 3 + FL 1 | 188.8 ± 1.7 | 0.26 ± 0.02 | −32.2 ± 0.9 | −2.42 ± 0.15 | 61.9 ± 4.1 |
| 4 | 183.4 ± 6.1 | 0.25 ± 0.09 | −33.1 ± 1.5 | −2.12 ± 0.21 | − |
| 4 + FL 1 | 185.2 ± 2.5 | 0.27 ± 0.1 | −34.9 ± 1.3 | −2.15 ± 0.18 | 75.1 ± 5.1 |
| 5 | 148.3 ± 1.6 | 0.14 ± 0.03 | −30.5 ± 1.4 | −2.3 ± 0.06 | − |
| 5 + FL 1 | 150.1 ± 1.6 | 0.16 ± 0.07 | −31.9 ± 1.7 | −2.5 ± 0.1 | 65.9 ± 5.7 |
| Mathematical Model | Akaike | Schwarz | Imbimbo | F-test |
|---|---|---|---|---|
| Higuchi | 29.7 | 31.3 | 0.057 | 0.242 |
| Weibul | 25.8 | 25.4 | 0.059 | — |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paolino, D.; Tudose, A.; Celia, C.; Di Marzio, L.; Cilurzo, F.; Mircioiu, C. Mathematical Models as Tools to Predict the Release Kinetic of Fluorescein from Lyotropic Colloidal Liquid Crystals. Materials 2019, 12, 693. https://doi.org/10.3390/ma12050693
Paolino D, Tudose A, Celia C, Di Marzio L, Cilurzo F, Mircioiu C. Mathematical Models as Tools to Predict the Release Kinetic of Fluorescein from Lyotropic Colloidal Liquid Crystals. Materials. 2019; 12(5):693. https://doi.org/10.3390/ma12050693
Chicago/Turabian StylePaolino, Donatella, Andra Tudose, Christian Celia, Luisa Di Marzio, Felisa Cilurzo, and Constantin Mircioiu. 2019. "Mathematical Models as Tools to Predict the Release Kinetic of Fluorescein from Lyotropic Colloidal Liquid Crystals" Materials 12, no. 5: 693. https://doi.org/10.3390/ma12050693
APA StylePaolino, D., Tudose, A., Celia, C., Di Marzio, L., Cilurzo, F., & Mircioiu, C. (2019). Mathematical Models as Tools to Predict the Release Kinetic of Fluorescein from Lyotropic Colloidal Liquid Crystals. Materials, 12(5), 693. https://doi.org/10.3390/ma12050693










