Application of Inner Radiation Baffles in the Bridgman Process for Flattening the Temperature Profile and Controlling the Columnar Grain Structure of Directionally Solidified Ni-Based Superalloys
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Castings
2.2. Numerical Simulation
3. Results and Discussion
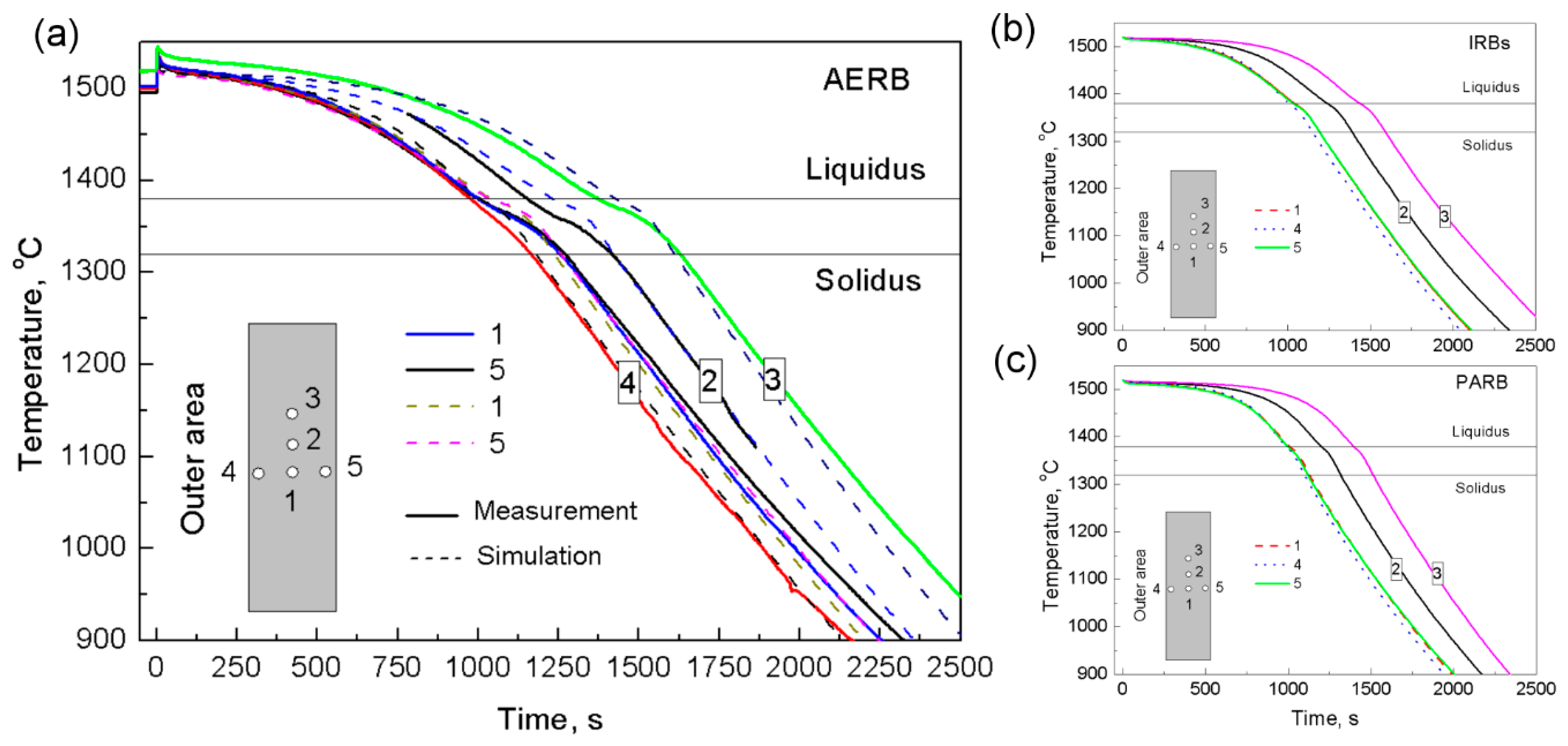
3.1. Thermal Analysis
3.2. Dendritic Microstructure
3.3. Structure of Grains
4. Conclusions
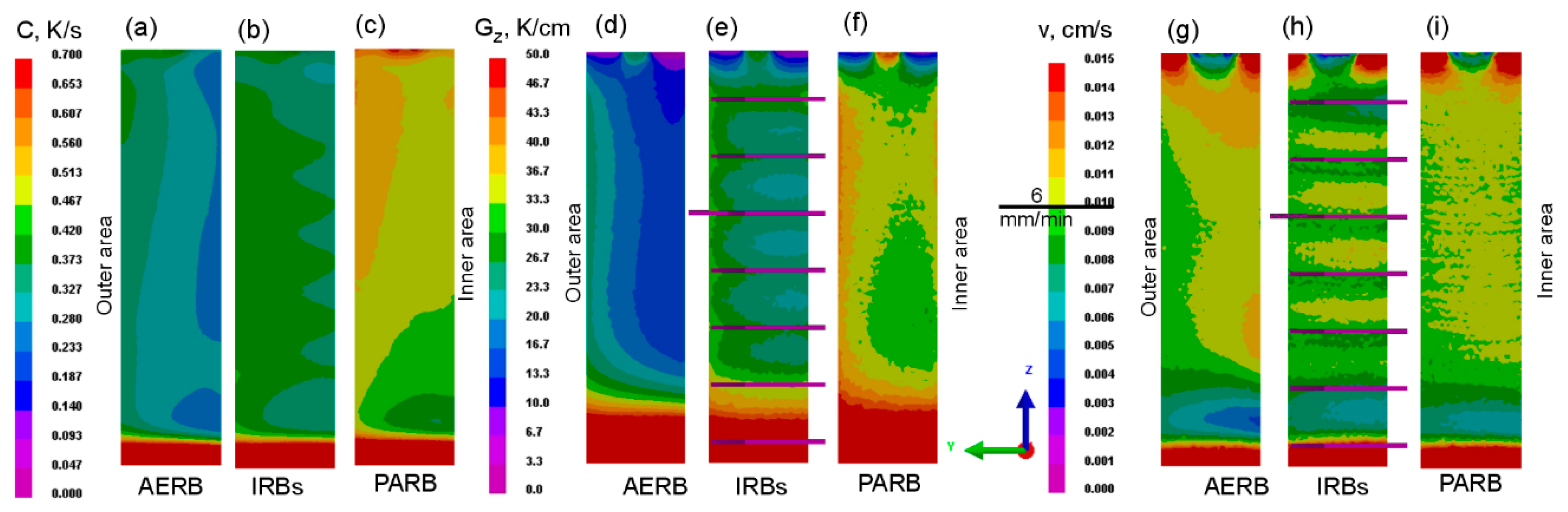
- For the process with IRBs, the temperature profile across the width of the casting plate and mold became more flattened than in the casting produced using only the standard ring-shaped adjusted radiation baffle (AERB). By the application of IRBs, the shadow effect in the inner area of the casting and mold was significantly reduced. Hence, the mushy zone reached a smaller curvature and attained a similar shape along the entire casting height.
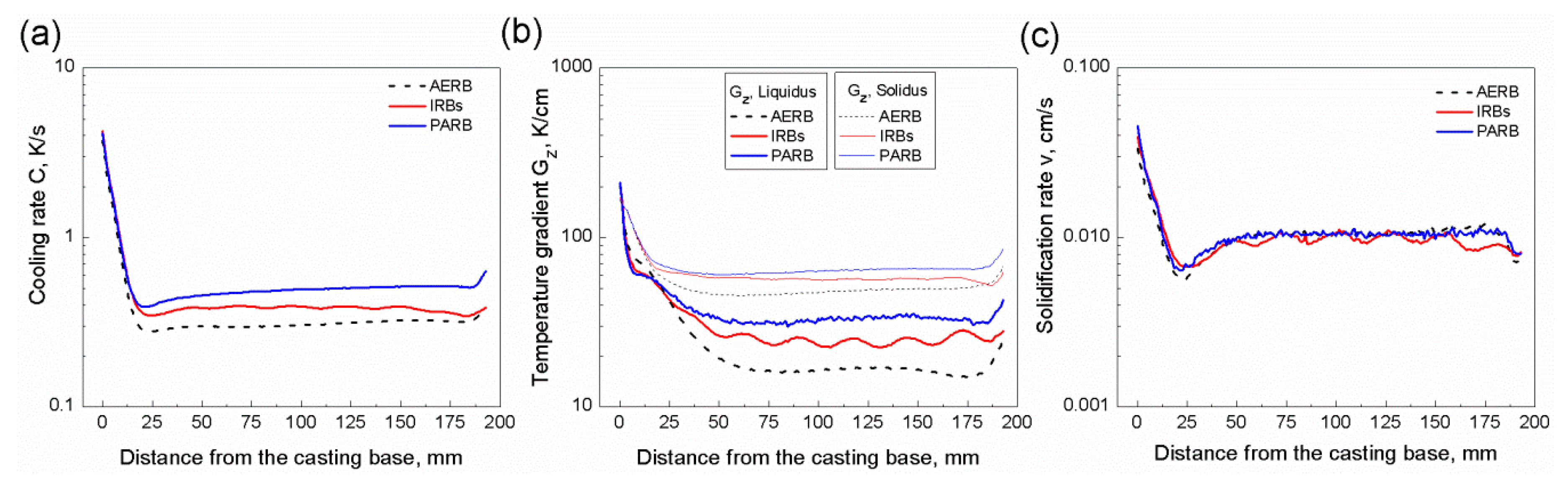
- The steady-state solidification conditions developed at a distance from the casting base ranged approximately from 45 to 170 mm. At the casting height of 100 mm, the cooling rate and axial temperature gradient increased favorably from approximately 0.3 K/s and 16 K/cm to 0.4 K/s and 25 K/cm for the process without and with the use of IRBs, respectively.
- Both the PDAS and SDAS decreased at the casting height of 100 mm due to an increase in axial temperature gradient and cooling rate. The PDAS was similar over the entire cross-section of the casting and reached approximately 370 μm, the value lowered even by 35% in the inner area of the plate, compared with the standard process. The average value of the SDAS equaled approximately 55 μm and 43 μm for the process with the use of AERB and IRBs, respectively. Consequently, the dendritic microstructure was more homogenized and favorably refined across the width of the cross-section of the casting.
- For the process with IRBs, it was possible to reach the solidification conditions and grain structure similar to those obtained in the manufacturing process with the application of the perfectly adjusted radiation baffle (PARB). In these castings, the grains are more elongated, and both their crystallographic orientation and inclination of boundaries towards withdrawal direction of the mold can be reduced, especially in the outer area of the plate.
- Employment of molybdenum IRBs thermophysical properties in simulation did not cause a significant change of temperature gradient along the casting height, compared to the process using graphite IRBs. The increase of graphite IRBs amount in mold from seven to 14 reduced the inhomogeneity of the axial temperature gradient along the casting height.
Author Contributions
Funding
Conflicts of Interest
References
- Reed, C.R. The Superalloys Fundamentals and Applications, 1st ed.; Cambridge University Press: Cambridge, UK, 2006; pp. 1–32. [Google Scholar]
- Miller, J.D.; Pollock, T.M. Process simulation for the directional solidification of a tri-crystal ring segment via the bridgman and liquid-metal-cooling processes. Metall. Mater. Trans. A 2012, 43, 2414–2425. [Google Scholar] [CrossRef]
- Kermanpur, A.; Rappaz, M.; Varahram, N.; Davami, P. Thermal and grain-structure simulation in a land-based turbine blade directionally solidified with the liquid metal cooling process. Metall. Mater. Trans. B 2000, 31, 1293–1304. [Google Scholar] [CrossRef]
- Rezaei, M.; Kermanpur, A.; Sadeghi, F. Effects of withdrawal rate and starter block size on crystal orientation of a single crystal Ni-based superalloy. J. Cryst. Growth 2018, 485, 19–27. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, Q. Simulation and Experimental Studies on Grain Selection and Structure Design of the Spiral Selector for Casting Single Crystal Ni-Based Superalloy. Materials 2017, 10, 1236. [Google Scholar] [CrossRef] [PubMed]
- Sun, D.; Liu, L.; Yang, W.; Huang, T.; Huo, M.; Hu, S.; Zhang, J.; Fu, H. Influence of Secondary Dendrite Orientation on the Evolution of Misorientation in the Platform Region of Single Crystal Superalloy Turbine Blades. Adv. Eng. Mater. 2018, 21, 1800933. [Google Scholar] [CrossRef]
- Kubiak, K.; Szeliga, D.; Sieniawski, J.; Onyszko, A. The Unidirectional Crystallization of Metals and Alloys (Turbine Blades). In Handbook of Crystal Growth: Bulk Crystal Growth, 2nd ed.; Nishinaga, T., Ed.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 413–457. [Google Scholar]
- Szeliga, D.; Kubiak, K.; Jarczyk, G. The Influence of the radiation baffle on predicted temperature gradient in single crystal CMSX-4 castings. Int. J. Metalcast. 2013, 7, 17–23. [Google Scholar] [CrossRef]
- Szeliga, D.; Kubiak, K.; Motyka, M.; Sieniawski, J. Directional solidification process of nickel based superalloy castings: Thermal analysis. Vacuum 2016, 131, 327–342. [Google Scholar] [CrossRef]
- Elliott, A.J.; Pollock, T.M. Thermal analysis of the Bridgman and liquid metal cooled directional solidification investment casting processes. Metall. Mater. Trans. A 2007, 38, 871–881. [Google Scholar] [CrossRef]
- Franke, M.M.; Hilbinger, R.M.; Lohmüller, A.; Singer, R.F. The effect of liquid metal cooling on thermal gradients in directional solidification of superalloys: Thermal analysis. J. Mater. Process. Technol. 2013, 213, 2081–2088. [Google Scholar] [CrossRef]
- Li, Y.; Liu, L.; Sun, D.; Yue, Q.; Huang, T.; Gan, B.; Zhang, J.; Fu, H. Quantitative analysis of withdrawal rate on stray grain formation in the platforms of a Ni-Based single crystal dummy blade. J. Alloys Compd. 2019, 773, 432–442. [Google Scholar] [CrossRef]
- Szeliga, D. Effect of processing parameters and shape of blade on the solidification of single crystal CMSX-4 Ni-based superalloy. Metall. Mater. Trans. B 2018, 49, 2550–2570. [Google Scholar] [CrossRef]
- Lian, Y.; Li, D.; Zhang, K. A method for flattening the solidification front in directional solidification technology. J. Cryst. Growth 2015, 426, 186–197. [Google Scholar] [CrossRef]
- Miller, J.D.; Pollock, T.M. Stability of dendrite growth during directional solidification in the presence of a non-axial thermal field. Acta Mater. 2014, 78, 23–36. [Google Scholar] [CrossRef]
- Elliott, A.J.; Tin, S.; King, W.T.; Huang, S.C.; Gigliotti, M.F.X.; Pollock, T.M. Directional solidification of large superalloy castings with radiation and liquid-metal cooling: A comparative assessment. Metall. Mater. Trans. A 2004, 35, 3221–3231. [Google Scholar] [CrossRef]
- Miller, J.D.; Pollock, T.M. The effect of processing conditions on heat transfer during directional solidification via the bridgman and liquid metal cooling processes. Metall. Mater. Trans. A 2014, 45, 411–425. [Google Scholar] [CrossRef]
- Ebrahimiyan, H.; Kermanpur, A.; Heydari, A.R.; Heydari, D.; Bahmani, M. On the formation of stray grains in directionally-solidified Ni-based superalloys with varying cross sections. Iranian J. Mater. Sci. Eng. 2017, 14, 12–24. [Google Scholar]
- Pollock, T.M.; Murphy, W.H. The breakdown of single-crystal solidification in high refractory nickel–base alloys. Metall. Mater. Trans. A 1996, 27, 1081–1094. [Google Scholar] [CrossRef]
- Brundidge, C.L.; van Drasek, D.; Wang, B.; Pollock, T.M. Structure refinement by a liquid metal cooling solidification process for single–crystal nickel-base superalloys. Metall. Mater. Trans. A 2012, 43, 965–976. [Google Scholar] [CrossRef]
- Hofmann, N.; Olive, S.; Laschet, G.; Hediger, F.; Wolf, J.; Sahm, P.R. Numerical optimization of process control variables for the Bridgman casting process. Model. Simul. Mater. Sci. Eng. 1997, 5, 23. [Google Scholar] [CrossRef]
- Matache, G.; Stefanescu, D.M.; Puscasu, C.; Alexandrescu, E.; Bührig-Polaczek, A. Investigation of solidification microstructure of single crystal CMSX-4 superalloy—Experimental measurements and modelling predictions. Int. J. Cast Met. Res. 2015, 28, 323–336. [Google Scholar] [CrossRef]
- Meyer ter Vehn, M.; Dedecke, D.; Paul, U.; Sahm, P.R. Undercooling related casting defects in single crystal turbine blades. In Proceedings of the Superalloys 1996; The Mineral, Metals and Materials Society: Pittsburgh, PA, USA, 1996; pp. 471–480. [Google Scholar]
- Li, Y.; Liu, L.; Huang, T.; Sun, D.; Zhang, J.; Fu, H. The Formation Mechanism, Influencing Factors and Processing Control of Stray Grains in Nickel-Based Single Crystal Superalloys. In Proceedings of the Superalloys 2016; The Mineral, Metals and Materials Society: Pittsburgh, PA, USA, 2016; pp. 293–301. [Google Scholar]
- Meng, X.; Li, J.; Zhu, S.; Du, H.; Yuan, Z.; Wang, J.; Jin, T.; Sun, X.; Hu, Z. Method of Stray Grain Inhibition in the Platforms with Different Dimensions During Directional Solidification of a Ni-Base Superalloy. Metall. Mater. Trans. A 2014, 45, 1230–1237. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, Q.; Liu, B. Numerical Simulation and Optimization of Directional Solidification Process of Single Crystal Superalloy Casting. Materials 2014, 7, 1625–1639. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Monastyrskiy, V. Modeling and Numerical Optimization of Withdrawal Rate in Directional Solidification Process. IOP Conf. Ser. Mater. Sci. Eng. 2012, 33, 012023. [Google Scholar] [CrossRef] [Green Version]
- Ma, D.; Bührig-Polaczek, A. Application of a heat conductor technique in the production of single-crystal turbine blades. Metall. Mater. Trans. B 2009, 40, 738–748. [Google Scholar] [CrossRef]
- Qin, L.; Shen, J.; Yang, G.; Li, Q.; Shang, Z. A design of non-uniform thickness mould for controlling temperature gradient and S/L interface shape in directionally solidified superalloy blade. Mater. Des. 2017, 116, 565–576. [Google Scholar] [CrossRef]
- Ma, D. Novel casting processes for single-crystal turbine blades of superalloys. Front. Mech. Eng. 2018, 13, 3–16. [Google Scholar] [CrossRef] [Green Version]
- Szeliga, D.; Gancarczyk, K.; Ziaja, W. The Control of Solidification of Ni-Based Superalloy Single-Crystal Blade by Mold Design Modification using Inner Radiation Baffle. Adv. Eng. Mater. 2018, 20, 1700973. [Google Scholar] [CrossRef]
- Szeliga, D.; Kubiak, K.; Sieniawski, J. Control of liquidus isotherm shape during solidification of Ni-based superalloy of single crystal platforms. J. Mater. Process. Technol. 2016, 234, 18–26. [Google Scholar] [CrossRef]
- Szeliga, D.; Kubiak, K.; Burbelko, A.; Motyka, M.; Sieniawski, J. Modeling of directional solidification of columnar grains structure in CMSX-4 nickel based superalloy castings. J. Mater. Eng. Perform. 2014, 23, 1088–1095. [Google Scholar] [CrossRef]
- Gandin, C.-A.; Desbiolles, J.-L.; Rappaz, M.; Thevoz, P. A Three-Dimensional Cellular Automaton-Finite Element Model for the Prediction of Solidification Grain Structures. Metall. Mater. Trans. A 1999, 30, 3153–3165. [Google Scholar] [CrossRef]
- Kurz, W.; Giovanola, B.; Trivedi, R. Theory of Microstructural Development During Rapid Solidification. Acta Metall. 1986, 34, 823–830. [Google Scholar] [CrossRef]
- Wang, R.; Yan, X.; Li, Z.; Xu, Q.; Liu, B. Effect of Construction Manner of Mould Cluster on Stray Grain Formation in Dummy Blade of DD6 Superalloy. High Temp. Mater. Proc. 2017, 36, 399–409. [Google Scholar] [CrossRef]
- Karwa, R. Heat and Mass Transfer, 1st ed.Springer: Singapore, 2017; pp. 762–770. [Google Scholar]
- Guo, Y.; Ge, N.; Wang, K.; Shen, M.; Wang, M. Effect of heat shield on the thermal fields during sapphire crystal growth by Kyropoulos method. J. Ceram. Process. Res. 2016, 17, 1175–1180. [Google Scholar]
- Alekseev, A.; Andreenko, E.; Orlovskiy, I.; Gorshkov, A.; Akhtyrsky, S.; Kozlov, A.; Smekalin, V.; Ulyanitskiy, V.; Khmelnitsky, R.; Evlashin, S.; et al. A study of methods to enhance infrared emissivity of Molybdenum surfaces. Fusion Eng. Des. 2018. [Google Scholar] [CrossRef]
- Available online: http://www-ferp.ucsd.edu/LIB/PROPS/PANOS/moa.html (accessed on 12 March 2019).
- Kurz, W.; Fisher, D.J. Dendrite growth at the limit of stability: Tip radius and spacing. Acta Metall. 1981, 29, 11–20. [Google Scholar] [CrossRef]
- Stefanescu, D.M. Science and Engineering of Casting Solidification, 2nd ed.; Springer: New York, NY, USA, 2009; pp. 177–183. [Google Scholar]
- Konter, M.; Kats, E.; Hofman, N. A novel casting process for single crystal turbine components. In Proceedings of the Superalloys 2000; The Mineral Metals and Materials Society: Pittsburgh, PA, USA, 2000; pp. 189–200. [Google Scholar]
- Wang, F.; Ma, D.; Bogner, S.; Bührig-Polaczek, A. Comparative Investigation of the Downward and Upward Directionally Solidified Single-Crystal Blades of Superalloy CMSX-4. Metall. Mater. Trans. A 2016, 47, 2376–2386. [Google Scholar] [CrossRef]
- Wang, F.; Ma, D.; Zhang, J.; Bogner, S.; Bührig-Polaczek, A. A high thermal gradient directional solidification method for growing superalloy single crystals. J. Mater. Process. Technol. 2014, 214, 3112–3121. [Google Scholar] [CrossRef]
- Hofmeister, M.; Franke, M.M.; Koerner, C.; Singer, R.F. Single Crystal Casting with Fluidized Carbon Bed Cooling: A Process Innovation for Quality Improvement and Cost Reduction. Metall. Mater. Trans. B 2017, 48, 3132–3142. [Google Scholar] [CrossRef]
- Xu, W.; Zhao, Y.; Sun, S.; Liu, M.; Ma, D.; Liang, X.; Wang, C.; Tao, R. Effect of modified mold shell on the microstructure and tensile fracture morphology of single-crystal nickel-base superalloy. Mater. Res. Express 2018, 5, 046504. [Google Scholar] [CrossRef] [Green Version]
- Derby, J.J.; Yeckel, A. Heat Transfer Analysis and Design for Bulk Crystal Growth: Perspectives on the Bridgman Method. In Handbook of Crystal Growth: Bulk Crystal Growth, 2nd ed.; Nishinaga, T., Ed.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 793–843. [Google Scholar]
- Walton, D.; Chalmers, B. The origin of the preferred orientation in the columnar zone of ingots. Trans. Am. Inst. Min. Metall. Eng. 1959, 215, 447–457. [Google Scholar]
- Zhou, Y.Z.; Volek, A.; Green, N.R. Mechanism of competitive grain growth in directional solidification of a nickel-base superalloy. Acta Mater. 2008, 56, 2631–2637. [Google Scholar] [CrossRef]
- Li, J.; Wang, Z.; Wang, Y.; Wang, J. Phase-field study of competitive dendritic growth of converging grains during directional solidification. Acta Mater. 2012, 60, 1478–1493. [Google Scholar] [CrossRef]

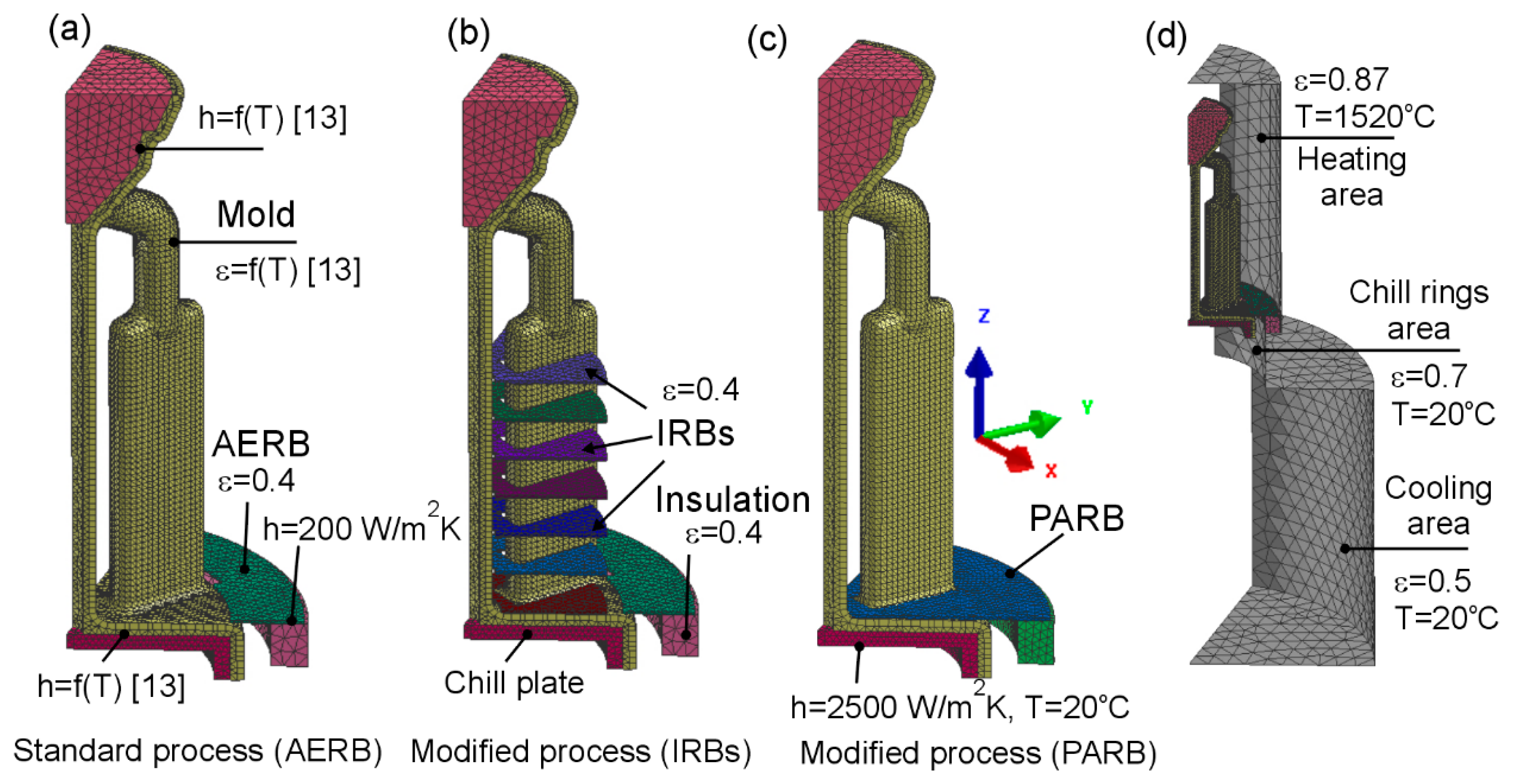





| Experiment (E) or Simulation (P) Designation | Inner Radiation Baffle | External Radiation Baffle | Process Designation | Solidification Process Conditions |
|---|---|---|---|---|
| 1 (E, P) | - | AERB, d = 200 mm graphite | Standard process or AERB | Mold temperature: 1520 °C; Pouring temperature: 1520 °C; Withdrawal rate 6 mm/min |
| 2 (E, P) | D = 180 mm quantity 7 graphite | AERB, d = 200 mm graphite | Modified process or IRBs | |
| 3 (P) | - | PARB graphite | Modified process or PARB | |
| 4 (P) | D = 180 mm quantity 7 molybdenum | AERB, d = 200 mm graphite | IRBs | |
| 5 (P) | D = 180 mm quantity 14 graphite | AERB, d = 200 mm graphite | IRBs |
| Experiment Designation | Alloy | Geometry (Section Thickness) | Withdrawal Rate mm/min | Manufacturing Process | PDAS μm | Reduction of PDAS % | Reference |
|---|---|---|---|---|---|---|---|
| 1 2 | CMSX-4 | Plate (6 mm) | 6 6 | Bridgman (AERB) Bridgman (IRB) | 500 370 | 26 | This work |
| 3 4 | CMSX-4 | Blade (5 mm) | 5 5 | Bridgman (AERB) Bridgman (IRB) | 480 360 | 25 | [31] |
| 5 6 | CMSX-4 | Blade (5 mm) | 3 5 | Bridgman (AERB) Bridgman (IRBs) | 415 360 | 13 | [31] |
| 7 8 | Rod (16 mm) | 3.4 8.5 | Bridgman LMC | 380 250 | 34 | [20] | |
| 9 10 | Rene 4 | IGT blade (10 mm) | 2.5 5.1 | Bridgman LMC | 550 300 | 45 | [16] |
| 11 12 | CMSX-4 | IGT blade (10 mm) | Bridgman GCC | 410 320 | 28 | [43] | |
| 13 14 | CMSX-4 | Blade (5 mm) | 2.5 2.5 | Bridgman DWDS | 445 299 | 33 | [44] |
| 15 16 | CMSX-6 | Rod (9 mm) | 3 3 | Bridgman DWDS | 520 250 | 52 | [45] |
| 17 18 | PWA1483 | Blade (6 mm) | 3 5 | Bridgman FCBC | 410 300 | 27 | [46] |
| 19 | - | - | - | Bridgman (decrease of mold thickness) | - | 8 | [47] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szeliga, D.; Ziaja, W.; Motyka, M.; Kubiak, K.; Sieniawski, J. Application of Inner Radiation Baffles in the Bridgman Process for Flattening the Temperature Profile and Controlling the Columnar Grain Structure of Directionally Solidified Ni-Based Superalloys. Materials 2019, 12, 935. https://doi.org/10.3390/ma12060935
Szeliga D, Ziaja W, Motyka M, Kubiak K, Sieniawski J. Application of Inner Radiation Baffles in the Bridgman Process for Flattening the Temperature Profile and Controlling the Columnar Grain Structure of Directionally Solidified Ni-Based Superalloys. Materials. 2019; 12(6):935. https://doi.org/10.3390/ma12060935
Chicago/Turabian StyleSzeliga, Dariusz, Waldemar Ziaja, Maciej Motyka, Krzysztof Kubiak, and Jan Sieniawski. 2019. "Application of Inner Radiation Baffles in the Bridgman Process for Flattening the Temperature Profile and Controlling the Columnar Grain Structure of Directionally Solidified Ni-Based Superalloys" Materials 12, no. 6: 935. https://doi.org/10.3390/ma12060935
APA StyleSzeliga, D., Ziaja, W., Motyka, M., Kubiak, K., & Sieniawski, J. (2019). Application of Inner Radiation Baffles in the Bridgman Process for Flattening the Temperature Profile and Controlling the Columnar Grain Structure of Directionally Solidified Ni-Based Superalloys. Materials, 12(6), 935. https://doi.org/10.3390/ma12060935







