Continuous Directional Water Delivery on the 3D-Printed Arrowhead Microstructure Array
Abstract
:1. Introduction
2. Materials and Methods
2.1. Theoretical and Simulation Models
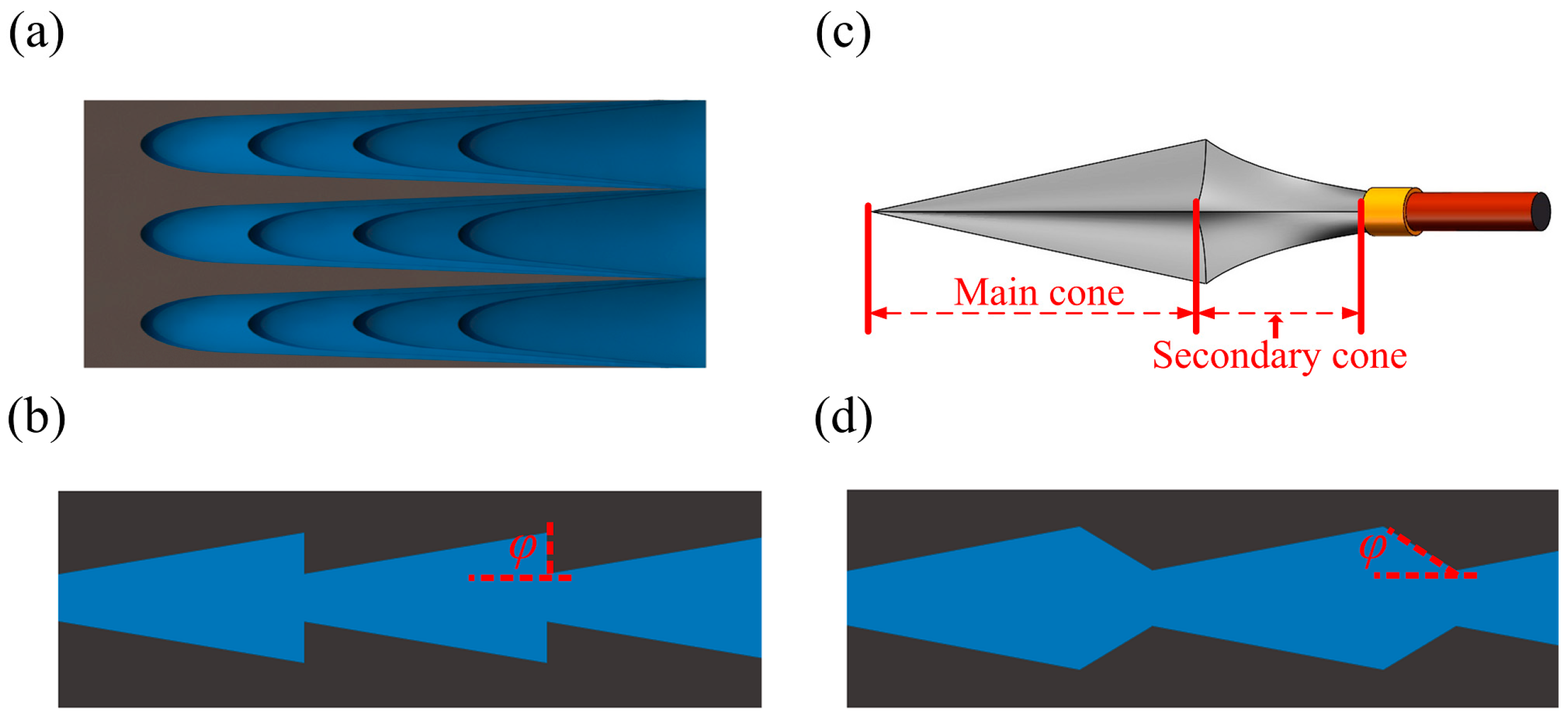
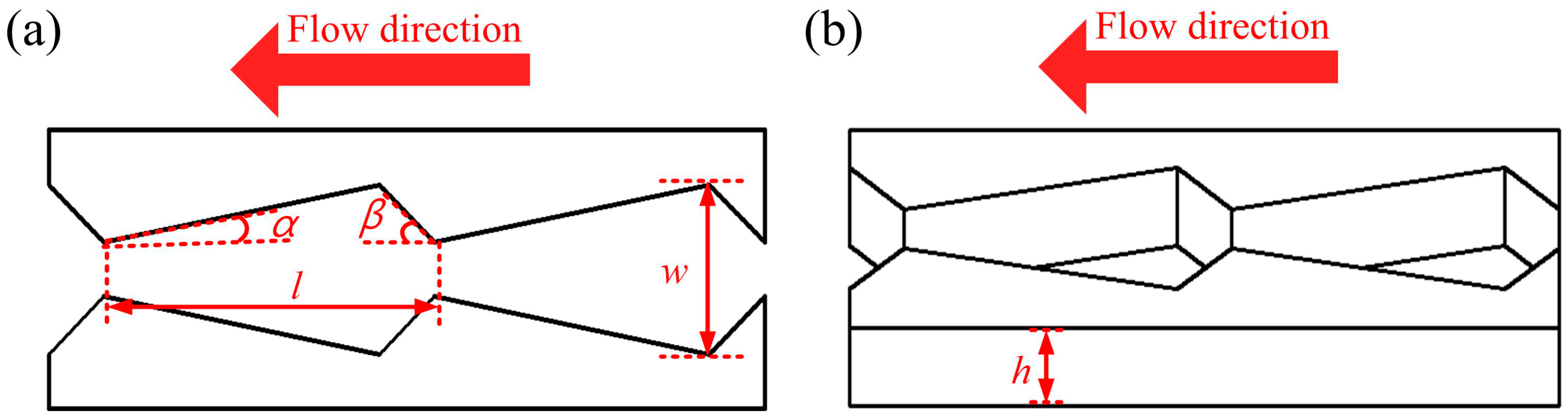
2.1.1. Arrowhead Microstructure Array Design
2.1.2. Theoretical Model of Arrowhead Microstructure Array
2.1.3. Simulation Model of Arrowhead Microstructure Array
2.2. Experiments
2.2.1. Preparation of Arrowhead Microstructure Array
2.2.2. Structural and Morphological Characterization
2.2.3. Superhydrophilic Treatment
2.2.4. Observation of Transport Phenomenon
3. Results
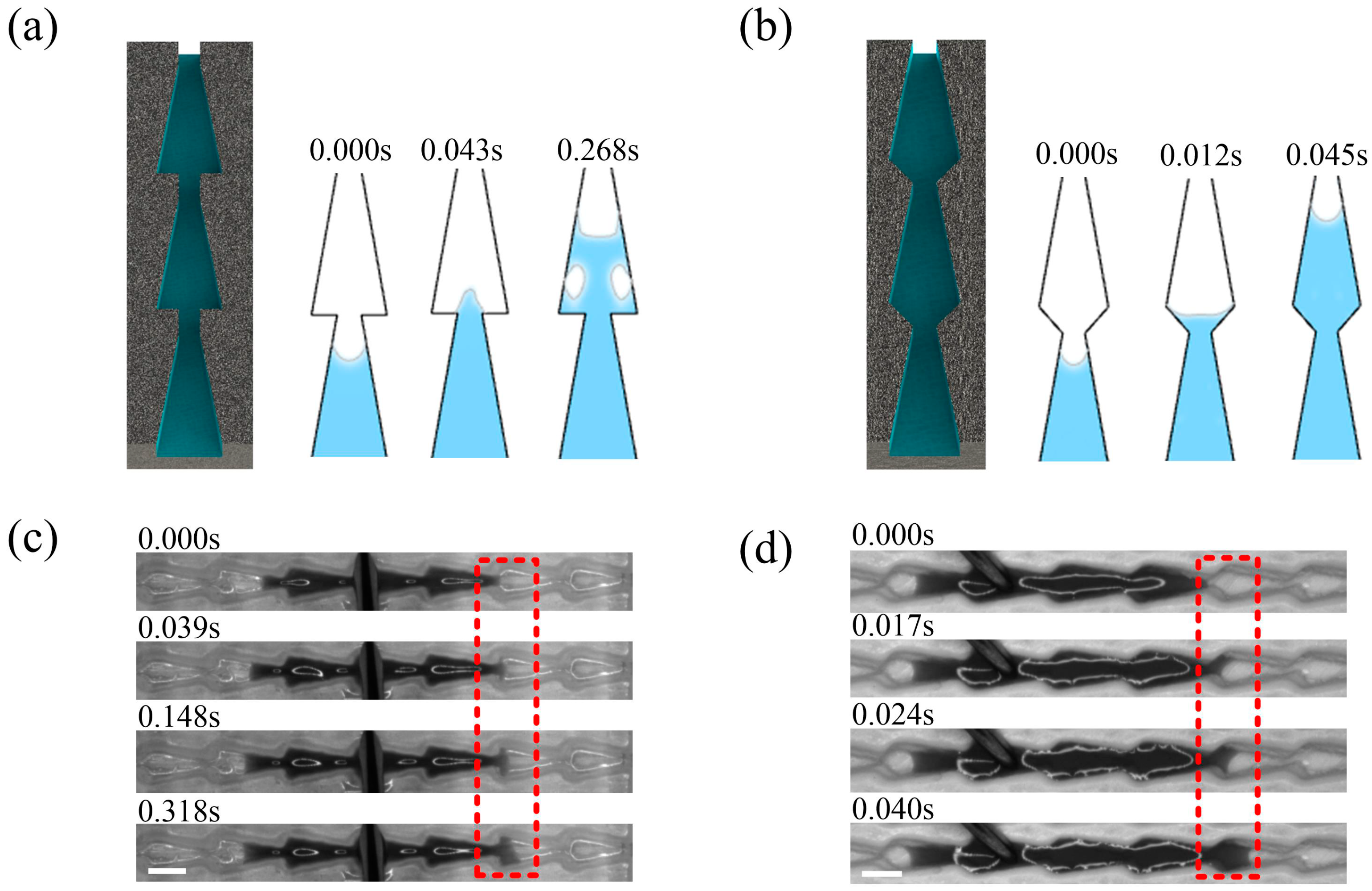
3.1. Comparison of Flat-Bottom and Double Conical Structure
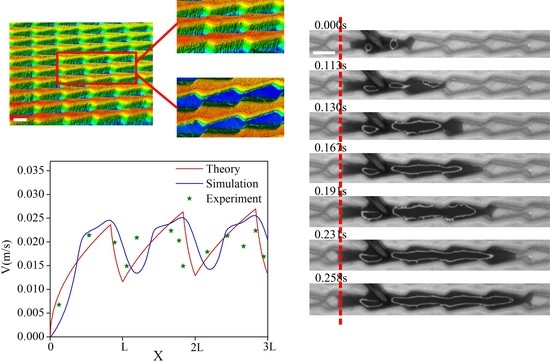
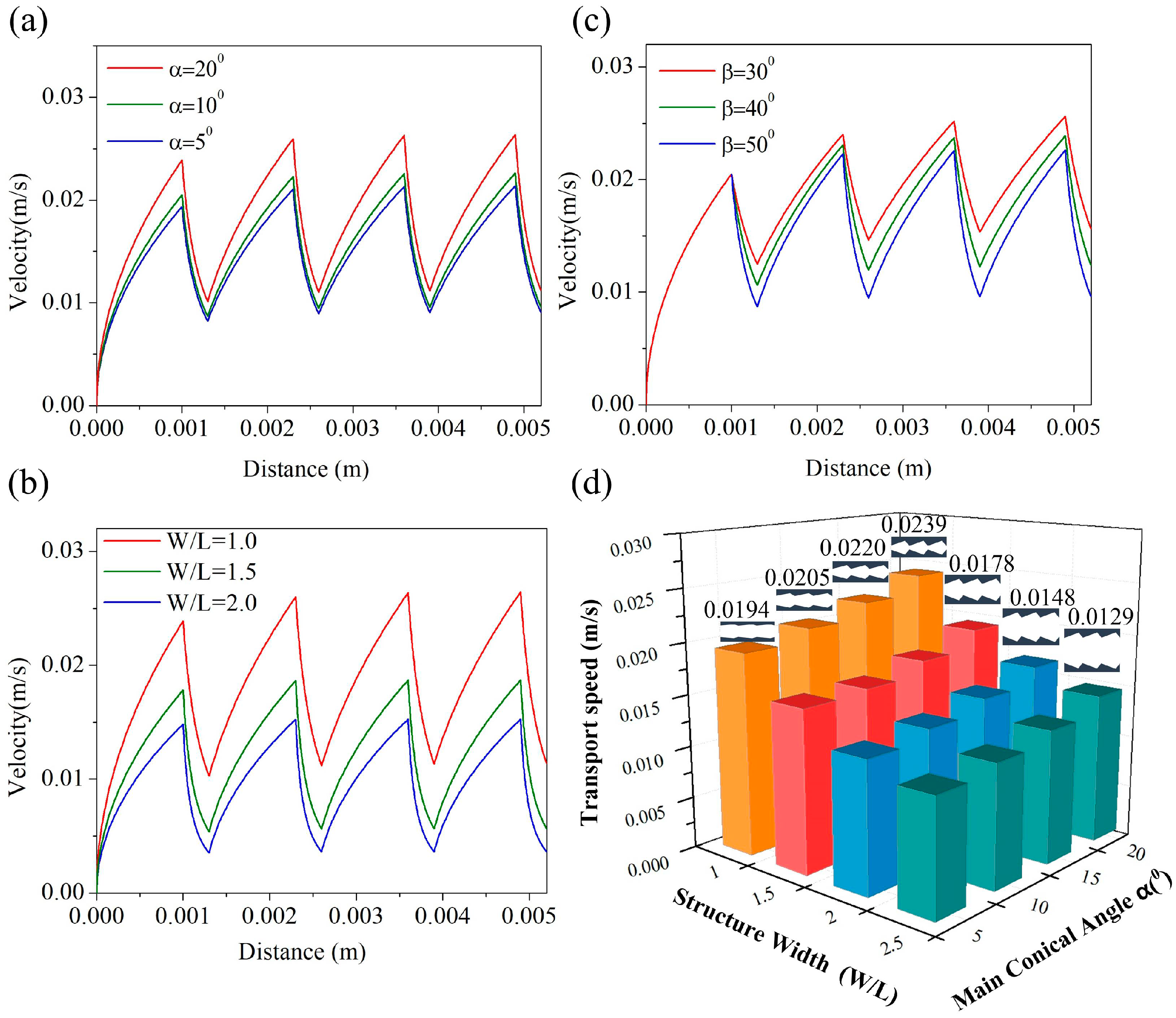
3.2. Effect of Size on Liquid Transport Velocity
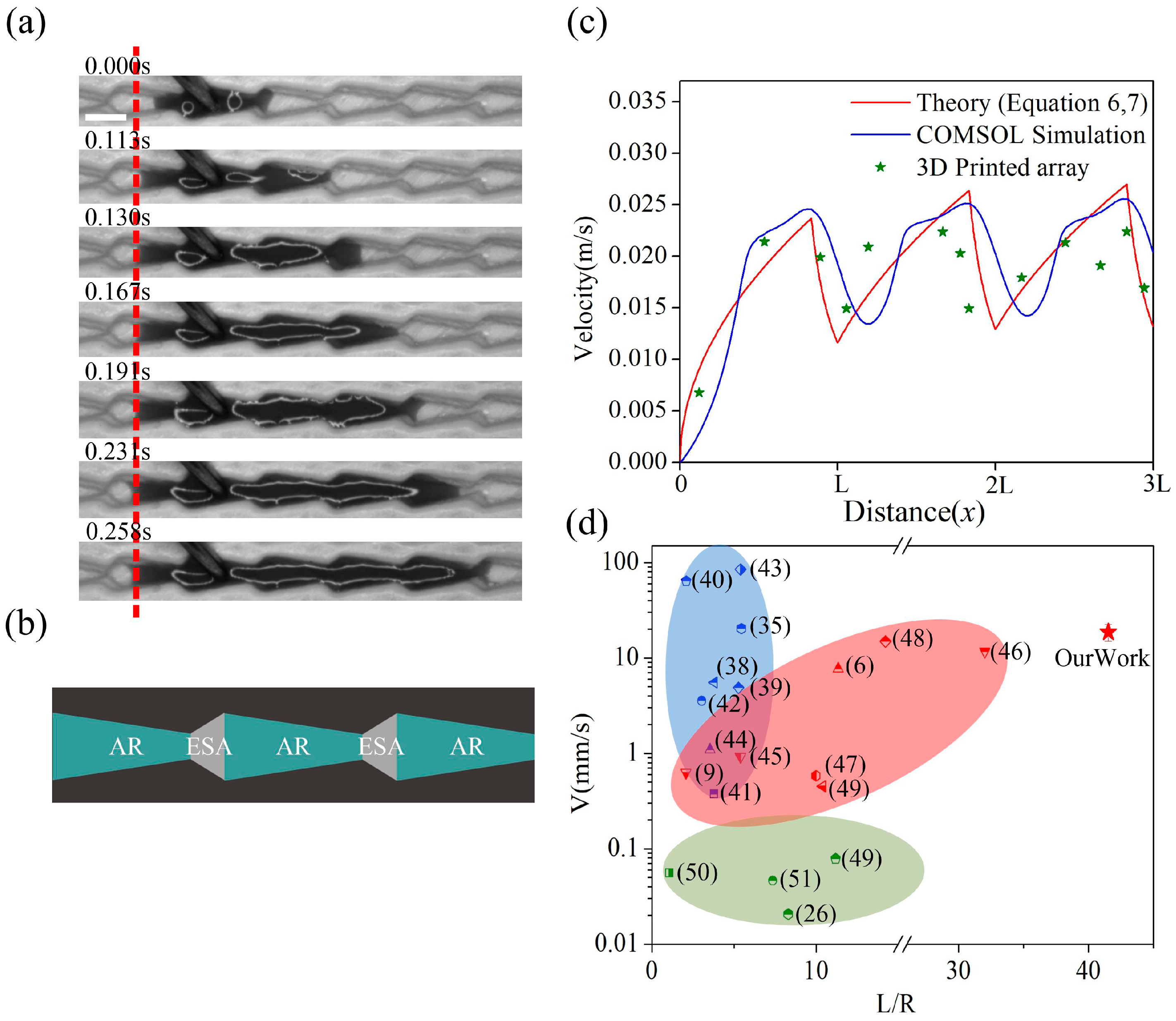
3.3. Experimental Analysis of Liquid Transport
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Koch, K.; Barthlott, W. Superhydrophobic and superhydrophilic plant surfaces: An inspiration for biomimetic materials. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2009, 367, 1487–1509. [Google Scholar] [CrossRef] [PubMed]
- Qu, M.; Liu, S.; He, J.; Yu, C.; Liu, X.; Yao, Y.; Feng, J. Bioinspired fabrication of mechanically durable superhydrophobic materials with abrasion-enhanced properties. RSC Adv. 2016, 6, 93403–93409. [Google Scholar] [CrossRef]
- Zheng, Y.; Bai, H.; Huang, Z.; Tian, X.; Nie, F.-Q.; Zhao, Y.; Zhai, J.; Jiang, L. Directional water collection on wetted spider silk. Nature 2010, 463, 640–643. [Google Scholar] [CrossRef]
- Liu, K.; Jiang, L. Bio-inspired design of multiscale structures for function integration. Nano Today 2011, 6, 155–175. [Google Scholar] [CrossRef]
- White, B.; Sarkar, A.; Kietzig, A.-M. Fog-harvesting inspired by the Stenocara beetle—An analysis of drop collection and removal from biomimetic samples with wetting contrast. Appl. Surf. Sci. 2013, 284, 826–836. [Google Scholar] [CrossRef]
- Hischen, F.; Buchberger, G.; Plamadeala, C.; Armbruster, O.; Heiss, E.; Winands, K.; Schwarz, M.; Jüttler, B.; Heitz, J.; Baumgartner, W. The external scent efferent system of selected European true bugs (Heteroptera): A biomimetic inspiration for passive, unidirectional fluid transport. J. R. Soc. 2018, 15, 20170975. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, P.; Zhang, L.; Liu, H.; Jiang, Y.; Zhang, D.; Han, Z.; Jiang, L. Continuous directional water transport on the peristome surface of Nepenthes alata. Nature 2016, 532, 85–89. [Google Scholar] [CrossRef] [PubMed]
- Wong, T.-S.; Kang, S.H.; Tang, S.K.Y.; Smythe, E.J.; Hatton, B.D.; Grinthal, A.; Aizenberg, J. Bioinspired self-repairing slippery surfaces with pressure-stable omniphobicity. Nature 2011, 477, 443–447. [Google Scholar] [CrossRef] [Green Version]
- Zhang, P.; Chen, H.; Li, L.; Liu, H.; Liu, G.; Zhang, L.; Zhang, D.; Jiang, L. Bioinspired Smart Peristome Surface for Temperature-Controlled Unidirectional Water Spreading. ACS Appl. Mater. Interfaces 2017, 9, 5645–5652. [Google Scholar] [CrossRef]
- Li, C.; Li, N.; Zhang, X.; Dong, Z.; Chen, H.; Jiang, L. Uni-Directional Transportation on Peristome-Mimetic Surfaces for Completely Wetting Liquids. Angew. Chem. Int. Ed. 2016, 55, 14988–14992. [Google Scholar] [CrossRef]
- Daniel, S.; Chaudhury, M.K.; Chen, J.C. Fast Drop Movements Resulting from the Phase Change on a Gradient Surface. Science 2001, 291, 633–636. [Google Scholar] [CrossRef] [PubMed]
- Feng, J.; Pang, Y.; Qin, Z.; Ma, R.; Yao, S. Why Condensate Drops Can Spontaneously Move Away on Some Superhydrophobic Surfaces but Not on Others. ACS Appl. Mater. Interfaces 2012, 4, 6618–6625. [Google Scholar] [CrossRef] [PubMed]
- Qiu, X.; Yang, Z.; Wu, H.; Guo, J.; Zhang, Z.; Feng, J.; Chai, G.; Liu, A. Excellent oil-water separation under external pressure: Controllable critical pressure and separation efficiency by well-designed hierarchical mesh structure. Appl. Surf. Sci. 2018, 456, 602–608. [Google Scholar] [CrossRef]
- Malvadkar, N.A.; Hancock, M.J.; Sekeroglu, K.; Dressick, W.J.; Demirel, M.C. An engineered anisotropic nanofilm with unidirectional wetting properties. Nat. Mater. 2010, 9, 1023–1028. [Google Scholar] [CrossRef]
- Qin, Z.; Feng, J.; Yao, S. Factors Affecting the Spontaneous Motion of Condensate Drops on Superhydrophobic Copper Surfaces. Langmuir 2012, 28, 6067–6075. [Google Scholar]
- Li, C.; Wu, L.; Yu, C.; Dong, Z.; Jiang, L. Peristome-Mimetic Curved Surface for Spontaneous and Directional Separation of Micro Water-in-Oil Drops. Angew. Chem. Int. Ed. 2017, 56, 13623–13628. [Google Scholar] [CrossRef]
- Gao, C.; Wang, L.; Lin, Y.; Li, J.; Liu, Y.; Li, X.; Feng, S.; Zheng, Y. Droplets Manipulated on Photothermal Organogel Surfaces. Adv. Funct. Mater. 2018, 28, 1803072. [Google Scholar] [CrossRef]
- Shi, D.; Chen, Y.; Chen, X.; Chen, X.; Gao, J.; He, Y.; Wong, C.-P. Ladderlike Tapered Pillars Enabling Spontaneous and Consecutive Liquid Transport. ACS Appl. Mater. Interfaces 2018, 10, 34735–34743. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Zhu, K.; Cao, B.; Zhang, Z.; Wu, B.; Liang, L.; Chai, G.; Liu, A. Smart design of wettability-patterned gradients on substrate-independent coated surfaces to control unidirectional spreading of droplets. Soft Matter 2017, 13, 2995–3002. [Google Scholar] [CrossRef]
- Dou, X.; Li, S.; Liu, J. Zero curvature-surface driven small objects. Appl. Phys. Lett. 2017, 111, 081602. [Google Scholar] [CrossRef]
- Liu, M.; Jiang, L.; Wang, S. Nature-inspired superwettability systems. Nat. Rev. Mater. 2017, 2, 17036. [Google Scholar] [CrossRef]
- Yu, Y.-S.; Xia, X.-L.; Zheng, X.; Huang, X.; Zhou, J.-Z. Quasi-static motion of microparticles at the depinning contact line of an evaporating droplet on PDMS surface. Sci. Physics, Mech. Astron. 2017, 60, 094612. [Google Scholar] [CrossRef]
- Wang, J.; Wen, Y.; Hu, J.; Song, Y.; Jiang, L. Fine Control of the Wettability Transition Temperature of Colloidal-Crystal Films: From Superhydrophilic to Superhydrophobic. Adv. Funct. Mater. 2007, 17, 219–225. [Google Scholar] [CrossRef]
- Zhu, W.; Feng, X.; Feng, L.; Jiang, L. UV-manipulated wettability between superhydrophobicity and superhydrophilicity on a transparent and conductive SnO2 nanorod film. Chem. Commun. 2006, 2753–2755. [Google Scholar] [CrossRef]
- Li, J.; Qin, Q.H.; Shah, A.; Ras, R.H.A.; Tian, X.; Jokinen, V. Oil droplet self-transportation on oleophobic surfaces. Sci. Adv. 2016, 2, e1600148. [Google Scholar] [CrossRef] [Green Version]
- Chu, K.-H.; Xiao, R.; Wang, E.N. Uni-directional liquid spreading on asymmetric nanostructured surfaces. Nat. Mater. 2010, 9, 413–417. [Google Scholar] [CrossRef]
- Bai, F.; Wu, J.; Gong, G.; Guo, L. Biomimetic “Cactus Spine” with Hierarchical Groove Structure for Efficient Fog Collection. Adv. Sci. 2015, 2, 1500047. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Zhang, L.; Zhang, Y.; Zhang, P.; Zhang, D.; Jiang, L. Uni-directional liquid spreading control on a bio-inspired surface from the peristome of Nepenthes alata. J. Mater. Chem. A 2017, 5, 6914–6920. [Google Scholar] [CrossRef]
- Li, J.; Zheng, H.; Yang, Z.; Wang, Z. Breakdown in the directional transport of droplets on the peristome of pitcher plants. Commun. Phys. 2018, 1, 35. [Google Scholar] [CrossRef]
- Feng, J.; Rothstein, J.P. One-way wicking in open micro-channels controlled by channel topography. J. Sci. 2013, 404, 169–178. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Zhu, K.; Wu, B.; Lou, J.; Zhang, Z.; Chai, G. Influence of structured sidewalls on the wetting states and superhydrophobic stability of surfaces with dual-scale roughness. Appl. Surf. Sci. 2016, 382, 111–120. [Google Scholar] [CrossRef]
- Wu, B.-B.; Wu, H.-P.; Zhang, Z.; Dong, C.-C.; Chai, G.-Z. Thermodynamic analysis of stable wetting states and wetting transition of micro/nanoscale structured surface. Acta Phys. Sinica 2015, 64, 176801. [Google Scholar] [CrossRef]
- Wu, H.; Yang, Z.; Cao, B.; Zhang, Z.; Zhu, K.; Wu, B.; Jiang, S.; Chai, G. Wetting and Dewetting Transitions on Submerged Superhydrophobic Surfaces with Hierarchical Structures. Langmuir 2016, 33, 407–416. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.-L.; Xia, R.; Li, B.-W.; Feng, X.-Q. Directional motion of droplets in a conical tube or on a conical fibre. Chin. Phys. Lett. 2007, 24, 3210–3213. [Google Scholar]
- Yu, Y.-S. Circular plate deformed by a sessile droplet. J. Adhes. Sci. Technol. 2014, 28, 1970–1979. [Google Scholar] [CrossRef]
- Lei, L.; Zhang, H.B.; Bergstrom, D.J.; Zhang, B.; Zhang, W.J. Modeling of Droplet Generation by a Modified T-Junction Device Using COMSOL. Appl. Mech. Mater. 2014, 705, 112–116. [Google Scholar] [CrossRef]
- Rezaeiravesh, S.; Vinuesa, R.; Liefvendahl, M.; Schlatter, P. Assessment of uncertainties in hot-wire anemometry and oil-film interferometry measurements for wall-bounded turbulent flows. Eur. J. Mech. B/Fluids 2018, 72, 57–73. [Google Scholar] [CrossRef] [Green Version]
- Bliznyuk, O.; Jansen, H.P.; Kooij, E.S.; Zandvliet, H.J.W.; Poelsema, B. Smart Design of Stripe-Patterned Gradient Surfaces to Control Droplet Motion. Langmuir 2011, 27, 11238–11245. [Google Scholar] [CrossRef]
- Sun, C.; Zhao, X.-W.; Han, Y.-H.; Gu, Z.-Z. Control of water droplet motion by alteration of roughness gradient on silicon wafer by laser surface treatment. Thin Films 2008, 516, 4059–4063. [Google Scholar] [CrossRef]
- Wu, J.; Ma, R.; Wang, Z.; Yao, S. Do droplets always move following the wettability gradient? Appl. Phys. Lett. 2011, 98, 204104. [Google Scholar] [CrossRef]
- Ito, Y.; Heydari, M.; Hashimoto, A.; Konno, T.; Hirasawa, A.; Hori, S.; Kurita, K.; Nakajima, A. The Movement of a Water Droplet on a Gradient Surface Prepared by Photodegradation. Langmuir 2007, 23, 1845–1850. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Wang, H.; Liao, Q.; Ding, Y.; Gu, Y. Experiments and analysis on self-motion behaviors of liquid droplets on gradient surfaces. Exp. Therm. Sci. 2009, 33, 947–954. [Google Scholar] [CrossRef]
- Khoo, H.S.; Tseng, F.-G. Spontaneous high-speed transport of subnanoliter water droplet on gradient nanotextured surfaces. Appl. Phys. Lett. 2009, 95, 63108. [Google Scholar] [CrossRef]
- Chaudhury, M.K.; Whitesides, G.M. How to Make Water Run Uphill. Science 1992, 256, 1539–1541. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Zhang, L.; Zhang, P.; Zhang, D.; Han, Z.; Jiang, L. A Novel Bioinspired Continuous Unidirectional Liquid Spreading Surface Structure from the Peristome Surface of Nepenthes alata. Small 2016, 13, 1601676. [Google Scholar] [CrossRef]
- Chen, H.; Ran, T.; Gan, Y.; Zhou, J.; Zhang, Y.; Zhang, L.; Zhang, D.; Jiang, L. Ultrafast water harvesting and transport in hierarchical microchannels. Nat. Mater. 2018, 17, 935. [Google Scholar] [CrossRef]
- Geng, H.; Bai, H.; Fan, Y.; Wang, S.; Ba, T.; Yu, C.; Cao, M.; Jiang, L. Unidirectional water delivery on a superhydrophilic surface with two-dimensional asymmetrical wettability barriers. Mater. Horizons 2018, 5, 303–308. [Google Scholar] [CrossRef]
- Li, J.; Zhou, X.; Li, J.; Che, L.; Yao, J.; McHale, G.; Chaudhury, M.K.; Wang, Z. Topological liquid diode. Sci. Adv. 2017, 3, eaao3530. [Google Scholar] [CrossRef] [PubMed]
- Jokinen, V.; Leinikka, M.; Franssila, S. Microstructured Surfaces for Directional Wetting. Adv. Mater. 2009, 21, 4835–4838. [Google Scholar] [CrossRef]
- Kim, T.-I.; Suh, K.Y. Unidirectional wetting and spreading on stooped polymer nanohairs. Soft Matter 2009, 5, 4131. [Google Scholar] [CrossRef]
- Yang, X.M.; Zhong, Z.W.; Li, E.Q.; Wang, Z.H.; Xu, W.; Thoroddsen, S.T.; Zhang, X.X. Asymmetric liquid wetting and spreading on surfaces with slanted micro-pillar arrays. Soft Matter 2013, 9, 11113. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, L.; Wang, W.; Chen, J.; Jiang, K.; Sheng, Y.; Peng, X.; Liu, A.; Wu, H. Continuous Directional Water Delivery on the 3D-Printed Arrowhead Microstructure Array. Materials 2019, 12, 1043. https://doi.org/10.3390/ma12071043
Liang L, Wang W, Chen J, Jiang K, Sheng Y, Peng X, Liu A, Wu H. Continuous Directional Water Delivery on the 3D-Printed Arrowhead Microstructure Array. Materials. 2019; 12(7):1043. https://doi.org/10.3390/ma12071043
Chicago/Turabian StyleLiang, Lihua, Wei Wang, Junjun Chen, Kunpeng Jiang, Yufeng Sheng, Xiang Peng, Aiping Liu, and Huaping Wu. 2019. "Continuous Directional Water Delivery on the 3D-Printed Arrowhead Microstructure Array" Materials 12, no. 7: 1043. https://doi.org/10.3390/ma12071043
APA StyleLiang, L., Wang, W., Chen, J., Jiang, K., Sheng, Y., Peng, X., Liu, A., & Wu, H. (2019). Continuous Directional Water Delivery on the 3D-Printed Arrowhead Microstructure Array. Materials, 12(7), 1043. https://doi.org/10.3390/ma12071043