Toward a Fully Analytical Contact Resistance Expression in Organic Transistors

Abstract

Contact resistance is a major characteristic of organic transistors, and its importance has received renewed attention due to the recent revelation of mobility overestimation. In this article, we propose a method to describe the contact resistance as a closed-form compact equation of the materials, interfaces, and geometrical parameters. The proposed model allows us to quantitatively understand the correlation between charge-injection and transport properties, while providing a tool for performance prediction and optimization. This theory is applied to a set of experimentally fabricated devices to exemplify how to utilize the model in practice.

1. Introduction

Clearly, the organic field-effect transistor (OFET) has experienced a tremendous progress over its now more than three decades of history [1]. The initially widespread concerns about stability and reliability have been largely overcome, and the device performance has increased so much that the OFET technologies could successfully demonstrate the applicability to flat-panel displays [2], active-matrix imagers [3], radio-frequency identification tags [4], and many other areas. However, relatively immature understanding of the basic operation of OFETs limits sustainable developments. A lack of holistic understanding directly translates into a lack of dedicated compact model, which otherwise is critical to circuit simulation [5]. In other words, there is still no standard OFET model in general-purpose simulators, and often one is obliged to go with a Si transistor model available in the library. Also, when an OFET is used as a test bed for material inspection, there is sometimes no better choice than picking up the simplistic current-voltage equation that is for an ideal field-effect transistor. Since the latter usage of a ‘model’ is broadly evoked, there has been much debate on whether the common practice of charge-carrier mobility (μ) extraction should be revised [6,7,8,9].

At the heart of these parameterization issues is the contact resistance (R_c) and its impact on the overall device behaviors. If we ‘assume’ that there is no parasitic R_c and the channel resistance (R_ch, which is a direct indicator of μ) is solely responsible for a measured drain current (I_D), it is easy to underestimate the real μ when there is a non-zero R_c, because we have got a higher R_ch than real [10]. Nonetheless, as explained by Liu and co-workers [11], both resistive components can be gate-voltage (V_G) dependent to different extents, and we may either under- or overestimate the actual μ depending on the relative strength of the V_G derivatives of these two resistances.

Completely eliminating R_c in a device might be the best way to produce a high current and avoid analysis problems, but in most case, especially with a high-mobility material and/or at a large V_G, this task is not straightforward. Therefore, it is recommended to directly measure the V_G-dependent R_c by e.g. transmission-line method (TLM) [12], four-probe measurement [13], or surface potentiometry [14], and then unambiguously deduce R_ch and μ. In parallel, deeply understanding what makes up R_c and capturing this knowledge into a widely valid parametric form is of fundamental importance, as such a model allows us to see one step further and discuss the extracted R_c and its implications.

In this article, we introduce a method to simplify the carrier distribution at the on-state of an OFET to build a fully analytical R_c model. The model is based on the idea of effective accumulation thickness and it provides a direct link between R_c and other key materials and device parameters, including μ. Therefore, it allows for the self-consistent decoupling and correlation between carrier injection and transport quantities, and provides a useful instrument for physical analysis.

2. Theoretical Modeling

An in-depth foundation of the following approach is given in our previous paper [15]. That study proposed the first theoretical model for the R_c in coplanar OFETs, by defining the sharp carrier-density-transition zone at the source/channel interface as the responsible volume and expressing the single effective macroscopic resistance therein. While it convincingly demonstrated both the analytic and predictive capability of such a model, a major drawback was that it suggested a ‘semi-analytical’ final equation in that solving for R_c involves numerical integration.

Therefore, we propose here a method to modify the theory toward a fully analytical and widely applicable compact model. We first summarize the major characteristics of the previous model using Figure 1, which visualizes the channel region of a p-type OFET. Here, W and L denote the channel width and length, respectively, and d is the semiconductor film thickness. The x, y, and z axes are defined as shown. Note that the model in [15] was originally dedicated to coplanar OFETs, but we believe that it can be a good approximation to staggered OFETs with a thin active layer where metal diffusion can shape vertically penetrating metal/organic interfaces [16].

From the Boltzmann statistics, the source hole density at y = 0 (p_s0) is injection-limited, written as

$$p_{s0}=N_v\exp \left(-\frac{E_b}{kT}\right),$$

(1)

where N_v is the effective density of states (DOS) at the highest-occupied molecular orbital (HOMO) edge, E_b is the hole injection barrier, k is the Boltzmann constant, and T is the absolute temperature. In contrast, the channel hole density at y = 0 (p_ch0) is capacitively modulated. The widely used charge per area versus V_G equation can be transformed to the carrier density dimension by assuming a strong vertical localization, as

$$p_{\mathrm{ch}0}=\frac{C_i^2{(V_G-V_T)}^2}{2{\epsilon }_{s}kT},$$

(2)

where C_i is the insulator capacitance per area, V_T is the threshold voltage, and ε_s is the semiconductor permittivity. As illustrated in Figure 1, p_s0 and p_ch0 are independently controlled by Equations (1) and (2) and they fix a boundary condition of the respective carrier distribution, which decreases as y increases. In [15], we formulated these distributions as p_s(y) and p_ch(y). The key finding was an orders-of-magnitude difference between p_s and p_ch values under realistic conditions (p_ch ≫ p_s), rationalizing the emergence of R_c at the source edge (a low carrier density means a high resistance). We therefore designated this transition zone with the length t as the physical R_c region. The parameter t basically is a balance factor that shows how large such a zone should be to regulate the horizontal relaxations of p_s and p_ch, and has the following dependence.

$$t=x_s\ln \left(\frac{p_{\mathrm{ch}}}{p_s}\right),$$

(3)

where x_s is the Debye length of source carriers. The average hole density p_m at this zone is given as

$$p_m=\frac{1}{t}{{\displaystyle \int }}_0^{t}p\left(x\right)dx\cong \frac{p_{\mathrm{ch}}}{\ln \left(p_{\mathrm{ch}}/p_s\right)}.$$

(4)

Therefore, the numerically integrated contact resistance, which we call R_num here, is obtained as

$$R_{\mathrm{num}}\left(d\right)={\left[{{\displaystyle \int }}_0^{d}q\mu p_m\left(y\right)\frac{W}{t\left(y\right)}dy\right]}^{-1}.$$

(5)

Note here that R_c does have a direct dependence on μ. Equation (5) can be supplemented by a specific functional form of μ such as

$$\mu =\kappa {\left|V_G-V_T\right|}^{\alpha },$$

(6)

which assumes a charge transport mediated by an exponential trap DOS [5]. Here, κ is the mobility pre-factor and α is the characteristic exponent.

Figure 2 shows the change of p_m with y and the numerically calculated R_num with a varying upper limit of integral d_i, under fixed materials, geometrical, and bias conditions. These results suggest the two important keys to the modeling.

(1)

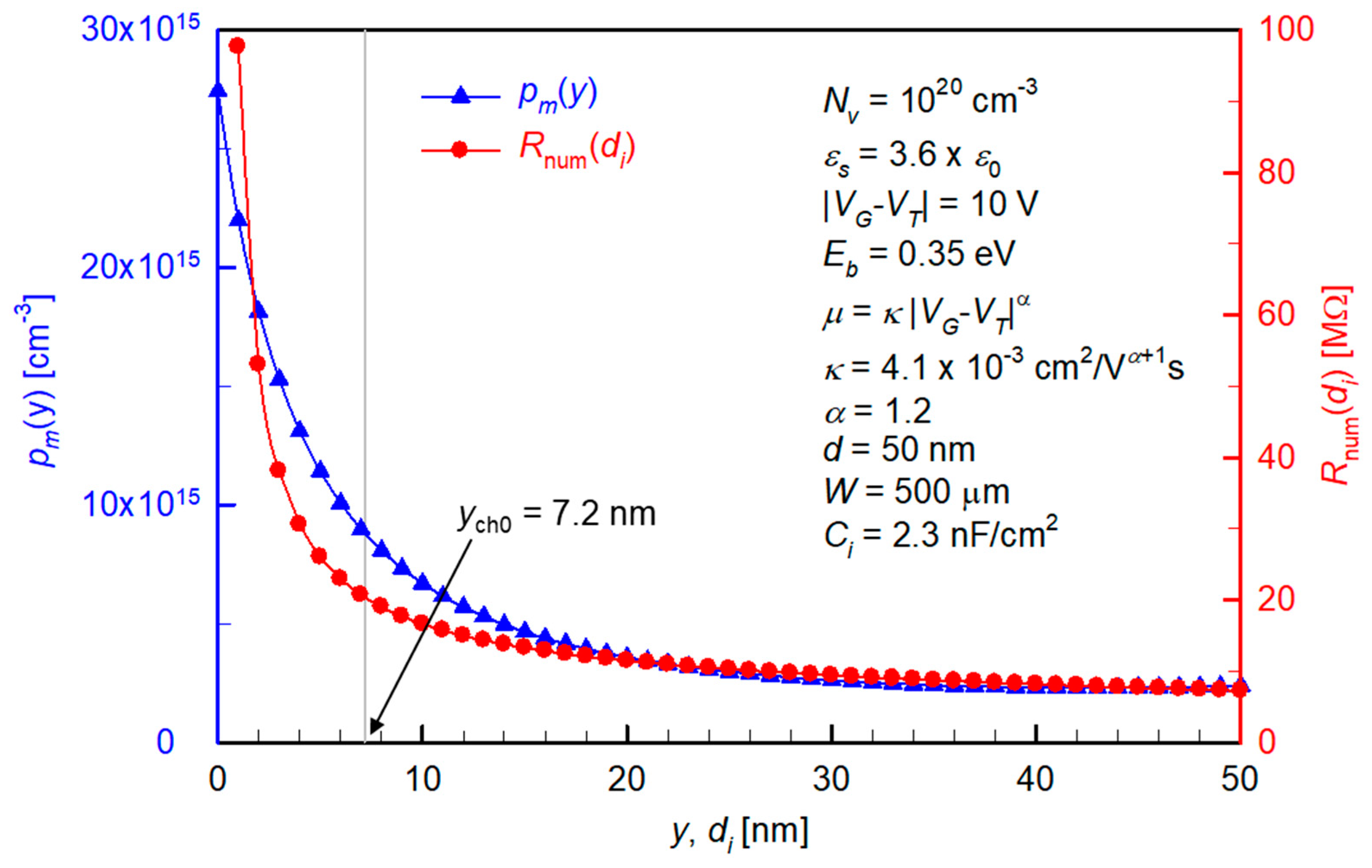
Here, both p_m and R_num decrease rapidly when moving from the insulator (y, d_i = 0) to the top surface of the semiconductor (y, d_i = 50 nm). Therefore, we choose to consider only the region 0 < y < y_ch0, with the y_ch0 being the effective accumulation thickness from the Mott–Gurney distribution. The value of y_ch0 therefore decreases when V_G increases (in magnitude) showing a smaller geometrical spread of the carriers at a higher gate field.

(2)

In order to replace an integral with a simpler multiplication, we now need to deal with those that change with y in Equation (5), namely p_m(y) and t(y). There are different ways to do this. For maximum simplicity, we take p_m0 and t₀ as the representative values that are determined by p_s0 and p_ch0, and are constant over 0 < y < y_ch0. Note that this choice is also justified by the fact that while p_m0 is the maximum of p_m(y) at an actual distribution (e.g., Figure 2), assuming a constantly high p_m0 over a certain physical distance can partly compensate the holes outside the effective accumulation space (i.e., those that are at y > y_ch0)

Finally, the new modified R_c model is constructed from

$$R_c=\frac{t_0}{q\mu p_{m0}W{y}_{\mathrm{ch}0}},$$

(7)

where

$$t_0=x_{s0}\ln \left(\frac{p_{\mathrm{ch}0}}{p_{s0}}\right),$$

(8)

$$p_{m0}=\frac{p_{\mathrm{ch}0}}{\ln \left(p_{\mathrm{ch}0}/p_{s0}\right)},$$

(9)

$$y_{\mathrm{ch}0}=\sqrt{\frac{2{\epsilon }_{s}kT}{q^2{p}_{\mathrm{ch}0}}},$$

(10)

Putting Equations (1), (2), (8)–(10), and $x_{s0}=\sqrt{{\epsilon }_{s}kT/q^2{p}_{s0}}$ into Equation (7), this equation can be re-written as

$$R_c=\frac{{\left[\ln \frac{C_i^2{\left(V_G-V_T\right)}^2}{2{\epsilon }_{s}kT{N}_v}+\frac{E_b}{kT}\right]}^2}{q\mu W\sqrt{N_v}\exp \left(-\frac{E_b}{2kT}\right)\frac{C_i\left|V_G-V_T\right|}{\sqrt{{\epsilon }_{s}kT}}},$$

(11)

which is a fully analytical model with explicit parametric impacts on the value of R_c. We additionally note that retaining the absolute sign in |V_G − V_T| generalizes the model to both n- and p-type OFETs, with an obvious need to replace N_v and E_b by values associated with the lowest-unoccupied molecular orbital (LUMO) and the electron injection when applying it to an n-type device.

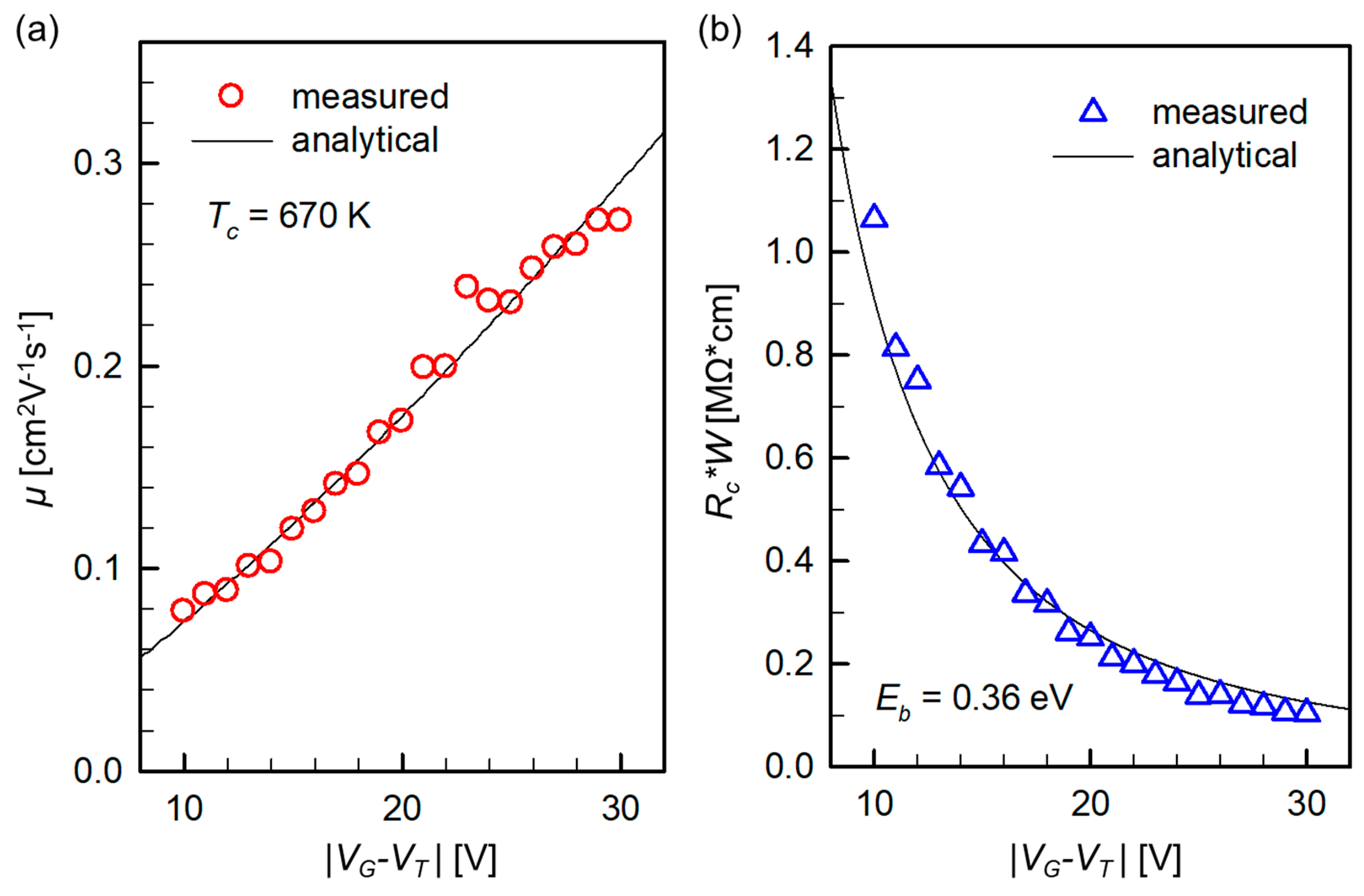
3. Application and Analysis

Major advantages of a closed-form analytical equation include an ease of application to practical research and a reduced computational load in circuit simulation. For instance, Equation (11) does not only illustrate the widely observed V_G and E_b dependence of R_c, but it also clearly and quantitatively demonstrates a considerable impact of e.g. ε_sand C_i, which have been less considered. Therefore, such a model allows for assessing critical parameters and setting a strategy for rational optimization.

Here, we briefly describe how to apply the model to fabricated devices, in this case to estimate the E_b. We repeat that it is crucial to robustly decouple contact and channel properties by systematic measurements before proceeding to any further analyses, to avoid parameter ambiguities [7,14]. We conducted the TLM on the pentacene OFETs with Au source/drain electrodes, whose fabrication and characterization details can be found in [15]. Note that full utilization of TLM gives access to both R_c and (intrinsic) μ as a function of V_G for a given set of length-variable transistors [12].

In Equation (11), we left the term μ intact, in view of possibly diverse transport scenarios and corresponding models. Once we have experimentally obtained a μ versus V_G plot, it can be a perfect moment to check which model suits best the given devices. As shown in Figure 3a, our pentacene OFETs exhibit a substantial gate-field enhancement, so we fit the measured curve to the power-law model in Equation (6). A satisfactory fit was obtained, from which we extracted the characteristic temperature for the trap distribution T_c [17,18] as 670 K by

T_c = T(α + 1)

(12)

Then, we inserted Equation (6) into Equation (11), assumed N_v and ε_s as those in Figure 2 [19], and fit the TLM-measured R_c versus V_G curve to Equation (11). Figure 3b shows that the model is in good agreement with the measurements, and the fitting process resulted in E_b = 0.36 eV, which is a realistic value for a pentacene/Au junction [20].

As a final note, we clarify that the Boltzmann approximation for Equation (1) is broadly valid in organic devices where a large HOMO-LUMO gap and trap-related level pinning sustains a sizable energetic distance between the transport orbital and the electrode Fermi level [21]. If we incorporate the Fermi–Dirac distribution into our model despite this fact, its analytical simplicity will be reduced, but the predicted R_c values will remain similar because of a sufficiently large E_b.

4. Conclusions

In this article, we have proposed the strategic modification of the existing charge-based model toward a new fully analytical R_c model. In addition to providing a convenient tool for OFET contact analysis and engineering, we believe that the systematic approach introduced here will inspire the physical and mathematical modeling of other key characteristics of OFETs, which will be ultimately necessary for a universal compact model of organic transistor technologies.