Structure–Property Relationships in Shape Memory Metallic Glass Composites
Abstract
:1. Introduction
2. Simulation Details
3. Results and Discussion
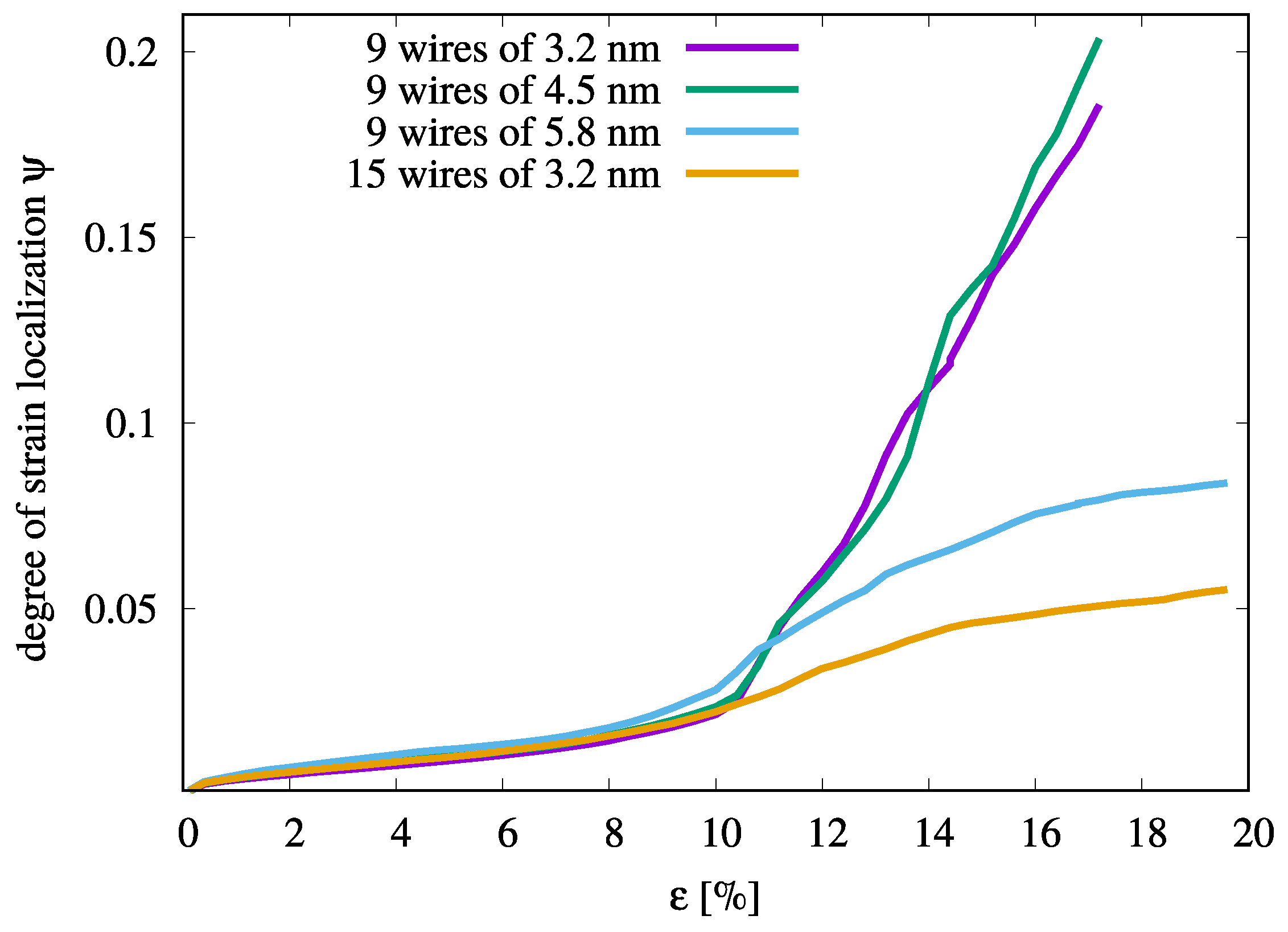
3.1. Effect of the Density of Inclusions
3.2. Effect of the Size of the Inclusions
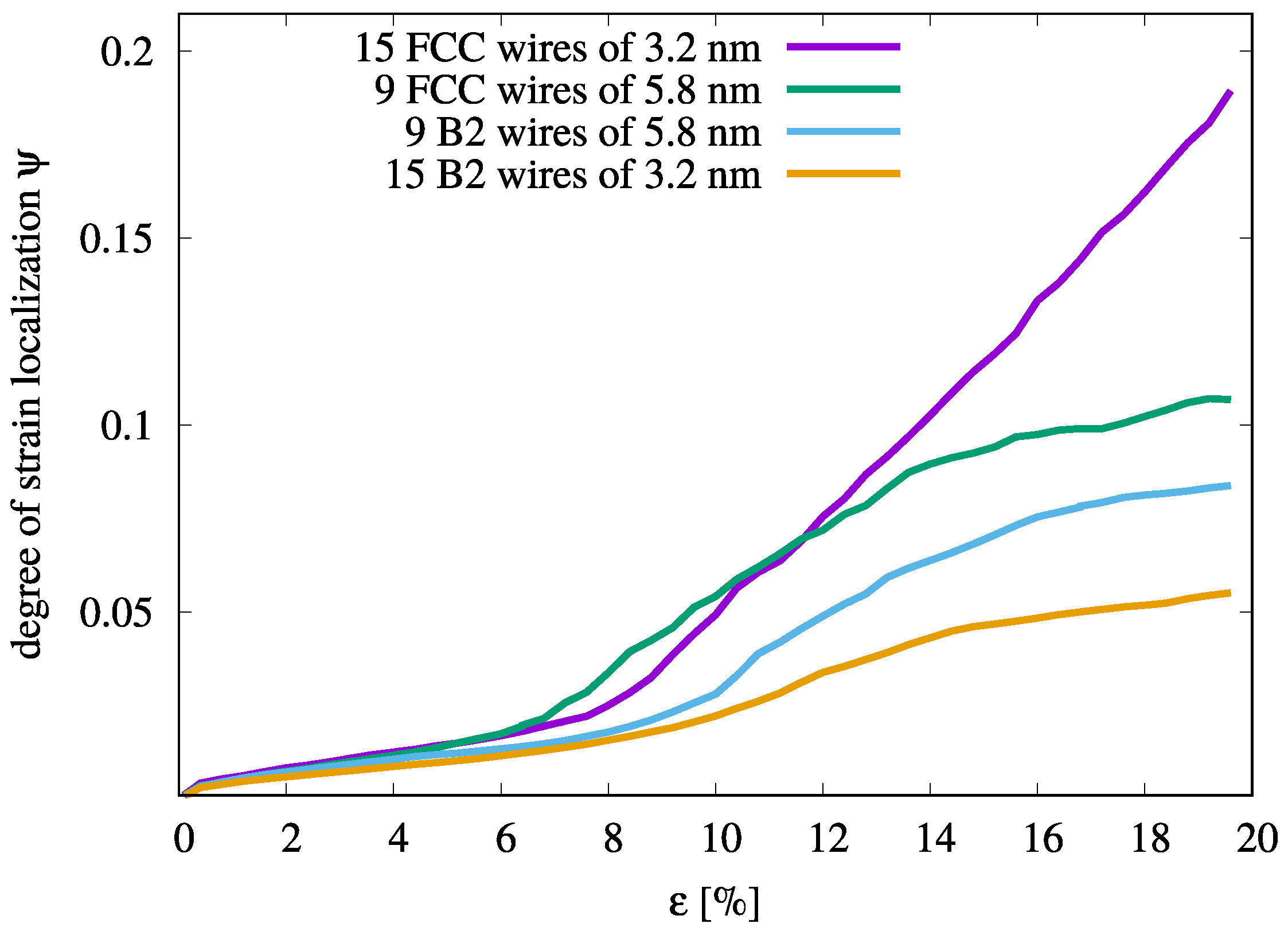
3.3. Effects of Crystal Structure
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- He, G.; Eckert, J.; Löser, W.; Schultz, L. Novel Ti-base nanostructure-dendrite composite with enhanced plasticity. Nat. Mater. 2003, 2, 33–37. [Google Scholar] [CrossRef] [PubMed]
- Fan, C.; Inoue, A. Improvement of mechanical properties by precipitation of nanoscale compound particles in Zr-Cu-Pd-Al amorphous alloys. Mater. Trans. JIM 1997, 38, 1040–1046. [Google Scholar] [CrossRef]
- Hays, C.C.; Kim, C.P.; Johnson, W.L. Microstructure controlled shear band pattern formation and enhanced plasticity of bulk metallic glasses containing in situ formed ductile phase dendrite dispersions. Phys. Rev. Lett. 2000, 84, 2901–2904. [Google Scholar] [CrossRef]
- Hays, C.C.; Kim, C.P.; Johnson, W.L. Improved mechanical behavior of bulk metallic glasses containing in situ formed ductile phase dendrite dispersions. Mater. Sci. Eng. A 2001, 304, 650–655. [Google Scholar] [CrossRef]
- Eckert, J.; Das, J.; Pauly, S.; Duhamel, C. Mechanical properties of bulk metallic glasses and composites. J. Mater. Res. 2007, 22, 285–301. [Google Scholar] [CrossRef]
- Conner, R.; Dandliker, R.; Johnson, W. Mechanical properties of tungsten and steel fiber reinforced Zr41.25Ti13.75Cu12.5Ni10Be22.5 metallic glass matrix composites. Acta Mater. 1998, 46, 6089–6102. [Google Scholar] [CrossRef]
- Pauly, S.; Gorantla, S.; Wang, G.; Kuhn, U.; Eckert, J. Transformation-mediated ductility in CuZr-based bulk metallic glasses. Nat. Mater. 2010, 9, 473–477. [Google Scholar] [CrossRef]
- Chen, M.; Inoue, A.; Zhang, W.; Sakurai, T. Extraordinary Plasticity of Ductile Bulk Metallic Glasses. Phys. Rev. Lett. 2006, 96, 245502. [Google Scholar] [CrossRef]
- Hofmann, D.C.; Suh, J.Y.; Wiest, A.; Duan, G.; Lind, M.L.; Demetriou, M.D.; Johnson, W.L. Designing metallic glass matrix composites with high toughness and tensile ductility. Nature 2008, 451, 1085–1089. [Google Scholar] [CrossRef] [PubMed]
- Kim, C.P.; Oh, Y.S.; Lee, S.; Kim, N.J. Realization of high tensile ductility in a bulk metallic glass composite by the utilization of deformation-induced martensitic transformation. Scr. Mater. 2011, 65, 304–307. [Google Scholar] [CrossRef]
- Liu, Z.; Li, R.; Liu, G.; Song, K.; Pauly, S.; Zhang, T.; Eckert, J. Pronounced ductility in CuZrAl ternary bulk metallic glass composites with optimized microstructure through melt adjustment. AIP Adv. 2012, 2. [Google Scholar] [CrossRef]
- Lee, M.; Lee, C.M.; Lee, K.R.; Ma, E.; Lee, J.C. Networked interpenetrating connections of icosahedra Effects on shear transformations in metallic glass. Acta Mater. 2011, 59, 159–170. [Google Scholar] [CrossRef]
- Wu, F.F.; Chan, K.; Li, S.T.; Wang, G. Stabilized shear banding of ZrCu-based metallic glass composites under tensile loading. J. Mater. Sci. 2014, 49, 2164–2170. [Google Scholar] [CrossRef]
- Barekar, N.; Pauly, S.; Kumar, R.; Kuhn, U.; Dhindaw, B.; Eckert, J. Structure–property relations in bulk metallic Cu–Zr–Al alloys. Mater. Sci. Eng. A 2010, 527, 5867–5872. [Google Scholar] [CrossRef]
- Pauly, S.; Liu, G.; Gorantla, S.; Wang, G.; Kühn, U.; Kim, D.H.; Eckert, J. Criteria for tensile plasticity in Cu-Zr-Al bulk metallic glasses. Acta Mater. 2010, 58, 4883–4890. [Google Scholar] [CrossRef]
- Hofmann, D.C. Shape Memory Bulk Metallic Glass Composites. Science 2010, 329, 1294–1295. [Google Scholar] [CrossRef]
- Wu, Y.; Xiao, Y.; Chen, G.; Liu, C.T.; Lu, Z. Bulk Metallic Glass Composites with Transformation-Mediated Work-Hardening and Ductility. Adv. Mater. 2010, 22, 2770–2773. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, H.; Li, W.; Gemming, T.; Wang, P.; Bönisch, M.; Şopu, D.; Eckert, J.; Pauly, S. Beta-type Ti-based bulk metallic glass composites with tailored structural metastability. J. Alloys Compd. 2017, 708, 972–981. [Google Scholar] [CrossRef]
- Hong, S.; Kim, J.; Park, H.; Kim, Y.; Suh, J.; Na, Y.; Lim, K.; Park, J.; Kim, K. Gradual martensitic transformation of B2 phase on TiCu-based bulk metallic glass composite during deformation. Intermetallics 2016, 75, 1–7. [Google Scholar] [CrossRef]
- Zhang, L.; Narayan, R.; Fu, H.; Ramamurty, U.; Li, W.; Li, Y.; Zhang, H. Tuning the microstructure and metastability of β-Ti for simultaneous enhancement of strength and ductility of Ti-based bulk metallic glass composites. Acta Mater. 2019, 168, 24–36. [Google Scholar] [CrossRef]
- Hajlaoui, K.; Yavari, A.; LeMoulec, A.; Botta, W.; Vaughan, F.; Das, J.; Greer, A.; Kvick, Å. Plasticity induced by nanoparticle dispersions in bulk metallic glasses. J. Non-Cryst. Solids 2007, 353, 327–331. [Google Scholar] [CrossRef]
- Luan, Y.W.; Li, C.H.; Han, X.J.; Li, J.G. Plastic deformation behaviours of CuZr amorphous/crystalline nanolaminate: A molecular dynamics study. Mol. Simul. 2017, 43, 1116–1124. [Google Scholar] [CrossRef]
- Seo, J.; Schryvers, D. TEM investigation of the microstructure and defects of CuZr martensite. Part I: Morphology and twin systems. Acta Mater. 1998, 46, 1165–1175. [Google Scholar] [CrossRef]
- Park, H.J.; Hong, S.H.; Park, H.J.; Kim, Y.S.; Kim, J.T.; Na, Y.S.; Lim, K.R.; Wang, W.M.; Kim, K.B. Development of High Strength Ni–Cu–Zr–Ti–Si–Sn In-Situ Bulk Metallic Glass Composites Reinforced by Hard B2 Phase. Met. Mater. Int. 2018, 24, 241–247. [Google Scholar] [CrossRef]
- Şopu, D.; Stoica, M.; Eckert, J. Deformation behavior of metallic glass composites reinforced with shape memory nanowires studied via molecular dynamics simulations. Appl. Phys. Lett. 2015, 106, 211902. [Google Scholar] [CrossRef] [Green Version]
- Şopu, D.; Albe, K.; Eckert, J. Metallic glass nanolaminates with shape memory alloys. Acta Mater. 2018, 159, 344–351. [Google Scholar] [CrossRef]
- Albe, K.; Ritter, Y.; Şopu, D. Enhancing the plasticity of metallic glasses: Shear band formation, nanocomposites and nanoglasses investigated by molecular dynamics simulations. Mech. Mater. 2013, 67, 94–103. [Google Scholar] [CrossRef]
- Brink, T.; Peterlechner, M.; Rösner, H.; Albe, K.; Wilde, G. Influence of Crystalline Nanoprecipitates on Shear-Band Propagation in Cu-Zr-Based Metallic Glasses. Phys. Rev. Appl. 2016, 5, 054005. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms For Short-Range Molecular-Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Mendelev, M.I.; Sordelet, D.J.; Kramer, M.J. Using atomistic computer simulations to analyze x-ray diffraction data from metallic glasses. J. Appl. Phys. 2007, 102, 043501. [Google Scholar] [CrossRef]
- Sutrakar, V.K.; Mahapatra, D.R. Stress-induced martensitic phase transformation in Cu-Zr nanowires. Mater. Lett. 2009, 63, 1289–1292. [Google Scholar] [CrossRef]
- Sutrakar, V.K.; Mahapatra, D.R. Single and multi-step phase transformation in CuZr nanowire under compressive/tensile loading. Intermetallics 2010, 18, 679–687. [Google Scholar] [CrossRef]
- Ward, L.; Agrawal, A.; Flores, K. Rapid production of accurate embedded-atom method potentials for metal alloys. arXiv 2012, arXiv:1209.0619. [Google Scholar]
- Shimizu, F.; Ogata, S.; Li, J. Theory of shear banding in metallic glasses and molecular dynamics calculations. Mater. Trans. 2007, 48, 2923–2927. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO-the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Honeycutt, J.D.; Andersen, H.C. Molecular dynamics study of melting and freezing of small Lennard-Jones clusters. J. Phys. Chem. 1987, 91, 4950–4963. [Google Scholar] [CrossRef]
- Şopu, D.; Stukowski, A.; Stoica, M.; Scudino, S. Atomic-Level Processes of Shear Band Nucleation in Metallic Glasses. Phys. Rev. Lett. 2017, 119, 195503. [Google Scholar] [CrossRef]
- Shi, Y.F. Size-independent shear band formation in amorphous nanowires made from simulated casting. Appl. Phys. Lett. 2010, 96, 121909. [Google Scholar] [CrossRef] [Green Version]
- Şopu, D.; Soyarslan, C.; Sarac, B.; Bargmann, S.; Stoica, M.; Eckert, J. Structure-property relationships in nanoporous metallic glasses. Acta Mater. 2016, 106, 199–207. [Google Scholar] [CrossRef] [Green Version]
- Cheng, Y.Q.; Cao, A.J.; Ma, E. Correlation between the elastic modulus and the intrinsic plastic behavior of metallic glasses: The roles of atomic configuration and alloy composition. Acta Mater. 2009, 57, 3253–3267. [Google Scholar] [CrossRef]
- Wang, Y.M.; Li, J.; Hamza, A.V.; Barbee, T.W. Ductile crystal line-amorphous nanolaminates. Proc. Natl. Acad. Sci. USA 2007, 104, 11155–11160. [Google Scholar] [CrossRef] [PubMed]
- Arman, B.; Brandl, C.; Luo, S.N.; Germann, T.C.; Misra, A.; Cagin, T. Plasticity in Cu(111)/Cu46Zr54 glass nanolaminates under uniaxial compression. J. Appl. Phys. 2011, 110. [Google Scholar] [CrossRef]
- Brandl, C.; Germann, T.; Misra, A. Structure and shear deformation of metallic crystalline–amorphous interfaces. Acta Mater. 2013, 61, 3600–3611. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Şopu, D.; Yuan, X.; Moitzi, F.; Stoica, M.; Eckert, J. Structure–Property Relationships in Shape Memory Metallic Glass Composites. Materials 2019, 12, 1419. https://doi.org/10.3390/ma12091419
Şopu D, Yuan X, Moitzi F, Stoica M, Eckert J. Structure–Property Relationships in Shape Memory Metallic Glass Composites. Materials. 2019; 12(9):1419. https://doi.org/10.3390/ma12091419
Chicago/Turabian StyleŞopu, Daniel, Xudong Yuan, Franco Moitzi, Mihai Stoica, and Jürgen Eckert. 2019. "Structure–Property Relationships in Shape Memory Metallic Glass Composites" Materials 12, no. 9: 1419. https://doi.org/10.3390/ma12091419
APA StyleŞopu, D., Yuan, X., Moitzi, F., Stoica, M., & Eckert, J. (2019). Structure–Property Relationships in Shape Memory Metallic Glass Composites. Materials, 12(9), 1419. https://doi.org/10.3390/ma12091419








