Prediction and Characteristics of Angular Distortion in Multi-Layer Butt Welding
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Study for the Database
2.1.1. Materials
2.1.2. Bead-on-Plate Welding Experiment
2.2. Databases for Algorithm
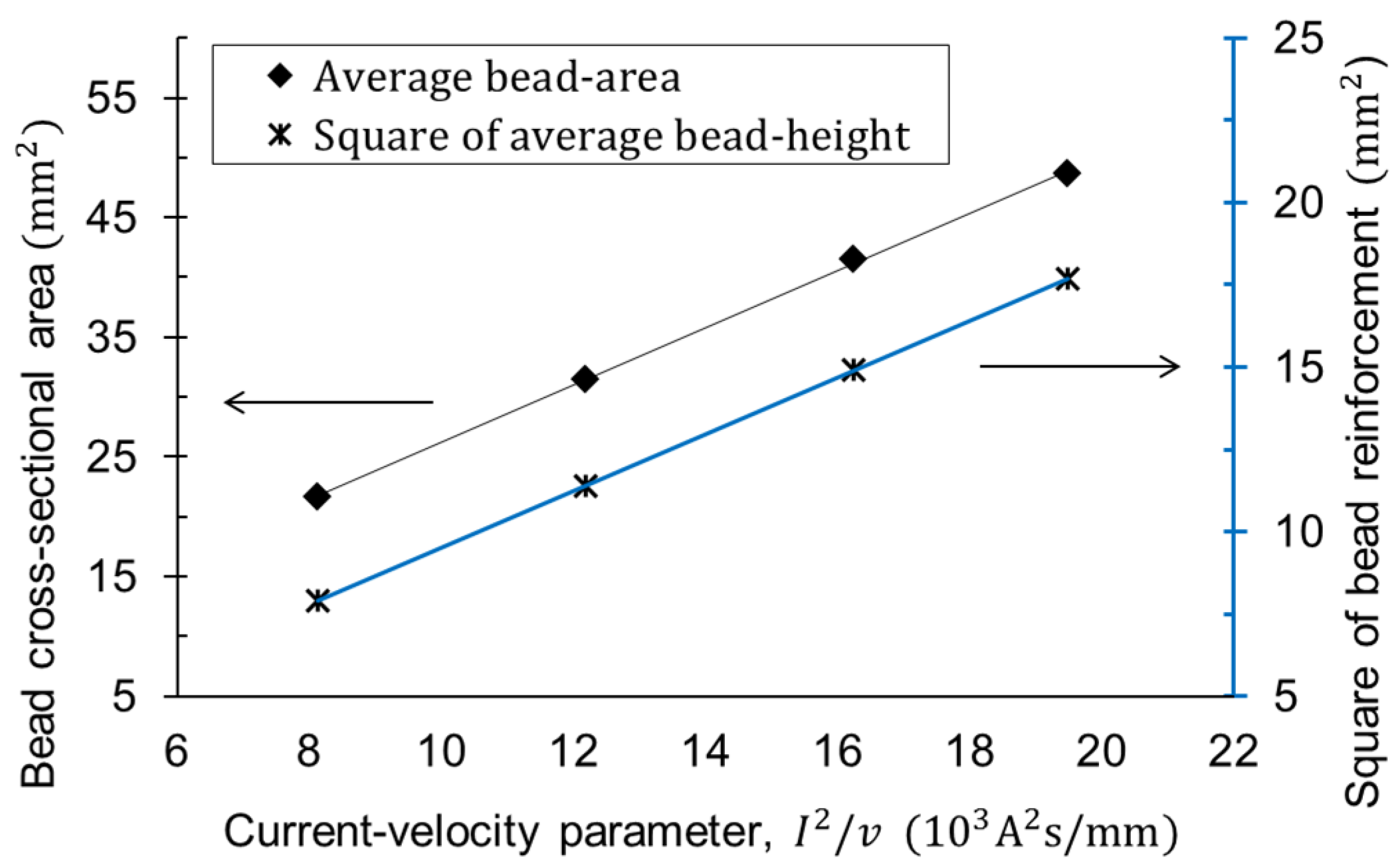
2.2.1. Database #1: Bead Area with Current-Velocity Parameter
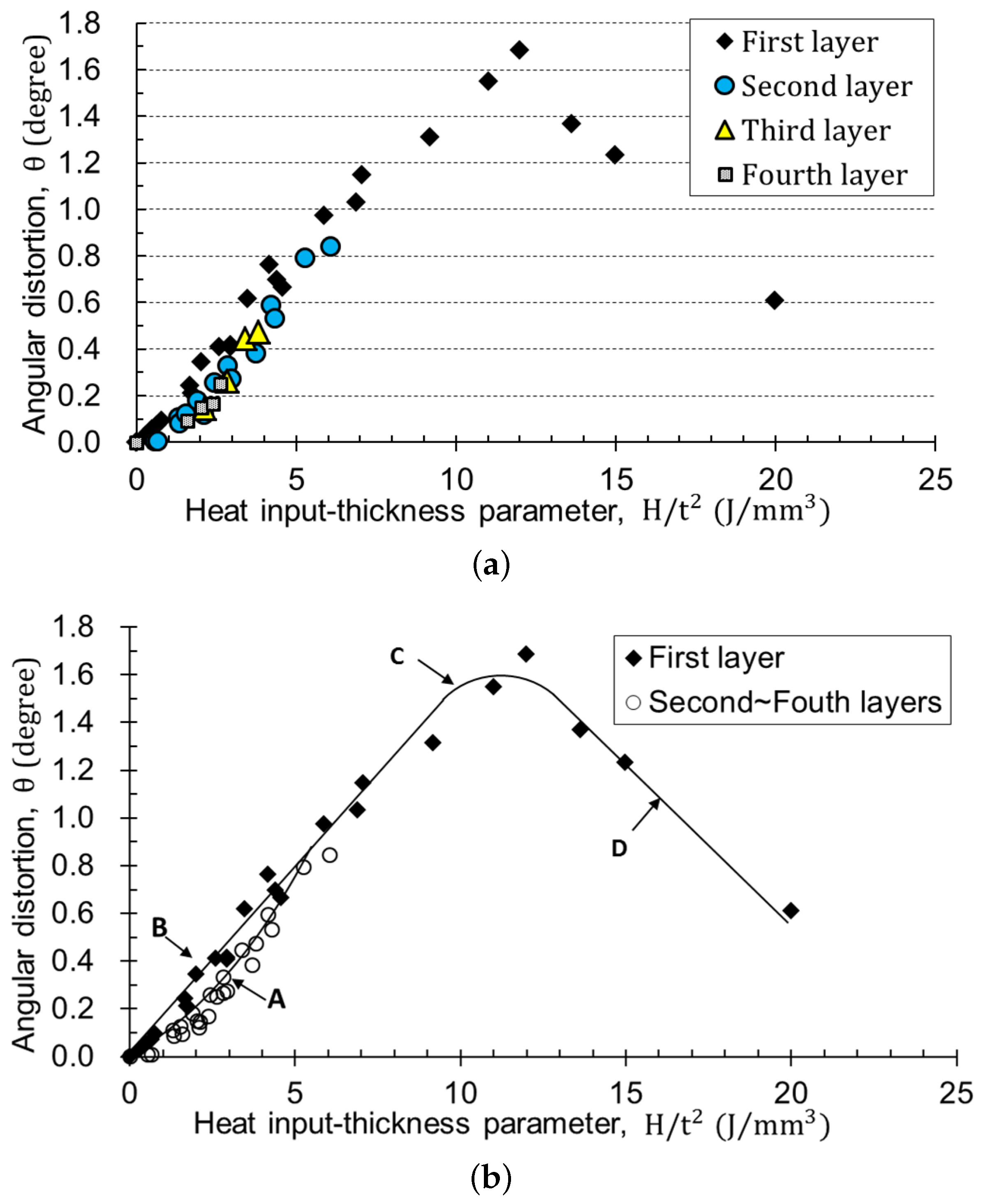
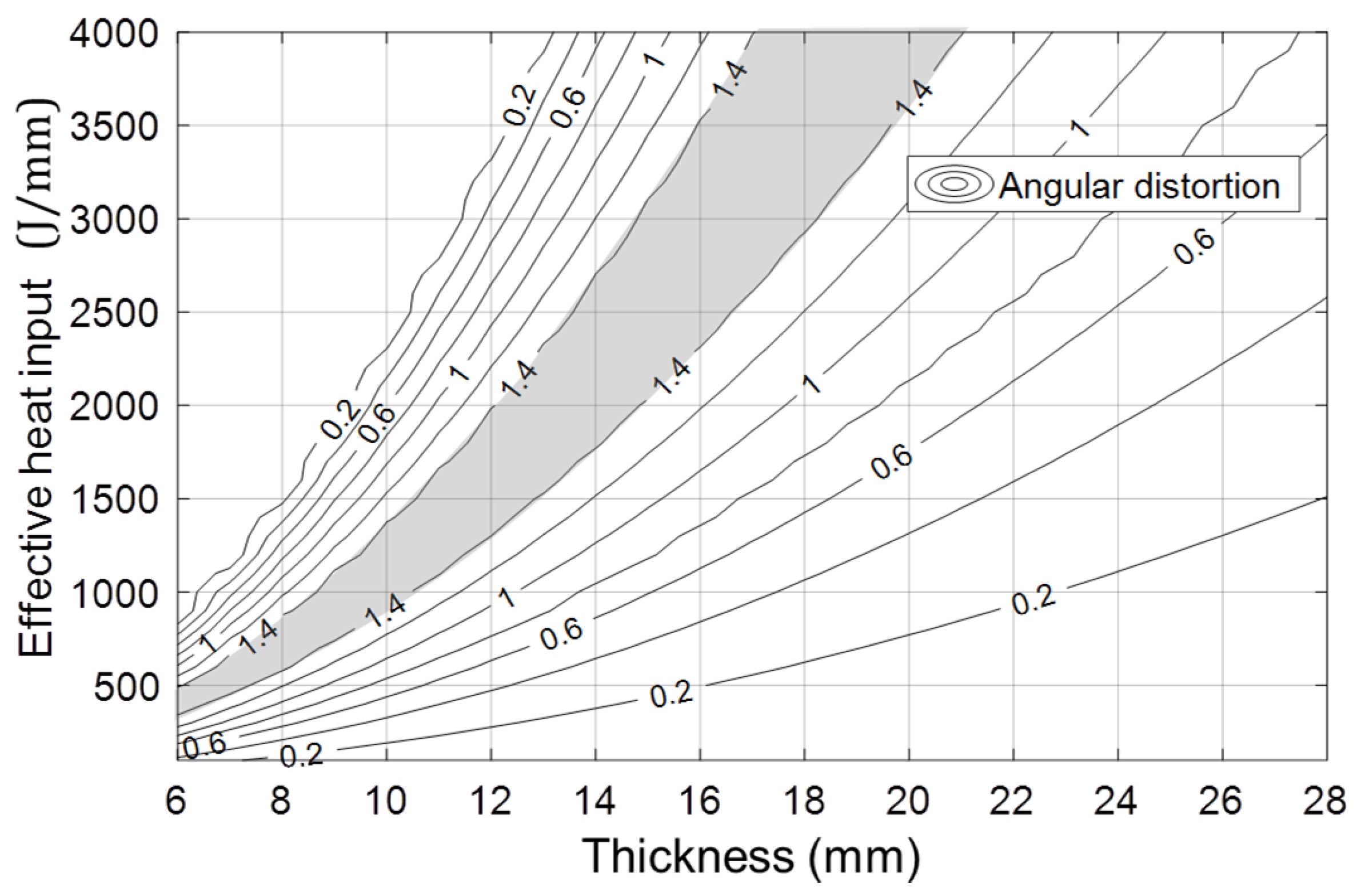
2.2.2. Database #2: Angular Distortion with Heat Input-Thickness Parameter
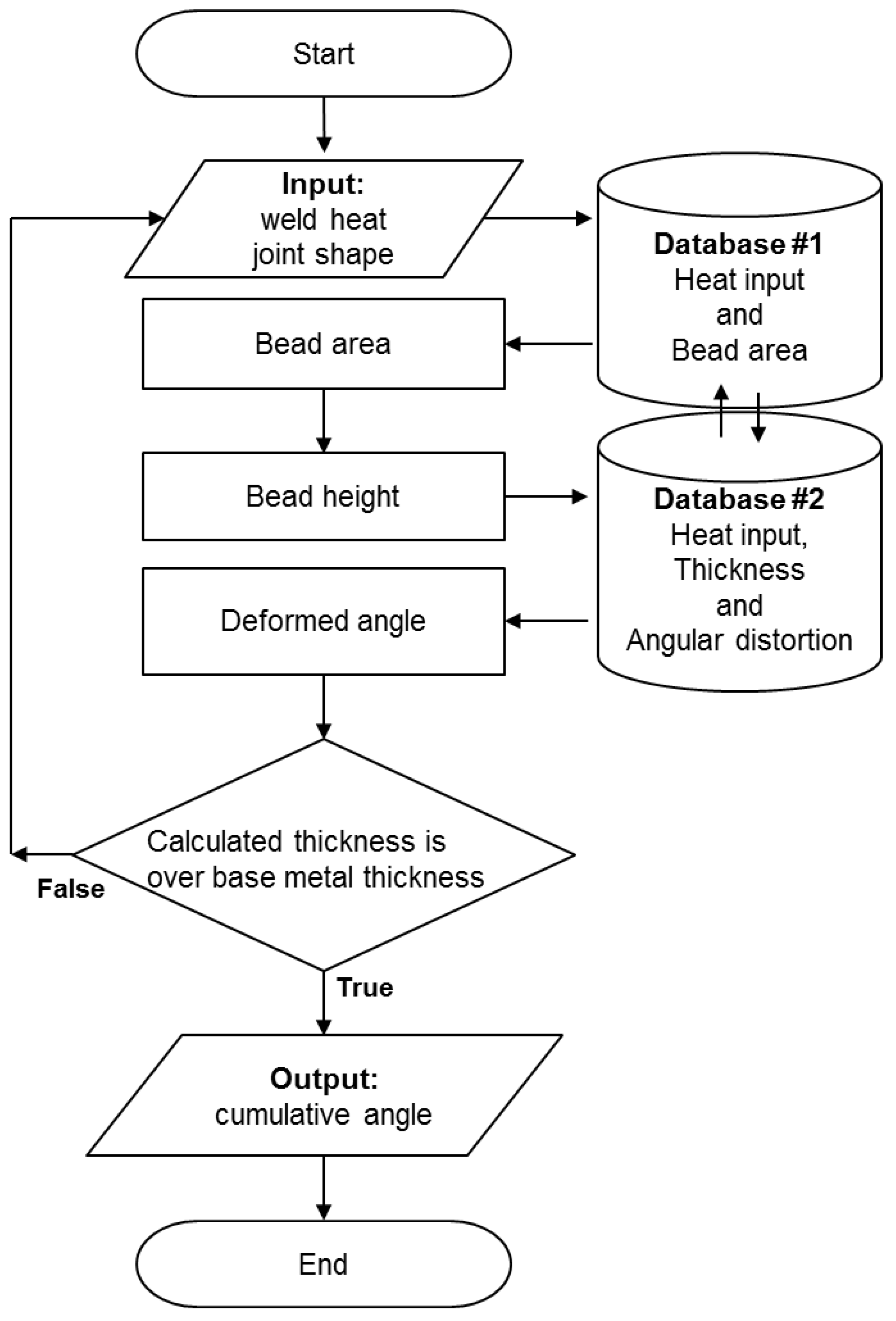
2.3. Algorithm for the Prediction of Angular Distortion
- Input information on weld joint geometry and the welding conditions in the current layer.Weld joint geometry consists of bevel angles, the thickness, the root gap, the root face, and the thickness below the weld root. The welding condition is the average of all passes in the current layer.
- Calculate the cross-sectional area of the bead using Database #1 and the input data of Step 1.Database #1 is composed of the relationship between the current-velocity parameter and the bead area.
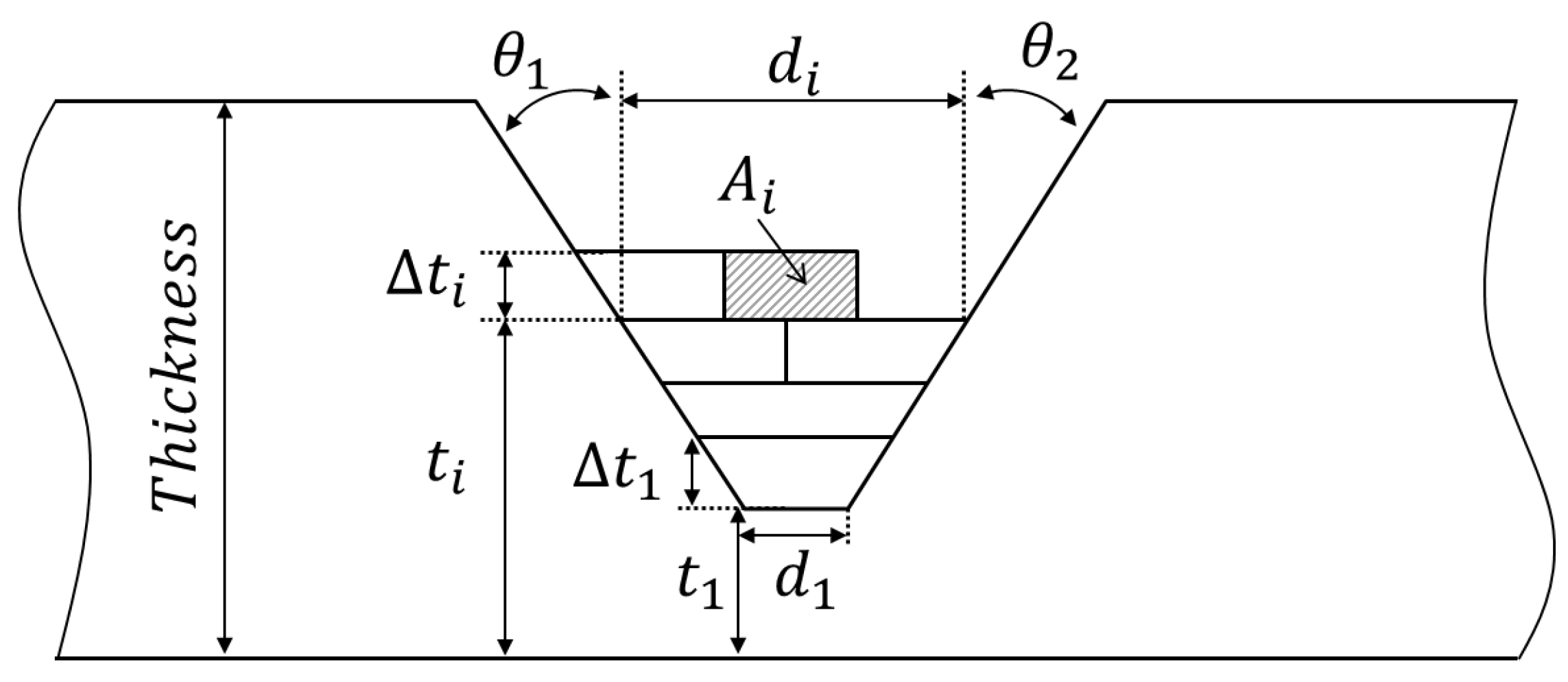
- Calculate the beat height from the bead area and the weld joint geometry.As shown in Figure 8, every layer has a trapezoidal shape in the case of the V-groove joint. Geometrically, the height of the trapezoid can be calculated with the bead area (), bevel angles (, ), and the bottom length of the bead (). The subscript i denotes the layer number, and j is for the bead number in the corresponding layer. The layer height () was updated as j was incremented one by one in the current layer i. The calculation was repeated until was greater than the reference height in Equation (4). At the time of termination, was determined as the bead height of the ith layer as written in Equation (9), and the value j was stored as the total number of beads in this layer.The current thickness plus the bead height will be used as the thickness for the calculation of the next layer, which is written as Equation (10).
- Calculate the top length of the layer:The top length () can be obtained by Equation (11) with the bottom length () and the height of the current layer (). The top length is used as the bottom length for the calculation of the next layer.
- Calculate the angular distortion at the current pass:In the current layer i, the angles from Bead Number 1 – j are extracted through Database #2 using the heat input and thickness (). The data were the thickness calculated in the previous layer. Database #2 was made up of the relationship between the heat input, the thickness, and the angular distortion. When the heat input-thickness parameter was less than 0 or greater than 25 kJ/mm, the output of the angular distortion was zero.
- The layer number i increased by one, and Steps 1–5 above were repeated.The value j was initialized to one before each layer calculation. The calculation terminated when was greater than the thickness of the base material.
- Calculate the accumulated angular distortion by summing the angles produced for each pass.
3. Results and Discussions
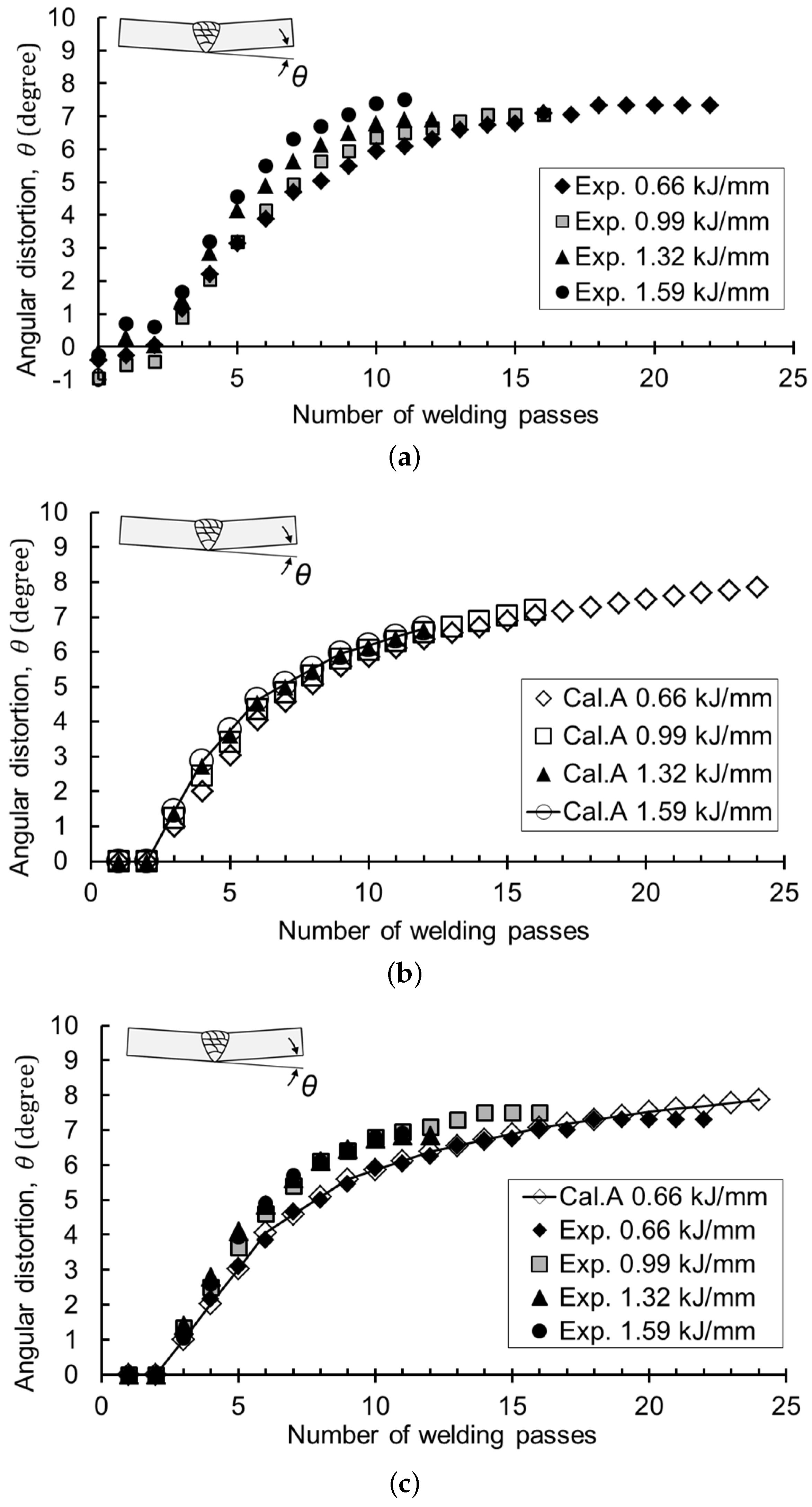
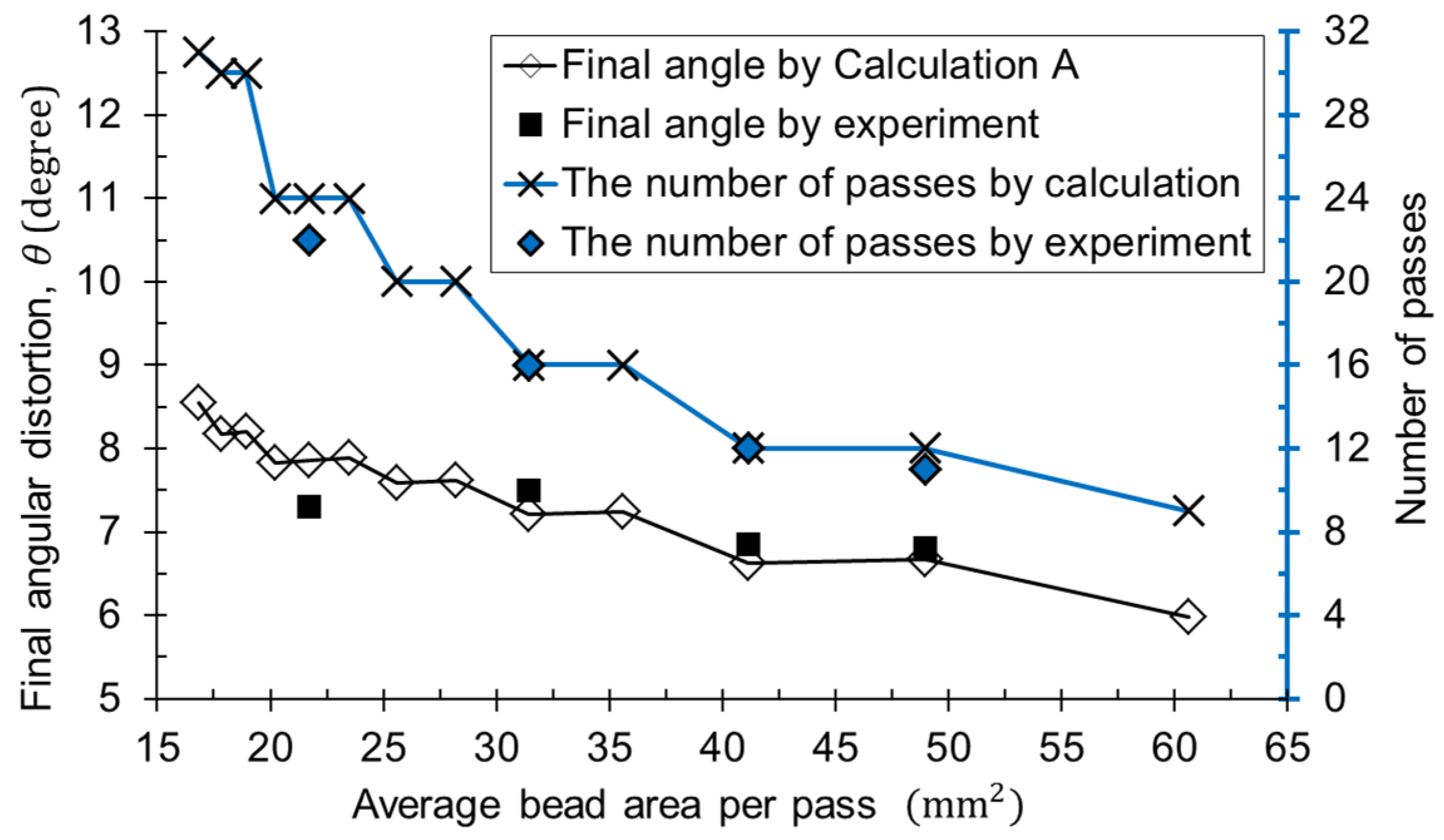
3.1. Algorithm Validation through Experiment
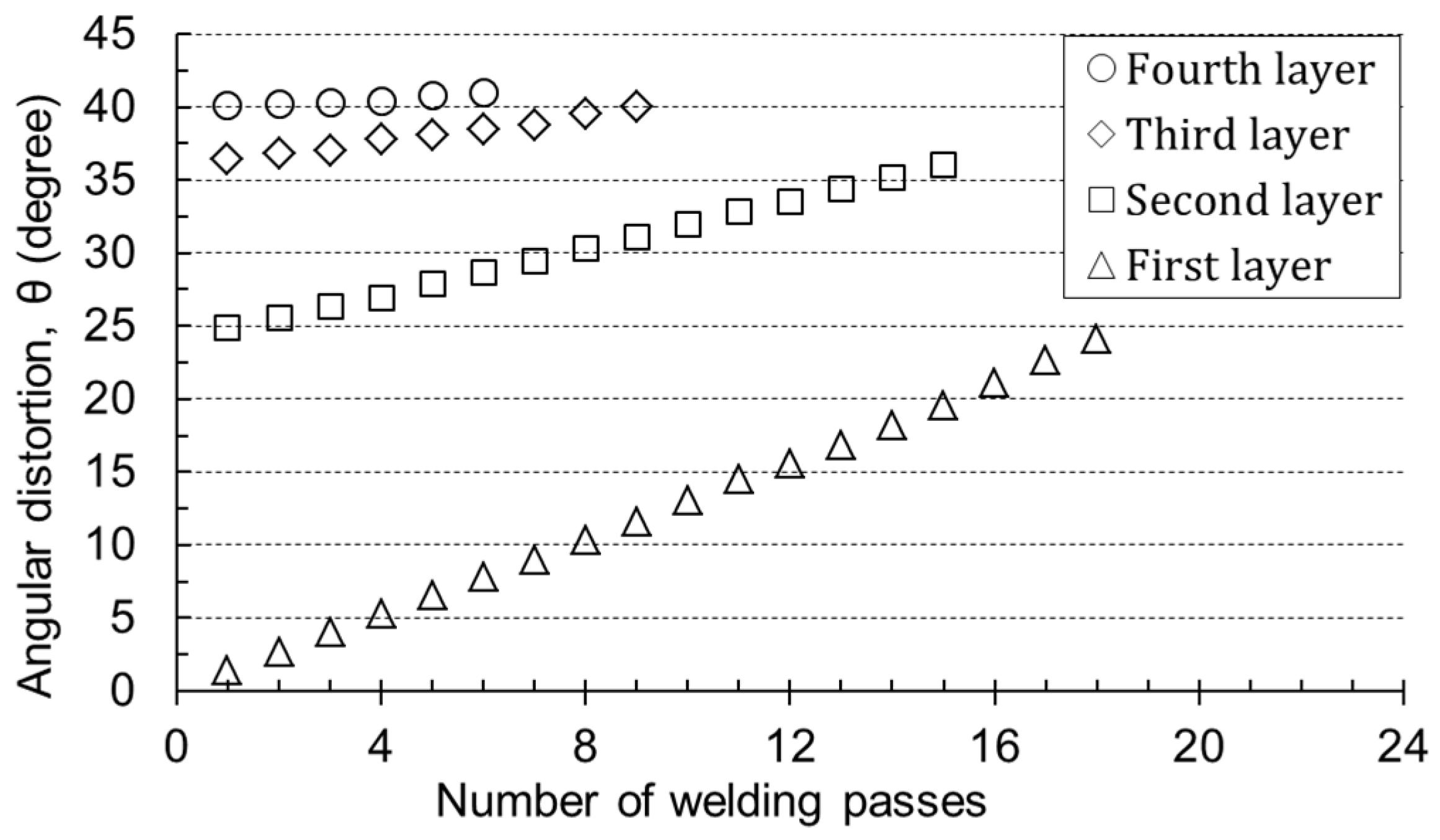
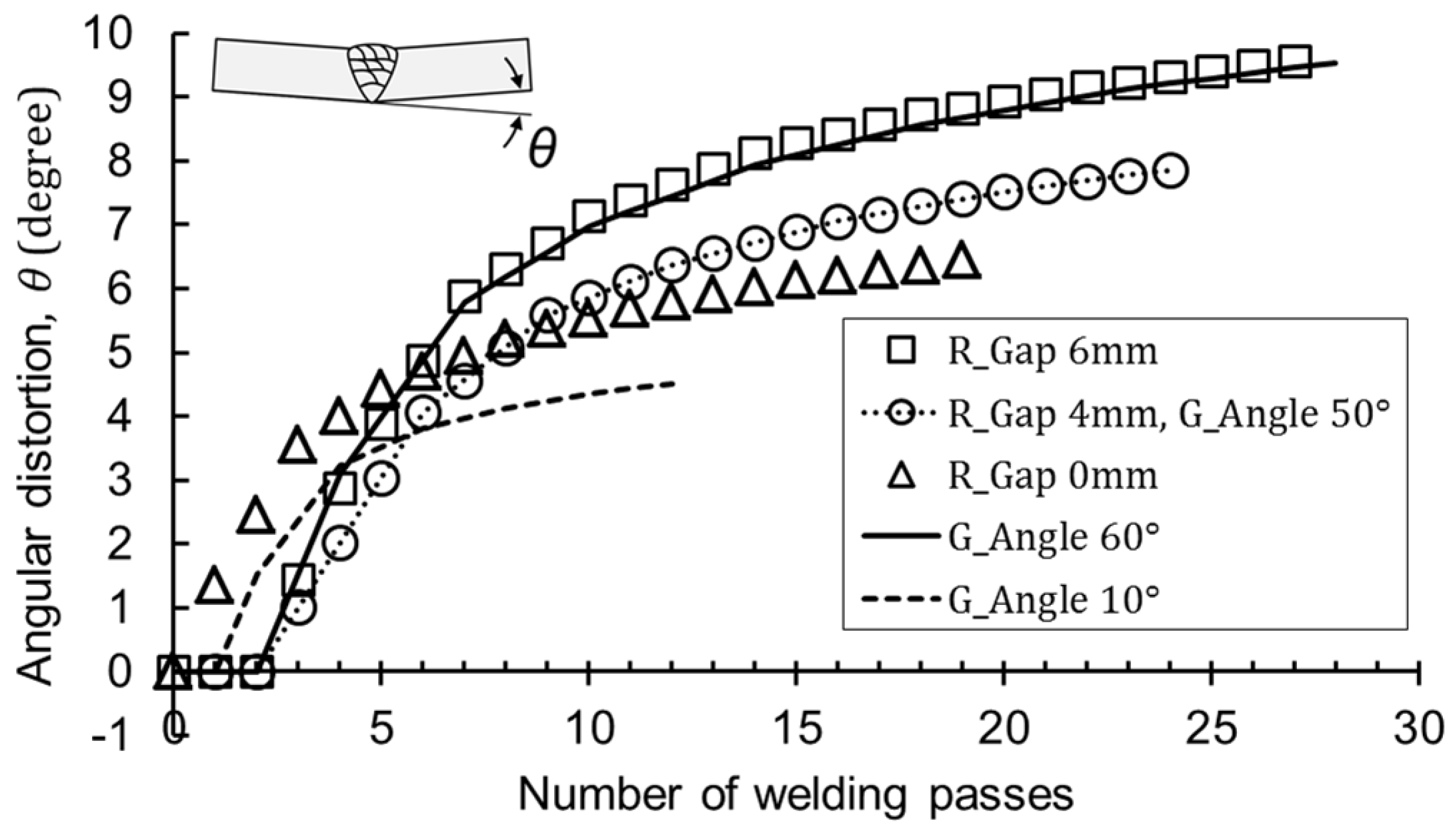
3.2. Effect of the Number of Welding Passes on Angular Distortion
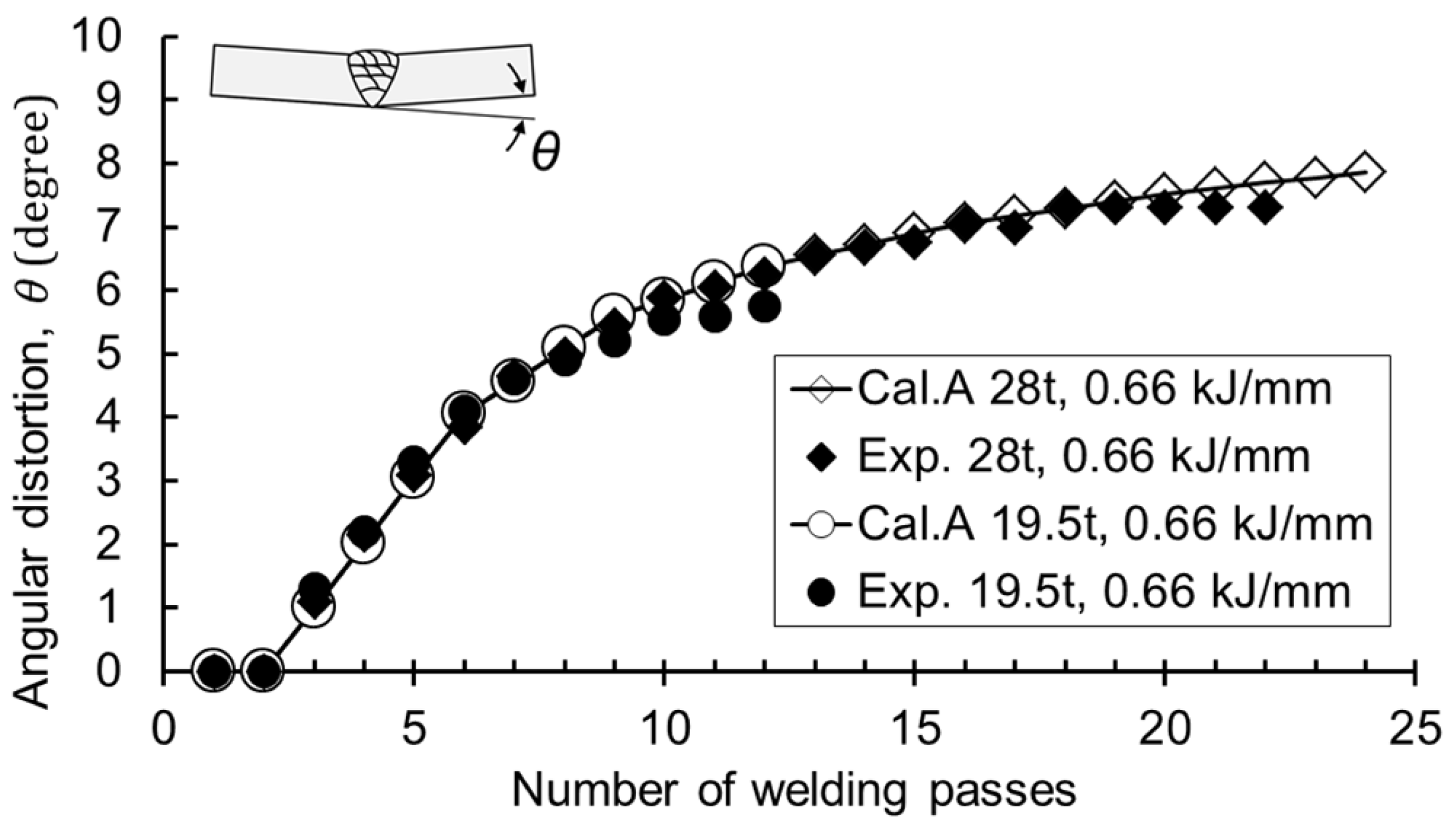
3.3. Effect of Parent Material Thickness on Angular Distortion
3.4. Effect of Previous Weld Beads on Angular Distortion
3.5. Effect of Bead Size on Angular Distortion
3.6. Effect of Weld Joint Geometry on Angular Distortion
4. Conclusions
- Information on the welding conditions and the weld joint geometry was the input.
- The bead area was calculated through Database #1, which consisted of the current-velocity parameter and bead size.
- The bead height was obtained from the geometric relationship between the bead area and the joint geometry, where the bead height plus previous thickness were used as the thickness in the next layer calculation.
- The angular distortion was estimated through Database #2, which is composed of the heat input-thickness parameters and the angular distortion.
- Accumulated angular distortions were obtained by iterative calculation of the above procedures.
- The bead cross-sectional area was proportional to the square of the electric current divided by the welding speed, and the angular distortion was a function of the heat input divided by the square of the thickness.
- The effect of the previous layer on reduction in angular distortion should be applied to the prediction method.
- In the same weld joint, the angular distortion with the number of passes created a single curve regardless of the welding conditions, so the final angle was determined by the final pass number. The predictive curve, on the other hand, varied with the shape of the weld joint.
- There existed a region where the angular distortion was the maximum at a specific thickness and heat input. In the case of V-butt welding, the change in angular distortion was greatest in between the third and fifth welding pass.
- Reducing the number of passes with a large bead size decreased the welding angular distortion in the same joint.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| HAZ | Heat-affected zone |
| FCAW | Flux cored arc welding |
| GMAW | Gas metal arc welding |
| SAW | Submerged arc welding |
References
- Murakawa, H. Computational welding mechanics and its interface with industrial application. Trans. JWRI 1996, 25, 191–204. [Google Scholar]
- Luo, Y.; Murakawa, H.; Ueda, Y. Prediction of Welding Deformation and Residual Stress by Elastic FEM Based on Inherent Strain. J. Soc. Nav. Archit. Jpn. 1997, 1997, 783–793. [Google Scholar] [CrossRef]
- Oliveira, J.; Fernandes, F.B.; Miranda, R.; Schell, N.; Ocaña, J. Residual stress analysis in laser welded NiTi sheets using synchrotron X-ray diffraction. Mater. Des. 2016, 100, 180–187. [Google Scholar] [CrossRef] [Green Version]
- Armentani, E.; Pozzi, A.; Sepe, R. Finite-Element Simulation of Temperature Fields and Residual Stresses in Butt Welded Joints and Comparison With Experimental Measurements. In Proceedings of the ASME 2014 12th Biennial Conference on Engineering Systems Design and Analysis Volume 1: Applied Mechanics, Automotive Systems, Biomedical Biotechnology Engineering, Computational Mechanics, Design, Digital Manufacturing, Education, Marine and Aerospace Applications, Copenhagen, Denmark, 25–27 July 2014. [Google Scholar] [CrossRef]
- Ahn, J.; He, E.; Chen, L.; Wimpory, R.; Dear, J.; Davies, C. Prediction and measurement of residual stresses and distortions in fibre laser welded Ti-6Al-4V considering phase transformation. Mater. Des. 2017, 115, 441–457. [Google Scholar] [CrossRef] [Green Version]
- Masubuchi, K. Analysis of Welded Structures: Residual Stresses, Distortion, and Their Consequences; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Timoshenko, S.P.; Gere, J.M.; Prager, W. Theory of Elastic Stability, Second Edition. J. Appl. Mech. 1962, 29, 220–221. [Google Scholar] [CrossRef] [Green Version]
- DNV GL. Structural Design of Offshore Units—WSD Method; DNV GL: Oslo, Norway, 2017. [Google Scholar]
- Mukherjee, T.; Zuback, J.S.; De, A.; DebRoy, T. Printability of alloys for additive manufacturing. Sci. Rep. 2016, 6, 19717. [Google Scholar] [CrossRef] [Green Version]
- Xie, D.; Zhao, J.; Liang, H.; Tian, Z.; Shen, L.; Xiao, M.; Ahsan, M.N.; Wang, C. Assumption of Constraining Force to Explain Distortion in Laser Additive Manufacturing. Materials 2018, 11, 2327. [Google Scholar] [CrossRef]
- Xie, D.; Zhao, J.; Liang, H.; Liu, S.; Tian, Z.; Shen, L.; Wang, C. Cause of Angular Distortion in Fusion Welding: Asymmetric Cross-Sectional Profile along Thickness. Materials 2019, 12, 58. [Google Scholar] [CrossRef] [PubMed]
- Deng, D.; Liang, W.; Murakawa, H. Determination of welding deformation in fillet-welded joint by means of numerical simulation and comparison with experimental measurements. J. Mater. Process. Technol. 2007, 183, 219–225. [Google Scholar] [CrossRef]
- Satoh, K.; Terasaki, T. Effect of Welding Conditions on Welding Deformations in Multipass Welded Butt Joint. J. Jpn. Weld. Soc. 1976, 45, 464–470. [Google Scholar] [CrossRef]
- Sepe, R.; Armentani, E.; Lamanna, G.; Caputo, F. Evaluation by FEM of the Influence of the Preheating and Post-Heating Treatments on Residual Stresses in Welding. Key Eng. Mater. 2015, 627, 93–96. [Google Scholar] [CrossRef]
- Okerblom, N.O. The Calculation of Deformation of Welded Metal Structures; H.M. Stationery Office: Richmond, UK, 1958. [Google Scholar]
- Rui, W.; Sherif, R.; Hisashi, S.; Hidekazu, M.; Zhang, J. Study on Welding Inherent Deformations in Welded Structural Materials. Trans. JWRI 2008, 37, 10. [Google Scholar]
- Tian, L.; Luo, Y.; Wang, Y.; Wu, X. Prediction of transverse and angular distortions of gas tungsten arc bead-on-plate welding using artificial neural network. Mater. Des. 2014, 54, 458–472. [Google Scholar] [CrossRef]
- Mochizuki, M.; Okano, S. Effect of Welding Process Conditions on Angular Distortion Induced by Bead-on-plate Welding. ISIJ Int. 2018, 58, 153–158. [Google Scholar] [CrossRef] [Green Version]
- Okano, S.; Tadano, S.; Nakatani, Y.; Mochizuki, M. Assembling a database of inherent strain for simplified distortion analysis in multi-layer and multi-pass welding of heavy section plate (Development of accuracy management system for high quality construction in welded structures on the basis of advanced theory of inherent strain). Trans. JSME 2016, 16-00005. (In Japanese) [Google Scholar] [CrossRef]
- Vega, A.; Rashed, S.; Tango, Y.; Ishiyama, M.; Murakawa, H. Analysis and Prediction of Multi-Heating Lines Effect on Plate Forming by Line Heating. CMES 2008, 28, 1–14. [Google Scholar]
- Sprenger, A.; Vollertsen, F.; Steen, W.M.; Watkins, K. Influence of strain hardening on laser bending. In Proceedings of the Laser Assisted Net Shape Engineering (LANE’94), Erlangen, Germany, 12–14 October 1994; pp. 361–370. [Google Scholar]
- Murugan, V.V.; Gunaraj, V. Effects of Process Parameters on Angular Distortion of Gas Metal Arc Welded Structural Steel Plates. Suppl. Weld. J. 2005, 7, 165–171. [Google Scholar]
- Khanna, P.; Maheshwari, S. Development of Mathematical Models for Prediction and Control of Weld Bead Dimensions in MIG Welding of Stainless Steel 409M. Mater. Today Proc. 2018, 5, 4475–4488. [Google Scholar] [CrossRef]
- Sadek, A.; Ibraham, R.N.; Price, J.W.H.; Shehata, T.; Ushio, M. Effect of Welding Parameters of FCAW Process and Shielding Gas Type on Weld Bead Geometry and Hardness Distribution(Materials, Metallurgy & Weldability). Trans. JWRI 2001, 30, 45–52. [Google Scholar]
- Palani, P.K.; Murugan, N. Optimization of weld bead geometry for stainless steel claddings deposited by FCAW. J. Mater. Process. Technol. 2007, 190, 291–299. [Google Scholar] [CrossRef]
- Connor, L.P.; O’Brien, R.L.; Society, A.W. Welding Handbook: Welding processes; American Welding Society: Miami, FL, USA, 1991. [Google Scholar]
- Olson, D.L.; Siewert, T.A.; Liu, S.; Edwards, G.R. ASM Handbook Volume 6: Welding, Brazing, and Soldering; ASM International: Novelty, OH, USA, 1993; Volme 6. [Google Scholar]
- Boccarusso, L.; Arleo, G.; Astarita, A.; Bernardo, F.; Fazio, P.D.; Durante, M.; Minutolo, F.M.C.; Sepe, R.; Squillace, A. A new approach to study the influence of the weld bead morphology on the fatigue behaviour of Ti-6Al-4V laser beam-welded butt joints. Int. J. Adv. Manuf. Technol. 2016, 88, 75–88. [Google Scholar] [CrossRef]
- Kim, H.G.; Shin, S.B.; Kim, D.S. A Study on the Angular Distortion Control for the Multi-Pass Butt Weldment of STS 316LN. Mater. Sci. Forum 2008, 580–582, 431–434. [Google Scholar] [CrossRef]
- Ha, Y.; Choi, J. Cumulative Angular Distortion Curve of Multi-Pass Welding at Thick Plate of Offshore Structures. J. Adv. Res. Ocean. Eng. 2015, 1, 106–114. [Google Scholar] [CrossRef] [Green Version]
- Adamczuk, P.C.; Machado, I.G.; Mazzaferro, J.A.E. Methodology for predicting the angular distortion in multi-pass butt-joint welding. J. Mater. Process. Technol. 2017, 240, 305–313. [Google Scholar] [CrossRef]
- AWS. Specification for Low-Alloy Steel Electrodes for Flux Cored Arc Welding; A5.29/A5.29M; Amazon Web Services: Seattle, WA, USA, 2010. [Google Scholar]
- TWI Distortion—Prevention by Design—Job Knowledge 34. Available online: www.twi-global.com/technical-knowledge/job-knowledge/distortion-prevention-by-design-034 (accessed on 29 April 2019).





| Type | Chemical Compositions (Mass %) | Mechanical Properties as Welded | |||||
|---|---|---|---|---|---|---|---|
| C | Mn | Ni | Cr | Yield strength | Tensile strength | Elongation | |
| LR-AH32 (base) | 0.16 | 1.12 | 0.04 | 0.03 | 348 MPa | 495 MPa | 30% |
| E81T1-K2C (wire) | 0.03 | 1.28 | 1.49 | 0.03 | 549 MPa | 617 MPa | 31% |
| Thickness (mm) | Voltage (V) | Current (A) | Speed (cm/min) | Number of Layers |
|---|---|---|---|---|
| 11.5 | 29 | 285 | 15, 20, 22, 25 | 1, (6–13 passes per layer) |
| 12 | 29 | 285 | 25, 30, 40, 60 | 4, (4–27 passes per layer) |
| 15 | 29 | 285 | 25, 30, 40, 60 | 2, (6–13 passes per layer) |
| 19.5 | 29 | 285 | 25, 30, 40, 60 | 2, (6–13 passes per layer) |
| 28 | 29 | 285 | 25, 30 | 2, (6–13 passes per layer) |
| 45 | 29 | 285 | 25, 30, 40, 60 | 2, (6–13 passes per layer) |
| Thickness (mm) | Voltage (V) | Current (A) | Speed (cm/min) | Effective Heat Input (kJ/mm) |
|---|---|---|---|---|
| 19.5, 28 | 29 | 285 | 60, 40, 20, 25 | 0.7, 1.0, 1.3, 1.6 |
| Effective Heat Input (kJ/mm) | 0.7 | 1.0 | 1.3 | 1.6 |
|---|---|---|---|---|
| Experiment (degree), [Number of passes] | 7.3, [22] | 7.5, [16] | 6.9, [12] | 6.9, [11] |
| Calculation (degree), [Number of passes] | 7.9, [24] | 7.2, [16] | 6.6, [12] | 6.7, [12] |
| Error (%) | −7.7 | 3.9 | 3.2 | 3.3 |
| Error (%) = (Experiment − Calculation)/Experiment × 100 | ||||
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seong, W.-J. Prediction and Characteristics of Angular Distortion in Multi-Layer Butt Welding. Materials 2019, 12, 1435. https://doi.org/10.3390/ma12091435
Seong W-J. Prediction and Characteristics of Angular Distortion in Multi-Layer Butt Welding. Materials. 2019; 12(9):1435. https://doi.org/10.3390/ma12091435
Chicago/Turabian StyleSeong, Woo-Jae. 2019. "Prediction and Characteristics of Angular Distortion in Multi-Layer Butt Welding" Materials 12, no. 9: 1435. https://doi.org/10.3390/ma12091435
APA StyleSeong, W.-J. (2019). Prediction and Characteristics of Angular Distortion in Multi-Layer Butt Welding. Materials, 12(9), 1435. https://doi.org/10.3390/ma12091435






