Effects of Adhesive Bond-Slip Behavior on the Capacity of Innovative FRP Retrofits for Fatigue and Fracture Repair of Hydraulic Steel Structures
Abstract
1. Introduction
1.1. Fatigue and Fracture
1.2. CFRP Fatigue and Fracture Repairs
1.3. Bond
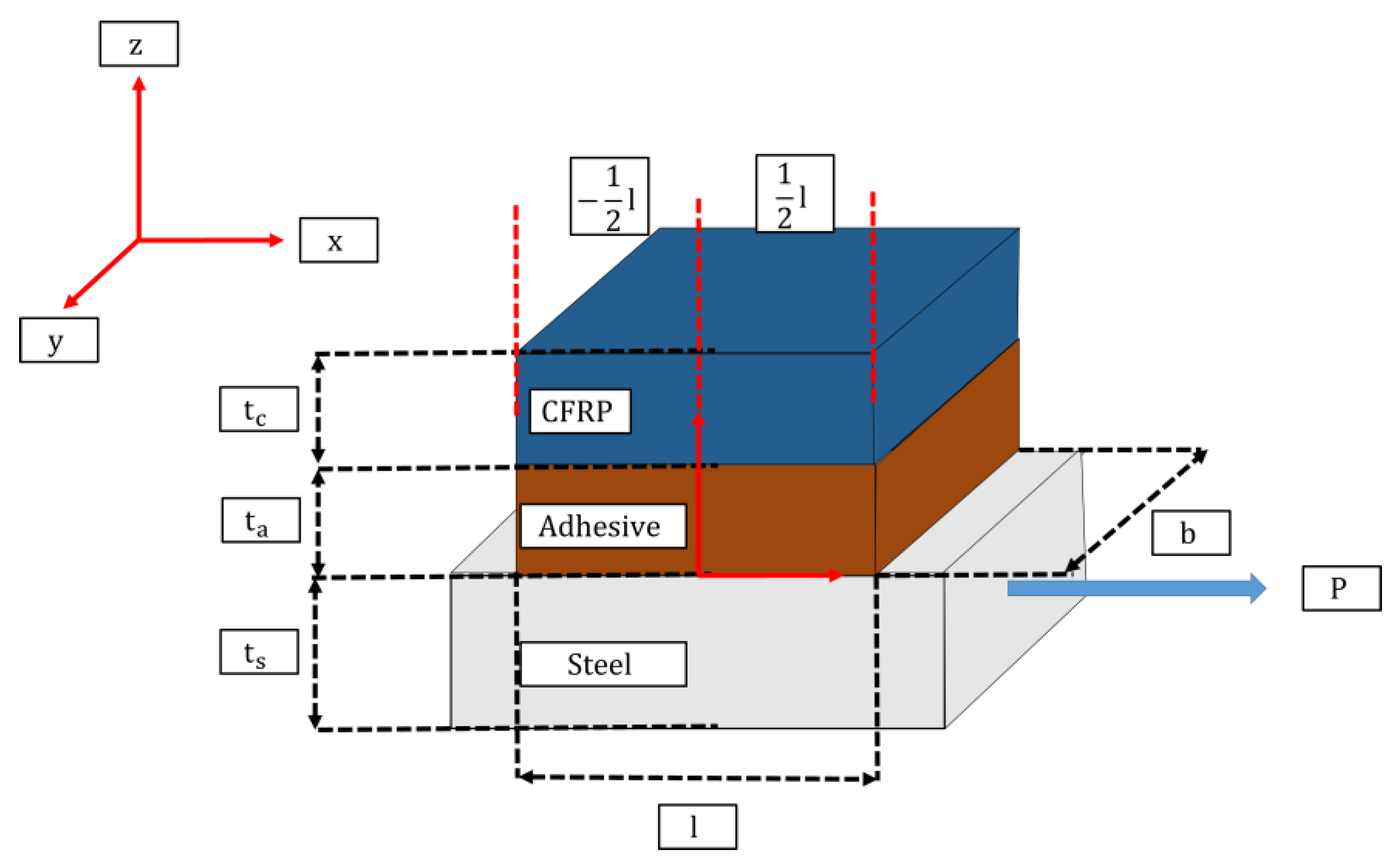
2. Methods
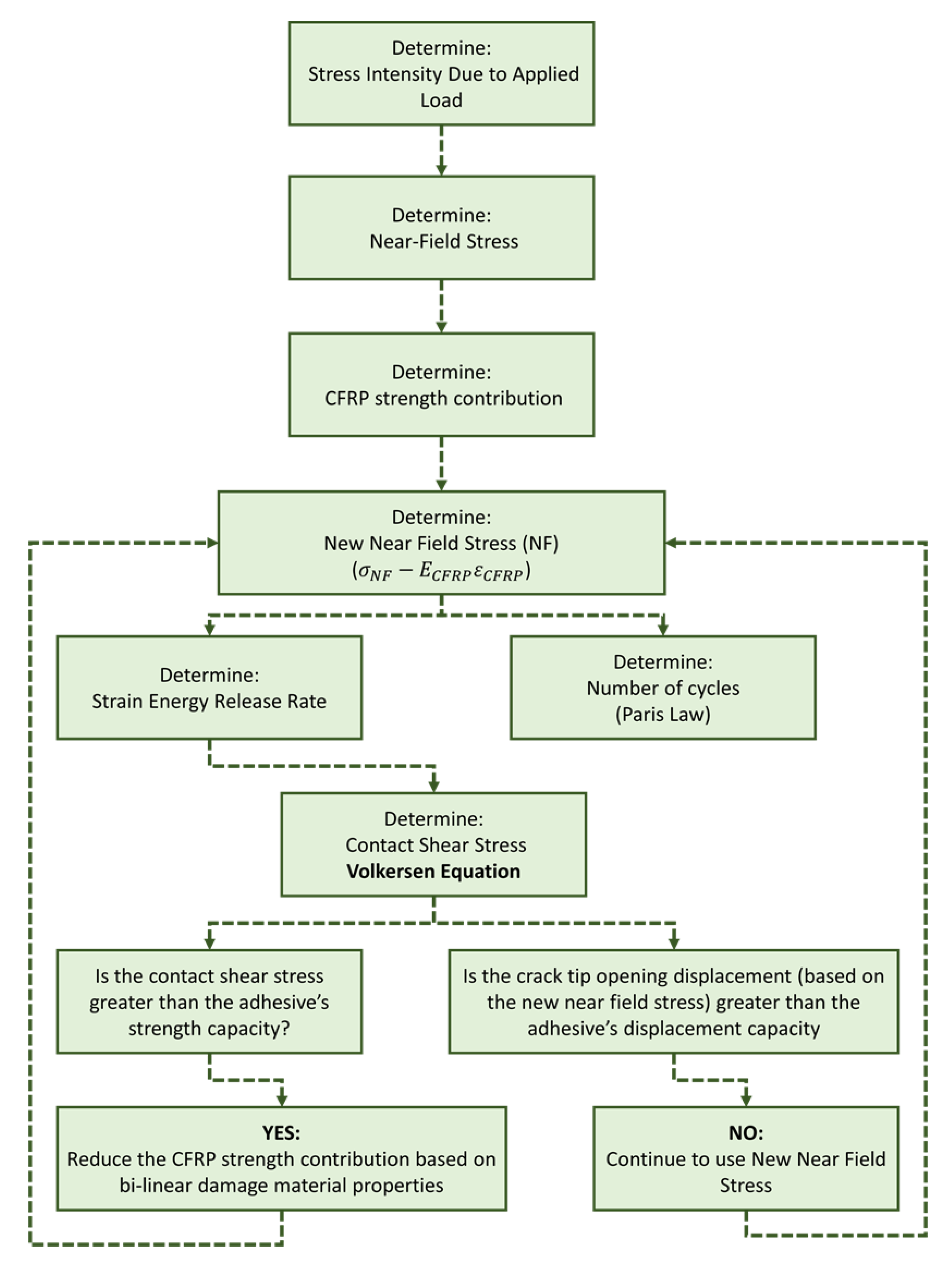
Analytical
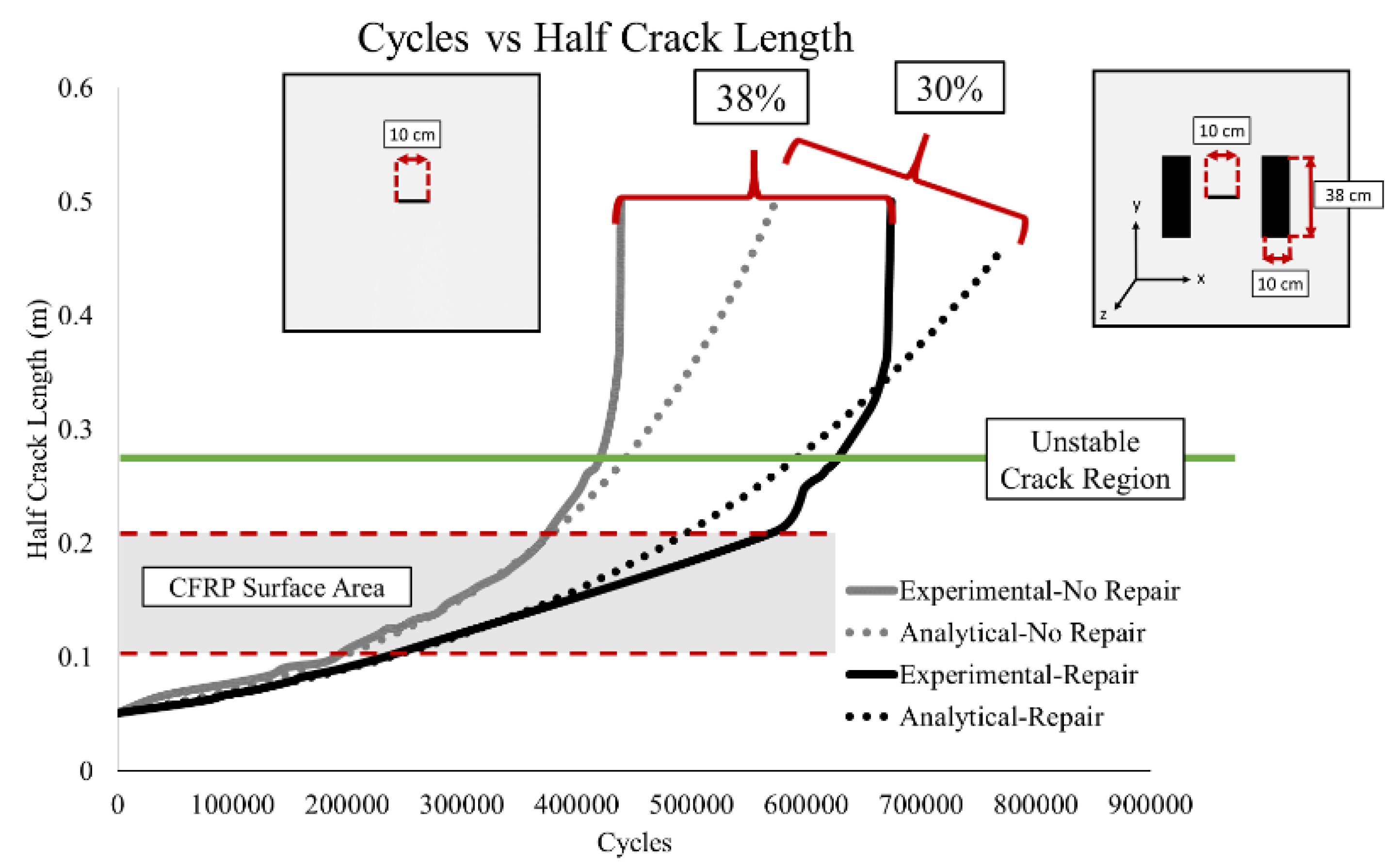
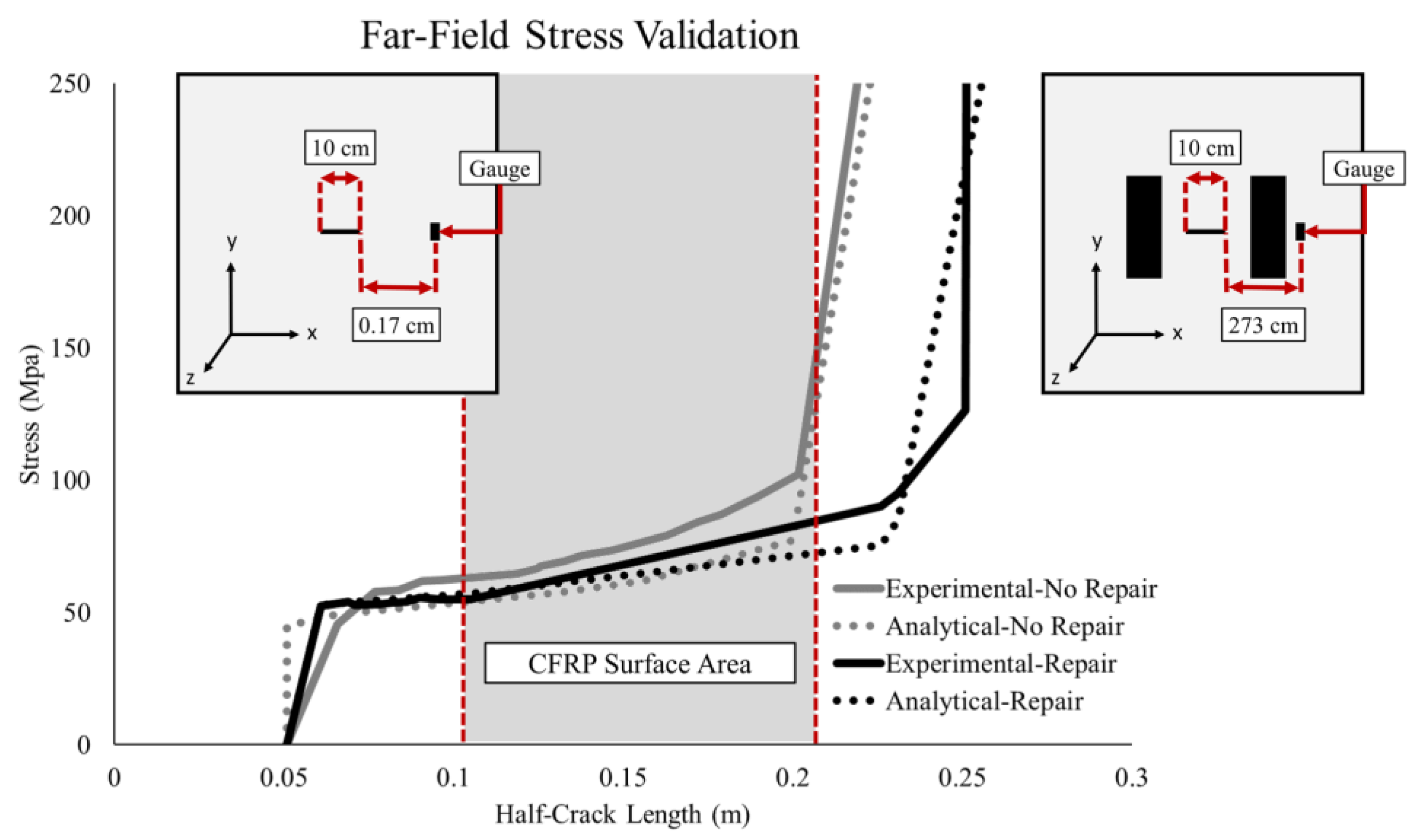
3. Results and Discussion
4. Conclusions
- The two adherends are highly rigid and experience linear elastic behavior;
- There is no eccentricity of the adherends;
- Shear and normal stresses of the adhesive are constant through the thickness of the adhesive;
- Linear elastic Mode I crack propagation is utilized;
- The occurrence of the adhesive’s localized debonding at the crack tip as the crack propagates under the CFRP patch;
- Fatigue and fracture linear crack growth.
Author Contributions
Funding
Conflicts of Interest
References
- Riveros, G.A.; Arredondo, E. Predicting Future Deterioration of Hydraulic Steel Structures with Markov Chain and Multivariate Samples of Statistical Distributions. J. Appl. Math. 2014, 2014, 360532. [Google Scholar] [CrossRef]
- Mahmoud, H.; Chulahwat, A.; Riveros, G. Fatigue and Fracture Life-Cycle Cost Assessment of a Miter Gate with Multiple Cracks. Eng. Fail. Anal. 2018, 83, 57–74. [Google Scholar] [CrossRef]
- Riveros, G.A.; Rosario-Pérez, M.E. Deriving the Transition Probability Matrix Using Computational mechanics. Eng. Comput. 2018, 35, 692–709. [Google Scholar] [CrossRef]
- Grier, D. The Declining Reliability of the U.S. Inland Waterway System; U.S. Army Corps of Engineers Institute for Water Resources: Alexandria, VA, USA, 2005. [Google Scholar]
- Grossardt, T.; Bray, L.; Burton, M. Inland Navigation in the United States an Evaluation of Economic Impacts and the Potential Effects of Infrastructure Investment; National Waterways Foundation: Washington, DC, USA, 2014. [Google Scholar]
- Litz, J.; Frank, J. Retaining the Value of the U.S. Inland Waterways System; U.S. Army War College: Carlisle, PA, USA, 2017. [Google Scholar]
- Kruse, C.J.; Ellis, D.; Protopapas, A.; Norboge, N. New Approaches for U.S. Lock and Dam Maintenance and Funding; Texas Transportation Institute: College Station, TX, USA, 2012; pp. 1–127.
- Mahmoud, H.N.; Riveros, G.A.; Memari, M.; Valsangkar, A.; Ahmadi, B. Underwater Large-Scale Experimental Fatigue Assessment of CFRP-Retrofitted Steel Panels. J. Struct. Eng. 2018, 144, 04018183. [Google Scholar] [CrossRef]
- Riveros, G.A.; Mahmoud, H.; Lozano, C.M. Fatigue repair of underwater navigation steel structures using Carbon Fiber Reinforced Polymer (CFRP). Eng. Struct. 2018, 173, 718–728. [Google Scholar] [CrossRef]
- Nor, N.M.; Boestamam, M.H.A.; Yusof, M.A. Carbon Fiber Reinforced Polymer (CFRP) as Reinforcement for Concrete Beam. Int. J. Emerg. Technol. Adv. Eng. 2013, 3, 6–10. [Google Scholar]
- Barsom, J.; Rolfe, S. Fracture and Fatigue Control in Structures, 3rd ed.; ASTM International: West Conshohocken, PA, USA, 1999; ISBN 78-0750673150. [Google Scholar]
- Volkersen, O. Die Niektraftverteilung in Zugbeanspruchten mit Konstanten Laschenquerschritten. Luftfahrtforschung 1938, 15, 41–47. [Google Scholar]
- Freudenthal, A.M. Fatigue and fracture mechanics. Eng. Fract. Mech. 1973, 5, 403–414. [Google Scholar] [CrossRef]
- Lozano, C. Development of Pre-Stressed Retrofit Strategies for Mitigating Fatigue Cracking in Steel Waterway Lock Gate Components. Master’s Thesis, University of Arkansas, Fayetteville, Arkansas, 2017. [Google Scholar]
- Wang, H.-T.; Wu, G.; Jiang, J.-B. Fatigue Behavior of Cracked Steel Plates Strengthened with Different CFRP Systems and Configurations. J. Compos. Constr. 2016, 20, 04015078. [Google Scholar] [CrossRef]
- ElSafty, A.; Graeff, M. The Repair of Damaged Bridge Girders with Carbon-Fiber-Reinforced Polymer “CFRP” Laminates; University of North Florida: Jacksonville, FL, USA, 2012. [Google Scholar]
- Dawood, M.; Rizkalla, S. Development of a Carbon Fiber Reinforced Polymer System for Strengthening and Repair of Steel Bridges and Structures; Culture for Effective Design of Structures. In Proceedings of the 2nd Canadian Conference on Effective Design of Structures, Hamilton, ON, Canada, 20–23 May 2003. [Google Scholar]
- Klaiber, F.W.; Wipf, T.J.; Kempers, B.J. Repair of Damaged Prestressed Concrete Bridges Using CFRP. In Proceedings of the 2003 Mid-Continental Transportation Research Symposium, Ames, IA, USA, 21–22 August 2003. [Google Scholar]
- Chandrathilaka, E.R.K.; Gamage, J.C.P.H.; Fawzia, S. Numerical Modelling of Bond Shear Stress Slip Behavior of CFRP/Steel Composites Cured and Tested at Elevated Temperature. Compos. Struct. 2019, 212, 1–10. [Google Scholar] [CrossRef]
- Da Silva, L.F.; das Neves, P.J.; Adams, R.D.; Spelt, J.K. Analytical Models of Adhesively Bonded Joints-Part I: Literature Survey. Int. J. Adhes. Adhes. 2009, 29, 319–330. [Google Scholar] [CrossRef]
- Da Silva, L.F.; das Neves, P.J.; Adams, R.D.; Wang, A.; Spelt, J.K. Analytical Models of Adhesively Bonded Joints-Part II: Comparative Study. Int. J. Adhes. Adhes. 2009, 331–341. [Google Scholar] [CrossRef]
- Fayyadh, M.M.; Razak, H.A. Analytical and Experimental Study on Repair Effectiveness of CFRP Sheets for RC Beams. J. Civ. Eng. Manag. 2014, 20, 21–31. [Google Scholar] [CrossRef]
- Rosenboom, O.; Rizkalla, S. Analytical Modeling of Flexural Debonding in CFRP Strengthened Reinforced or Prestressed Concrete. In Proceedings of the 8th International Symposium on Fiber Reinforced Polymer Reinforcement for Concrete Structures (FRPRCS-8), Patras, Greece, 16–18 July 2007. [Google Scholar]
- Adderley, C.S. Adhesive Bonding. Mater. Des. 1988, 9, 287–293. [Google Scholar] [CrossRef]
- Alkhrdaji, T. Strengthening of Concrete Structures Using FRP Composites. Struct. Mag. 2015, 12, 18–20. [Google Scholar]
- Wang, H.-T.; Wu, G.; Pang, Y.-Y. Theoretical and Numerical Study on Stress Intensity Factors for FRP-Strengthened Steel Plates with Double-Edged Cracks. Sensors 2018, 18, 2356. [Google Scholar] [CrossRef]
- Liu, H.B.; Xiao, Z.G.; Zhao, X.L. Fracture Mechanics Analysis of Cracked Steel Plates Repaired with Composite Sheets. In Proceedings of the Asia-Pacific Conference on FRP in Structures (APFIS 2007), Hong Kong, China, 12–14 December 2007. [Google Scholar]
- Ghafoori, E.; Motavalli, M. A Retrofit Theory to Prevent Fatigue Crack Initiation in Aging Riveted Bridges Using Carbon Fiber-Reinforced Polymer Materials. Polymers 2016, 8, 308. [Google Scholar] [CrossRef]
- Yang, Y.; Biscaia, H.; Chastre, C.; Silva, M.A.G. Bond Characteristics of CFRP-to-steel Joints. J. Constr. Steel Res. 2017, 138, 401–419. [Google Scholar] [CrossRef]
- Al-Mosawe, A.; Al-Mahaidi, R. Bond Characteristics between Steel and CFRP Laminate under Impact Loads. In Proceedings of the 23rd Australasian Conference on the Mechanics of Structures and Materials, Byron Bay, Australia, 9–12 December 2014. [Google Scholar]
- Schnerch, D.; Dawood, M.; Rizkalla, S.; Sumner, E.; Stanford, K. Bond Behavior of CFRP Strengthened Steel Structures. Adv. Struct. Eng. 2006, 9, 805–817. [Google Scholar] [CrossRef]
- Fawzia, S.; Karim, M.A. Investigation into the Bond between CFRP and Steel Plates. Int. J. Civ. Environ. Eng. 2009, 3, 5. [Google Scholar]
- Wu, C.; Zhao, X.-L.; Al-Mahaidi, R.; Duan, W.H. Experimental Study on Bond Behaviour between UHM CFRP Laminate and Steel. In Advances in FRP Composites in Civil Engineering; Ye, L., Feng, P., Yue, Q., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 890–893. [Google Scholar]
- Sahin, M.; Dawood, M. Experimental Investigation of Bond between High-Modulus CFRP and Steel at Moderately Elevated Temperatures. J. Compos. Constr. 2016, 20, 04016049. [Google Scholar] [CrossRef]
- Tyfo® SCH-41 Composite Using Tyfo® S Epoxy 2015. Available online: https://www.aegion.com/-/media/Files/Fyfe/2013-Products/Tyfo%20SCH%2041.ashx (accessed on 11 February 2019).
- Tyfo® S Saturant Epoxy 2015. Available online: http://fyfeasia.com/-/media/Files/Fyfe/2013-Products/Tyfo%20S%20Epoxy.ashx?la=en (accessed on 11 February 2019).



| Analytical Model | Assumptions | ||||
|---|---|---|---|---|---|
| Linear Elastic | Deformation | Bending | Transverse Stress | Type of Joint 1 | |
| Volkersen | x | Shear only | Equal | SLJ & DLJ | |
| Goland and Reissner | x | Shear & Normal | x | Equal | SLJ & DLJ |
| Frostig et al. | x | Shear & Normal | x | Equal | SLJ & DLJ |
| Hart-Smith | x | Shear & Normal | x | Equal | SLJ & DLJ |
| Bigwood and Crocombe | x | Shear & Normal | x | Equal | Multiple Configuration |
| Mechanical Property | Steel | Tyfo SCH-41 (Carbon Fiber) [35] | Tyfo S (Adhesive) [36] |
|---|---|---|---|
| Ex 1 (Gpa) | - | 5.93 | - |
| Ey 1 (Gpa) | 206 | 82.7 | 2.9 |
| Gxy (Gpa) | - | 29.5 | 1.03 |
| ε | - | 0.0085 | - |
| σy (Gpa) | 344.7 | 82 | - |
| τu (Gpa) | - | - | 1.69 × 10−2 |
| Gc (Gpa) (Fracture Energy) | - | - | 2.10 × 10−7 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lozano, C.M.; Riveros, G.A. Effects of Adhesive Bond-Slip Behavior on the Capacity of Innovative FRP Retrofits for Fatigue and Fracture Repair of Hydraulic Steel Structures. Materials 2019, 12, 1495. https://doi.org/10.3390/ma12091495
Lozano CM, Riveros GA. Effects of Adhesive Bond-Slip Behavior on the Capacity of Innovative FRP Retrofits for Fatigue and Fracture Repair of Hydraulic Steel Structures. Materials. 2019; 12(9):1495. https://doi.org/10.3390/ma12091495
Chicago/Turabian StyleLozano, Christine M., and Guillermo A. Riveros. 2019. "Effects of Adhesive Bond-Slip Behavior on the Capacity of Innovative FRP Retrofits for Fatigue and Fracture Repair of Hydraulic Steel Structures" Materials 12, no. 9: 1495. https://doi.org/10.3390/ma12091495
APA StyleLozano, C. M., & Riveros, G. A. (2019). Effects of Adhesive Bond-Slip Behavior on the Capacity of Innovative FRP Retrofits for Fatigue and Fracture Repair of Hydraulic Steel Structures. Materials, 12(9), 1495. https://doi.org/10.3390/ma12091495





