Euler’s Elastica-Based Biomechanics of the Papillary Muscle Approximation in Ischemic Mitral Valve Regurgitation: A Simple 2D Analytical Model
Abstract
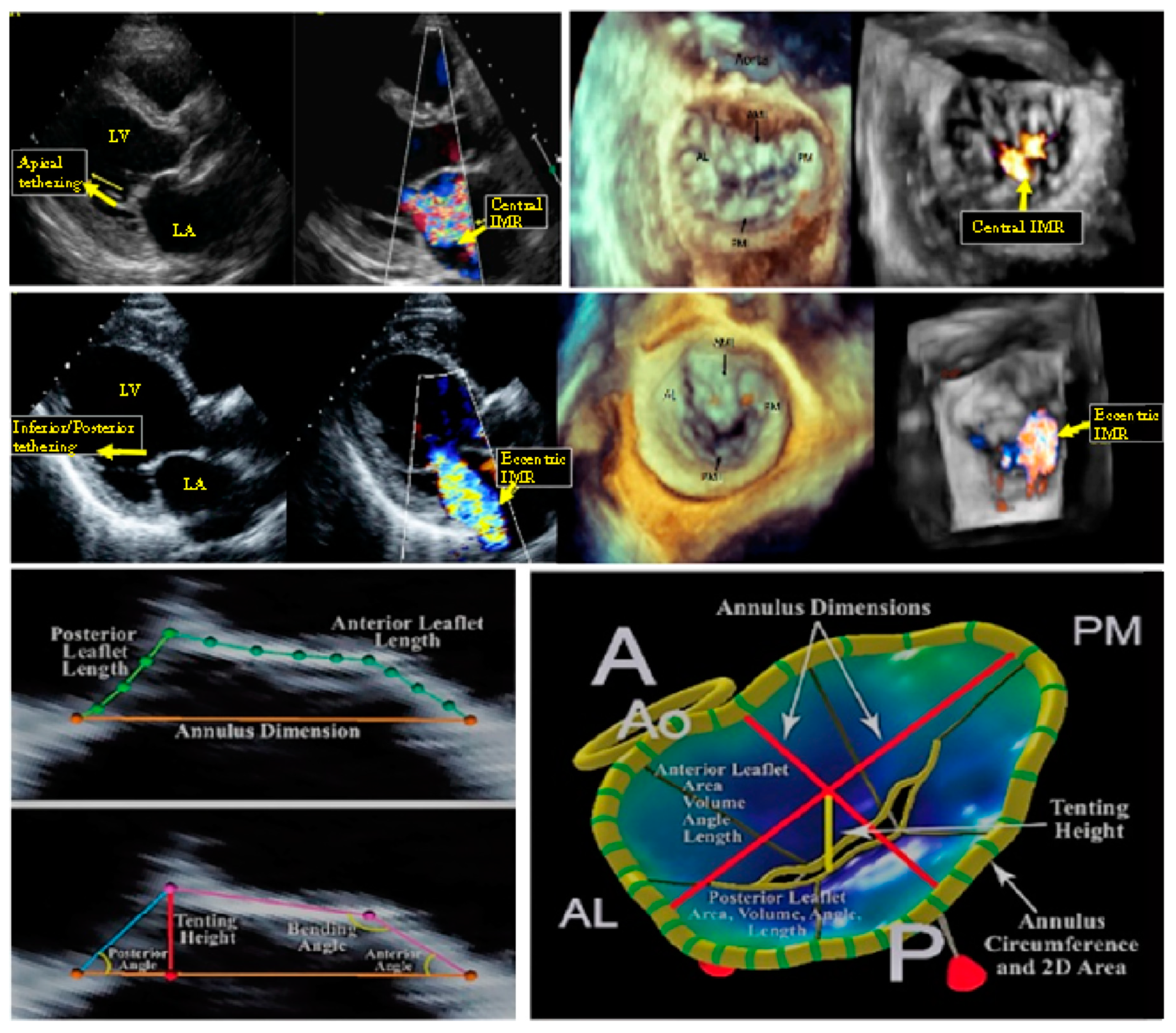
:1. Introduction
2. Materials and Methods
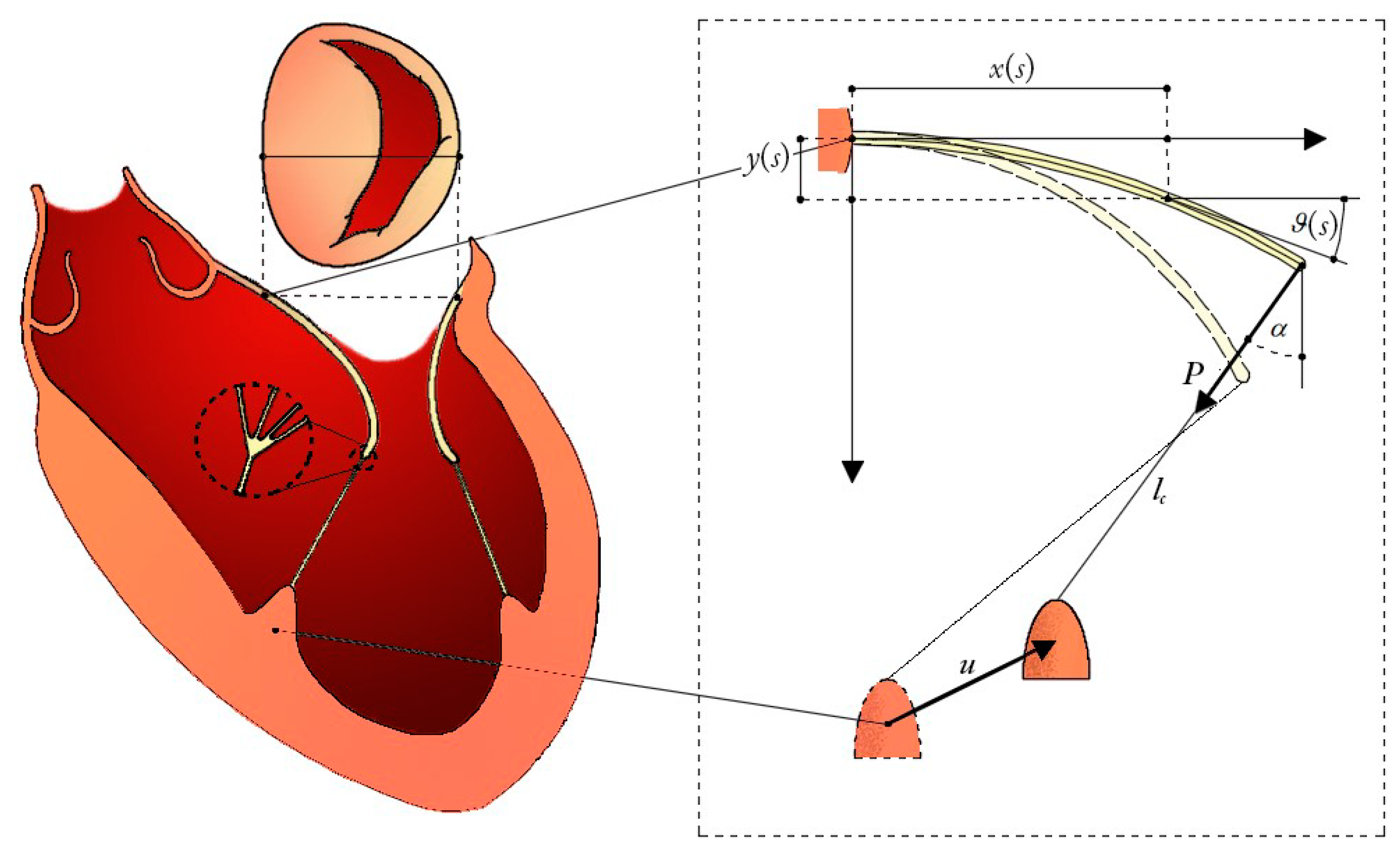
2.1. Mitral Leaflets Modelled as Euler’s Elastica
2.2. Hyperelasticity of the Chordae Tendinee
2.3. Chorda-Leaflet Coupling and Overall System Interaction
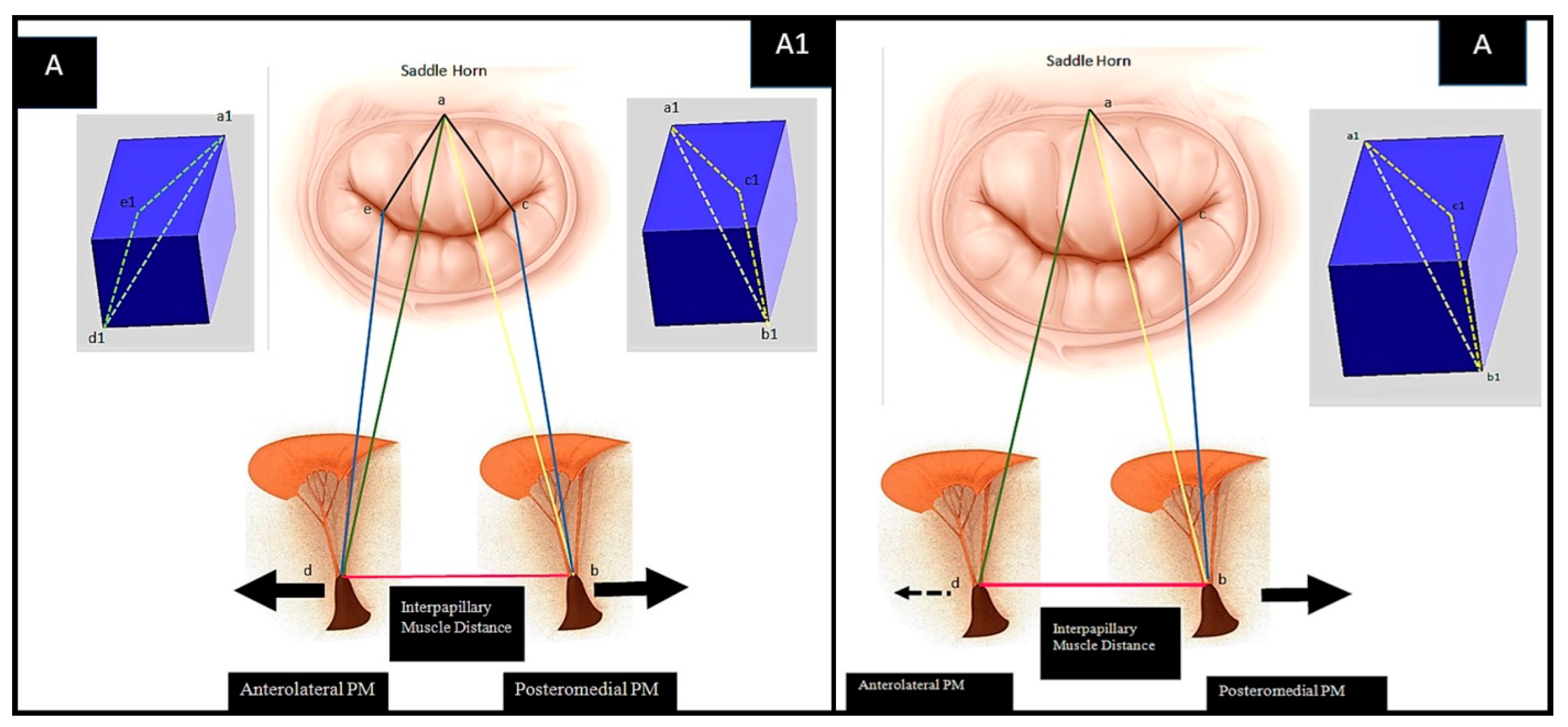
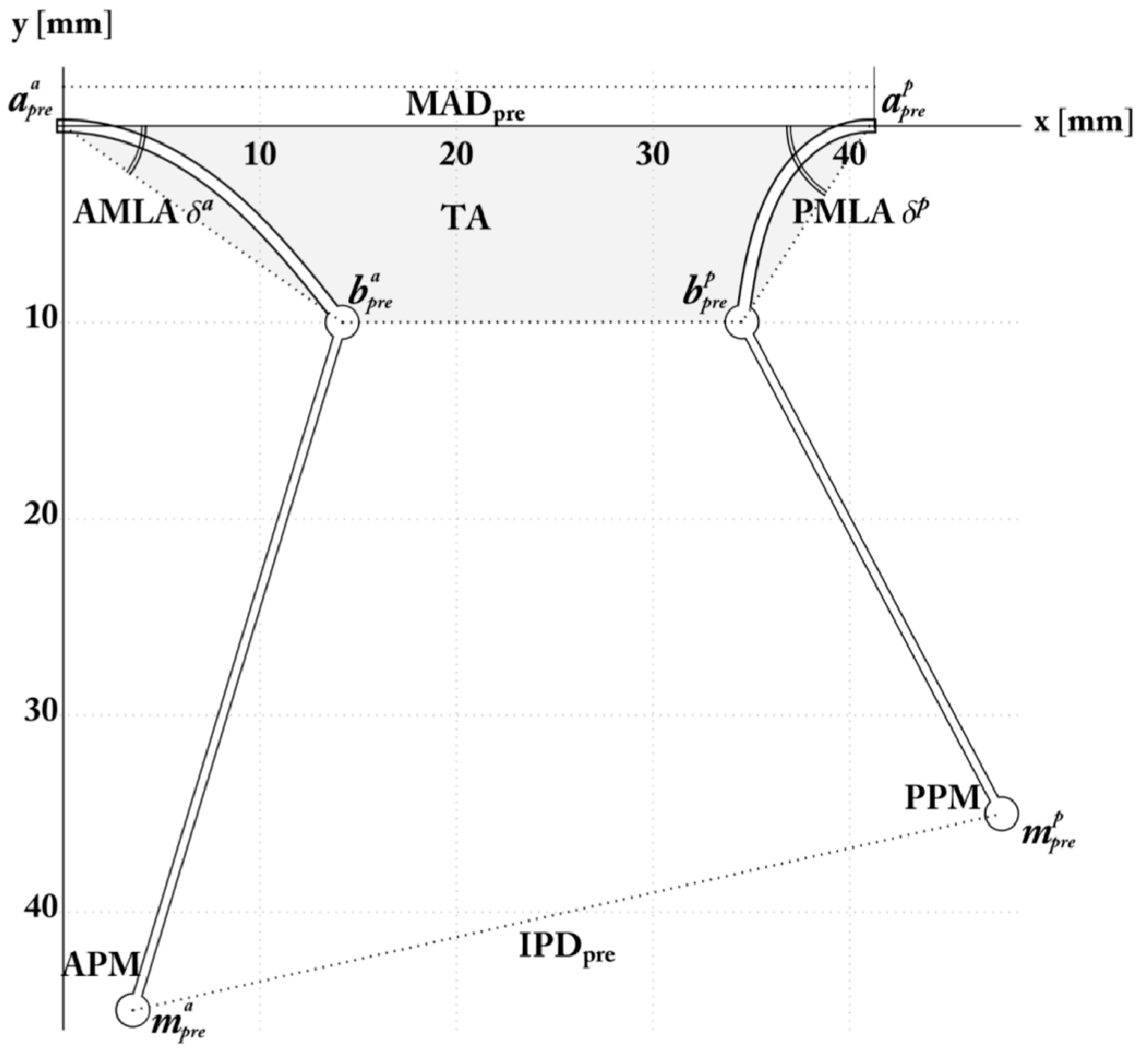
The Pre-Operative Configuration
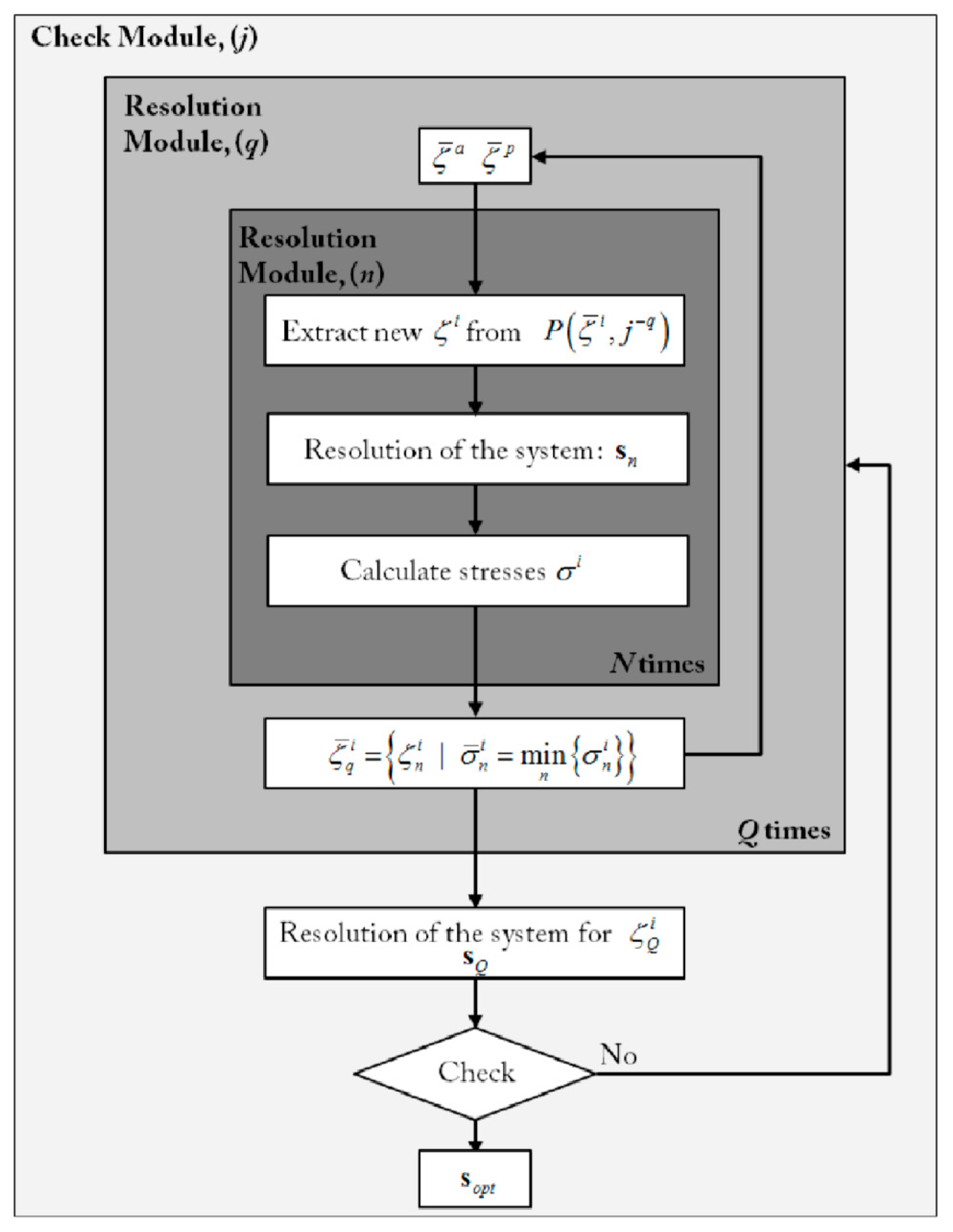
2.4. Simulation and Optimization of RA and PMA
3. Results
3.1. Mitral Valve: Annulus and Leaflet
3.2. Mitral Valve: Subvalvular Apparatus
3.3. Combined Valvular and Subvalvular Model
4. Discussion
5. Limitation and Perspective
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MV | Mitral Valve |
| LV | Left Ventricle |
| RA | Restrictive Annuloplasty |
| PMA | Papillary Muscle Approximation |
| PM(s) | Papillary Muscle(s) |
| IPD or IPMD | Interpapillary Muscle Distance |
| ES, ED | End Systolic, End Diastolic |
| MAD | Mitral Annulus Diameter |
| PMPM | Posteromedial Muscle |
| ALPM | Anterolateral Papillary Muscle |
| TH | Tenting Height |
| LVESD | Left Ventricular End Systolic Diameter |
| LVEDD | Left Ventricular End Diastolic Diameter |
| EROA | Effective Regurgitant Orifice Area |
| ACC | American College of Cardiology |
| AHA | American Heart Association |
References
- Nishimura, R.A.; Otto, C.M.; Bonow, R.O.; Carabello, B.A.; Erwin, J.P., III; Guyton, R.A.; O’Gara, P.T.; Ruiz, C.E.; Skubas, N.J.; Sorajja, P. 2014 AHA/ACC guideline for the management of patients with valvular heart disease: A report of the American college of cardiology/American heart association task force on practice guidelines. J. Am. Coll. Cardiol. 2014, 63, e57–e185. [Google Scholar] [CrossRef]
- Acker, M.A.; Parides, M.K.; Perrault, L.P.; Moskowitz, A.J.; Gelijns, A.C.; Voisine, P.; Smith, P.K.; Hung, J.W.; Blackstone, E.H. Mitral-valve repair versus replacement for severe ischemic mitral regurgitation. N. Engl. J. Med. 2014, 370, 23–32. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, D.; Moskowitz, A.J.; Gelijns, A.C.; Ailawadi, G.; Parides, M.K.; Perrault, L.P.; Hung, J.W.; Voisine, P.; Dagenais, F.; Gillinov, A.M. Two-year outcomes of surgical treatment of severe ischemic mitral regurgitation. N. Engl. J. Med. 2016, 374, 344–353. [Google Scholar] [CrossRef] [PubMed]
- Nappi, F.; Lusini, M.; Spadaccio, C.; Nenna, A.; Covino, E.; Acar, C.; Chello, M. Papillary muscle approximation versus restrictive annuloplasty alone for severe ischemic mitral regurgitation. J. Am. Coll. Cardiol. 2016, 67, 2334–2346. [Google Scholar] [CrossRef] [PubMed]
- Nappi, F.; Spadaccio, C.; Fraldi, M. Reply: Papillary muscle approximation is an anatomically correct repair for ischemic mitral regurgitation. J. Am. Coll. Cardiol. 2016, 68, 1147–1148. [Google Scholar] [CrossRef]
- Nappi, F.; Spadaccio, C.; Nenna, A.; Lusini, M.; Fraldi, M.; Acar, C.; Chello, M. Is subvalvular repair worthwhile in severe ischemic mitral regurgitation? Subanalysis of the papillary muscle approximation trial. J. Thorac. Cardiovasc. Surg. 2017, 153, 286–295.e2. [Google Scholar] [CrossRef]
- Dudzinski, D.M.; Hung, J. Echocardiographic assessment of ischemic mitral regurgitation. Cardiovasc. Ultrasound 2014, 12. [Google Scholar] [CrossRef]
- Rama, A.; Nappi, F.; Praschker, B.G.; Gandjbakhch, I. Papillary muscle approximation for ischemic mitral valve regurgitation. J. Card. Surg. 2008, 23, 733–735. [Google Scholar] [CrossRef]
- Nappi, F.; Carotenuto, A.R.; Vito, D.D.; Spadaccio, C.; Acar, C.; Fraldi, M. Stress shielding, growth and remodeling of pulmonary artery reinforced with copolymer scaffold and transposed into aortic position. Biomech. Modeling Mechanobiol. 2015, 15, 1141–1157. [Google Scholar] [CrossRef] [PubMed]
- Rausch, M.K.; Famaey, N.; Shultz, T.O.; Bothe, W.; Miller, D.C.; Kuhl, E. Mechanics of the mitral valve. Biomech. Modeling Mechanobiol. 2012, 12, 1053–1071. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wenk, J.F.; Zhang, Z.; Cheng, G.; Malhotra, D.; Acevedo-Bolton, G.; Burger, M.; Suzuki, T.; Saloner, D.A.; Wallace, A.W.; Guccione, J.M.; et al. First finite element model of the left ventricle with mitral valve: Insights into ischemic mitral regurgitation. Ann. Thorac. Surg. 2010, 89, 1546–1553. [Google Scholar] [CrossRef] [PubMed]
- Bisshopp, K.E.; Drucker, D.C. Large deflection of cantilevere beams. Q. Appl. Math. 1945, 3, 272–275. [Google Scholar] [CrossRef]
- Nallathambi, A.K.; Rao, C.L.; Srinivasan, S.M. Large deflection of constant curvature cantilever beam under follower load. Int. J. Mech. Sci. 2010, 52, 440–445. [Google Scholar] [CrossRef]
- Zhang, A.; Chen, G. A comprehensive elliptic integral solution to the large deflection problems of thin beams in compliant mechanisms. J. Mech. Robot. 2013, 5, 021006. [Google Scholar] [CrossRef]
- Murdock, K.; Martin, C.; Sun, W. Characterization of mechanical properties of pericardium tissue using planar biaxial tension and flexural deformation. J. Mech. Behav. Biomed. Mater. 2018, 77, 148–156. [Google Scholar] [CrossRef]
- Bigoni, D. Introduction. In Nonlinear Solid Mechanics; Cambridge University Press (CUP): New York, NY, USA, 2012; pp. 1–90. [Google Scholar]
- Kunzelman, K.; Cochran, R. Mechanical properties of basal and marginal mitral valve chordae tendineae. ASAIO Trans. 1990, 36, 405–408. [Google Scholar]
- Kongsaerepong, V.; Shiota, M.; Gillinov, A.M.; Song, J.M.; Fukuda, S.; McCarthy, P.M.; Williams, T.; Savage, R.; Daimon, M.; Thomas, J.D. Echocardiographic predictors of successful versus unsuccessful mitral valve repair in ischemic mitral regurgitation. Am. J. Cardiol. 2006, 98, 504–508. [Google Scholar] [CrossRef]
- Stone, G.W.; Adams, D.H.; Abraham, W.T.; Kappetein, A.P.; Généreux, P.; Vranckx, P.; Mehran, R.; Kuck, K.H.; Leon, M.B.; Piazza, N. Clinical trial design principles and endpoint definitions for transcatheter mitral valve repair and replacement: Part 2: Endpoint definitions. J. Am. Coll. Cardiol. 2015, 66, 308–321. [Google Scholar] [CrossRef]
- Stone, G.W.; Vahanian, A.S.; Adams, D.H.; Abraham, W.T.; Borer, J.S.; Bax, J.J.; Schofer, J.; Cutlip, D.E.; Krucoff, M.W.; Blackstone, E.H. Clinical trial design principles and endpoint definitions for transcatheter mitral valve repair and replacement: Part 1: Clinical trial design principles. Eur. Heart J. 2015, 36, 1851–1877. [Google Scholar] [CrossRef]
- Lancellotti, P.; Moura, L.; Pierard, L.A.; Agricola, E.; Popescu, B.A.; Tribouilloy, C.; Hagendorff, A.; Monin, J.L.; Badano, L.; Zamorano, J.L. European association of echocardiography recommendations for the assessment of valvular regurgitation. part 2: Mitral and tricuspid regurgitation (native valve disease). Eur. J. Echocardiogr. 2010, 11, 307–332. [Google Scholar] [CrossRef]
- Lancellotti, P.; Zamorano, J.L.; Vannan, M.A. Imaging challenges in secondary mitral regurgitation: Unsolved issues and perspectives. Circ. Cardiovasc. Imaging 2014, 7, 735–746. [Google Scholar] [CrossRef]
- Magne, J.; Pibarot, P.; Dagenais, F.; Hachicha, Z.; Dumesnil, J.G.; Senechal, M. Preoperative posterior leaflet angle accurately predicts outcome after restrictive mitral valve annuloplasty for ischemic mitral regurgitation. Circulation 2007, 115, 782–791. [Google Scholar] [CrossRef]
- Alotti, N.; Gombocz, K.; Rashed, A.; D´ezsi, C.; Sayur, A. Surgical approximation of the posterior papillary muscle in chronic ischemic mitral regurgitation—Presentation of a new method of mitral valve repair. J. Cardiothorac. Surg. 2013, 8. [Google Scholar] [CrossRef]
- Kron, I.L.; Hung, J.; Overbey, J.R.; Bouchard, D.; Gelijns, A.C.; Moskowitz, A.J.; Voisine, P.; O’Gara, P.T.; Argenziano, M.; Michler, R.E.; et al. Predicting recurrent mitral regurgitation after mitral valve repair for severe ischemic mitral regurgitation. J. Thorac. Cardiovasc. Surg. 2015, 149, 752–761.e1. [Google Scholar] [CrossRef]
- Nappi, F.; Spadaccio, C.; Chello, M.; Lusini, M.; Acar, C. Double row of overlapping sutures for downsizing annuloplasty decreases the risk of residual regurgitation in ischaemic mitral valve repair. Eur. J. Cardiothorac. Surg. 2016, 49, 1182–1187. [Google Scholar] [CrossRef]
- Roshanali, F.; Mandegar, M.H.; Yousefnia, M.A.; Rayatzadeh, H.; Alaeddini, F. A prospective study of predicting factors in ischemic mitral regurgitation recurrence after ring annuloplasty. Ann. Thorac. Surg. 2007, 84, 745–749. [Google Scholar] [CrossRef]
- Kron, I.L.; Green, G.; Cope, J.T. Surgical relocation of the posterior papillary muscle in chronic ischemic mitral regurgitation. Ann. Thorac. Surg. 2002, 74, 600–601. [Google Scholar] [CrossRef]
- Lu, S.; Zhang, P.; Sun, X.; Gong, F.; Yang, S.; Shen, L.; Huang, Z.; Wang, C. Synthetic ePTFE grafts coated with an anti-CD133 antibody-functionalized heparin/collagen multilayer with rapid in vivo endothelialization properties. ACS Appl. Mater. Interfaces 2013, 5, 7360–7369. [Google Scholar] [CrossRef]
- Rechtsman, M.C.; Stillinger, F.H.; Torquato, S. Negative Poisson’s ratio materials via isotropicinteractions. Phys. Rev. Lett. 2008, 101, 085501. [Google Scholar] [CrossRef]
- Fernandes, A.M.; Rathi, V.; Biederman, R.W.; Doyle, M.; Yamrozik, J.A.; Willians, R.B.; Hedge, V.; Graunt, S.; Aras, R., Jr. Cardiovascular magnetic resonance imaging-derived mitral valve geometry in determining mitral regurgitation severity. Arq. Bras. De Cardiol. 2013. [Google Scholar] [CrossRef]
- Millard, L.; Espino, D.M.; Shepherd, D.E.T.; Hukins, D.W.L.; Buchan, K.G. Mechanical properties of chordae tendineae of the mitral heart valve: Young modulus, structural stiffness and effects of aging. J. Mech. Med. Biol. 2011, 11, 221–230. [Google Scholar] [CrossRef]

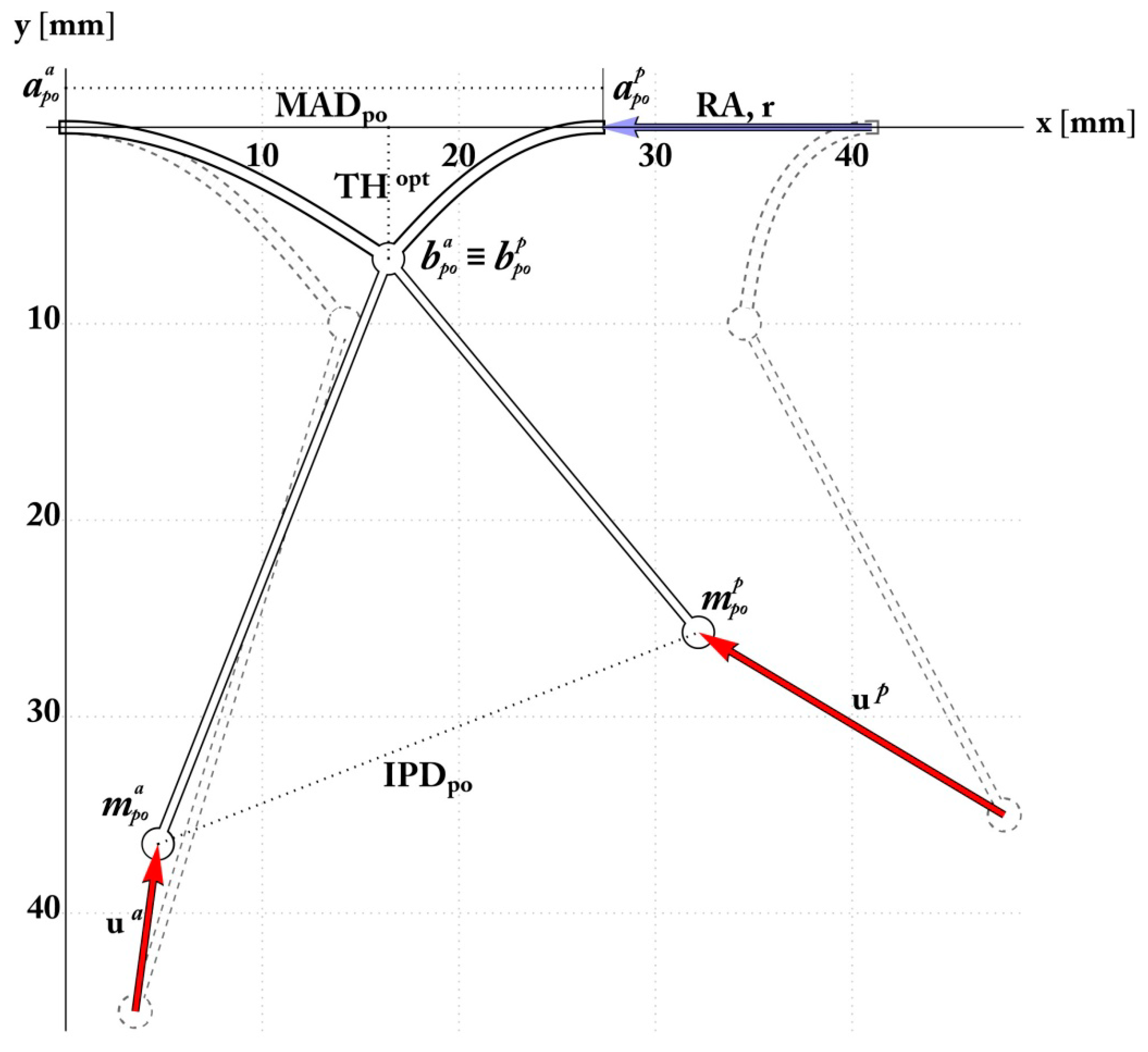

| Preoperative Measurement Namesource and Unit | Value (mean ± std) |
| Mitral Annulus Diameter ADpre, mm End-Diastolic Interpapillary | 40 ± 1.9 |
| Muscle Distance ED IPMD, mm | 44.6 ± 0.39 |
| Tenting Height THpre, mm | 12.4 ± 0.13 |
| Target Coaptation Distance THopt, mm | 6.8 |
| Anterior Mitral Leaflet Angle δa [°] | 32.6° ± 2.5° |
| Posterior Mitral Leaflet Angle δp [°] | 56.8° ± 5.2° |
| Anterior Annulus to Papillary Head ha, mm | 45 ± 8.6 |
| Posterior Annulus to Papillary Head hp, mm | 28 ± 8.1 |
| Model Parameters Namesource and Unit | Value |
| Anterior leaflet length31 la, mm | 18 |
| Posterior leaflet length31 lp, mm | 13 |
| Leaflet bending stiffness10 B, mN mm2 | 500 |
| Chordae tendineae material constants31 c1, mN mm−2 c2, [-] | 352.4 0.1907 |
| Chordae tendineae nominal area32 Aref, mm2 | 0.197 |
| Postoperative Configuration | Analytical Prediction (Preoperative Value) | Surgical Outcome (mean ± std) |
|---|---|---|
| MAD, mm | 26.9(41) | 24.6 ± 2.4 |
| ES IPMD, mm | 27.5 | 32.7 ± 3.2 |
| ha, mm | 38(45) | 37.5 ± 8.2 |
| hp, mm | 26(35) | 23 ± 7.4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nappi, F.; Carotenuto, A.R.; Avtaar Singh, S.S.; Mihos, C.; Fraldi, M. Euler’s Elastica-Based Biomechanics of the Papillary Muscle Approximation in Ischemic Mitral Valve Regurgitation: A Simple 2D Analytical Model. Materials 2019, 12, 1518. https://doi.org/10.3390/ma12091518
Nappi F, Carotenuto AR, Avtaar Singh SS, Mihos C, Fraldi M. Euler’s Elastica-Based Biomechanics of the Papillary Muscle Approximation in Ischemic Mitral Valve Regurgitation: A Simple 2D Analytical Model. Materials. 2019; 12(9):1518. https://doi.org/10.3390/ma12091518
Chicago/Turabian StyleNappi, Francesco, Angelo Rosario Carotenuto, Sanjeet Singh Avtaar Singh, Christos Mihos, and Massimiliano Fraldi. 2019. "Euler’s Elastica-Based Biomechanics of the Papillary Muscle Approximation in Ischemic Mitral Valve Regurgitation: A Simple 2D Analytical Model" Materials 12, no. 9: 1518. https://doi.org/10.3390/ma12091518
APA StyleNappi, F., Carotenuto, A. R., Avtaar Singh, S. S., Mihos, C., & Fraldi, M. (2019). Euler’s Elastica-Based Biomechanics of the Papillary Muscle Approximation in Ischemic Mitral Valve Regurgitation: A Simple 2D Analytical Model. Materials, 12(9), 1518. https://doi.org/10.3390/ma12091518




