The Effect of Alloying Elements on the Structural Stability, and Mechanical and Electronic Properties of Al3Sc: A First-Principles Study
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Structural Stability
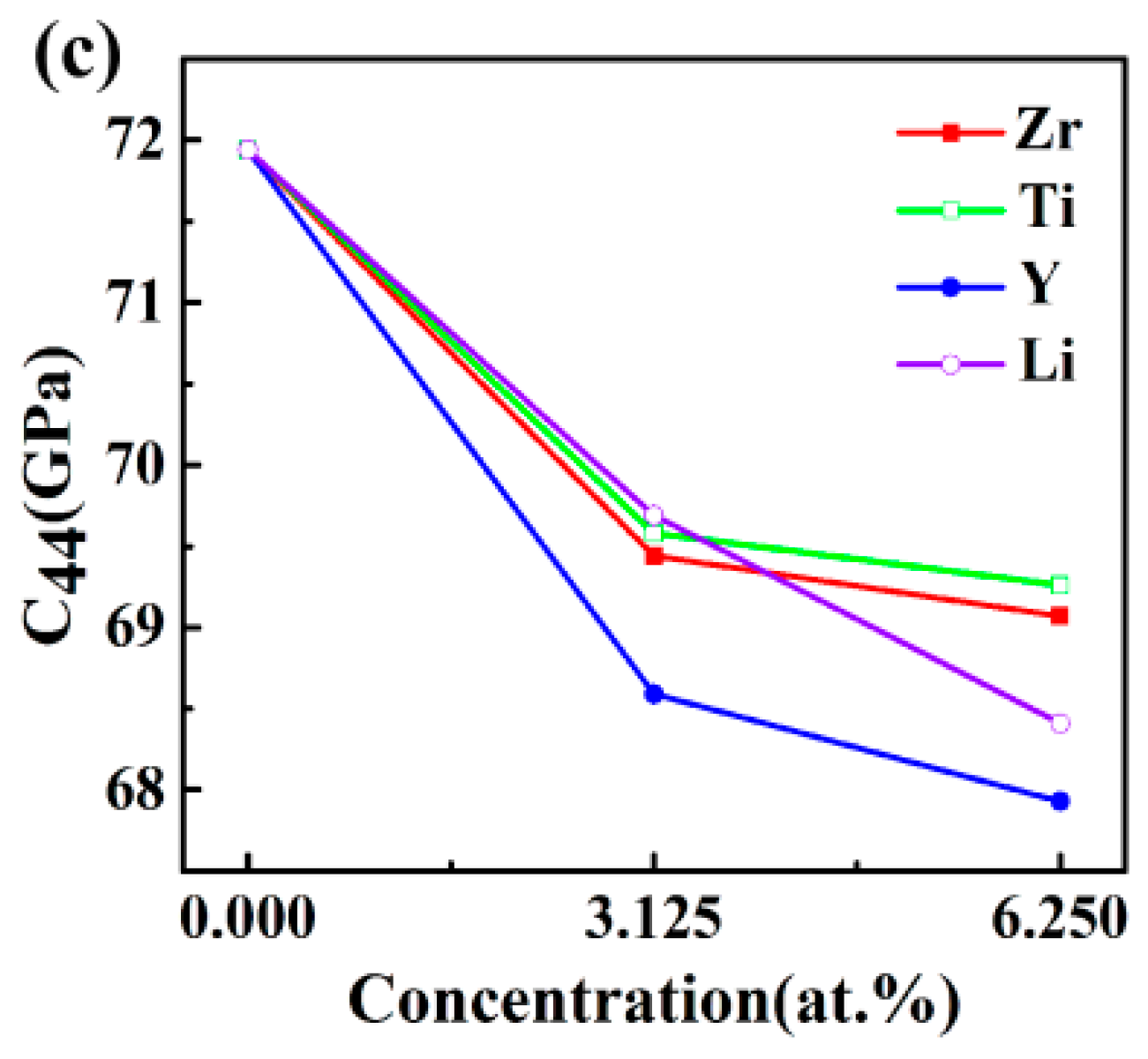
3.2. Elastic Properties
3.3. Debye Temperature
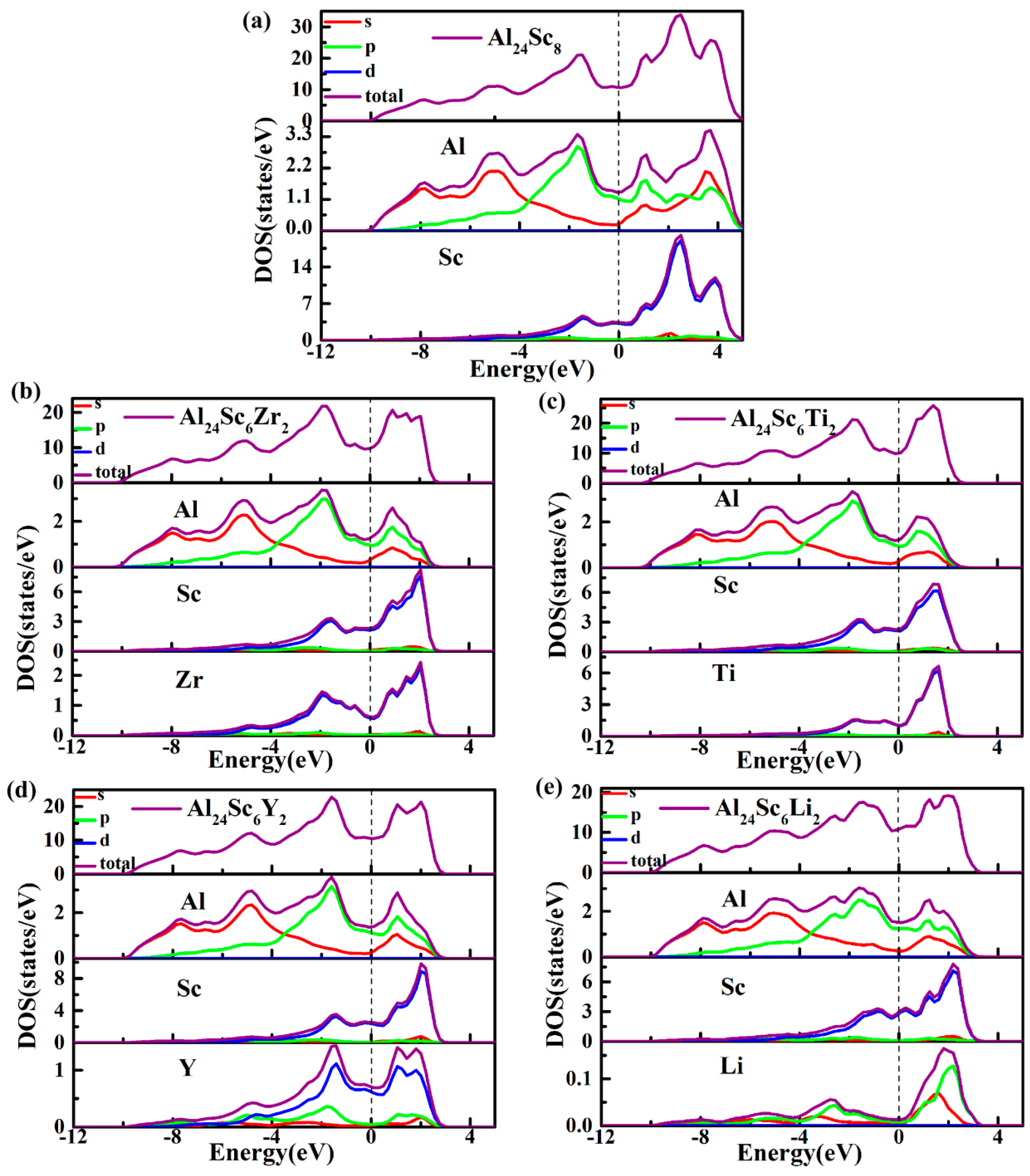
3.4. Electronic Properties
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Asta, M.; Ozoliņš, V. Structural, vibrational, and thermodynamic properties of Al-Sc alloys and intermetallic compounds. Phys. B 2001, 64, 094104. [Google Scholar] [CrossRef]
- Asta, M.; Ozolins, V.; Woodward, C. A first-principles approach to modeling alloy phase equilibria. JOM 2001, 53, 16–19. [Google Scholar] [CrossRef]
- Marquis, E.A.; Seidman, D.N. Nanoscale structural evolution of Al3Sc precipitates in Al(Sc) alloys. Acta Mater. 2001, 49, 1909–1919. [Google Scholar] [CrossRef]
- Ebrahimi, Z.; Ebrahimi, H. Effects of elastic contributions on the evolution of nano-structure Al3Sc phase: A phase-field study. Sci. Iran. 2016, 23, 1539–1548. [Google Scholar] [CrossRef]
- Raghukiran, N.; Sujith, R.; Agrawal, H.; Shabadi, R.; Kumar, R. In situ age hardening and grain refinement in as-sprayed Al-Sc binary alloy deposits. J. Alloys Compd. 2018, 735, 1596–1602. [Google Scholar] [CrossRef]
- Kundu, S.; Thirunavukarasu, G.; Chatterjee, S.; Mishra, B. Effect of Bonding Temperature on Phase Transformation of Diffusion-Bonded Joints of Duplex Stainless Steel and Ti-6Al-4V Using Nickel and Copper as Composite Intermediate Metals. Met. Mater. Trans. A 2015, 46, 5756–5771. [Google Scholar] [CrossRef]
- Jiang, C.; Sordelet, D.; Gleeson, B. Effects of Pt on the elastic properties of B2 NiAl: A combined first-principles and experimental study. Acta Mater. 2006, 54, 2361–2369. [Google Scholar] [CrossRef]
- Jia, M.; Zheng, Z.; Gong, Z. Microstructure evolution of the 1469 Al-Cu-Li-Sc alloy during homogenization. J. Alloys Compd. 2014, 614, 131–139. [Google Scholar] [CrossRef]
- Lai, J.; Zhang, Z.; Chen, X.-G. Precipitation strengthening of Al-B4C metal matrix composites alloyed with Sc and Zr. J. Alloy. Compd. 2013, 552, 227–235. [Google Scholar] [CrossRef]
- Mo, Y.; Pang, M.; Yang, W.; Zhan, Y. Effects of alloying elements on structural, electronic and mechanical properties of AlSc2 by first-principles calculations. Comput. Mater. Sci. 2013, 69, 160–167. [Google Scholar] [CrossRef]
- Park, N.; Lee, S.-C.; Cha, P.-R. Effects of alloying elements on the stability and mechanical properties of Fe3Al from first-principles calculations. Comput. Mater. Sci. 2018, 146, 303–309. [Google Scholar] [CrossRef]
- Tian, J.; Zhao, Y.; Hou, H.; Wang, B. The effect of alloying elements on the structural stability, mechanical properties, and Debye temperature of Al3Li: A first-principles study. Materials 2018, 11, 1471. [Google Scholar] [CrossRef] [PubMed]
- Fuller, C.B.; Seidman, D.N.; Dunand, D.C. Mechanical properties of Al(Sc,Zr) alloys at ambient and elevated temperatures. Acta Mater. 2003, 51, 4803–4814. [Google Scholar] [CrossRef]
- Van Dalen, M.E.; Dunand, D.C.; Seidman, D.N. Effects of Ti additions on the nanostructure and creep properties of precipitation-strengthened Al-Sc alloys. Acta Mater. 2005, 53, 4225–4235. [Google Scholar] [CrossRef]
- Mao, Z.; Chen, W.; Seidman, D.; Wolverton, C. First-principles study of the nucleation and stability of ordered precipitates in ternary Al-Sc-Li alloys. Acta Mater. 2011, 59, 3012–3023. [Google Scholar] [CrossRef]
- Harada, Y.; Dunand, D.; Dunand, D. Thermal expansion of Al3Sc and Al3(Sc0.75X0.25). Scr. Mater. 2003, 48, 219–222. [Google Scholar] [CrossRef] [Green Version]
- Harada, Y.; Dunand, D.; Dunand, D. Creep properties of Al3Sc and Al3(Sc, X) intermetallics. Acta Mater. 2000, 48, 3477–3487. [Google Scholar] [CrossRef]
- Li, D.L.; Chen, P.; Yi, J.X.; Tang, B.Y.; Peng, L.M.; Ding, W.J. Ab initio study on the thermal properties of the fcc Al3Mg and Al3Sc alloys. J. Phys. D Appl. Phys. 2009, 42, 225407. [Google Scholar] [CrossRef]
- Hu, W.-C.; Liu, Y.; Li, D.-J.; Zeng, X.-Q.; Xu, C.-S. Mechanical and thermodynamic properties of Al3Sc and Al3Li precipitates in Al-Li-Sc alloys from first-principles calculations. Phys. B Condens. Matter. 2013, 427, 85–90. [Google Scholar] [CrossRef]
- Chen, D.; Chen, Z.; Wu, Y.; Wang, M.; Ma, N.; Wang, H. First-principles investigation of mechanical, electronic and optical properties of Al3Sc intermetallic compound under pressure. Comput. Mater. Sci. 2014, 91, 165–172. [Google Scholar] [CrossRef]
- Pan, R.-K.; Wang, H.-C.; Shao, L.; Zheng, J.; Pan, X.-Z.; Tang, B.-Y. Temperature dependence of elastic properties of L12-Al3Sc: A first-principles study. Comput. Mater. Sci. 2016, 111, 424–429. [Google Scholar] [CrossRef]
- Duan, Y.H.; Sun, Y.; Peng, M.J.; Zhou, S.G. Ab-initio investigations on elastic properties in L12 structure Al3Sc and Al3Y under high pressure. J. Alloys Compd. 2014, 585, 587–593. [Google Scholar] [CrossRef]
- Wang, R.N.; Ma, L.; Pan, R.K.; Luo, T.P.; Zhou, S.C.; Tang, B.Y. First-principles study of L12-Al3(Sc1−xTMx) alloys using special quasirandom structures. Comput. Mater. Sci. 2013, 79, 136–142. [Google Scholar] [CrossRef]
- Huang, Y.C.; Guo, X.F.; Ma, Y.L.; Shao, H.B.; Xiao, Z.B. Stabilities, electronic and elastic properties of L12-Al3(Sc1−x,Zrx) with different Zr content: A first-principles study. Phys. B Condens. Matter 2018, 548, 27–33. [Google Scholar] [CrossRef]
- Khenioui, Y.; Boulechfar, R.; Maazi, N.; Ghemid, S. FP-LAPW investigation of Al3(Sc1−xTix) alloys properties in L12 and D022 structures. Int. J. Mod. Phys. B 2018, 32, 1850167. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Qian, Y.; Xue, J.L.; Wang, Z.J.; Yang, Z.H.; Qian, P. Mechanical properties evaluation of Zr addition in L12-Al3(Sc1−xZrx) using first-principles calculation. JOM 2016, 68, 1293–1300. [Google Scholar] [CrossRef]
- Tian, T.; Wang, X.F.; Li, W. Ab initio calculations on elastic properties in L12 structure Al3X and X3Al-type (X= transition or main group metal) intermetallic compounds. Solid State Commun. 2013, 156, 69–75. [Google Scholar] [CrossRef]
- Shi, D.; Wen, B.; Melnik, R.; Yao, S.; Li, T. First-principles studies of Al-Ni intermetallic compounds. J. Solid State Chem. 2009, 182, 2664–2669. [Google Scholar] [CrossRef]
- Hill, R. The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Zhou, L.J.; Su, K.H.; Wang, Y.L.; Zeng, Q.F.; Li, Y.L. First-principles study of the properties of Li, Al and Cd doped Mg alloys. J. Alloys Compd. 2014, 596, 63–68. [Google Scholar] [CrossRef]
- Young, A.F.; Sanloup, C.; Gregoryanz, E.; Scandolo, S.; Hemley, R.J.; Mao, H.-K. Synthesis of Novel Transition Metal NitridesIrN2andOsN2. Phys. Lett. 2006, 96, 155501. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.N.; Tang, B.Y.; Peng, L.M.; Ding, W.J. Ab initio study of the effect of Zr content on elastic and electronic properties of L12-Al3(Sc1−xZrx) alloys. Comput. Mater. Sci. 2012, 59, 87–93. [Google Scholar] [CrossRef]
- Teter, D.M. Computational Alchemy: The Search for New Superhard Materials. MRS Bull. 1998, 23, 22–27. [Google Scholar] [CrossRef]
- Pugh, S. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Pettifor, D.G. Theoretical predictions of structure and related properties of intermetallics. Mater. Sci. Technol. 1992, 8, 345–349. [Google Scholar] [CrossRef]
- Mattesini, M.; Ahuja, R.; Johansson, B. Cubic Hf3N4 and Zr3N4: A class of hard materials. Phys. B 2003, 68, 184108. [Google Scholar]
- Tvergaard, V.; Hutchinson, J.W. Microcracking in Ceramics Induced by Thermal Expansion or Elastic Anisotropy. J. Am. Ceram. Soc. 1988, 71, 157–166. [Google Scholar] [CrossRef]
- Anderson, O.L. A simplified method for calculating the debye temperature from elastic constants. J. Phys. Chem. Solids 1963, 24, 909–917. [Google Scholar] [CrossRef]
- Ravindran, P.; Fast, L.; Korzhavyi, P.A.; Johansson, B.; Wills, J.; Eriksson, O. Density functional theory for calculation of elastic properties of orthorhombic crystals: Application to TiSi2. J. Appl. Phys. 1998, 84, 4891–4904. [Google Scholar] [CrossRef]
- Sun, Z.M.; Ahuja, R.; Schneider, J.M. Theoretical investigation of the solubility in (MxM’2−x)AlC (M and M’= Ti,V, Cr). Phys. Rev. B 2003, 68, 224112. [Google Scholar] [CrossRef]
- Tian, J.; Han, G.; Wei, H.; Zheng, Q.; Jin, T.; Sun, X.; Hu, Z. Effects of alloying elements on the electronic structure and ductility of NiAl compounds investigated by X-ray absorption fine structure. Philos. Mag. 2013, 93, 2161–2171. [Google Scholar] [CrossRef]
- Nylén, J.; Garcìa, F.G.; Mosel, B.; Pöttgen, R.; Häussermann, U. Structural relationships, phase stability and bonding of compounds PdSnn (n = 2, 3, 4). Solid State Sci. 2004, 6, 147–155. [Google Scholar] [CrossRef]
- Electronic structure and hybridization effects in Hume-Rothery alloys containing transition elements. Phys. Rev. B 1995, 52, 7920–7933. [CrossRef]
- Bader, R. Atoms in Moledules: A Quantum Theory; Oxford University Press: New York, NY, USA, 1990. [Google Scholar]
- Delaire, O.; Fultz, B. Charge redistribution and rhonon entropy of Vanadium alloys. Phys. Rev. Lett. 2006, 97, 245701. [Google Scholar] [CrossRef]







| Structures | a/Å | ρ/g·cm−3 | ΔHf/eV·atom−1 |
|---|---|---|---|
| Al3Sc | 4.107 | 3.108 | −0.443 |
| Al24Sc7Zr | 8.210 | 3.160 | −0.449 |
| Al24Sc6Zr2 | 8.211 | 3.298 | −0.456 |
| Al24Sc7Ti | 8.180 | 3.064 | −0.435 |
| Al24Sc6Ti2 | 8.144 | 3.155 | −0.427 |
| Al24Sc7Y | 8.252 | 3.106 | −0.438 |
| Al24Sc6Y2 | 8.291 | 3.19 | −0.432 |
| Al24Sc7Li | 8.201 | 2.917 | −0.396 |
| Al24Sc6Li2 | 8.193 | 2.812 | −0.35 |
| Structures | C11 (GPa) | C12 (GPa) | C44 (GPa) | C11 − C12 (GPa) | C12 − C44 (GPa) |
|---|---|---|---|---|---|
| Al3Sc | 183.99 | 37.81 | 71.94 | 146.18 | −34.13 |
| Exp. [31] | 183 | 46 | 68 | 137 | −22 |
| DFT [15] | 180.67 | 40.62 | 72 | 140.05 | −31.38 |
| Al24Sc7Zr | 181.2 | 40.89 | 69.44 | 140.31 | −28.55 |
| Al24Sc6Zr2 | 183.93 | 42.9 | 69.07 | 141.03 | −26.17 |
| Al24Sc7Ti | 181.66 | 40.88 | 69.58 | 140.79 | −28.7 |
| Al24Sc6Ti2 | 186.41 | 43.325 | 69.26 | 143.09 | −25.94 |
| Al24Sc7Y | 175.77 | 38.08 | 68.59 | 137.69 | −30.51 |
| Al24Sc6Y2 | 171.96 | 38.55 | 67.93 | 133.41 | −29.38 |
| Al24Sc7Li | 167.18 | 38.05 | 69.69 | 129.37 | −31.64 |
| Al24Sc6Li2 | 163.42 | 39.34 | 68.41 | 124.08 | −29.07 |
| Structures | B (GPa) | G (GPa) | E (GPa) | ν | B/G | A | H (GPa) | ΘD (K) |
|---|---|---|---|---|---|---|---|---|
| Al3Sc | 86.53 | 72.4 | 169.84 | 0.173 | 1.195 | 0.98 | 15.78 | 607 |
| Exp. [31] | 91.7 | 71.7 | 170.63 | 0.201 | 1.28 | 0.99 | ||
| DFT [15] | 87.3 | 71.2 | 167.94 | 0.179 | 1.23 | 1.03 | ||
| Al24Sc7Zr | 87.66 | 69.73 | 165.34 | 0.186 | 1.257 | 0.99 | 14.59 | 596 |
| Al24Sc6Zr2 | 89.91 | 69.64 | 166.06 | 0.192 | 1.291 | 0.98 | 14.3 | 590 |
| Al24Sc7Ti | 87.81 | 69.91 | 165.74 | 0.185 | 1.256 | 0.98 | 14.68 | 610 |
| Al24Sc6Ti2 | 91.02 | 70.16 | 167.48 | 0.193 | 1.297 | 0.97 | 14.37 | 608 |
| Al24Sc7Y | 83.98 | 68.64 | 161.93 | 0.179 | 1.223 | 0.99 | 14.7 | 594 |
| Al24Sc6Y2 | 83.02 | 67.44 | 159.21 | 0.18 | 1.23 | 1.02 | 14.39 | 580 |
| Al24Sc7Li | 81.09 | 67.64 | 158.77 | 0.174 | 1.199 | 1.07 | 14.61 | 611 |
| Al24Sc6Li2 | 80.97 | 65.78 | 155.43 | 0.18 | 1.231 | 1.10 | 14.05 | 619 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, D.; Xia, C.; Liu, X.; Wu, Y.; Wang, M. The Effect of Alloying Elements on the Structural Stability, and Mechanical and Electronic Properties of Al3Sc: A First-Principles Study. Materials 2019, 12, 1539. https://doi.org/10.3390/ma12091539
Chen D, Xia C, Liu X, Wu Y, Wang M. The Effect of Alloying Elements on the Structural Stability, and Mechanical and Electronic Properties of Al3Sc: A First-Principles Study. Materials. 2019; 12(9):1539. https://doi.org/10.3390/ma12091539
Chicago/Turabian StyleChen, Dong, Cunjuan Xia, Xiaomin Liu, Yi Wu, and Mingliang Wang. 2019. "The Effect of Alloying Elements on the Structural Stability, and Mechanical and Electronic Properties of Al3Sc: A First-Principles Study" Materials 12, no. 9: 1539. https://doi.org/10.3390/ma12091539
APA StyleChen, D., Xia, C., Liu, X., Wu, Y., & Wang, M. (2019). The Effect of Alloying Elements on the Structural Stability, and Mechanical and Electronic Properties of Al3Sc: A First-Principles Study. Materials, 12(9), 1539. https://doi.org/10.3390/ma12091539




