Experimental Verification of Isotropic and Anisotropic Anhysteretic Magnetization Models
Abstract
:1. Introduction
2. Models of Anhysteretic Curve
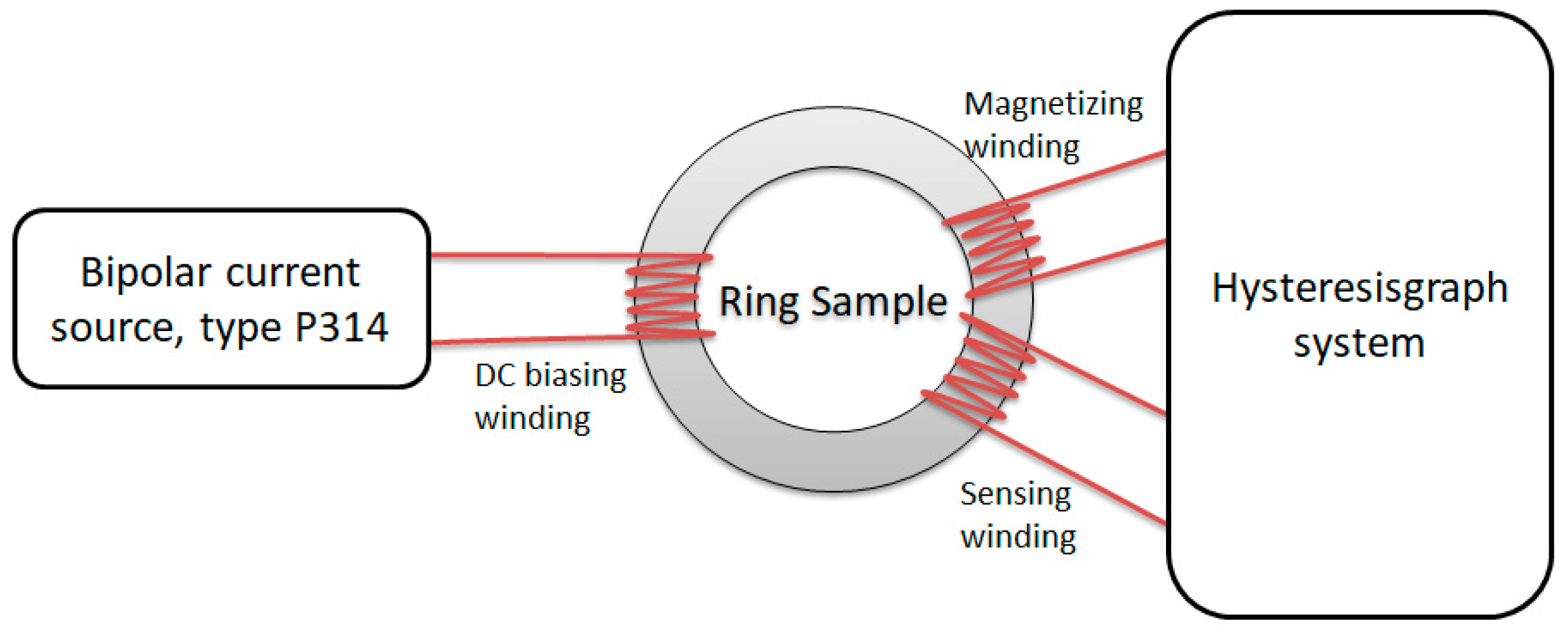
3. Materials and Methods
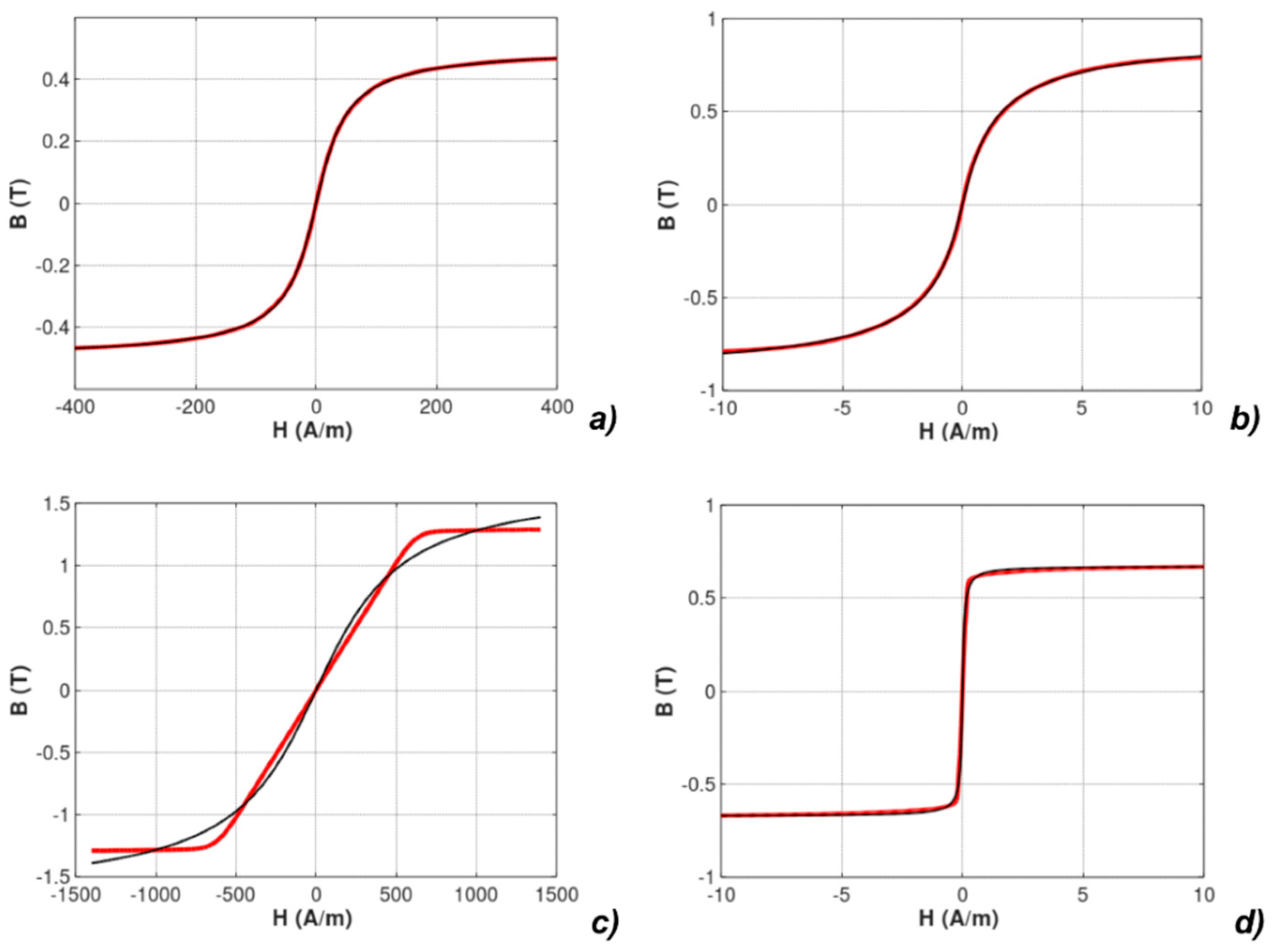
4. Identification of Parameters of the Models
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jiles, D.C.; Atherton, D. Theory of ferromagnetic hysteresis. J. Appl. Phys. 1984, 55, 2115–2120. [Google Scholar] [CrossRef]
- Jiles, D.C.; Atherton, D. Theory of ferromagnetic hysteresis. J. Magn. Magn. Mater. 1986, 61, 48–60. [Google Scholar] [CrossRef]
- Venkataraman, R.; Krishnaprasad, P.S. Qualitative analysis of a bulk ferromagnetic hysteresis model. In Proceedings of the 37th IEEE Conference on Decision and Control, Tampa, FL, USA, 16–18 December 1998. [Google Scholar] [CrossRef]
- Szewczyk, R.; Cheng, P. Open Source Implementation of Different Variants of Jiles-Atherton Model of Magnetic Hysteresis Loops. Acta Phys. Pol. A 2018, 133, 654–656. [Google Scholar] [CrossRef]
- Chwastek, K.; Szczygłowski, J.; Wilczyński, W. Minor Loops in the Harrison Model. Acta Phys. Pol. A 2012, 121, 941–944. [Google Scholar] [CrossRef]
- Szewczyk, R. Validation of the Anhysteretic Magnetization Model for Soft Magnetic Materials with Perpendicular Anisotropy. Materials 2014, 7, 5109–5116. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiles, D.C. Introduction to Magnetism and Magnetic Materials, 2nd ed.; Chapman and Hall: London, UK, 1998; ISBN 978-0412798603. [Google Scholar]
- Kvasnica, B.; Kundracik, F. Fitting experimental anhysteretic curves of ferromagnetic materials and investigation of the effect of temperature and tensile stress. J. Magn. Magn. Mater. 1996, 162, 43–49. [Google Scholar] [CrossRef]
- Nowicki, M. Anhysteretic Magnetization Measurement Methods for Soft Magnetic Materials. Materials 2018, 11, 2021. [Google Scholar] [CrossRef] [PubMed]
- Estakhri, N.M.; Edwards, B.; Engheta, N. Inverse-designed metastructures that solve equations. Science 2019, 363, 1333–1338. [Google Scholar]
- La Spada, L.; Spooner, C.; Haq, S.; Hao, Y. Curvilinear MetaSurfaces for Surface Wave Manipulation. Sci. Rep. 2019, 9, 3107. [Google Scholar] [CrossRef] [PubMed]
- Kittel, C. Introduction to Solid State Physics, 2nd ed.; John Wiley and Sons: Hoboken, NJ, USA, 1960; ISBN 1114173568. [Google Scholar]
- Sablik, M.; Jiles, D.C. Coupled magnetoelastic theory of magnetic and magnetostrictive hysteresis. IEEE Trans. Magn. 1993, 29, 2113–2123. [Google Scholar] [CrossRef] [Green Version]
- Kokornaczyk, E.; Gutowski, M.W. Anhysteretic Functions for the Jiles-Atherton Model. IEEE Trans. Magn. 2015, 51, 7300305. [Google Scholar] [CrossRef]
- Ponjavic, M.M.; Duric, R.M. Nonlinear modeling of the self-oscillating fluxgate current sensor. IEEE Sens. J. 2007, 7, 1546. [Google Scholar] [CrossRef]
- La Spada, L.; Vegni, L. Electromagnetic nanoparticles for sensing and medical diagnostic applications. Materials 2018, 11, 603. [Google Scholar] [CrossRef] [PubMed]
- Sablik, M.J.; Augustyniak, B.; Chmielewski, M. Modeling biaxial stress effects on magnetic hysteresis in steel with the field and stress axes noncoaxial. J. Appl. Phys. 1999, 85, 4391–4393. [Google Scholar] [CrossRef]
- Sablik, M.J.; Burkhardt, G.L.; Kwun, H.; Jiles, D.C. A model for the effect of stress on the low-frequency harmonic content of the magnetic induction in ferromagnetic materials. J. Appl. Phys. 1988, 63, 3930–3932. [Google Scholar] [CrossRef]
- Chwastek, K.; Szczygłowski, J.; Najgebauer, M. A Direct Search algorithm for estimation of Jiles-Atherton hysteresis model parameters. Mater. Sci. Eng. B 2006, 131, 22–26. [Google Scholar] [CrossRef]
- Chwastek, K.; Szczygłowski, J. An alternative method to estimate the parameters of Jiles-Atherton model. J. Magn. Magn. Mater. 2007, 314, 47–51. [Google Scholar] [CrossRef]
- Culity, B.D. Introduction to Magnetic Materials, 2nd ed.; Wiley-IEEE Press: Hoboken, NJ, USA, 2011; ISBN 978-1-118-21149-6. [Google Scholar]
- Ramesh, A.; Jiles, D.C.; Bi, Y. Generalization of hysteresis modeling to anisotropic materials. J. Appl. Phys. 1997, 81, 5585–5587. [Google Scholar] [CrossRef] [Green Version]
- Ramesh, A.; Jiles, D.; Roderik, J. A model of anisotropic anhysteretic magnetization. IEEE Trans. Magn. 1996, 32, 4234–4236. [Google Scholar] [CrossRef]
- Charubin, T.; Nowicki, M.; Marusenkov, A.; Szewczyk, R.; Nosenko, A.; Kyrylchuk, V. Mobile ferrograph system for ultrahigh permeability alloys. J. Autom. Mob. Rob. Intell. Syst. 2018, 12, 40–42. [Google Scholar] [CrossRef]
- Frydrych, P.; Szewczyk, R.; Salach, J. Magnetic Fluxgate Sensor Characteristics Modeling Using Extended Preisach Model. Acta Phys. Pol. A 2014, 126, 18–19. [Google Scholar] [CrossRef]
- La Spada, L. Metasurfaces for Advanced Sensing and Diagnostics. Sensors 2019, 19, 355. [Google Scholar] [CrossRef] [PubMed]
- Dahal, J.N.; Ali, K.S.S.; Mishra, S.R.; Alam, J. Structural, Magnetic, and Mössbauer Studies of Transition Metal-Doped Gd2Fe16Ga0.5TM0.5 Intermetallic Compounds (TM = Cr, Mn, Co, Ni, Cu, and Zn). Magnetochemistry 2018, 4, 54. [Google Scholar] [CrossRef]





| Parameter | Unit | Mn-Zn ferrite F3001 | Co67Fe4Mo1B11Si17 | Fe73.5Cu1Nb3Si15.5B7 Perpendicular Anisotropy | Fe67Co18B14Si1 Parallel Anisotropy |
|---|---|---|---|---|---|
| Ms | A/m | 356,460 | 643,597 | 820,551 | 521,407 |
| a | A/m | 87.52 | 11.20 | 50.00 | 0.52 |
| α | 7.65 × 10−7 | 1.31 × 10−5 | 2.92 × 10−8 | 5.96 × 10−7 | |
| R2 | % | 99.79 | 99.9989 | 88.47 | 99.96 |
| Parameter | Unit | Mn-Zn ferrite F3001 | Co67Fe4Mo1B11Si17 | Fe73.5Cu1Nb3Si15.5B7 Perpendicular Anisotropy | Fe67Co18B14Si1 Parallel Anisotropy |
|---|---|---|---|---|---|
| Ms | A/m | 360,958 | 649,693 | 1,073,424 | 523,969 |
| a | A/m | 55.90 | 3.99 | 264.94 | 0.10 |
| α | 1.34 × 10−5 | 9.91 × 10−6 | 2.92 × 10−8 | 5.64 × 10−8 | |
| R2 | % | 99.94 | 99.9977 | 99.74 | 99.96 |
| Parameter | Unit | Mn-Zn ferrite F3001 | Co67Fe4Mo1B11Si17 | Fe73.5Cu1Nb3Si15.5B7 Perpendicular Anisotropy | Fe67Co18B14Si1 Parallel Anisotropy |
|---|---|---|---|---|---|
| Ms | A/m | 399,291 | 727,548 | 1,330,538 | 533,825 |
| a | A/m | 44.01 | 2.36 | 385.76 | 0.08 |
| α | 2.26 × 10−5 | 2.68 × 10−6 | 2.94 × 10−8 | 5.64 × 10−8 | |
| R2 | % | 99.9992 | 99.995 | 99.50 | 99.97 |
| Parameter | Unit | Mn-Zn ferrite | Co67Fe4Mo1B11Si17 | Fe73.5Cu1Nb3Si15.5B7 Perpendicular Anisotropy | Fe67Co18B14Si1 Parallel Anisotropy |
|---|---|---|---|---|---|
| Ms | A/m | 402,878 | 737,851 | 948,825 | 537,164 |
| a | A/m | 32.67 | 1.84 | 50.00 | 0.10 |
| α | 9.17 × 10−5 | 5.07 × 10−5 | 2.92 × 10−8 | 3.68 × 10−7 | |
| R2 | % | 99.9990 | 99.995 | 95.11 | 99.95 |
| Parameter | Unit | Mn-Zn ferrite F-3001 | Co67Fe4Mo1B11Si17 | Fe73.5Cu1Nb3Si15.5B7 Perpendicular Anisotropy | Fe67Co18B14Si1 Parallel Anisotropy |
|---|---|---|---|---|---|
| Ms | A/m | 403,075 | 736,367 | 1,028,169 | 602,000 |
| a | A/m | 32.98 | 1.80 | 2.72 | 28.86 |
| α | 9.5 × 10−5 | 4.8 × 10−5 | 4.48 × 10−6 | 6.85 × 10−5 | |
| Κan | J/m3 | 0.05 | 0.04 | 411.42 | 487.98 |
| R2 | % | 99.9990 | 99.995 | 99.9993 | 99.65 |
| R2 (%) | Mn-Zn ferrite F-3001 | Co67Fe4Mo1B11Si17 | Fe73.5Cu1Nb3Si15.5B7 Perpendicular Anisotropy | Fe67Co18B14Si1 Parallel Anisotropy |
|---|---|---|---|---|
| erf-based | 99.79 | 99.9989 | 88.47 | 99.96 |
| exp-based | 99.94 | 99.9977 | 99.74 | 99.96 |
| arctan-based | 99.9992 | 99.995 | 99.50 | 99.97 |
| Langevin function-based | 99.9990 | 99.995 | 95.11 | 99.95 |
| Anisotropic extension-based | 99.9990 | 99.995 | 99.9993 | 99.65 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nowicki, M.; Szewczyk, R.; Nowak, P. Experimental Verification of Isotropic and Anisotropic Anhysteretic Magnetization Models. Materials 2019, 12, 1549. https://doi.org/10.3390/ma12091549
Nowicki M, Szewczyk R, Nowak P. Experimental Verification of Isotropic and Anisotropic Anhysteretic Magnetization Models. Materials. 2019; 12(9):1549. https://doi.org/10.3390/ma12091549
Chicago/Turabian StyleNowicki, Michał, Roman Szewczyk, and Paweł Nowak. 2019. "Experimental Verification of Isotropic and Anisotropic Anhysteretic Magnetization Models" Materials 12, no. 9: 1549. https://doi.org/10.3390/ma12091549
APA StyleNowicki, M., Szewczyk, R., & Nowak, P. (2019). Experimental Verification of Isotropic and Anisotropic Anhysteretic Magnetization Models. Materials, 12(9), 1549. https://doi.org/10.3390/ma12091549






