Effects of Defects on Bond Behavior of Fiber Reinforced Cementitious Matrix Materials
Abstract
:1. Introduction
- Phase 1 (uncracked stage): The matrix is not yet cracked and the mechanical tensile behavior is governed by the mechanical properties of the matrix;
- Phase 2 (crack developing stage): The tensile strength of the matrix is exceeded, hence cracking begins to take place and the load is gradually transferred to the fibers;
- Phase 3 (crack-stabilized stage): The load is almost completely transferred to the fibers and the mechanical tensile behavior is governed by the mechanical properties of the fibers (i.e., E3 ≅ Ef).
- Debonding with cohesive failure of the support of the reinforcement;
- Debonding at the matrix interface-support;
- Debonding at the matrix-fiber interface;
- Slip of the fiber inside the matrix;
- Slip of the fiber and cracking of the outer layer of mortar;
- Tensile failure of the fiber.
2. Bond Test Simulation
2.1. Material Constitutive Laws
2.2. Interface Bond Relationships
3. Single Bundle Algorithm
3.1. General Problem
3.2. Numerical Procedure
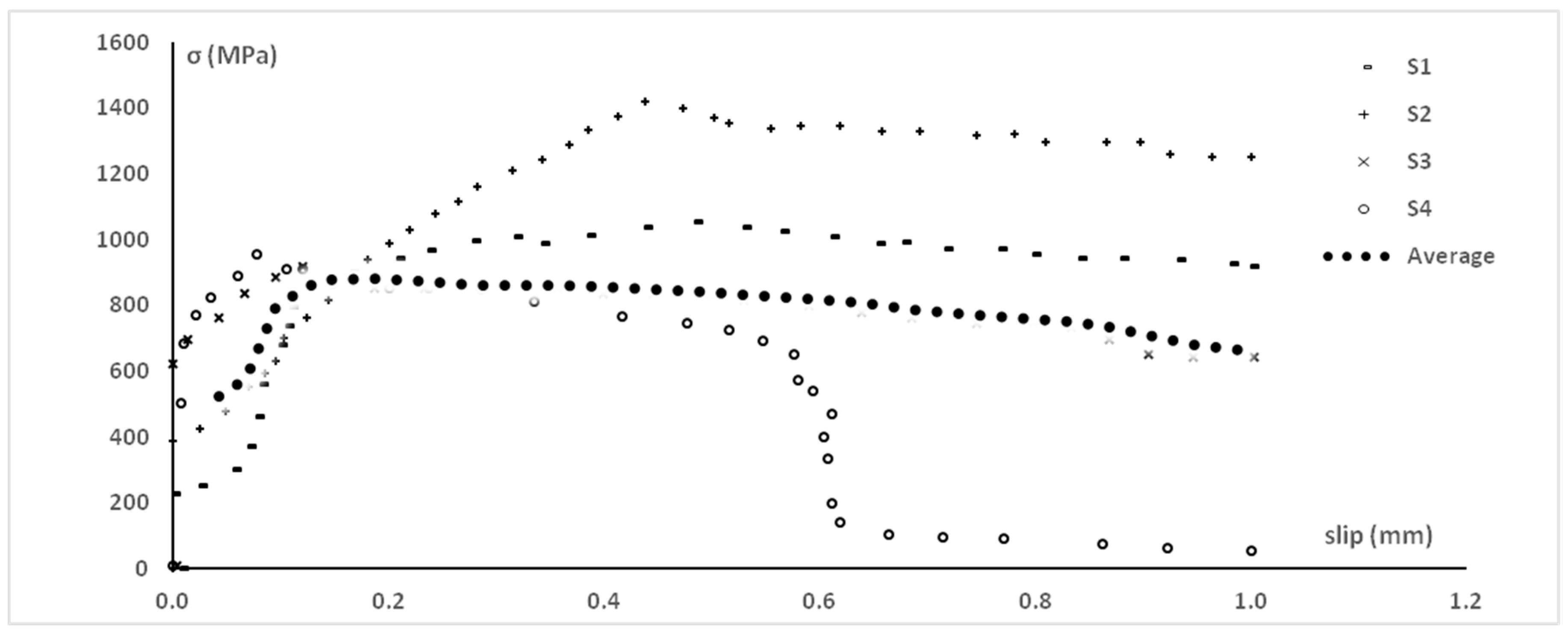
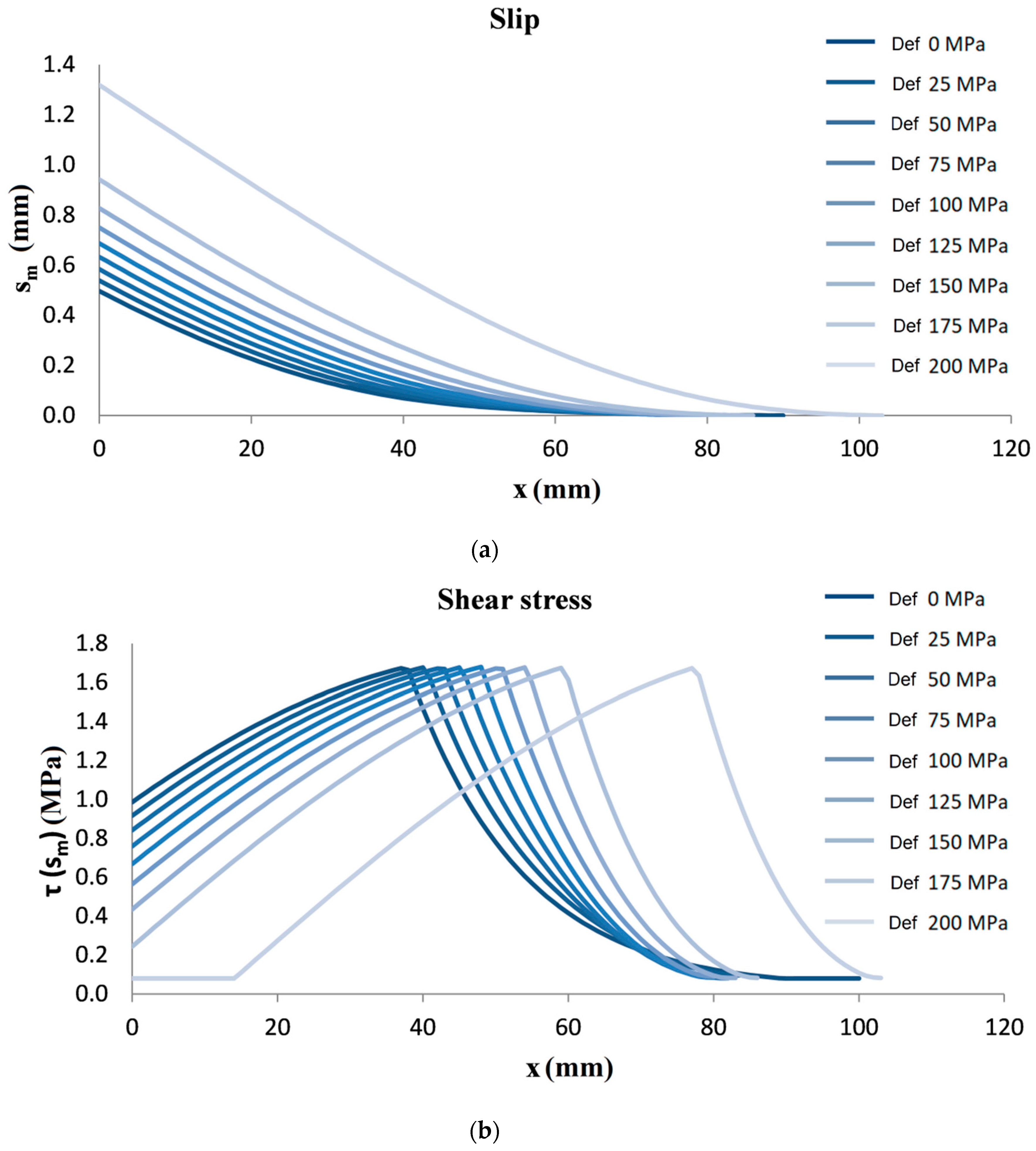
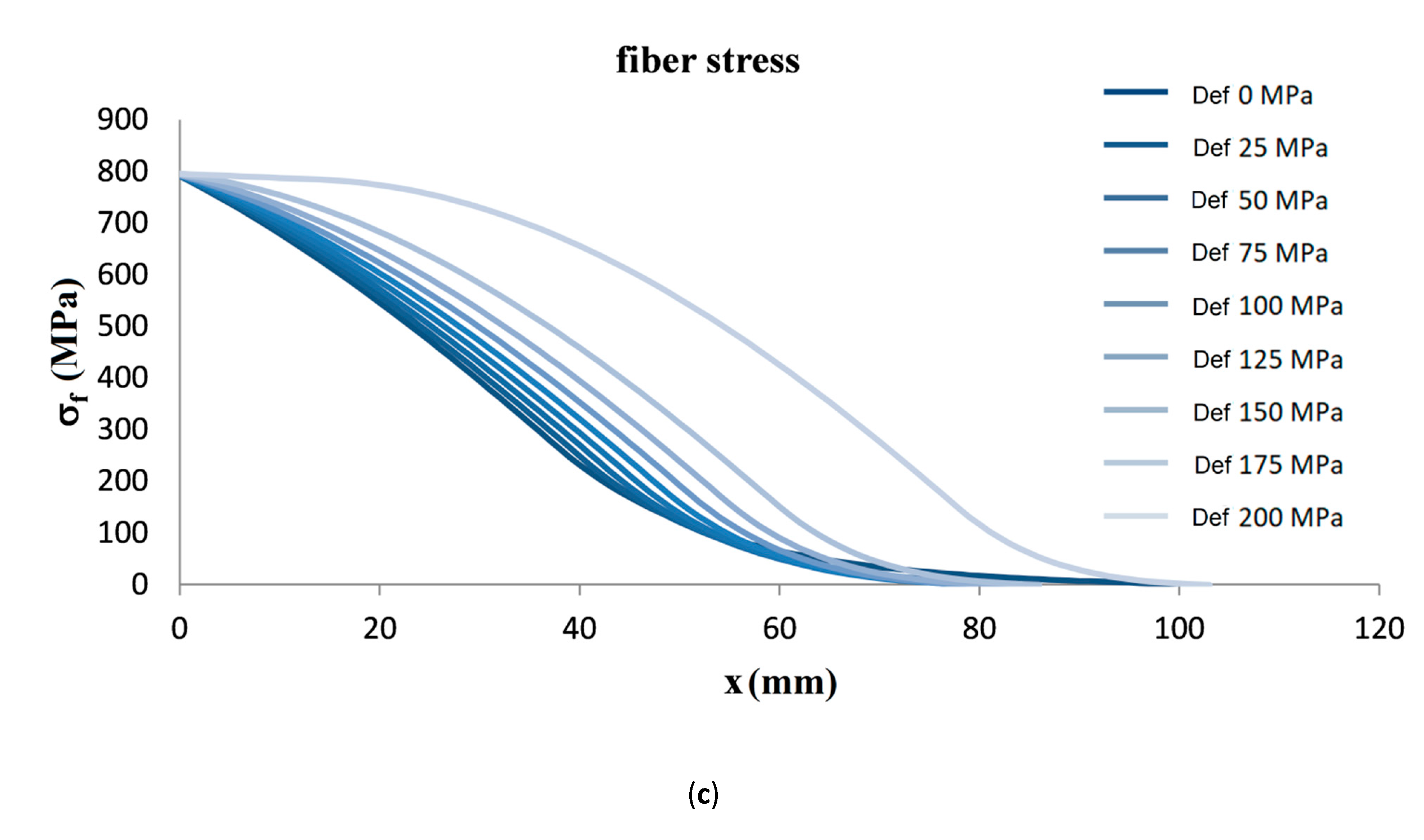
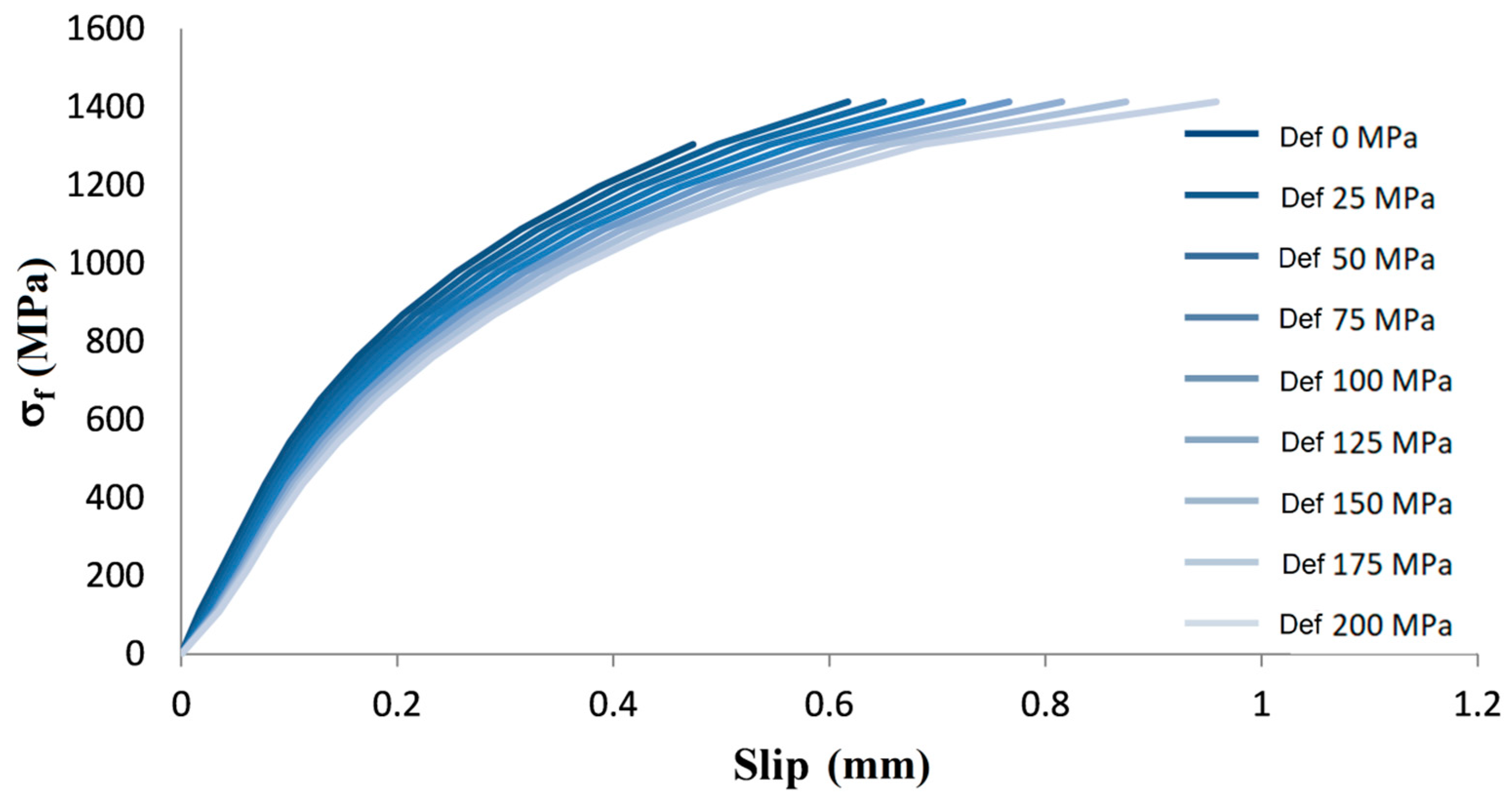
3.3. Example of Some Numerical Results
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Menna, C.; Parisi, F.; Prota, A.; Sodano, S. Analisi sezionale a fibre di pannelli murari rinforzati con sistemi FRCM. In Proceedings of the IfCrasc ’17: IV Convegno di Ingegneria Forense-VII Convegno su CRolli, Affidabilità Strutturale, Consolidamento, Milano, Italy, 14–16 September 2017; pp. 683–692. [Google Scholar]
- Papanicolaou, C.; Triantafillou, T.; Papathanasiou, M.; Karlos, K. Textile reinforced mortar (TRM) versus FRP as strengthening material of URM walls: Out of Plane cyclic loading. Mater. Struct. 2008, 41, 143–157. [Google Scholar] [CrossRef]
- Parisi, F.; Iovinella, I.; Balsamo, A.; Augenti, N.; Prota, A. In-plane behaviour of tuff masonry strengthendened with inorganic matrix-grid composites. Compos. Part B Eng. 2013, 45, 1657–1666. [Google Scholar] [CrossRef]
- Prota, A.; Marcari, G.; Fabbrocino, G.; Manfredi, G. Experimental In-Plane Behavior of Tuff Masonry Strengthened with Cementitious-Grid Composites. J. Compos. Constr. 2006, 10, 223–233. [Google Scholar] [CrossRef]
- Menna, C.; Asprone, D.; Ferone, C.; Colangelo, F.; Balsamo, A.; Prota, A.; Cioffi, R.; Manfredi, G. Use of geopolymers for composite external reinforcement of RC members. Compos. Part B Eng. 2013, 45, 1667–1676. [Google Scholar] [CrossRef]
- Harajli, M.; ElKhatib, H.; San-Jose, J.T. Static and Cyclic Out-of-Plane Response of Masonry Walls Strengthened Using Textile-Mortar System. J. Mater. Civ. Eng. 2010, 22, 1171–1180. [Google Scholar] [CrossRef]
- D’Ambrisi, A.; Feo, L.; Focacci, F. Bond-Slip relations for PBO-FRCM materials externally bonded to concrete. Compos. Part B Eng. 2012, 43, 2938–2949. [Google Scholar] [CrossRef]
- D’Ambrisi, A.; Feo, L.; Focacci, F. Experimental and analytical investigation on bond between Carbon-FRCM materials and masonry. Compos. Part B Eng. 2013, 46, 15–20. [Google Scholar] [CrossRef]
- Koutas, L.N.; Tetta, Z.; Bournas, D.A.; Triantafillou, T.C. Strengthening of Concrete Structures with Textile Reinforced Mortars: State-of-the-Art Review. J. Compos. Constr. 2019, 23, 1–20. [Google Scholar] [CrossRef]
- Kouris, L.A.S.; Triantafillou, T.C. State-of-the-art on strengthening of masonry structures with textile reinforced mortar (TRM). Constr. Build. Mater. 2018, 188, 1221–1233. [Google Scholar] [CrossRef]
- Loreto, G.; Babaeidarabad, S.; Leardini, L.; Nanni, A. RC beams shear-strengthened with fabric-reinforced-cementitious-matrix (FRCM) composite. Int. J. Adv. Struct. Eng. 2015, 7, 341–352. [Google Scholar] [CrossRef] [Green Version]
- Pino, V.; Akbari Hadad, H.; De Caso y Basalo, F.; Nanni, A.; Ebead, U.; El Refai, A. Performance of FRCM-strengthened RC beams subject to fatigue. J. Bridge Eng. 2017, 22, 04017079. [Google Scholar] [CrossRef]
- Pino, V.; Nanni, A.; Arboleda, D.; Roberts-Wollmann, C.; Cousins, T. Repair of damaged prestressed concrete girders with FRP and FRCM composites. J. Compos. Constr. 2017, 21, 04016111. [Google Scholar] [CrossRef]
- Sneed, L.H.; Verre, S.C.; Carloni, C.; Ombres, L. Flexural behaviour of RC beams strengthened with steel-FRCM composite. Eng. Struct. 2016, 127, 686–699. [Google Scholar] [CrossRef]
- Tran, C.T.M.; Stitmannaithum, B.; Ueda, T. Investigation of the bond behaviour between PBO-FRCM strengthening material and concrete. J. Adv. Concr. Technol. 2014, 12, 545–557. [Google Scholar] [CrossRef] [Green Version]
- Carozzi, F.G.; Poggi, C. Mechanical properties and debonding strength of fabric reinforced cementitious matrix (FRCM) systems for masonry strengthening. Compos. Part B 2015, 70, 215–230. [Google Scholar] [CrossRef]
- Lignola, G.P.; Caggegi, C.; Ceroni, F.; De Santis, S.; Krajewskie, P.; Lourenço, P.B.; Morganti, M.; Papanicolaou, C.; Pellegrino, C.; Prota, A.; et al. Performance assessment of basalt FRCM for retrofit applications on masonry. Compos. Part B Eng. 2017, 128, 1–18. [Google Scholar] [CrossRef]
- Leone, M.; Aiello, M.A.; Balsamo, A.; Carozzi, F.G.; Ceroni, F.; Corradi, M.; Gams, M.; Garbin, E.; Gattesco, N.; Krajewski, P.; et al. Glass fabric reinforced cementitious matrix: Tensile properties and bond performance on masonry substrate. Compos. Part B Eng. 2017, 127, 196–214. [Google Scholar] [CrossRef] [Green Version]
- Caggegi, C.; Carozzi, F.G.; De Santis, S.; Fabbrocino, F.; Focacci, F.; Hojdys, Ł.; Lanoye, E.; Zuccarino, L. Experimental analysis on tensile and bond properties of PBO and aramid fabric reinforced cementitious matrix for strengthening masonry structures. Compos. Part B Eng. 2017, 127, 175–195. [Google Scholar] [CrossRef]
- De Santis, S.; Ceroni, F.; de Felice, G.; Fagone, M.; Ghiassi, B.; Kwiecieńe, A.; Lignola, G.P.; Morganti, M.; Santandrea, M.; Valluzzi, M.R.; et al. Round Robin Test on tensile and bond behaviour of Steel Reinforced Grout systems. Compos. Part B Eng. 2017, 127, 100–120. [Google Scholar] [CrossRef]
- Valluzzi, M.R.; Oliveira, D.V.; Caratelli, A.; Castori, G.; Corradi, M.; de Felice, G.; Garbin, E.; Garcia, D.; Garmendia, L.; Grande, E.; et al. Round robin test for composite to brick shear bond characterization. Mater. Struct. 2012, 45, 1761–1791. [Google Scholar] [CrossRef] [Green Version]
- De Felice, G.; Aiello, M.A.; Bellini, A.; Ceroni, F.; De Santis, S.; Garbin, E.; Leone, M.; Lignola, G.P.; Malena, M.; Mazzotti, C.; et al. Experimental characterization of composite-to-brick masonry shear bond. Mater. Struct. 2015, 49, 2581–2596. [Google Scholar] [CrossRef]
- De Felice, G.; Aiello, M.A.; Caggegi, C.; Ceroni, F.; De Santis, S.; Garbin, E.; Gattesco, N.; Hojdys, Ł.; Krajewski, P.; Kwiecień, A.; et al. Recommendation of RILEM Technical Committee 250-CSM: Test method for Textile Reinforced Mortar to substrate bond characterization. Mater. Struct. 2018, 51, 95. [Google Scholar] [CrossRef]
- Istruzioni per la Progettazione, l’Esecuzione ed il Controllo di Interventi di Consolidamento Statico Mediante l’utilizzo di Compositi Fibrorinforzati a Matrice Inorganica; CNR-DT 215/2018; National Research Council: Roma, Italy, 2019.
- Bilotta, A.; Ceroni, F.; Lignola, G.P.; Prota, A. Use of DIC technique for investigating the behaviour of FRCM materials for strengthening masonry elements. Compos. Part B Eng. 2017, 129, 251–270. [Google Scholar] [CrossRef]
- Brice, L.P. Adherence des Barres d’Acier Dans le Beton, Annales de Institut Technique du Batiment et des Travaux Publics; No. 179 (March–April 1951); Serie: Essais et Mesures, No. 19; Société de la Diffusion des Techniques du Bâtiment et de Travaux Publics: Paris, France, 1951. [Google Scholar]
- Carloni, C.; D’Antino, T.; Sneed, L.H.; Pellegrino, C. Role of the Matrix Layers in the Stress-Transfer Mechanism of FRCM Composites Bonded to a Concrete Substrate. J. Eng. Mech. 2015, 141, 04014165. [Google Scholar] [CrossRef]


| Matrix (M) | Matrix Cross section effective in tension | mm2 | |
| Matrix thickness | mm | ||
| Matrix width/distance between bundles | mm | ||
| Matrix Young’s modulus | MPa | ||
| Compressive strength | MPa | ||
| Tensile strength | MPa | ||
| Matrix stress | MPa | ||
| Axial strain in the matrix | - | ||
| Fiber (F) | Equivalent bundle diameter | mm | |
| Bundle Cross section | mm2 | ||
| Bundle Young’s modulus | MPa | ||
| Axial fiber stress | MPa | ||
| Axial fiber strain | - | ||
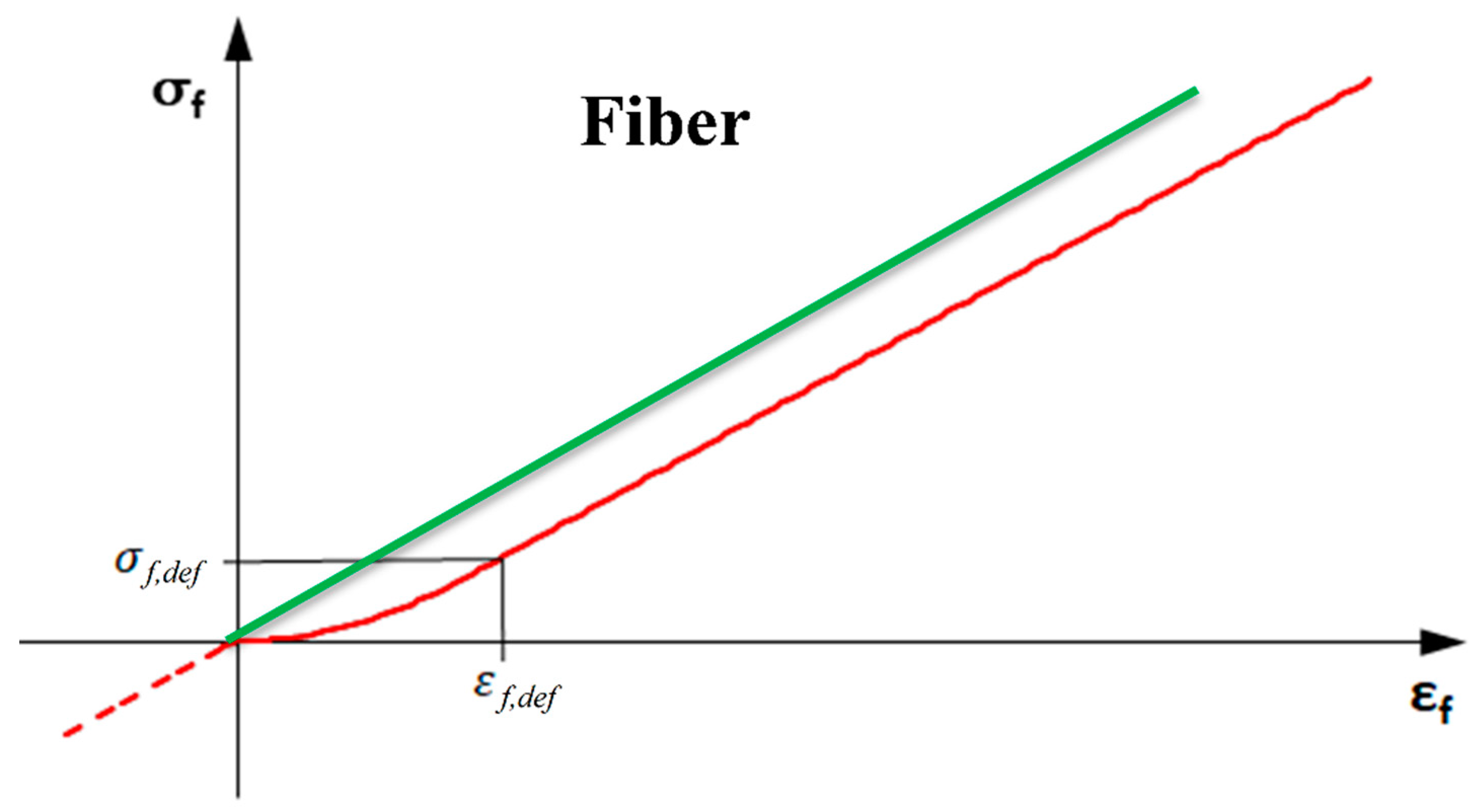
| Fiber defect stress | MPa | ||
| Fiber defect strain | - | ||
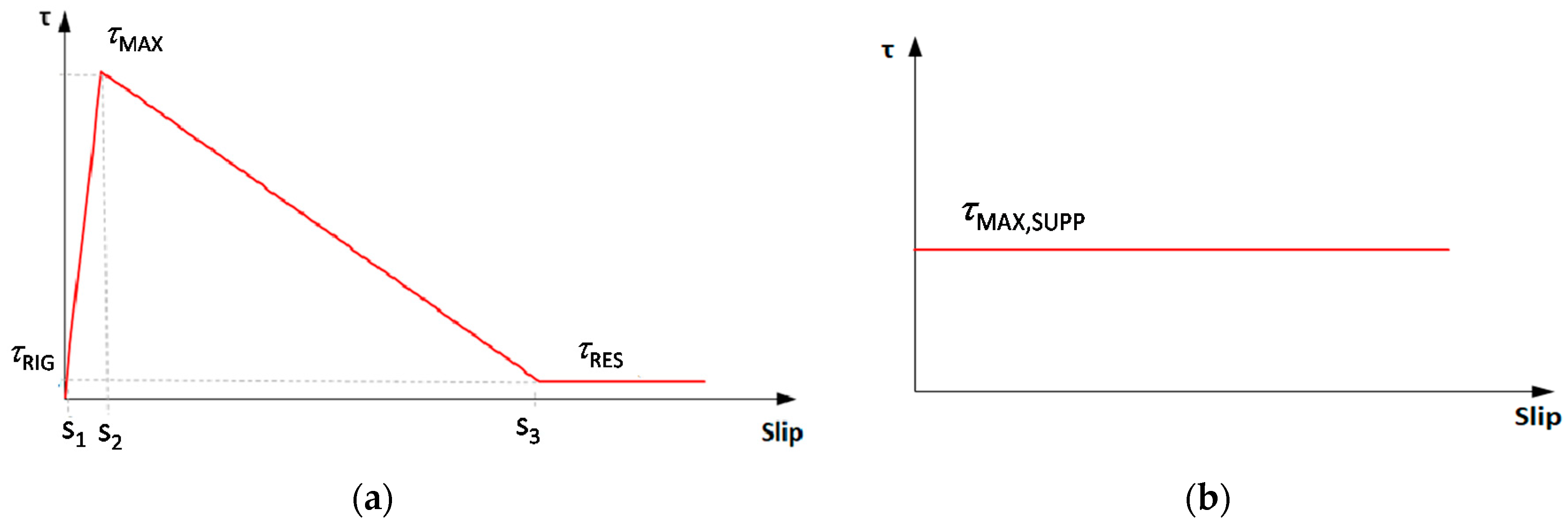
| F-M interface | Rigid shear stress | MPa | |
| Maximum shear stress | MPa | ||
| Residual shear stress | MPa | ||
| Slip at | mm | ||
| Slip at | mm | ||
| Slip at | mm | ||
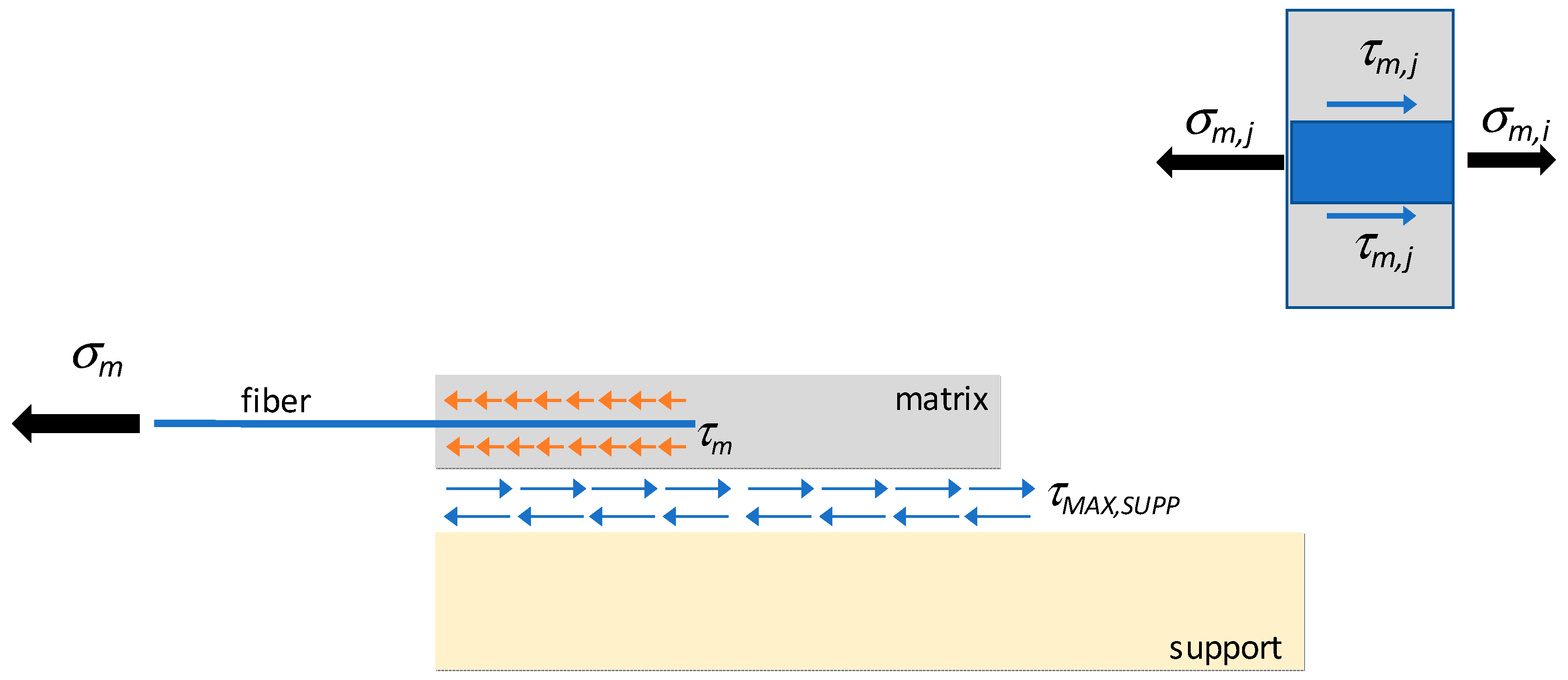
| M-support interface | Maximum shear stress | MPa |
| N | Tensile force along the FRCM | N |
| N0 | Tensile force in the FRCM at x0 | N |
| Δx | FRCM step discretization, hence distance between 2 control sections | mm |
| sn,TARGET | Slip target at the end of the FRCM, at xn | mm |
| xi | Current control section | - |
| xj | xi + Δx | - |
| uf | Fiber axial displacement | mm |
| um | Matrix axial displacement | mm |
| s | Slip between fiber and matrix | mm |
| x | Reference axis | - |
| sm,i−j | Average slip between fiber and matrix at xi and at xj | mm |
| τ(sm,i−j) | Average shear stress between fiber and matrix at xi and at xj | N/mm2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bilotta, A.; Lignola, G.P. Effects of Defects on Bond Behavior of Fiber Reinforced Cementitious Matrix Materials. Materials 2020, 13, 164. https://doi.org/10.3390/ma13010164
Bilotta A, Lignola GP. Effects of Defects on Bond Behavior of Fiber Reinforced Cementitious Matrix Materials. Materials. 2020; 13(1):164. https://doi.org/10.3390/ma13010164
Chicago/Turabian StyleBilotta, Antonio, and Gian Piero Lignola. 2020. "Effects of Defects on Bond Behavior of Fiber Reinforced Cementitious Matrix Materials" Materials 13, no. 1: 164. https://doi.org/10.3390/ma13010164
APA StyleBilotta, A., & Lignola, G. P. (2020). Effects of Defects on Bond Behavior of Fiber Reinforced Cementitious Matrix Materials. Materials, 13(1), 164. https://doi.org/10.3390/ma13010164






