Development of an Analytical Model for Optimization of Direct Laser Interference Patterning
Abstract
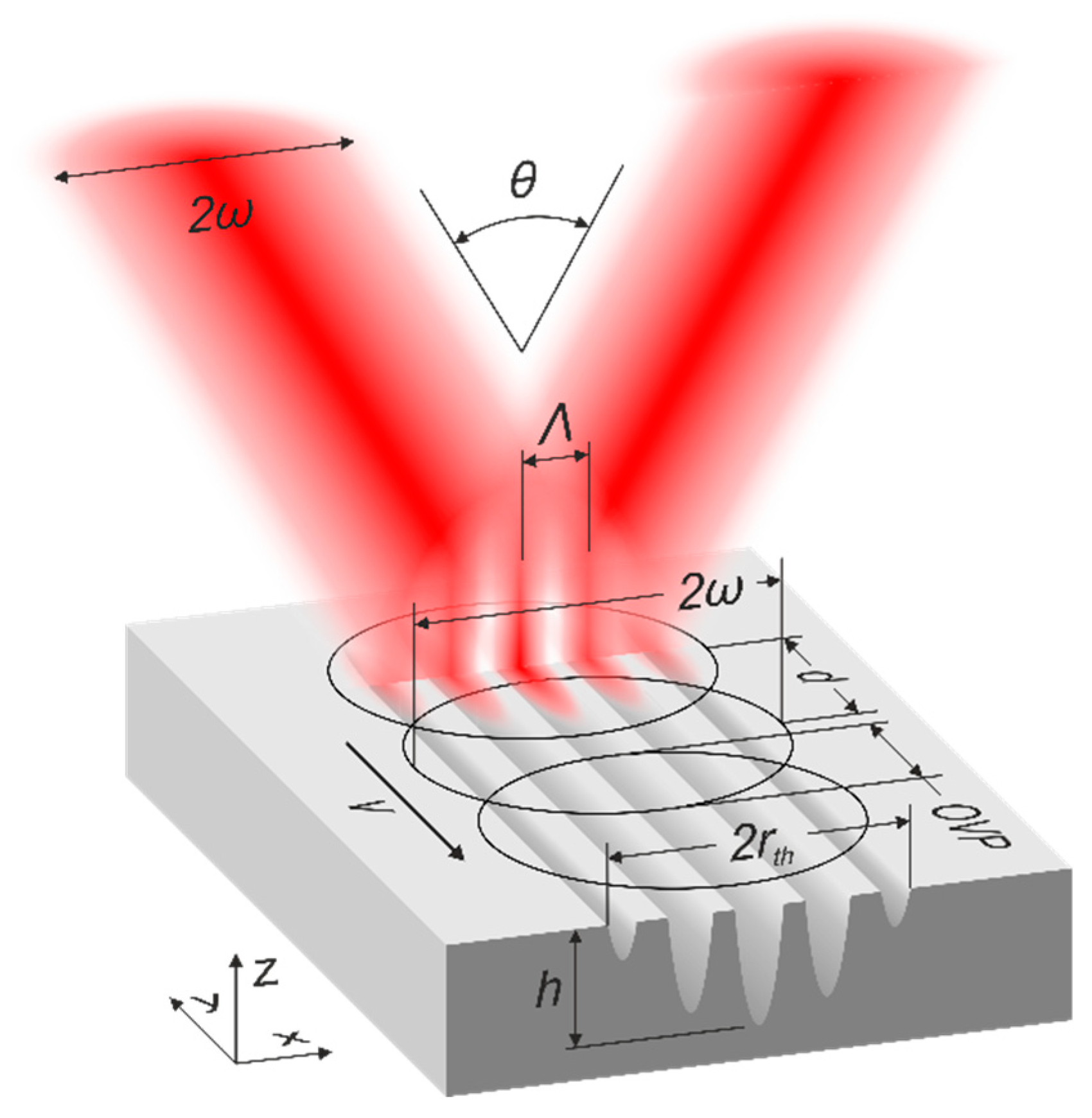
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Experimental Setup
2.3. Surface Characterization
3. Results and Discussion
3.1. Development of an Analytical Ablation Model for DLIP
3.2. Validation of the Simulation Model
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lasagni, A.; Alamri, S.; Aguilar-Morales, A.; Rößler, F.; Voisiat, B.; Kunze, T. Biomimetic Surface Structuring Using Laser Based Interferometric Methods. Appl. Sci. 2018, 8, 1260. [Google Scholar] [CrossRef] [Green Version]
- Nakata, Y. Interference laser processing. Adv. Opt. Technol. 2016, 5, 29–38. [Google Scholar] [CrossRef]
- Bae, W.G.; Kim, H.N.; Kim, D.; Park, S.H.; Jeong, H.E.; Suh, K.Y. In 25th anniversary article: Scalable multiscale patterned structures inspired by nature: The role of hierarchy. Adv. Mater. 2014, 26, 675–699. [Google Scholar] [CrossRef]
- Liu, M.; Wang, S.; Jiang, L. Nature-inspired superwettability systems. Nat. Rev. Mater. 2017, 2, 17036. [Google Scholar] [CrossRef]
- Abdel-Aal, H.A. Functional surfaces for tribological applications: Inspiration and design. Surf. Topogr. Metrol. Prop. 2016, 4. [Google Scholar] [CrossRef]
- Valle, J.; Burgui, S.; Langheinrich, D.; Gil, C.; Solano, C.; Toledo-Arana, A.; Helbig, R.; Lasagni, A.; Lasa, I. Evaluation of Surface Microtopography Engineered by Direct Laser Interference for Bacterial Anti-Biofouling. Macromol. Biosci. 2015, 15, 1060–1069. [Google Scholar] [CrossRef] [Green Version]
- Milles, S.; Voisiat, B.; Nitschke, M.; Lasagni, A.F. Influence of roughness achieved by periodic structures on the wettability of aluminum using direct laser writing and direct laser interference patterning technology. J. Mater. Process. Technol. 2019, 270, 142–151. [Google Scholar] [CrossRef]
- Rosenkranz, A.; Hans, M.; Gachot, C.; Thome, A.; Bonk, S.; Mücklich, F. Direct Laser Interference Patterning: Tailoring of Contact Area for Frictional and Antibacterial Properties. Lubricants 2016, 4, 2. [Google Scholar] [CrossRef] [Green Version]
- Voisiat, B.; Wang, W.; Holzhey, M.; Lasagni, A.F. Improving the homogeneity of diffraction based colours by fabricating periodic patterns with gradient spatial period using Direct Laser Interference Patterning. Sci. Rep. 2019, 9, 7801. [Google Scholar] [CrossRef] [Green Version]
- Tamulevičius, T.; Juodėnas, M.; Klinavičius, T.; Paulauskas, A.; Jankauskas, K.; Ostreika, A.; Žutautas, A.; Tamulevičius, S. Dot-Matrix Hologram Rendering Algorithm and its Validation through Direct Laser Interference Patterning. Sci. Rep. 2018, 8, 14245. [Google Scholar] [CrossRef] [Green Version]
- Park, I.-Y.; Ahn, S.; Kim, Y.; Bae, H.-S.; Kang, H.-S.; Yoo, J.; Noh, J. Serial number coding and decoding by laser interference direct patterning on the original product surface for anti-counterfeiting. Opt. Express 2017, 25, 14644. [Google Scholar] [CrossRef] [PubMed]
- Neuenschwander, B.; Jaeggi, B.; Schmid, M.; Hennig, G. Surface structuring with ultra-short laser pulses: Basics, limitations and needs for high throughput. Phys. Procedia 2014, 56, 1047–1058. [Google Scholar] [CrossRef] [Green Version]
- Lang, V.; Roch, T.; Lasagni, A.F. High-Speed Surface Structuring of Polycarbonate Using Direct Laser Interference Patterning: Toward 1 m 2 min −1 Fabrication Speed Barrier. Adv. Eng. Mater. 2016, 18, 1342–1348. [Google Scholar] [CrossRef]
- Lang, V.; Roch, T.; Lasagni, A.F. World record in high speed laser surface microstructuring of polymer and steel using direct laser interference patterning. In Proceedings of the International Society for Optical Engineering, San Francisco, CA, USA, 13–18 February 2016; Volume 9736, p. 97360Z-9736-8. [Google Scholar]
- Aguilar-Morales, A.I.; Alamri, S.; Lasagni, A.F. Micro-fabrication of high aspect ratio periodic structures on stainless steel by picosecond direct laser interference patterning. J. Mater. Process. Technol. 2018, 252, 313–321. [Google Scholar] [CrossRef]
- He, C.; Steger, M.; Gillner, A. High-efficiency nanostructuring using multi-beam interference by consecutively deposited ultrashort laser pulses on tool steel. J. Laser Micro Nanoeng. 2018, 13, 1–5. [Google Scholar]
- D’Alessandria, M.; Lasagni, A.; Mücklich, F. Direct micro-patterning of aluminum substrates via laser interference metallurgy. Appl. Surf. Sci. 2008, 255, 3210–3216. [Google Scholar] [CrossRef]
- Aguilar-Morales, A.I.; Alamri, S.; Kunze, T.; Lasagni, A.F. Influence of processing parameters on surface texture homogeneity using Direct Laser Interference Patterning. Opt. Laser Technol. 2018, 107, 216–227. [Google Scholar] [CrossRef]
- Bieda, M.; Siebold, M.; Lasagni, A.F. Fabrication of sub-micron surface structures on copper, stainless steel and titanium using picosecond laser interference patterning. Appl. Surf. Sci. 2016, 387, 175–182. [Google Scholar] [CrossRef]
- Liu, J.M. Simple technique for measurements of pulsed Gaussian-beam spot sizes. Opt. Lett. 1982, 7, 196. [Google Scholar] [CrossRef]
- Chichkov, B.N.; Momma, C.; Nolte, S.; von Alvensleben, F.; Tünnermann, A. Femtosecond, picosecond and nanosecond laser ablation of solids. Appl. Phys. A Mater. Sci. Process. 1996, 63, 109–115. [Google Scholar] [CrossRef]
- Hecht, E. Optics; Addison-Wesley: San Francisco, CA, USA, 2002; ISBN 9780805385663. [Google Scholar]
- Jee, Y.; Becker, M.F.; Walser, R.M. Laser-induced damage on single-crystal metal surfaces. J. Opt. Soc. Am. B 2008, 5, 648. [Google Scholar] [CrossRef]
- Weber, R.; Graf, T.; Berger, P.; Onuseit, V.; Wiedenmann, M.; Freitag, C.; Feuer, A. Heat accumulation during pulsed laser materials processing. Opt. Express 2014, 22, 11312. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Voisiat, B.; Rank, A.; Lasagni, A.F. One step fabrication of asymmetric saw-tooth-like surface structures using direct laser interference patterning. Mater. Lett. 2019, 245, 183–187. [Google Scholar] [CrossRef]
- Jaeggi, B.; Neuenschwander, B.; Zimmermann, M.; De Loor, R.; Penning, L. High throughput ps-laser micro machining with a synchronized polygon line scanner. In Proceedings of the 8th International Conference on Photonic Technologies LANE 2014, Furth, German, 8–11 September 2014; pp. 1–8. [Google Scholar]






© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Voisiat, B.; Aguilar-Morales, A.I.; Kunze, T.; Lasagni, A.F. Development of an Analytical Model for Optimization of Direct Laser Interference Patterning. Materials 2020, 13, 200. https://doi.org/10.3390/ma13010200
Voisiat B, Aguilar-Morales AI, Kunze T, Lasagni AF. Development of an Analytical Model for Optimization of Direct Laser Interference Patterning. Materials. 2020; 13(1):200. https://doi.org/10.3390/ma13010200
Chicago/Turabian StyleVoisiat, Bogdan, Alfredo I. Aguilar-Morales, Tim Kunze, and Andrés Fabián Lasagni. 2020. "Development of an Analytical Model for Optimization of Direct Laser Interference Patterning" Materials 13, no. 1: 200. https://doi.org/10.3390/ma13010200
APA StyleVoisiat, B., Aguilar-Morales, A. I., Kunze, T., & Lasagni, A. F. (2020). Development of an Analytical Model for Optimization of Direct Laser Interference Patterning. Materials, 13(1), 200. https://doi.org/10.3390/ma13010200






