Numerical Modeling for Simulation of Compaction of Refractory Materials for Secondary Steelmaking
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Procedure
2.2. DEM Simulations
2.3. Methodology
3. Results and Discussion
3.1. Preliminary Analysis
3.2. Calibration of the DEM Models
3.3. DEM Model Validation
4. Conclusions
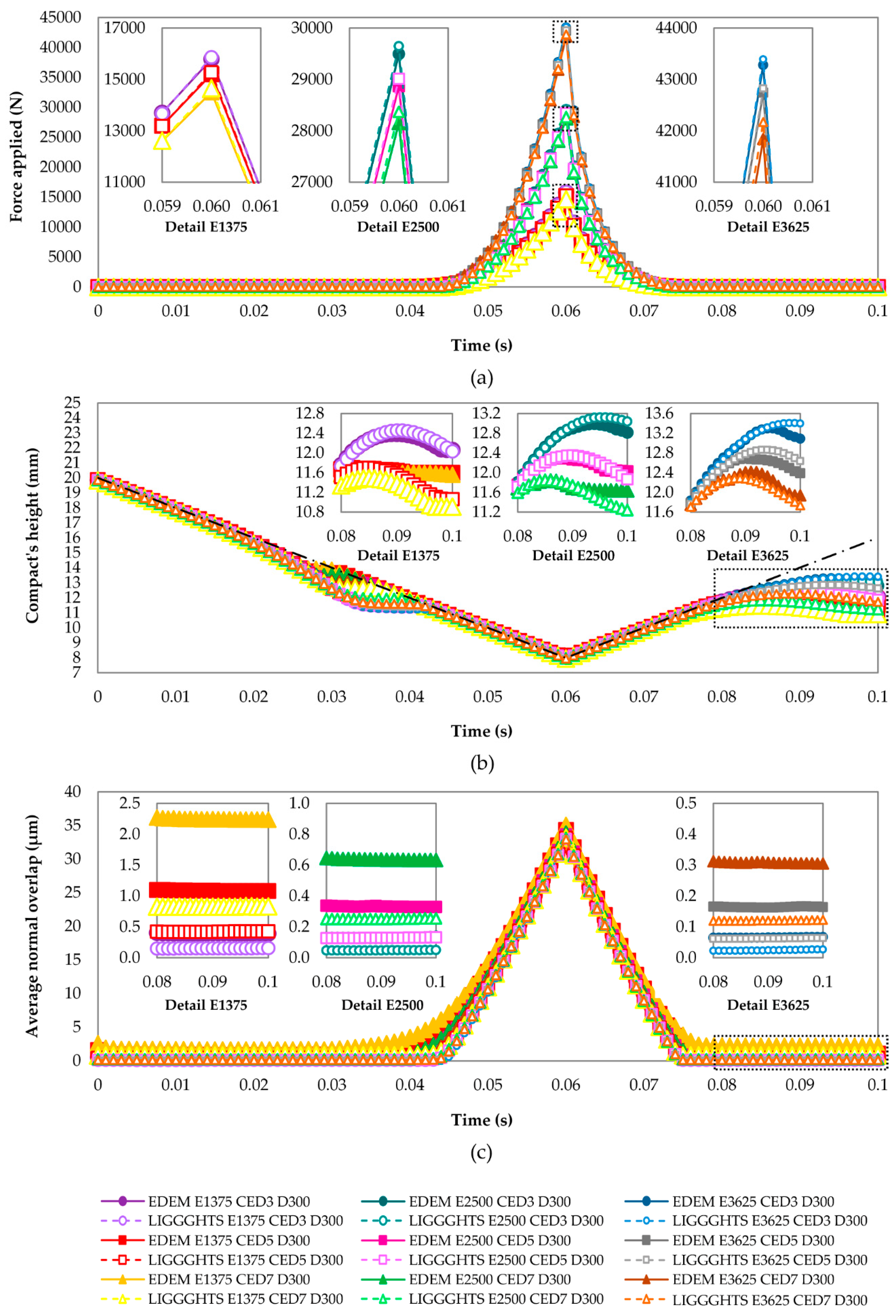
- The maximum force was mainly influenced by Young’s modulus. It increased significantly as Young’s modulus increased and decreased slightly as CED increased. The maximum force was also affected by the diameter of the Al2O3 particles, especially in EDEM.
- The porosity of the compacts increased with Young’s modulus and decreased with CED. The effect of both factors on the porosity was similar. Additionally, the porosity increased as the particle size of Al2O3 was larger. The effect of the diameter was also more remarkable in EDEM.
- SQC got better as CED increased, but it worsened with the increment of Young’s modulus. The effect of the particle size on SQC was negligible.
- The values of the maximum force and porosity of the compact were very similar in both software packages. On the contrary, there was not an equivalence between the values assigned to SQC in EDEM and LIGGGHTS. However, the trend in both software packages was the same.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gupta, N.; Basu, B. Hot pressing and spark plasma sintering techniques of intermetallic matrix composites. In Intermetallic Matrix Composites; Mitra, R., Ed.; Elsevier Woodhead Publishing: Amsterdam, The Netherlands, 2018; pp. 243–302. ISBN 9780857093462. [Google Scholar]
- Braulio, M.A.L.; Bittencourt, L.R.M.; Pandolfelli, V.C. Magnesia grain size effect on in situ spinel refractory castables. J. Eur. Ceram. Soc. 2008, 28, 2845–2852. [Google Scholar] [CrossRef]
- Ye, X.; Li, Y.; Ai, Y.; Nie, Y. Novel powder packing theory with bimodal particle size distribution-application in superalloy. Adv. Powder Technol. 2018. [Google Scholar] [CrossRef]
- Qian, Q.; An, X.; Zhao, H.; Dong, K.; Yang, X. Numerical investigations on random close packings of cylindrical particles with different aspect ratios. Powder Technol. 2018. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, N.; Zhou, X.; Zhang, L. Particle shape effects on fabric of granular random packing. Powder Technol. 2017. [Google Scholar] [CrossRef]
- Wang, H.; Glaser, B.; Sichen, D. Improvement of Resistance of MgO-Based Refractory to Slag Penetration by In Situ Spinel Formation. Metall. Mater. Trans. B Process Metall. Mater. Process. Sci. 2015, 46, 749–757. [Google Scholar] [CrossRef] [Green Version]
- Braulio, M.A.L.; Martinez, A.G.T.; Luz, A.P.; Liebske, C.; Pandolfelli, V.C. Basic slag attack of spinel-containing refractory castables. Ceram. Int. 2011. [Google Scholar] [CrossRef]
- Tomba Martinez, A.G.; Luz, A.P.; Braulio, M.A.L.; Pandolfelli, V.C. Ceramics International Al2O3 -based binders for corrosion resistance optimization of Al2O3 –MgAl2O4 and Al2O3 –MgO refractory castables. Ceram. Int. 2015, 41, 9947–9956. [Google Scholar] [CrossRef]
- Weerasekara, N.S.; Powell, M.S.; Cleary, P.W.; Tavares, L.M.; Evertsson, M.; Morrison, R.D.; Quist, J.; Carvalho, R.M. The contribution of DEM to the science of comminution. Powder Technol. 2013, 248, 3–24. [Google Scholar] [CrossRef]
- Metzger, M.J.; Glasser, B.J. Simulation of the breakage of bonded agglomerates in a ball mill. Powder Technol. 2013, 237, 286–302. [Google Scholar] [CrossRef]
- Ghodki, B.M.; Charith Kumar, K.; Goswami, T.K. Modeling breakage and motion of black pepper seeds in cryogenic mill. Adv. Powder Technol. 2018, 29, 1055–1071. [Google Scholar] [CrossRef]
- Pantaleev, S.; Yordanova, S.; Janda, A.; Marigo, M.; Ooi, J.Y. An experimentally validated DEM study of powder mixing in a paddle blade mixer. Powder Technol. 2017. [Google Scholar] [CrossRef] [Green Version]
- Sebastian Escotet-Espinoza, M.; Foster, C.J.; Ierapetritou, M. Discrete Element Modeling (DEM) for mixing of cohesive solids in rotating cylinders. Powder Technol. 2018. [Google Scholar] [CrossRef]
- Janda, A.; Ooi, J.Y. DEM modeling of cone penetration and unconfined compression in cohesive solids. Powder Technol. 2016. [Google Scholar] [CrossRef]
- Thakur, S.C.; Morrissey, J.P.; Sun, J.; Chen, J.F.; Ooi, J.Y. Micromechanical analysis of cohesive granular materials using the discrete element method with an adhesive elasto-plastic contact model. Granul. Matter 2014. [Google Scholar] [CrossRef]
- Thakur, S.C.; Ooi, J.Y.; Ahmadian, H. Scaling of discrete element model parameters for cohesionless and cohesive solid. Powder Technol. 2016. [Google Scholar] [CrossRef] [Green Version]
- Yoon, J. Application of experimental design and optimization to PFC model calibration in uniaxial compression simulation. Int. J. Rock Mech. Min. Sci. 2007. [Google Scholar] [CrossRef]
- He, Y.; Wang, Z.; Evans, T.J.; Yu, A.B.; Yang, R.Y. DEM study of the mechanical strength of iron ore compacts. Int. J. Miner. Process. 2015. [Google Scholar] [CrossRef]
- He, Y.; Evans, T.J.; Yu, A.B.; Yang, R.Y. DEM investigation of the role of friction in mechanical response of powder compact. Powder Technol. 2017. [Google Scholar] [CrossRef]
- He, Y.; Guo, F. Micromechanical analysis on the compaction of tetrahedral particles. Chem. Eng. Res. Des. 2018, 136, 610–619. [Google Scholar] [CrossRef]
- He, Y.; Evans, T.J.; Shen, Y.S.; Yu, A.B.; Yang, R.Y. Discrete modelling of the compaction of non-spherical particles using a multi-sphere approach. Miner. Eng. 2018. [Google Scholar] [CrossRef]
- Wiącek, J.; Molenda, M. Effect of particle size distribution on micro-and macromechanical response of granular packings under compression. Int. J. Solids Struct. 2014. [Google Scholar] [CrossRef] [Green Version]
- Wiacek, J.; Molenda, M.; Horabik, J.; Ooi, J.Y. Influence of grain shape and intergranular friction on material behavior in uniaxial compression: Experimental and DEM modeling. Powder Technol. 2012. [Google Scholar] [CrossRef]
- Nordström, J.; Alderborn, G.; Frenning, G. Compressibility and tablet forming ability of bimodal granule mixtures: Experiments and DEM simulations. Int. J. Pharm. 2018, 540, 120–131. [Google Scholar] [CrossRef]
- Martin, C.L.; Schneider, L.C.R.; Olmos, L.; Bouvard, D. Discrete element modeling of metallic powder sintering. Scr. Mater. 2006, 55, 425–428. [Google Scholar] [CrossRef]
- Henrich, B.; Wonisch, A.; Kraft, T.; Moseler, M.; Riedel, H. Simulations of the influence of rearrangement during sintering. Acta Mater. 2007, 55, 753–762. [Google Scholar] [CrossRef]
- Olmos, L.; Martin, C.L.; Bouvard, D. Sintering of mixtures of powders: Experiments and modelling. Powder Technol. 2009, 190, 134–140. [Google Scholar] [CrossRef]
- Martin, S.; Guessasma, M.; Léchelle, J.; Fortin, J.; Saleh, K.; Adenot, F. Simulation of sintering using a Non Smooth Discrete Element Method. Application to the study of rearrangement. Comput. Mater. Sci. 2014. [Google Scholar] [CrossRef]
- Nosewicz, S.; Rojek, J.; Pietrzak, K.; Chmielewski, M. Viscoelastic discrete element model of powder sintering. Powder Technol. 2013, 246, 157–168. [Google Scholar] [CrossRef]
- Parhami, F.; McMeeking, R.M.; Cocks, A.C.F.; Suo, Z. A model for the sintering and coarsening of rows of spherical particles. Mech. Mater. 1999, 31, 43–61. [Google Scholar] [CrossRef]
- Garner, S.; Strong, J.; Zavaliangos, A. Study of the die compaction of powders to high relative densities using the discrete element method. Powder Technol. 2018. [Google Scholar] [CrossRef]
- Jiménez-Herrera, N.; Barrios, G.K.P.; Tavares, L.M. Comparison of breakage models in DEM in simulating impact on particle beds. Adv. Powder Technol. 2018, 29, 692–706. [Google Scholar] [CrossRef]
- Markauskas, D.; Ramírez-Gómez, Á.; Kacianauskas, R.; Zdancevicius, E. Maize grain shape approaches for DEM modelling. Comput. Electron. Agric. 2015, 118, 247–258. [Google Scholar] [CrossRef]
- Wei, H.; Zhao, Y.; Zhang, J.; Saxén, H.; Yu, Y. LIGGGHTS and EDEM application on charging system of ironmaking blast furnace. Adv. Powder Technol. 2017. [Google Scholar] [CrossRef]
- Soltanbeigi, B.; Podlozhnyuk, A.; Papanicolopulos, S.A.; Kloss, C.; Pirker, S.; Ooi, J.Y. DEM study of mechanical characteristics of multi-spherical and superquadric particles at micro and macro scales. Powder Technol. 2018. [Google Scholar] [CrossRef] [Green Version]
- Ramírez-Aragón, C.; Ordieres-Meré, J.; Alba-Elías, F.; González-Marcos, A. Comparison of Cohesive Models in EDEM and LIGGGHTS for Simulating Powder Compaction. Materials 2018, 11, 2341. [Google Scholar] [CrossRef] [Green Version]
- Roessler, T.; Katterfeld, A. Scaling of the angle of repose test and its influence on the calibration of DEM parameters using upscaled particles. Powder Technol. 2018. [Google Scholar] [CrossRef]
- Thornton, C.; Antony, S.J. Quasi-static shear deformation of a soft particle system. Powder Technol. 2000. [Google Scholar] [CrossRef]
- Washino, K.; Chan, E.L.; Tanaka, T. DEM with attraction forces using reduced particle stiffness. Powder Technol. 2018. [Google Scholar] [CrossRef]
- Thakur, S.C.; Ahmadian, H.; Sun, J.; Ooi, J.Y. Scaling of discrete element model parameters in uniaxial test simulation. In Proceedings of the Sixth International Conference on Discrete Element Methods (DEM 6), Golden, CO, USA, 5–6 August 2013; pp. 457–462. [Google Scholar]
- Sako, E.Y.; Braulio, M.A.L.; Pandolfelli, V.C. How effective is the addition of nanoscaled particles to alumina–magnesia refractory castables? Ceram. Int. 2012, 38, 5157–5164. [Google Scholar] [CrossRef]
- Luz, A.P.; Tomba Martinez, A.G.; Braulio, M.A.L.; Pandolfelli, V.C. Thermodynamic evaluation of spinel containing refractory castables corrosion by secondary metallurgy slag. Ceram. Int. 2011. [Google Scholar] [CrossRef]
- German, R.M. Particulate Composites; Springer International Publishing: Cham, Switzerland, 2016; ISBN 978-3-319-29915-0. [Google Scholar]
- Kong, L.B.; Huang, Y.; Que, W.; Zhang, T.; Li, S.; Zhang, J.; Dong, Z.; Tang, D. Powder characterization and compaction. In Metallurgy and Materials Engineering; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]

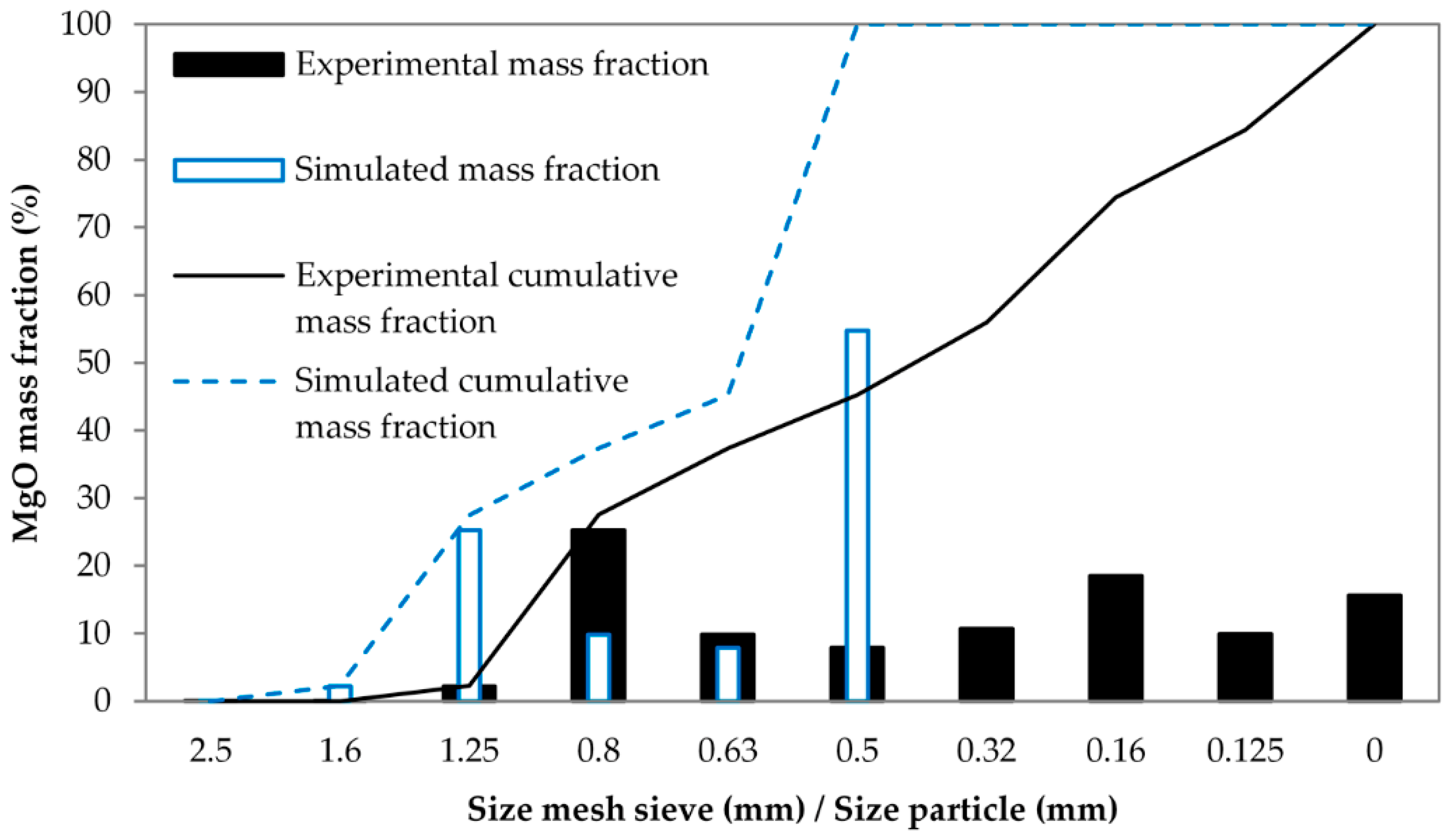




| Material Properties | |||
|---|---|---|---|
| MgO | Al2O3 | Wall | |
| Density (kg/m3) | 3500 | 3000 | 8000 |
| Young’s modulus (MPa) | 250–3625 | 250–3625 | 200–2900 |
| Poisson’s ratio | 0.25 | 0.25 | 0.29 |
| Interaction Parameters | |||
|---|---|---|---|
| Particle-Particle | Particle-Wall | Wall-Wall | |
| Coefficient of restitution | 0.5 | 0.5 | 0.5 |
| Coefficient of static friction | 0.2 | 0.2 | 0.2 |
| Coefficient of rolling friction | 0 | 0 | 0 |
| Cohesion energy density (J/m3) | 1 × 106–7 × 106 | – | – |
| Setup No. | Nomenclature | Young’s Modulus [MPa] | Cohesion Energy Density [J/m3] | Al2O3 Diameter [µm] |
|---|---|---|---|---|
| 1 | E0250 CED1 D300 | 250 | 1 × 106 | 300 |
| 2 | E0250 CED1 D500 | 250 | 1 × 106 | 500 |
| 3 | E0250 CED3 D400 | 250 | 3 × 106 | 400 |
| 4 | E0250 CED5 D300 | 250 | 5 × 106 | 300 |
| 5 | E0250 CED5 D500 | 250 | 5 × 106 | 500 |
| 6 | E1375 CED1 D400 | 1375 | 1 × 106 | 400 |
| 7 | E1375 CED3 D300 | 1375 | 3 × 106 | 300 |
| 8 | E1375 CED3 D400 | 1375 | 3 × 106 | 400 |
| 9 | E1375 CED3 D500 | 1375 | 3 × 106 | 500 |
| 10 | E1375 CED5 D400 | 1375 | 5 × 106 | 400 |
| 11 | E2500 CED1 D300 | 2500 | 1 × 106 | 300 |
| 12 | E2500 CED1 D500 | 2500 | 1 × 106 | 500 |
| 13 | E2500 CED3 D400 | 2500 | 3 × 106 | 400 |
| 14 | E2500 CED5 D300 | 2500 | 5 × 106 | 300 |
| 15 | E2500 CED5 D500 | 2500 | 5 × 106 | 500 |
| Setup No. | Nomenclature | Young’s Modulus [MPa] | Cohesion Energy Density [J/m3] | Al2O3 Diameter [µm] |
|---|---|---|---|---|
| 1 | E1375 CED3 D300 | 1375 | 3 × 106 | 300 |
| 2 | E1375 CED5 D300 | 1375 | 5 × 106 | 300 |
| 3 | E1375 CED7 D300 | 1375 | 7 × 106 | 300 |
| 4 | E2500 CED3 D300 | 2500 | 3 × 106 | 300 |
| 5 | E2500 CED5 D300 | 2500 | 5 × 106 | 300 |
| 6 | E2500 CED7 D300 | 2500 | 7 × 106 | 300 |
| 7 | E3625 CED3 D300 | 3625 | 3 × 106 | 300 |
| 8 | E3625 CED5 D300 | 3625 | 5 × 106 | 300 |
| 9 | E3625 CED7 D300 | 3625 | 7 × 106 | 300 |
| Setup No. | Nomenclature | DEM Simulator | Young’s Modulus [MPa] | Cohesion Energy Density [J/m3] | Al2O3 Diameter [µm] |
|---|---|---|---|---|---|
| 1 | E2250 CED7 D300 | EDEM | 2250 | 7 × 106 | 300 |
| 2 | E2230 CED7 D300 | LIGGGHTS | 2230 | 7 × 106 | 300 |
| 3 | E2341 CED7 D250 | EDEM | 2341 | 7 × 106 | 250 |
| 4 | E2322 CED7 D250 | LIGGGHTS | 2322 | 7 × 106 | 250 |
| 5 | E2535 CED7 D200 | EDEM | 2535 | 7 × 106 | 200 |
| 6 | E2525 CED7 D200 | LIGGGHTS | 2525 | 7 × 106 | 200 |
| 7 | E2910 CED7 D150 | EDEM | 2910 | 7 × 106 | 150 |
| 8 | E2903 CED7 D150 | LIGGGHTS | 2903 | 7 × 106 | 150 |
| EDEM | LIGGGHTS | ||||||
|---|---|---|---|---|---|---|---|
| Setup No. | Nomenclature | F [N] | P [%] | SQC [-] | F [N] | P [%] | SQC [-] |
| 1 | E0250 CED1 D300 | 2729 | 41.86 | 5 | 2750 | 38.25 | 4 |
| 2 | E0250 CED1 D500 | 2333 | 54.20 | 5 | 2919 | 41.90 | 4 |
| 3 | E0250 CED3 D400 | 2260 | 48.02 | 5 | 2250 | 35.60 | 5 |
| 4 | E0250 CED5 D300 | 1424 | 32.81 | 1 | 1457 | 29.37 | 5 |
| 5 | E0250 CED5 D500 | 1182 | 45.21 | 5 | 1628 | 31.66 | 5 |
| 6 | E1375 CED1 D400 | 17,091 | 55.29 | 2 | 17,276 | 47.95 | 2 |
| 7 | E1375 CED3 D300 | 15,787 | 41.48 | 5 | 15,865 | 41.34 | 3 |
| 8 | E1375 CED3 D400 | 16,551 | 51.24 | 5 | 16,624 | 43.47 | 3 |
| 9 | E1375 CED3 D500 | 12,475 | 55.13 | 5 | 16,858 | 44.41 | 3 |
| 10 | E1375 CED5 D400 | 15,922 | 48.94 | 5 | 15,986 | 38.24 | 5 |
| 11 | E2500 CED1 D300 | 30,093 | 47.07 | 2 | 30,297 | 47.59 | 2 |
| 12 | E2500 CED1 D500 | 23,613 | 58.17 | 2 | 31,987 | 48.94 | 2 |
| 13 | E2500 CED3 D400 | 29,909 | 54.22 | 3 | 31,053 | 47.35 | 2 |
| 14 | E2500 CED5 D300 | 28,867 | 41.32 | 5 | 29,015 | 40.51 | 4 |
| 15 | E2500 CED5 D500 | 22,453 | 54.14 | 5 | 30,807 | 43.98 | 3 |
| EDEM | LIGGGHTS | ||||||
|---|---|---|---|---|---|---|---|
| Setup no. | Nomenclature | F [N] | P [%] | SQC [-] | F [N] | P [%] | SQC [-] |
| 1 | E1375 CED3 D300 | 15,787 | 41.48 | 5 | 15,865 | 41.34 | 3 |
| 2 | E1375 CED5 D300 | 15,201 | 39.14 | 5 | 15,283 | 36.20 | 5 |
| 3 | E1375 CED7 D300 | 14,506 | 38.95 | 5 | 14,662 | 35.32 | 5 |
| 4 | E2500 CED3 D300 | 29,495 | 44.93 | 4 | 29,647 | 45.87 | 2 |
| 5 | E2500 CED5 D300 | 28,867 | 41.32 | 5 | 29,015 | 40.51 | 4 |
| 6 | E2500 CED7 D300 | 28,155 | 39.37 | 5 | 28,369 | 37.23 | 5 |
| 7 | E3625 CED3 D300 | 43,279 | 46.08 | 3 | 43,393 | 47.31 | 2 |
| 8 | E3625 CED5 D300 | 42,745 | 43.02 | 5 | 42,827 | 44.14 | 2 |
| 9 | E3625 CED7 D300 | 41,846 | 40.90 | 5 | 42,172 | 39.87 | 4 |
| Setup No. | Nomenclature | DEM Simulator | F [N] | P [%] | SQC [-] |
|---|---|---|---|---|---|
| 1 | E2250 CED7 D300 | EDEM | 25,153 | 38.90 | 5 |
| 2 | E2230 CED7 D300 | LIGGGHTS | 25,134 | 36.83 | 5 |
| 3 | E2341 CED7 D250 | EDEM | 25,089 | 37.24 | 5 |
| 4 | E2322 CED7 D250 | LIGGGHTS | 25,075 | 35.19 | 5 |
| 5 | E2535 CED7 D200 | EDEM | 24,970 | 34.37 | 5 |
| 6 | E2525 CED7 D200 | LIGGGHTS | 25,012 | 33.28 | 5 |
| 7 | E2910 CED7 D150 | EDEM | 25,159 | 31.57 | 5 |
| 8 | E2903 CED7 D150 | LIGGGHTS | 25,135 | 30.37 | 5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramírez-Aragón, C.; Ordieres-Meré, J.; Alba-Elías, F.; González-Marcos, A. Numerical Modeling for Simulation of Compaction of Refractory Materials for Secondary Steelmaking. Materials 2020, 13, 224. https://doi.org/10.3390/ma13010224
Ramírez-Aragón C, Ordieres-Meré J, Alba-Elías F, González-Marcos A. Numerical Modeling for Simulation of Compaction of Refractory Materials for Secondary Steelmaking. Materials. 2020; 13(1):224. https://doi.org/10.3390/ma13010224
Chicago/Turabian StyleRamírez-Aragón, Cristina, Joaquín Ordieres-Meré, Fernando Alba-Elías, and Ana González-Marcos. 2020. "Numerical Modeling for Simulation of Compaction of Refractory Materials for Secondary Steelmaking" Materials 13, no. 1: 224. https://doi.org/10.3390/ma13010224
APA StyleRamírez-Aragón, C., Ordieres-Meré, J., Alba-Elías, F., & González-Marcos, A. (2020). Numerical Modeling for Simulation of Compaction of Refractory Materials for Secondary Steelmaking. Materials, 13(1), 224. https://doi.org/10.3390/ma13010224







