Pressure Effects on the Magnetic Phase Diagram of the CeNMSb2 (NM: Au and Ag): A DFT Study
Abstract
1. Introduction
2. Calculation Details
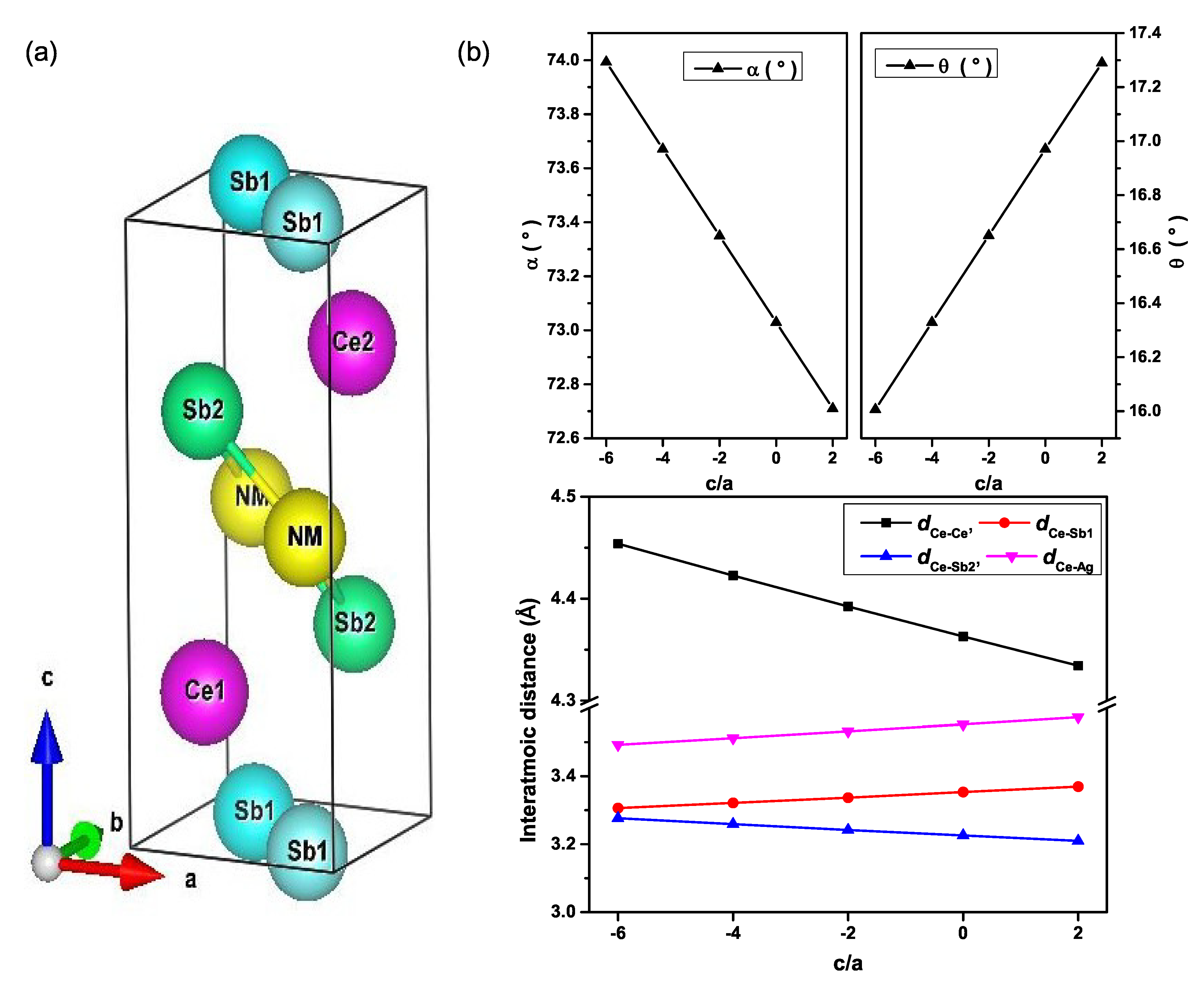
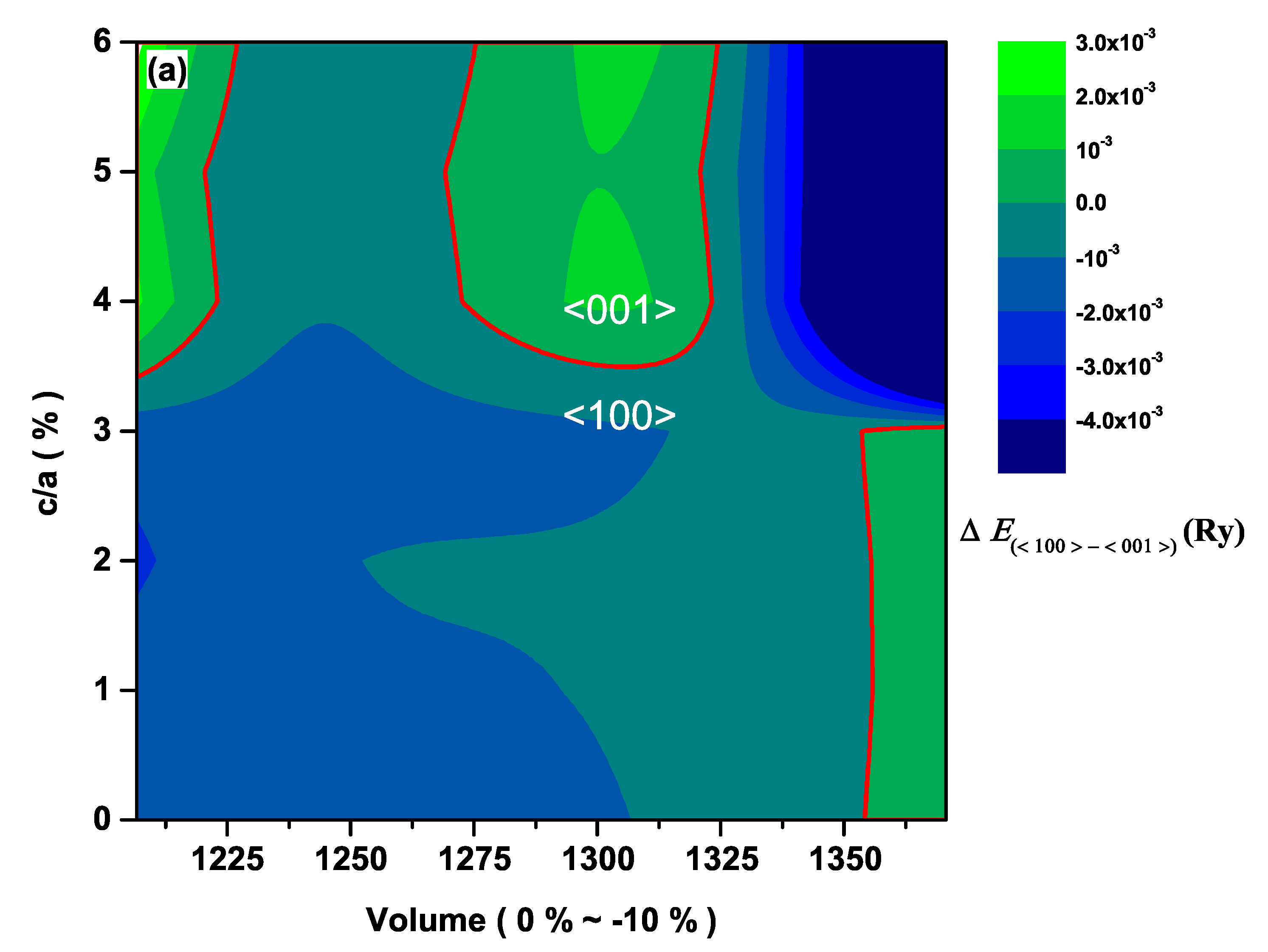
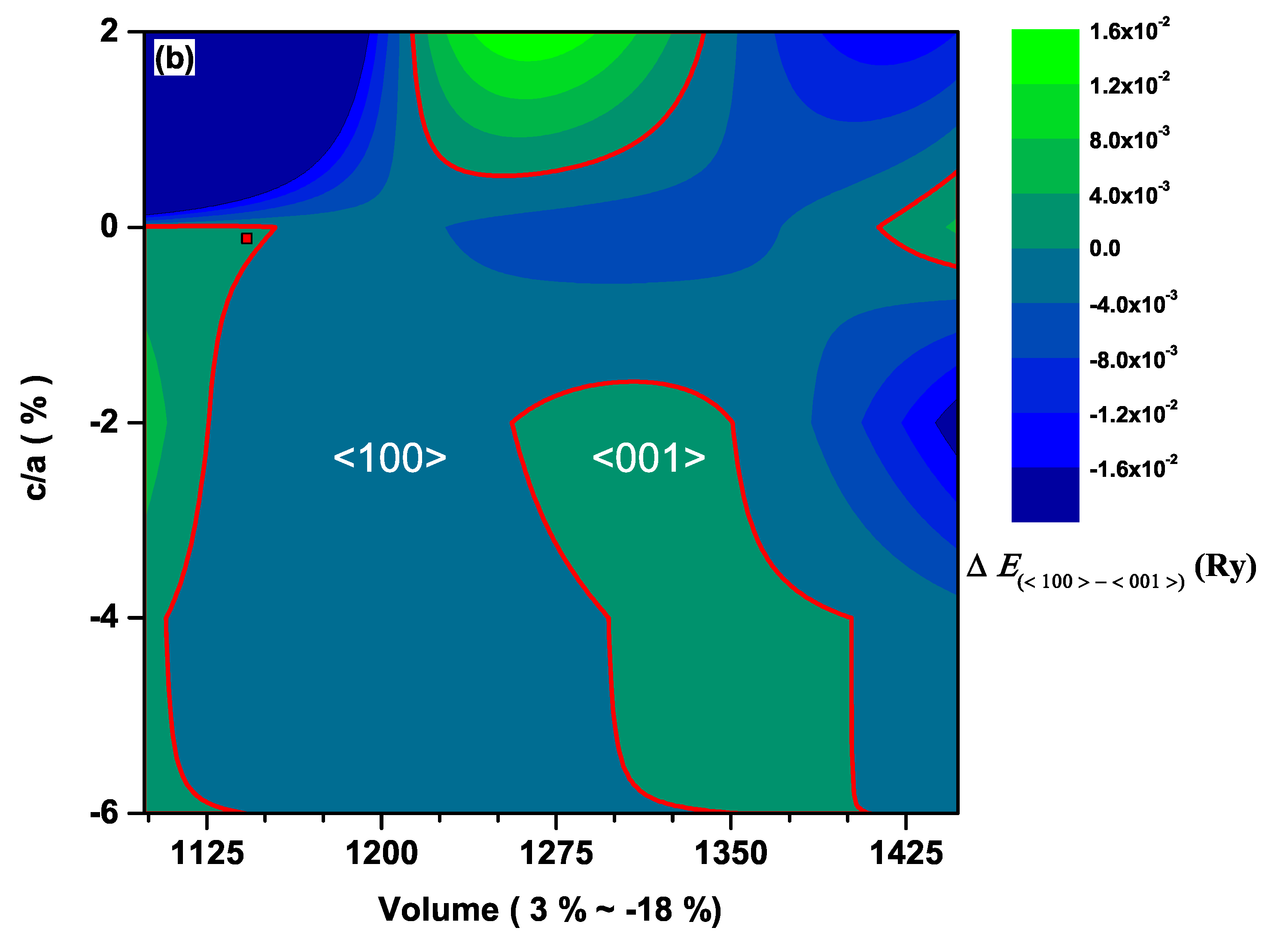
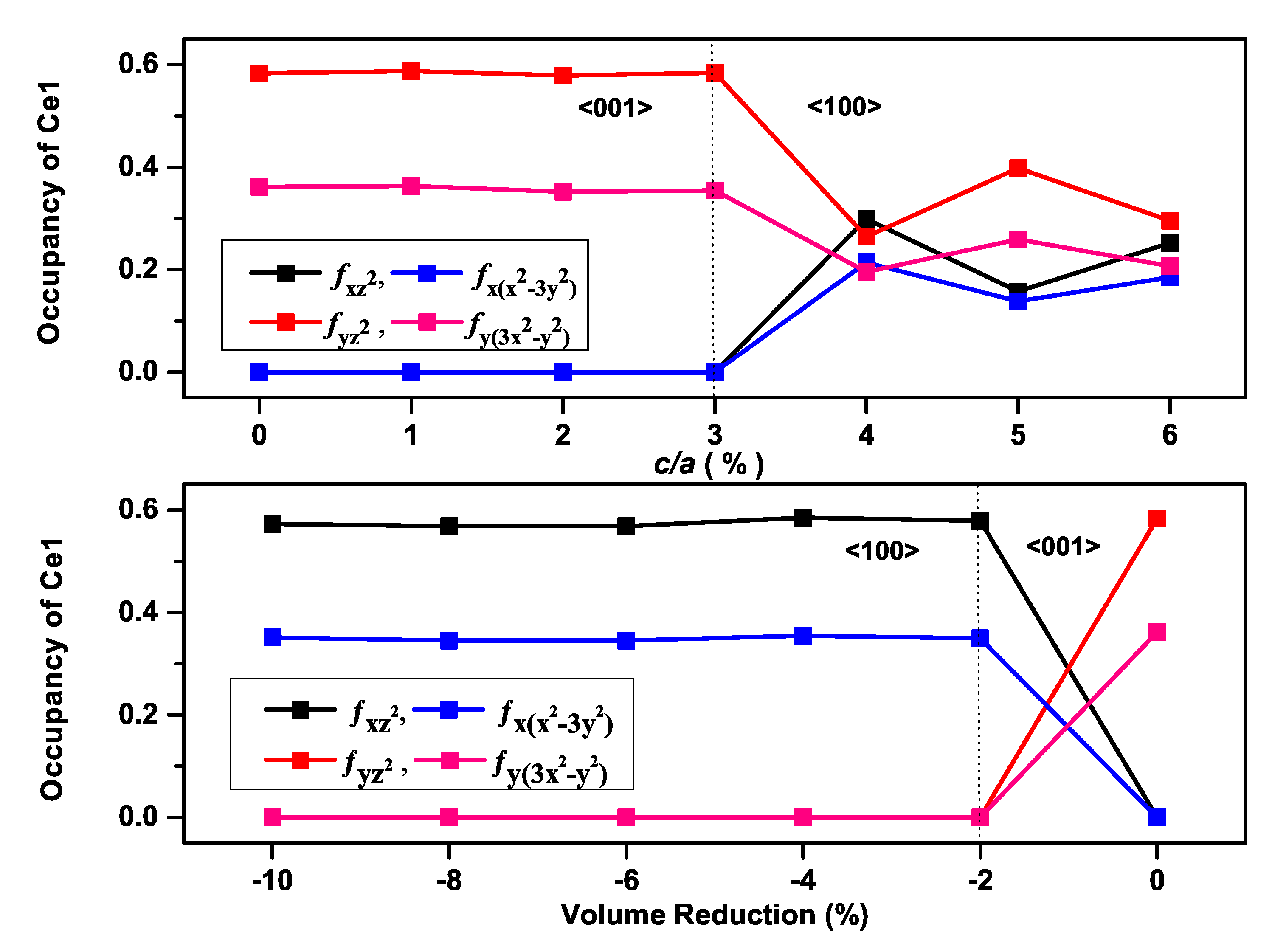
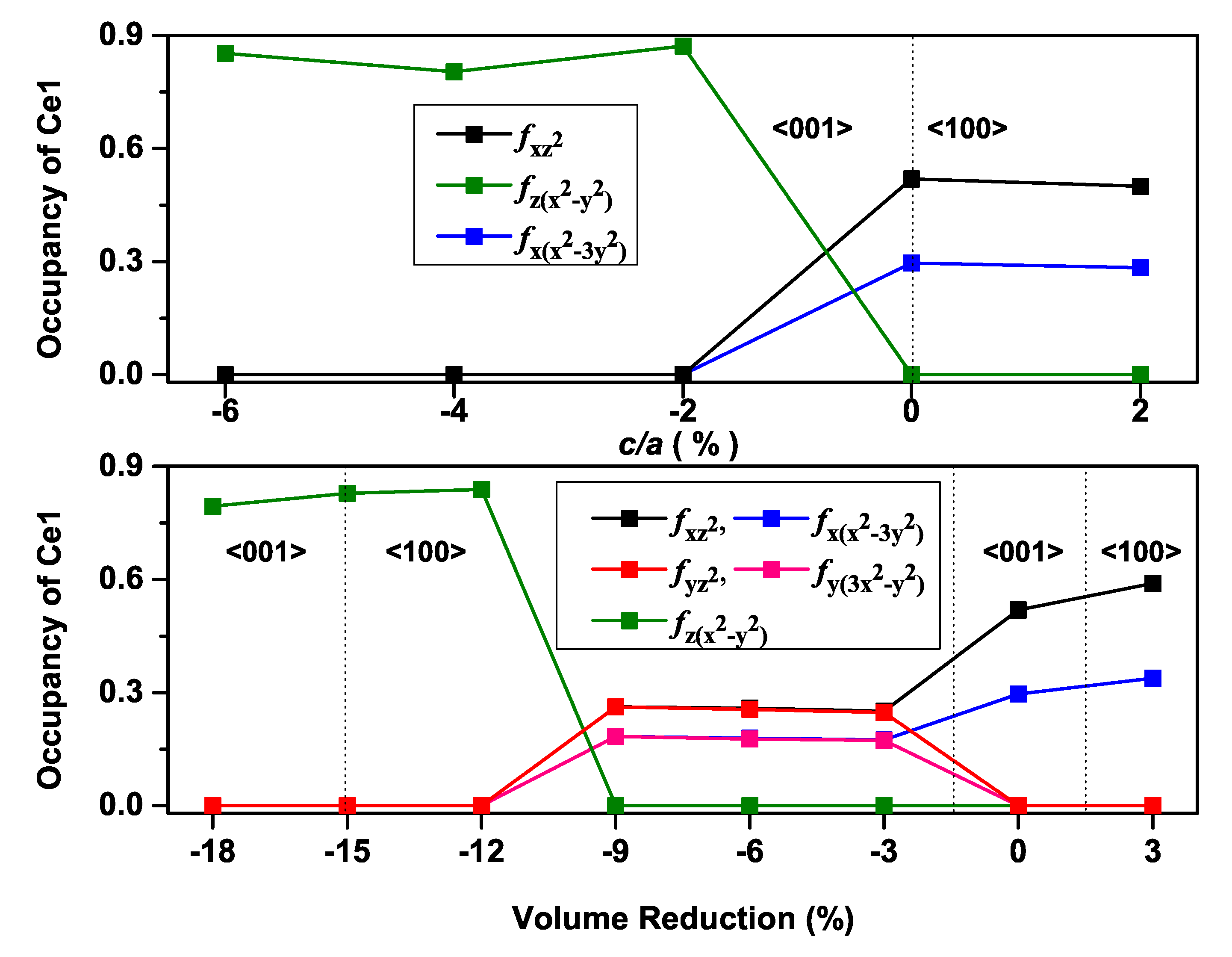
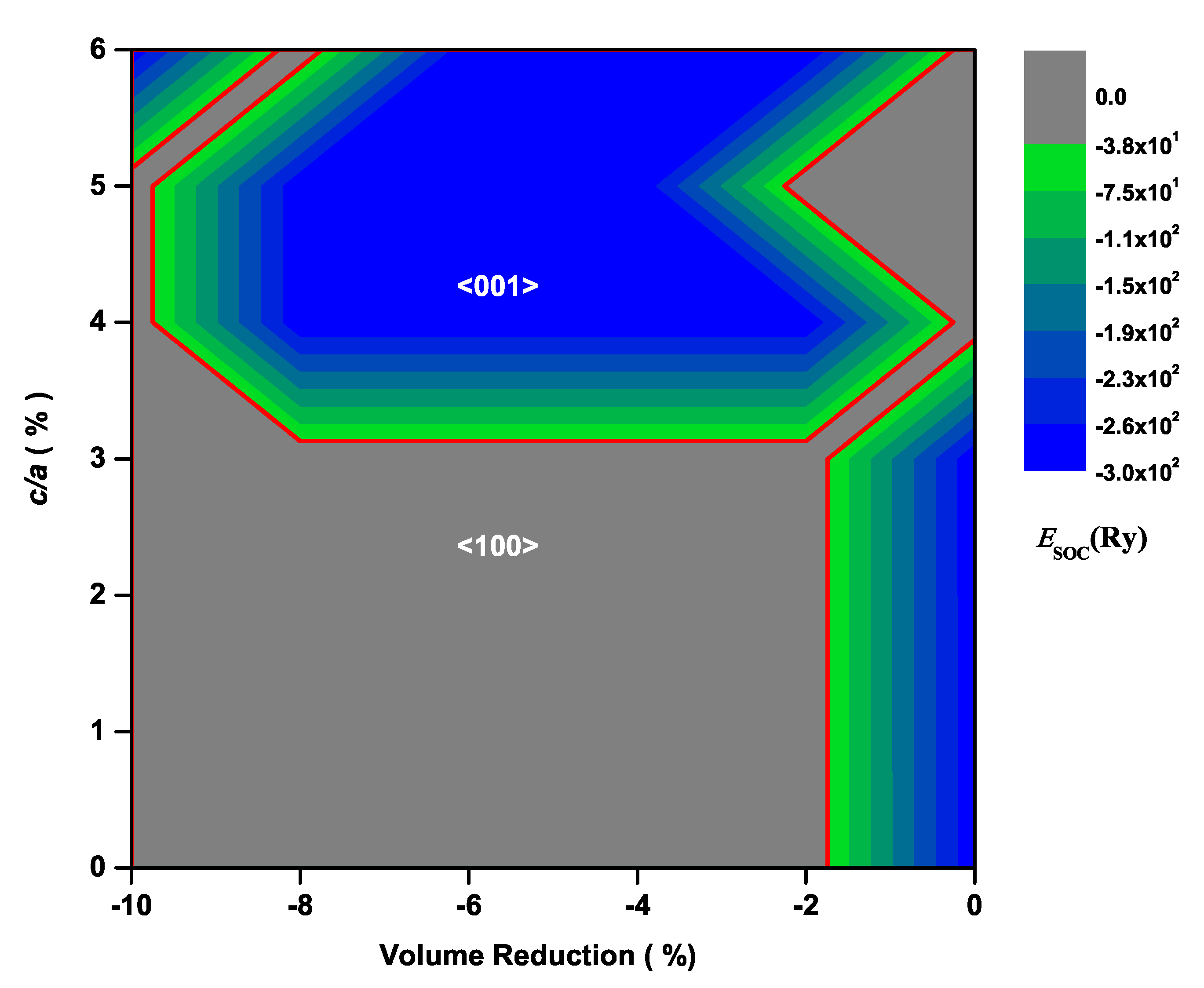
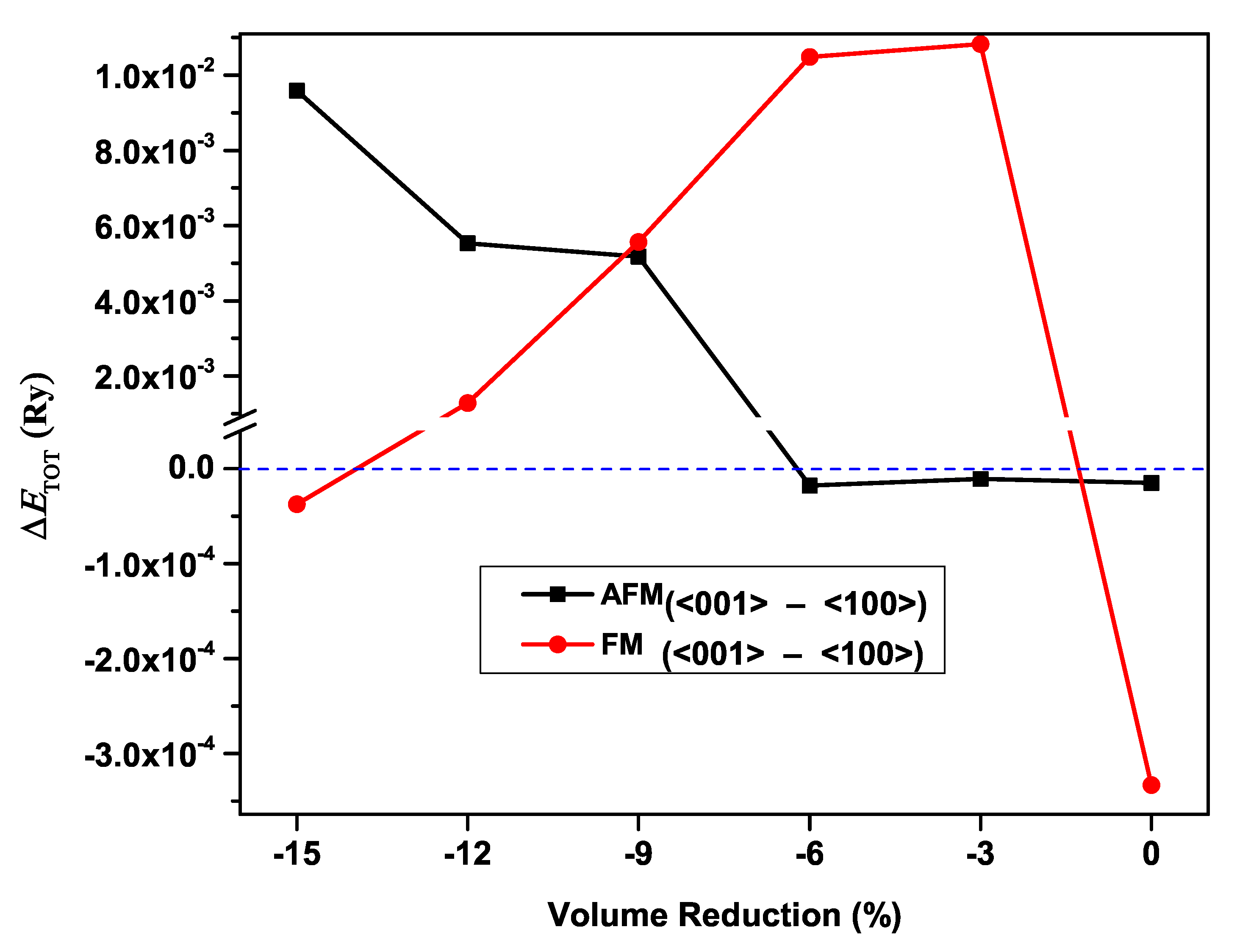
3. Results and Discussion
4. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Stewart, G.R. Heavy-fermion systems. Rev. Mod. Phys. 1984, 56, 755–787. [Google Scholar] [CrossRef]
- Hiroi, M.; Kobayashi, S.; Sera, M.; Kobayashi, N.; Kunii, S. Unusual Magnetic Phase Diagram of CexLa1-xB6 (x= 0.5, 0.75) Studied by the Magnetoresistance. J. Phys. Soc. Jpn. 1997, 66, 1762–1770. [Google Scholar] [CrossRef]
- Thompson, J.; Movshovich, R.; Fisk, Z.; Bouquet, F.; Curro, N.; Fisher, R.; Hammel, P.; Hegger, H.; Hundley, M.; Jaime, M.; et al. Superconductivity and magnetism in a new class of heavy-fermion materials. J. Magn. Magn. Mater. 2001, 226–230, 5–10. [Google Scholar] [CrossRef]
- Fisk, Z.; Hess, D.; Pethick, C.; Pines, D.; Smith, J.; Thompson, J.; Willis, J. Heavy-electron metals: New highly correlated states of matter. Science 1988, 239, 33–42. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Coleman, P. Dimensions are critical. Nat. Mater. 2012, 11, 185–187. [Google Scholar] [CrossRef] [PubMed]
- Stewart, G.R. Non-Fermi-liquid behavior in d- and f-electron metals. Rev. Mod. Phys. 2001, 73, 797–855. [Google Scholar] [CrossRef]
- Bianchi, A.; Movshovich, R.; Vekhter, I.; Pagliuso, P.G.; Sarrao, J.L. Avoided Antiferromagnetic Order and Quantum Critical Point in CeCoIn5. Phys. Rev. Lett. 2003, 91, 257001. [Google Scholar] [CrossRef]
- Seo, S.; Sidorov, V.A.; Lee, H.; Jang, D.; Fisk, Z.; Thompson, J.D.; Park, T. Pressure effects on the heavy-fermion antiferromagnet CeAuSb2. Phys. Rev. B 2012, 85, 205145. [Google Scholar] [CrossRef]
- Sidorov, V.A.; Bauer, E.D.; Frederick, N.A.; Jeffries, J.R.; Nakatsuji, S.; Moreno, N.O.; Thompson, J.D.; Maple, M.B.; Fisk, Z. Magnetic phase diagram of the ferromagnetic Kondo-lattice compound CeAgSb2 up to 80 kbar. Phys. Rev. B 2003, 67, 224419. [Google Scholar] [CrossRef]
- Tayama, T.; Sakakibara, T.; Tenya, K.; Amitsuka, H.; Kunii, S. Magnetic Phase Diagram of CexLa1-xB6 Studied by Static Magnetization Measurement at Very Low Temperatures. J. Phys. Soc. Jpn. 1997, 66, 2268–2271. [Google Scholar] [CrossRef]
- Present, P.; Si, Q.; Steglich, F. Quantum criticality in heavy-fermion metals. Nat. Phys. 2008, 4, 186–197. [Google Scholar]
- Löhneysen, H.V.; Rosch, A.; Vojta, M.; Wölfle, P. Fermi-liquid instabilities at magnetic quantum phase transitions. Rev. Mod. Phys. 2007, 79, 1015–1075. [Google Scholar] [CrossRef]
- Bogenberger, B.; Löhneysen, H.V. Tuning of Non-Fermi-Liquid Behavior with Pressure. Phys. Rev. Lett. 1995, 74, 1016–1019. [Google Scholar] [CrossRef] [PubMed]
- Grosche, F.; Julian, S.; Mathur, N.; Lonzarich, G. Magnetic and superconducting phases of CePd2Si2. Physica B Condens. Matter 1996, 223, 50–52. [Google Scholar] [CrossRef]
- Doniach, S. The Kondo lattice and weak antiferromagnetism. Phys. B+C 1977, 91, 231–234. [Google Scholar] [CrossRef]
- Hoshino, S.; Kuramoto, Y. Itinerant Versus Localized Heavy-Electron Magnetism. Phys. Rev. Lett. 2013, 111, 026401. [Google Scholar] [CrossRef]
- Fisk, Z.; Ott, H.; Rice, T.; Smith, J. Heavy-electron metals. Nature 1986, 320, 124–129. [Google Scholar] [CrossRef]
- Park, T.; Tokiwa, Y.; Ronning, F.; Lee, H.; Bauer, E.D.; Movshovich, R.; Thompson, J.D. Field-induced quantum critical point in the pressure-induced superconductor CeRhIn5. Phys. Status Solidi B 2010, 247, 553–556. [Google Scholar] [CrossRef]
- Seo, S.; Wang, X.; Thomas, S.M.; Rahn, M.C.; Carmo, D.; Ronning, F.; Bauer, E.D.; dos Reis, R.D.; Janoschek, M.; Thompson, J.D.; et al. Nematic State in CeAuSb2. Phys. Rev. X 2020, 10, 011035. [Google Scholar] [CrossRef]
- Logg, P.; Feng, Z.; Ebihara, T.; Zou, Y.; Friedemann, S.; Alireza, P.; Goh, S.; Grosche, F.M. Pressure and field tuning in the Kondo lattice ferromagnet CeAgSb2. Phys. Status Solidi B 2013, 250, 515–518. [Google Scholar] [CrossRef]
- Thamizhavel, A.; Takeuchi, T.; Okubo, T.; Yamada, M.; Asai, R.; Kirita, S.; Galatanu, A.; Yamamoto, E.; Ebihara, T.; Inada, Y.; et al. Anisotropic electrical and magnetic properties of CeTSb2 (T = Cu, Au, and Ni) single crystals. Phys. Rev. B 2003, 68, 054427. [Google Scholar] [CrossRef]
- Balicas, L.; Nakatsuji, S.; Lee, H.; Schlottmann, P.; Murphy, T.P.; Fisk, Z. Magnetic field-tuned quantum critical point in CeAuSb2. Phys. Rev. B 2005, 72, 064422. [Google Scholar] [CrossRef]
- Muro, Y.; Takeda, N.; Ishikawa, M. Magnetic and transport properties of dense Kondo systems, CeTSb2 (T= Ni, Cu, Pd and Ag). J. Alloys Compd. 1997, 257, 23–29. [Google Scholar] [CrossRef]
- Thamizhavel, A.; Okubo, T.; Yamada, M.; Galatanu, A.; Yamamoto, E.; Inada, Y.; Ebihara, T.; Ōnuki, Y. Electrical and magnetic properties of the cerium–transition metal intermetallics CeTSb2 (T: Cu, Au, Ni). Phys. B 2003, 327, 374–377. [Google Scholar] [CrossRef]
- Jang, J.K.; Rhee, J.Y. Peculiar role of f-orbital occupancy in heavy-fermion antiferromagnetic CeNMSb2 (NM: Cu and Au) compounds. Curr. Appl. Phys. 2016, 16, 475–480. [Google Scholar] [CrossRef]
- Jang, J.; Alsardia, M.; Rhee, J.Y. Magnetic ground state of ferromagnetic CeAgSb2. J. Magn. Magn. Mater. 2019, 477, 283–286. [Google Scholar] [CrossRef]
- Araki, S.; Metoki, N.; Galatanu, A.; Yamamoto, E.; Thamizhavel, A.; Ōnuki, Y. Crystal structure, magnetic ordering, and magnetic excitation in the 4f-localized ferromagnet CeAgSb2. Phys. Rev. B 2003, 68, 024408. [Google Scholar] [CrossRef]
- Brylak, M.; Möller, M.H.; Jeitschko, W. Ternary arsenides ACuAs2 and ternary antimonides AAgSb2 (A= rare-earth elements and uranium) with HfCuSi2-type structure. J. Solid State Chem. 1995, 115, 305–308. [Google Scholar] [CrossRef]
- Myers, K.; Bud’ko, S.; Fisher, I.; Islam, Z.; Kleinke, H.; Lacerda, A.; Canfield, P. Systematic study of anisotropic transport and magnetic properties of RAgSb2 (R= Y, La–Nd, Sm, Gd–Tm). J. Magn. Magn. Mater. 1999, 205, 27–52. [Google Scholar] [CrossRef]
- Adriano, C.; Rosa, P.F.S.; Jesus, C.B.R.; Mardegan, J.R.L.; Garitezi, T.M.; Grant, T.; Fisk, Z.; Garcia, D.J.; Reyes, A.P.; Kuhns, P.L.; et al. Physical properties and magnetic structure of the intermetallic CeCuBi2 compound. Phys. Rev. B 2014, 90, 235120. [Google Scholar] [CrossRef]
- Thomas, S.M.; Rosa, P.F.S.; Lee, S.B.; Parameswaran, S.A.; Fisk, Z.; Xia, J. Hall effect anomaly and low-temperature metamagnetism in the Kondo compound CeAgBi2. Phys. Rev. B 2016, 93, 075149. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Madsen, G.K.; Kvasnicka, D.; Luitz, J. WIEN2k, An Augmented Plane Wave + Local Orbitals Program For Calculating Crystal Properties; Karlheinz Schwarz, Techn. Universität Wien: Wien, Austria, 2001. [Google Scholar]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Anisimov, V.I.; Solovyev, I.V.; Korotin, M.A.; Czyżyk, M.T.; Sawatzky, G.A. Density-functional theory and NiO photoemission spectra. Phys. Rev. B 1993, 48, 16929–16934. [Google Scholar] [CrossRef] [PubMed]
- Sologub, O.; Hiebl, K.; Rogl, P.; Noël, H.; Bodak, O. On the crystal structure and magnetic properties of the ternary rare earth compounds RETSb2 with RE ≡ rare earth and T ≡ Ni, Pd, Cu and Au. J. Alloys Compd. 1994, 210, 153–157. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsardia, M.M.; Jang, J.; Rhee, J.Y. Pressure Effects on the Magnetic Phase Diagram of the CeNMSb2 (NM: Au and Ag): A DFT Study. Materials 2020, 13, 2237. https://doi.org/10.3390/ma13102237
Alsardia MM, Jang J, Rhee JY. Pressure Effects on the Magnetic Phase Diagram of the CeNMSb2 (NM: Au and Ag): A DFT Study. Materials. 2020; 13(10):2237. https://doi.org/10.3390/ma13102237
Chicago/Turabian StyleAlsardia, Mowafaq Mohammad, Jaekyung Jang, and Joo Yull Rhee. 2020. "Pressure Effects on the Magnetic Phase Diagram of the CeNMSb2 (NM: Au and Ag): A DFT Study" Materials 13, no. 10: 2237. https://doi.org/10.3390/ma13102237
APA StyleAlsardia, M. M., Jang, J., & Rhee, J. Y. (2020). Pressure Effects on the Magnetic Phase Diagram of the CeNMSb2 (NM: Au and Ag): A DFT Study. Materials, 13(10), 2237. https://doi.org/10.3390/ma13102237




