Correlation of Strain Path, Texture, Twinning, and Mechanical Properties in Twinning-Induced Plasticity Steel during Wire Drawing
Abstract
1. Introduction
2. Experimental and Numerical Procedures
2.1. Experimental Procedure
2.1.1. Casting and Hot Rolling of TWIP
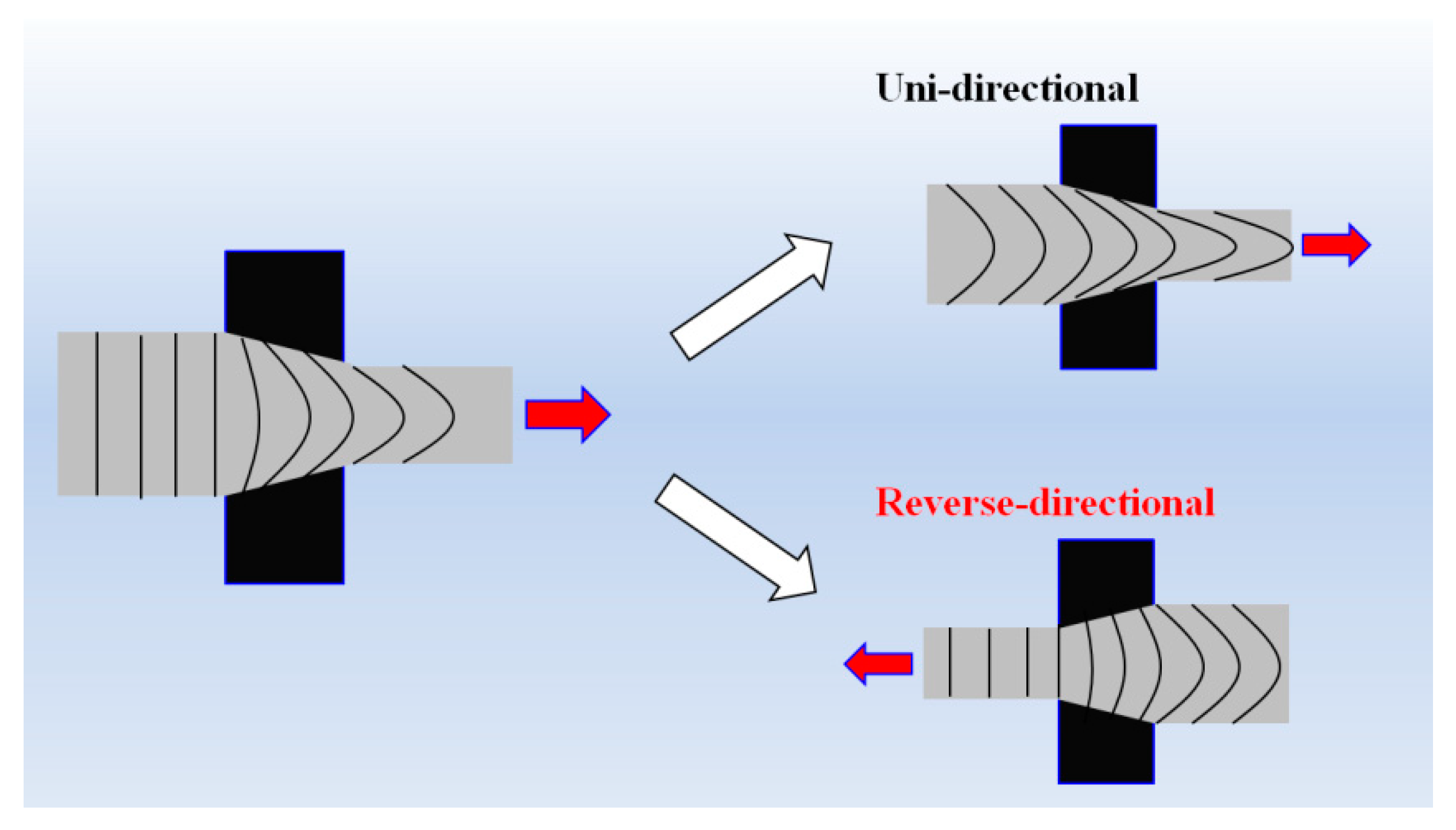
2.1.2. Wire Drawing
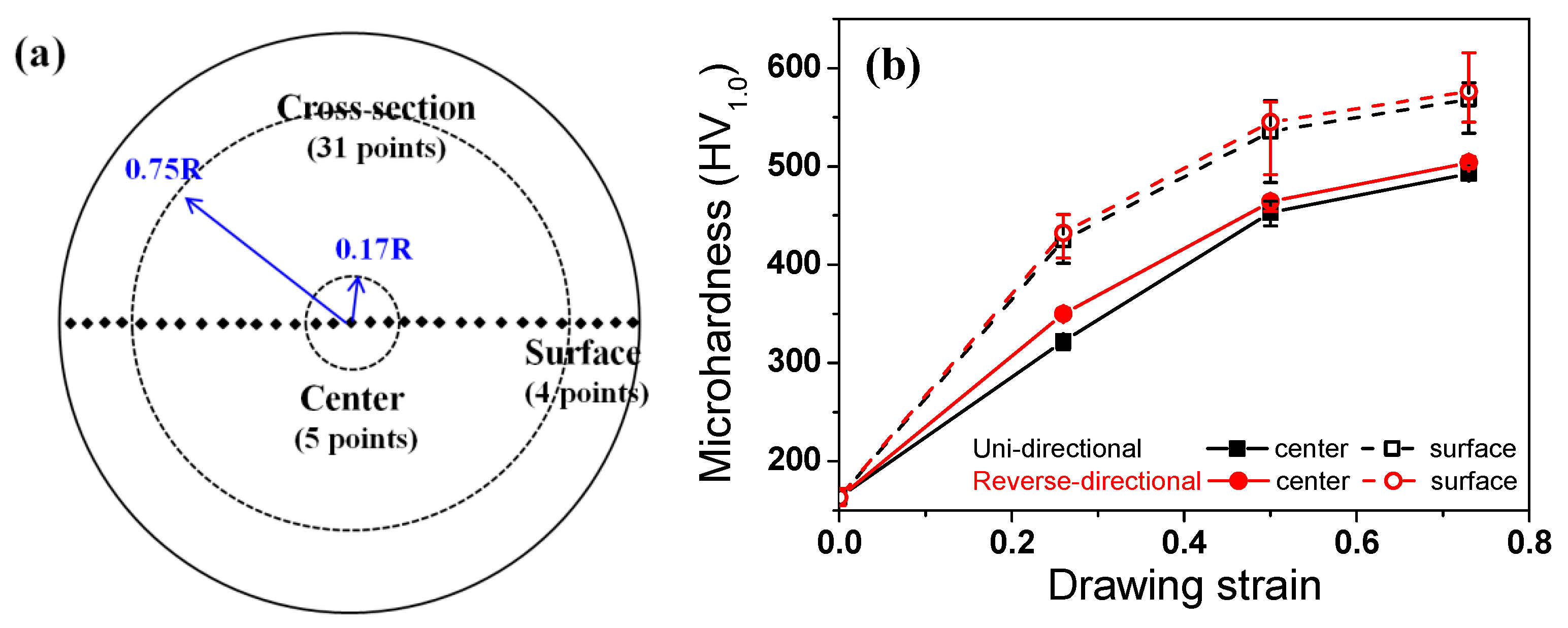
2.1.3. Microstructure and Mechanical Properties
2.2. Numerical Modelling
3. Results
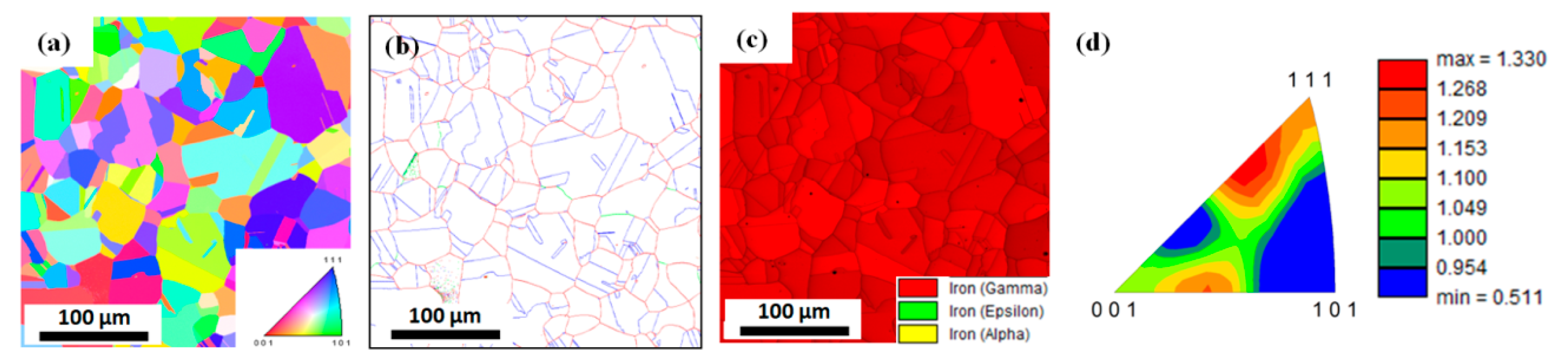
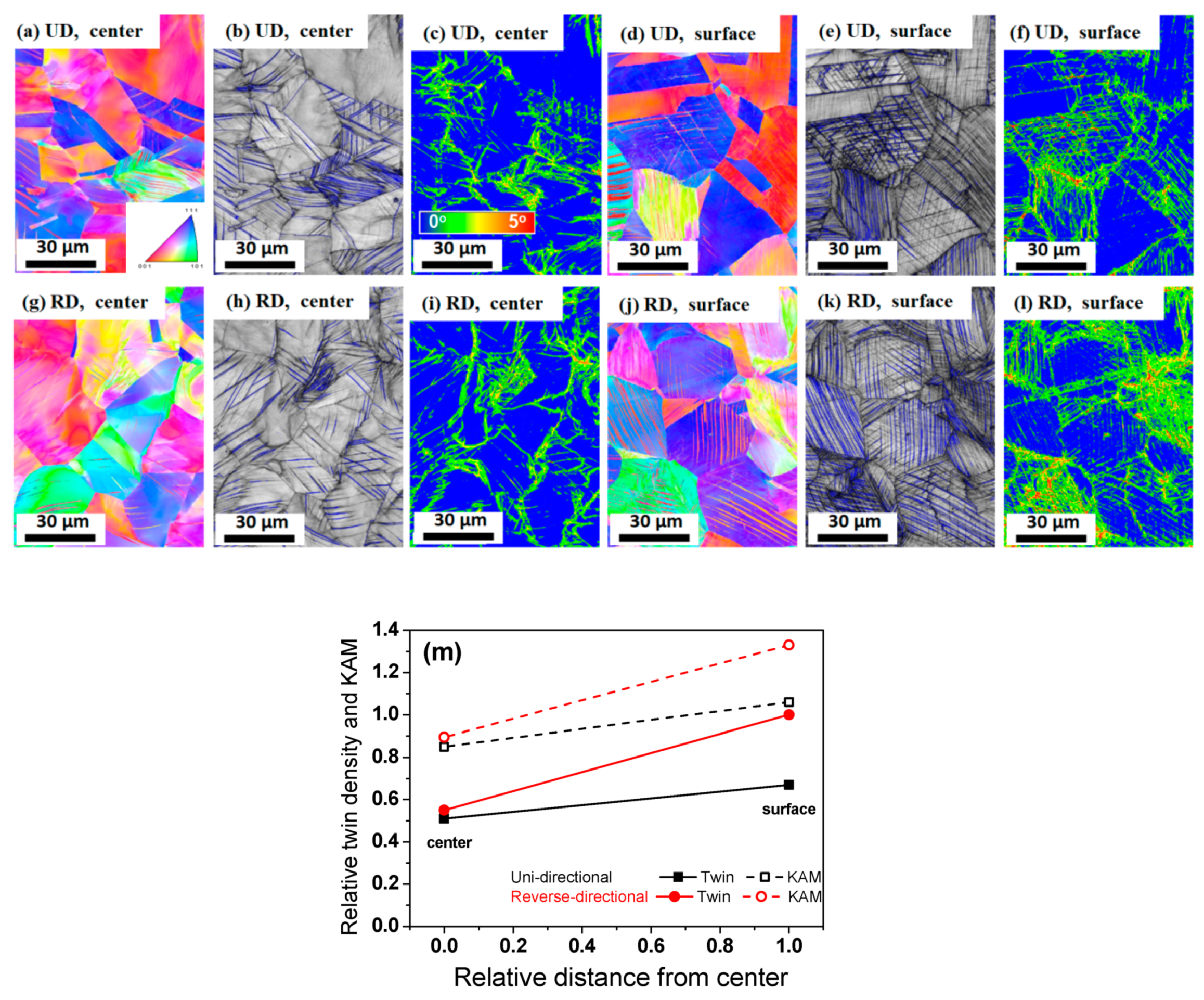
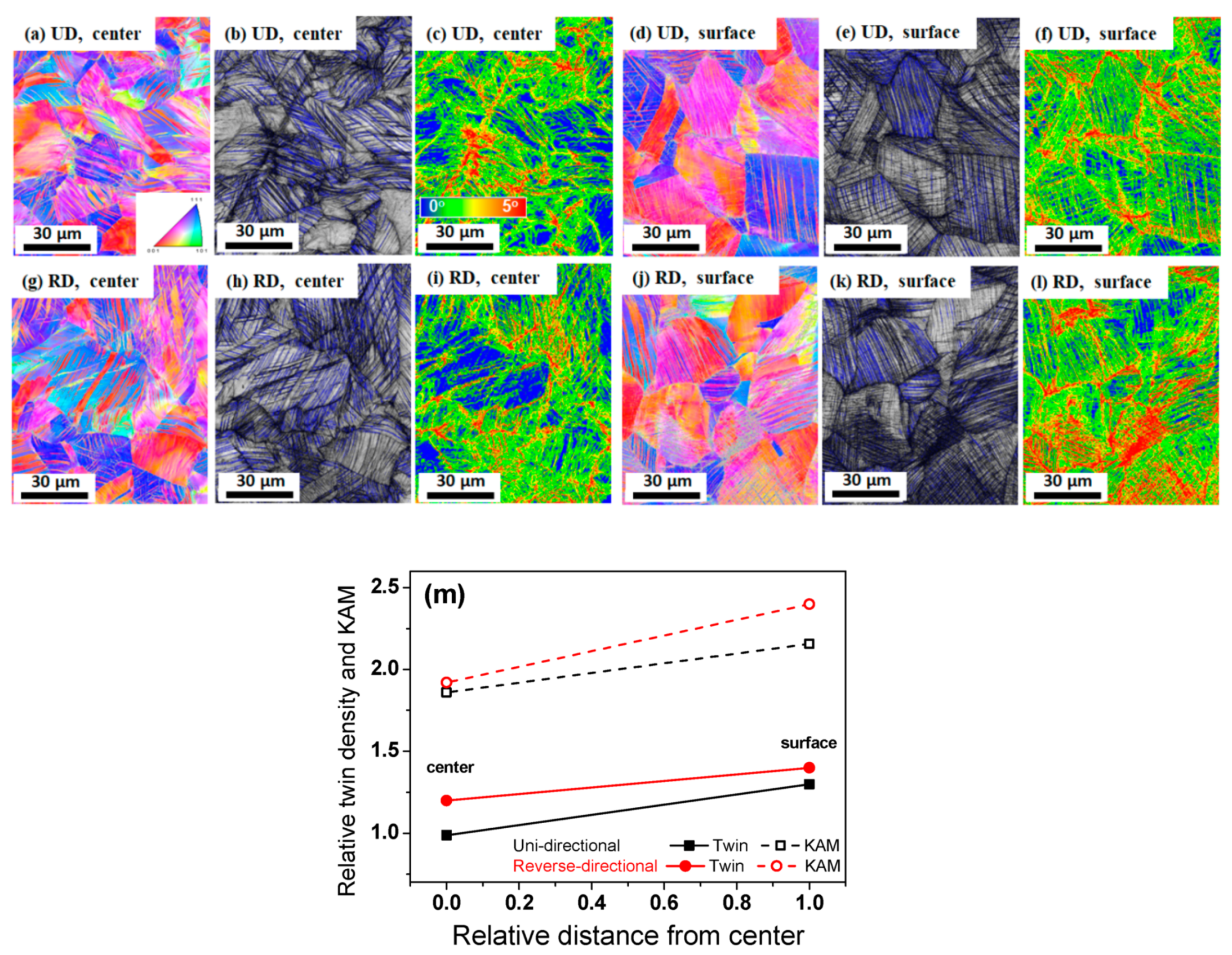
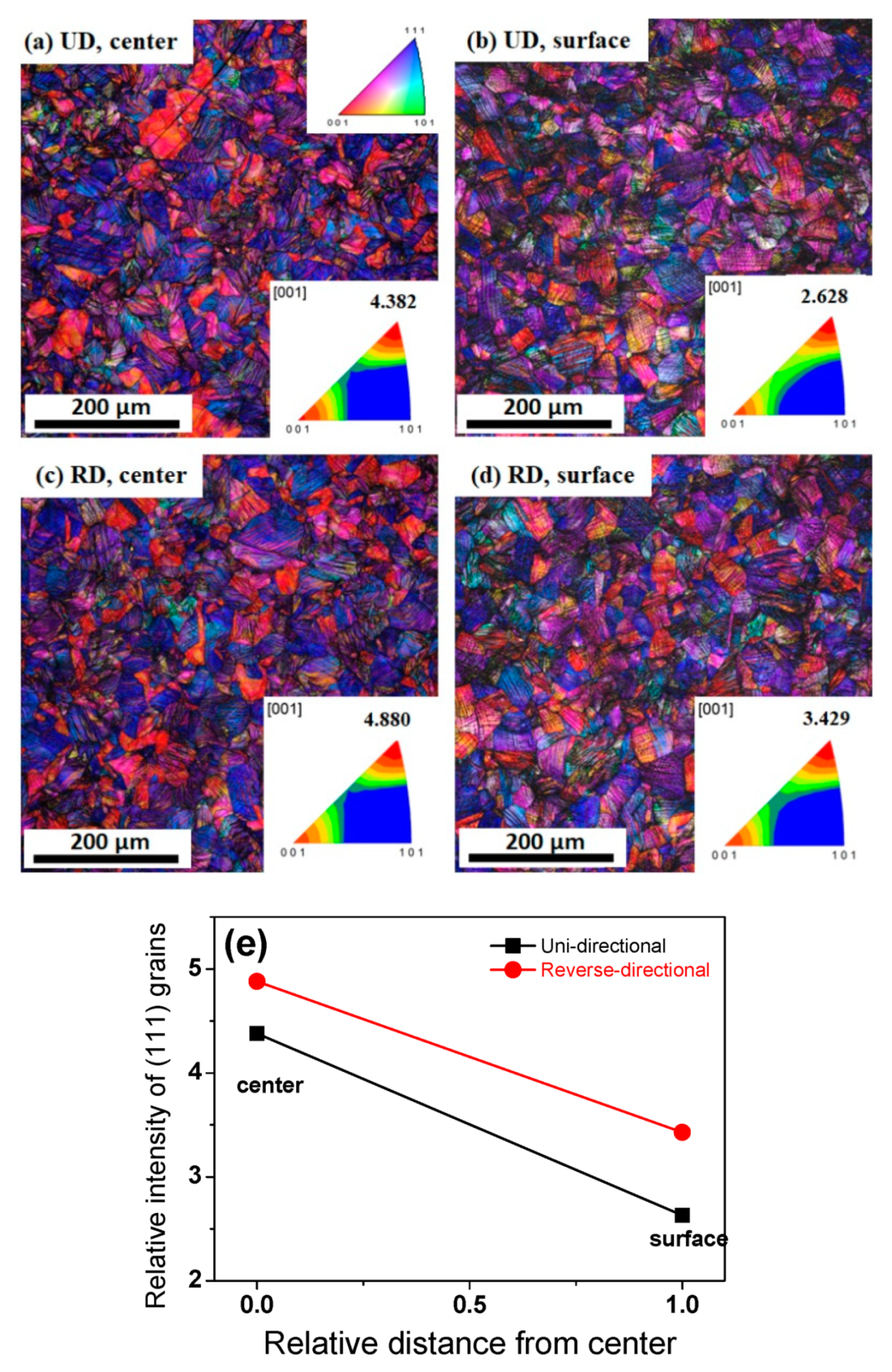
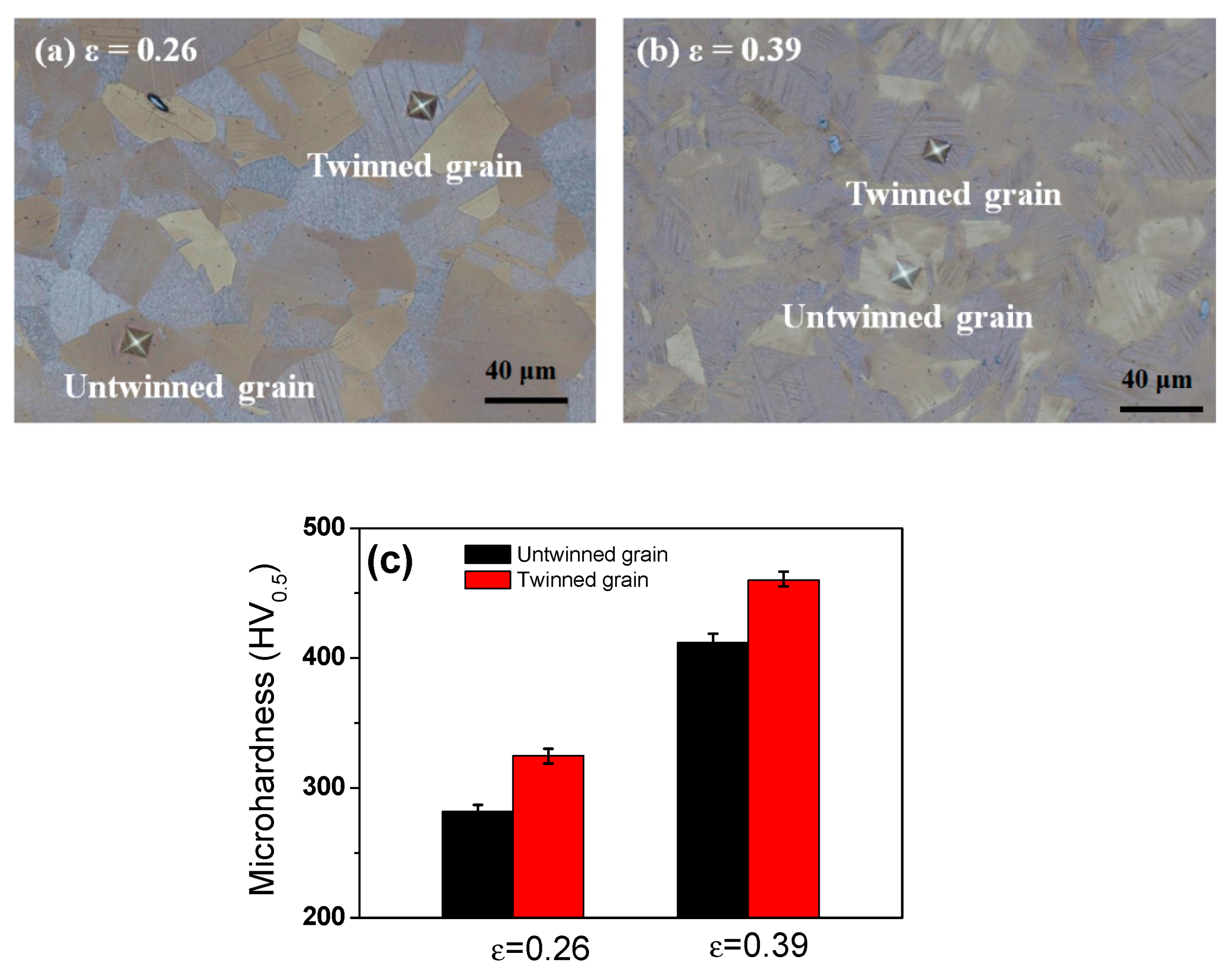
3.1. Microstructural Evolution
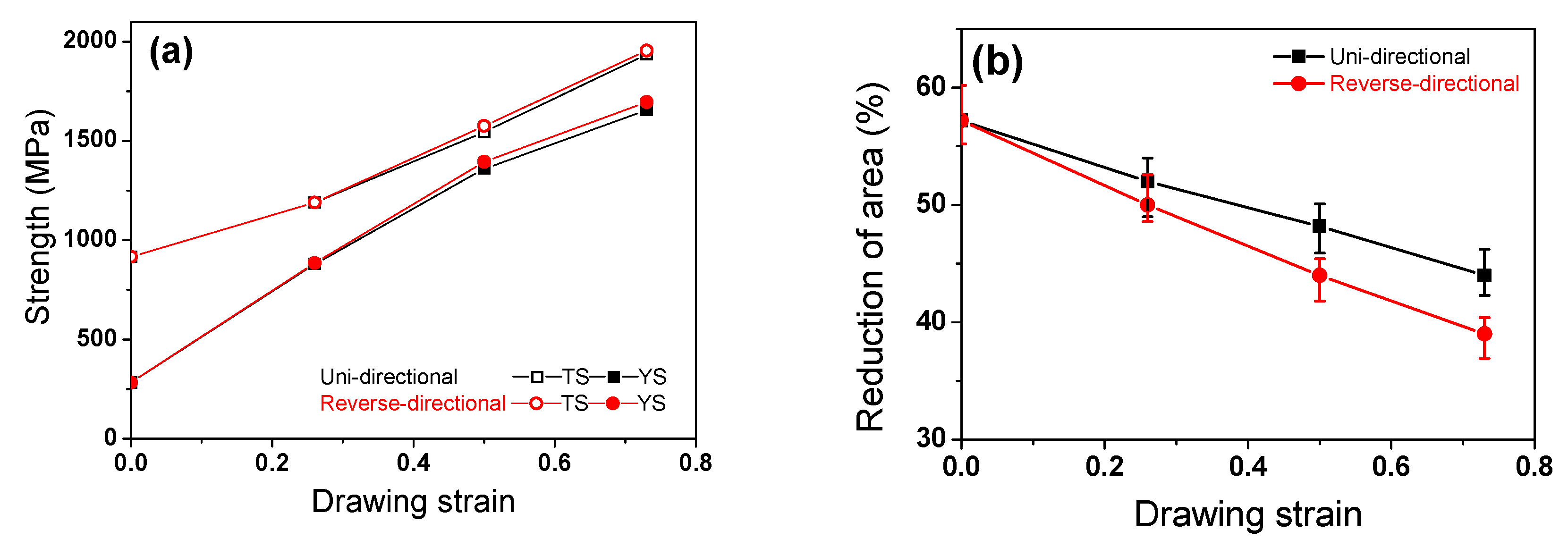
3.2. Mechanical Properties
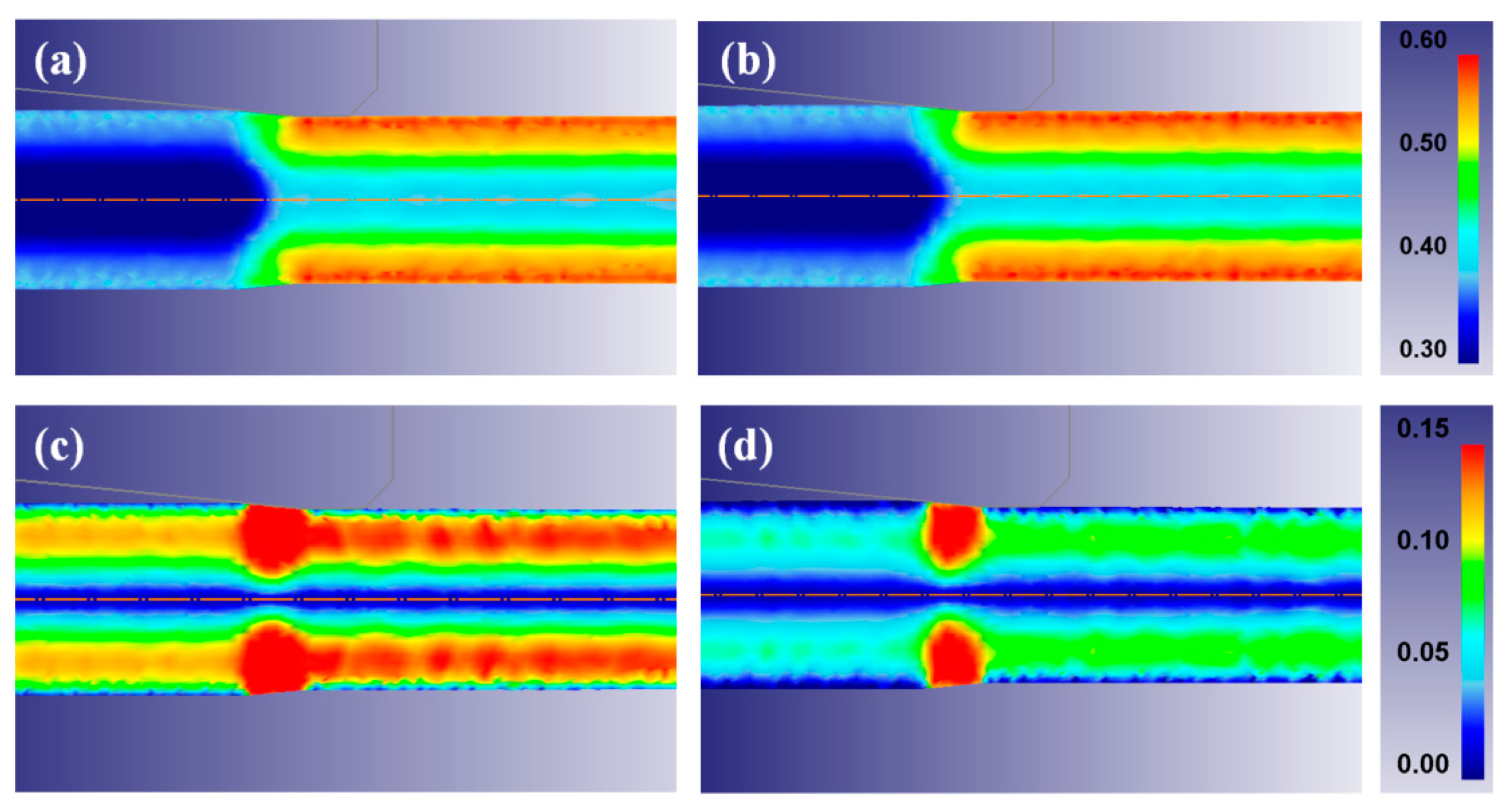
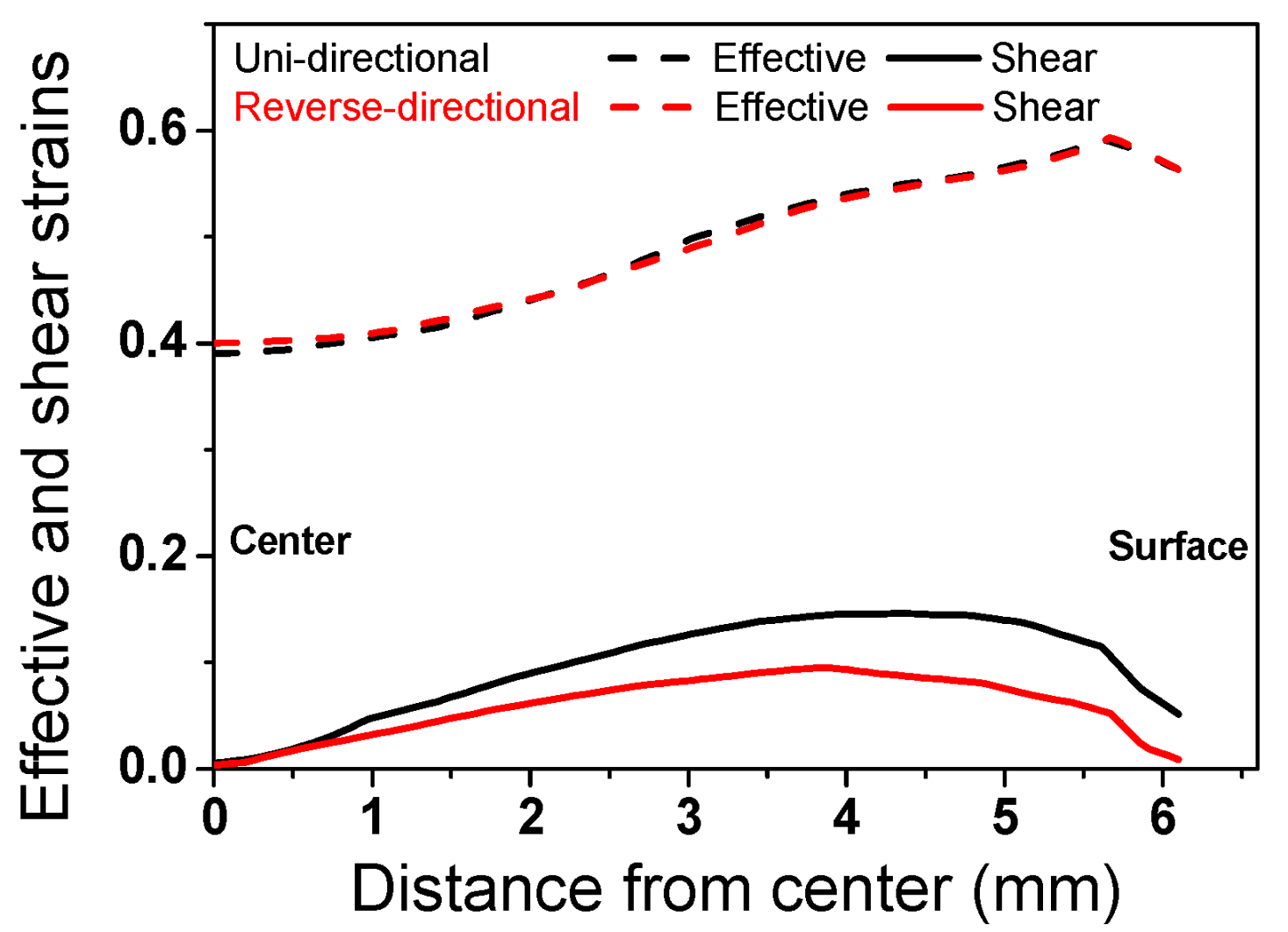
3.3. Analysis of Strain and Stress
4. Discussion
5. Conclusions
Funding
Conflicts of Interest
References
- Grassel, O.; Kruger, L.; Frommeyer, G.; Meyer, L.W. High strength Fe-Mn-(Al, Si) TRIP/TWIP steels development-properties-application. Int. J. Plast. 2000, 16, 1391–1409. [Google Scholar] [CrossRef]
- Bouaziz, O.; Allain, S.; Scott, C.P.; Cugy, P.; Barbier, D. High manganese austenitic twinning induced plasticity steels: A review of the microstructure properties relationships. Curr. Opin. Solid State Mater. Sci. 2011, 15, 141–168. [Google Scholar] [CrossRef]
- Barbier, D.; Gey, N.; Allain, S.; Bozzolo, N.; Humbert, M. Analysis of the tensile behavior of a TWIP steel based on the texture and microstructure evolutions. Mater. Sci. Eng. A 2009, 500, 196–206. [Google Scholar] [CrossRef]
- Jin, J.E.; Lee, Y.K. Strain hardening behavior of a Fe-18Mn-0.6C-1.5Al TWIP steel. Mater. Sci. Eng. A 2009, 527, 157–161. [Google Scholar] [CrossRef]
- De Cooman, B.C.; Estrin, Y.; Kim, S.K. Twinning-induced plasticity (TWIP) steels. Acta Mater. 2018, 142, 283–362. [Google Scholar] [CrossRef]
- Bouaziz, O.; Guelton, N. Modeling of TWIP effect on work-hardening. Mater. Sci. Eng. A 2001, 319, 246–249. [Google Scholar] [CrossRef]
- Zambrano, O.A. A general perspective of Fe–Mn–Al–C steels. J. Mater. Sci. 2018, 53, 14003–14062. [Google Scholar] [CrossRef]
- Karaman, I.; Sehitoglu, H.; Gall, K.; Chumlyakov, Y.I.; Maier, H.J. Deformation of single crystal Hadfield steel by twinning and slip. Acta Mater. 2000, 48, 1345–1359. [Google Scholar] [CrossRef]
- Yang, P.; Xie, Q.; Meng, L.; Ding, H.; Tang, Z. Dependence of deformation twinning on grain orientation in a high manganese steel. Scr. Mater. 2006, 55, 629–631. [Google Scholar] [CrossRef]
- Meng, L.; Yang, P.; Xie, Q.; Ding, H.; Tang, Z. Dependence of deformation twinning on grain orientation in compressed high manganese steels. Scr. Mater. 2007, 56, 931–934. [Google Scholar] [CrossRef]
- Brake, L.; Kestens, L.; Penning, J. Direct observation of the twinning mechanism in an austenitic Fe–Mn–C steel. Scr. Mater. 2009, 61, 220–222. [Google Scholar] [CrossRef]
- Gutierrez-Urrutia, I.; Zaefferer, S.; Rabbe, D. The effect of grain size and orientation on deformation twinning in a Fe-22Mn-0.6C TWIP steel. Mater. Sci. Eng. A 2010, 527, 3552–3560. [Google Scholar] [CrossRef]
- Sato, S.; Kwon, E.P.; Imafuku, M.; Wagatsuma, K.; Suzuki, S. Microstructural characterization of high-manganese austenitic steels with different stacking fault energies. Mater. Charact. 2011, 62, 781–788. [Google Scholar] [CrossRef]
- Renard, K.; Idrissi, H.; Schryvers, D.; Jacques, P.J. On the stress state dependence of the twinning rate and work hardening in twinning-induced plasticity steels. Scr. Mater. 2012, 66, 966–971. [Google Scholar] [CrossRef]
- Liu, F.; Dan, W.J.; Zhang, W.G. The effects of stress state on the strain hardening behaviors of TWIP steel. J. Mater. Eng. Perform. 2017, 26, 2721–2728. [Google Scholar] [CrossRef]
- Nakada, N.; Ito, H.; Matsuoka, Y.; Tsuchiyama, T.; Takaki, S. Deformation-induced martensitic transformation behavior in cold-rolled and cold-drawn type 316 stainless steels. Acta Mater. 2010, 58, 895–903. [Google Scholar] [CrossRef]
- Hwang, J.K. Effect of stress states on the twinning behavior in twinning-induced plasticity steel. J. Mater. Eng. Perform. 2019, 28, 4811–4825. [Google Scholar] [CrossRef]
- Pinheiro, P.; Monteiro, W.A.; Barbosa, R.; Cetlin, P.R. The effect of strain path on the mechanical behavior and dislocation arrangements in the hot working of copper. Mater. Sci. Eng. A 2004, 368, 280–285. [Google Scholar] [CrossRef]
- Sakharova, N.A.; Fernandes, J.V. Strain path change effect on dislocation microstructure of multicrystalline copper sheets. Mater. Chem. Phys. 2006, 98, 44–50. [Google Scholar] [CrossRef]
- Koohbor, B.; Serajzadeh, S. Influence of deformation path change on static strain aging of cold rolled steel strip. Int. J. Adv. Manuf. Technol. 2012, 61, 901–909. [Google Scholar] [CrossRef]
- Koohbor, B. On the influence of rolling path change on static recrystallization behavior of commercial purity aluminum. Int. J. Mater. Form. 2014, 7, 53–63. [Google Scholar] [CrossRef]
- Higginson, R.L.; Sellars, C.M. The effect of strain path reversal during hot rolling on austenitic stainless steel. Mater. Sci. Eng. A 2002, 338, 323–330. [Google Scholar] [CrossRef]
- Wright, R.N. Wire Technology: Process Engineering and Metallurgy; Butterworth-Heinemann: Oxford, UK, 2011. [Google Scholar]
- Lee, S.K.; Lee, I.K.; Lee, S.M.; Lee, S.Y. Prediction of Effective Strain Distribution in Two-Pass Drawn Wire. Materials 2019, 12, 3923. [Google Scholar] [CrossRef] [PubMed]
- Allain, S.; Chateau, J.P.; Bouaziz, O.; Migot, S.; Guelton, N. Correlations between the calculated stacking fault energy and the plasticity mechanisms in Fe–Mn–C alloys. Mater. Sci. Eng. A 2004, 387, 158–162. [Google Scholar] [CrossRef]
- Ghasri-Khouzani, M.; McDermid, J.R. Effect of carbon content on the mechanical properties and microstructure evolution of Fe–22Mn–C steels. Mater. Sci. Eng. A 2015, 621, 118–127. [Google Scholar] [CrossRef]
- Saeed-Akbari, A.; Imlau, J.; Prahl, U.; Bleck, W. Derivation and variation in composition-dependent stacking fault energy maps based on subregular solution model in high-manganese steels. Metall. Mater. Trans. A 2009, 40, 3076–3090. [Google Scholar] [CrossRef]
- Dumay, A.; Chateau, J.P.; Allain, S.; Migot, S.; Bouaziz, O. Influence of addition elements on the stacking-fault energy and mechanical properties of an austenite Fe-Mn-C steel. Mater. Sci. Eng. A 2008, 483, 184–187. [Google Scholar] [CrossRef]
- Hwang, J.K. The microstructure dependence of drawability in ferritic, pearlitic and TWIP steels during wire drawing. J. Mater. Sci. 2019, 54, 8743–8759. [Google Scholar] [CrossRef]
- Hwang, J.K.; Yi, I.C.; Son, I.H.; Yoo, J.Y.; Kim, B.; Zargaran, A.; Kim, N.J. Microstructural evolution and deformation behavior of twinning-induced plasticity (TWIP) steel during wire drawing. Mater. Sci. Eng. A 2015, 644, 41–52. [Google Scholar] [CrossRef]
- Hwang, J.K. Effect of copper and aluminum contents on wire drawing behavior in twinning-induced plasticity steels. Mater. Sci. Eng. A 2018, 737, 188–197. [Google Scholar] [CrossRef]
- Yang, H.K.; Zhang, Z.J.; Dong, F.Y.; Duan, Q.Q.; Zhang, Z.F. Strain rate effects on tensile deformation behaviors for Fe–22Mn–0.6C–(1.5Al) twinning-induced plasticity steel. Mater. Sci. Eng. A 2014, 607, 551–558. [Google Scholar] [CrossRef]
- Yang, H.K.; Zhang, Z.J.; Tian, Y.Z.; Zhang, Z.F. Negative to positive transition of strain rate sensitivity in Fe–22Mn–0.6C–x(Al) twinning-induced plasticity steels. Mater. Sci. Eng. A 2017, 690, 146–157. [Google Scholar] [CrossRef]
- Yang, H.K.; Zhang, Z.J.; Zhang, Z.F. Comparison of twinning evolution with work hardening ability in twinning-induced plasticity steel under different strain rates. Mater. Sci. Eng. A 2015, 622, 184–188. [Google Scholar] [CrossRef]
- Lee, S.Y.; Lee, S.I.; Hwang, B. Effect of strain rate on tensile and serration behaviors of an austenitic Fe–22Mn–0.7C twinning-induced plasticity steel. Mater. Sci. Eng. A 2018, 711, 22–28. [Google Scholar] [CrossRef]
- Liang, Z.Y.; Wang, X.; Huang, W.; Huang, M.X. Strain rate sensitivity and evolution of dislocations and twins in a twinning-induced plasticity steel. Acta Mater. 2015, 88, 170–179. [Google Scholar] [CrossRef]
- Lee, S.J.; Kim, J.; Kane, S.N.; De Cooman, B.C. On the origin of dynamic strain aging in twinning-induced plasticity steels. Acta Mater. 2011, 59, 6809–6819. [Google Scholar] [CrossRef]
- Hwang, S.K.; Jin, Y.G.; Son, I.H.; Rhee, K.H.; Lee, D.L.; Im, Y.T. Flow characteristics of continuous shear drawing of high carbon steel. Int. J. Mech. Sci. 2011, 53, 479–484. [Google Scholar] [CrossRef]
- Baek, H.M.; Hwang, S.K.; Joo, H.S.; Im, Y.T.; Son, I.H.; Bae, C.M. The effect of a non-circular drawing sequence on delamination characteristics of pearlitic steel wire. Mater. Des. 2014, 62, 137–148. [Google Scholar] [CrossRef]
- Hwang, S.K.; Baek, H.M.; Lee, J.W.; Son, I.H.; Im, Y.T.; Bae, C.M. The effect of microstructure and texture evolution on mechanical properties of low carbon steel in a non-circular drawing sequence. J. Mater. Process. Technol. 2014, 214, 318–325. [Google Scholar] [CrossRef]
- Saleh, A.A.; Pereloma, E.V.; Gazder, A.A. Texture evolution of cold rolled and annealed Fe–24Mn–3Al–2Si–1Ni–0.06C TWIP steel. Mater. Sci. Eng. A 2011, 528, 4537–4549. [Google Scholar] [CrossRef]
- Zambrano, O.A.; Valdes, J.; Aguilar, Y.; Coronado, J.J.; Rodriguez, S.A.; Loge, R.E. Hot deformation of a Fe–Mn–Al–C steel susceptible of k-carbide precipitation. Mater. Sci. Eng. A 2017, 689, 269–285. [Google Scholar] [CrossRef]
- Hwang, J.K. Deformation behaviors of various Fe–Mn–C twinning-induced plasticity steels: Effect of stacking fault energy and chemical composition. J. Mater. Sci. 2020, 55, 1779–1795. [Google Scholar] [CrossRef]
- Schwartz, A.J.; Kumar, M.; Adams, B.L.; Field, D.P. Electron Backscatter Diffraction in Materials Science, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 251–262. [Google Scholar]
- Badji, R.; Chauveau, T.; Bacroix, B. Texture, misorientation and mechanical anisotropy in a deformed dual phase stainless steel weld joint. Mater. Sci. Eng. A 2013, 575, 94–103. [Google Scholar] [CrossRef]
- Park, J.; Kang, M.; Sohn, S.S.; Kim, S.H.; Kim, K.S.; Nack, J.K.; Lee, S. Quasi-static and dynamic deformation mechanisms interpreted by microstructural evolution in TWinning Induced Plasticity (TWIP) steel. Mater. Sci. Eng. A 2017, 684, 54–63. [Google Scholar] [CrossRef]
- Chen, J.; Yan, W.; Liu, C.X.; Ding, R.G.; Fan, X.H. Dependence of texture evolution on initial orientation in drawn single crystal copper. Mater. Charact. 2011, 62, 237–242. [Google Scholar] [CrossRef]
- English, A.T.; Chin, G.Y. On the variation of wire texture with stacking fault energy in FCC metals and alloys. Acta Metall. 1965, 13, 1013–1016. [Google Scholar] [CrossRef]
- Hwang, J.K.; Son, I.H.; Yoo, J.Y.; Zargaran, A.; Kim, N.J. Effect of reduction of area on microstructure and mechanical properties of twinning-induced plasticity steel during wire drawing. Met. Mater. Int. 2015, 21, 815–822. [Google Scholar] [CrossRef]
- Hwang, J.K. Drawing direction effect on microstructure and mechanical properties of twinning-induced plasticity steel during wire drawing. J. Mater. Eng. Perform. 2019, 28, 2834–2844. [Google Scholar] [CrossRef]
- Nagashima, H.; Yoshida, K. Ductility improvement of high carbon steel by alternate wire drawing method. J. AMME 2015, 70, 29–35. [Google Scholar]
- Yoshida, K.; Doi, K. Improvement of ductility of aluminum wire for automotive wiring hardness by alternate drawing. Procedia Eng. 2014, 81, 706–711. [Google Scholar] [CrossRef]
- Valberg, H. Understanding metal flow in aluminum extrusion by means of emptying diagrams. Int. J. Mater. Form. 2010, 3, 391–394. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, H.Y.; Xie, J.X. Texture evolution and flow stress of columnar-grained polycrystalline copper during intense plastic deformation process at room temperature. Mater. Sci. Eng. A 2011, 530, 418–425. [Google Scholar] [CrossRef]
- Hou, J.P.; Wang, Q.; Yang, H.J.; Wu, X.M.; Li, C.H.; Li, X.W.; Zhang, Z.F. Microstructure evolution and strengthening mechanisms of cold-drawn commercially pure aluminum wire. Mater. Sci. Eng. A 2015, 639, 103–106. [Google Scholar] [CrossRef]
- Schuman, C.; Esling, C.; Philippe, M.J.; Hergesheimer, M.; Jallon, M.; Lefort, A. Texture evolution during the drawing of low carbon steel. Textures Microstruct. 1994, 22, 261–278. [Google Scholar] [CrossRef]
- Estrin, Y.; Toth, L.S.; Molinari, A.; Bréchet, Y. A dislocation-based model for all hardening stages in large strain deformation. Acta Mater. 1998, 46, 5509–5522. [Google Scholar] [CrossRef]
| C | Mn | Cu | Fe | SFE (mJ/m2) |
|---|---|---|---|---|
| 0.72 | 16.94 | 1.52 | Bal. | 20.1 |
| Diameter of Drawn Wire (mm) | No. of Passes | RA per Pass (%) | Drawing Direction | Total RA (%) | Drawing Strain | |
|---|---|---|---|---|---|---|
| Unidirectional (UD) | Reverse-Directional (RD) | |||||
| 15.0 | - | - | - | - | 0 | 0 |
| 14.0 | 1 | 12.8 | Forward | Forward | 12.8 | 0.13 |
| 13.18 | 2 | 11.3 | Forward | Reverse | 22.7 | 0.26 |
| 12.30 | 3 | 12.9 | Forward | Forward | 32.7 | 0.39 |
| 11.63 | 4 | 10.5 | Forward | Reverse | 39.8 | 0.50 |
| 10.97 | 5 | 11.1 | Forward | Forward | 46.7 | 0.62 |
| 10.40 | 6 | 10.1 | Forward | Reverse | 51.9 | 0.73 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hwang, J.-K. Correlation of Strain Path, Texture, Twinning, and Mechanical Properties in Twinning-Induced Plasticity Steel during Wire Drawing. Materials 2020, 13, 2250. https://doi.org/10.3390/ma13102250
Hwang J-K. Correlation of Strain Path, Texture, Twinning, and Mechanical Properties in Twinning-Induced Plasticity Steel during Wire Drawing. Materials. 2020; 13(10):2250. https://doi.org/10.3390/ma13102250
Chicago/Turabian StyleHwang, Joong-Ki. 2020. "Correlation of Strain Path, Texture, Twinning, and Mechanical Properties in Twinning-Induced Plasticity Steel during Wire Drawing" Materials 13, no. 10: 2250. https://doi.org/10.3390/ma13102250
APA StyleHwang, J.-K. (2020). Correlation of Strain Path, Texture, Twinning, and Mechanical Properties in Twinning-Induced Plasticity Steel during Wire Drawing. Materials, 13(10), 2250. https://doi.org/10.3390/ma13102250





