Reliability and Lifetime Assessment of Glider Wing’s Composite Spar through Accelerated Fatigue Life Testing
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Static Mechanical Proprieties
3.2. Accelerated Fatigue Life Testing of the GFRP-Foam Specimens
3.3. Reliability Analysis of Accelerated Life-Test Data
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zaharia, S.M. Reliability, Maintenance and Testing of Aerospace Systems; Lambert Academic Publishing: Riga, Latvia, 2019; pp. 25–26. [Google Scholar]
- Nelson, W. Accelerated Testing: Statistical Models, Test Plans, and Data Analysis; John Wiley & Sons, Inc.: New York, NY, USA, 2004; pp. 15–17. [Google Scholar]
- Sha, N. Statistical Inference for Progressive Stress Accelerated Life Testing with Birnbaum-Saunders Distribution. Stats 2018, 1, 189–203. [Google Scholar] [CrossRef]
- Kim, S.K.; Lim, H.; Sung, S.-I.; Kim, Y.S. Planning of Partially Accelerated Degradation Test with Two Stress Variables for Practical Lifetime Estimation. Appl. Sci. 2018, 8, 2162. [Google Scholar] [CrossRef]
- Hu, C.H.; Plante, R.D.; Tang, J. Statistical equivalency and optimality of simple step-stress accelerated test plans for the exponential distribution. Nav. Res. Logist. 2013, 60, 19–30. [Google Scholar] [CrossRef]
- Escobar, L.A.; Meeker, W.Q. A Review of Accelerated Test Models. Stat. Sci. 2006, 21, 552–577. [Google Scholar] [CrossRef]
- Nakada, M.; Miyano, Y. Accelerated testing for long-term fatigue strength of various FRP laminates for marine use. Compos. Sci. Technol. 2009, 69, 805–813. [Google Scholar] [CrossRef]
- Chen, Y.; Davalos, J.F.; Ray, I.; Kim, H.Y. Accelerated aging tests for evaluations of durability performance of FRP reinforcing bars for concrete structures. Compos. Struct. 2007, 78, 101–111. [Google Scholar] [CrossRef]
- Zaharia, S.M.; Morariu, C.O.; Nedelcu, A.; Pop, M.A. Experimental Study of Static and Fatigue Behavior of CFRP-Balsa Sandwiches under Three-point Flexural Loading. BioResources 2017, 12, 2673–2689. [Google Scholar] [CrossRef]
- He, Q.; Chen, W.; Pan, J.; Qian, P. Improved step stress accelerated life testing method for electronic product. Microelectron. Reliab. 2012, 52, 2773–2780. [Google Scholar]
- Cai, M.; Yang, D.; Tian, K.; Zhang, P.; Chen, X.; Liu, L.; Zhang, G. Step-stress accelerated testing of high-power LED lamps based on subsystem isolation method. Microelectron. Reliab. 2015, 55, 1784–1789. [Google Scholar] [CrossRef]
- Cai, M.; Yang, D.; Zheng, J.; Mo, Y.; Huang, J.; Xu, J.; Chen, W.; Zhang, G.; Chen, X. Thermal degradation kinetics of LED lamps in step-up-stress and step-down-stress accelerated degradation testing. Appl. Eng. 2016, 107, 918–926. [Google Scholar] [CrossRef]
- Qian, C.; Fan, J.; Fang, J.; Yu, C.; Ren, Y.; Fan, X.; Zhang, G. Photometric and Colorimetric Assessment of LED Chip Scale Packages by Using a Step-Stress Accelerated Degradation Test (SSADT) Method. Materials 2017, 10, 1181. [Google Scholar] [CrossRef] [PubMed]
- Tseng, S.T.; Wen, Z.C. Step-Stress Accelerated Degradation Analysis for Highly Reliable Products. J. Qual. Technol. 2000, 32, 209–216. [Google Scholar] [CrossRef]
- Coutu, R.A.; Lake, R.A.; Christiansen, B.D.; Heller, E.R.; Bozada, C.A.; Poling, B.S.; Via, G.D.; Theimer, J.P.; Tetlak, S.E.; Vetury, R.; et al. Benefits of Considering More than Temperature Acceleration for GaN HEMT Life Testing. Electronics 2016, 5, 32. [Google Scholar] [CrossRef]
- Yang, X.; Sun, B.; Wang, Z.; Qian, C.; Ren, Y.; Yang, D.; Feng, Q. An Alternative Lifetime Model for White Light Emitting Diodes under Thermal–Electrical Stresses. Materials 2018, 11, 817. [Google Scholar] [CrossRef]
- Hernández-López, A.M.; Aguilar-Garib, J.A.; Guillemet-Fritsch, S.; Nava-Quintero, R.; Dufour, P.; Tenailleau, C.; Durand, B.; Valdez-Nava, Z. Reliability of X7R Multilayer Ceramic Capacitors During High Accelerated Life Testing (HALT). Materials 2018, 11, 1900. [Google Scholar] [CrossRef]
- Coro, A.; Abasolo, M.; Aguirrebeitia, J.; López de Lacalle, L.N. Inspection scheduling based on reliability updating of gas turbine welded structures. Adv. Mech. Eng. 2019, 11, 1–20. [Google Scholar] [CrossRef]
- Coro, A.; Macareno, L.M.; Aguirrebeitia, J.; López de Lacalle, L.N. A Methodology to Evaluate the Reliability Impact of the Replacement of Welded Components by Additive Manufacturing Spare Parts. Metals 2019, 9, 932. [Google Scholar] [CrossRef]
- Wang, L.; Li, Y. Boundary for aviation bearing accelerated life test based on quasi-dynamic analysis. Tribol. Int. 2017, 116, 414–421. [Google Scholar] [CrossRef]
- Lok, S.; Paul, J.; Upendranath, V. Prescience life of landing gear using multiaxial fatigue numerical analysis. Procedia Eng. 2014, 86, 775–779. [Google Scholar] [CrossRef]
- Zhang, M.; Meng, Q.; Hu, W.; Shi, S.; Hu, M.; Zhang, X. Damage mechanics method for fatigue life prediction of PitchChange-Link. Int. J. Fatigue 2010, 32, 1683–1688. [Google Scholar] [CrossRef]
- Shahani, A.R.; Mohammadi, S. Damage tolerance approach for analyzing a helicopter main rotor blade. Eng. Fail. Anal. 2015, 57, 56–71. [Google Scholar] [CrossRef]
- Van der Ven, H.; Bakker, R.J.J.; van Tongeren, J.H.; Bos, M.J.; Münninghoff, N. A modelling framework for the calculation of structural loads for fatigue life prediction of helicopter airframe components. Aerosp. Sci. Technol. 2012, 23, 26–33. [Google Scholar] [CrossRef]
- Özsoy, S.; Çelik, M.; Kadıoğlu, F.S. An accelerated life test approach for aerospace structural components. Eng. Fail. Anal. 2008, 15, 946–957. [Google Scholar] [CrossRef]
- Zaharia, S.M. The methodology of fatigue lifetime prediction and validation based on accelerated reliability testing of the rotor pitch links. Eksploat. Niezawodn. 2019, 21, 638–644. [Google Scholar] [CrossRef]
- Zaharia, S.M.; Martinescu, I. Management of accelerated reliability testing. Teh. Vjesn. 2016, 23, 1447–1455. [Google Scholar]
- Zaharia, S.M.; Martinescu, I.; Morariu, C.O. Life time prediction using accelerated test data of the specimens from mechanical element. Eksploat. Niezawodn. 2012, 14, 99–106. [Google Scholar]
- Orkisz, M.; Święch, L.; Zacharzewski, J. Fatigue tests of motor glider wing’s composite spar. Eksploat. Niezawodn. 2012, 14, 228–232. [Google Scholar]
- Święch, Ł. Calibration of a Load Measurement System for an Unmanned Aircraft Composite Wing Based on Fibre Bragg Gratings and Electrical Strain Gauges. Aerospace 2020, 7, 27. [Google Scholar] [CrossRef]
- Petrašinović, N.; Petrašinović, D.; Rašuo, B.; Milković, D. Aircraft duraluminum wing spar fatigue testing. FME Trans. 2017, 45, 531–536. [Google Scholar] [CrossRef]
- Eldwaib, K.A.; Grbović, A.; Sedmak, A.; Kastratović, G.; Petrasinović, D.; Sedmak, S. Fatigue life estimation of damaged integral wing spar using XFEM. Teh. Vjesn. 2018, 25, 1837–1842. [Google Scholar]
- Grbović, A.; Rasuo, B. FEM based fatigue crack growth predictions for spar of light aircraft under variable amplitude loading. Eng. Fail. Anal. 2012, 26, 50–64. [Google Scholar]
- Rasuo, B.; Grbović, A.; Petrasinović, D. Investigation of fatigue life of 2024-T3 aluminum spar using Extended Finite Element Method (XFEM). SAE Int. J. Aerosp. 2013, 6, 408–416. [Google Scholar] [CrossRef]
- IAR Ghimbav. Composite Glider Flight Manual; IAR Ghimbav: Brașov, Romania, 2000. [Google Scholar]
- Divinycell F. Available online: http://www.diabgroup.com/Products-and-services/Core-Material/Divinycell-F (accessed on 4 April 2020).
- Interglas Technologies. Available online: https://www.pd-interglas.com/en/index.php (accessed on 4 April 2020).
- Miyano, Y.; Nakada, M.; Nishigaki, K. Prediction of long-term fatigue life of quasi-isotropic CFRP laminates for aircraft use. Int. J. Fatigue 2006, 28, 1217–1225. [Google Scholar] [CrossRef]
- Miyano, Y.; Nakada, M.; Ichimura, J.; Hayakawa, E. Accelerated testing for long-term strength of innovative CFRP laminates for marine use. Compos. Part B Eng. 2008, 39, 5–12. [Google Scholar] [CrossRef]
- Rajaneesh, A.; Satrio, W.; Chai, G.B.; Sridhar, I. Long-term life prediction of woven CFRP laminates under three point flexural fatigue. Compos. Part B Eng. 2016, 91, 539–547. [Google Scholar] [CrossRef]
- ReliaSoft Corp. Accelerated Life Testing Reference eBook. Available online: http://reliawiki.org/index.php/ReliaWiki:Books/Accelerated_Life_Testing_Reference_eBook (accessed on 4 April 2020).
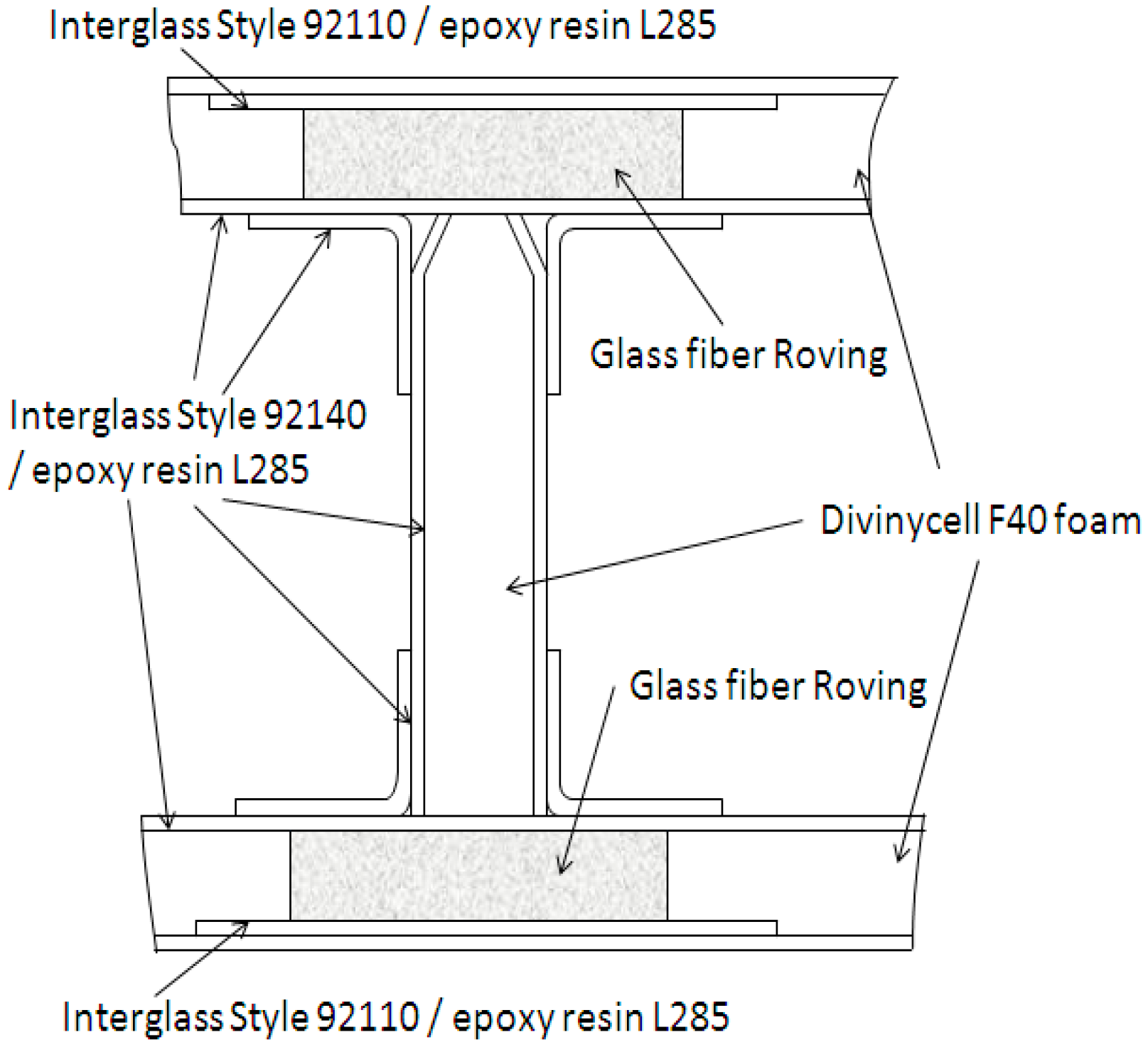







| Material | Length L (mm) | Thickness d (mm) | Width b (mm) | Span Length S (mm) | Core Thickness c (mm) | Facing Thickness t (mm) |
|---|---|---|---|---|---|---|
| GFRP-Foam | 150 | 10 | 15 | 110 | 9 | 0.5 |
| Material | Mean (μ) | Standard Deviation (s) | Coefficient of Variation (δ)% |
|---|---|---|---|
| GFRP-Foam—Bending Strength (MPa) | 26.5 | 3.3 | 12.452 |
| GFRP-Foam Bending Modulus (GPa) | 2.8 | 0.4 | 14.285 |
| Core shear ultimate strength (MPa) | 0.843 | 0.105 | 12.455 |
| Core shear yield stress (MPa) | 0.069 | 0.009 | 13.043 |
| Facing stress (MPa) | 92.8 | 11.6 | 12.5 |
| Specimen No. | The Number of Cycles to Failure in Accelerated Conditions | Accelerated Frequency Level (Hz) |
|---|---|---|
| 1 | 20,756 | 2 |
| 2 | 22,321 | 2 |
| 3 | 24,759 | 2 |
| 4 | 26,098 | 2 |
| 5 | 27,479 | 2 |
| 6 | 14,389 | 3 |
| 7 | 16,342 | 3 |
| 8 | 17,743 | 3 |
| 9 | 19,902 | 3 |
| 10 | 21,872 | 3 |
| 11 | 2763 | 4 |
| 12 | 3473 | 4 |
| 13 | 4093 | 4 |
| 14 | 5764 | 4 |
| 15 | 6034 | 4 |
| 16 | 1234 | 5 |
| 17 | 1456 | 5 |
| 18 | 1789 | 5 |
| 19 | 2021 | 5 |
| 20 | 2341 | 5 |
| Specimen No. | The Number of Cycles to Failure in Accelerated Testing Conditions | Accelerated Frequency Level (Hz) | Acceleration Factor | The Number of Cycles to Failure in Normal Testing Conditions |
|---|---|---|---|---|
| 1 | 20,756 | 2 | 2.504 | 51,973 |
| 2 | 22,321 | 55,892 | ||
| 3 | 24,759 | 61,997 | ||
| 4 | 26,098 | 65,349 | ||
| 5 | 27,479 | 68,807 | ||
| 6 | 14,389 | 3 | 9.133 | 131,415 |
| 7 | 16,342 | 149,251 | ||
| 8 | 17,743 | 162,047 | ||
| 9 | 19,902 | 181,765 | ||
| 10 | 21,872 | 199,757 | ||
| 11 | 2763 | 4 | 22.87 | 63,190 |
| 12 | 3473 | 79,428 | ||
| 13 | 4093 | 93,607 | ||
| 14 | 5764 | 131,823 | ||
| 15 | 6034 | 137,998 | ||
| 16 | 1234 | 5 | 46.614 | 57,522 |
| 17 | 1456 | 67,870 | ||
| 18 | 1789 | 83,392 | ||
| 19 | 2021 | 94,207 | ||
| 20 | 2341 | 109,123 |
| The Number of Cycles to Failure in Normal Testing Conditions | Reliability R (t) | Unreliability F (t) | Pdf f(t) × 10−6 | Failure Rate λ(t) × 10−6 |
|---|---|---|---|---|
| 51,973 | 0.965 | 0.035 | 5.67 | 21.7 |
| 55,892 | 0.917 | 0.083 | 6.15 | 23.8 |
| 57,522 | 0.868 | 0.132 | 6.35 | 24.7 |
| 61,997 | 0.819 | 0.181 | 6.85 | 27.2 |
| 63,190 | 0.770 | 0.230 | 6.98 | 27.9 |
| 65,349 | 0.721 | 0.279 | 7.20 | 29.1 |
| 67,870 | 0.672 | 0.328 | 7.44 | 30.6 |
| 68,807 | 0.622 | 0.378 | 7.52 | 31.2 |
| 79,428 | 0.573 | 0.427 | 8.29 | 37.8 |
| 83,392 | 0.524 | 0.476 | 8.48 | 40.4 |
| 93,607 | 0.475 | 0.525 | 8.70 | 47.4 |
| 94,207 | 0.426 | 0.574 | 8.70 | 47.9 |
| 109,123 | 0.377 | 0.623 | 8.32 | 59.0 |
| 131,415 | 0.327 | 0.673 | 6.61 | 77.5 |
| 131,823 | 0.278 | 0.722 | 6.57 | 77.9 |
| 137,998 | 0.229 | 0.771 | 5.96 | 83.5 |
| 149,251 | 0.180 | 0.82 | 4.80 | 94.0 |
| 162,047 | 0.131 | 0.869 | 3.53 | 106.7 |
| 181,765 | 0.082 | 0.918 | 1.95 | 127.8 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaharia, S.M.; Pop, M.A.; Udroiu, R. Reliability and Lifetime Assessment of Glider Wing’s Composite Spar through Accelerated Fatigue Life Testing. Materials 2020, 13, 2310. https://doi.org/10.3390/ma13102310
Zaharia SM, Pop MA, Udroiu R. Reliability and Lifetime Assessment of Glider Wing’s Composite Spar through Accelerated Fatigue Life Testing. Materials. 2020; 13(10):2310. https://doi.org/10.3390/ma13102310
Chicago/Turabian StyleZaharia, Sebastian Marian, Mihai Alin Pop, and Răzvan Udroiu. 2020. "Reliability and Lifetime Assessment of Glider Wing’s Composite Spar through Accelerated Fatigue Life Testing" Materials 13, no. 10: 2310. https://doi.org/10.3390/ma13102310
APA StyleZaharia, S. M., Pop, M. A., & Udroiu, R. (2020). Reliability and Lifetime Assessment of Glider Wing’s Composite Spar through Accelerated Fatigue Life Testing. Materials, 13(10), 2310. https://doi.org/10.3390/ma13102310






