Prediction of the Long-Term Performance and Durability of GFRP Bars under the Combined Effect of a Sustained Load and Severe Environments
Abstract
:1. Introduction
- The residual tensile properties of stressed GFRP bars in a corrosive environment were evaluated and the obtained results were compared with the literature and the design limits given by ACI 440.1R-15 [22];
- The experimental phenomena and SEM analysis results were analysed to investigate the degradation mechanism of GFRP bars exposed to simulated seawater solution and concrete pore solution;
- The long-term performance of GFRP bars exposed to concrete pore solution under different stress levels was predicted based on Arrhenius theory.
2. Experimental Program
2.1. The GFRP Bars Used in this Study Were Prepared
2.2. Test Parameters
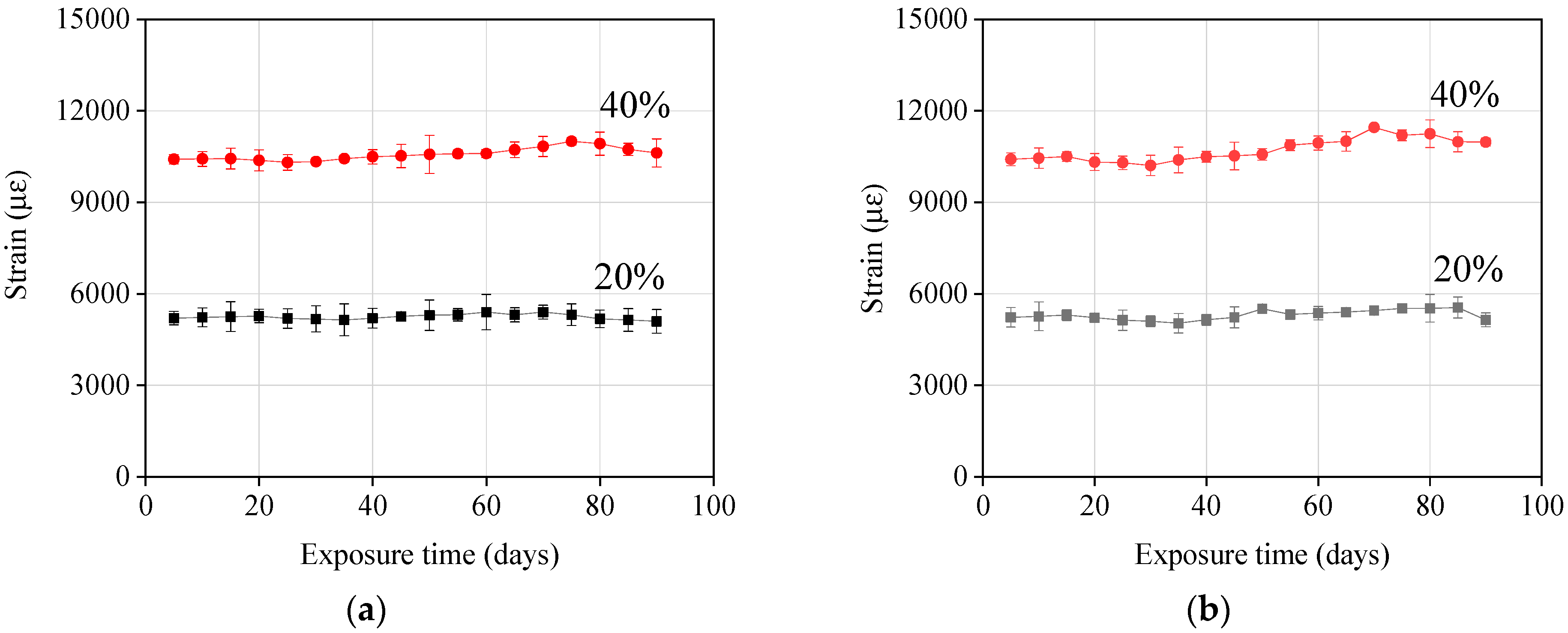
- Sustained tensile stresses: 20% and 40% of the ultimate tensile strength were selected in this test. The corresponding strains were 5200 and 10,400 με, respectively. These levels of strain are about 1.68–3.35 times the values recommended by ACI 440.1R-15 for creep rupture strain (Table 2). This was done to explore the material’s potential and evaluate how conservative the current codes and guidelines are;
- Temperature: Both ambient and elevated temperatures were used, with the ambient temperature being 23 °C and elevated temperatures being 40 and 60 °C.
2.3. Specimen Design and Test Procedure
2.4. Specimen Numbering
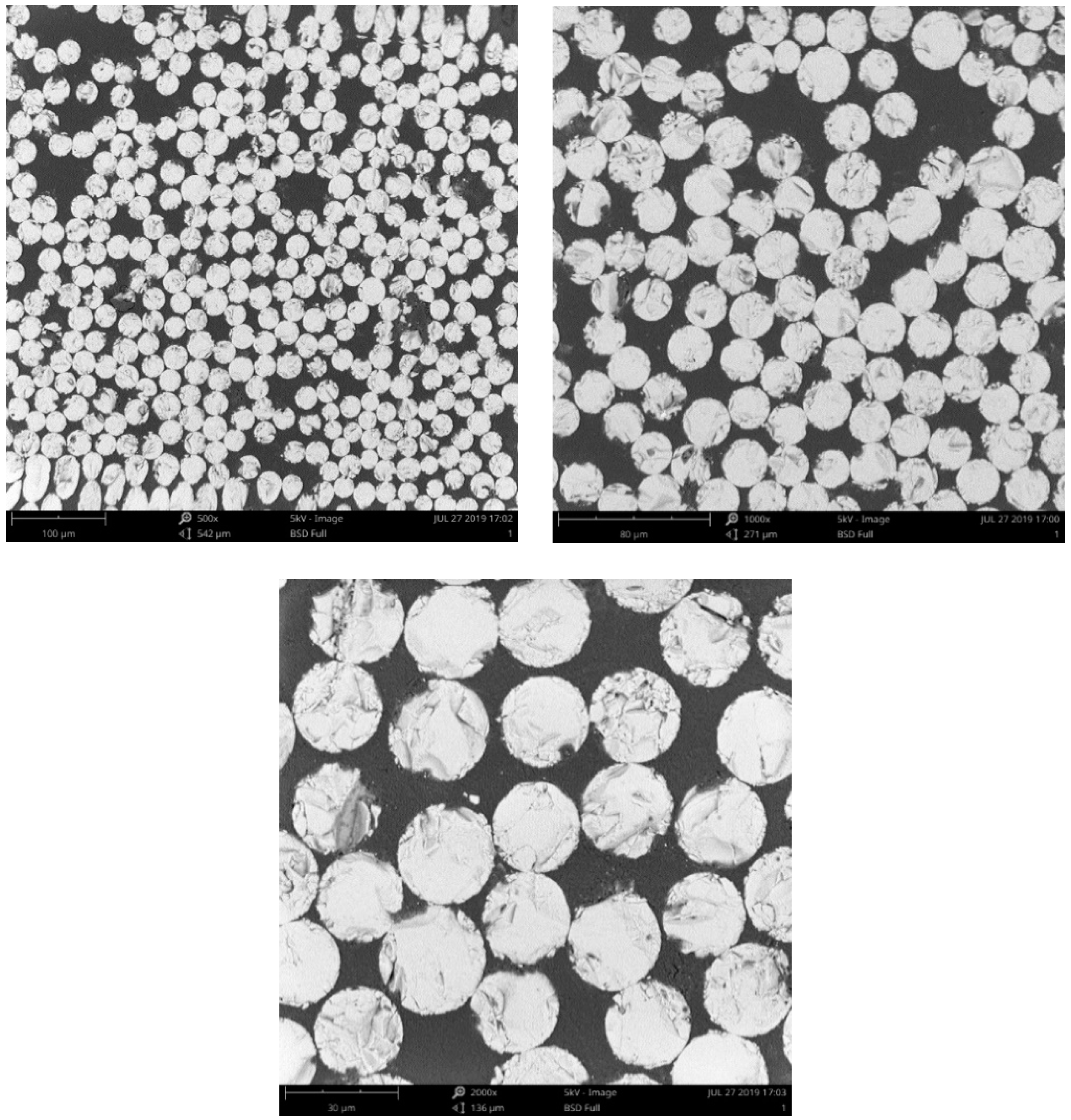
2.5. Scanning Electron Microscope (SEM)
3. Results and Discussion
3.1. Residual Tensile Strength and Strain
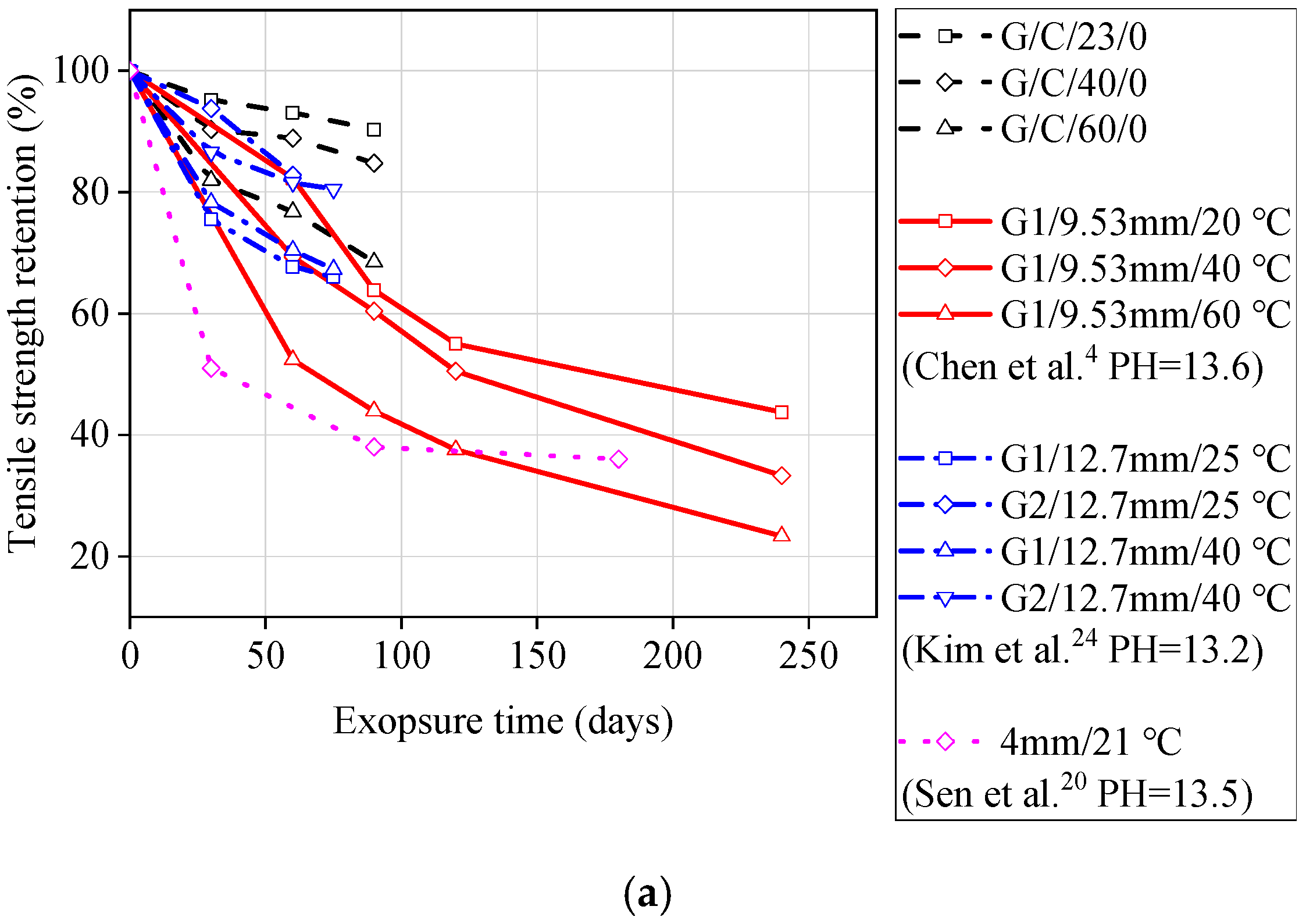
3.2. Comparing Obtained Results with Literature
3.3. Residual Modulus of Elasticity
3.4. Comparison with ACI 440.1R-15
3.5. Microstructure Analysis
4. Prediction of the Long-Term Performance of GFRP Bars
4.1. Prediction Model Selection
4.2. Arrheneius Theory
4.3. Prediction Procedure
4.4. Discussion on Predicted Results
5. Conclusions
- (1)
- The degradation rate of GFRP bars in seawater solution is significantly lower than that in concrete pore solution, and the difference in degradation rate becomes more obvious as the temperature and stress level increase;
- (2)
- A stress level of 40% is able to cause micro-cracks in the resin matrix of the GFRP bars, accelerating the degradation rate of the GFRP bar. In the design of GFRP-RC structures, the stress level in the GFRP bars should be limited to under 40% of the ultimate tensile strength;
- (3)
- It has been found that a lower stress level of 20% does not affect the degradation rate of GFRP bars. However, based on the prediction analysis of the service life of GFRP bars, it has been found that for the same tensile strength retention, the time required for a stress level of 20% is significantly reduced compared to a 0% stress level. With the increase of the exposure time of GFRP bars, the damage of GFRP bars increases continuously and the degradation rate of damage GFRP bars is accelerated by a 20% stress level;
- (4)
- The elastic modulus of GFRP bars is not affected by the corrosive environment and stress level, and the degradation rate for tensile strength and tensile strain tends to remain at the same level;
- (5)
- The residual tensile properties of all GFRP bars can meet the requirements of ACI 440.1R-15, except for those tested under a 40% stress level in 60 °C concrete pore solution for 90 days;
- (6)
- Since the GFRP bars were directly exposed to the corrosion solution, the long-term performance prediction results of the GFRP bars obtained using Arrheneius theory are considered to be conservative. Future research is needed to establish the correlation between the degradation of GFRP bars in laboratory-simulated and field conditions, in order to provide practical guidelines for GFRP-RC structures.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Clear, K.C.; Hartt, W.H.; McIntyre, J.; Lee, S.K. Performance of Epoxy-Coated Reinforcing Steel in Highway Bridges; NCHRP Report 370; Transportation Research Board: Washington, DC, USA, 1995. [Google Scholar]
- Gonenc, O. Durability and Service-Life Prediction of Concrete Reinforcing Materials. Master’s Thesis, University of Wisconsin-Madison, Madison, WI, USA, 2001. [Google Scholar]
- Chen, Y.; Davalos, J.F.; Ray, I.; Kim, H.Y. Accelerated aging tests for evaluations of durability performance of FRP reinforcing bars for concrete structures. Compos. Struct. 2007, 78, 101–111. [Google Scholar] [CrossRef]
- Chen, Y.; Davalos, J.F.; Ray, I. Durability prediction for GFRP reinforcing bars using short-term data of accelerated aging tests. J. Compos. Constr. 2006, 10, 279–286. [Google Scholar] [CrossRef]
- Kamal, A.S.M.; Boulfiza, M. Durability of GFRP rebars in simulated concrete solutions under accelerated aging Conditions. J. Compos. Constr. 2011, 15, 473–481. [Google Scholar] [CrossRef]
- Robert, M.; Cousin, P.; Benmokrane, B. Durability of GFRP Reinforcing Bars embedded in moist concrete. J. Compos. Constr. 2009, 13, 66–73. [Google Scholar] [CrossRef] [Green Version]
- Robert, M.; Benmokrane, B. Combined effects of saline solution and moist concrete on long-term durability of GFRP reinforcing bars. Constr. Build. Mater. 2013, 38, 274–284. [Google Scholar] [CrossRef]
- Benmokrane, B.; Wang, P.; Ton-That, T.M.; Rahman, H.; Robert, J.F. Durability of glass fiber-reinforced polymer reinforcing bars in concrete environment. J. Compos. Constr. 2002, 6, 143–153. [Google Scholar] [CrossRef]
- Debaiky, A.S.; Nkurunziza, G.; Benmokrane, B.; Cousin, P. Residual tensile properties of GFRP reinforcing bars after loading in severe environments. J. Compos. Constr. 2006, 10, 370–380. [Google Scholar] [CrossRef]
- Micelli, F.; Nanni, A. Durability of FRP rods for concrete structures. Constr. Build. Mater. 2004, 18, 491–503. [Google Scholar] [CrossRef]
- Benmokrane, B.; Manalo, A.; Bouhet, J.C.; Mohamed, K.; Robert, M. Effects of diameter on the durability of glass fiber-reinforced polymer bars conditioned in alkaline solution. J. Compos. Constr. 2017, 21, 04017040. [Google Scholar] [CrossRef] [Green Version]
- Benmokrane, B.; Elgabbas, F.; Ahmed, E.A.; Cousin, P. Characterization and comparative durability study of glass/vinylester, basalt/vinylester, and basalt/epoxy FRP bars. J. Compos. Constr. 2015, 19, 04015008. [Google Scholar] [CrossRef]
- Benmokrane, B.; Ali, A.H.; Mohamed, H.M.; Elsafty, A.; Manalo, A. Laboratory assessment and durability performance of vinyl-ester, polyester, and epoxy glass-FRP bars for concrete structures. Compos. Part B Eng. 2017, 114, 163–174. [Google Scholar] [CrossRef] [Green Version]
- Benmokrane, B.; Robert, M.; Mohamed, H.M.; Ali, A.H.; Cousin, P. Durability assessment of glass FRP solid and hollow bars (rock bolts) for application in ground control of Jurong rock caverns in Singapore. J. Compos. Constr. 2017, 21, 06016002. [Google Scholar] [CrossRef]
- Nkurunziza, G.; Debaiky, A.; Cousin, P.; Benmokrane, B. Durability of GFRP bars: A critical review of the literature. Prog. Struct. Eng. Mater. 2005, 7, 194–209. [Google Scholar] [CrossRef]
- Nkurunziza, G.; Benmokrane, B.; Debaiky, A.S.; Masmoudi, R. Effect of sustained load and environment on long-term tensile properties of glass fiber-reinforced polymer reinforcing bars. ACI Struct. J. 2005, 102, 615–621. [Google Scholar]
- Almusallam, T.H.; Al-Salloum, Y.A. Durability of GFRP rebars in concrete beams under sustained loads at severe environments. J. Compos. Constr. 2006, 40, 623–637. [Google Scholar] [CrossRef]
- Davalos, J.F.; Chen, Y.; Ray, I. Long-term durability prediction models for GFRP bars in concrete environment. J. Compos. Mater. 2012, 46, 1899–1914. [Google Scholar] [CrossRef]
- Wu, G.; Dong, Z.; Wang, X.; Zhu, Y.; Wu, Z.S. Prediction of long-term performance and durability of BFRP bars under the combined effect of sustained load and corrosive solutions. J. Compos. Constr. 2014, 19, 04014058. [Google Scholar] [CrossRef]
- Sen, R.; Mullins, G.; Salem, T. Durability of E-glass/vinylester reinforcement in alkaline solution. ACI Struct. J. 2002, 99, 369–375. [Google Scholar]
- Wang, Z.; Zhao, X.L.; Xian, G.; Wu, G.; Raman, R.K.S.; Al-Saadi, S.; Haque, A. Long-term durability of basalt- and glass-fibre reinforced polymer (BFRP/GFRP) bars in seawater and sea sand concrete environment. Constr. Build. Mater. 2017, 139, 467–489. [Google Scholar] [CrossRef]
- American Concrete Institute (ACI). Guide for the Design and Construction of Concrete Reinforced with FRP Bars; ACI 440.1R 15; ACI: Farmington Hills, MI, USA, 2015. [Google Scholar]
- American Concrete Institute (ACI). Guide Test Methods for Fiber Reinforced Polymers (FRPs) for Reinforcing or Strengthening Concrete Structures; ACI 440.3R-04; ACI: Farmington Hills, MI, USA, 2003. [Google Scholar]
- Kim, H.Y.; Park, Y.H.; You, Y.J.; Moon, C.K. Short-term durability test for GFRP rods under various environmental conditions. Compos. Struct. 2008, 83, 37–47. [Google Scholar] [CrossRef]
- Barris, C.; Torres, L.; Vilanova, I.; Mias, C.; Llorens, M. Experimental study on crack width and crack spacing for Glass-FRP reinforced concrete beams. Eng. Struct. 2017, 131, 231–242. [Google Scholar] [CrossRef]
- Kassem, C.; Farghaly, A.S.; Benmokrane, B. Evaluation of flexural behavior and serviceability performance of concrete beams reinforced with FRP bars. J. Compos. Constr. 2011, 15, 682–695. [Google Scholar] [CrossRef]
- El-Nemr, A.; Ahmed, E.; Benmokrane, B. Flexural behavior and serviceability of normal- and high-strength concrete beams reinforced with glass fiber reinforced polymer bars. ACI Struct. J. 2013, 110, 1077–1088. [Google Scholar]
- Wang, Z.; Zhao, X.L.; Xian, G.; Wu, G.; Raman, R.K.S.; Al-Saadi, S. Effect of sustained load and seawater and sea sand concrete environment on durability of basalt- and glass-fibre reinforced polymer (B/GFRP) bars. Corros. Sci. 2018, 138, 200–218. [Google Scholar] [CrossRef]
- Phani, K.K.; Bose, N.R. Temperature dependence of hydrothermal ageing of CSM-laminate during water immersion. Compos. Sci. Technol. 1987, 29, 79–87. [Google Scholar] [CrossRef]
- Nelson, W. Accelerated Testing—Statistical Models, Test Plans, and Data Analyses; Wiley: New York, NY, USA, 1990. [Google Scholar]
- Mufti, A.; Banthia, N.; Benmokrane, B.; Boulfiza, M.; Newhook, J.P. Durability of GFRP composite rods. Concr. Int. 2007, 29, 37–42. [Google Scholar]
- Dejke, V. Durability of FRP Reinforcement in Concrete-Literature Review and Experiments. Ph.D. Thesis, Chalmers University of Technology, Goteborg, Sweden, 2001. [Google Scholar]














| Type | Nominal Diameter (mm) | Reinforced Fiber | Resin Matrix | |||||
|---|---|---|---|---|---|---|---|---|
| Brand | Diameter (μm) | Tensile Strength (MPa) | Tensile Modulus (GPa) | Density (g/cm3) | Epoxy | Hardener | ||
| GFRP | 8 | E-glass 9600 Tex | 28 | 2250 | 82 | 2.66 | Bisphenol-A E44 | MeHHPA a |
| Property | Symbol | GFRP Bars | |
|---|---|---|---|
| Tensile properties | Ultimate tensile strength (MPa) | fu,ave | 1200 ± 25 |
| Guaranteed tensile strength (MPa) | f*fu = fu,ave−3σ | 1125 | |
| Environmental reduction factor (ACI 440.1R-15) | CE | 0.7 | |
| Design tensile strength (ACI 440.1R-15) (MPa) | ffu = CE f*fu | 787.5 | |
| Modulus of elasticity (GPa) | Ef,ave | 45 ± 0.8 | |
| Ultimate strain (%) | εu,ave | 2.6 ± 0.12 | |
| Guaranteed strain (%) | ε*u = εu, ave−3σ | 2.24 | |
| Design strain (%) | εu = CEε*u | 1.57 | |
| Creep strain (%) | 20%εu | 0.31 | |
| Physical properties | Glass transition temperature (°C) | Tg | 140 |
| Fiber content by volume (%) | Vf | 71.2 | |
| Fiber content by weight (%) | Wf | 82.5 | |
| Transverse coefficient of thermal expansion (×10−6/°C) | αT | 23.2 |
| Solution Type | Quantities (Gram Per Liter) | pH | ||||
|---|---|---|---|---|---|---|
| seawater | NaCl | MgCl2 | Na2SO4 | CaCl2 | KCl | 8.1 |
| 24.53 | 5.20 | 4.10 | 1.16 | 0.71 | ||
| concrete pore solutions | NaOH | KOH | Ca(OH)2 | - | - | 13.4 |
| 2.11 | 19.63 | 2.10 | - | - | ||
| Specimen | Applied Stress, % fu,ave | Specimen (Tension Test) | Strain (Tension Test) | Residual Elastic Modulus (GPa) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Residual (MPa) | fres/fu,ave (%) | fres/f*fu (%) | fres/ffu (%) | Residual μεres (%) | εres/εu,ave (%) | εres/ε*u (%) | εres/εu (%) | |||
| G/S/23/0/30 | 0 | 1199.4 | 99.95 | 106.61 | 1.52 | 2.64 | 99.54 | 117.86 | 168.15 | 45.45 |
| G/S/23/0/60 | 1175.64 | 97.97 | 104.50 | 1.49 | 2.69 | 98.46 | 120.09 | 171.34 | 43.65 | |
| G/S/23/0/90 | 1186.92 | 98.91 | 105.50 | 1.51 | 2.54 | 97.69 | 113.39 | 161.78 | 46.8 | |
| G/S/40/0/30 | 1169.76 | 97.48 | 103.97 | 1.49 | 2.65 | 101.92 | 118.3 | 168.79 | 44.1 | |
| G/S/40/0/60 | 1119.24 | 93.27 | 99.48 | 1.42 | 2.51 | 96.54 | 112.05 | 159.87 | 44.55 | |
| G/S/40/0/90 | 1080.12 | 90.01 | 96.01 | 1.37 | 2.38 | 91.54 | 106.25 | 151.59 | 45.45 | |
| G/S/60/0/30 | 1126.32 | 93.86 | 100.1 | 1.43 | 2.58 | 99.23 | 115.18 | 164.33 | 43.65 | |
| G/S/60/0/60 | 1092.84 | 91.07 | 97.14 | 1.39 | 2.53 | 97.31 | 112.95 | 161.15 | 43.2 | |
| G/S/60/0/90 | 991.56 | 82.63 | 88.13 | 1.26 | 2.14 | 82.31 | 95.54 | 136.31 | 46.35 | |
| G/S/23/20/30 | 20 | 1194.24 | 99.52 | 106.15 | 1.52 | 2.63 | 101.15 | 117.41 | 167.52 | 45.45 |
| G/S/23/20/60 | 1156.08 | 96.34 | 102.76 | 1.47 | 2.49 | 95.77 | 111.16 | 158.6 | 46.35 | |
| G/S/23/20/90 | 1181.64 | 98.47 | 105.03 | 1.5 | 2.6 | 100 | 116.07 | 165.61 | 45.45 | |
| G/S/40/20/30 | 1180.32 | 98.36 | 104.91 | 1.5 | 2.76 | 106.15 | 123.21 | 175.8 | 42.75 | |
| G/S/40/20/60 | 1094.76 | 91.23 | 97.31 | 1.39 | 2.39 | 91.92 | 106.7 | 152.23 | 45.9 | |
| G/S/40/20/90 | 1050.72 | 87.56 | 93.39 | 1.33 | 2.41 | 92.69 | 107.59 | 153.5 | 43.65 | |
| G/S/60/20/30 | 1143.84 | 95.32 | 101.67 | 1.45 | 2.59 | 99.62 | 115.63 | 164.97 | 44.1 | |
| G/S/60/20/60 | 1049.4 | 87.45 | 93.28 | 1.33 | 2.29 | 88.08 | 102.23 | 145.86 | 45.9 | |
| G/S/60/20/90 | 962.76 | 80.23 | 85.57 | 1.22 | 2.25 | 86.54 | 100.45 | 143.31 | 42.75 | |
| G/S/23/40/30 | 40 | 1195.08 | 99.59 | 106.22 | 1.52 | 2.71 | 104.23 | 120.98 | 172.61 | 44.1 |
| G/S/23/40/60 | 1162.2 | 96.85 | 103.30 | 1.48 | 2.66 | 102.31 | 118.75 | 169.43 | 43.65 | |
| G/S/23/40/90 | 1148.04 | 95.67 | 102.04 | 1.46 | 2.66 | 102.31 | 118.75 | 169.43 | 43.2 | |
| G/S/40/40/30 | 1121.04 | 93.42 | 99.64 | 1.42 | 2.42 | 93.08 | 108.04 | 154.14 | 46.35 | |
| G/S/40/40/60 | 1035.84 | 86.32 | 92.07 | 1.32 | 2.33 | 89.62 | 104.02 | 148.41 | 44.55 | |
| G/S/40/40/90 | 987.24 | 82.27 | 87.75 | 1.25 | 2.17 | 83.46 | 96.88 | 138.22 | 45.45 | |
| G/S/60/40/30 | 1055.4 | 87.95 | 93.81 | 1.34 | 2.5 | 96.15 | 111.61 | 159.24 | 42.3 | |
| G/S/60/40/60 | 980.16 | 81.68 | 87.12 | 1.24 | 2.29 | 88.08 | 102.23 | 145.86 | 42.75 | |
| G/S/60/40/90 | 897.72 | 74.81 | 79.79 | 1.14 | 2.08 | 80 | 92.86 | 132.48 | 43.2 | |
| Specimen | Applied Stress, % fu,ave | Specimen (Tension Test) | Strain (Tension Test) | Residual Elastic Modulus (GPa) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Residual (MPa) | fres/fu,ave (%) | fres/f*fu (%) | fres/ffu (%) | Residual μεres (%) | εres/εu,ave (%) | εres/ε*u (%) | εres/εu (%) | |||
| G/C/23/0/30 | 0 | 1142.4 | 95.2 | 101.55 | 145.07 | 94.36 | 96.54 | 112.05 | 159.87 | 45.45 |
| G/C/23/0/60 | 1117.2 | 93.1 | 99.31 | 141.87 | 95.11 | 97.31 | 112.95 | 161.15 | 44.1 | |
| G/C/23/0/90 | 1083.6 | 90.3 | 96.32 | 137.6 | 91.35 | 93.46 | 108.48 | 154.78 | 44.55 | |
| G/C/40/0/30 | 1083.6 | 90.3 | 96.32 | 137.6 | 93.23 | 95.38 | 110.71 | 157.96 | 43.65 | |
| G/C/40/0/60 | 1066.8 | 88.4 | 94.83 | 135.47 | 87.22 | 89.23 | 103.57 | 147.77 | 45.9 | |
| G/C/40/0/90 | 1017.6 | 85.8 | 90.45 | 129.22 | 82.71 | 84.62 | 98.21 | 140.13 | 46.35 | |
| G/C/60/0/30 | 984 | 82 | 87.47 | 124.95 | 79.7 | 81.54 | 94.64 | 135.03 | 46.35 | |
| G/C/60/0/60 | 921.6 | 75.8 | 81.92 | 117.03 | 78.57 | 80.38 | 93.3 | 133.12 | 44.1 | |
| G/C/60/0/90 | 822 | 67.8 | 73.07 | 104.38 | 71.43 | 73.08 | 84.82 | 121.02 | 43.2 | |
| G/C/23/20/30 | 20 | 1125.6 | 93.8 | 100.05 | 142.93 | 90.6 | 92.69 | 107.59 | 153.5 | 46.8 |
| G/C/23/20/60 | 1094.4 | 91.2 | 97.28 | 138.97 | 96.24 | 98.46 | 114.29 | 163.06 | 42.75 | |
| G/C/23/20/90 | 1036.8 | 86.4 | 92.16 | 131.66 | 85.71 | 87.69 | 101.79 | 145.22 | 45.45 | |
| G/C/40/20/30 | 1095.6 | 91.3 | 97.39 | 139.12 | 88.72 | 90.77 | 105.36 | 150.32 | 46.35 | |
| G/C/40/20/60 | 1020.84 | 85.07 | 90.74 | 129.63 | 86.09 | 88.08 | 102.23 | 145.86 | 44.55 | |
| G/C/40/20/90 | 985.32 | 82.11 | 87.58 | 125.12 | 84.96 | 86.92 | 100.89 | 143.95 | 43.65 | |
| G/C/60/20/30 | 998.88 | 83.24 | 88.79 | 126.84 | 86.84 | 88.85 | 103.13 | 147.13 | 43.2 | |
| G/C/60/20/60 | 892.92 | 74.41 | 79.37 | 113.39 | 75.94 | 77.69 | 90.18 | 128.66 | 44.1 | |
| G/C/60/20/90 | 782.76 | 65.23 | 69.58 | 1.01 | 64.29 | 65.77 | 76.34 | 108.92 | 45.9 | |
| G/C/23/40/30 | 40 | 1093.56 | 91.13 | 97.21 | 138.86 | 87.97 | 90 | 104.46 | 149.04 | 46.8 |
| G/C/23/40/60 | 1016.64 | 84.72 | 90.37 | 129.1 | 84.21 | 86.15 | 100 | 142.68 | 45.45 | |
| G/C/23/40/90 | 938.88 | 78.24 | 83.46 | 119.22 | 77.82 | 79.62 | 92.41 | 131.85 | 45.45 | |
| G/C/40/40/30 | 1018.56 | 84.88 | 90.54 | 129.34 | 87.59 | 89.62 | 104.02 | 148.41 | 43.65 | |
| G/C/40/40/60 | 943.44 | 78.62 | 83.86 | 119.8 | 81.95 | 83.85 | 97.32 | 138.85 | 43.2 | |
| G/C/40/40/90 | 816.48 | 68.04 | 72.58 | 103.68 | 72.56 | 74.23 | 86.16 | 122.93 | 42.3 | |
| G/C/60/40/30 | 914.64 | 76.22 | 81.3 | 116.14 | 75.56 | 77.31 | 89.73 | 128.03 | 45.45 | |
| G/C/60/40/60 | 800.76 | 66.73 | 71.18 | 101.68 | 68.42 | 70 | 81.25 | 115.92 | 44.1 | |
| G/C/60/40/90 | 638.52 | 53.21 | 56.76 | 81.08 | 56.02 | 57.31 | 66.52 | 94.9 | 42.75 | |
| Temperature (°C) | 0 Stress Level | 20% Stress Level | 40% Stress Level | |||
|---|---|---|---|---|---|---|
| τ | R2 | τ | R2 | τ | R2 | |
| 23 | 840 | 0.96 | 610 | 0.98 | 361 | 0.99 |
| 40 | 499 | 0.87 | 413 | 0.99 | 232 | 0.98 |
| 60 | 221 | 0.94 | 202 | 0.99 | 139 | 0.98 |
| Tensile Strength Retention (%) | 0% Stress Level | 20% Stress Level | 40% Stress Level | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Ea/R | R2 | Ea (KJ/mol) | Ea/R | R2 | Ea (KJ/mol) | Ea/R | R2 | Ea (KJ/mol) | |
| 50 | 3235 | 0.97 | 26.9 | 2680 | 0.99 | 22.3 | 2317 | 0.99 | 19.2 |
| 60 | 3235 | 0.97 | 26.9 | 2680 | 0.99 | 22.3 | 2317 | 0.99 | 19.2 |
| 70 | 3235 | 0.97 | 26.9 | 2680 | 0.99 | 22.3 | 2317 | 0.99 | 19.2 |
| 80 | 3237 | 0.97 | 26.9 | 2680 | 0.99 | 22.3 | 2317 | 0.99 | 19.2 |
| Temperature (°C) | 0% Stress Level | 20% Stress Level | 40% Stress Level |
|---|---|---|---|
| 23 | 0.894 | 0.912 | 0.923 |
| 40 | 1.809 | 1.635 | 1.529 |
| 60 | 3.364 | 2.733 | 2.385 |
| Stress Level (%) | τ | R2 |
|---|---|---|
| 0 | 781 | 0.92 |
| 20 | 583 | 0.96 |
| 40 | 339 | 0.98 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tu, J.; Xie, H.; Gao, K. Prediction of the Long-Term Performance and Durability of GFRP Bars under the Combined Effect of a Sustained Load and Severe Environments. Materials 2020, 13, 2341. https://doi.org/10.3390/ma13102341
Tu J, Xie H, Gao K. Prediction of the Long-Term Performance and Durability of GFRP Bars under the Combined Effect of a Sustained Load and Severe Environments. Materials. 2020; 13(10):2341. https://doi.org/10.3390/ma13102341
Chicago/Turabian StyleTu, Jianwei, Hua Xie, and Kui Gao. 2020. "Prediction of the Long-Term Performance and Durability of GFRP Bars under the Combined Effect of a Sustained Load and Severe Environments" Materials 13, no. 10: 2341. https://doi.org/10.3390/ma13102341




