Investigation of Notch-Induced Precise Splitting of Different Bar Materials under High-Speed Load
Abstract
1. Introduction
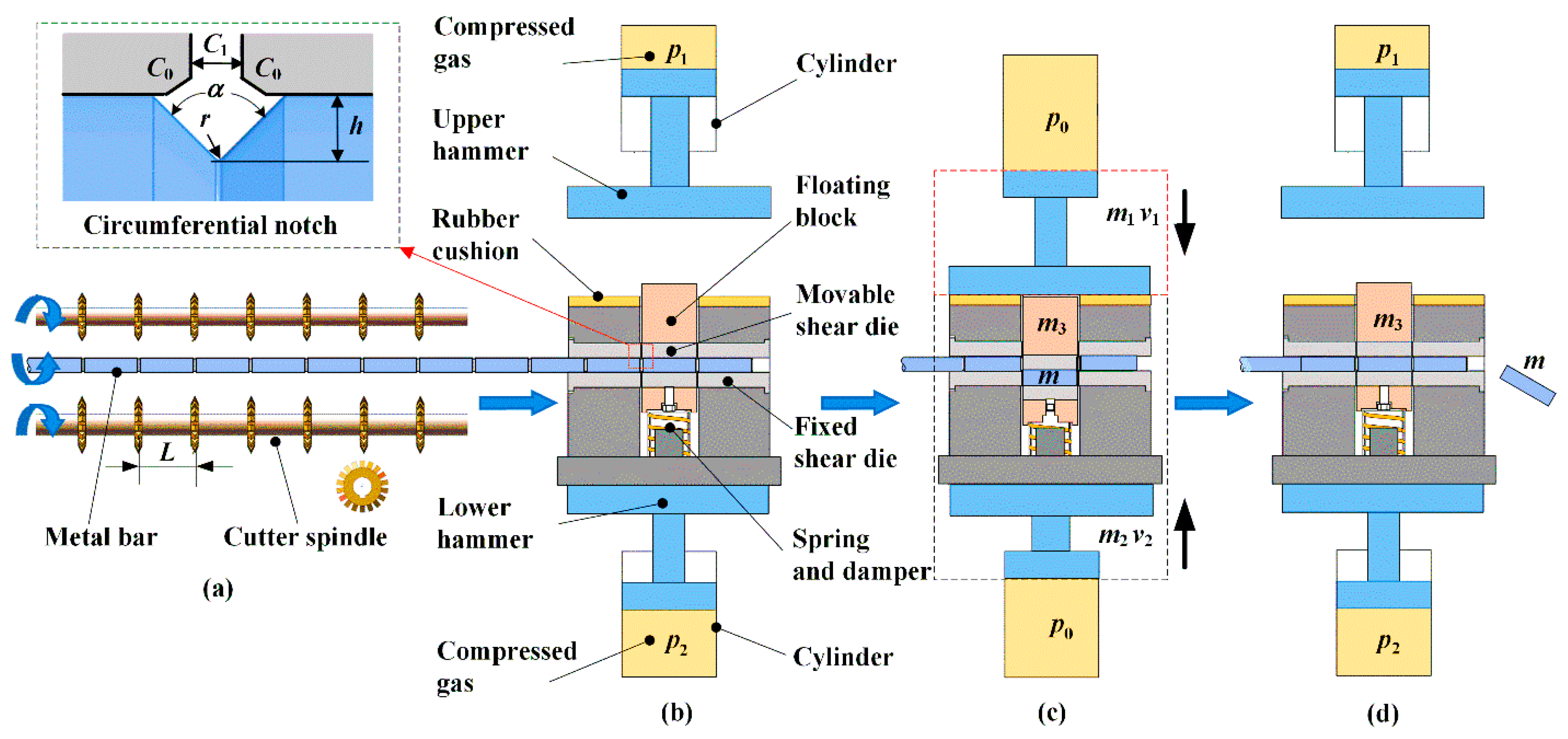
2. The Method of Notch-induced High-speed Splitting
3. Experimental Tests and FE Modeling
3.1. Experimental Tests and Materials
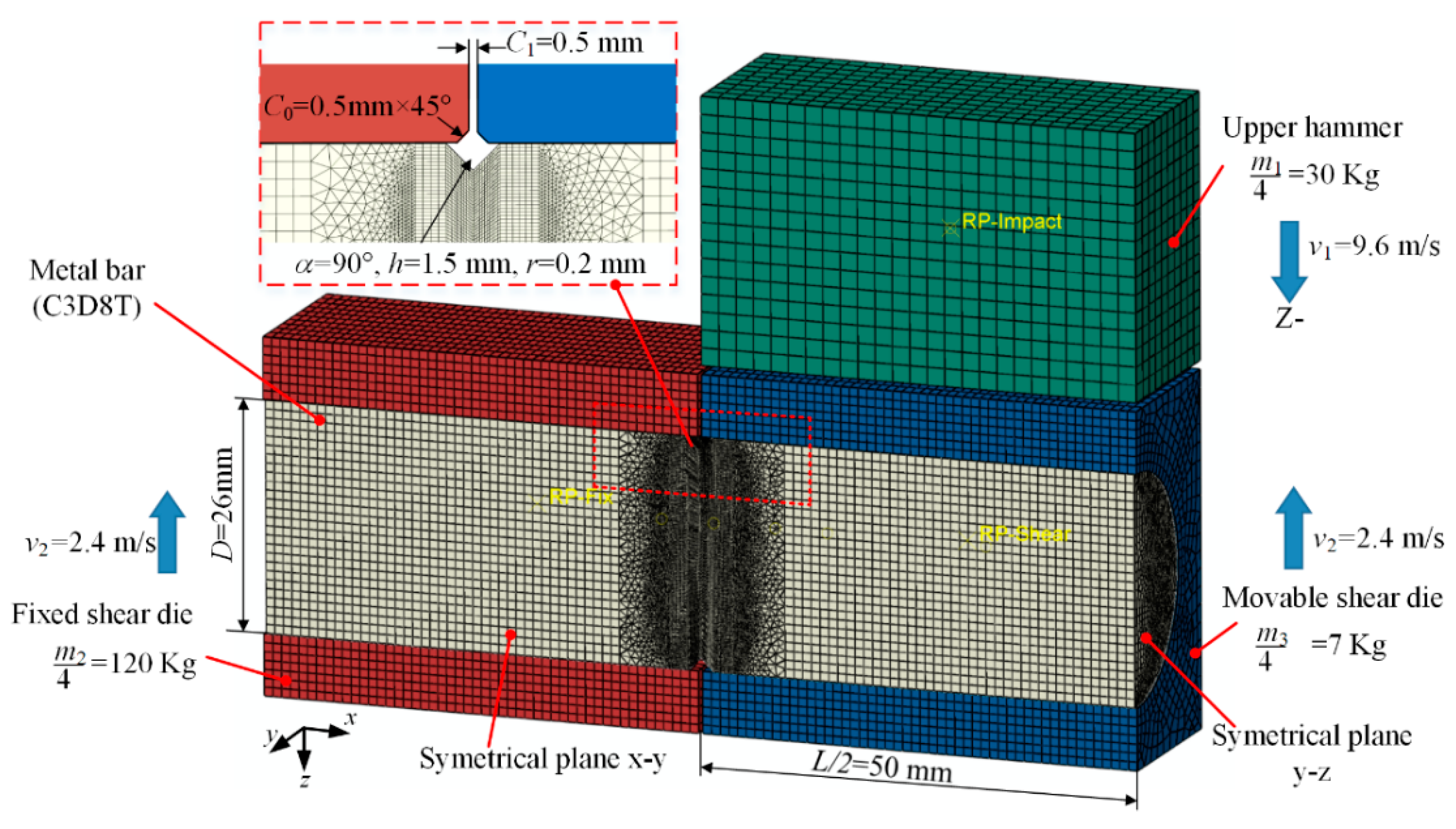
3.2. Details of the FE Model
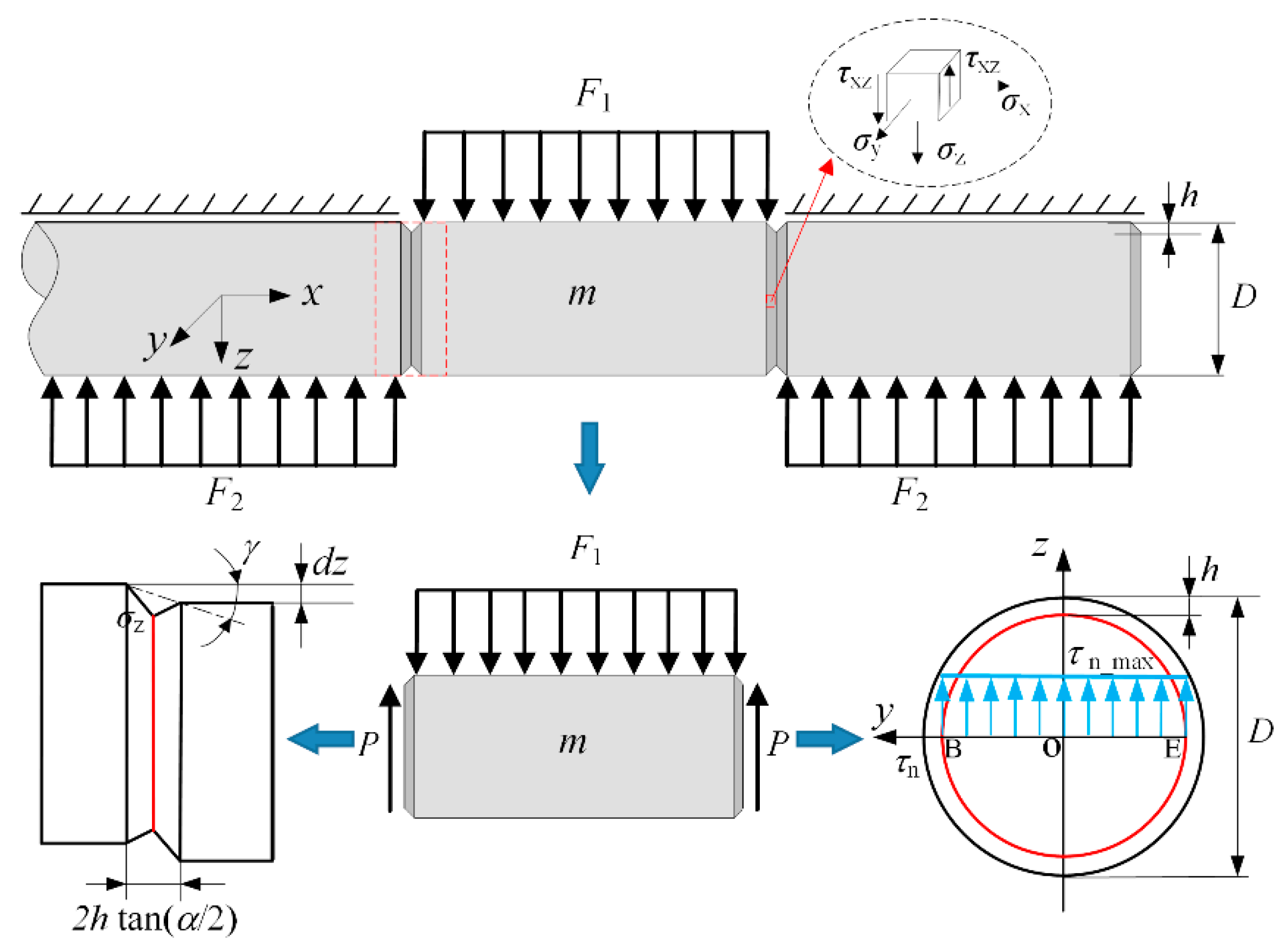
4. Results and Discussion
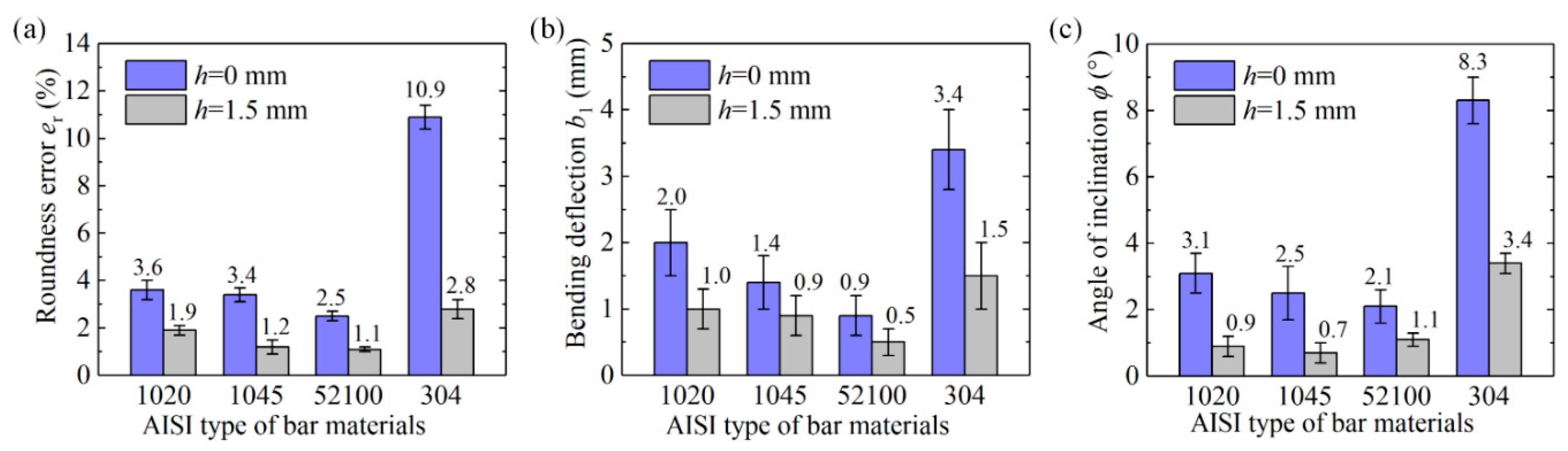
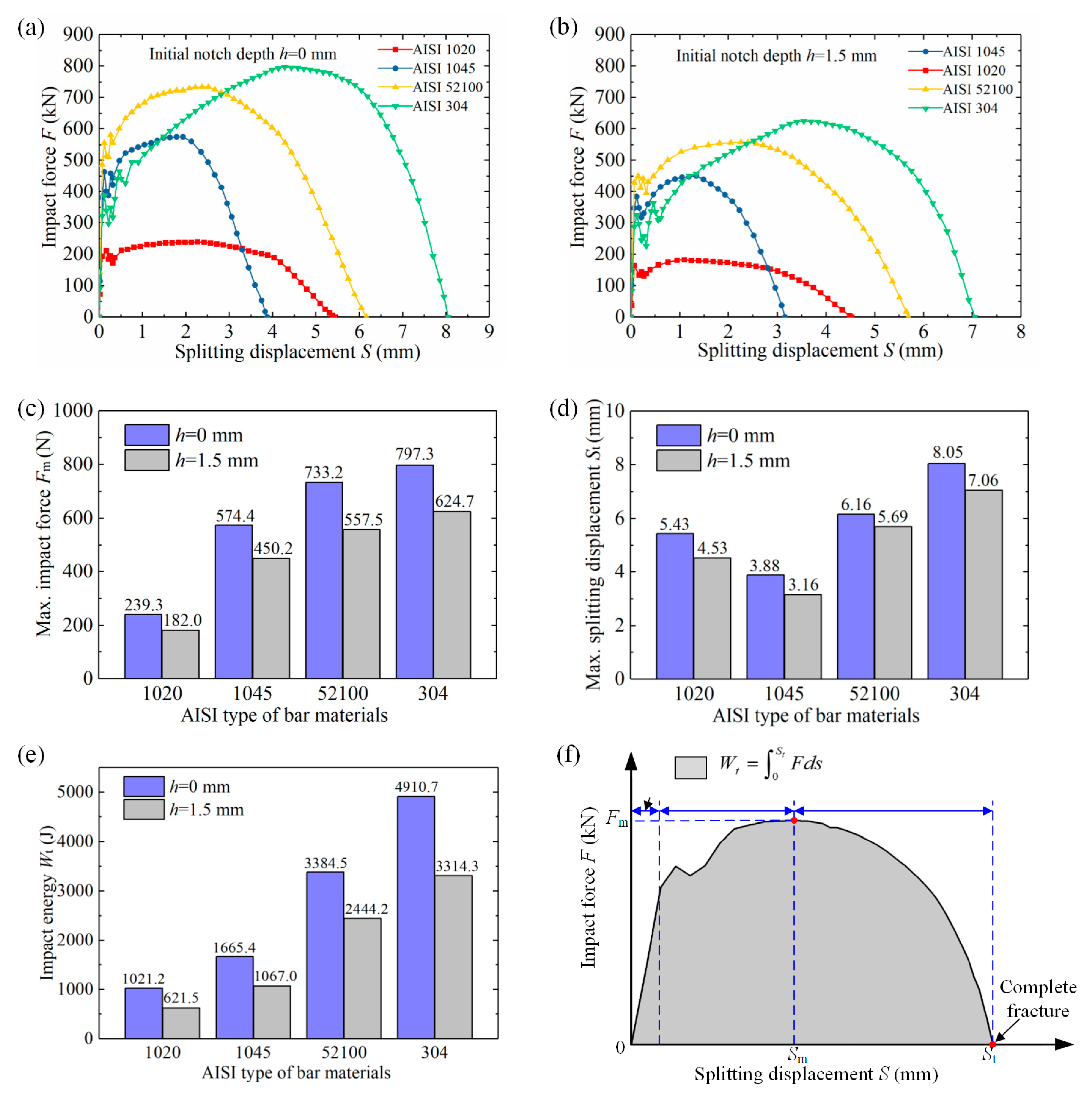
4.1. Fracture Behavior and Section Quality
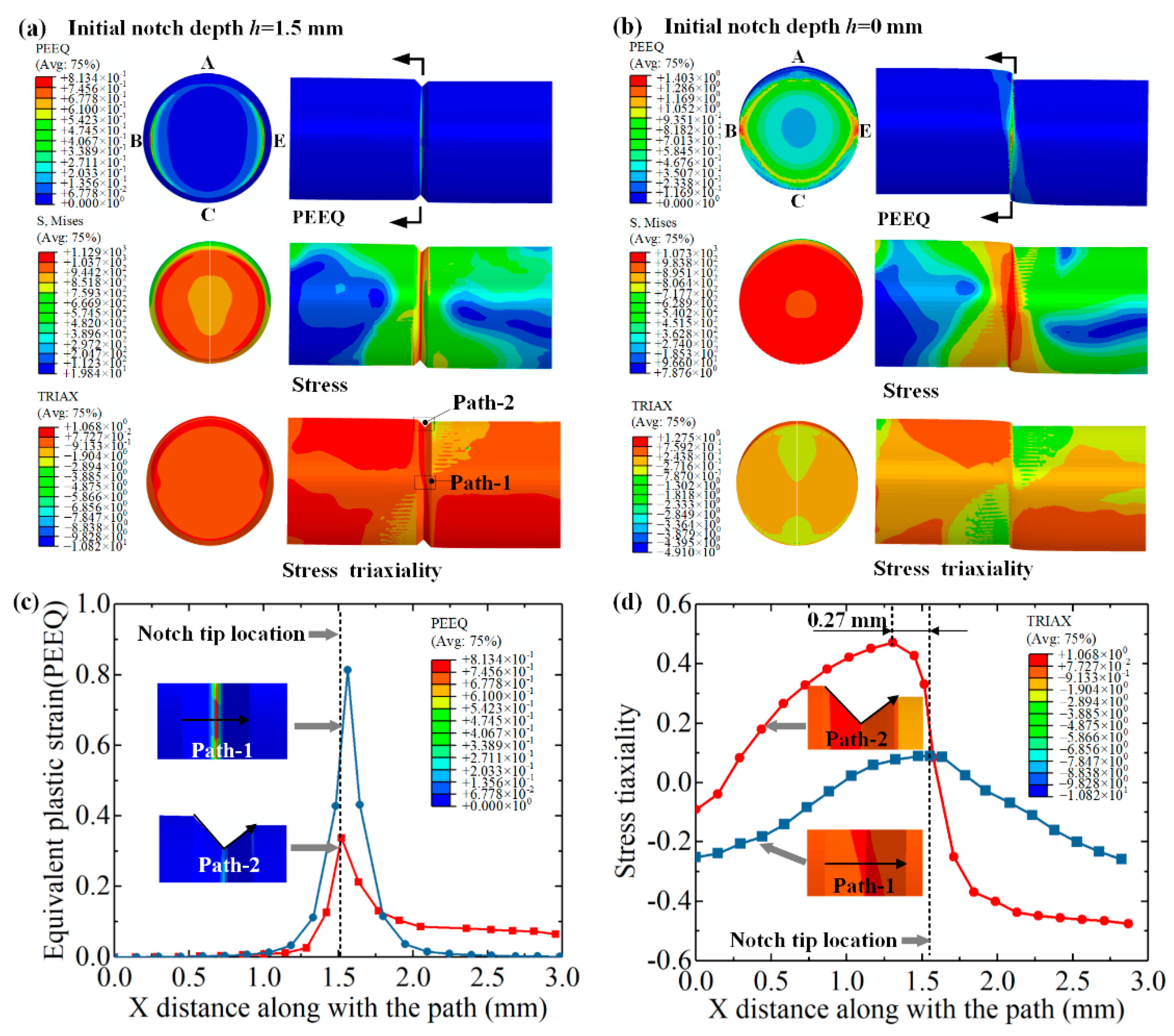
4.2. FE Simulation Results
4.3. Microfracture Mechanism Analysis
4.3.1. Crack Initiation Zone I
4.3.2. Final Rupture Zone II
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Thipprakmas, S.; Jin, M.; Murakawa, M. An investigation of material flow analysis in fineblanking process. J. Mater. Process. Technol. 2007, 192–193, 237–242. [Google Scholar] [CrossRef]
- Hu, C.; Chen, L.; Zhao, Z.; Li, J.; Li, Z. Study on the pre-shearing cropping process of steel bars. Int. J. Adv. Manuf. Technol. 2018, 97, 783–793. [Google Scholar] [CrossRef]
- Chen, M.; Li, H.; Li, X.; Liu, C. Characterization of deformation microstructure and fractured surface of plastic shearing of copper bar. Mater. Sci. Eng. A 2007, 452–453, 454–461. [Google Scholar] [CrossRef]
- Chen, J.; Yu, D.; Wang, Y.; Zhang, Z. Plastic precision cropping of metal materials. Int. J. Mach. Tools Manuf. 1992, 32, 425–433. [Google Scholar] [CrossRef]
- Kajino, S.; Asakawa, M. New billet cutting process combining torsion and shear load to reduce droop height. J. Mater. Process. Technol. 2020, 282, 1–11. [Google Scholar] [CrossRef]
- Zhao, R.; Zhao, S.; Zhong, B.; Tang, Y. Experimental investigation on new low cycle fatigue precision cropping process. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2015, 229, 1470–1476. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, X.; Wang, H.; Zhao, S.; Li, N.; Zhang, D. Research on critical loading force in precision cropping system based on hydraulic compensation. Int. J. Mech. Sci. 2018, 142–143, 44–50. [Google Scholar] [CrossRef]
- Dong, Y.; Li, J.; Ren, Y.; Fan, S.; Zhao, S. Laser-assisted cyclic chipless splitting for hard-to-cut thick wall tubes and fatigue fracture mechanism analysis. Int. J. Mech. Sci. 2020, 168, 105308. [Google Scholar] [CrossRef]
- Zhong, B.; Zhao, S.; Zhao, R.; Guo, T. Investigation on the influences of clearance and notch-sensitivity on a new type of metal-bar non-chip fine-cropping system. Int. J. Mech. Sci. 2013, 76, 144–151. [Google Scholar] [CrossRef]
- Armstrong, R.W.; Walley, S.M. High strain rate properties of metals and alloys. Int. Mater. Rev. 2008, 53, 105–128. [Google Scholar] [CrossRef]
- Singh, N.K.; Cadoni, E.; Singha, M.K.; Gupta, N.K. Dynamic tensile and compressive behaviors of mild steel at wide range of strain rates. J. Eng. Mech. 2013, 139, 1197–1206. [Google Scholar] [CrossRef]
- Hor, A.; Morel, F.; Lebrun, J.L.; Germain, G. An experimental investigation of the behaviour of steels over large temperature and strain rate ranges. Int. J. Mech. Sci. 2013, 67, 108–122. [Google Scholar] [CrossRef]
- Lu, Y.; Zhu, Z.; Li, D.; Xie, Q. Constitutive model of 42CrMo steel under a wide range of strain rates based on crystal plasticity theory. Mater. Sci. Eng. A 2017, 679, 215–222. [Google Scholar] [CrossRef]
- Zhu, Z.; Lu, Y.; Xie, Q.; Li, D.; Gao, N. Mechanical properties and dynamic constitutive model of 42CrMo steel. Mater. Des. 2017, 119, 171–179. [Google Scholar] [CrossRef]
- Figiel, Ł.; Kamiński, M.; Lauke, B. Analysis of a compression shear fracture test for curved interfaces in layered composites. Eng. Fract. Mech. 2004, 71, 967–980. [Google Scholar] [CrossRef]
- Organ, A.J.; Mellor, P.B. Mechanics of High-Speed Bar Cropping. Proc. Inst. Mech. Eng. Conf. Proc. 1965, 180, 151–162. [Google Scholar] [CrossRef]
- Chen, J.; Wang, Y.; Yu, D.; Zhang, Z. Brittle precision cropping of metal materials. Int. J. Mach. Tools Manuf. 1992, 32, 415–424. [Google Scholar] [CrossRef]
- Song, J.L.; Li, Y.T.; Liu, Z.Q.; Fu, J.H.; Ting, K.L. Numerical simulation and experiments of precision bar cutting based on high speed and restrained state. Mater. Sci. Eng. A 2009, 499, 225–229. [Google Scholar] [CrossRef]
- Xu, H.; Zhou, H.; Ma, Z.; Dai, L.; Jing, X.; Li, G.; Sun, Y. The influence of tool rake surface geometry on the hard turning process of AISI52100 hardened steel. Materials 2019, 12, 3096. [Google Scholar] [CrossRef]
- Wu, J.; Zhan, G.; He, L.; Zou, Z.; Zhou, T.; Du, F. Tribological performance of micro-groove tools of improving tool wear resistance in turning AISI 304 process. Materials 2020, 13, 1236. [Google Scholar] [CrossRef]
- Radaj, D.; Zhang, S. Notch effect of welded joints subjected to antiplane shear loading. Eng. Fract. Mech. 1992, 43, 663–669. [Google Scholar] [CrossRef]
- Zappalorto, M.; Berto, F.; Lazzarin, P. Practical expressions for the notch stress concentration factors of round bars under torsion. Int. J. Fatigue 2011, 33, 382–395. [Google Scholar] [CrossRef]
- Zappalorto, M.; Lazzarin, P.; Yates, J.R. Elastic stress distributions for hyperbolic and parabolic notches in round shafts under torsion and uniform antiplane shear loadings. Int. J. Solids Struct. 2008, 45, 4879–4901. [Google Scholar] [CrossRef]
- Gu, L.; Wang, M.; Duan, C. On adiabatic shear localized fracture during serrated chip evolution in high speed machining of hardened AISI 1045 steel. Int. J. Mech. Sci. 2013, 75, 288–298. [Google Scholar] [CrossRef]
- Osovski, S.; Rittel, D.; Venkert, A. The respective influence of microstructural and thermal softening on adiabatic shear localization. Mech. Mater. 2013, 56, 11–22. [Google Scholar] [CrossRef]
- Wang, B.; Liu, Z.; Hou, X.; Zhao, J. Influences of cutting speed and material mechanical properties on chip deformation and fracture during high-speed cutting of inconel 718. Materials 2018, 11, 461. [Google Scholar] [CrossRef]
- Chen, G.; Ren, C.; Yang, X.; Jin, X.; Guo, T. Finite element simulation of high-speed machining of titanium alloy (Ti-6Al-4V) based on ductile failure model. Int. J. Adv. Manuf. Technol. 2011, 56, 1027–1038. [Google Scholar] [CrossRef]
- Seriacopi, V.; Mezghani, S.; Crequy, S.; Machado, I.F.; El Mansori, M.; Souza, R.M. Study of angular cutting conditions using multiple scratch tests onto low carbon steel: An experimental-numerical approach. Wear 2019, 426–427, 128–136. [Google Scholar] [CrossRef]
- Chen, G.; Huang, X. Simulation of Deformation and Fracture Characteristics of a 45 Steel Taylor Impact Specimen. Eng. Trans. 2016, 64, 225–240. [Google Scholar]
- Kim, D.M.; Bajpai, V.; Kim, B.H.; Park, H.W. Finite element modeling of hard turning process via a micro-textured tool. Int. J. Adv. Manuf. Technol. 2015, 78, 1393–1405. [Google Scholar] [CrossRef]
- Dean, J.; S-Fallah, A.; Brown, P.M.; Louca, L.A.; Clyne, T.W. Energy absorption during projectile perforation of lightweight sandwich panels with metallic fibre cores. Compos. Struct. 2011, 93, 1089–1095. [Google Scholar] [CrossRef]
- Martinez, J.; Patin, R.; Figert, J. Failure analysis of international low impact docking system latch hooks. Microsc. Microanal. 2013, 19, 1830–1831. [Google Scholar] [CrossRef]





| Materials | Johnson-Cook Plasticity Parameters | Damage Parameters | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A (Mpa) | B (MPa) | n | m | C | d1 | d2 | d3 | d4 | d5 | ||
| 1020 [28] | 213 | 53 | 0.345 | 0.81 | 0.055 | 0.004 | 0.05 | 3.44 | −2.12 | 0.002 | 0.61 |
| 1045 [29] | 506 | 320 | 0.28 | 1.06 | 0.064 | 1 | 0.1 | 0.76 | −1.57 | 0.005 | −0.84 |
| 52100 [30] | 774.78 | 134 | 0.37 | 3.171 | 0.018 | 1 | 0.0368 | 2.34 | −1.484 | 0.0035 | 0.411 |
| 304 [31] | 310 | 1000 | 0.65 | 1 | 0.07 | 0.1 | 0.53 | 0.5 | −6.8 | −0.014 | 0.0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Y.; Ren, Y.; Fan, S.; Wang, Y.; Zhao, S. Investigation of Notch-Induced Precise Splitting of Different Bar Materials under High-Speed Load. Materials 2020, 13, 2461. https://doi.org/10.3390/ma13112461
Dong Y, Ren Y, Fan S, Wang Y, Zhao S. Investigation of Notch-Induced Precise Splitting of Different Bar Materials under High-Speed Load. Materials. 2020; 13(11):2461. https://doi.org/10.3390/ma13112461
Chicago/Turabian StyleDong, Yuanzhe, Yujian Ren, Shuqin Fan, Yongfei Wang, and Shengdun Zhao. 2020. "Investigation of Notch-Induced Precise Splitting of Different Bar Materials under High-Speed Load" Materials 13, no. 11: 2461. https://doi.org/10.3390/ma13112461
APA StyleDong, Y., Ren, Y., Fan, S., Wang, Y., & Zhao, S. (2020). Investigation of Notch-Induced Precise Splitting of Different Bar Materials under High-Speed Load. Materials, 13(11), 2461. https://doi.org/10.3390/ma13112461







