Axial Compressive Behaviour of Square Through-Beam Joints between CFST Columns and RC Beams with Multi-Layers of Steel Meshes
Abstract
:1. Introduction
2. Tests of Joint with CFST Columns (Series I Tests)
2.1. General
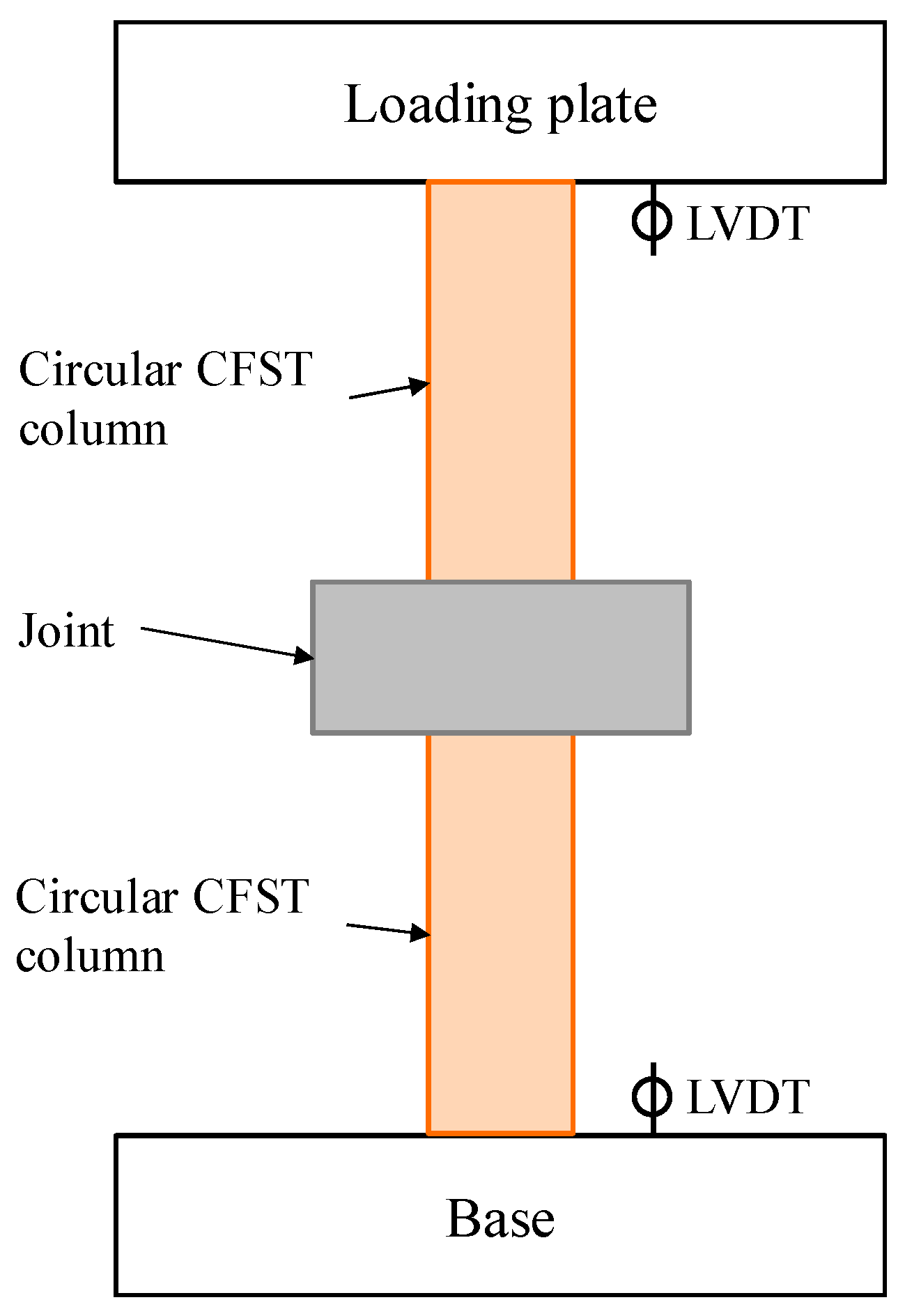
2.2. Experimental Test Setup
2.3. Experimental Results
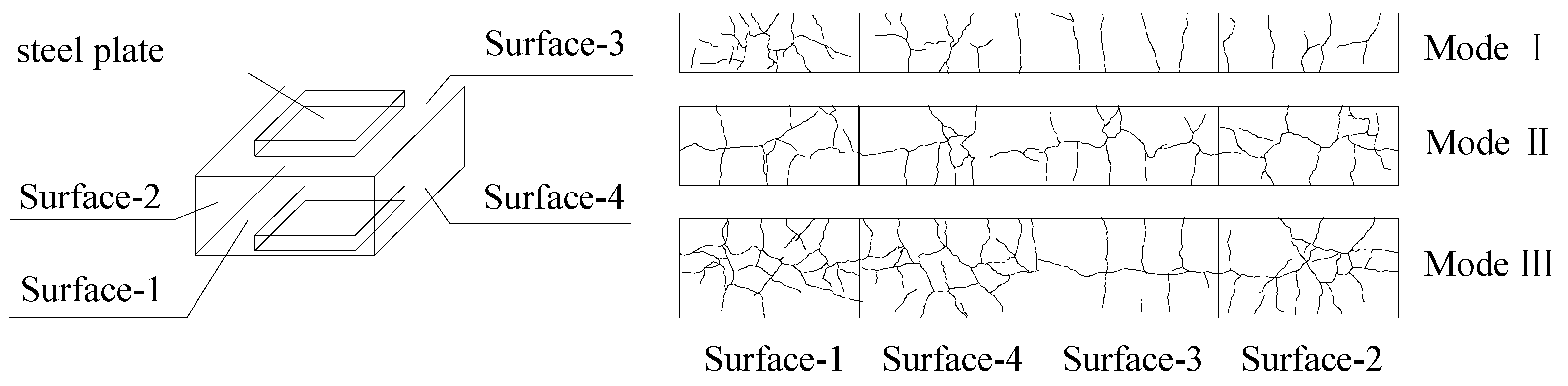
2.3.1. Failure Modes
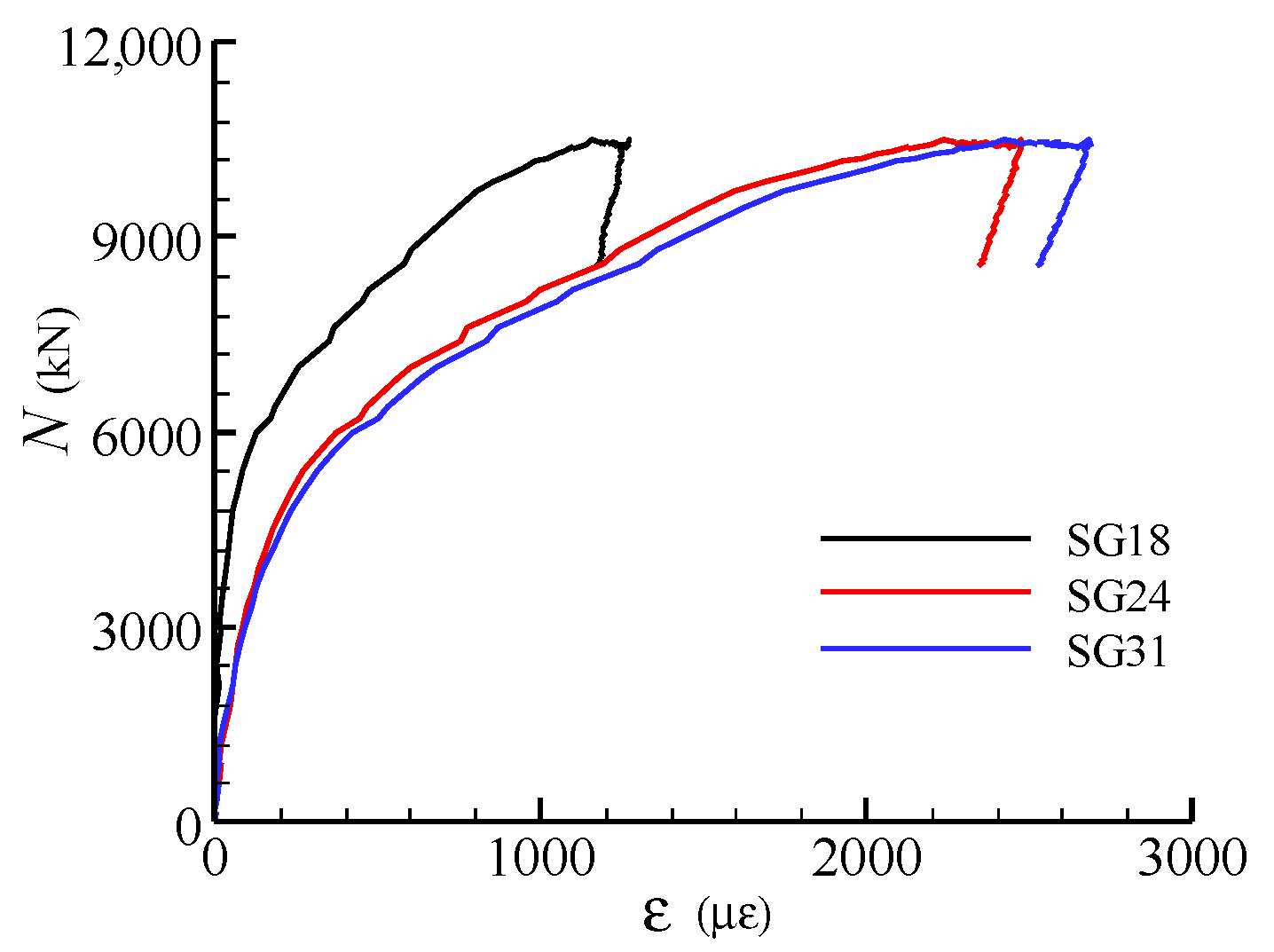
2.3.2. Load-Deformation and Load-Strain Curves
2.4. Summary for the Series I Tests
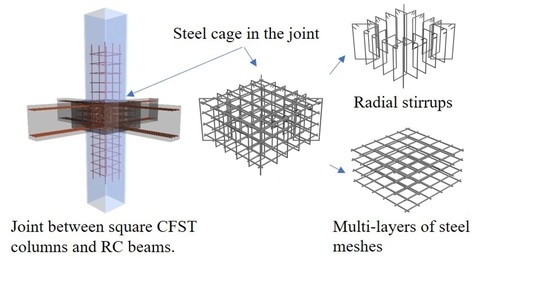
3. Axial Compression Tests on Innovative Joints (Series II Tests)
3.1. General
3.2. Experimental Test Setup
3.3. Failure Modes
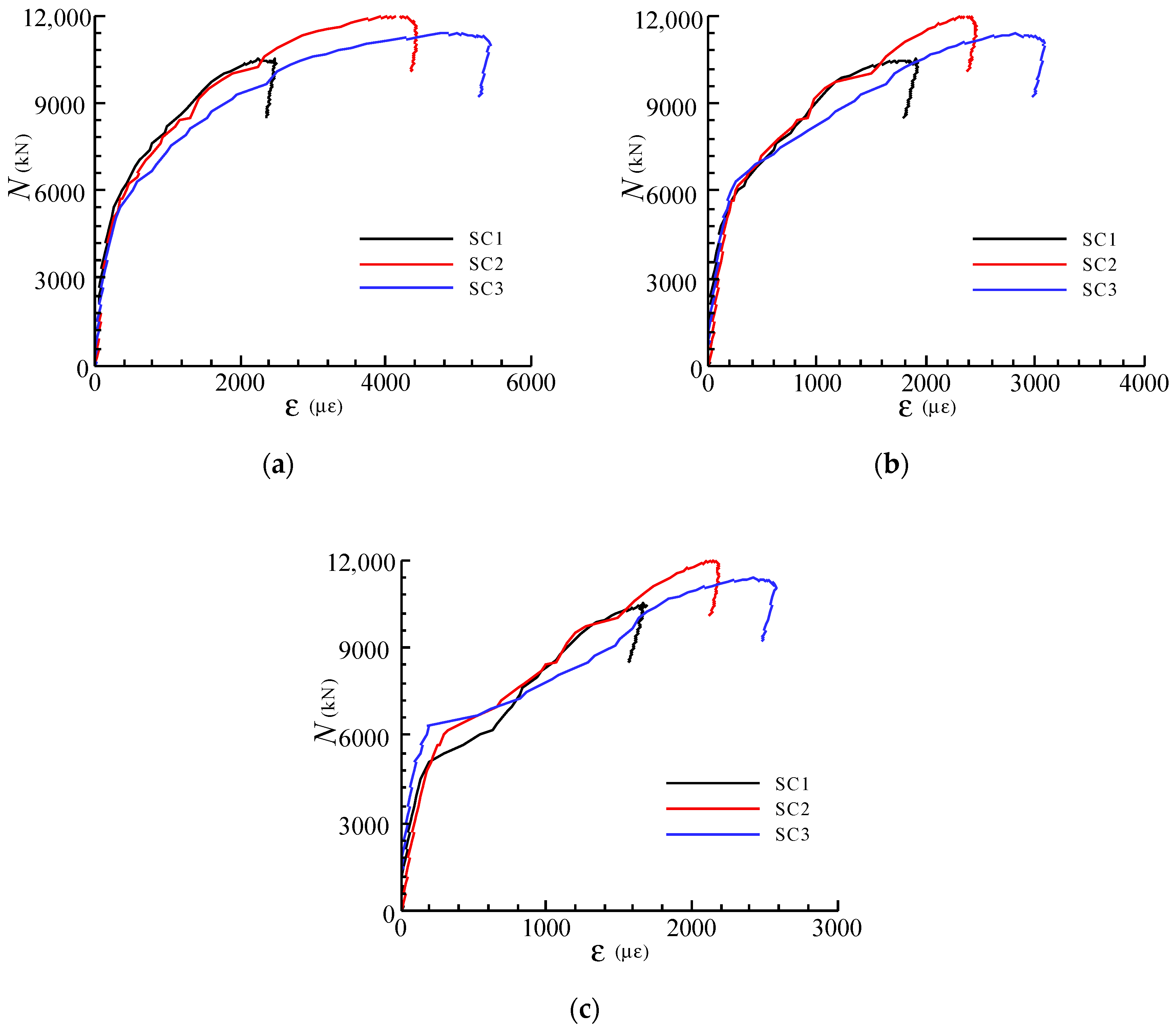
3.4. Load-Deformation Curves and Load-Strain Curves
3.5. Summary for the Series II Tests
4. Calculation of Axial Compression Capacity of the Joints
4.1. General
4.2. Effect of Local Compression
4.3. Confinement Effect Provided by the Multi-Layers of Steel Meshes
4.4. Height Effect of Concrete
4.5. Prediction and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Roeder, C.W. Overview of hybrid and composite systems for seismic design in the United States. Eng. Struct. 1998, 20, 355–363. [Google Scholar] [CrossRef]
- Miller, D.K. Lessons learned from the Northridge earthquake. Eng. Struct. 1998, 20, 249–260. [Google Scholar] [CrossRef]
- Popov, E.P.; Yang, T.-S.; Chang, S.-P. Design of steel MRF connections before and after 1994 Northridge earthquake. Eng. Struct. 1998, 20, 1030–1038. [Google Scholar] [CrossRef]
- Fang, X.; Li, S.; Qian, J.; Yang, R. Experimental Research on Seismic Behavior of Concrete Filled Steel Tubular Column Ring Beam Joint Under Cyclic Loading. J. Build. Struct. 2002, 23, 10–18. [Google Scholar]
- Han, L.-H.; Qu., H.; Tao, Z.; Wang, Z.-F. Experimental behaviour of thin-walled steel tube confined concrete column to RC beam joints under cyclic loading. Thin-Walled Struct. 2009, 47, 847–857. [Google Scholar] [CrossRef]
- Pan, P.; Lam, A.; Lin, X.; Li, Y.; Ye, L. Cyclic loading tests and finite element analyses on performance of ring beam connections. Eng. Struct. 2013, 56, 682–690. [Google Scholar] [CrossRef]
- Zha, X.; Wan, C.; Yu, H.; Dassekpo, J.-B.M. Seismic behavior study on RC-beam to CFST-column non-welding joints in field construction. J. Constr. Steel Res. 2016, 116, 204–217. [Google Scholar] [CrossRef]
- Nie, J.; Bai, Y.; Cai, C. New connection system for confined concrete columns and beams. I: Experimental study. J. Struct. Eng. 2008, 134, 1787–1799. [Google Scholar] [CrossRef]
- Bai, Y.; Nie, J.; Cai, C. New connection system for confined concrete columns and beams. II: Theoretical modeling. J. Struct. Eng. 2008, 134, 1800–1809. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, J.; Cai, C. Seismic behavior of ring beam joints between concrete-filled twin steel tubes columns and reinforced concrete beams. Eng. Struct. 2012, 39, 1–10. [Google Scholar] [CrossRef]
- Chen, Q.; Cai, J.; Bradford, M.A.; Liu, X.; Wu, Y. Axial compressive behavior of through-beam connections between concrete-filled steel tubular columns and reinforced concrete beams. J. Struct. Eng. 2015, 141, 04015016. [Google Scholar] [CrossRef]
- Chen, Q.-J.; Cai, J.; Bradford, M.A.; Liu, X.; Zuo, Z.-L. Seismic behaviour of a through-beam connection between concrete-filled steel tubular columns and reinforced concrete beams. Eng. Struct. 2014, 80, 24–39. [Google Scholar] [CrossRef]
- Zhou, X.; Cheng, G.; Liu, J.; Gan, D.; Frank Chen, Y. Behavior of circular tubed-RC column to RC beam connections under axial compression. J. Constr. Steel Res. 2017, 130, 96–108. [Google Scholar] [CrossRef]
- Zhou, X.; Zhou, Z.; Gan, D. Cyclic testing of square tubed-reinforced-concrete column to RC beam joints. Eng. Struct. 2018, 176, 439–454. [Google Scholar] [CrossRef]
- Tang, X.-L.; Cai, J.; Chen, Q.-J.; Liu, X.; He, A. Seismic behaviour of through-beam connection between square CFST columns and RC beams. J. Constr. Steel Res. 2016, 122, 151–166. [Google Scholar] [CrossRef]
- Code for Design of Concrete Structures, National Standard of PRC GB 50010; National Standards of People’s Republic of China: Beijing, China, 2010.
- Hawkins, N.M. The bearing strength of concrete loaded through rigid plates. Mag. Concr. Res. 1968, 20, 31–40. [Google Scholar] [CrossRef]
- Niyogi, S.K. Bearing strength of reinforced concrete blocks. J. Struct. Div. 1975, 101, 1125–1137. [Google Scholar]
- Ahmed, T.; Burley, E.; Rigden, S. Bearing capacity of plain and reinforced concrete loaded over a limited area. Struct. J. 1998, 95, 330–342. [Google Scholar]
- Ince, R.; Arici, E. Size effect in bearing strength of concrete cubes. Constr. Build. Mater. 2004, 18, 603–609. [Google Scholar] [CrossRef]
- Au, T.; Baird, D.L. Bearing capacity of concrete blocks. ACI Struct. J. 1960, 56, 869–880. [Google Scholar]
- Meyerhof, G.G. The bearing capacity of concrete and rock. Mag. Concr. Res. 1953, 4, 107–116. [Google Scholar] [CrossRef]
- Komendant, A.E. Prestressed Concrete Structures, 1st ed.; McGraw-Hill: New York, NY, USA, 1952. [Google Scholar]
- ACI Committee, American Concrete Institute; International Organization for Standardization. Building Code Requirements for Structural Concrete (ACI 318-08) and Commentary; American Concrete Institute: Farmington Hills, MI, USA, 2008. [Google Scholar]
- Mander, J.B.; Priestley, M.J.; Park, R. Theoretical stress-strain model for confined concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef] [Green Version]
- Dehestani, M.; Nikbin, I.; Asadollahi, S. Effects of specimen shape and size on the compressive strength of self-consolidating concrete (SCC). Constr. Build. Mater. 2014, 66, 685–691. [Google Scholar] [CrossRef]
- Yi, S.-T.; Yang, E.-I.; Choi, J.-C. Effect of specimen sizes, specimen shapes, and placement directions on compressive strength of concrete. Nucl. Eng. Des. 2006, 236, 115–127. [Google Scholar] [CrossRef]
- British Standards Institution. Eurocode 2: Design of Concrete Structures: Part 1-1: General Rules and Rules for Buildings; British Standards Institution: London, UK, 2004. [Google Scholar]


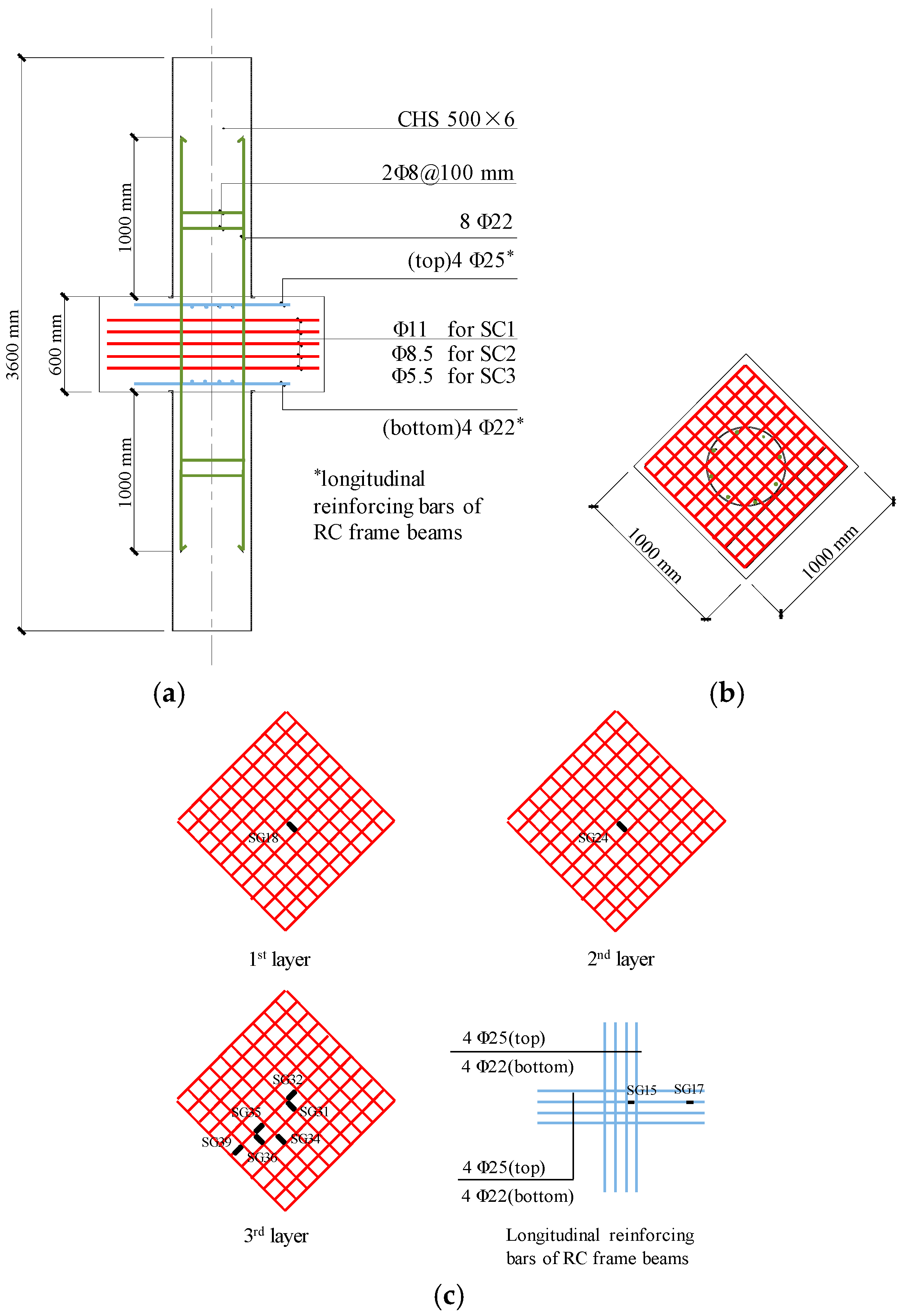












| Specimen | D × t (mm × mm) | A × A × H (mm × mm × mm) | fcu,u (MPa) | fcu (MPa) | fcu,l (MPa) | dbar (mm) | ρv (%) | Ncr (kN) | Nu (kN) | Ncr/Nu | Ncal (kN) | Ncal/Nu |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SC1 | 500 × 6 | 1000 × 1000 × 600 | 46.3 | 40.8 | 44.7 | 11 | 1.65 | 6000 | 10,534 | 0.57 | 20,112 | 1.91 |
| SC2 | 500 × 6 | 1000 × 1000 × 600 | 46.3 | 40.8 | 44.7 | 8.5 | 0.99 | 5300 | 12,004 | 0.44 | 18,395 | 1.53 |
| SC3 | 500 × 6 | 1000 × 1000 × 600 | 46.3 | 40.8 | 44.7 | 5.5 | 0.41 | 5100 | 11,404 | 0.45 | 15,954 | 1.40 |
| Member | Bar Φ5.5 | Bar Φ8 | Bar Φ8.5 | Bar Φ11 | Bar Φ22 | Bar Φ25 | Steel Tube |
|---|---|---|---|---|---|---|---|
| Yield strength fy (MPa) | 517 | 318 | 510 | 448 | 386 | 368 | 330 |
| Ultimate strength fu (MPa) | 578 | 460 | 608 | 540 | 575 | 575 | 460 |
| Specimen | A × A × H | a × a | fcu | γ | β | ρv | Layers of Steel Meshes | 1st Layer Steel Mesh | 2nd Layer Steel Mesh | 3rd Layer Steel Mesh | 4st Layer Steel Mesh |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (mm × mm × mm) | (mm) | (MPa) | (%) | ||||||||
| C20-L1-H3-S2 | 480 × 480 × 300 | 300 × 300 | 15.35 | 1.6 | 1.0 | 1.5 | 4 | 6Φ8 | 6Φ8 | 6Φ8 | 6Φ8 |
| C20-L2-H1-S2 | 540 × 540 × 180 | 300 × 300 | 15.35 | 1.8 | 0.6 | 1.5 | 3 | 6Φ8 | 4Φ6 + 2Φ8 | 6Φ8 | - |
| C20-L2-H2-S2 | 540 × 540 × 240 | 300 × 300 | 15.35 | 1.8 | 0.8 | 1.5 | 4 | 6Φ8 | 3Φ6 + 3Φ8 | 3Φ6 + 3Φ8 | 6Φ8 |
| C20-L2-H3-S1 | 540 × 540 × 300 | 300 × 300 | 15.35 | 1.8 | 1.0 | 1.0 | 4 | 6Φ6 | 5Φ8 + 1Φ6 | 5Φ8 + 1Φ6 | 6Φ6 |
| C20-L2-H3-S2 | 540 × 540 × 300 | 300 × 300 | 15.35 | 1.8 | 1.0 | 1.5 | 4 | 6Φ6 | 3Φ8 + 3Φ10 | 3Φ8 + 3Φ10 | 6Φ6 |
| C20-L2-H3-S3 | 540 × 540 × 300 | 300 × 300 | 15.35 | 1.8 | 1.0 | 2.0 | 4 | 6Φ10 | 1Φ8 + 5Φ10 | 1Φ8 + 5Φ10 | 6Φ10 |
| C20-L3-H3-S2 | 600 × 600 × 300 | 300 × 300 | 15.35 | 2.0 | 1.0 | 1.5 | 4 | 6Φ8 | 5Φ10 + 1Φ8 | 5Φ10 + 1Φ8 | 6Φ8 |
| C30-L2-H1-S2 | 540 × 540 × 180 | 300 × 300 | 32.96 | 1.8 | 0.6 | 1.5 | 3 | 6Φ8 | 4Φ6 + 2Φ8 | 6Φ8 | - |
| C30-L2-H2-S1 | 540 × 540 × 240 | 300 × 300 | 32.96 | 1.8 | 0.8 | 1.0 | 4 | 6Φ6 | 5Φ6 + 1Φ8 | 5Φ6 + 1Φ8 | 6Φ6 |
| C30-L2-H2-S2 | 540 × 540 × 240 | 300 × 300 | 32.96 | 1.8 | 0.8 | 1.5 | 4 | 6Φ8 | 3Φ6 + 3Φ8 | 3Φ6 + 3Φ8 | 6Φ8 |
| C30-L2-H2-S3 | 540 × 540 × 240 | 300 × 300 | 32.96 | 1.8 | 0.8 | 2.0 | 4 | 6Φ10 | 4Φ8 + 2Φ6 | 4Φ8 + 2Φ6 | 6Φ10 |
| C30-L2-H3-S1 | 540 × 540 × 300 | 300 × 300 | 32.96 | 1.8 | 1.0 | 1.0 | 4 | 6Φ6 | 5Φ8 + 1Φ6 | 5Φ8 + 1Φ6 | 6Φ6 |
| C30-L2-H3-S2 | 540 × 540 × 300 | 300 × 300 | 32.96 | 1.8 | 1.0 | 1.5 | 4 | 6Φ8 | 3Φ8 + 3Φ10 | 3Φ8 + 3Φ10 | 6Φ8 |
| C30-L2-H3-S3 | 540 × 540 × 300 | 300 × 300 | 32.96 | 1.8 | 1.0 | 2.0 | 4 | 6Φ10 | 1Φ8 + 5Φ10 | 1Φ8 + 5Φ10 | 6Φ10 |
| Member | Series C20 | Series C30 | ||||
|---|---|---|---|---|---|---|
| BarΦ6 | Bar Φ8 | Bar Φ10 | Bar Φ6 | Bar Φ8 | Bar Φ10 | |
| Yielding strength fy (MPa) | 259.9 | 472 | 422 | 260 | 300 | 340 |
| Ultimate strength fu (MPa) | 430 | 536.1 | 480.4 | 440 | 340 | 430 |
| Specimens | Ncr (kN) | Ncr/Nu | N0.2 (kN) | N0.2/Nu | N0.3 (kN) | N0.3/Nu | Nu (kN) | Crack Mode | Ncal (kN) | Ncal/Nu |
|---|---|---|---|---|---|---|---|---|---|---|
| C20-L1-H3-S2 | 300 | 0.122 | 800 | 0.325 | 1000 | 0.406 | 2465 | III | 3097 | 1.26 |
| C20-L2-H1-S2 | 400 | 0.116 | 1100 | 0.320 | 1500 | 0.437 | 3435 | I | 3763 | 1.10 |
| C20-L2-H2-S2 | 600 | 0.178 | 1400 | 0.416 | 1500 | 0.445 | 3369 | II | 3592 | 1.07 |
| C20-L2-H3-S1 | 600 | 0.280 | 1200 | 0.559 | 1400 | 0.652 | 2146 | III | 3103 | 1.45 |
| C20-L2-H3-S2 | 600 | 0.240 | 1000 | 0.400 | 1400 | 0.560 | 2498 | III | 3484 | 1.39 |
| C20-L2-H3-S3 | 600 | 0.221 | 750 | 0.277 | 1000 | 0.369 | 2712 | III | 3813 | 1.41 |
| C20-L3-H3-S2 | 600 | 0.235 | 1050 | 0.412 | 1400 | 0.549 | 2550 | III | 3871 | 1.52 |
| C30-L2-H1-S2 | 800 | 0.103 | 1100 | 0.141 | 1800 | 0.231 | 7801 | I | 6845 | 0.88 |
| C30-L2-H2-S1 | 900 | 0.156 | 2100 | 0.363 | 2700 | 0.467 | 5782 | II | 5938 | 1.03 |
| C30-L2-H2-S2 | 1200 | 0.184 | 2400 | 0.369 | 3300 | 0.507 | 6505 | II | 6380 | 0.98 |
| C30-L2-H2-S3 | 1200 | 0.180 | 2400 | 0.360 | 2700 | 0.405 | 6659 | II | 6789 | 1.02 |
| C30-L2-H3-S1 | 900 | 0.193 | 1500 | 0.321 | 2400 | 0.514 | 4673 | III | 5612 | 1.20 |
| C30-L2-H3-S2 | 900 | 0.162 | 1500 | 0.270 | 1800 | 0.324 | 5550 | III | 6081 | 1.10 |
| C30-L2-H3-S3 | 900 | 0.147 | 1500 | 0.245 | 1800 | 0.294 | 6122 | III | 6512 | 1.06 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, W.; Cai, J.; Tang, X.-L.; Chen, Q.-J.; Yang, C.; He, A. Axial Compressive Behaviour of Square Through-Beam Joints between CFST Columns and RC Beams with Multi-Layers of Steel Meshes. Materials 2020, 13, 2482. https://doi.org/10.3390/ma13112482
Duan W, Cai J, Tang X-L, Chen Q-J, Yang C, He A. Axial Compressive Behaviour of Square Through-Beam Joints between CFST Columns and RC Beams with Multi-Layers of Steel Meshes. Materials. 2020; 13(11):2482. https://doi.org/10.3390/ma13112482
Chicago/Turabian StyleDuan, Weining, Jian Cai, Xu-Lin Tang, Qing-Jun Chen, Chun Yang, and An He. 2020. "Axial Compressive Behaviour of Square Through-Beam Joints between CFST Columns and RC Beams with Multi-Layers of Steel Meshes" Materials 13, no. 11: 2482. https://doi.org/10.3390/ma13112482
APA StyleDuan, W., Cai, J., Tang, X.-L., Chen, Q.-J., Yang, C., & He, A. (2020). Axial Compressive Behaviour of Square Through-Beam Joints between CFST Columns and RC Beams with Multi-Layers of Steel Meshes. Materials, 13(11), 2482. https://doi.org/10.3390/ma13112482