Author Contributions
Conceptualization, T.H. and H.-f.L.; Data curation, T.H., M.L., H.-f.L.; Formal analysis, T.H. and H.-f.L.; Funding acquisition, T.H. and H.-f.L.; Methodology, T.H.; Project administration, T.H. and H.-f.L.; Resources, T.H. and H.-f.L.; Supervision, T.H. and H.-f.L.; Writing—original draft, T.H., M.L., M.-y.H., H.-h.J., Y.T.; Writing—review & editing, T.H., M.L., M.-y.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the: National Key R&D Program of China (grant number 2018YFB1600-100), Natural Science Foundation of Hunan Province (grant number2019JJ40297), the education department of Hunan Province (grant number 18B143, 18B144), Science and Technology progress and Innovation Project of Hunan Provincial Department of Transportation (grant number 201904), National Natural Science Foundation of China (grant number 51608055, 51608058), Open Found of Key Laboratory of Special Environment Road Engineering of Hunan Province (Changsha University of Science and Technology grant number Kfj190501), State Scholarship Fund (grant number 201908430034), the project of Changsha science and Technology Bureau (grant number kq1901107).
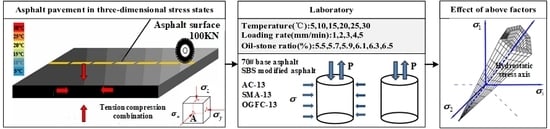
Figure 1.
The research program of the failure strength models of asphalt mixtures under various factors.
Figure 1.
The research program of the failure strength models of asphalt mixtures under various factors.
Figure 2.
The gradation of three type of asphalt mixture.
Figure 2.
The gradation of three type of asphalt mixture.
Figure 3.
Gyratory compactor device and test specimens.
Figure 3.
Gyratory compactor device and test specimens.
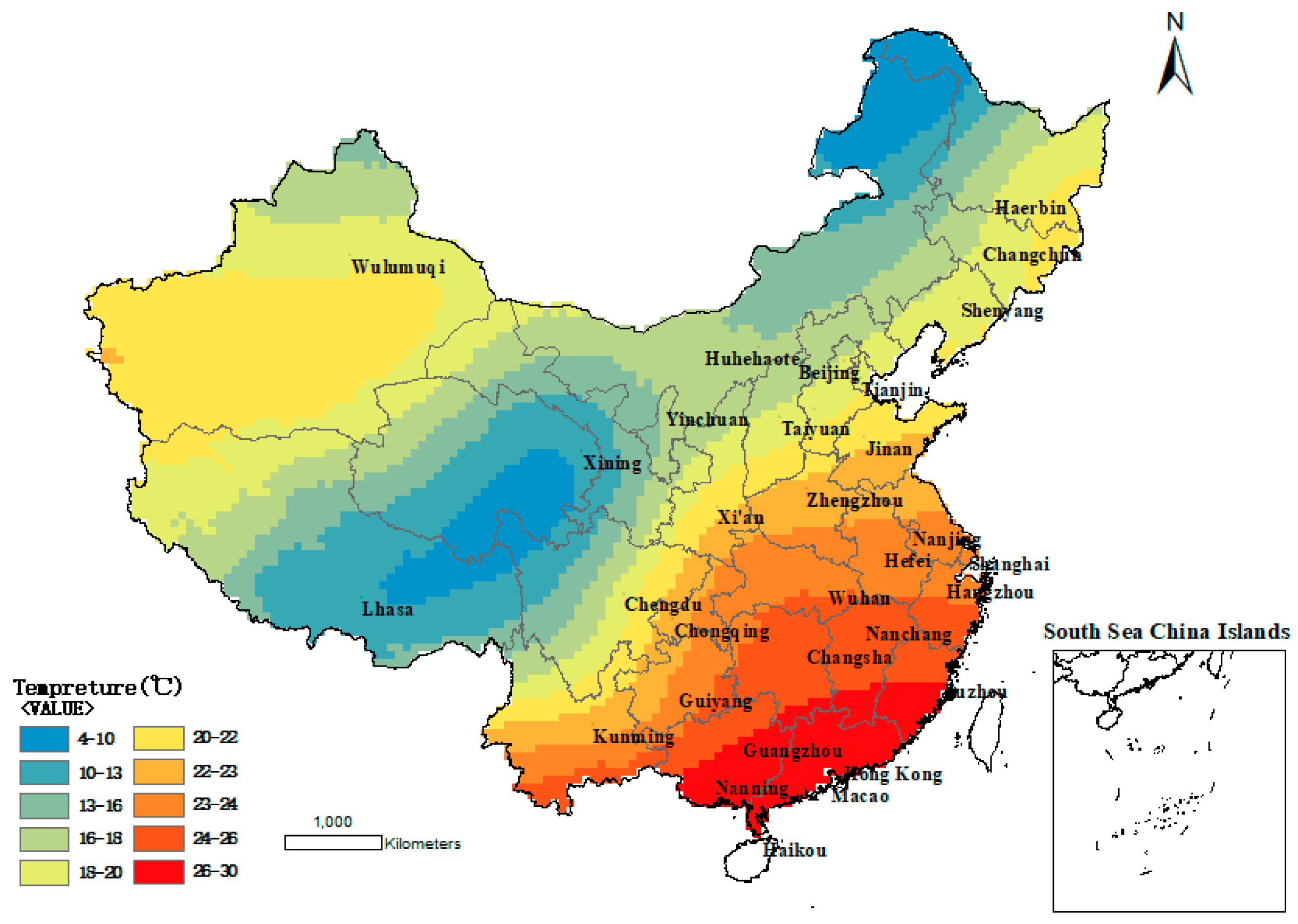
Figure 4.
China benchmark equivalent temperature map.
Figure 4.
China benchmark equivalent temperature map.
Figure 5.
The nonlinear and linear strength models of asphalt mixture.
Figure 5.
The nonlinear and linear strength models of asphalt mixture.
Figure 6.
Strength test under various stress states.
Figure 6.
Strength test under various stress states.
Figure 7.
Linear compressive and tensile meridian under three type of gradation. (a) The compressive and tensile meridian under three type of gradation (b) The strength comparison between three type of gradation.
Figure 7.
Linear compressive and tensile meridian under three type of gradation. (a) The compressive and tensile meridian under three type of gradation (b) The strength comparison between three type of gradation.
Figure 8.
Linear compressive and tensile meridian under different oil-stone ratios. (a) The compressive and tensile meridian under six different oil-stone ratios (b) The strength comparison between six different oil-stone ratios.
Figure 8.
Linear compressive and tensile meridian under different oil-stone ratios. (a) The compressive and tensile meridian under six different oil-stone ratios (b) The strength comparison between six different oil-stone ratios.
Figure 9.
Linear failure envelope in
plane under different oil-stone ratios.
Figure 9.
Linear failure envelope in
plane under different oil-stone ratios.
Figure 10.
Linear compressive and tensile meridian under different temperature. (a) The compressive and tensile meridian under six different temperatures (b) The strength comparison between six different temperatures.
Figure 10.
Linear compressive and tensile meridian under different temperature. (a) The compressive and tensile meridian under six different temperatures (b) The strength comparison between six different temperatures.
Figure 11.
Linear failure envelope in
plane under different temperatures.
Figure 11.
Linear failure envelope in
plane under different temperatures.
Figure 12.
Linear compressive and tensile meridian under different loading rates. (a) The compressive and tensile meridian under six different temperatures (b) The strength comparison between six different temperatures.
Figure 12.
Linear compressive and tensile meridian under different loading rates. (a) The compressive and tensile meridian under six different temperatures (b) The strength comparison between six different temperatures.
Figure 13.
Linear failure envelope in
plane under different loading rates.
Figure 13.
Linear failure envelope in
plane under different loading rates.
Figure 14.
Linear failure criterion under different test conditions.
Figure 14.
Linear failure criterion under different test conditions.
Figure 15.
Three-factor range analysis.
Figure 15.
Three-factor range analysis.
Table 1.
The density of basalt aggregate at all levels.
Table 1.
The density of basalt aggregate at all levels.
| Sieve Size (mm) | Apparent Density (g/cm3) | Standard Requirement | Test Methods |
|---|
| 13.2 | 2.680 | ≥2.6 | T0304-2004 |
| 9.5 | 2.682 | ≥2.6 | T0304-2004 |
| 4.75 | 2.673 | ≥2.6 | T0304-2004 |
| 2.36 | 2.660 | ≥2.5 | T0328-2004 |
| 1.18 | 2.651 | ≥2.5 | T0328-2004 |
| 0.6 | 2.617 | ≥2.5 | T0328-2004 |
| 0.3 | 2.604 | ≥2.5 | T0328-2004 |
| 0.15 | 2.594 | ≥2.5 | T0328-2004 |
| 0.075 | 2.627 | ≥2.5 | T0328-2004 |
| Ore powder | 2.763 | ≥2.5 | T0352-2004 |
Table 2.
The key index of two type of asphalt.
Table 2.
The key index of two type of asphalt.
| Test | Test Methods | Test Results | Standard Requirement |
|---|
| SBS Asphalt | Base Asphalt | SBS Asphalt | Base Asphalt |
|---|
| Penetration (25 °C, 100 g, 5 s) | T0604-2004 | 56.1 | 69 | 40~60 | 60–80 |
| Penetration Index | T0604-2004 | 0.533 | −0.78 | ≥0 | −1.5~+1.0 |
| Softening point (°C) | T0606-2004 | 80 | 48 | ≥60 | ≥46 |
| Ductility, cm | T0605-2004 | 32(5 °C) | 22.8(10 °C) | ≥20 | ≥20 |
| Kinematic viscosity 135 °C (Pa·s) | T0625-2004 | 2.30 | - | ≤3 | - |
| Dynamic viscosity 60 °C (Pa·s) | T0620-2004 | - | 192 | - | ≥180 |
| Solubility (%) | T0607-2004 | 99.9 | 99.8 | ≥99 | ≥99.5 |
Table 3.
The Marshall test results.
Table 3.
The Marshall test results.
| Mixture Type | VV (%) | Oil-Stone Ratio (%) | VMA (%) | VFA (%) | MS (KN) | FL (mm) |
|---|
| AC-13 | SBS | 4.5 | 5.7 | 15.2 | 70.4 | 15.7 | 2.7 |
| Base | 4.2 | 5.2 | 14.6 | 71.2 | 14.1 | 2.4 |
| SMA-13 | SBS | 4.7 | 6.1 | 19.8 | 76.3 | 6.3 | – |
| Base | 4.3 | 5.7 | 17.2 | 75 | 5.8 | 3.7 |
| OGFC-13 | SBS | 19.5 | 5.4 | 12.8 | – | 6.9 | – |
| Base | 20.9 | 4.9 | 10.5 | – | 4.1 | – |
Table 4.
Test results of three type of asphalt mixture under Marshall optimum oil-stone ratio.
Table 4.
Test results of three type of asphalt mixture under Marshall optimum oil-stone ratio.
| Asphalt Type | Mixture Type | | | | | | |
|---|
| Base asphalt | AC-13 | 0 | 0 | −5.835 | −0.333 | 0.471 | 60 |
| −0.2 | −0.2 | −7.417 | −0.447 | 0.583 | 60 |
| 0.845 | 0 | 0 | 0.0483 | 0.068 | 0 |
| 0.748 | −0.5 | −0.5 | −0.014 | 0.101 | 0 |
| SMA-13 | 0 | 0 | −6.265 | −0.333 | 0.471 | 60 |
| −0.2 | −0.2 | −7.905 | −0.442 | 0.58 | 60 |
| 0.885 | 0 | 0 | 0.0471 | 0.067 | 0 |
| 0.806 | −0.5 | −0.5 | −0.01 | 0.098 | 0 |
| OGFC-13 | 0 | 0 | −5.245 | −0.333 | 0.471 | 60 |
| −0.2 | −0.2 | −6.625 | −0.446 | 0.577 | 60 |
| 0.727 | 0 | 0 | 0.0462 | 0.065 | 0 |
| 0.698 | −0.5 | −0.5 | −0.019 | 0.108 | 0 |
| SBS asphalt | SMA-13 | 0 | 0 | −6.449 | −0.333 | 0.471 | 60 |
| −0.2 | −0.2 | −8.146 | −0.442 | 0.581 | 60 |
| 0.918 | 0 | 0 | 0.0474 | 0.067 | 0 |
| 0.883 | −0.5 | −0.5 | −0.006 | 0.101 | 0 |
Table 5.
Fitting parameters of linear model under different gradation.
Table 5.
Fitting parameters of linear model under different gradation.
| Modeling Parameters | A | B | C |
| Fitting Results | 0.1 | −0.64 | 1.512 |
Table 6.
Test results of asphalt mixture under different oil-stone ratio.
Table 6.
Test results of asphalt mixture under different oil-stone ratio.
| Oil-Stone Ratio | | | | | | |
|---|
| 5.5% | 0 | 0 | −5.873 | −0.33 | 0.47 | 60 |
| −0.2 | −0.2 | −7.441 | −0.45 | 0.58 | 60 |
| 0.885 | 0 | 0 | 0.05 | 0.07 | 0 |
| 0.777 | −0.5 | −0.5 | −0.01 | 0.1 | 0 |
| 5.7% | 0 | 0 | −6.306 | −0.333 | 0.471 | 60 |
| −0.2 | −0.2 | −7.991 | −0.443 | 0.582 | 60 |
| 0.905 | 0 | 0 | 0.0478 | 0.068 | 0 |
| 0.795 | −0.5 | −0.5 | −0.011 | 0.097 | 0 |
| 5.9% | 0 | 0 | −6.819 | −0.333 | 0.471 | 60 |
| −0.2 | −0.2 | −8.501 | −0.435 | 0.574 | 60 |
| 0.981 | 0 | 0 | 0.0479 | 0.068 | 0 |
| 0.853 | −0.5 | −0.5 | −0.007 | 0.094 | 0 |
| 6.1% | 0 | 0 | −6.449 | −0.333 | 0.471 | 60 |
| −0.2 | −0.2 | −8.146 | −0.442 | 0.581 | 60 |
| 0.918 | 0 | 0 | 0.0474 | 0.067 | 0 |
| 0.826 | −0.5 | −0.5 | −0.009 | 0.097 | 0 |
| 6.3% | 0 | 0 | −6.005 | −0.333 | 0.471 | 60 |
| −0.2 | −0.2 | −7.685 | −0.449 | 0.588 | 60 |
| 0.864 | 0 | 0 | 0.048 | 0.068 | 0 |
| 0.774 | −0.5 | −0.5 | −0.013 | 0.1 | 0 |
| 6.5% | 0 | 0 | −5.183 | −0.333 | 0.471 | 60 |
| −0.2 | −0.2 | −6.868 | −0.467 | 0.606 | 60 |
| 0.743 | 0 | 0 | 0.0478 | 0.068 | 0 |
| 0.689 | −0.5 | −0.5 | −0.02 | 0.108 | 0 |
Table 7.
Fitting parameters of linear model under different oil-stone ratio.
Table 7.
Fitting parameters of linear model under different oil-stone ratio.
| Asphalt Type | A | B | C | | | c |
| SBS Modified Asphalt | 0.1 | −0.64 | 1.512 | −4.51 | 53.45 | −151.69 |
Table 8.
Test results of asphalt mixture under different temperatures.
Table 8.
Test results of asphalt mixture under different temperatures.
| Temperature | | | | | | |
|---|
| 5 °C | 0 | 0 | −9.059 | −0.333 | 0.471 | 60 |
| −0.2 | −0.2 | −10.74 | −0.41 | 0.548 | 60 |
| 1.304 | 0 | 0 | 0.048 | 0.068 | 0 |
| 1.213 | −0.5 | −0.5 | 0.0078 | 0.089 | 0 |
| 10 °C | 0 | 0 | −8.177 | −0.333 | 0.471 | 60 |
| −0.2 | −0.2 | −9.862 | −0.418 | 0.557 | 60 |
| 1.174 | 0 | 0 | 0.0479 | 0.068 | 0 |
| 1.038 | −0.5 | −0.5 | 0.0015 | 0.089 | 0 |
| 15 °C | 0 | 0 | −7.301 | −0.333 | 0.471 | 60 |
| −0.2 | −0.2 | −8.979 | −0.428 | 0.567 | 60 |
| 1.052 | 0 | 0 | 0.048 | 0.068 | 0 |
| 0.987 | −0.5 | −0.5 | −0.0006 | 0.096 | 0 |
| 20 °C | 0 | 0 | −6.819 | −0.333 | 0.471 | 60 |
| −0.2 | −0.2 | −8.501 | −0.435 | 0.574 | 60 |
| 0.981 | 0 | 0 | 0.0479 | 0.068 | 0 |
| 0.905 | −0.5 | −0.5 | −0.005 | 0.097 | 0 |
| 25 °C | 0 | 0 | −6.049 | −0.333 | 0.471 | 60 |
| −0.2 | −0.2 | −7.727 | −0.448 | 0.587 | 60 |
| 0.872 | 0 | 0 | 0.048 | 0.068 | 0 |
| 0.785 | −0.5 | −0.5 | −0.012 | 0.1 | 0 |
| 30 °C | 0 | 0 | −5.012 | −0.333 | 0.471 | 60 |
| −0.2 | −0.2 | −6.145 | −0.435 | 0.559 | 60 |
| 0.747 | 0 | 0 | 0.0497 | 0.07 | 0 |
| 0.698 | −0.5 | −0.5 | −0.02 | 0.113 | 0 |
Table 9.
Fitting parameters of linear model under different temperatures.
Table 9.
Fitting parameters of linear model under different temperatures.
| Asphalt Type | A | B | C | | |
| SBS Modified Asphalt | 0.1 | −0.64 | 1.512 | 9.78 | −0.155 |
Table 10.
Test results of asphalt mixture under different loading rates.
Table 10.
Test results of asphalt mixture under different loading rates.
| Loading Rates | | | | | | |
|---|
| 1 mm/min | 0 | 0 | −5.678 | 0.317 | −0.471 | 60 |
| −0.2 | −0.2 | −7.359 | 0.435 | −0.594 | 60 |
| 0.817 | 0 | 0 | −0.05 | −0.068 | 0 |
| 0.732 | −0.5 | −0.5 | −0.01 | −0.102 | 0 |
| 2 mm/min | 0 | 0 | −6.819 | 0.317 | −0.471 | 60 |
| −0.2 | −0.2 | −8.501 | 0.415 | −0.574 | 60 |
| 0.981 | 0 | 0 | −0.05 | −0.068 | 0 |
| 0.905 | −0.5 | −0.5 | −0.02 | −0.097 | 0 |
| 3 mm/min | 0 | 0 | −7.555 | 0.317 | −0.471 | 60 |
| −0.2 | −0.2 | −9.268 | 0.407 | −0.566 | 60 |
| 1.064 | 0 | 0 | −0.05 | −0.066 | 0 |
| 0.943 | −0.5 | −0.5 | −0.02 | −0.09 | 0 |
| 4 mm/min | 0 | 0 | −8.422 | 0.317 | −0.471 | 60 |
| −0.2 | −0.2 | −10.13 | 0.398 | −0.556 | 60 |
| 1.192 | 0 | 0 | −0.05 | −0.067 | 0 |
| 1.107 | −0.5 | −0.5 | −0.02 | −0.09 | 0 |
| 5 mm/min | 0 | 0 | −9.546 | 0.317 | −0.471 | 60 |
| −0.2 | −0.2 | −11.26 | 0.389 | −0.546 | 60 |
| 1.339 | 0 | 0 | −0.05 | −0.066 | 0 |
| 1.231 | −0.5 | −0.5 | −0.03 | −0.085 | 0 |
Table 11.
Fitting parameters of linear model under different loading rates.
Table 11.
Fitting parameters of linear model under different loading rates.
| Asphalt type | A | B | C | a3 | b3 |
| SBS modified asphalt | 0.1 | −0.64 | 1.56 | 4.803 | 0.934 |
Table 12.
Design plane of orthogonal test.
Table 12.
Design plane of orthogonal test.
| Asphalt Type | N | T (°C) | V mm/min | O(%) | UC | TC | UT |
|---|
| Base bitumen | 1 | 5 | 1 | 5.7 | −4.598 | −5.925 | 0.728 |
| 2 | 5 | 3 | 5.9 | −5.449 | −6.844 | 0.849 |
| 3 | 5 | 5 | 6.1 | −6.556 | −7.983 | 0.999 |
| 4 | 15 | 1 | 5.9 | −3.848 | −5.08 | 0.624 |
| 5 | 15 | 3 | 6.1 | −4.071 | −5.39 | 0.651 |
| 6 | 15 | 5 | 5.7 | −6.165 | −7.606 | 0.929 |
| 7 | 25 | 1 | 6.1 | −1.938 | −2.88 | 0.325 |
| 8 | 25 | 3 | 5.7 | −3.432 | −4.673 | 0.543 |
| 9 | 25 | 5 | 5.9 | −3.929 | −5.239 | 0.577 |
| SBS bitumen | 1 | 5 | 1 | 5.7 | −6.595 | −7.947 | 0.953 |
| 2 | 5 | 3 | 5.9 | −8.352 | −9.939 | 1.195 |
| 3 | 5 | 5 | 6.1 | −8.778 | −10.4 | 1.249 |
| 4 | 15 | 1 | 5.9 | −5.848 | −7.23 | 0.858 |
| 5 | 15 | 3 | 6.1 | −6.014 | −7.563 | 0.89 |
| 6 | 15 | 5 | 5.7 | −8.62 | −10.27 | 1.185 |
| 7 | 25 | 1 | 6.1 | −3.028 | −4.196 | 0.456 |
| 8 | 25 | 3 | 5.7 | −5.458 | −6.88 | 0.752 |
| 9 | 25 | 5 | 5.9 | −5.903 | −7.511 | 0.824 |
Table 13.
The results of orthogonal test.
Table 13.
The results of orthogonal test.
| | Base Asphalt | SBS Modified Asphalt |
|---|
| T | V | O | T | V | O |
|---|
| 5.534 | 3.462 | 4.732 | 7.908 | 5.157 | 6.891 |
| 4.695 | 4.317 | 4.409 | 6.827 | 6.608 | 6.701 |
| 3.1 | 5.55 | 4.188 | 4.796 | 7.767 | 5.94 |
| 6.917 | 4.628 | 6.068 | 9.427 | 6.457 | 8.365 |
| 6.025 | 5.636 | 5.721 | 8.353 | 8.127 | 8.227 |
| 4.264 | 5.418 | 5.418 | 6.196 | 7.385 | 7.385 |
| 0.806 | 0.525 | 0.733 | 1.124 | 0.75 | 0.963 |
| 0.69 | 0.608 | 0.684 | 0.97 | 0.847 | 0.959 |
| 0.452 | 0.835 | 0.658 | 0.672 | 1.086 | 0.865 |
| 2.434 | 2.088 | 0.543 | 3.112 | 2.61 | 0.951 |
| 2.654 | 1.008 | 0.65 | 3.231 | 1.67 | 0.98 |
| 0.354 | 0.311 | 0.075 | 0.451 | 0.336 | 0.098 |