A Peridynamic Computational Scheme for Thermoelectric Fields
Abstract
:1. Introduction
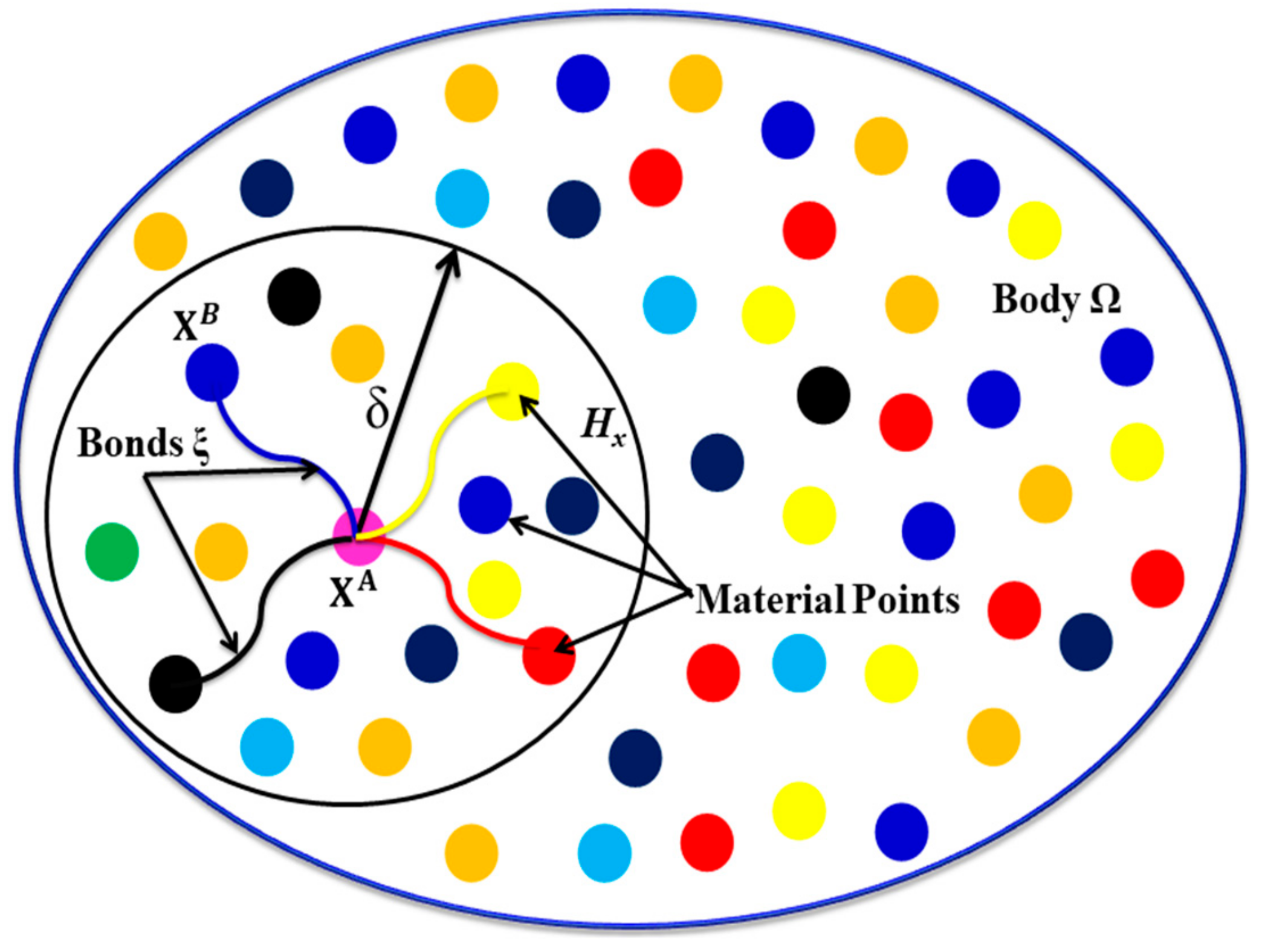
2. Peridynamics (PD) Formulation
2.1. PD Electric Conduction
2.2. PD Formulation for Heat Conduction
2.3. Peridynamic Formulation for the System of Thermoelectric
2.3.1. Peridynamic Constitutive Equations
2.3.2. Peridynamic Balance Laws
3. Numerical Procedures
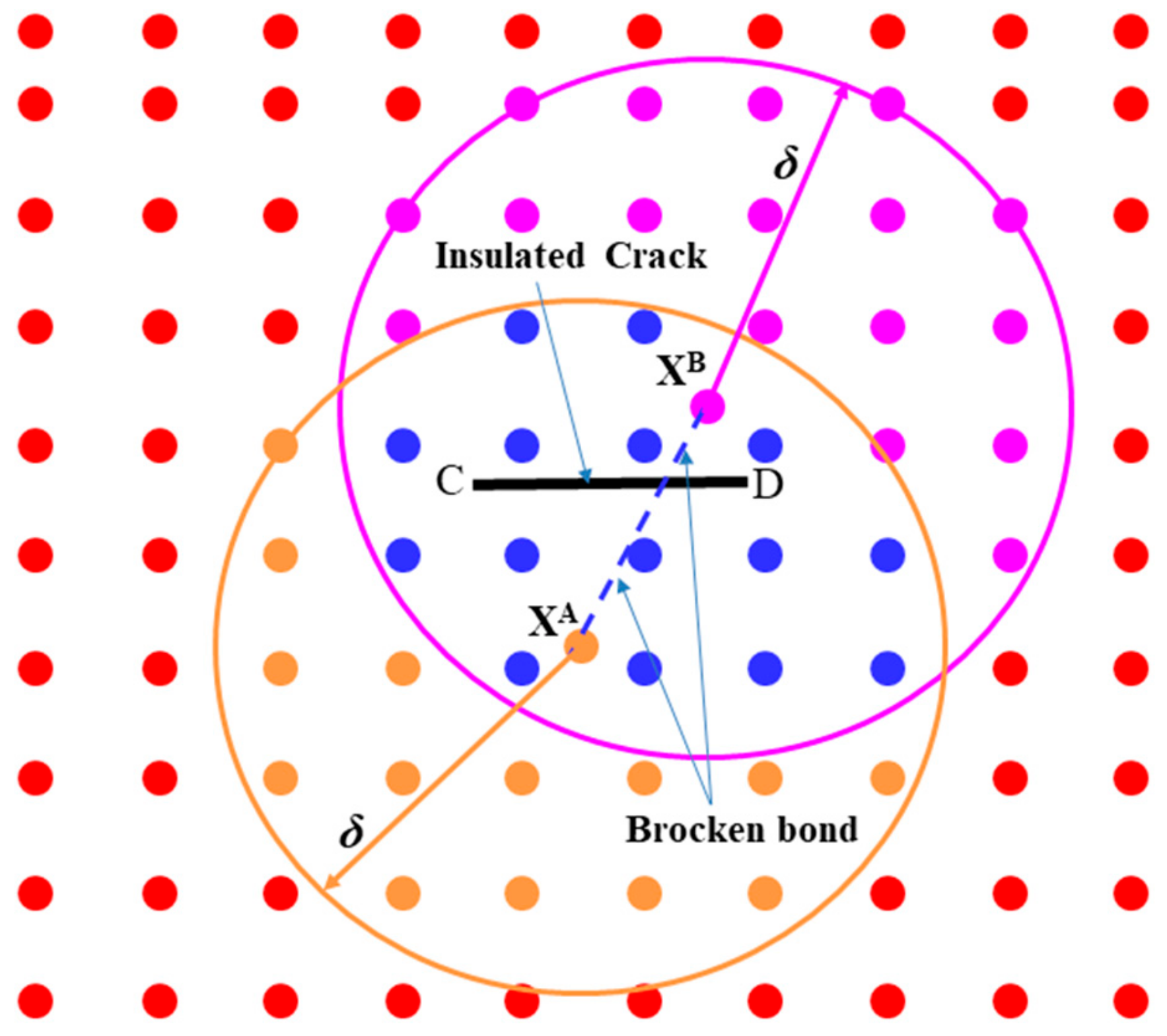
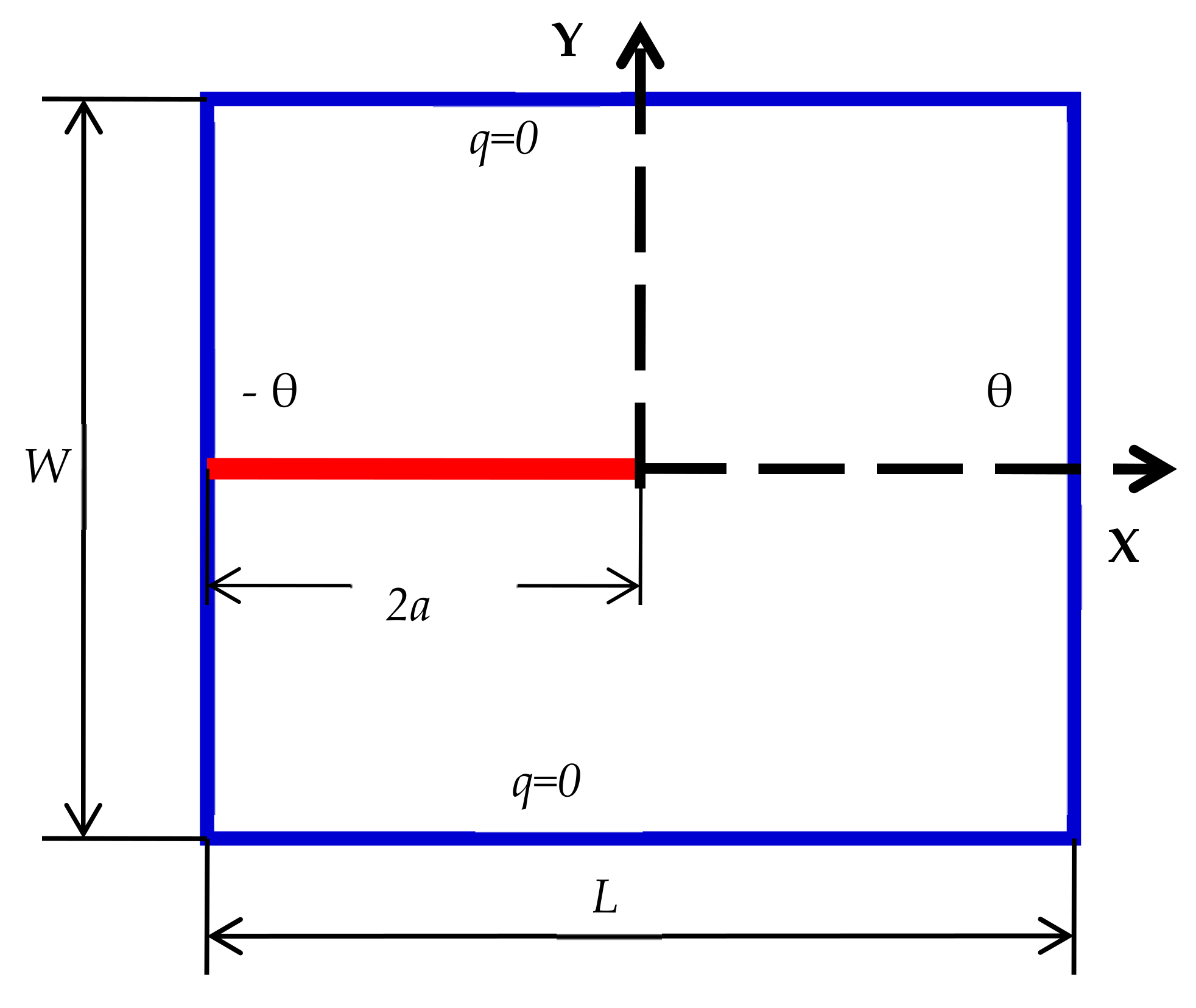
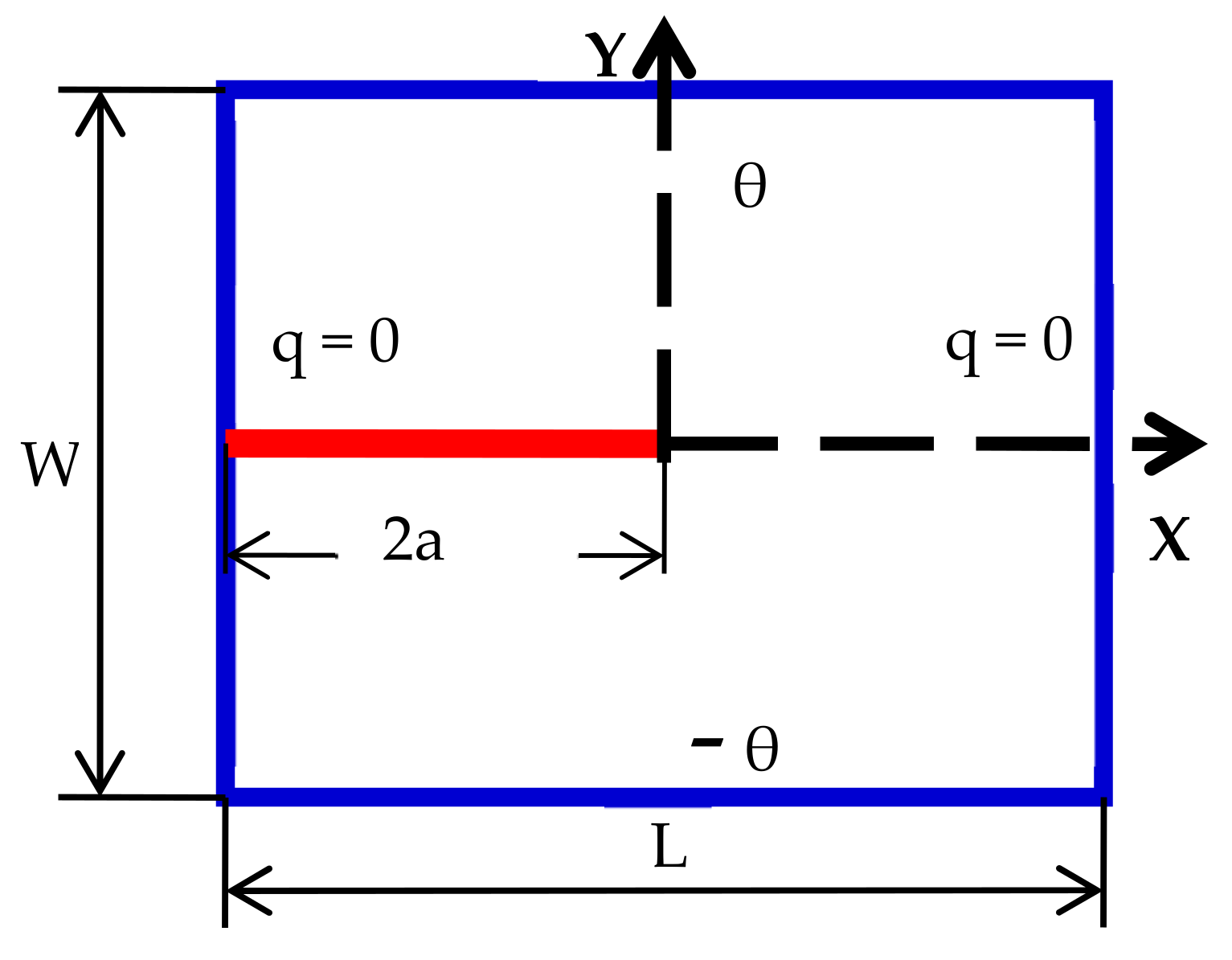
Modeling of Insulated Crack
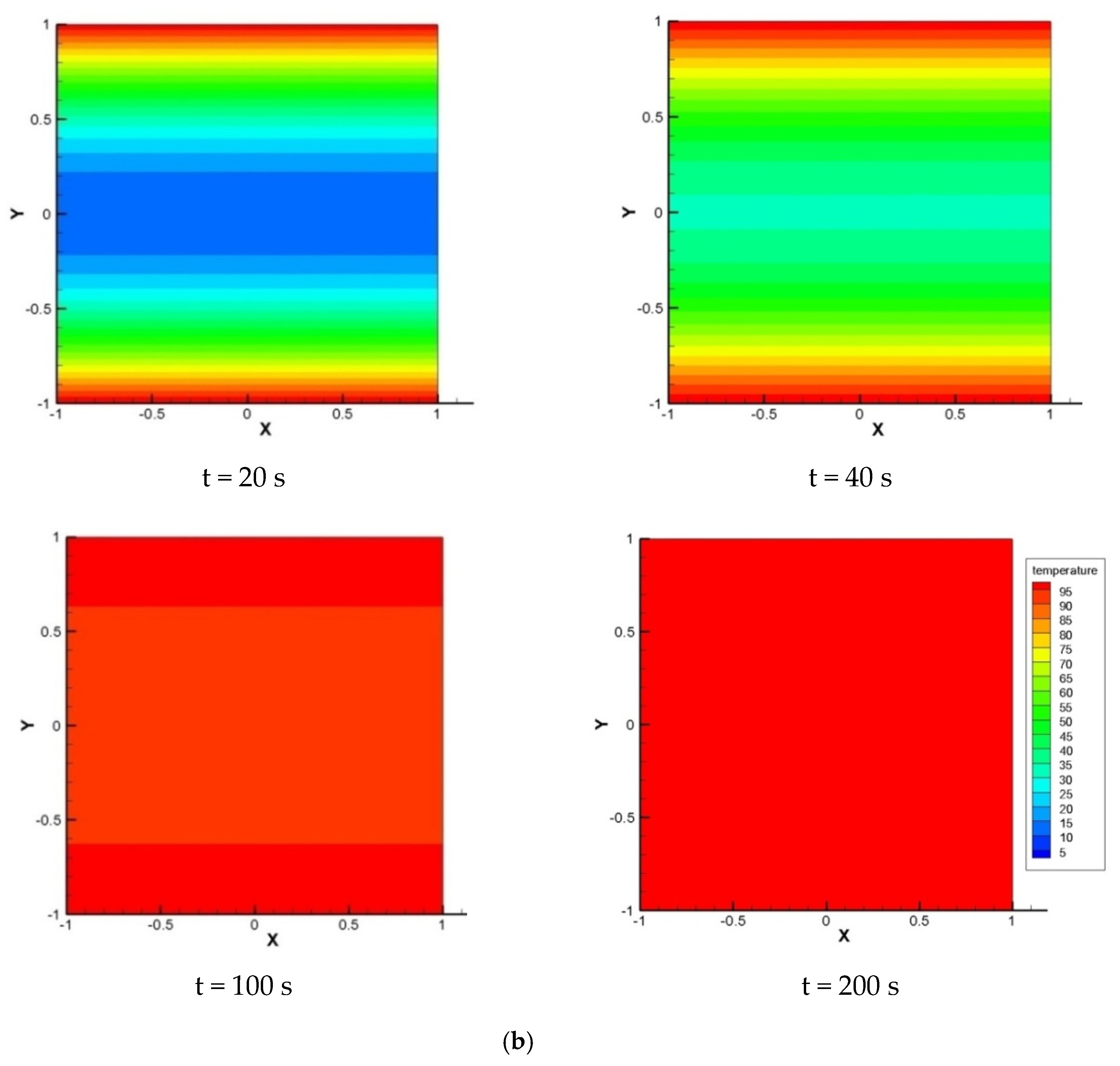
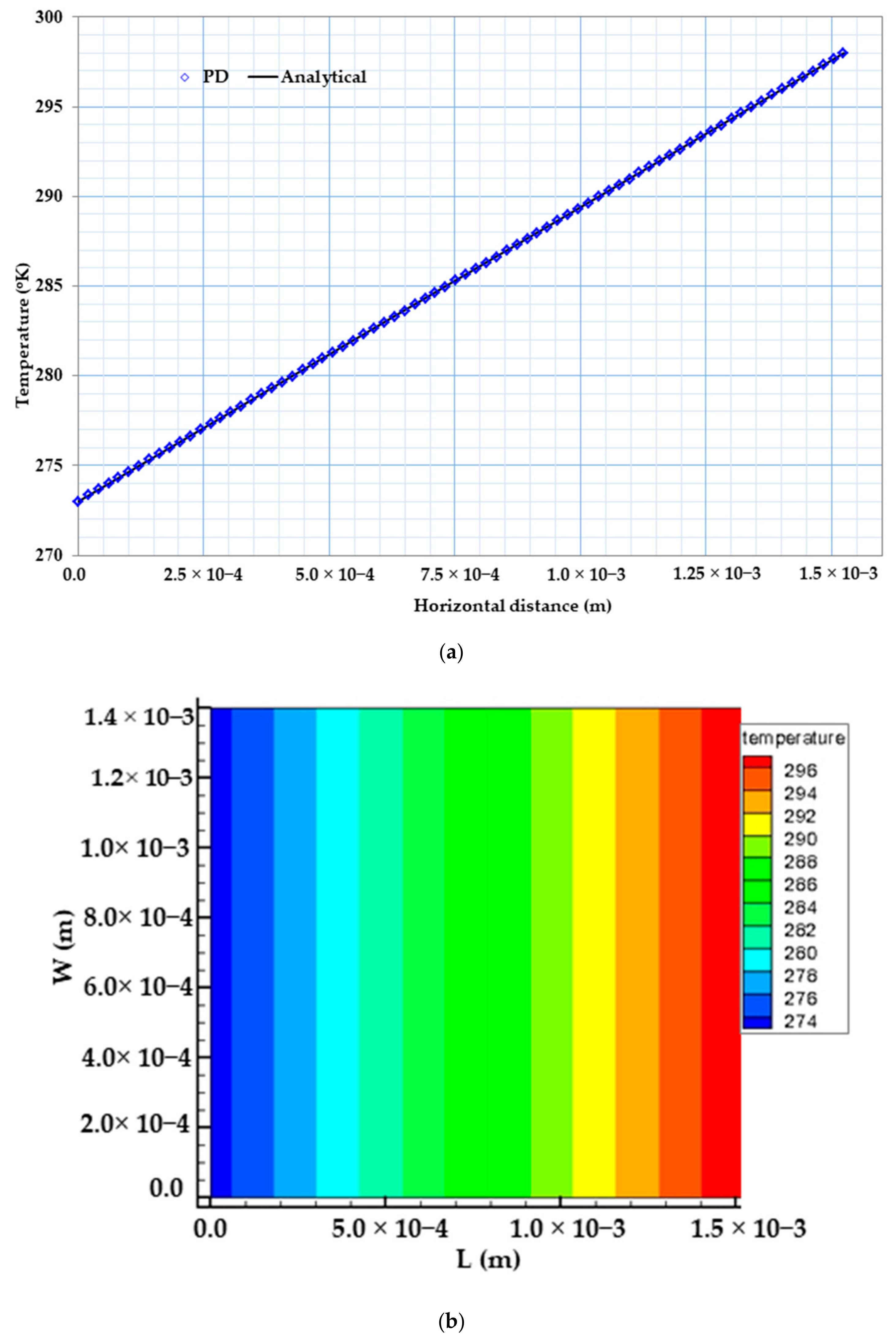
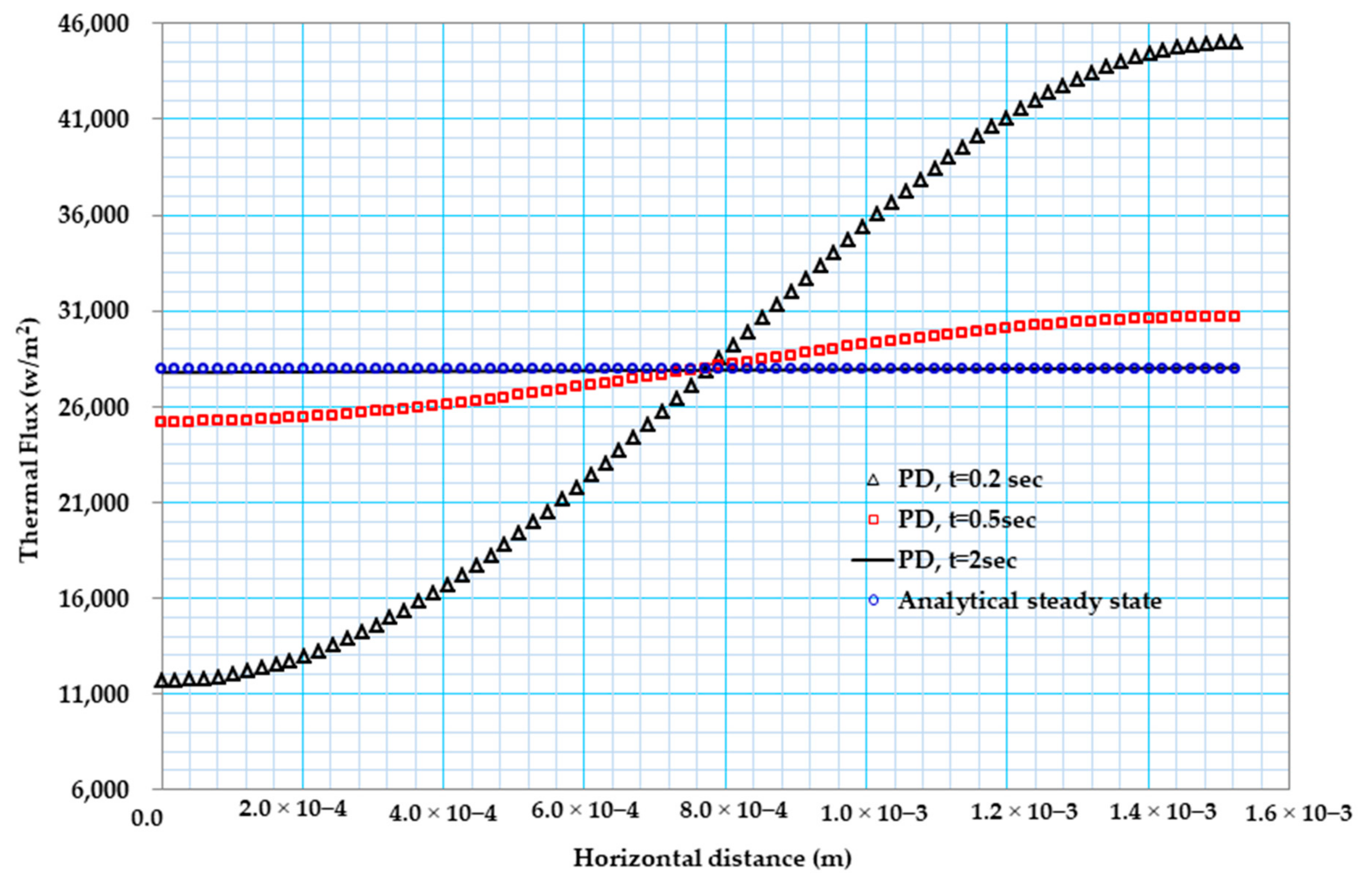
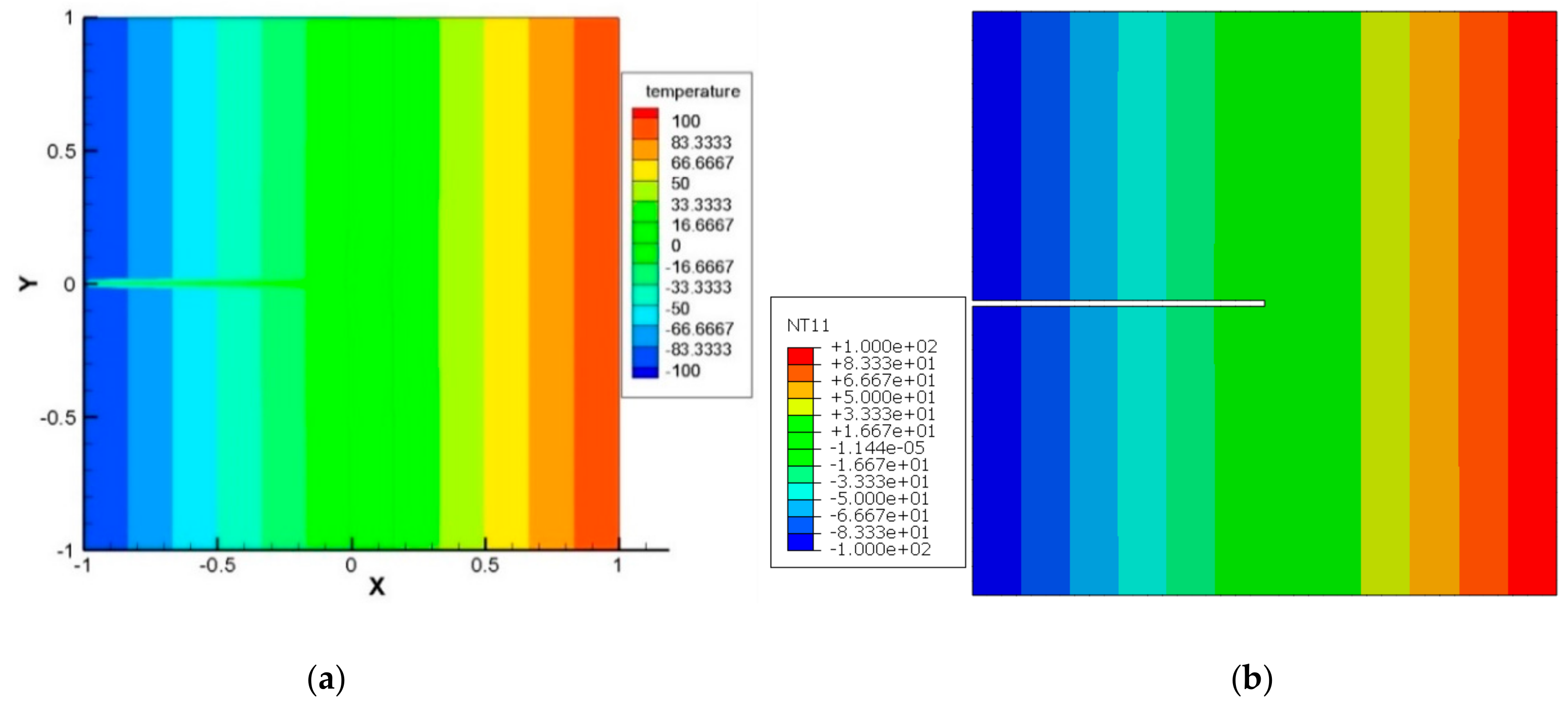
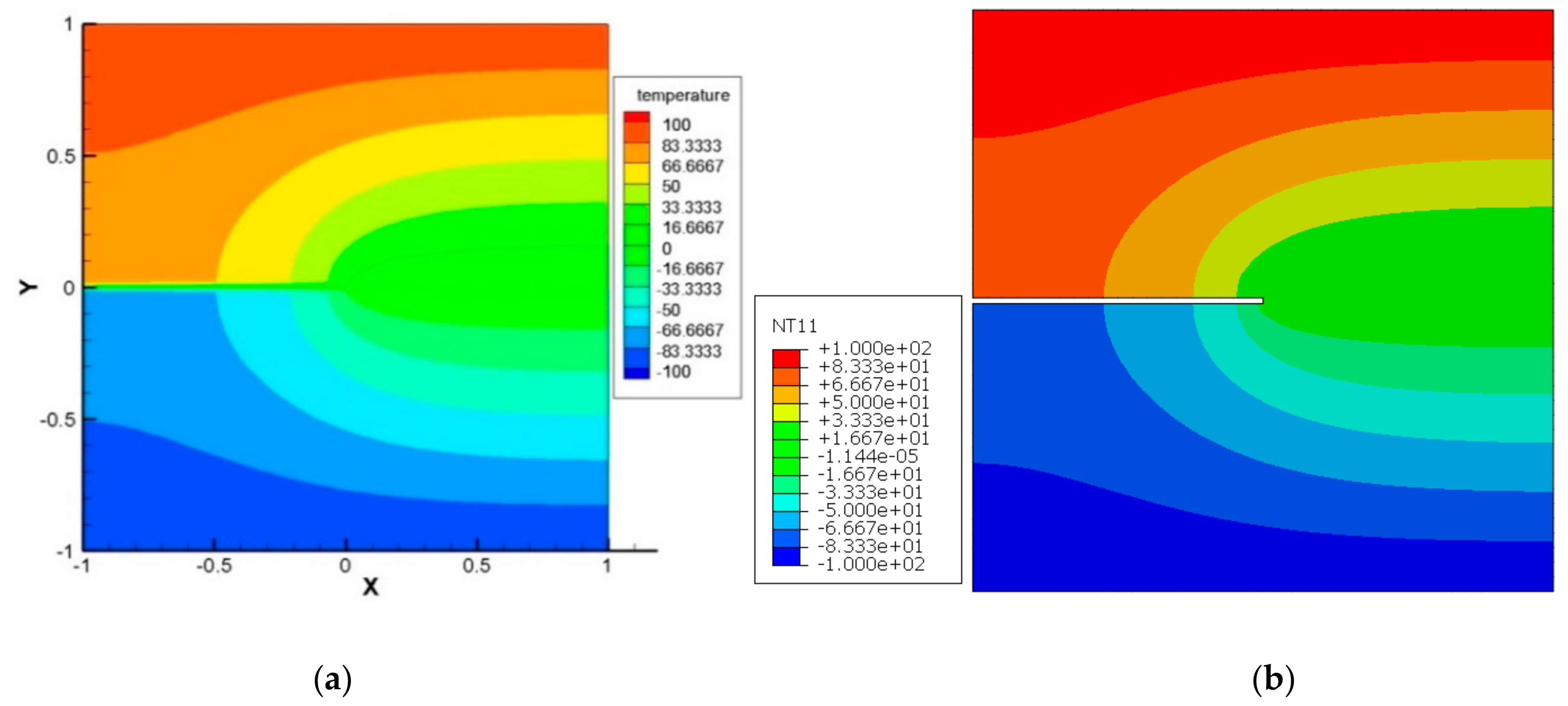
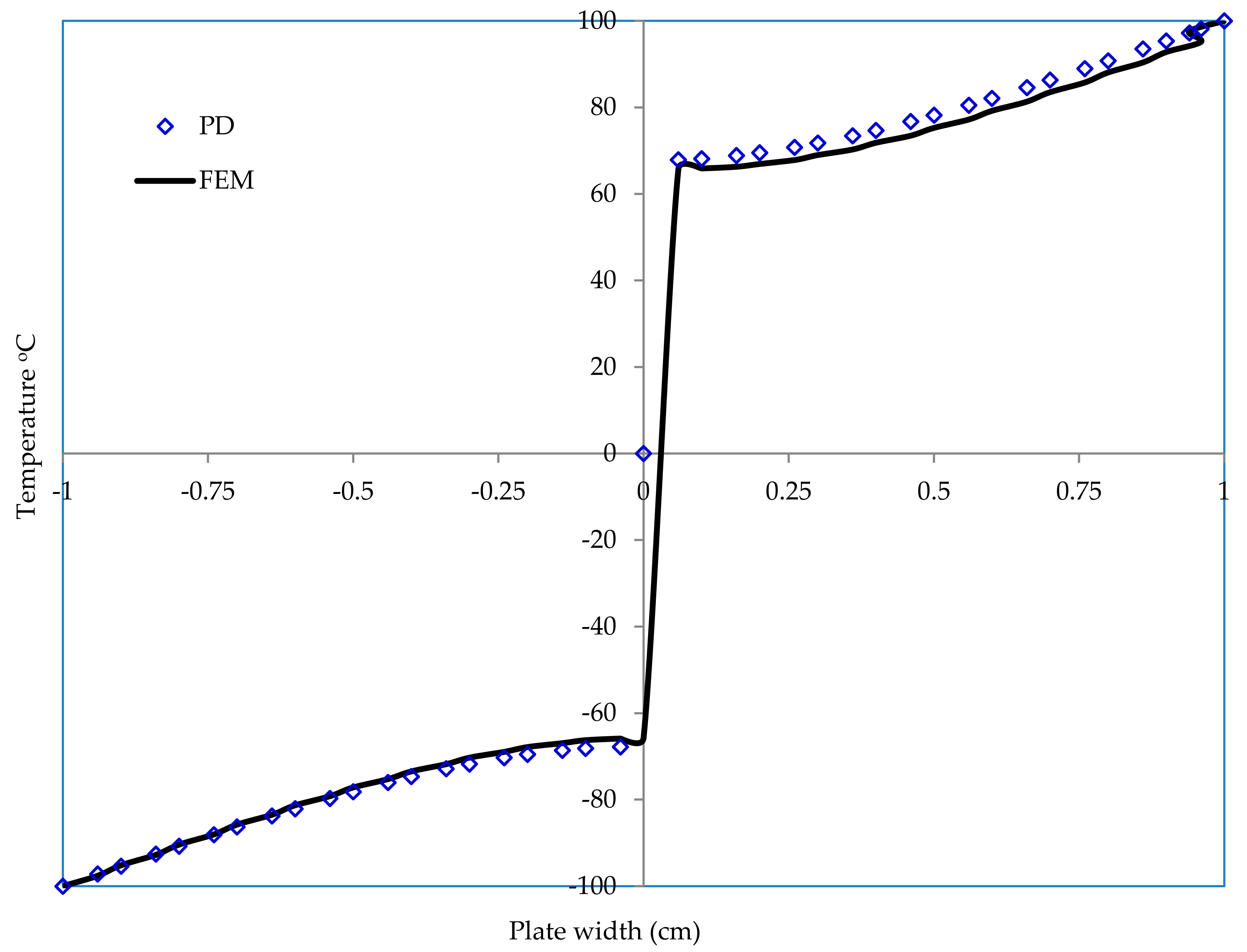
4. Results and Discussions
4.1. Validation of PD Theory
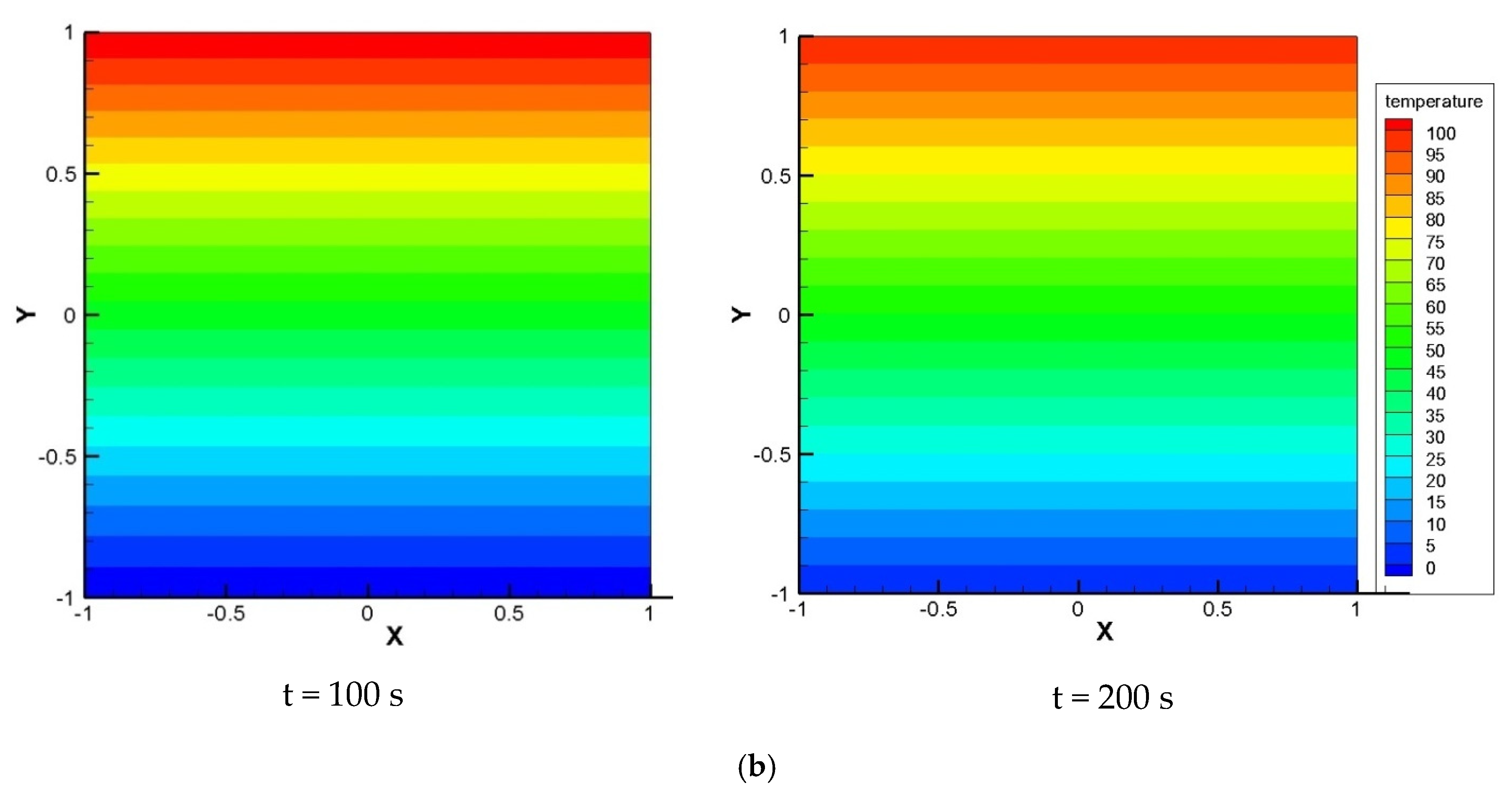
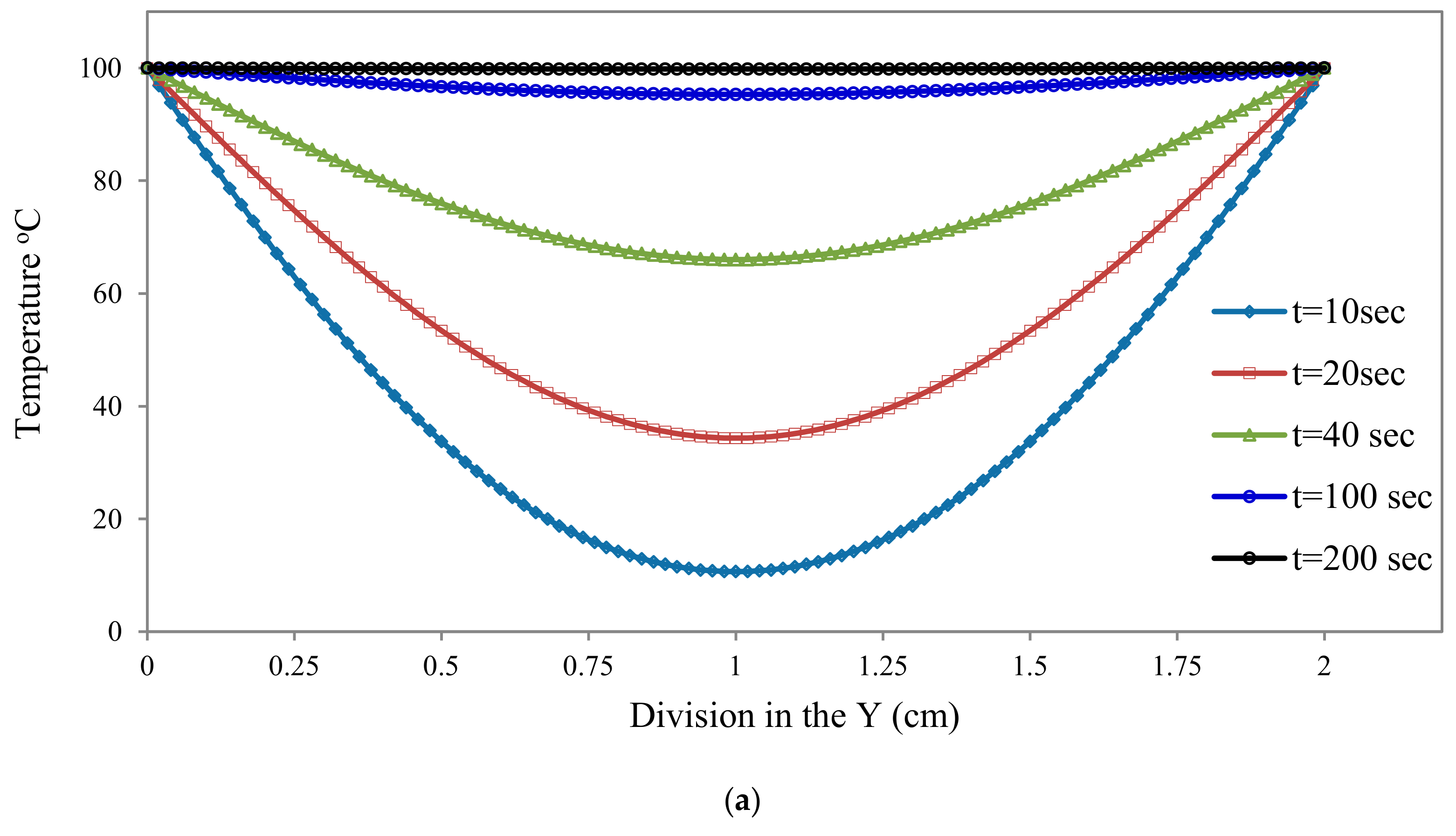
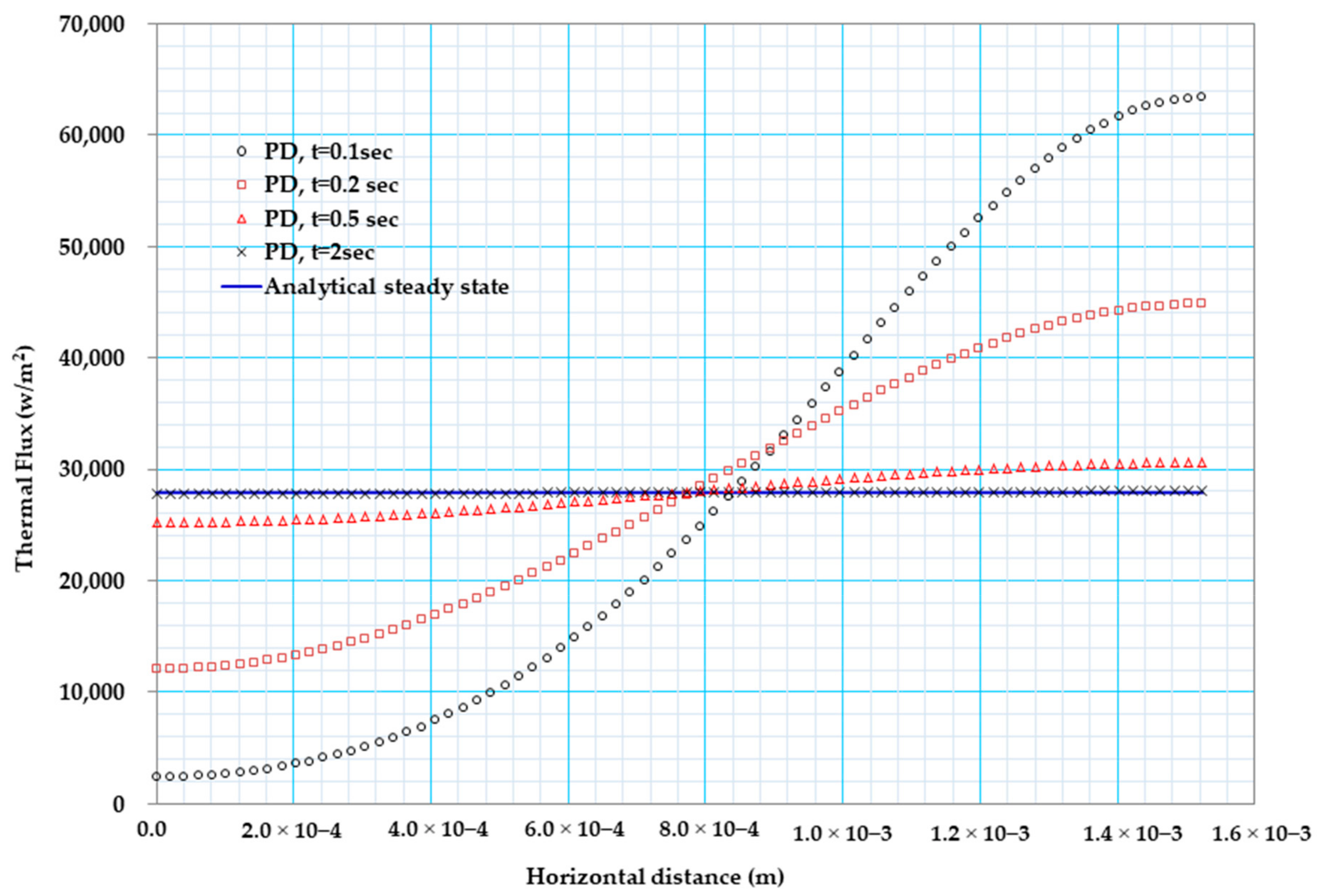
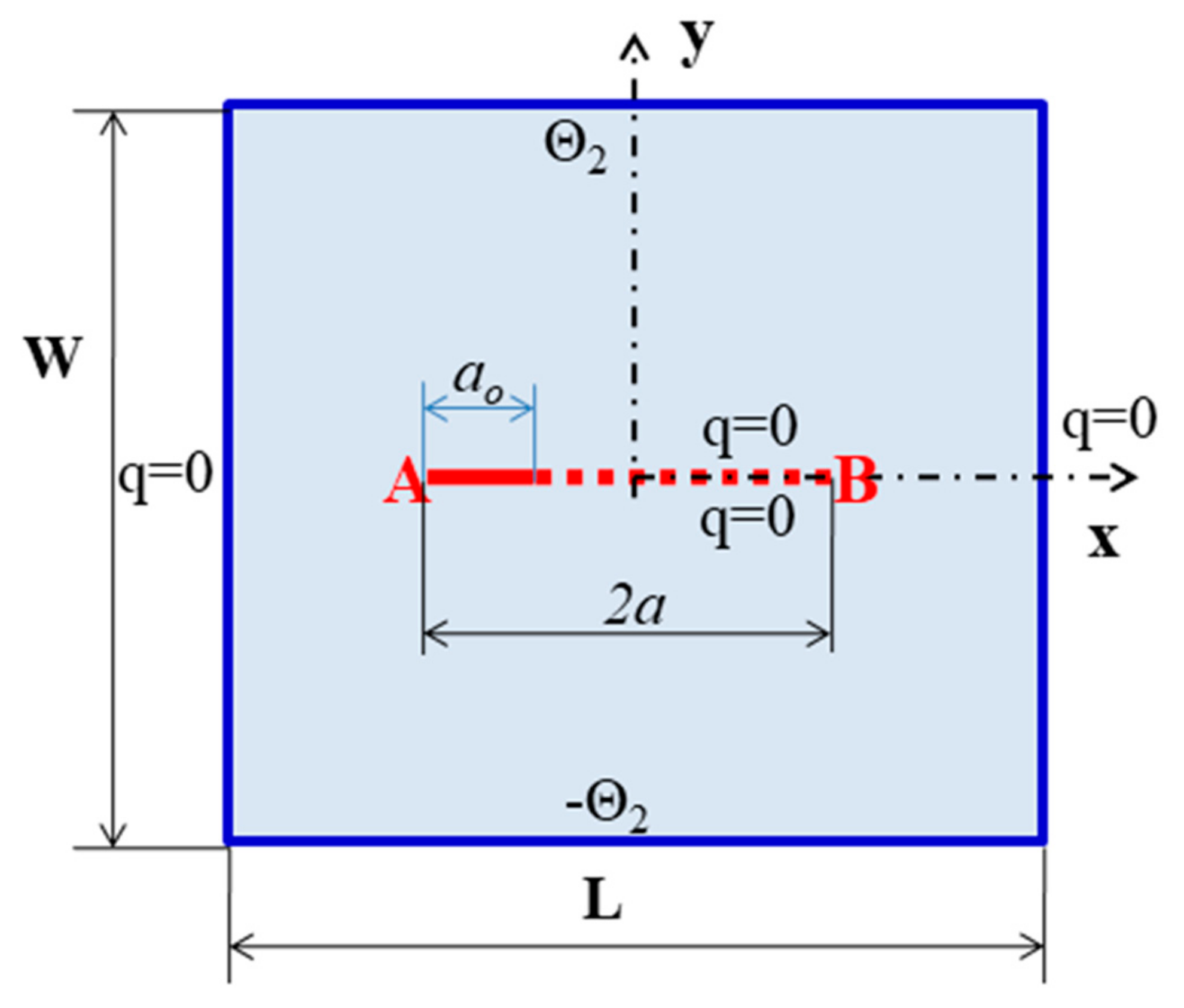
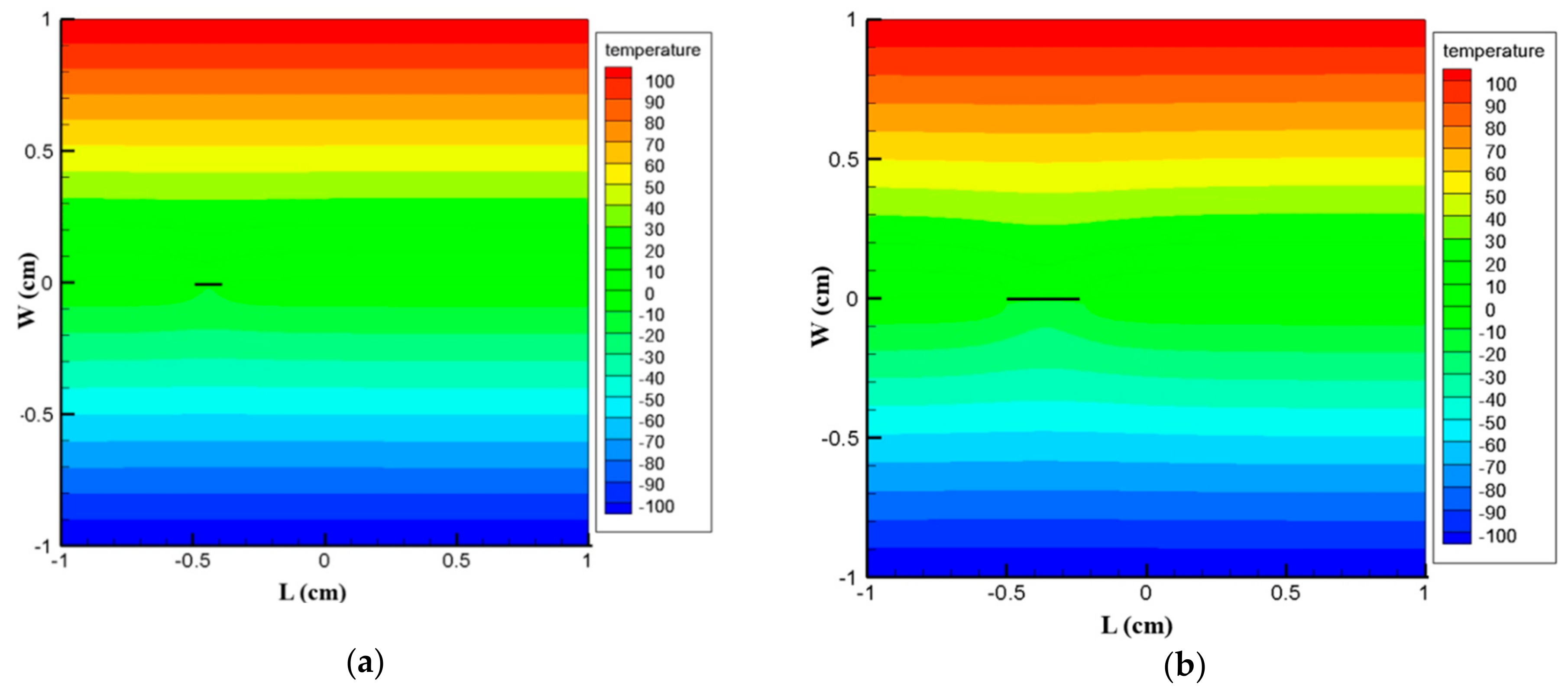
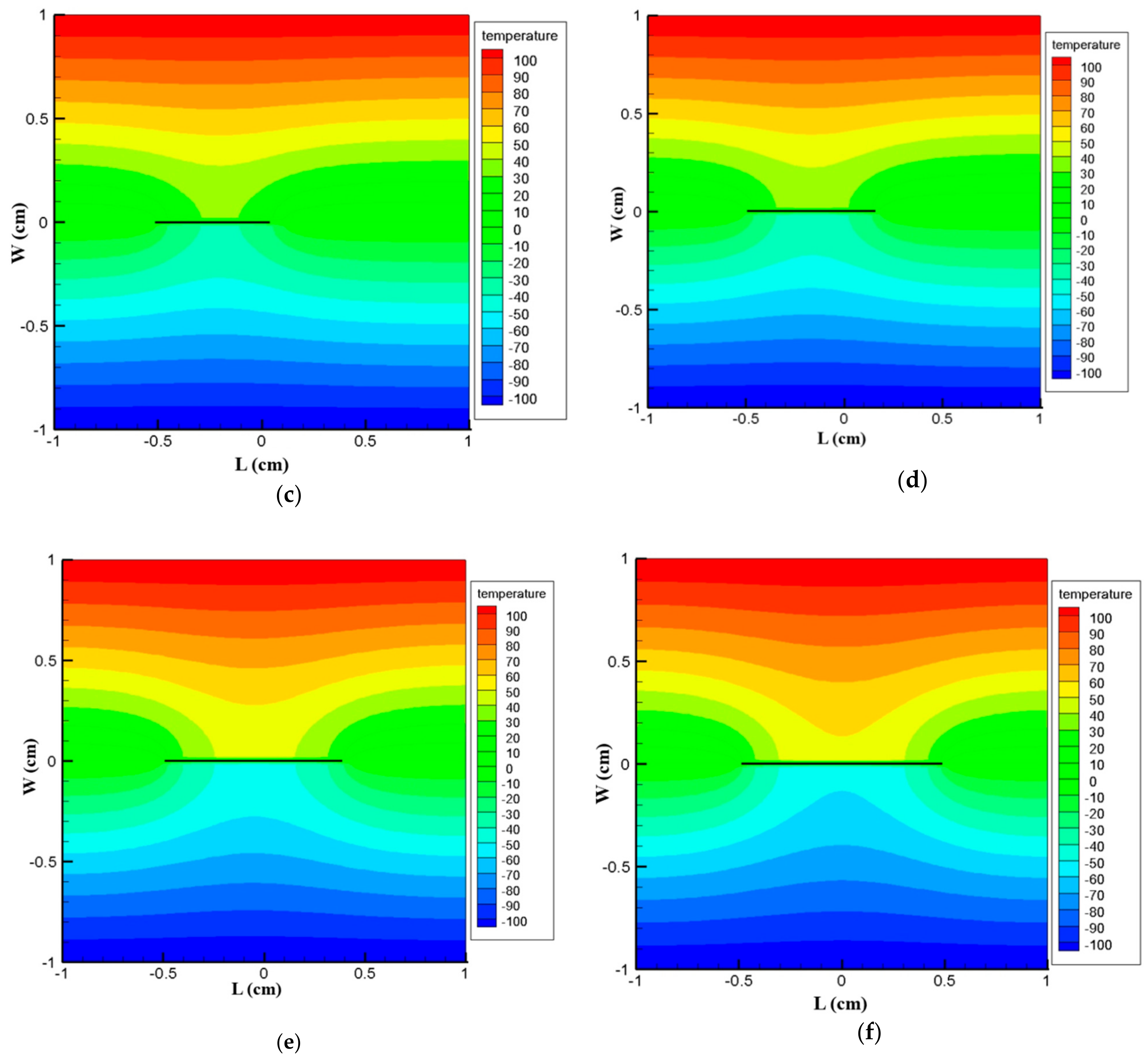
4.2. Examples on Thermoelectric Plate with Stationary and Moving Crack
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ling Bing, K.; Li, T.; Hng, H.H.; Boey, F.; Zhang, T.; Li, S. Waste Energy Harvesting Mechanical and Thermal Energies; Springer: New York, NY, USA, 2014. [Google Scholar]
- Liu, X.; Li, C.; Deng, Y.D.; Su, C.Q. An energy-harvesting system using thermoelectric power generation for automotive application. Electr. Power Energy Syst. 2015, 67, 510–516. [Google Scholar] [CrossRef]
- Ssennoga, T.; Jie, Z.; Yuying, Y.; Boi, L. A comprehensive review of thermoelectric technology: Materials, applications. Model. Perform. Improve. 2016, 65, 698–726. [Google Scholar]
- Rowe, D.M. CRC Handbook of Thermoelectrics; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Gigliotti, M.; Lafarie-Frenot, M.C.; Lin, Y.; Pugliese, A. Electro-mechanical fatigue of CFRP laminates for aircraft applications. Compos. Struct. 2015, 127, 436–449. [Google Scholar] [CrossRef]
- Liu, L. A continuum theory of thermoelectric bodies and effective properties of thermoelectric composites. Int. J. Eng. Sci. 2012, 55, 35–53. [Google Scholar] [CrossRef] [Green Version]
- Zhang, A.B.; Wang, B.L. Crack tip field in thermoelectric media. Theor. Appl. Fract. Mech. 2013, 66, 33–36. [Google Scholar] [CrossRef]
- Silling, S.A. Reformulation of elasticity theory for discontinuities and long-range forces. J. Mech. Phys. Solids 2000, 48, 175–209. [Google Scholar] [CrossRef] [Green Version]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Meth. Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Belytschko, T.; Parimi, C.; Moes, N.; Sukumar, N.; Usui, S. Structured extended finite element methods for solids defined by implicit surfaces. Int. J. Numer. Methods Eng. 2003, 56, 609–635. [Google Scholar] [CrossRef] [Green Version]
- Moes, N.; Dolbow, J.; Belytschko, T. A finite element method for crack growth without remeshing. Int. J. Numer. Meth. Eng. 1999, 46, 131–150. [Google Scholar] [CrossRef]
- Areias, P.; Belytschko, T. Analysis of three-dimensional crack initiation and propagation using the extended finite element method. Int. J. Numer. Meth. Eng. 2005, 63, 760–788. [Google Scholar] [CrossRef]
- Silling, S.A.; Zimmermann, M.; Abeyaratne, R. Deformation of a peridynamic bar. J. Elast. 2003, 73, 173–190. [Google Scholar] [CrossRef]
- Silling, S.A.; Epton, M.; Weckner, O.; Xu, J.; Askari, E. Peridynamic States and Constitutive Modeling. J. Elast. 2007, 88, 151–184. [Google Scholar] [CrossRef] [Green Version]
- Warren, T.L.; Silling, S.A.; Askari, A.; Weckner, O.; Epton, M.A.; Xu, J. A non-ordinary state-based peridynamic method to model solid material deformation and fracture. Int. J. Solids Struct. 2009, 46, 1186–1195. [Google Scholar] [CrossRef] [Green Version]
- O’Grady, J.; Foster, J. Peridynamic beams: A non-ordinary, state-based model. Int. J. Solids Struct. 2014, 51, 3177–3183. [Google Scholar] [CrossRef] [Green Version]
- Kilic, B.; Madenci, E. Peridynamic theory for thermomechanical analysis. Adv. Packag IEEE Trans. 2010, 33, 97–105. [Google Scholar] [CrossRef]
- Agwai, A. Peridynamic Approach for Coupled Fields. Ph.D. Thesis, University of Arizona, Tucson, AZ, USA, 2011. [Google Scholar]
- Oterkus, S.; Fox, J.; Madenci, E. Simulation of electro-migration through peridynamics. In Proceedings of the 63rd Electronic Components and Technology Conference (ECTC), Las Vegas, NV, USA, 28–31 May 2013; pp. 1488–1493. [Google Scholar]
- Gerstle, W.; Silling, S.A.; Read, D.; Tewary, V.; Lehoucq, R. Peridynamic simulation of electromigration. CMC 2008, 8, 75–92. [Google Scholar]
- Oterkus, S.; Madenci, E.; Agwai, A. Fully coupled peridynamic thermomechanics. J. Mech. Phys. Solids 2014, 64, 1–23. [Google Scholar] [CrossRef] [Green Version]
- Oterkus, S.; Madenci, E.; Oterkus, E.; Hwang, Y.; Bae, J.; Han, S. Hygro-thermo-mechanical analysis and failure prediction in electronic packages by using peridynamics. In Proceedings of the 64th Electronic Components and Technology Conference (ECTC), Walt Disney Swan & Dolphin Orlando, Lake Buena Vista, FL, USA, 27–30 May 2014; pp. 973–982. [Google Scholar]
- Raymond, A.W.; George, A.G.A. Dynamic electro-thermo-mechanical model of dielectric breakdown in solids using peridynamics. J. Mech. Mater. Struct. 2015, 10, 613–630. [Google Scholar]
- Assefa, M.; Lai, X.; Liu, L.; Liao, Y. Peridynamic Formulation for Coupled Thermoelectric Phenomena. Adv. Mater. Sci. Eng. 2017, 2017, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Hu, Y.; Spencer, B.W. A MOOSE-Based Implicit Peridynamic ThermoMechanical Model. In Proceedings of the ASME 2016 International Mechanical Engineering Congress and Exposition, Phoenix, AZ, USA, 11–17 November 2016. IMECE2016-65552. [Google Scholar]
- Bobaru, F.; Duangpanya, M. The peridynamic formulation for transient heat conduction. Int. J. Heat Mass Transf. 2010, 53, 4047–4059. [Google Scholar] [CrossRef]
- Bobaru, F.; Duangpanya, M. A peridynamic formulation for transient heat conduction in bodies with evolving discontinuities. J. Comput. Phys. 2012, 231, 2764–2785. [Google Scholar] [CrossRef] [Green Version]
- Oterkus, S.; Madenci, E.; Agwai, A. Peridynamic thermal diffusion. J. Comput. Phys. 2014, 265, 71–96. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Bobaru, F. Selecting the kernel in a peridynamic formulation: A study for transient heat diffusion. Comput. Phys. Commun. 2015, 197, 51–60. [Google Scholar] [CrossRef]
- Oterkus, S.; Madenci, E.; Oterkus, E. Fully coupled poroelastic peridynamic formulation for fluid-filled fractures. Eng. Geol. 2017, 225, 19–28. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Xu, J.; Wang, J. A peridynamic framework and simulation of non-Fourier and nonlocal heat conduction. Int. J. Heat Mass Transf. 2018, 118, 1284–1292. [Google Scholar] [CrossRef]
- Dorduncu, M. Peridynamic solution of the steady state heat conduction problem in plates with insulated cracks. J. Aeronaut. Space Technol. 2019, 12, 145–155. [Google Scholar]
- Zhao, J.; Chen, Z.; Mehrmashhadi, J.; Bobaru, F. Construction of a peridynamic model for transient advection-diffusion problems. Int. J. Heat Mass Trans. 2018, 126, 1253–1266. [Google Scholar] [CrossRef]
- Zhang, H.; Qiao, P. An extended state-based peridynamic model for damage growth prediction of bimaterial structures under thermomechanical loading. Eng. Fract. Mech. 2018, 189, 81–97. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, X.; Kou, M. A coupled thermo-mechanical bond-based peridynamics for simulating thermal cracking in rocks. Int. J. Fract. 2018, 211, 13–42. [Google Scholar] [CrossRef]
- Bazazzadeh, S.; Mossaiby, F.; Shojaei, A. An adaptive thermo-mechanical peridynamic model for fracture analysis in ceramics. Eng. Fract. Mech. 2020, 223, 106708. [Google Scholar] [CrossRef]
- Prakash, N.; Seidel, G.D. Electromechanical peridynamics modeling of piezoresistive response of carbon nanotube nanocomposites. Comput. Mater. Sci. 2016, 113, 154–170. [Google Scholar] [CrossRef]
- Prakash, N.; Seidel, G.D. Computational electromechanical peridynamics modeling of strain and damage sensing in nanocomposite bonded explosive materials (NCBX). Eng. Fract. Mech. 2017, 177, 180–202. [Google Scholar] [CrossRef]
- Prakash, N.; Seidel, G.D. Effects of microscale damage evolution on piezoresistive sensing in nanocomposite bonded explosives under dynamic loading via electromechanical peridynamics. Model. Simul. Mater. Sci. Eng. 2017, 26, 015003. [Google Scholar] [CrossRef]
- Diana, V.; Carvelli, V. An electromechanical micropolar peridynamic model. Comput. Methods Appl. Mech. Eng. 2020, 365, 112998. [Google Scholar] [CrossRef]
- Chen, H.; Hu, Y.; Spencer, B.W. Peridynamics using Irregular Domain Discretization with MOOSE-Based Implementation. In Proceedings of the ASME 2017 International Mechanical Engineering Congress and Exposition, Tampa, FL, USA, 3–9 November 2017. IMECE2017-71527. [Google Scholar]
- Hu, Y.; Chen, H.; Spencer, B.W.; Madenci, E. Thermomechanical peridynamic analysis with irregular non-uniform domain discretization. Eng. Fract. Mech. 2018, 197, 92–113. [Google Scholar] [CrossRef]
- Assefa, Z.M.; Xin, L.; Liu, L. Bond Based Peridynamic Formulation for Thermoelectric Materials. Mater. Sci. Forum 2016, 883, 51–59. [Google Scholar]
- Pérez-Aparicio, J.L.; Palma, R.; Taylor, R.L. Multiphysics and Thermodynamic Formulations for Equilibrium and Non-equilibrium Interactions: Non-linear Finite Elements Applied to Multi-coupled Active Materials. Arch. Comput. Methods Eng. 2016, 23, 535–583. [Google Scholar] [CrossRef] [Green Version]
- Zhao, L.-D.; Lo, S.-H.; Zhang, Y.; Sun, H.; Tan, G.; Uher, C.; Wolverton, C.; Dravid, V.P.; Kanatzidis, M.G. Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals. Nat. Lett. 2014, 508, 373–377. [Google Scholar] [CrossRef]
- Pérez-Aparicio, J.L.; Taylor, R.L.; Gavela, D. Finite element analysis of nonlinear fully coupled thermoelectric materials. Comput. Mech. 2007, 40, 35–45. [Google Scholar] [CrossRef]
- Wang, B.L. A finite element computational scheme for transient and nonlinear coupling thermoelectric fields and the associated thermal stresses in thermoelectric materials. Appl. Therm. Eng. 2017, 110, 136–143. [Google Scholar] [CrossRef]



| Physical Problem | Heat Conduction | Electrical Conduction |
|---|---|---|
| Conservation principles | Conservation of energy | Conservation of electric charge |
| Classical Equations | ||
| Peridynamic Equations | ||
| Constitutive Equations | Generalized Fourier’s law | Generalized Ohm’s law |
| Classical Equatons | Generalized Fourier’s law | Generalized Ohm’s law |
| Peridynamic Equations |
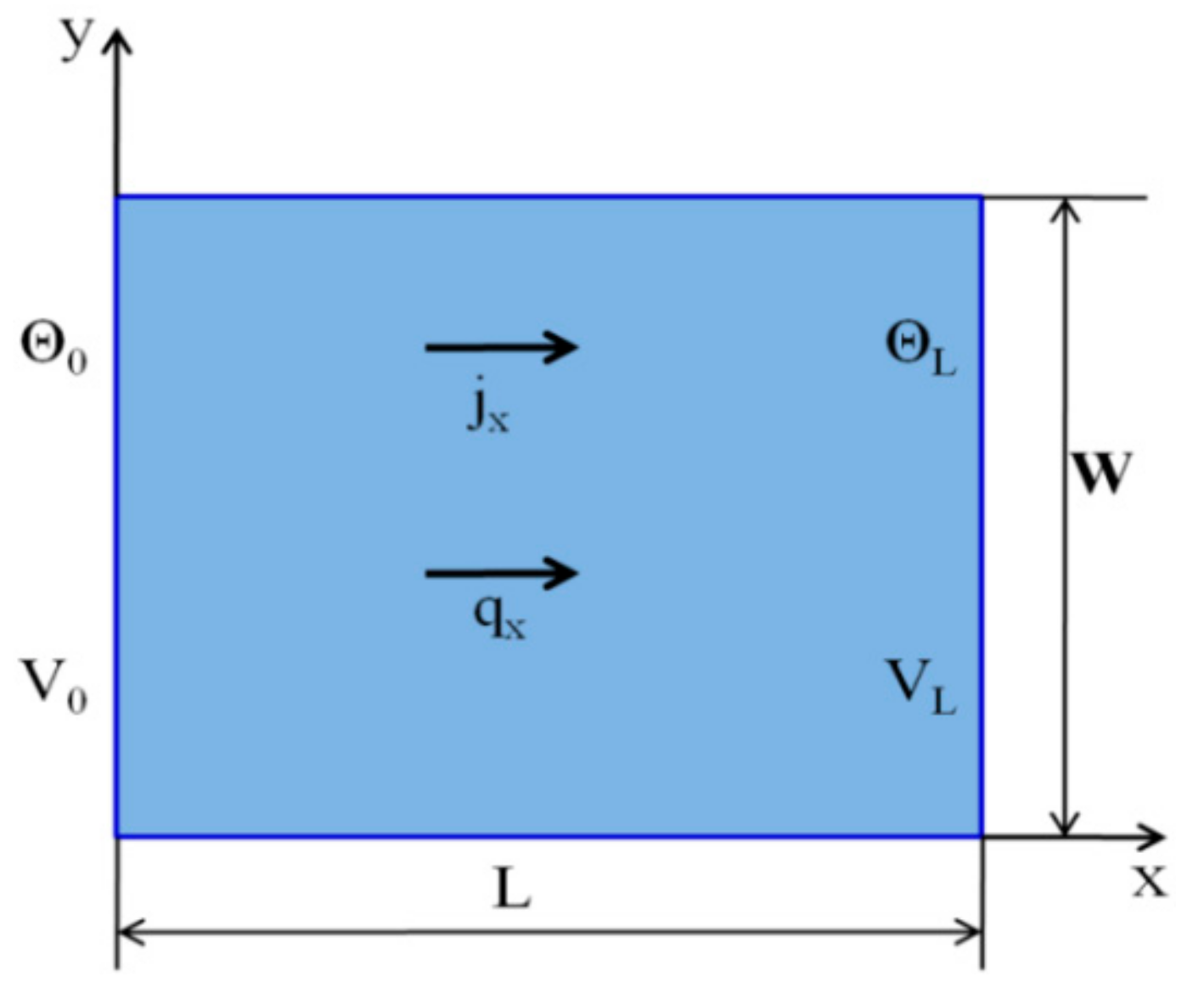
| Geometric Parameters | Material Properties |
|---|---|
| Length, L = 2 cm | |
| Width, W = 2 cm | |
| Thickness, t = 0.01 cm |
| Geometric Parameters | Material Properties |
|---|---|
| Length, L = 1.524 mm, Width, W = 1.4 mm, |
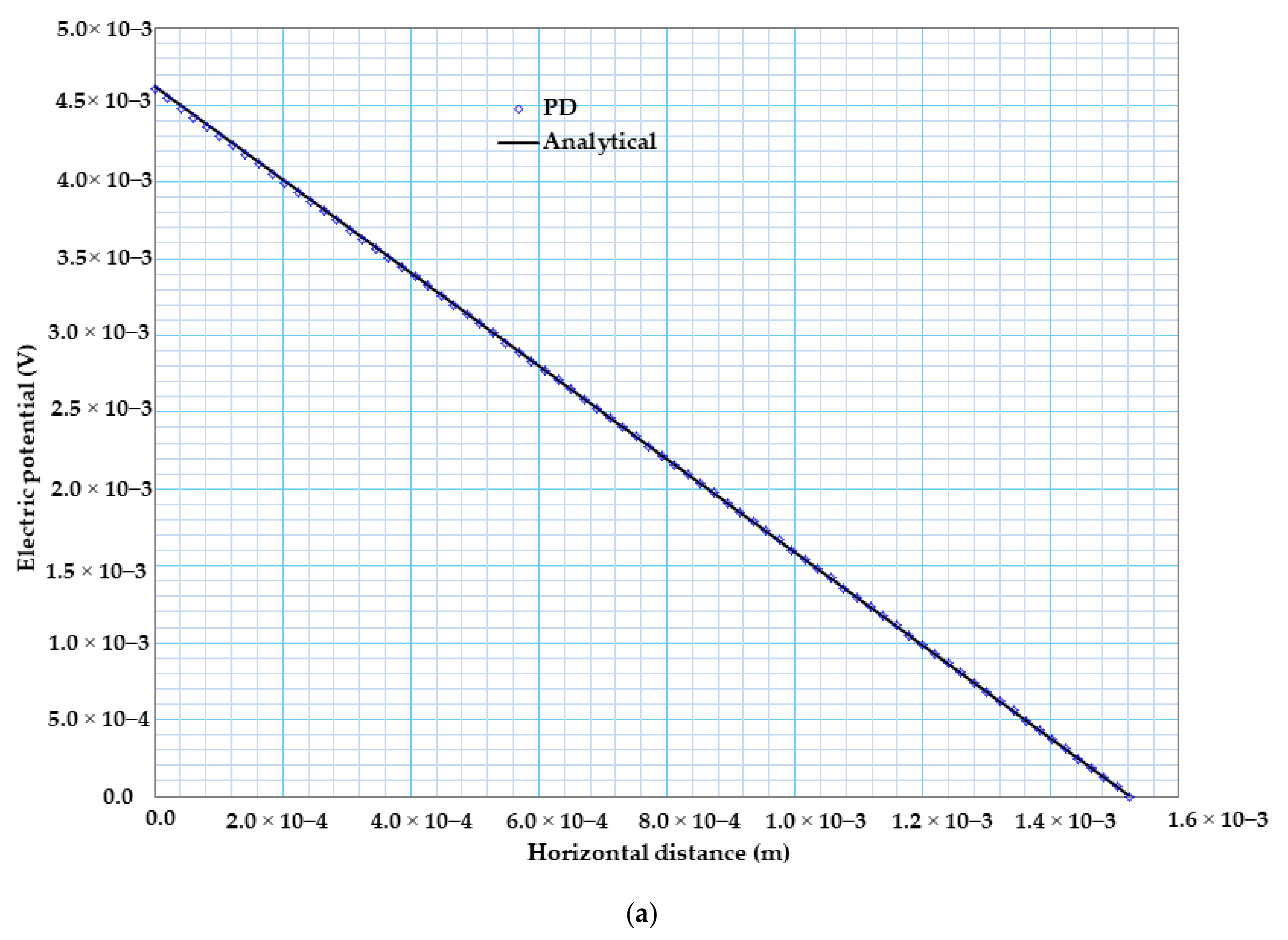
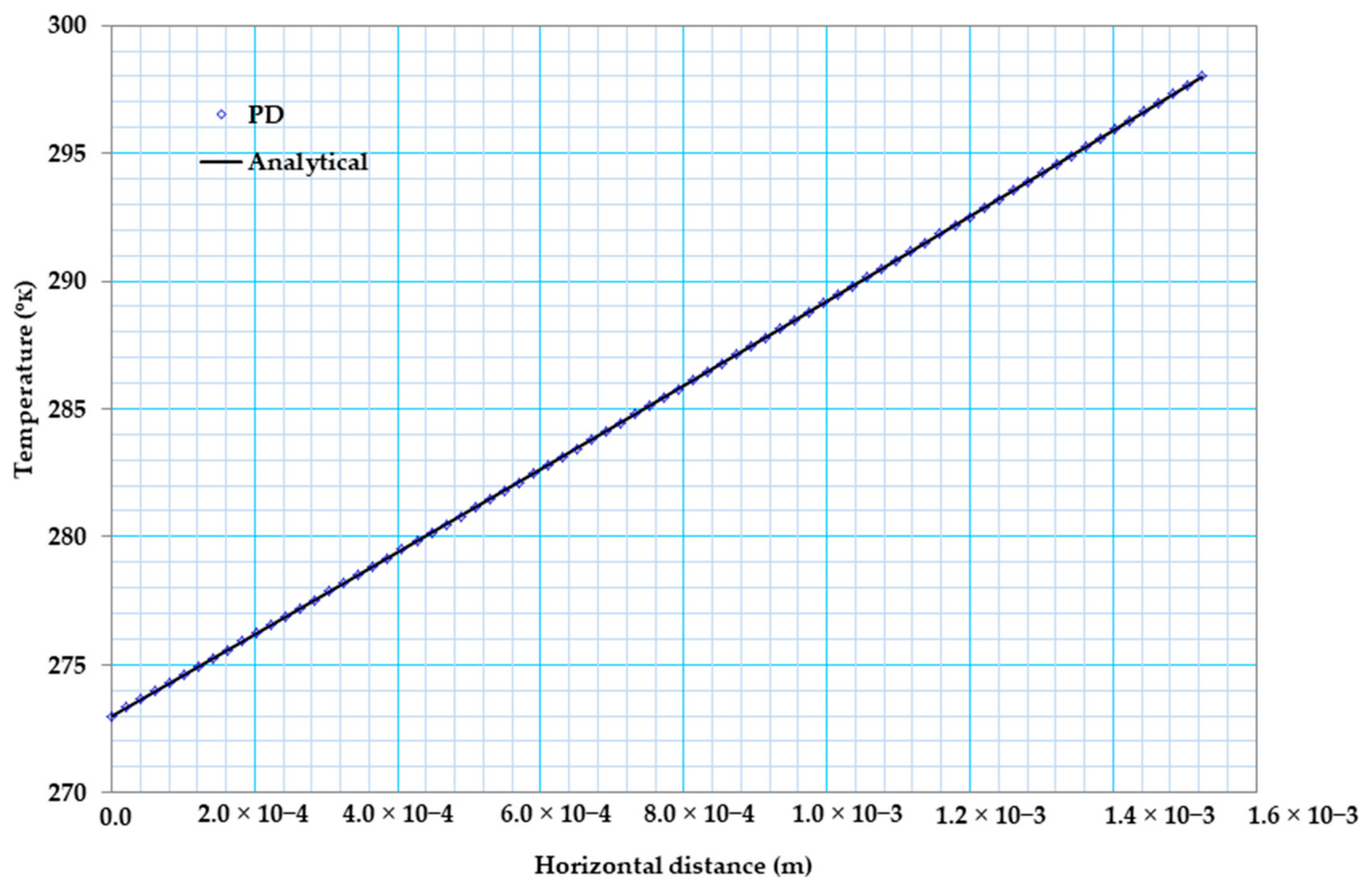
| Horizontal Distance (mm) | Electric Potential (10−3 V) (This Study) | Electric Potential (10−3 V) Ref. [46] | Electric Potential (10−3 V) Ref. [47] | Temperature (K) (This Study) | Temperature (K) Ref. [46] | Temperature (K) Ref. [47] |
|---|---|---|---|---|---|---|
| 0 | 4.603 | 4.622 | 4.622 | 273 | 273 | 273 |
| 0.762 | 2.311 | 2.311 | 2.311 | 285.45 | 285.3 | 285.3 |
| 1.143 | 1.143 | 1.156 | 1.156 | 291.8 | 291.8 | 291.7 |
| 1.524 | 0 | 0 | 0 | 298 | 298 | 298 |
| Geometric Parameters | Material Properties |
|---|---|
| Length (L) = 1.524 mm, Width (W) = 1.4 mm, |
| Horizontal Distance (mm) | Electric Potential (10−3 V) (This Study) | Electric Potential (10−3 V) Ref. [46] | Electric Potential (10−3 V) Ref. [47] | Temperature (K) (This Study) | Temperature (K) Ref. [46] | Temperature (K) Ref. [47] |
|---|---|---|---|---|---|---|
| 0 | 4.35 | 4.636 | 4.622 | 273 | 273 | 273 |
| 0.381 | 3.362 | 3.524 | 3.514 | 279.17 | 279.1 | 279.1 |
| 0.762 | 2.309 | 2.380 | 2.375 | 285.28 | 285.3 | 285.3 |
| 1.143 | 1.19 | 1.205 | 1.205 | 291.56 | 291.6 | 291.6 |
| 1.524 | 0 | 0 | 0 | 298 | 298 | 298 |
| Geometric Parameters | Material Properties |
|---|---|
| Length, L = 0.02 m Width, W = 0.02 m | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeleke, M.A.; Lai, X.; Liu, L. A Peridynamic Computational Scheme for Thermoelectric Fields. Materials 2020, 13, 2546. https://doi.org/10.3390/ma13112546
Zeleke MA, Lai X, Liu L. A Peridynamic Computational Scheme for Thermoelectric Fields. Materials. 2020; 13(11):2546. https://doi.org/10.3390/ma13112546
Chicago/Turabian StyleZeleke, Migbar Assefa, Xin Lai, and Lisheng Liu. 2020. "A Peridynamic Computational Scheme for Thermoelectric Fields" Materials 13, no. 11: 2546. https://doi.org/10.3390/ma13112546





