Multi-Mode Buckling Analysis of FGM Channel Section Beams
Abstract
1. Introduction
2. Materials and Methods
- The location of the aluminum and titanium layer (variant A and B),
- The thickness of aluminium and titanium sheet (tAl/tTi = 1/3, tAl/tTi = 1 and tAl/tTi = 3),
- The existence of adhesive layer tAd (samples with and without an adhesive layer—tAd = 0 or tAd = 0.1 mm),
- The length of the beam (L = 300 mm and L = 400 mm).
3. Results
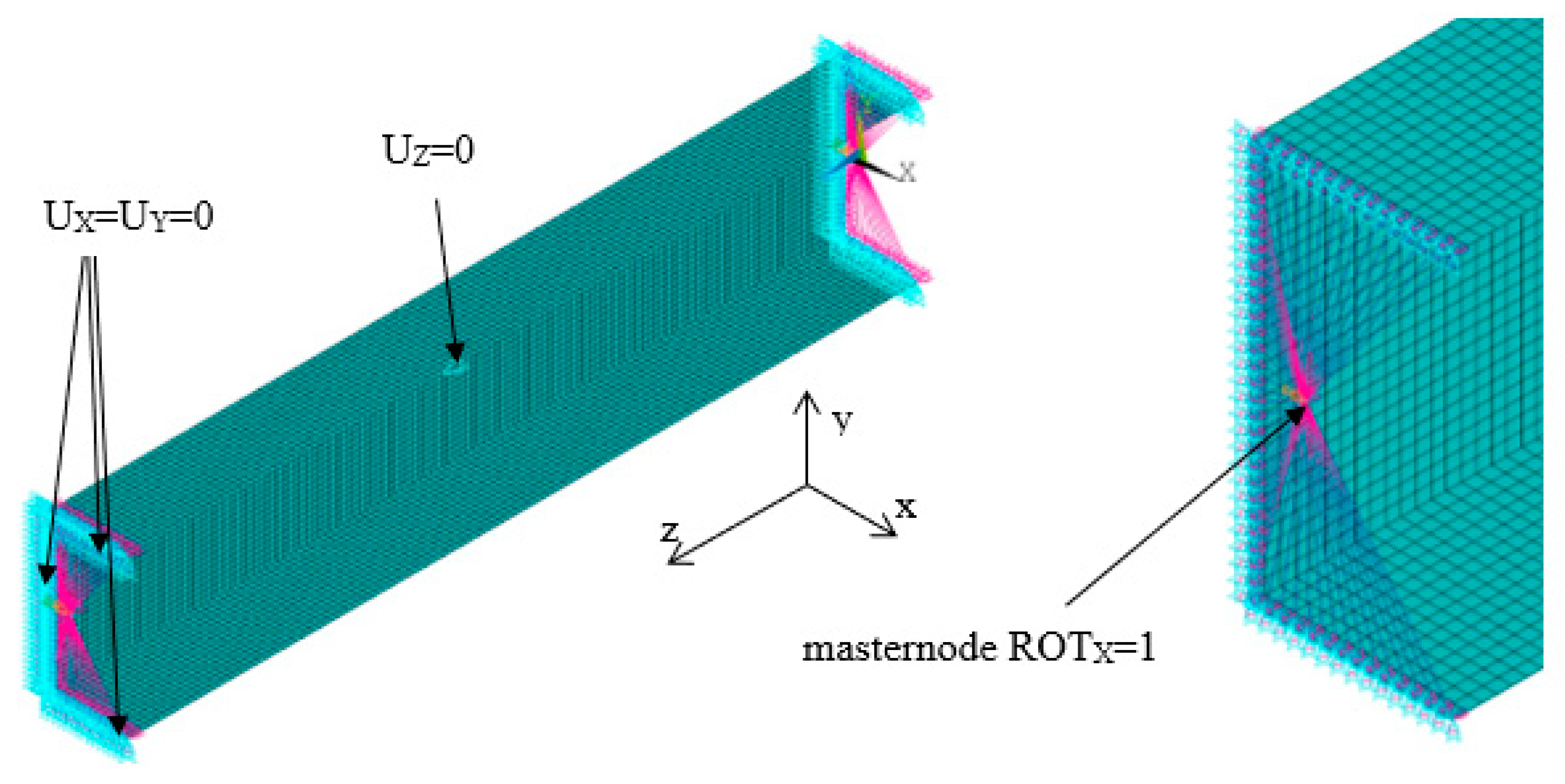
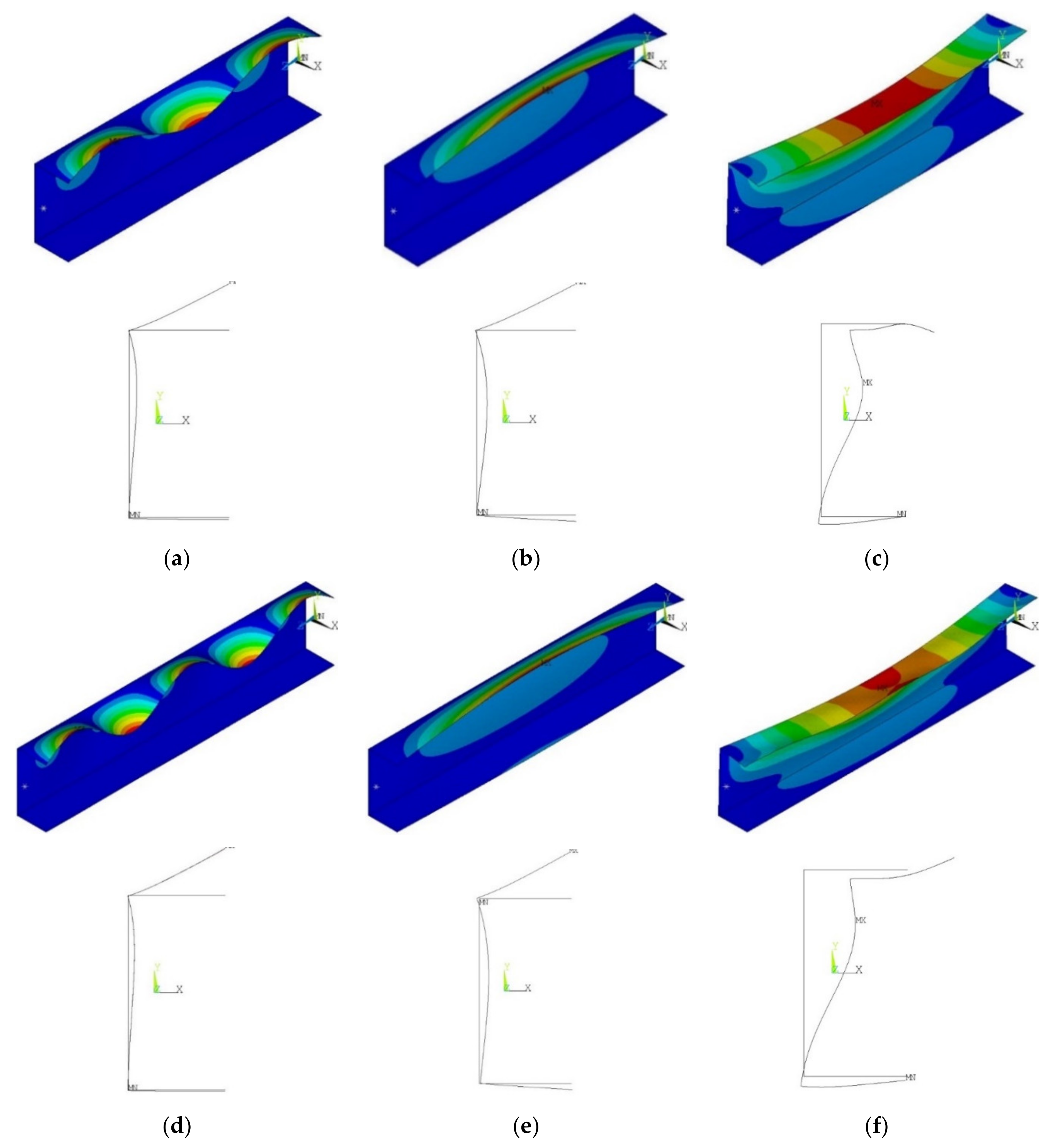
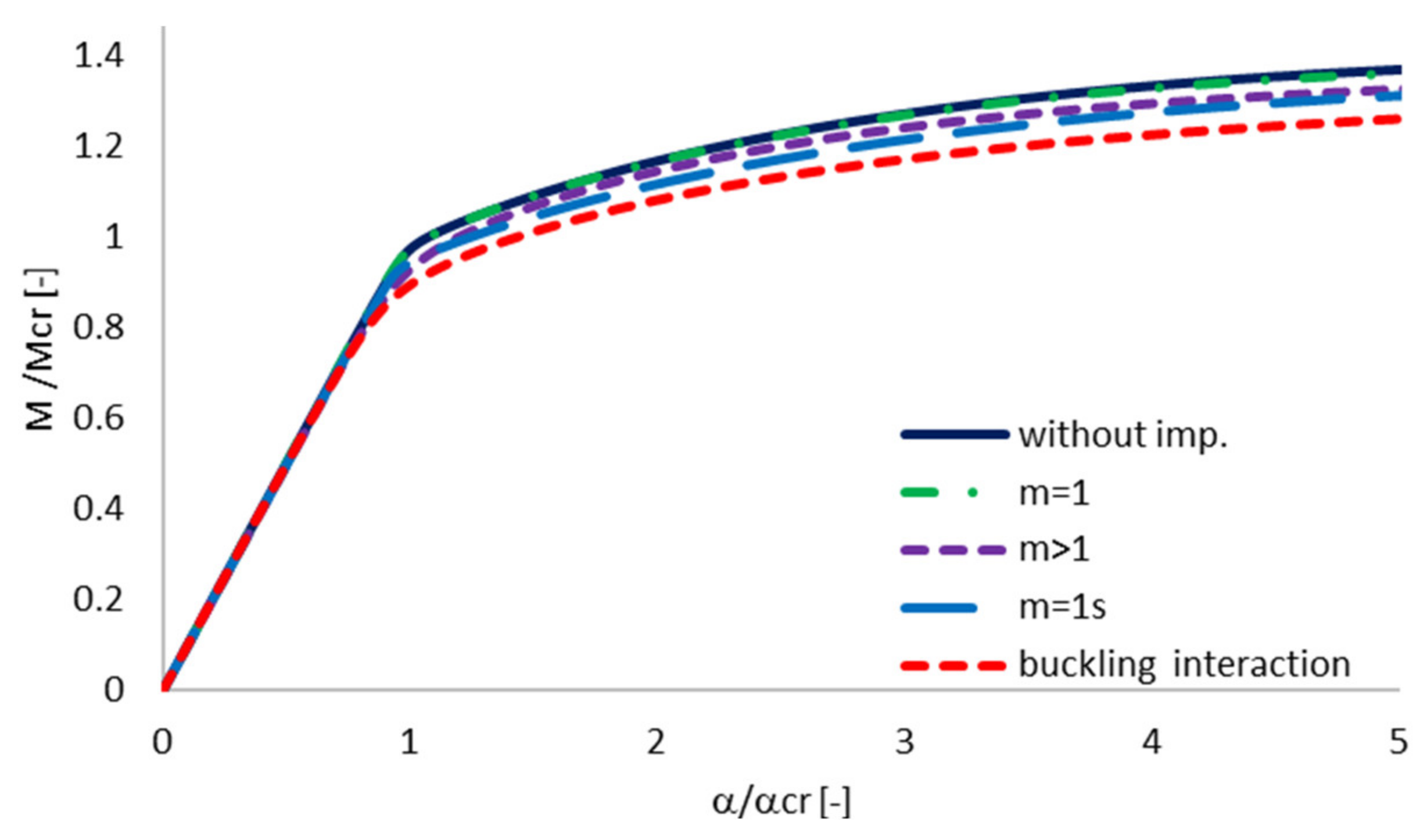
3.1. Linear Buckling Analysis
- Local buckling mode (m > 1, where m is the number of half-waves in the longitudinal direction)
- Primary global-distortional buckling mode (m = 1)
- Secondary global-distortional buckling mode (m = 1 s)
3.2. Non-Linear Buckling Analysis
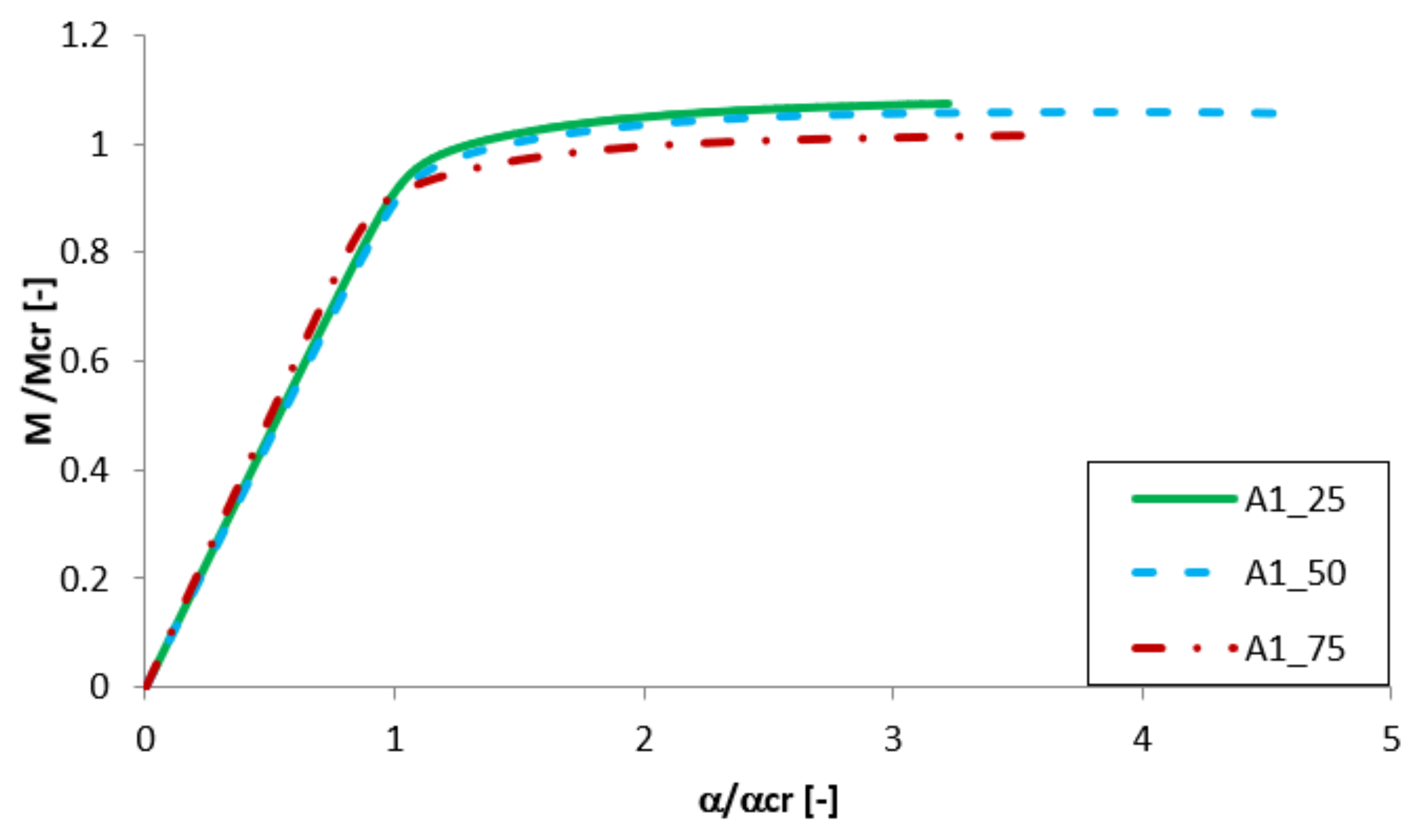
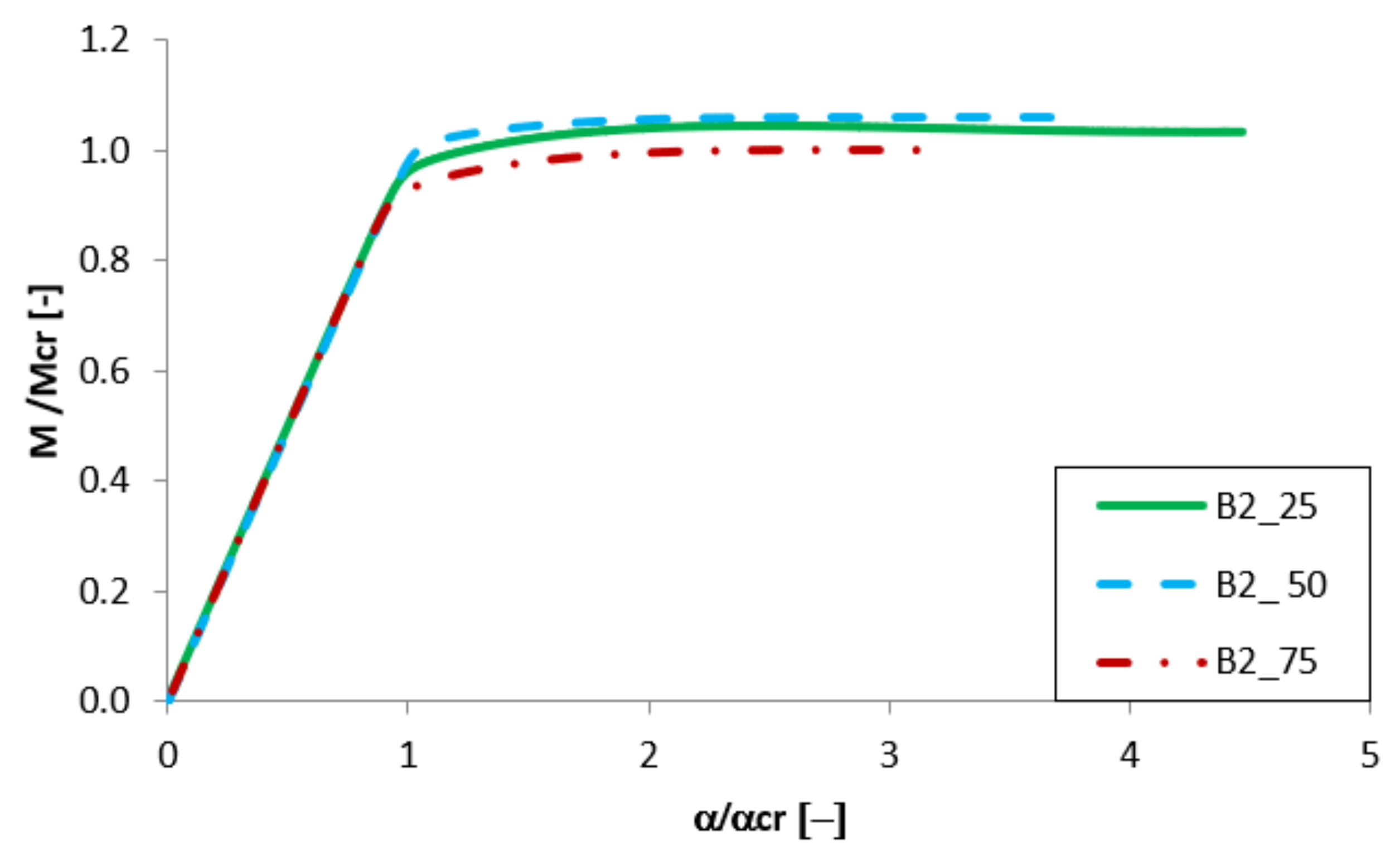
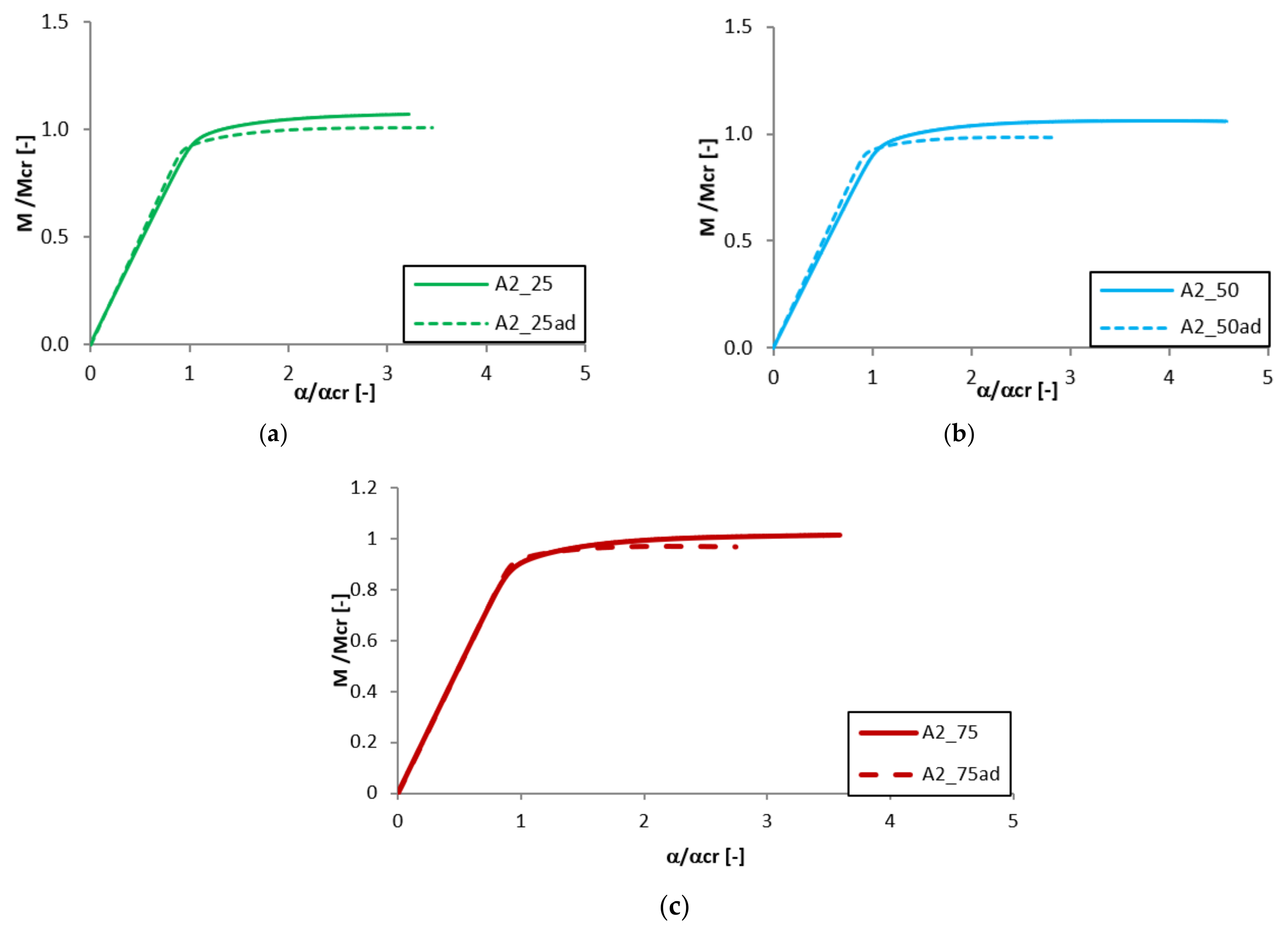
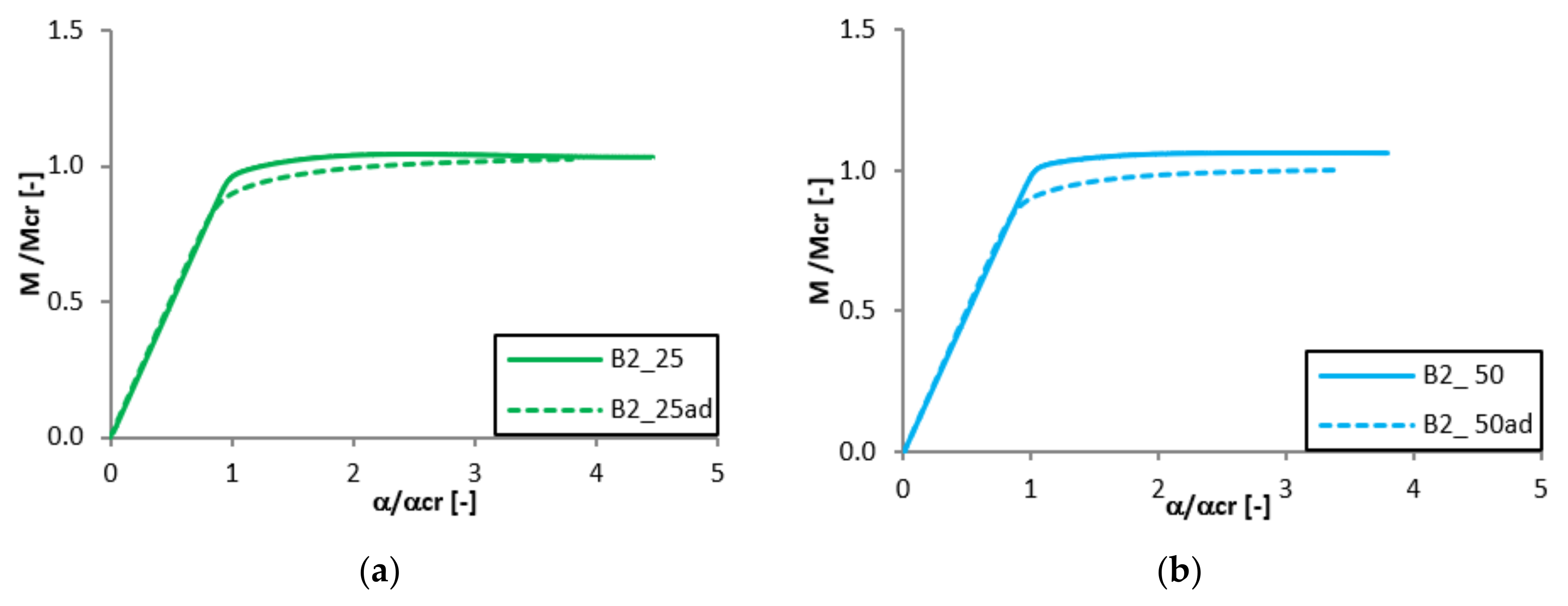
3.3. The Effect of Aluminium and Titanium Thickness and Position
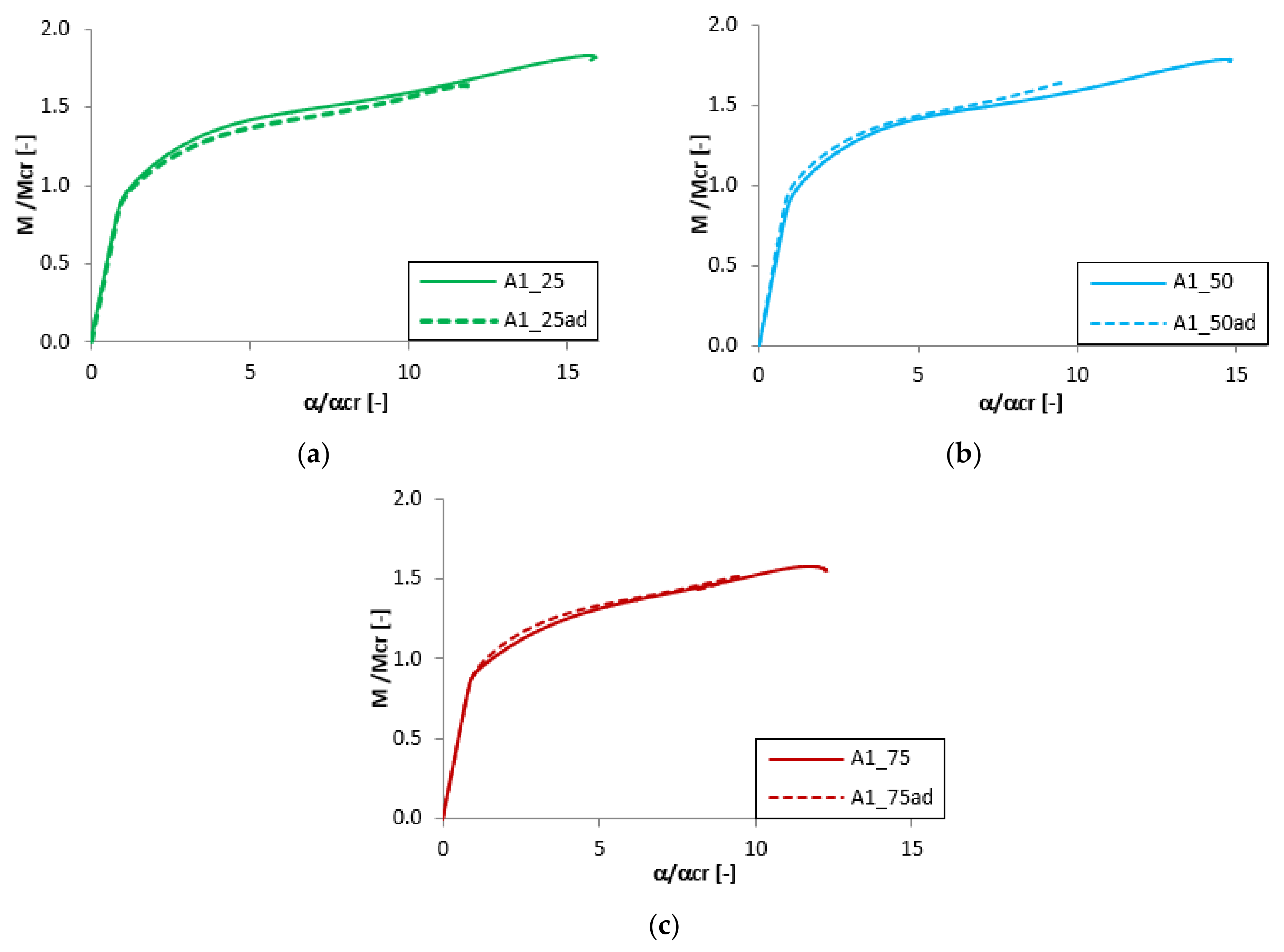
3.4. The Effect of the Adhesive Layer
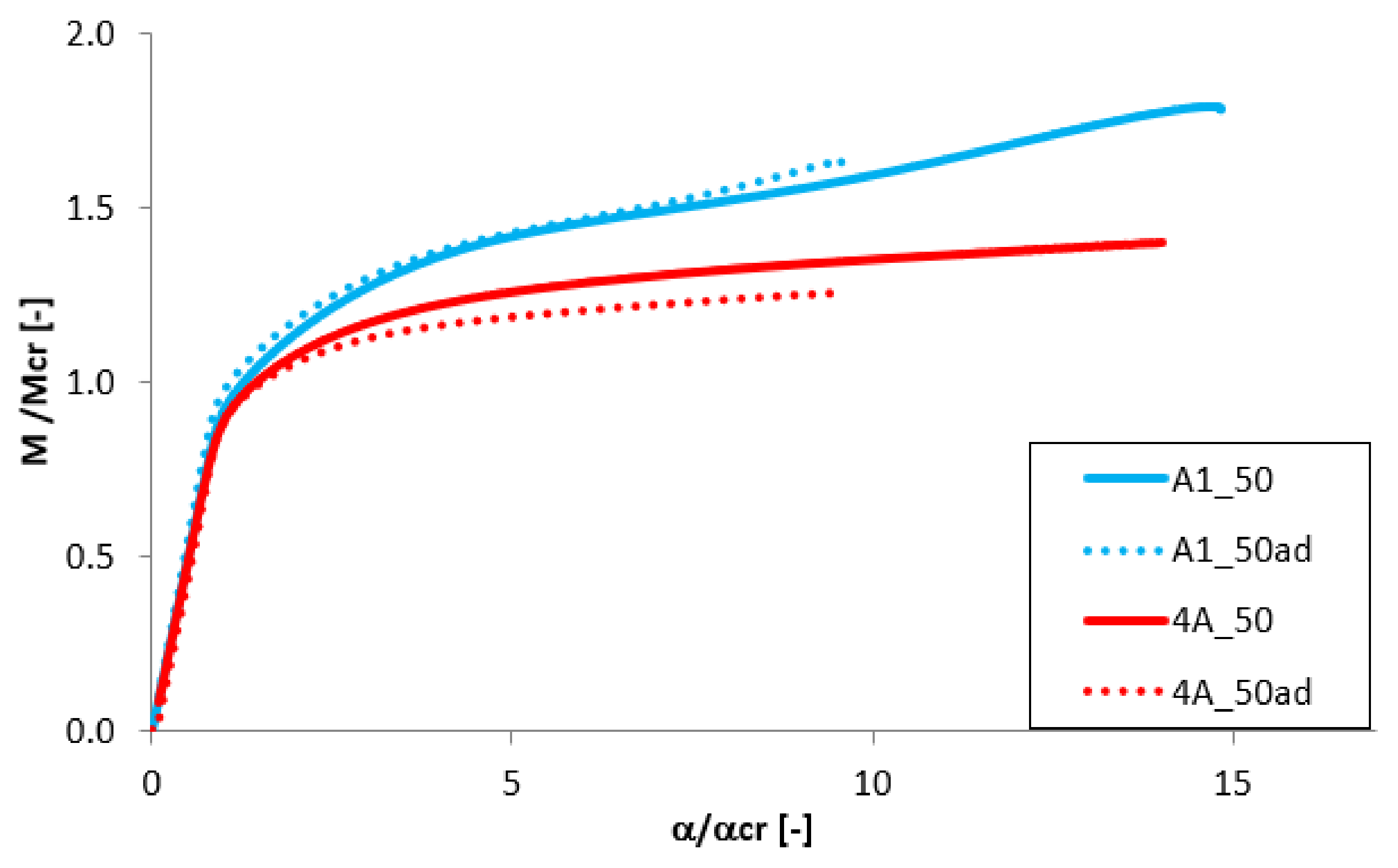
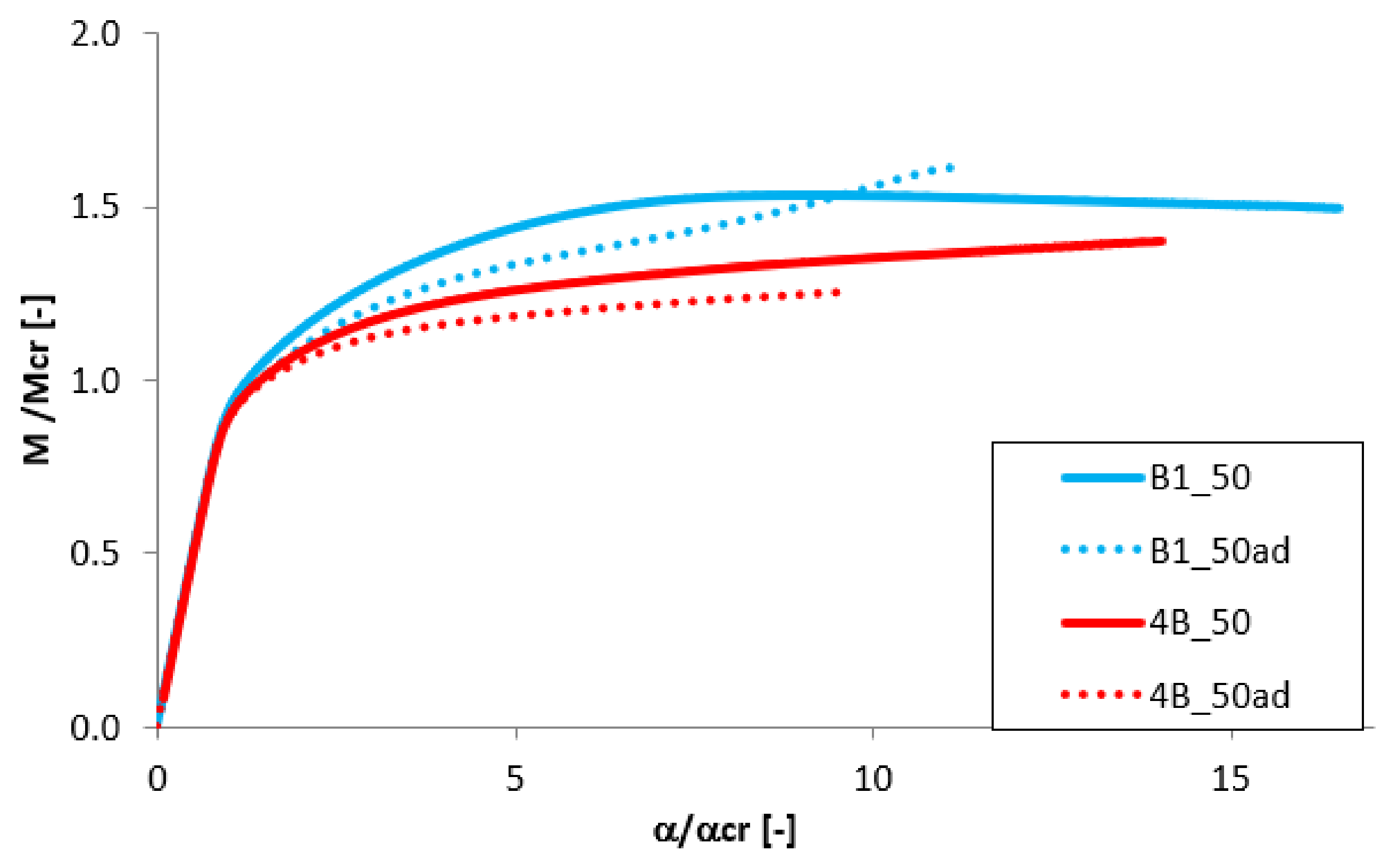
3.5. The Effect of the Beam’s Length
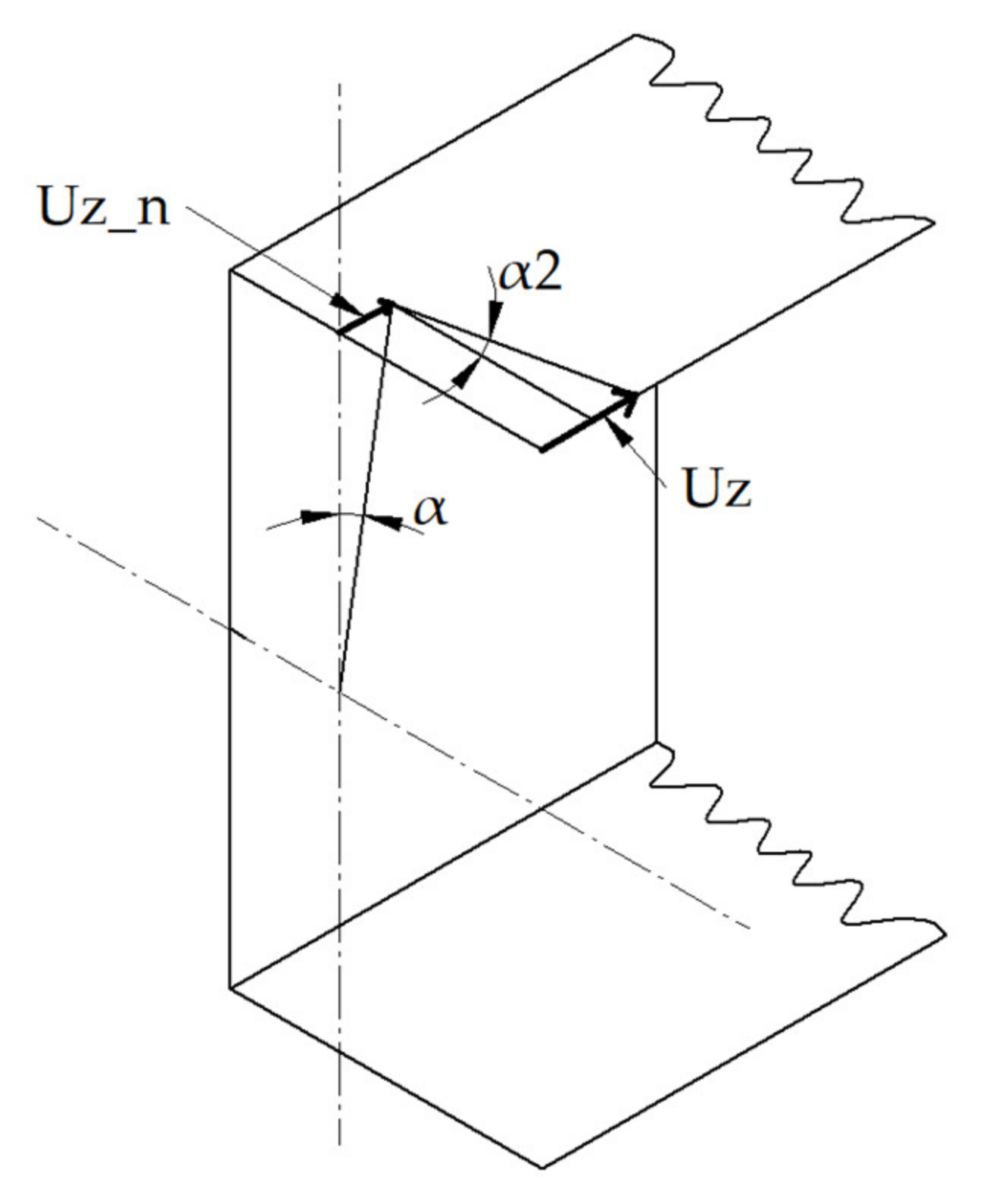
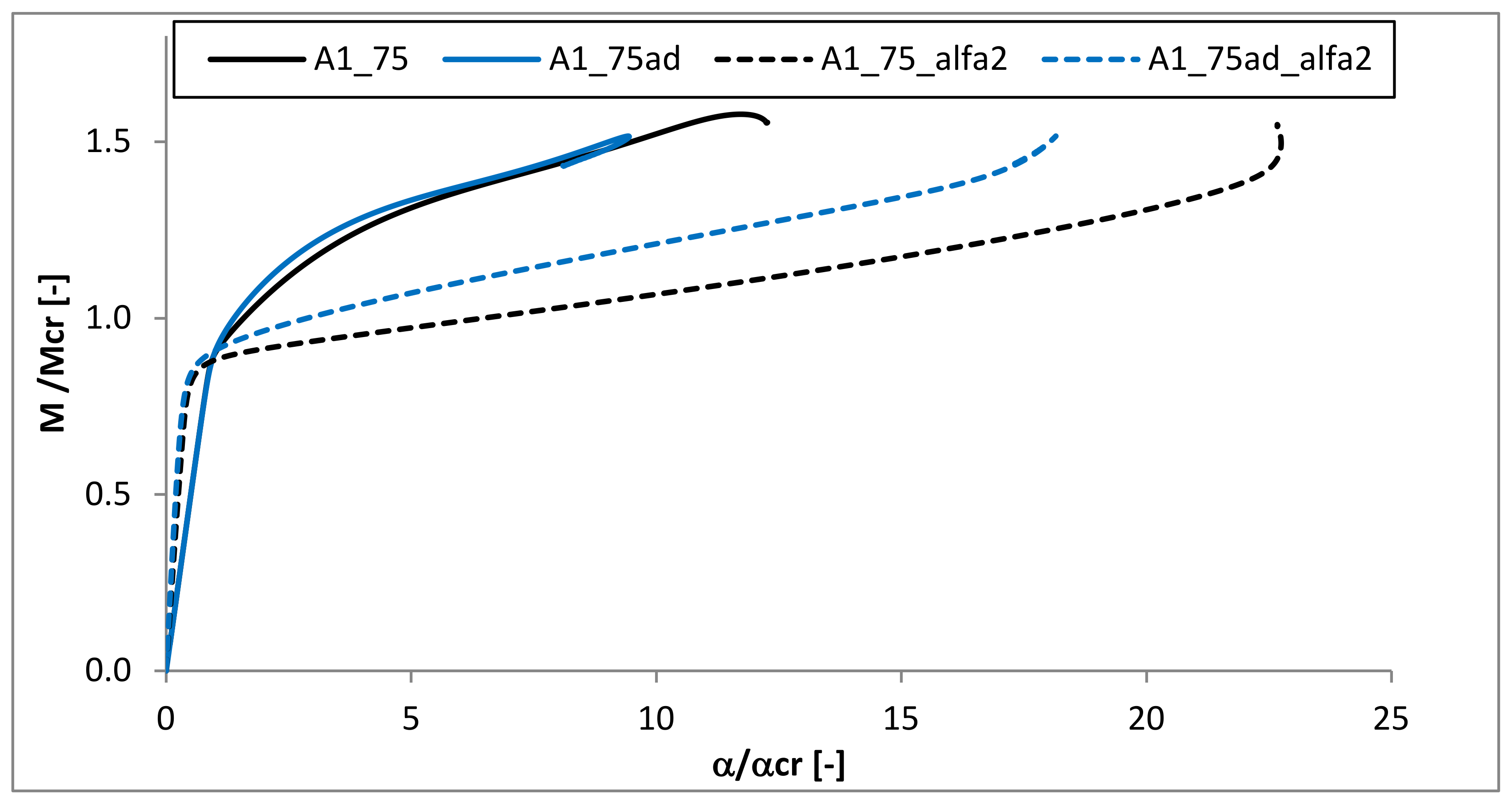
3.6. The Angle of Rotation at the Beam Ends
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sai, H. A review on functionally gradient materials (FGMs) and their applications. Int. J. Curr. Eng. Technol. 2018, 8, 79–84. [Google Scholar] [CrossRef]
- Mahamood, M.; Akinlabi, E.T. Functionally Graded Materials, Topics in Mining, Metallurgy and Materials Engineering; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Reddy, J.N. Analysis of functionally graded plates. Int. J. Numer. Meth. Eng. 2000, 47, 663–684. [Google Scholar] [CrossRef]
- Aydogdu, M.; Taskin, V. Free vibration analysis of functionally graded beams with simply supported edges. Mater. Des. 2007, 28, 1651–1656. [Google Scholar] [CrossRef]
- Suresh, S.; Mortensen, A. Fundamentals of Functionally Graded Materials: Processing and Thermomechanical Behavior of Graded Metals and Metallic-Ceramic Composites; IOM Communications Ltd.: London, UK, 1998. [Google Scholar]
- Zhang, X.; Chen, F.; Zhang, H. Stability and local bifurcation analysis of functionally graded material plate under transversal and in-plane excitations. Appl. Math. Model. 2013, 37, 6639–6651. [Google Scholar] [CrossRef]
- Babaei, H.; Eslami, M.R.; Khorshidvand, A.R. Thermal buckling and postbuckling responses of geometrically imperfect FG porous beams based on physical neutral plane. J. Therm. Stresses 2020, 43, 109–131. [Google Scholar] [CrossRef]
- Do, V.N.V.; Lee, C.H. Quasi-3D higher-order shear deformation theory for thermal buckling analysis of FGM plates based on a meshless method. Aerosp. Sci. Technol. 2018, 82, 450–465. [Google Scholar] [CrossRef]
- Do, V.N.V.; Lee, C. Thermal buckling analyses of FGM sandwich plates using the improved radial point interpolation mesh-free method. Compos. Struct. 2017, 177, 171–186. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, L.; Lv, Y. Elastoplastic thermal buckling of functionally graded material beams. Compos. Struct. 2019, 224, 111014. [Google Scholar] [CrossRef]
- Sohn, K.J.; Kim, J.H. Structural stability of functionally graded material plates subjected to aero-thermal loads. Compos. Struct. 2008, 82, 317–325. [Google Scholar] [CrossRef]
- Moita, J.S.; Araújo, A.L.; Correia, V.F.; Mota Soares, C.M.; Herskovits, J. Buckling behavior of composite and functionally graded material plates. Eur. J. Mech. A/Solids 2020, 80, 1–10. [Google Scholar] [CrossRef]
- Taczała, M.; Buczkowski, R.; Kleiber, M. Postbuckling analysis of functionally graded plates on an elastic foundation. Compos. Struct. 2015, 132, 842–847. [Google Scholar] [CrossRef]
- Prakash, T.; Singha, M.; Ganapathi, M. Influence of neutral surface position on the nonlinear stability behavior of functionally graded plates. Comput. Mech. 2009, 43, 341–350. [Google Scholar] [CrossRef]
- Shen, H.S. Post buckling of FGM plates with piezoelectric actuators under thermo-electro-mechanical loadings. Int. J. Solids Struct. 2005, 42, 6101–6121. [Google Scholar] [CrossRef]
- Burzynski, S.; Chroscielewski, J.; Daszkiewicz, K.; Witkowski, W. Geometrically nonlinear FEM analysis of FGM shells based on neutral physical surface approach in 6-parameter shell theory. Compos. Part B Eng. 2016, 107, 203–213. [Google Scholar] [CrossRef]
- Burzynski, S.; Chroscielewski, J.; Daszkiewicz, K.; Witkowski, W. Elastoplastic nonlinear FEM analysis of FGM shells of Cosserat type. Compos. Part B Eng. 2018, 154, 478–491. [Google Scholar] [CrossRef]
- Sobhy, M. An accurate shear deformation theory for vibration and buckling of FGM sandwich plates in hygrothermal environment. Int. J. Mech. Sci. 2016, 10, 62–77. [Google Scholar] [CrossRef]
- Kumar, R.; Lal, A.; Singh, B.N.; Singh, J. New transverse shear deformation theory for bending analysis of FGM plate under patch load. Compos. Struct. 2019, 208, 91–100. [Google Scholar] [CrossRef]
- Meiche, N.E.; Tounsi, A.; Ziane, N.; Mechab, I.; Addia Bedia, E.A. A new hyperbolic shear deformation theory for buckling and vibration of functionally graded sandwich plate. Int. J. Mech. Sci. 2011, 53, 237–241. [Google Scholar] [CrossRef]
- Daneshmehra, A.; Heydaria, M.; Khorshidia, M.A. Post-buckling analysis of FGM beams according to different shear deformation theories. Int. J. Multidiscip. Curr. Res. 2013, 1, 37–49. [Google Scholar]
- Farhatnia, F.; Sarami, M. Finite element approach of bending and buckling analysis of FG beams based on refined zigzag theory. Uni. J. Mech. Eng. 2019, 7, 147–158. [Google Scholar] [CrossRef]
- Ghiasian, S.E.; Kiani, Y.; Eslami, M.R. Nonlinear thermal dynamic buckling of FGM beams. Eur. J. Mech. A/Solids 2015, 54, 232–242. [Google Scholar] [CrossRef]
- Zeverdejeni, M.K.; Beni, Y.T.; Kiani, Y. Multi-scale buckling and post-buckling analysis of functionally graded laminated composite plates reinforced by defective graphene sheets. Int. J. Struct. Stab. Dynam. 2019, 20, 1. [Google Scholar] [CrossRef]
- Kiani, Y. Axisymmetric static and dynamics snap-through phenomena in a thermally postbuckled temperature-dependent FGM circular plate. Int. J. Non-Linear Dynam. 2016, 89, 1–13. [Google Scholar] [CrossRef]
- Czechowski, L. Study of dynamic buckling of FG plate due to heat flux pulse. Int. J. Appl. Mech. Eng. 2015, 20, 19–31. [Google Scholar] [CrossRef]
- Czechowski, L. Analysis of dynamic response of functionally graded plate due to temperature pulse load. Compos. Struct. 2016, 160, 625–634. [Google Scholar] [CrossRef]
- Czechowski, L.; Kowal-Michalska, K. Static and dynamic buckling of rectangular functionally graded plates subjected to thermal loading. Strength Mater. 2013, 45, 666–673. [Google Scholar] [CrossRef]
- Zhang, J.; Li, S. Dynamic buckling of FGM truncated conical shells subjected to non-uniform normal impact load. Compos. Struct. 2010, 92, 2979–2983. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, S.; Zweng, W. Dynamic buckling analysis of functionally graded material cylindrical shells under thermal shocks. Contin. Mech. Thermodyn. 2019, 55, 1–14. [Google Scholar] [CrossRef]
- Kolakowski, Z. Some aspects of interactive dynamic stability of thin-walled trapezoidal FGM beam-columns under axial load. Thin-Walled Struct. 2016, 98, 431–442. [Google Scholar] [CrossRef]
- Kolakowski, Z.; Teter, A. Static interactive buckling of functionally graded columns with close cross-sections subjected to axial compression. Compos. Struct. 2015, 123, 257–262. [Google Scholar] [CrossRef]
- Kolakowski, Z.; Teter, A. Load carrying capacity of functionally graded columns with open cross-sections under static compression. Compos. Struct. 2015, 129, 1–7. [Google Scholar] [CrossRef]
- Kolakowski, Z.; Mania, R.J. Influence of the coupling matrix B on the interactive buckling of FML-FGM columns with closed cross-sections under axial compression. Compos. Struct. 2017, 173, 70–77. [Google Scholar] [CrossRef]
- Teter, A.; Mania, R.J.; Kolakowski, Z. Non-linear multi-mode buckling of non-symmetric FML/FGM thin-walled columns with open cross-sections under compression. Compos. Struct. 2017, 167, 38–49. [Google Scholar] [CrossRef]
- Huang, X.H.; Yang, J.; Liu, Q.; Zhu, J.; Bai, L.; Wang, F.; Wang, J. A simplified flange-lip model for distortional buckling of cold-formed steel channel-sections with stiffened web. Int. J. Mech. Sci. 2018, 136, 451–459. [Google Scholar] [CrossRef]
- Camotim, D.; Dinis, P.B. Coupled instabilities with distortional buckling in cold-formed steel lipped channel columns. Thin-Wall Struct. 2011, 49, 562–575. [Google Scholar] [CrossRef]
- Camotim, D.; Dinis, P.B.; Martins, A.D.; Young, B. Review: Interactive behaviour, failure and DSM design of cold-formed steel members prone to distortional buckling. Thin-Wall Struct. 2018, 128, 12–42. [Google Scholar] [CrossRef]
- Chen, M.T.; Young, B.; Martins, A.D.; Camotim, D.; Dinis, P.B. Experimental investigation on cold-formed steel stiffened lipped channel columns undergoing local-distortional interaction. Thin-Walled Struct. 2020, 150, 106682. [Google Scholar] [CrossRef]
- Martins, A.D.; Gonçalves, R.; Camotim, D. Post-buckling behaviour of thin-walled regular polygonal tubular columns undergoing local–distortional interaction. Thin-Walled Struct. 2019, 138, 373–391. [Google Scholar] [CrossRef]
- Niu, R.; Rasmussen, K.J.R.; Fan, F. Distortional–global interaction buckling of stainless steel C-beams: Part I—Experimental investigation. J. Constr. Steel Res. 2014, 96, 127–139. [Google Scholar] [CrossRef]
- Niu, R.; Rasmussen, K.J.R.; Fan, F. Distortional–global interaction buckling of stainless steel C-beams: Part II—Numerical study and design. J. Constr. Steel Res. 2014, 96, 40–53. [Google Scholar] [CrossRef]
- Kolakowski, Z. A semi-analytical method of interactive buckling of thin-walled elastic structures in the second order approximation. Int. J. Solids Struct. 1996, 33, 3779–3790. [Google Scholar] [CrossRef]
- Kolakowski, Z.; Jankowski, J. Interactive buckling of steel C-beams with different lengths—From short to long beams. Thin-Walled Struct. 2018, 125, 203–210. [Google Scholar] [CrossRef]
- Kolakowski, Z.; Jankowski, J. Interactive buckling of steel LC-beams under bending. Materials 2019, 12, 1440. [Google Scholar] [CrossRef] [PubMed]
- Kolakowski, Z.; Kubiak, T.; Kamocka, M. Coupled buckling of steel LC-beams under bending. In Stability and Ductility of Steel Structures; Wald, F., Jandera, M., Eds.; CRC Press: Boca Raton, FL, USA, 2019; pp. 614–621. [Google Scholar]
- Zaczynska, M.; Kolakowski, Z. The influence of the internal forces of the buckling modes on the load-carrying capacity of composite medium length beams under bending. Materials 2020, 13, 445. [Google Scholar] [CrossRef]
- ANSYS, Inc. User’s Guide ANSYS® 18.2; Ansys, Inc.: Canonsburg, PA, USA, 2018. [Google Scholar]
- Huntsman. Available online: https://prostech.vn/wp-content/uploads/2019/01/Araldite-AW-4804-_-Hardener-HW-4804.pdf (accessed on 4 June 2019).
- Kolakowski, Z.; Kubiak, T.; Zaczynska, M.; Kazmierczyk, F. Global-distortional buckling mode influence on post-buckling behaviour of lip-channel beams. Int. J. Mech. Sci. 2020, 105723, in press. [Google Scholar] [CrossRef]
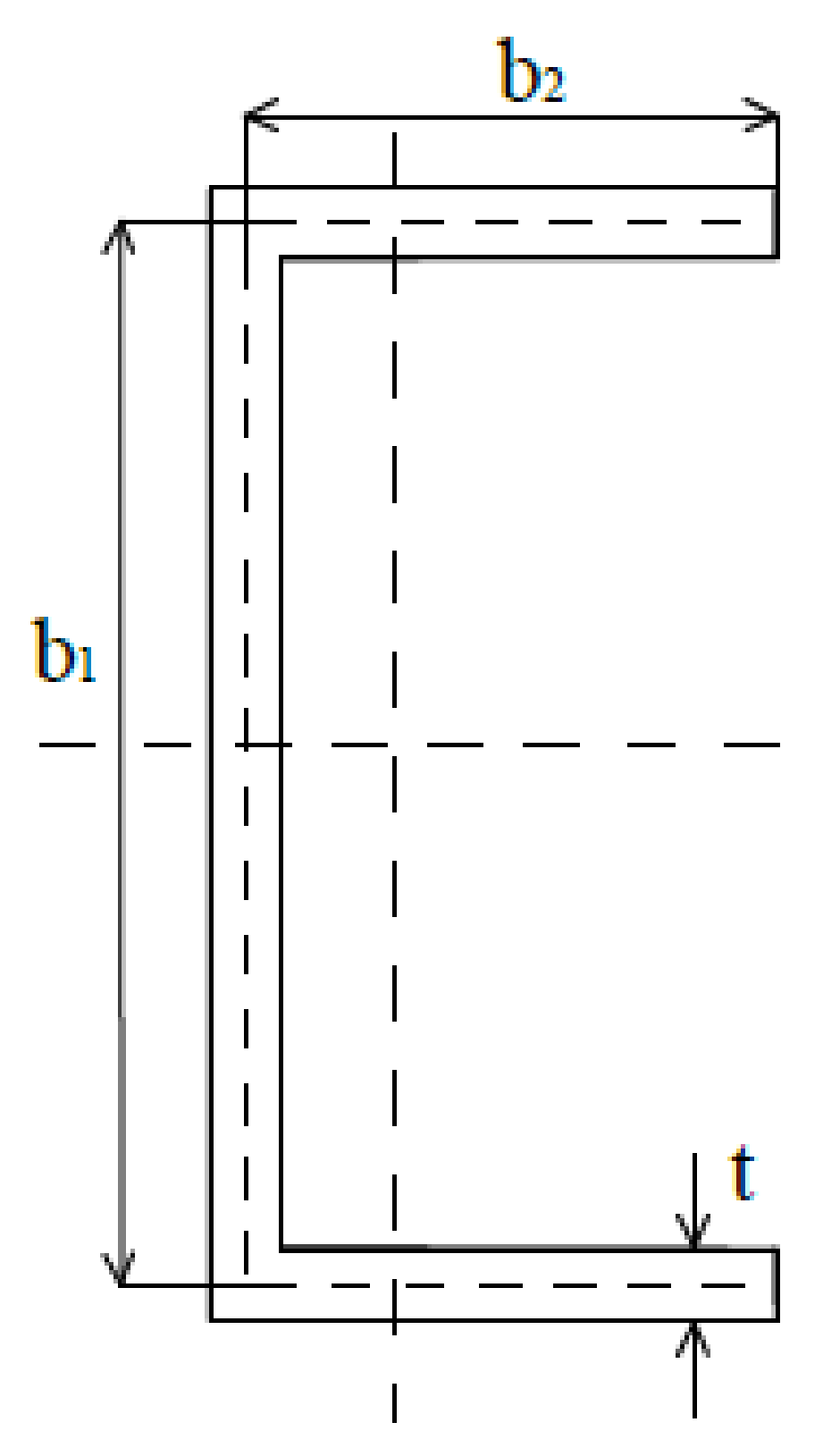





| Total Wall Thickness—t (mm) | Width of the Web—b1 (mm) | Width of the Flange—b2 (mm) | Length of the Beam—L (mm) |
|---|---|---|---|
| 1–2.1 | 80 | 40 | 300; 400 |
| L (mm) | Name | Case | Thickness (mm) | Name | Case | Thickness (mm) | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| tAl | tTi | tAd | tAl | tTi | tAd | |||||
| 300 | A1_75 | A | 0.25 | 0.75 | 0.00 | B1_75 | B | 0.25 | 0.75 | 0.00 |
| A1_75ad | A | 0.25 | 0.75 | 0.10 | B1_75ad | B | 0.25 | 0.75 | 0.10 | |
| A1_50 | A | 0.50 | 0.50 | 0.00 | B1_50 | B | 0.50 | 0.50 | 0.00 | |
| A1_50ad | A | 0.50 | 0.50 | 0.10 | B1_50ad | B | 0.50 | 0.50 | 0.10 | |
| A1_25 | A | 0.75 | 0.25 | 0.00 | B1_25 | B | 0.75 | 0.25 | 0.00 | |
| A1_25ad | A | 0.75 | 0.25 | 0.10 | B1_25ad | B | 0.75 | 0.25 | 0.10 | |
| A2_75 | A | 1.50 | 0.50 | 0.00 | B2_75 | B | 1.50 | 0.50 | 0.00 | |
| A2_75ad | A | 1.50 | 0.50 | 0.10 | B2_75ad | B | 1.50 | 0.50 | 0.10 | |
| A2_50 | A | 1.00 | 1.00 | 0.00 | B2_50 | B | 1.00 | 1.00 | 0.00 | |
| A2_50ad | A | 1.00 | 1.00 | 0.10 | B2_50ad | B | 1.00 | 1.00 | 0.10 | |
| A2_25 | A | 0.50 | 1.50 | 0.00 | B2_25 | B | 0.50 | 1.50 | 0.00 | |
| A2_25ad | A | 0.50 | 1.50 | 0.10 | B2_25ad | B | 0.50 | 1.50 | 0.10 | |
| 400 | 4A_50 | A | 0.50 | 0.50 | 0.00 | 4B_50 | B | 0.50 | 0.50 | 0.00 |
| 4A_50ad | A | 0.50 | 0.50 | 0.10 | 4B_50ad | B | 0.50 | 0.50 | 0.10 | |
| Material | E (GPa) | ν |
|---|---|---|
| Titanium Ti-5Al-2.5Sn | 107 | 0.34 |
| Aluminium EN AW-2024 (AlCu4Mg1) | 71 | 0.33 |
| Adhesive Araldite AW 4804 [49] | 6.2 | 0.4 |
| Name | Mode | Mcr (Nm) | αcr (°) | Name | Mode | Mcr (Nm) | αcr (°) | Mcr(A)/Mcr(B) (-) |
|---|---|---|---|---|---|---|---|---|
| A1_75 | 3 | 178 | 0.11 | B1_75 | 3 | 177 | 0.11 | 1.01 |
| 1 | 502 | 0.32 | 1 | 497 | 0.31 | 1.01 | ||
| 1 s | 6516 | 4.11 | 1 s | 6546 | 4.12 | 0.99 | ||
| A1_75ad | 3 | 226 | 0.14 | B1_75ad | 3 | 225 | 0.14 | 1.00 |
| 1 | 635 | 0.40 | 1 | 631 | 0.39 | 1.01 | ||
| 1 s | 6732 | 4.21 | 1 s | 6774 | 4.23 | 0.99 | ||
| A1_50 | 3 | 181 | 0.10 | B1_50 | 3 | 179 | 0.10 | 1.01 |
| 1 | 510 | 0.29 | 1 | 505 | 0.29 | 1.01 | ||
| 1 s | 7170 | 4.07 | 1 s | 7241 | 4.10 | 0.99 | ||
| A1_50ad | 3 | 237 | 0.13 | B1_50ad | 3 | 235 | 0.13 | 1.01 |
| 1 | 670 | 0.38 | 1 | 662 | 0.37 | 1.01 | ||
| 1 s | 7419 | 4.18 | 1 s | 7503 | 4.22 | 0.99 | ||
| A1_25 | 3 | 188 | 0.10 | B1_25 | 3 | 187 | 0.10 | 1.01 |
| 1 | 532 | 0.27 | 1 | 528 | 0.27 | 1.01 | ||
| 1 s | 7815 | 40.39 | 1 s | 7889 | 4.05 | 0.99 | ||
| A1_25ad | 3 | 229 | 0.12 | B1_25ad | 3 | 227 | 0.12 | 1.01 |
| 1 | 647 | 0.33 | 1 | 639 | 0.33 | 1.01 | ||
| 1 s | 8053 | 4.13 | 1 s | 8143 | 4.16 | 0.99 | ||
| A2_75 | 3 | 1389 | 0.43 | B2_75 | 3 | 1408 | 0.44 | 0.83 |
| 1 | 3726 | 1.18 | 1 | 3666 | 1.15 | 0.85 | ||
| 1 s | 14810 | 4.66 | 1 s | 15008 | 4.72 | 0.88 | ||
| A2_75ad | 3 | 1574 | 0.49 | B2_75ad | 3 | 1556 | 0.49 | 1.01 |
| 1 | 4147 | 1.30 | 1 | 4089 | 1.30 | 1.01 | ||
| 1 s | 15083 | 4.74 | 1 s | 15257 | 4.74 | 0.99 | ||
| A2_50 | 3 | 1410 | 0.36 | B2_50 | 3 | 1433 | 0.41 | 0.98 |
| 1 | 3821 | 1.09 | 1 | 3748 | 1.06 | 1.02 | ||
| 1 s | 16,226 | 4.61 | 1 s | 16,519 | 4.67 | 0.98 | ||
| A2_50ad | 3 | 1629 | 0.46 | B2_50ad | 3 | 1600 | 0.46 | 1.02 |
| 1 | 4332 | 1.23 | 1 | 4242 | 1.23 | 1.02 | ||
| 1 s | 16,566 | 4.69 | 1 s | 16,851 | 4.69 | 0.98 | ||
| A2_25 | 3 | 1474 | 0.38 | B2_25 | 3 | 1491 | 0.38 | 0.99 |
| 1 | 3991 | 1.03 | 1 | 3939 | 1.01 | 1.01 | ||
| 1 s | 17,873 | 4.60 | 1 s | 18,067 | 4.64 | 0.99 | ||
| A2_25ad | 3 | 1638 | 0.42 | B2_25ad | 3 | 1612 | 0.42 | 1.02 |
| 1 | 4370 | 1.12 | 1 | 4293 | 1.12 | 1.02 | ||
| 1 s | 18060 | 4.64 | 1 s | 18330 | 4.64 | 0.99 | ||
| 4A1_50 | 5 | 181 | 0.14 | 4B1_50 | 5 | 179 | 0.14 | 1.01 |
| 1 | 784 | 0.59 | 1 | 776 | 0.59 | 1.01 | ||
| 1 s | 4643 | 3.51 | 1 s | 4684 | 3.53 | 0.99 | ||
| 4A1_50ad | 5 | 237 | 0.18 | 4B1_50ad | 5 | 235 | 0.18 | 1.01 |
| 1 | 1017 | 0.76 | 1 | 1004 | 0.75 | 1.01 | ||
| 1 s | 4786 | 3.60 | 1 s | 4836 | 3.62 | 0.99 |
| Name | Mmax/Mcr | Name | Mmax/Mcr |
|---|---|---|---|
| A1_75 | 1.578 | B1_75 | 1.589 |
| A1_75ad | 1.516 | B1_75ad | 1.539 |
| A1_50 | 1.788 | B1_50 | 1.532 |
| A1_50ad | 1.637 | B1_50ad | 1.613 |
| A1_25 | 1.832 | B1_25 | 1.649 |
| A1_25ad | 1.646 | B1_25ad | 1.695 |
| A2_75 | 1.014 | B2_75 | 1.002 |
| A2_75ad | 0.971 | B2_75ad | 0.977 |
| A2_50 | 1.060 | B2_50 | 1.062 |
| A2_50ad | 0.986 | B2_50ad | 0.99 |
| A2_25 | 1.074 | B2_25 | 1.045 |
| A2_25ad | 1.016 | B2_25ad | 1.028 |
| 4A1_50 | 1.399 | 4B1_50 | 1.437 |
| 4A1_50ad | 1.256 | 4B1_50ad | 1.267 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaczynska, M.; Kazmierczyk, F. Multi-Mode Buckling Analysis of FGM Channel Section Beams. Materials 2020, 13, 2567. https://doi.org/10.3390/ma13112567
Zaczynska M, Kazmierczyk F. Multi-Mode Buckling Analysis of FGM Channel Section Beams. Materials. 2020; 13(11):2567. https://doi.org/10.3390/ma13112567
Chicago/Turabian StyleZaczynska, Monika, and Filip Kazmierczyk. 2020. "Multi-Mode Buckling Analysis of FGM Channel Section Beams" Materials 13, no. 11: 2567. https://doi.org/10.3390/ma13112567
APA StyleZaczynska, M., & Kazmierczyk, F. (2020). Multi-Mode Buckling Analysis of FGM Channel Section Beams. Materials, 13(11), 2567. https://doi.org/10.3390/ma13112567




