Numerical Study of Concrete Mesostructure Effect on Lamb Wave Propagation
Abstract
1. Introduction
2. Theoretical Background
2.1. Theory of Lamb Waves
2.2. Two-Dimensional Fourier Transform
3. Concrete Model Generation
3.1. Concrete Mesostructure
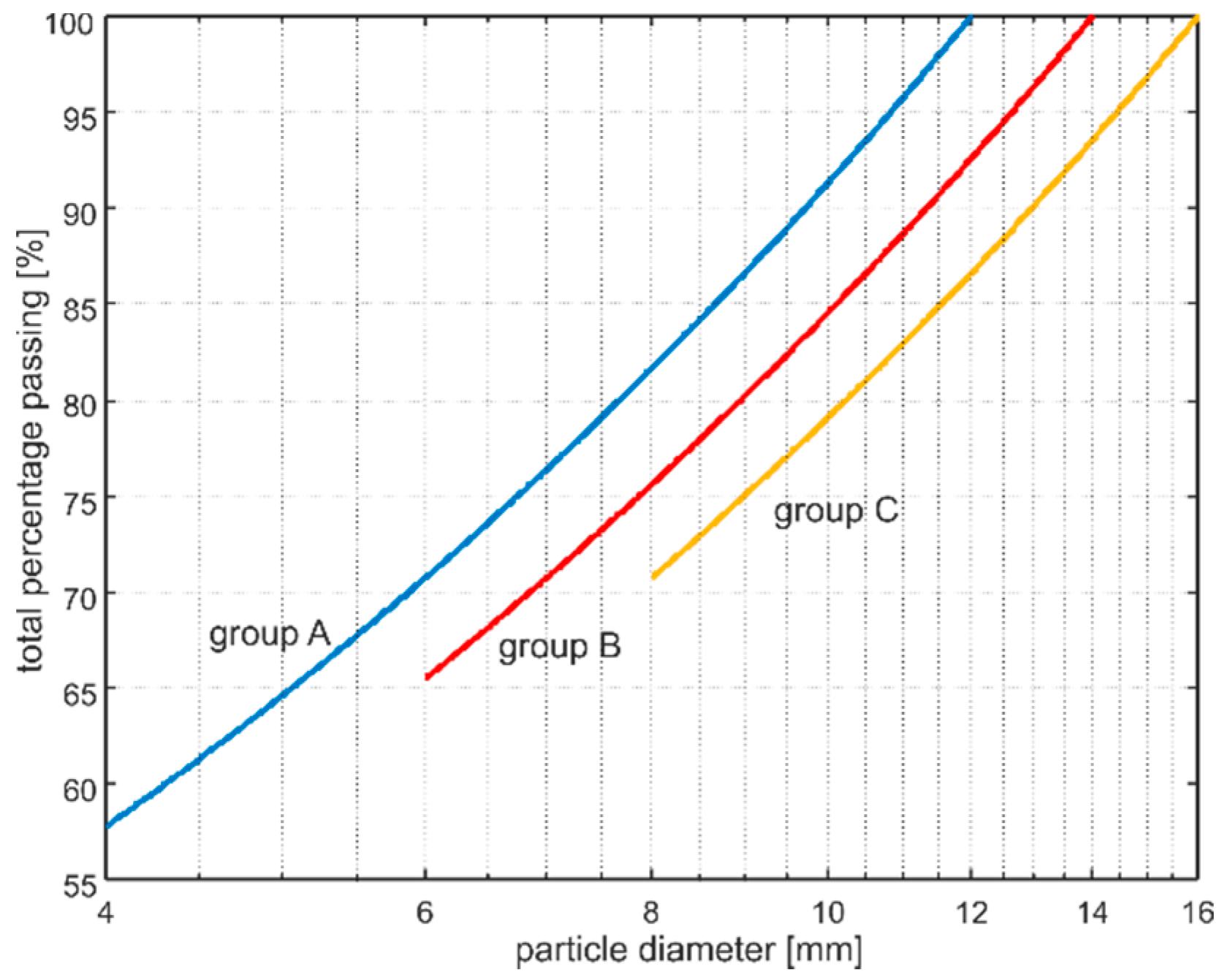
3.2. Aggregate Particles Size
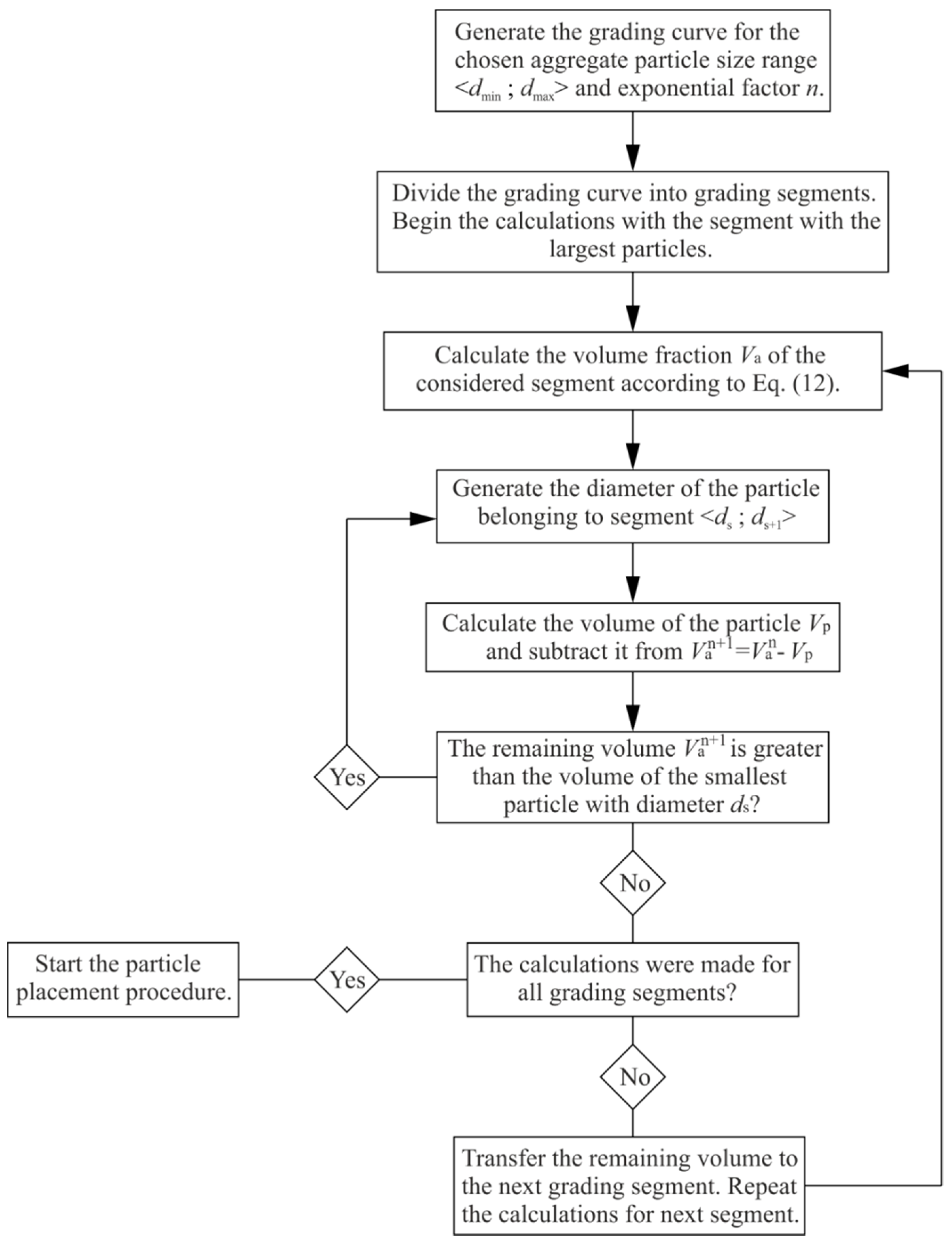
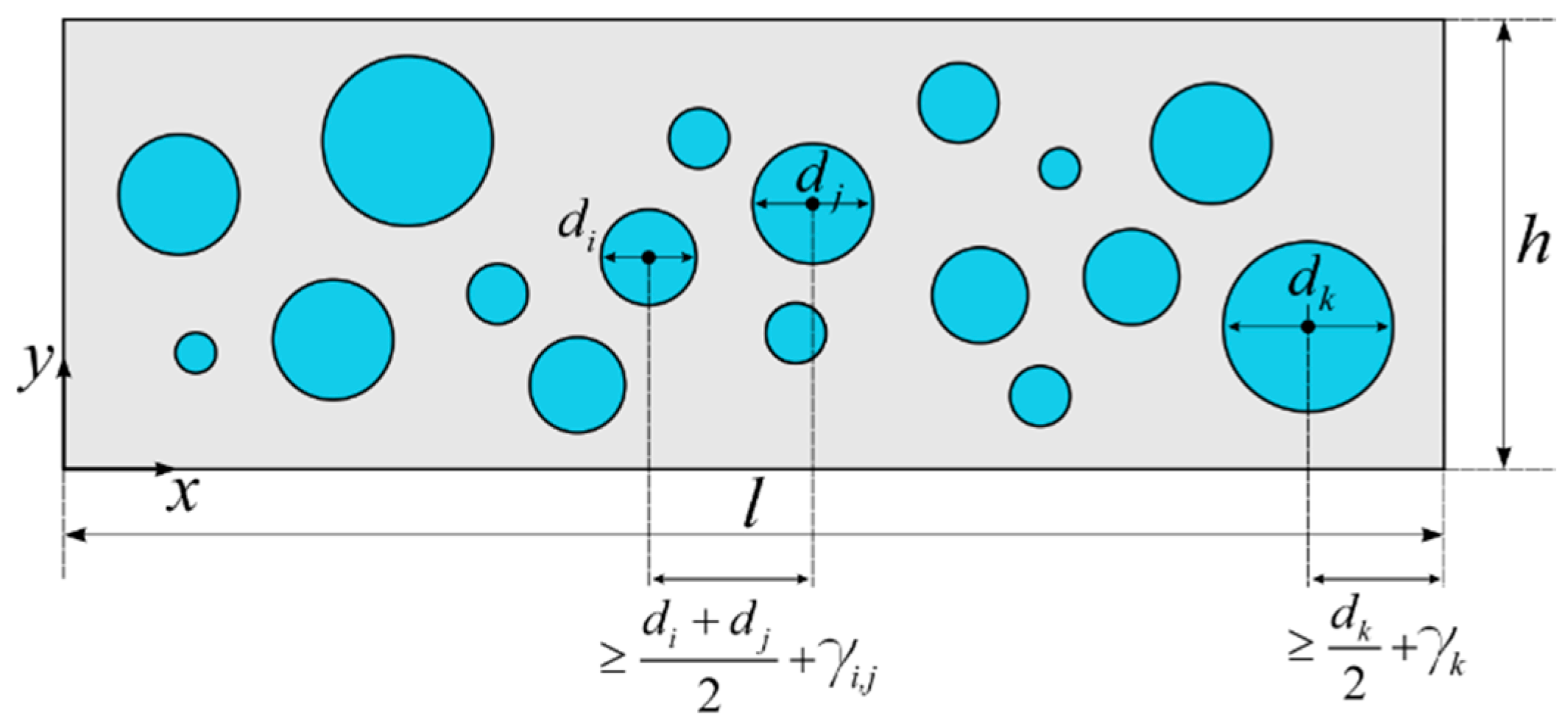
3.3. Particle Placement
- Step I: For the particle with diameter di, generate the coordinates of its mass center. It is recommended to begin from the largest particles, which significantly facilities the placement process.
- Step II: Check if the particle covered with the mortar film does not overlap with any other previously generated particle. If it does, generate new coordinates and check again. If particles do not overlap, generate the coordinates for the next particle.
- Step III: Repeat Steps I and II for all particles.
3.4. Description of Numerical Models
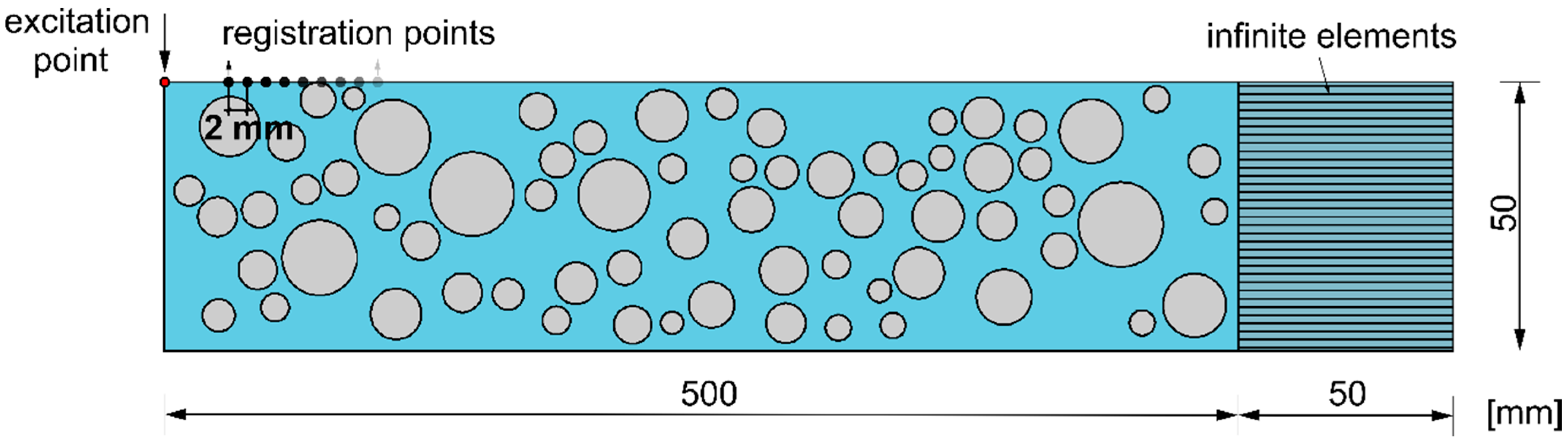
3.4.1. Model Geometry and Material Parameters
3.4.2. Excitation Function
4. Results
4.1. Visualization of Lamb Wave Propagation
4.2. Dispersion Curves
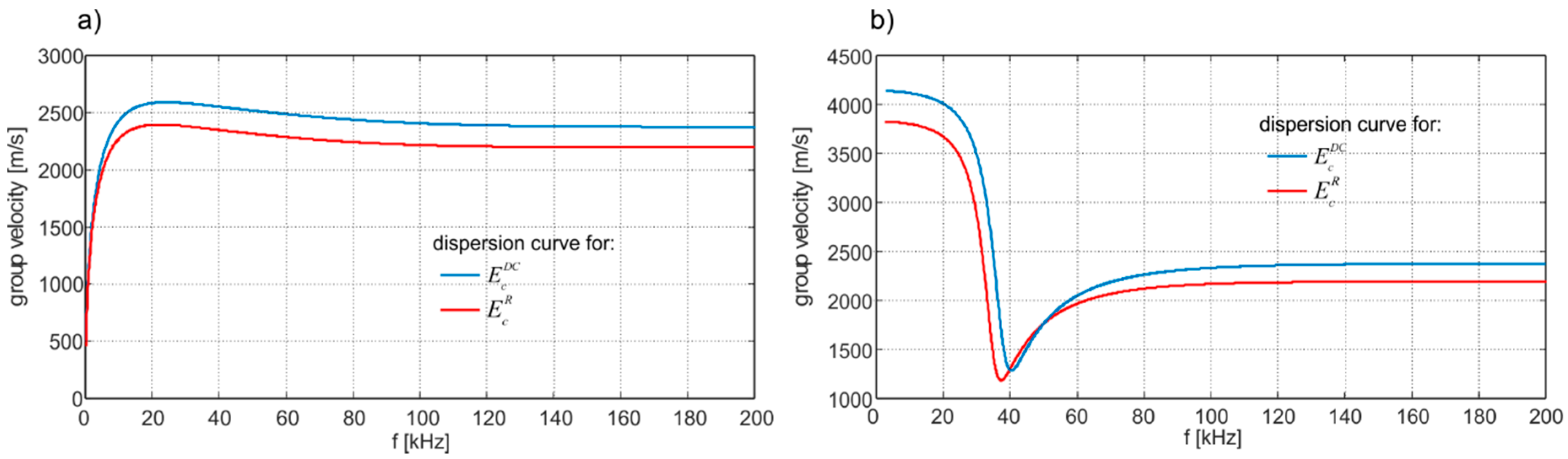
4.3. Determining the Elastic Modulus of Concrete Plates
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liu, P.-L.; Lee, K.-H.; Wu, T.T.; Kuo, M.-K. Scan of surface-opening cracks in reinforced concrete using transient elastic waves. NDT E Int. 2001, 34, 219–226. [Google Scholar] [CrossRef]
- Yang, Y.; Cascante, G.; Polak, M.-A. Depth detection of surface-breaking cracks in concrete plates using fundamental Lamb modes. NDT E Int. 2009, 42, 501–512. [Google Scholar] [CrossRef]
- Pahlavan, L.; Zhang, F.; Blacquiere, G.; Yang, Y.; Hordijk, D. Interaction of ultrasonic waves with partially-closed cracks in concrete structures. Constr. Build. Mater. 2018, 167, 899–906. [Google Scholar] [CrossRef]
- Choi, P.; Kim, D.-H.; Lee, B.-H.; Won, M.C. Application of ultrasonic shear-wave tomography to identify horizontal crack or delamination in concrete pavement and bridge. Constr. Build. Mater. 2016, 12, 81–91. [Google Scholar] [CrossRef]
- Ham, S.; Song, H.; Oelze, M.; Popovics, J.S. A contactless ultrasonic surface wave approach to characterize distributed cracking damage in concrete. Ultrasonics 2017, 75, 46–57. [Google Scholar] [CrossRef]
- Aggelis, D.G.; Shiotani, T. Repair evaluation of concrete cracks using surface and through-transmission wave measurement. Cem. Concr. Compos. 2007, 29, 700–711. [Google Scholar] [CrossRef]
- Quiviger, A.; Girard, A.; Payan, C.; Chaix, J.F.; Garnier, V.; Salin, J. Influence of the depth and morphology of real cracks on diffuse ultrasound in concrete: A simulation study. NDT E Int. 2013, 60, 11–16. [Google Scholar] [CrossRef]
- Del Rio, L.M.; Jimenez, A.; Lopez, F.; Rosa, F.J.; Rufo, M.M.; Paniagua, J.M. Characterization and hardening of concrete with ultrasonic testing. Ultrasonics 2004, 42, 527–530. [Google Scholar] [CrossRef]
- Dumoulin, C.; Karaiskos, G.; Carette, J.; Staquet, S.; Deraemaeker, A. Monitoring of the ultrasonic P-wave velocity in early-age concrete with embedded piezoelectric transducers. Smart Mater. Struct. 2012, 21, 1–4. [Google Scholar] [CrossRef]
- Lee, C.; Park, S.; Bolander, J.; Pyo, S. Monitoring the hardening process of ultra high performance concrete using decomposed modes of guided waves. Constr. Build. Mater. 2018, 163, 267–276. [Google Scholar] [CrossRef]
- Liu, S.; Zhu, J.; Seeaj, S.; Cano, R.; Juenger, M. Monitoring setting and hardening process of mortar and concrete using ultrasonic shear waves. Constr. Build. Mater. 2014, 72, 248–255. [Google Scholar] [CrossRef]
- Yang, W.; Yang, X.; Li, S. Monitoring of Interfacial Debonding of Concrete Filled Pultrusion-GFRP Tubular Column Based on Piezoelectric Smart Aggregate and Wavelet Analysis. Sensors 2020, 20, 2149. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.; Jiang, J.; Deng, X.; Deng, Z. Detecting Debonding between Steel Beam and Reinforcing CFRP Plate Using Active Sensing with Removable PZT-Based Transducers. Sensors 2020, 20, 41. [Google Scholar] [CrossRef] [PubMed]
- Zhao, G.; Zhang, D.; Zhang, L.; Wang, B. Detection of defects in reinforced concrete structures using ultrasonic nondestructive evaluation with piezoceramic transducers and time reversal method. Sensors 2018, 18, 4176. [Google Scholar] [CrossRef]
- Giri, P.; Mishra, S.; Clark, S.M.; Samali, B. Detection of gaps in concrete-metal composite structures based on the feature extraction method using piezoelectric transducers. Sensors 2019, 19, 1769. [Google Scholar] [CrossRef]
- Zima, B.; Kędra, R. Debonding size estimation in reinforced concrete beams using guided wave-based method. Sensors 2020, 20, 389. [Google Scholar] [CrossRef]
- Xu, B.; Chen, H.; Mo, Y.-L.; Zhou, T. Dominance of debonding defect of CFST on PZT sensor response considering the meso-scale structure of concrete with multi-scale simulation. Mech. Syst. Sig. Proc. 2018, 107, 515–528. [Google Scholar] [CrossRef]
- Abo-Qudais, S.A. Effect of concrete mixing parameters on propagation of ultrasonic waves. Constr. Build. Mater. 2005, 19, 257–263. [Google Scholar] [CrossRef]
- Ramaniraka, M.; Rokotonarivo, S.; Payan, C.; Garnier, V. Effect of the Interfacial Transition Zone on ultrasonic wave attenuation and velocity in concrete. Cem. Concr. Res. 2019, 124, 105809. [Google Scholar] [CrossRef]
- Lamb, H. On waves in elastic plate. Proc. R. Soc. Lond. Ser. A 1917, 93, 114–128. [Google Scholar]
- Alleyne, D.; Cawley, P. A two-dimensional Fourier transform method for the measurement of propagating multimode signals. J. Acoust. Soc. Am. 1991, 89, 1159–1168. [Google Scholar] [CrossRef]
- Wriggers, P.; Moftah, S.O. Mesoscale models for concrete: Homogenisation and damage behavior. Finite Elem. Anal. Des. 2006, 42, 623–636. [Google Scholar] [CrossRef]
- Concrete, Reinforced and Prestressed Concrete Structures; German Institute for Standardisation: Berlin, Germany, 2008.
- Schlangen, E.; van Mier, J.G.M. Simple lattice model for numerical simulation of fracture of concrete materials and structures. Mater. Struct. 1992, 25, 534–542. [Google Scholar] [CrossRef]
- Du, X.; Jin, L.; Ma, G. Numerical modeling tensile failure behavior of concrete at mesoscale using the extended finite element method. Int. J. Dam. Mech. 2014, 23, 872–898. [Google Scholar] [CrossRef]
- Giurgiutiu, V. Structural Health Monitoring with Piezoelectric Wafer Active Sensors; Academic Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Zhou, F.P.; Lydon, F.D.; Barr, B.I.G. Effect of coarse aggregate on elastic modulus and compressive strength of high performance concrete. Cem. Concr. Res. 1995, 25, 177–186. [Google Scholar] [CrossRef]




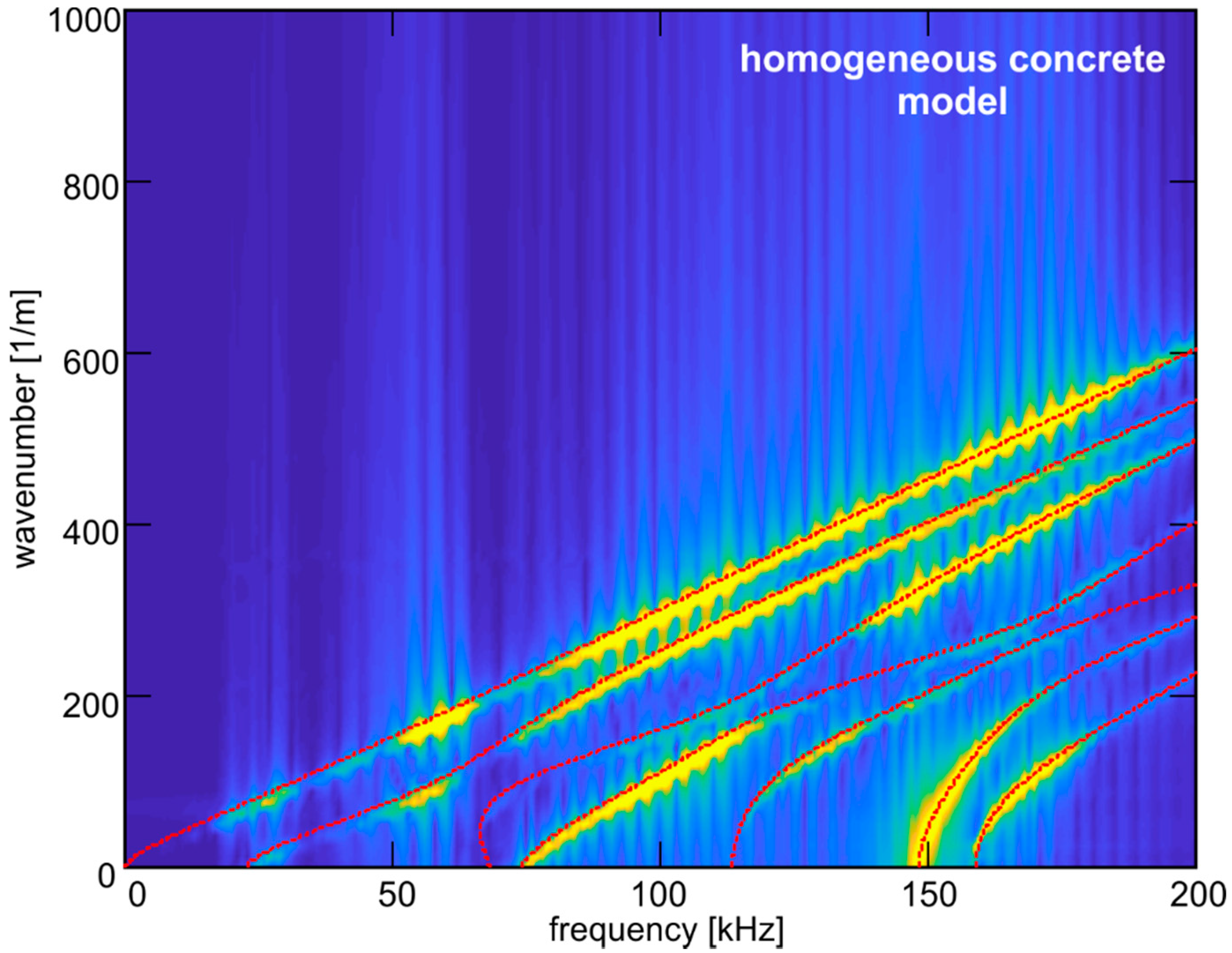

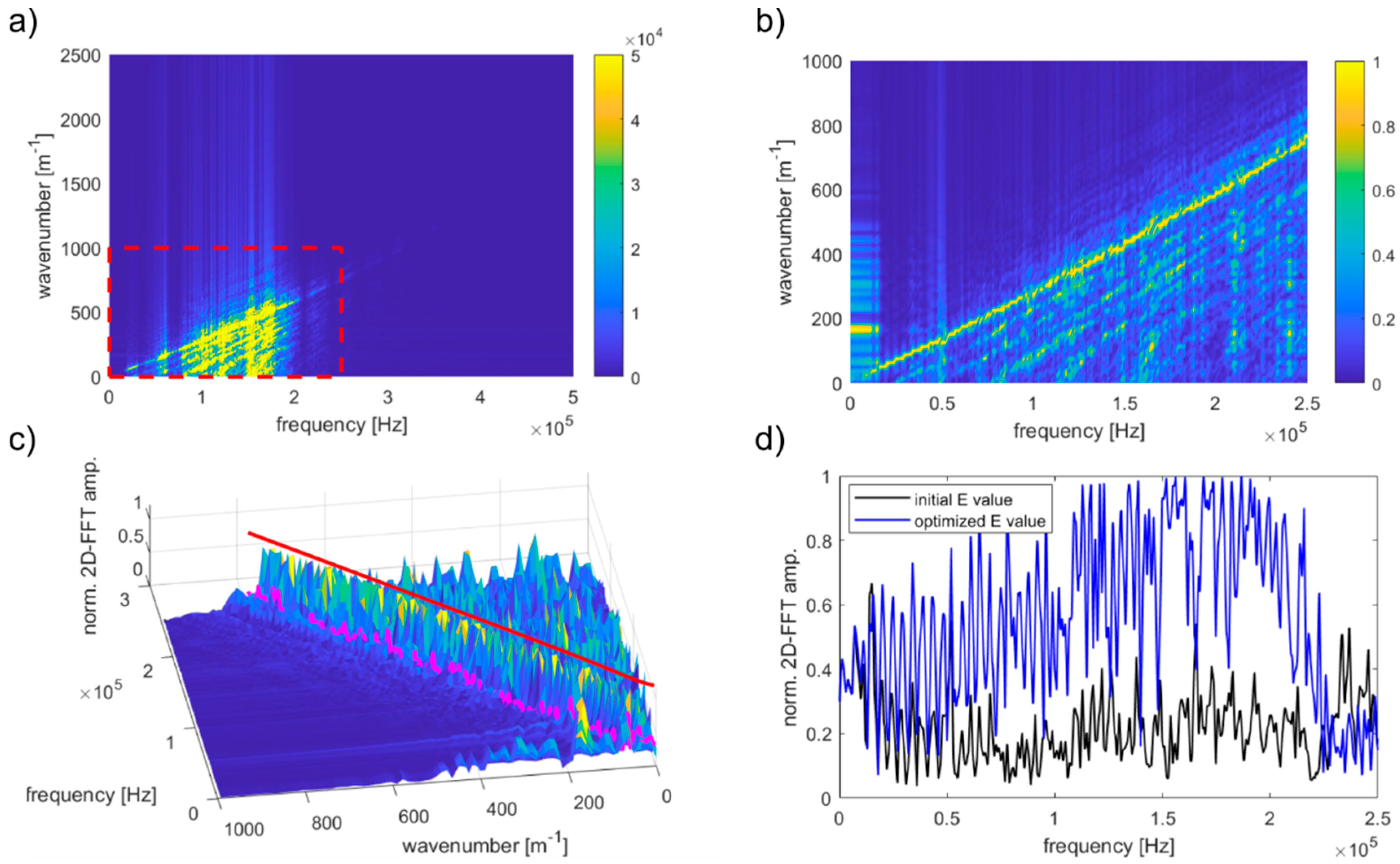
| Material Parameter | Mortar Matrix | Aggregate Particles |
|---|---|---|
| Elastic modulus (GPa) | 26 | 60 |
| Poisson’s ratio (-) | 0.2 | 0.22 |
| Density (kg/m3) | 2100 | 2700 |
| Model | Aggregate Ratio | Aggregate Particle Size (mm) |
|---|---|---|
| A1 | 20% | |
| A2 | 30% | 4–12 |
| A3 | 40% | |
| B1 | 20% | |
| B2 | 30% | 6–14 |
| B3 | 40% | |
| C1 | 20% | |
| C2 | 30% | 8–16 |
| C3 | 40% |
| Model | Aggregate Volume Fraction (-) | Density (kg/m3) | acc. Voigt Model (GPa) | acc. Reuss Model (GPa) | Based on Dispersion Curves (GPa) |
|---|---|---|---|---|---|
| homogeneous concrete model | 0 | 2100 | 26 | 26 | 25.92 |
| A1 | 0.163 | 2197.8 | 31.542 | 28.650 | 30.310 |
| A2 | 0.250 | 2250.0 | 34.500 | 30.290 | 29.459 |
| A3 | 0.342 | 2305.2 | 37.628 | 32.250 | 35.290 |
| B1 | 0.163 | 2197.8 | 31.542 | 28.650 | 28.734 |
| B2 | 0.250 | 2250.0 | 34.500 | 30.290 | 29.119 |
| B3 | 0.342 | 2305.2 | 37.628 | 32.250 | 35.689 |
| C1 | 0.163 | 2197.9 | 31.542 | 28.650 | 29.400 |
| C2 | 0.250 | 2250.0 | 34.500 | 30.290 | 29.104 |
| C3 | 0.342 | 2305.2 | 37.628 | 32.250 | 37.475 |
| Model | The Difference (GPa) | Percentage Error (%) | The Difference (GPa) | Percentage Error (%) |
|---|---|---|---|---|
| homogeneous concrete model | 0.08 | 0.309 | 0.08 | 0.309 |
| A1 | 1.232 | 4.065 | 1.66 | 5.477 |
| A2 | 5.041 | 17.111 | 0.831 | 2.820 |
| A3 | 2.338 | 6.625 | 3.040 | 8.614 |
| B1 | 2.808 | 9.772 | 0.084 | 0.292 |
| B2 | 5.381 | 18.479 | 1.171 | 4.021 |
| B3 | 1.939 | 5.433 | 3.439 | 9.636 |
| C1 | 1.842 | 6.265 | 0.750 | 2.551 |
| C2 | 5.396 | 18.540 | 1.186 | 4.075 |
| C3 | 0.153 | 0.408 | 5.225 | 13.943 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zima, B.; Kędra, R. Numerical Study of Concrete Mesostructure Effect on Lamb Wave Propagation. Materials 2020, 13, 2570. https://doi.org/10.3390/ma13112570
Zima B, Kędra R. Numerical Study of Concrete Mesostructure Effect on Lamb Wave Propagation. Materials. 2020; 13(11):2570. https://doi.org/10.3390/ma13112570
Chicago/Turabian StyleZima, Beata, and Rafał Kędra. 2020. "Numerical Study of Concrete Mesostructure Effect on Lamb Wave Propagation" Materials 13, no. 11: 2570. https://doi.org/10.3390/ma13112570
APA StyleZima, B., & Kędra, R. (2020). Numerical Study of Concrete Mesostructure Effect on Lamb Wave Propagation. Materials, 13(11), 2570. https://doi.org/10.3390/ma13112570





